Теорема Байеса

Вероятность, основанная на предварительных знаниях

В теории вероятностей и статистике теорема Байеса (альтернативно закон Байеса или правило Байеса ) , названная в честь Томаса Байеса , описывает вероятность события , основанную на предварительном знании условий, которые могут быть связаны с событием. ^[1] Например, если известно, что риск развития проблем со здоровьем увеличивается с возрастом, теорема Байеса позволяет более точно оценить риск для человека известного возраста, обусловливая его относительно его возраста, а не просто предполагая что индивидуум типичен для популяции в целом.

Одним из многих применений теоремы Байеса является байесовский вывод , особый подход к статистическому выводу . При применении вероятности, включенные в теорему, могут иметь разные вероятностные интерпретации . Используя байесовскую вероятностную интерпретацию, теорема выражает, как степень убеждения, выраженная как вероятность, должна рационально меняться, чтобы учесть наличие соответствующих доказательств. Байесовский вывод является фундаментальным для байесовской статистики , и один авторитетный специалист считает его «для теории вероятностей тем же, чем теорема Пифагора является для геометрии». ^[2]

История

Теорема Байеса названа в честь преподобного Томаса Байеса ( / b eɪ z / ), также статистика и философа. Байес использовал условную вероятность, чтобы создать алгоритм (его Предложение 9), который использует доказательства для расчета пределов неизвестного параметра. Его работа была опубликована в 1763 году как «Очерк решения проблемы учения о шансах» . Байес изучал, как вычислить распределение вероятностного параметра биномиального распределения (в современной терминологии). После смерти Байеса его семья передала его бумаги другу, министру, философу и математику Ричарду Прайсу .

За два года Ричард Прайс существенно отредактировал неопубликованную рукопись, прежде чем отправить ее другу, который прочитал ее вслух в Королевском обществе 23 декабря 1763 года. ^[3] Прайс редактировал ^[4] основную работу Байеса «Очерк решения проблемы в «Доктрина шансов» (1763), появившаяся в «Философских трудах » ^[5] и содержащая теорему Байеса. Прайс написал введение к статье, в котором представлены некоторые философские основы байесовской статистики , и выбрал одно из двух решений, предложенных Байесом. В 1765 году Прайс был избран членом Королевского общества в знак признания его работы над наследием Байеса. ^{[6] [7]} 27 апреля письмо, отправленное его другу Бенджамину Франклину, было зачитано в Королевском обществе, а затем опубликовано, где Прайс применяет эту работу к населению и вычислению «пожизненной ренты». ^[8]

Независимо от Байеса, Пьер-Симон Лаплас в 1774 году, а позже в своей «Аналитической теории вероятностей» 1812 года использовал условную вероятность, чтобы сформулировать связь обновленной апостериорной вероятности с априорной вероятностью при наличии доказательств. Он воспроизвел и расширил результаты Байеса в 1774 году, очевидно, не зная о работах Байеса. ^{[примечание 1] [9]} Байесовская интерпретация вероятности была разработана главным образом Лапласом. ^[10]

Примерно 200 лет спустя сэр Гарольд Джеффрис поставил алгоритм Байеса и формулировку Лапласа на аксиоматическую основу, написав в книге 1973 года, что теорема Байеса «является для теории вероятностей тем же, чем теорема Пифагора является для геометрии». ^[2]

Стивен Стиглер использовал байесовский аргумент, чтобы прийти к выводу, что теорема Байеса была открыта Николасом Сондерсоном , слепым английским математиком, незадолго до Байеса; ^{[11] [12]} эта интерпретация, однако, оспаривается. ^[13] Мартин Хупер ^[14] и Шэрон МакГрейн ^[15] утверждают, что вклад Ричарда Прайса был существенным:

По современным меркам нам следует обратиться к правилу Байеса-Прайса. Прайс обнаружил работу Байеса, осознал ее важность, исправил ее, внес свой вклад в статью и нашел ей применение. Современная традиция использовать только имя Байеса несправедлива, но настолько укоренилась, что все остальное не имеет смысла. ^[15]

Формулировка теоремы

Теорема Байеса математически формулируется в виде следующего уравнения: ^[16]

${\displaystyle P(A\vert B)={\frac {P(B\vert A)P(A)}{P(B)}}}$

где и – события и . ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle P(B)\neq 0}$

• ${\displaystyle P(A\vert B)}$— условная вероятность : вероятность того, что событие произойдет, если оно истинно. Ее еще называют апостериорной вероятностью данного . ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle B}$
• ${\displaystyle P(B\vert A)}$также является условной вероятностью: вероятностью события, если оно истинно. Его также можно интерпретировать как вероятность заданного фиксированного значения , поскольку . ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle P(B\vert A)=L(A\vert B)}$
• ${\displaystyle P(A)}$и – вероятности наблюдения и соответственно без каких-либо заданных условий; они известны как априорная вероятность и предельная вероятность . ${\displaystyle P(B)}$ ${\displaystyle A}$ ${\displaystyle B}$

Доказательство

Наглядное доказательство теоремы Байеса

Для мероприятий

Теорему Байеса можно вывести из определения условной вероятности :

${\displaystyle P(A\vert B)={\frac {P(A\cap B)}{P(B)}},{\text{ if }}P(B)\neq 0,}$

где вероятность того, что А и Б верны. Сходным образом, ${\displaystyle P(A\cap B)}$

${\displaystyle P(B\vert A)={\frac {P(A\cap B)}{P(A)}},{\text{ if }}P(A)\neq 0.}$

Решение и подстановка в приведенное выше выражение дает теорему Байеса: ${\displaystyle P(A\cap B)}$ ${\displaystyle P(A\vert B)}$

${\displaystyle P(A\vert B)={\frac {P(B\vert A)P(A)}{P(B)}},{\text{ if }}P(B)\neq 0.}$

Для непрерывных случайных величин

Для двух непрерывных случайных величин X и Y теорема Байеса может быть получена аналогичным образом из определения условной плотности :

${\displaystyle f_{X\vert Y=y}(x)={\frac {f_{X,Y}(x,y)}{f_{Y}(y)}}}$

${\displaystyle f_{Y\vert X=x}(y)={\frac {f_{X,Y}(x,y)}{f_{X}(x)}}}$

Поэтому,

${\displaystyle f_{X\vert Y=y}(x)={\frac {f_{Y\vert X=x}(y)f_{X}(x)}{f_{Y}(y)}}.}$

Общий случай

Пусть – условное распределение данного и пусть – распределение . Тогда совместное распределение . Тогда условное распределение данного определяется формулой ${\displaystyle P_{Y}^{x}}$ ${\displaystyle Y}$ ${\displaystyle X=x}$ ${\displaystyle P_{X}}$ ${\displaystyle X}$ ${\displaystyle P_{X,Y}(dx,dy)=P_{Y}^{x}(dy)P_{X}(dx)}$ ${\displaystyle P_{X}^{y}}$ ${\displaystyle X}$ ${\displaystyle Y=y}$

$${\displaystyle P_{X}^{y}(A)=E(1_{A}(X)|Y=y)}$$

Существование и единственность необходимого условного ожидания является следствием теоремы Радона–Никодима . Это было сформулировано Колмогоровым в его знаменитой книге 1933 года. Колмогоров подчеркивает важность условной вероятности, написав в предисловии: «Я хочу обратить внимание на... и особенно на теорию условных вероятностей и условных ожиданий...». ^[17] Теорема Байеса определяет апостериорное распределение на основе предварительного распределения. Теорему Байеса можно обобщить, включив в нее неправильные априорные распределения, такие как равномерное распределение на действительной прямой. ^[18] Современные методы Монте-Карло для цепей Маркова повысили важность теоремы Байеса, включая случаи с неправильными априорными значениями. ^[19]

Примеры

Рекреационная математика

Правило Байеса и вычисление условных вероятностей обеспечивают метод решения ряда популярных головоломок, таких как проблема трёх узников , проблема Монти Холла , проблема двух детей и проблема двух конвертов .

Тестирование на наркотики

Рисунок 1. Использование рамки частоты для визуального отображения путем сравнения заштрихованных областей. ${\displaystyle P({\text{User}}\vert {\text{Positive}})}$

Предположим, что конкретный тест на то, употреблял ли кто-то каннабис, имеет чувствительность 90% , что означает, что истинно положительный уровень (TPR) = 0,90. Таким образом, это приводит к 90% истинно положительных результатов (правильная идентификация употребления наркотиков) для потребителей каннабиса.

Специфичность теста также составляет 80 % , что означает долю истинно отрицательных результатов (TNR) = 0,80. Таким образом, тест правильно определяет 80% случаев неиспользования для непользователей, но также генерирует 20% ложноположительных результатов или уровень ложноположительных результатов (FPR) = 0,20 для непользователей.

Если предположить, что распространенность составляет 0,05 , то есть 5% людей употребляют каннабис, какова вероятность того , что случайный человек с положительным результатом теста действительно является потребителем каннабиса?

Положительная прогностическая ценность (PPV) теста — это доля людей, которые действительно имеют положительный результат, среди всех тех, кто дал положительный результат теста, и ее можно рассчитать на основе выборки как:

PPV = истинно положительный результат/положительный результат теста

Если известны чувствительность, специфичность и распространенность, PPV можно рассчитать с помощью теоремы Байеса. Пусть это означает «вероятность того, что кто-то употребляет каннабис при условии, что его тест положительный», что подразумевается под PPV. Мы можем написать: ${\displaystyle P({\text{User}}\vert {\text{Positive}})}$

${\displaystyle {\begin{aligned}P({\text{User}}\vert {\text{Positive}})&={\frac {P({\text{Positive}}\vert {\text{User}})P({\text{User}})}{P({\text{Positive}})}}\\&={\frac {P({\text{Positive}}\vert {\text{User}})P({\text{User}})}{P({\text{Positive}}\vert {\text{User}})P({\text{User}})+P({\text{Positive}}\vert {\text{Non-user}})P({\text{Non-user}})}}\\[8pt]&={\frac {0.90\times 0.05}{0.90\times 0.05+0.20\times 0.95}}={\frac {0.045}{0.045+0.19}}\approx 19\%\end{aligned}}}$

Дело в том, что это прямое применение Закона полной вероятности . В этом случае говорится, что вероятность того, что кто-то даст положительный результат теста, равна вероятности того, что пользователь даст положительный результат, умноженной на вероятность того, что он является пользователем, плюс вероятность того, что непользователь получит положительный результат теста, умноженной на вероятность того, что он не является пользователем. . Это верно, поскольку классификации «пользователь» и «непользователь» образуют раздел множества , а именно множества людей, которые проходят тест на наркотики. В сочетании с определением условной вероятности это приводит к приведенному выше утверждению. ${\displaystyle P({\text{Positive}})=P({\text{Positive}}\vert {\text{User}})P({\text{User}})+P({\text{Positive}}\vert {\text{Non-user}})P({\text{Non-user}})}$

Другими словами, даже если у кого-то положительный результат теста, вероятность того, что он употребляет каннабис, составляет всего 19% — это потому, что в этой группе только 5% людей являются потребителями, а большинство положительных результатов — это ложные срабатывания, исходящие от остальных 95%. .

Если протестировано 1000 человек:

• 950 человек не являются пользователями, и 190 из них дают ложноположительный результат (0,20 × 950)
• 50 из них являются пользователями и 45 из них дают истинно положительный результат (0,90 × 50)

Таким образом, на 1000 человек приходится 235 положительных тестов, из которых только 45 являются настоящими потребителями наркотиков, или около 19%. На рисунке 1 представлена ​​иллюстрация с использованием рамки частоты и обратите внимание, насколько мала розовая область истинных положительных результатов по сравнению с синей областью ложных положительных результатов.

Чувствительность или специфичность

Важность специфичности можно увидеть, показав, что даже если чувствительность повышается до 100%, а специфичность остается на уровне 80%, вероятность того, что кто-то с положительным результатом теста действительно является потребителем каннабиса, возрастает только с 19% до 21%, но если чувствительность при 90% и повышении специфичности до 95% вероятность возрастает до 49%.

Уровень рака

Даже если у 100% пациентов с раком поджелудочной железы имеется определенный симптом, наличие такого же симптома у кого-то не означает, что у этого человека есть 100% вероятность заболеть раком поджелудочной железы. Если предположить, что уровень заболеваемости раком поджелудочной железы составляет 1/100 000, в то время как 10 из 99 999 здоровых людей во всем мире имеют одинаковые симптомы, вероятность заболевания раком поджелудочной железы с учетом этих симптомов составляет всего 9,1%, а остальные 90,9% могут быть «ложноположительными» (ложноположительные результаты). то есть ошибочно говорят, что у них рак; термин «положительный» сбивает с толку, когда, как в данном случае, тест дает плохие новости).

В зависимости от уровня заболеваемости в следующей таблице представлены соответствующие цифры на 100 000 человек.

Затем это можно использовать для расчета вероятности заболевания раком при наличии следующих симптомов:

${\displaystyle {\begin{aligned}P({\text{Cancer}}|{\text{Symptoms}})&={\frac {P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})}{P({\text{Symptoms}})}}\\&={\frac {P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})}{P({\text{Symptoms}}|{\text{Cancer}})P({\text{Cancer}})+P({\text{Symptoms}}|{\text{Non-Cancer}})P({\text{Non-Cancer}})}}\\[8pt]&={\frac {1\times 0.00001}{1\times 0.00001+(10/99999)\times 0.99999}}={\frac {1}{11}}\approx 9.1\%\end{aligned}}}$

Уровень бракованного товара

Фабрика производит продукцию с использованием трех машин — A, B и C, на долю которых приходится 20%, 30% и 50% ее продукции соответственно. Из изделий, произведенных машиной А, 5% являются бракованными; Аналогично, 3% изделий машины B и 1% машин C являются дефектными. Если случайно выбранный предмет окажется бракованным, какова вероятность того, что он был изготовлен машиной С?

И снова ответ можно получить без использования формулы, применив условия к гипотетическому числу случаев. Например, если завод производит 1000 изделий, 200 будет произведено машиной А, 300 — машиной Б и 500 — машиной С. Машина А будет производить 5% × 200 = 10 дефектных изделий, машина Б — 3% × 300 = 9. , а машина C 1% × 500 = 5, всего 24. Таким образом, вероятность того, что случайно выбранная дефектная деталь была произведена машиной C, равна 5/24 (~20,83%).

Эту проблему также можно решить с помощью теоремы Байеса: Пусть X _i обозначает событие, когда случайно выбранный предмет был изготовлен i- ^й машиной (для i  = A,B,C). Пусть Y обозначает событие, когда случайно выбранный товар оказывается бракованным. Далее нам предоставляется следующая информация:

${\displaystyle P(X_{A})=0.2,\quad P(X_{B})=0.3,\quad P(X_{C})=0.5.}$

Если деталь изготовлена ​​на первом станке, то вероятность того, что она бракованная, равна 0,05; то есть P ( Y  |  X _A ) = 0,05. В целом у нас есть

${\displaystyle P(Y|X_{A})=0.05,\quad P(Y|X_{B})=0.03,\quad P(Y|X_{C})=0.01.}$

Чтобы ответить на исходный вопрос, мы сначала находим P (Y). Это можно сделать следующим образом:

${\displaystyle P(Y)=\sum _{i}P(Y|X_{i})P(X_{i})=(0.05)(0.2)+(0.03)(0.3)+(0.01)(0.5)=0.024.}$

Следовательно, 2,4% от общего объема выпуска являются бракованными.

Нам дано, что событие Y произошло, и мы хотим вычислить условную вероятность события X _C . По теореме Байеса

${\displaystyle P(X_{C}|Y)={\frac {P(Y|X_{C})P(X_{C})}{P(Y)}}={\frac {0.01\cdot 0.50}{0.024}}={\frac {5}{24}}}$

Учитывая, что деталь бракованная, вероятность того, что она была изготовлена ​​на машине С, равна 5/24. Хотя машина С производит половину всей продукции, она производит гораздо меньшую долю бракованных изделий. Следовательно, знание того, что выбранный элемент был дефектным, позволяет нам заменить априорную вероятность P ( X _C ) = 1/2 меньшей апостериорной вероятностью P (X _C  |  Y ) = 5/24.

Интерпретации

Рисунок 2. Геометрическая визуализация теоремы Байеса.

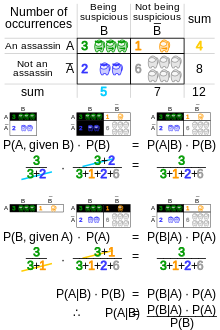
Интерпретация правила Байеса зависит от интерпретации вероятности, приписываемой этим терминам. Ниже описаны две преобладающие интерпретации. На рисунке 2 показана геометрическая визуализация.

Байесовская интерпретация

В байесовской (или эпистемологической) интерпретации вероятность измеряет «степень веры». Теорема Байеса связывает степень веры в утверждение до и после учета доказательств. Например, предположим, что с 50% уверенностью считается, что монета выпадет орел в два раза чаще, чем решка. Если монету подбросить несколько раз и наблюдать за результатами, эта степень веры, вероятно, повысится или упадет, но может даже остаться прежней, в зависимости от результатов. Для предложения A и доказательства B ,

• P  ( A ), априор , является начальной степенью веры в A.
• P  ( A  |  B ), апостериорный показатель , представляет собой степень уверенности после включения новостей в то, что B является правдой.
• частноеП ( Б  |  А )/П ( Б )представляет поддержку B , предоставляемую A.

Дополнительную информацию о применении теоремы Байеса в байесовской интерпретации вероятности см. в разделе « Байесовский вывод» .

Частотная интерпретация

Рисунок 3. Иллюстрация частотной интерпретации с помощью древовидных диаграмм.

В частотной интерпретации вероятность измеряет «долю результатов». Например, предположим, что эксперимент проводится много раз. P ( A ) — это доля результатов со свойством A (априорным), а P ( B ) — это доля со свойством B. P ( B  |  A ) — это доля результатов со свойством B среди результатов со свойством A , а P ( A  |  B ) — это доля результатов со свойством A среди результатов со свойством  A (апостериорный).

Роль теоремы Байеса лучше всего визуализировать с помощью древовидных диаграмм, таких как рисунок 3. Две диаграммы делят одни и те же результаты на A и B в противоположных порядках, чтобы получить обратные вероятности. Теорема Байеса связывает различные разделения.

Пример

Рисунок 4: Древовидная диаграмма, иллюстрирующая пример жука. R, C, P и — события редкие, распространенные, закономерности и отсутствия закономерности. Проценты в скобках рассчитаны. Даны три независимых значения, поэтому можно вычислить обратное дерево. ${\displaystyle {\overline {P}}}$

Энтомолог замечает существо, судя по рисунку на его спине, которое может быть редким подвидом жука . Полные 98% представителей редкого подвида имеют этот образец, поэтому P (Шаблон | Редкий) = 98%. Только 5% представителей общего подвида имеют этот рисунок. Редкий подвид составляет 0,1% от общей численности популяции. Насколько вероятно, что жук с рисунком будет редким: что такое P (Редкий | Образец)?

Из расширенной формы теоремы Байеса (поскольку любой жук либо редкий, либо обычный):

${\displaystyle {\begin{aligned}P({\text{Rare}}\vert {\text{Pattern}})&={\frac {P({\text{Pattern}}\vert {\text{Rare}})P({\text{Rare}})}{P({\text{Pattern}})}}\\[8pt]&={\frac {P({\text{Pattern}}\vert {\text{Rare}})P({\text{Rare}})}{P({\text{Pattern}}\vert {\text{Rare}})P({\text{Rare}})+P({\text{Pattern}}\vert {\text{Common}})P({\text{Common}})}}\\[8pt]&={\frac {0.98\times 0.001}{0.98\times 0.001+0.05\times 0.999}}\\[8pt]&\approx 1.9\%\end{aligned}}}$

Формы

События

Простая форма

Для событий A и B при условии, что P ( B ) ≠ 0,

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B)}}.}$

Во многих приложениях, например в байесовском выводе , событие B фиксируется в обсуждении, и мы хотим рассмотреть влияние его наблюдения на нашу веру в различные возможные события A. В такой ситуации знаменатель последнего выражения, вероятность данного свидетельства B , фиксирована; мы хотим изменить A . Теорема Байеса затем показывает, что апостериорные вероятности пропорциональны числителю , поэтому последнее уравнение принимает вид:

${\displaystyle P(A|B)\propto P(A)\cdot P(B|A).}$

Другими словами, апостериорная вероятность пропорциональна предыдущему времени. ^[20]

Если события A ₁ , A ₂ , ... являются взаимоисключающими и исчерпывающими, т. е. одно из них обязательно произойдет, но никакие два не могут произойти вместе, мы можем определить константу пропорциональности, используя тот факт, что их вероятности должны складываться. к одному. Например, для данного события A само событие A и его дополнение ¬A являются исключительными и исчерпывающими. Обозначая константу пропорциональности через c , имеем

${\displaystyle P(A|B)=c\cdot P(A)\cdot P(B|A){\text{ and }}P(\neg A|B)=c\cdot P(\neg A)\cdot P(B|\neg A).}$

Сложив эти две формулы, мы приходим к выводу, что

${\displaystyle 1=c\cdot (P(B|A)\cdot P(A)+P(B|\neg A)\cdot P(\neg A)),}$

или

${\displaystyle c={\frac {1}{P(B|A)\cdot P(A)+P(B|\neg A)\cdot P(\neg A)}}={\frac {1}{P(B)}}.}$

Альтернативная форма

Другая форма теоремы Байеса для двух конкурирующих утверждений или гипотез:

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B|A)P(A)+P(B|\neg A)P(\neg A)}}.}$

Для эпистемологической интерпретации:

Для предложения A и доказательств или предпосылок B [ ^21]

• ${\displaystyle P(A)}$— априорная вероятность , начальная степень веры в A.
• ${\displaystyle P(\neg A)}$— соответствующая начальная степень веры в не-А , в то, что А ложно, где ${\displaystyle P(\neg A)=1-P(A)}$
• ${\displaystyle P(B|A)}$— это условная вероятность или правдоподобие, степень веры в B при условии, что утверждение A истинно.
• ${\displaystyle P(B|\neg A)}$— это условная вероятность или правдоподобие, степень веры в B при условии, что утверждение A ложно.
• ${\displaystyle P(A|B)}$— апостериорная вероятность , вероятность A после учета B.

Расширенная форма

Часто для некоторого раздела { A _j } выборочного пространства пространство событий задается в терминах P ( A _j ) и P ( B  |  A _j ). Тогда полезно вычислить P ( B ), используя закон полной вероятности :

${\displaystyle P(B)=\sum _{j}P(B\cap A_{j}),}$

Или (используя правило умножения условной вероятности) ^[22]

${\displaystyle P(B)={\sum _{j}P(B|A_{j})P(A_{j})},}$

${\displaystyle \Rightarrow P(A_{i}|B)={\frac {P(B|A_{i})P(A_{i})}{\sum \limits _{j}P(B|A_{j})P(A_{j})}}\cdot }$

В особом случае, когда A — двоичная переменная :

${\displaystyle P(A|B)={\frac {P(B|A)P(A)}{P(B|A)P(A)+P(B|\neg A)P(\neg A)}}\cdot }$

Случайные переменные

Рисунок 5: Теорема Байеса, примененная к пространству событий, генерируемому непрерывными случайными величинами X и Y с известными распределениями вероятностей. Для каждой точки области существует пример теоремы Байеса . На практике эти случаи можно параметризовать, записав указанные плотности вероятности как функции x и y .

Рассмотрим выборочное пространство Ω, порожденное двумя случайными величинами X и Y с известными распределениями вероятностей. В принципе, теорема Байеса применима к событиям A  = { X  =  x } и B  = { Y  =  y }.

${\displaystyle P(X{=}x|Y{=}y)={\frac {P(Y{=}y|X{=}x)P(X{=}x)}{P(Y{=}y)}}}$

Однако члены становятся равными 0 в точках, где любая переменная имеет конечную плотность вероятности . Чтобы оставаться полезной, теорему Байеса можно сформулировать в терминах соответствующих плотностей (см. Вывод).

Простая форма

Если X непрерывен, а Y дискретен,

${\displaystyle f_{X|Y{=}y}(x)={\frac {P(Y{=}y|X{=}x)f_{X}(x)}{P(Y{=}y)}}}$

где каждая представляет собой функцию плотности. ${\displaystyle f}$

Если X дискретно, а Y непрерывно,

${\displaystyle P(X{=}x|Y{=}y)={\frac {f_{Y|X{=}x}(y)P(X{=}x)}{f_{Y}(y)}}.}$

Если и X, и Y непрерывны,

${\displaystyle f_{X|Y{=}y}(x)={\frac {f_{Y|X{=}x}(y)f_{X}(x)}{f_{Y}(y)}}.}$

Расширенная форма

Рисунок 6. Способ концептуализации пространств событий, генерируемых непрерывными случайными величинами X и Y.

Непрерывное пространство событий часто концептуализируется с точки зрения числителя. Тогда полезно исключить знаменатель, используя закон полной вероятности . Для f _Y ( y ) это становится интегралом:

${\displaystyle f_{Y}(y)=\int _{-\infty }^{\infty }f_{Y|X=\xi }(y)f_{X}(\xi )\,d\xi .}$

Правило Байеса в форме шансов

Теорема Байеса в форме шансов :

${\displaystyle O(A_{1}:A_{2}\vert B)=O(A_{1}:A_{2})\cdot \Lambda (A_{1}:A_{2}\vert B)}$

где

${\displaystyle \Lambda (A_{1}:A_{2}\vert B)={\frac {P(B\vert A_{1})}{P(B\vert A_{2})}}}$

называется фактором Байеса или отношением правдоподобия . Шансы между двумя событиями — это просто отношение вероятностей двух событий. Таким образом

${\displaystyle O(A_{1}:A_{2})={\frac {P(A_{1})}{P(A_{2})}},}$

${\displaystyle O(A_{1}:A_{2}\vert B)={\frac {P(A_{1}\vert B)}{P(A_{2}\vert B)}},}$

Таким образом, правило гласит, что апостериорные шансы — это априорные шансы, умноженные на коэффициент Байеса , или, другими словами, апостериорные шансы пропорциональны предыдущему произведению вероятности.

В особом случае и пишут , и используют аналогичную аббревиатуру для фактора Байеса и для условных шансов. Шансы на – это, по определению, шансы за и против . Тогда правило Байеса можно записать в сокращенной форме ${\displaystyle A_{1}=A}$ ${\displaystyle A_{2}=\neg A}$ ${\displaystyle O(A)=O(A:\neg A)=P(A)/(1-P(A))}$ ${\displaystyle A}$ ${\displaystyle A}$

${\displaystyle O(A\vert B)=O(A)\cdot \Lambda (A\vert B),}$

или, другими словами, апостериорные шансы равны априорным шансам, умноженным на отношение правдоподобия для данной информации . Короче говоря, апостериорные шансы равны априорным шансам, умноженным на отношение правдоподобия . ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle B}$

Например, если медицинский тест имеет чувствительность 90% и специфичность 91%, то положительный фактор Байеса равен . Теперь, если распространенность этого заболевания составляет 9,09% и если мы примем это за априорную вероятность, то априорные шансы составят примерно 1:10. Таким образом, после получения положительного результата теста апостериорная вероятность наличия заболевания становится 1:1, что означает, что апостериорная вероятность наличия заболевания составляет 50%. Если второй тест проводится при серийном тестировании и он также оказывается положительным, то апостериорная вероятность фактического наличия заболевания становится 10:1, что означает апостериорную вероятность около 90,91%. Отрицательный фактор Байеса можно рассчитать как 91%/(100%-90%)=9,1, поэтому, если второй тест окажется отрицательным, то апостериорные шансы на самом деле иметь заболевание составляют 1:9,1, что означает апостериорная вероятность около 9,9%. ${\displaystyle \Lambda _{+}=P({\text{True Positive}})/P({\text{False Positive}})=90\%/(100\%-91\%)=10}$

Приведенный выше пример можно понять и с помощью более точных цифр: предположим, что пациент, проходящий тест, принадлежит к группе из 1000 человек, из которых 91 человек действительно болен (распространенность 9,1%). Если все эти 1000 человек пройдут медицинское обследование, то 82 из больных получат истинно положительный результат (чувствительность 90,1%), 9 из больных получат ложноотрицательный результат (ложноотрицательный результат 9,9%), 827 человек без заболевания получат истинно отрицательный результат (специфичность 91,0%), а 82 человека без заболевания получат ложноположительный результат (частота ложноположительных результатов 9,0%). До прохождения какого-либо теста вероятность наличия у пациента заболевания составляет 91:909. После получения положительного результата вероятность заболевания у пациента равна

${\displaystyle {\frac {91}{909}}\times {\frac {90.1\%}{9.0\%}}={\frac {91\times 90.1\%}{909\times 9.0\%}}=1:1}$

что согласуется с тем фактом, что в группе из 1000 человек имеется 82 истинных положительных результата и 82 ложных положительных результата.

Соответствие другим математическим основам

Логика высказываний

Используя дважды, можно использовать теорему Байеса, чтобы также выразить через отрицания и без них: ${\displaystyle P(\neg B\vert A)=1-P(B\vert A)}$ ${\displaystyle P(\neg B\vert \neg A)}$ ${\displaystyle P(A\vert B)}$

${\displaystyle P(\neg B\vert \neg A)=1-\left(1-P(A\vert B)\right){\frac {P(B)}{P(\neg A)}}}$,

когда . Из этого мы можем прочитать вывод ${\displaystyle P(\neg A)=1-P(A)\neq 0}$

${\displaystyle P(A\vert B)=1\implies P(\neg B\vert \neg A)=1}$.

Другими словами: если, конечно, подразумевается , мы делаем вывод, что, безусловно, подразумевает . Где , если два импликации являются достоверными, являются эквивалентными утверждениями. В формулах вероятности условная вероятность обобщает логическое следствие , где теперь помимо присвоения истинного или ложного утверждениям мы присваиваем значения вероятности. Утверждение о схвачено уверенностью в условном, утверждение о . Связывая направления импликации, теорема Байеса представляет собой обобщение закона противопоставления , который в классической логике высказываний может быть выражен как: ${\displaystyle B}$ ${\displaystyle A}$ ${\displaystyle \neg A}$ ${\displaystyle \neg B}$ ${\displaystyle P(B)\neq 0}$ ${\displaystyle P(A\vert B)}$ ${\displaystyle B\implies A}$ ${\displaystyle B\implies A}$ ${\displaystyle P(A\vert B)=1}$

${\displaystyle (B\implies A)\iff (\neg A\implies \neg B)}$.

В этом отношении между импликациями позиции соотв. перевернуться. ${\displaystyle A}$ ${\displaystyle B}$

Соответствующей формулой в терминах исчисления вероятностей является теорема Байеса, которая в своей расширенной форме, включающая только априорную вероятность / базовую ставку , выражается как: ^[23] ${\displaystyle a}$ ${\displaystyle A}$

${\displaystyle P(A\vert B)=P(B\vert A){\frac {a(A)}{P(B\vert A)\,a(A)+P(B\vert \neg A)\,a(\neg A)}}}$.

Субъективная логика

Теорема Байеса представляет собой частный случай вывода перевернутых условных мнений в субъективной логике , выраженных как:

${\displaystyle (\omega _{A{\tilde {|}}B}^{S},\omega _{A{\tilde {|}}\lnot B}^{S})=(\omega _{B\vert A}^{S},\omega _{B\vert \lnot A}^{S}){\widetilde {\phi }}a_{A},}$

где обозначает оператор инвертирования условных мнений. Аргумент обозначает пару биномиальных условных мнений, данных источником , а аргумент обозначает априорную вероятность (т. е. базовую ставку ) . Обозначается пара производных перевернутых условных суждений . Условное мнение обобщает вероятностное условное мнение , т.е. помимо присвоения вероятности источник может приписать условному высказыванию любое субъективное мнение . Биномиальное субъективное мнение — это вера в истинность утверждения со степенью эпистемической неопределенности, выраженная источником . Каждое субъективное мнение имеет соответствующую прогнозируемую вероятность . Применение теоремы Байеса к прогнозируемым вероятностям мнений является гомоморфизмом , что означает, что теорему Байеса можно выразить через прогнозируемые вероятности мнений: ${\displaystyle {\widetilde {\phi }}}$ ${\displaystyle (\omega _{B\vert A}^{S},\omega _{B\vert \lnot A}^{S})}$ ${\displaystyle S}$ ${\displaystyle a_{A}}$ ${\displaystyle A}$ ${\displaystyle (\omega _{A{\tilde {|}}B}^{S},\omega _{A{\tilde {|}}\lnot B}^{S})}$ ${\displaystyle \omega _{A\vert B}^{S}}$ ${\displaystyle P(A\vert B)}$ ${\displaystyle S}$ ${\displaystyle (A\vert B)}$ ${\displaystyle \omega _{A}^{S}}$ ${\displaystyle A}$ ${\displaystyle S}$ ${\displaystyle P(\omega _{A}^{S})}$

${\displaystyle P(\omega _{A{\tilde {|}}B}^{S})={\frac {P(\omega _{B\vert A}^{S})a(A)}{P(\omega _{B\vert A}^{S})a(A)+P(\omega _{B\vert \lnot A}^{S})a(\lnot A)}}.}$

Следовательно, субъективная теорема Байеса представляет собой обобщение теоремы Байеса. ^[24]

Обобщения

Теорема Байеса для трех событий

Версия теоремы Байеса для трех событий ^[25] возникает в результате добавления третьего события , которым обусловлены все вероятности: ${\displaystyle C}$ ${\displaystyle P(C)>0,}$

${\displaystyle P(A\vert B\cap C)={\frac {P(B\vert A\cap C)\,P(A\vert C)}{P(B\vert C)}}}$

Вывод

Использование правила цепочки

${\displaystyle P(A\cap B\cap C)=P(A\vert B\cap C)\,P(B\vert C)\,P(C)}$

И, с другой стороны

${\displaystyle P(A\cap B\cap C)=P(B\cap A\cap C)=P(B\vert A\cap C)\,P(A\vert C)\,P(C)}$

Желаемый результат получается путем идентификации обоих выражений и решения для . ${\displaystyle P(A\vert B\cap C)}$

Использование в генетике

В генетике правило Байеса можно использовать для оценки вероятности наличия у человека определенного генотипа. Многие люди пытаются приблизительно оценить свои шансы заболеть генетическим заболеванием или вероятность того, что они являются носителями интересующего рецессивного гена. Байесовский анализ может быть проведен на основе семейного анамнеза или генетического тестирования , чтобы предсказать, разовьется ли у человека заболевание или передаст ли его своим детям. Генетическое тестирование и прогнозирование — обычная практика среди пар, которые планируют завести детей, но обеспокоены тем, что они оба могут быть носителями заболевания, особенно в сообществах с низкой генетической вариативностью. ^[26]

Первым шагом в байесовском анализе генетики является выдвижение взаимоисключающих гипотез: для конкретного аллеля человек либо является носителем, либо не является носителем. Затем рассчитываются четыре вероятности: априорная вероятность (вероятность каждой гипотезы с учетом такой информации, как семейный анамнез или прогнозы, основанные на менделевском наследовании), условная вероятность (определенного результата), совместная вероятность (произведение первых двух) и апостериорная вероятность. Вероятность (взвешенное произведение, рассчитанное путем деления совместной вероятности для каждой гипотезы на сумму обеих совместных вероятностей). Этот тип анализа может быть проведен исключительно на основе семейного анамнеза заболевания или в сочетании с генетическим тестированием. ^{[ нужна цитата ]}

Использование родословной для расчета вероятностей

Пример таблицы байесовского анализа риска заболевания у женщины, основанной на знании того, что заболевание присутствует у ее братьев и сестер, но не у ее родителей или кого-либо из ее четырех детей. Основываясь исключительно на статусе братьев, сестер и родителей субъекта, она с одинаковой вероятностью может быть носителем и не носителем (эта вероятность обозначается априорной гипотезой). Однако вероятность того, что все четыре сына субъекта не пострадают, составляет 1/16 ( 1 ⁄ 2 · 1 ⁄ 2 · 1 ⁄ 2 · 1 ⁄ 2 ), если она является носителем, и около 1, если она не является носителем ( это условная вероятность). Совместная вероятность согласовывает эти два предсказания, умножая их вместе. Последняя строка (апостериорная вероятность) рассчитывается путем деления совместной вероятности для каждой гипотезы на сумму обеих совместных вероятностей. ^[27]

Использование результатов генетического теста

Родительское генетическое тестирование может обнаружить около 90% известных аллелей заболеваний у родителей, которые могут привести к носительству или пораженному статусу у их ребенка. Муковисцидоз — наследственное заболевание, вызываемое аутосомно-рецессивной мутацией гена CFTR, ^[28] , расположенного на плече q хромосомы 7. ^[29]

Байесовский анализ пациентки с семейным анамнезом муковисцидоза (МВ), у которой результат теста на МВ оказался отрицательным, демонстрирующий, как этот метод использовался для определения риска рождения ребенка с МВ:

Поскольку пациентка не затронута этим заболеванием, она либо гомозиготна по аллелю дикого типа, либо гетерозиготна. Для установления априорных вероятностей используется квадрат Пеннета, основанный на знании того, что ни один из родителей не был затронут болезнью, но оба могли быть носителями:

Учитывая, что пациент не пострадал, есть только три возможности. Среди этих трех есть два сценария, в которых пациент является носителем мутантного аллеля. Таким образом, априорные вероятности равны 2 ⁄ 3 и 1 ⁄ 3 .

Далее пациент проходит генетическое тестирование и дает отрицательный результат на муковисцидоз. Уровень обнаружения этого теста составляет 90%, поэтому условные вероятности отрицательного результата теста равны 1/10 и 1. Наконец, совместная и апостериорная вероятности рассчитываются, как и раньше.

После проведения того же анализа на партнере-мужчине пациента (с отрицательным результатом теста) вероятность того, что у их ребенка будет выявлено заболевание, равна произведению соответствующих апостериорных вероятностей родителей быть носителями, умноженных на шансы того, что два носителя произведут пораженное потомство ( 1 ⁄ 4 ).

Генетическое тестирование проводится параллельно с выявлением других факторов риска.

Байесовский анализ можно провести с использованием фенотипической информации, связанной с генетическим заболеванием, а в сочетании с генетическим тестированием этот анализ становится намного сложнее. Например, муковисцидоз можно идентифицировать у плода с помощью УЗИ, направленного на поиск эхогенного кишечника, то есть такого, который на сканировании выглядит ярче, чем обычно. Это не надежный тест, поскольку эхогенный кишечник может присутствовать и у совершенно здорового плода. В этом случае большое влияние оказывает родительское генетическое тестирование, поскольку фенотипический аспект может иметь чрезмерное влияние на расчет вероятности. В случае плода с эхогенной кишкой, мать которого прошла тестирование и известна как носительница МВ, апостериорная вероятность того, что плод действительно болен заболеванием, очень высока (0,64). Однако, как только у отца отрицательный результат теста на МВ, апостериорная вероятность значительно падает (до 0,16). ^[27]

Расчет факторов риска является мощным инструментом генетического консультирования и репродуктивного планирования, но его нельзя рассматривать как единственный важный фактор, который следует учитывать. Как указано выше, неполное тестирование может дать ложно высокую вероятность статуса носителя, а тестирование может быть финансово недоступным или неосуществимым в отсутствие родителя.

Смотрите также

• Математический портал

• Байесовская эпистемология
• Индуктивная вероятность
• Квантовый байесианство
• «Почему большинство опубликованных результатов исследований ложны» , эссеДжона Иоаннидиса по метанауке 2005 года.
• Регулярная условная вероятность
• Байесовское убеждение

Примечания

1. Лаплас уточнял теорему Байеса в течение десятилетий:
   • Лаплас объявил о своем независимом открытии теоремы Байеса в книгах: Лаплас (1774) «Mémoire sur la вероятностные причины par les événements», «Mémoires de l'Académie royale des Sciences de MI (Savants étrangers)», 4 : 621–656. Перепечатано в: Лаплас, «Oeuvres complètes» (Париж, Франция: Gauthier-Villars et fils, 1841), vol. 8, стр. 27–65. Доступно в Интернете по адресу: Gallica. Теорема Байеса приведена на стр. 29.
   • Лаплас представил уточнение теоремы Байеса в: Лапласе (читай: 1783 г. / опубликовано: 1785 г.) «Mémoire sur les Appliance des Formulas qui sont fonctions de très grands nombres», «Mémoires de l'Académie Royale des Sciences de Paris», 423. –467. Перепечатано в: Лаплас, «Oeuvres complètes» (Париж, Франция: Gauthier-Villars et fils, 1844), vol. 10, стр. 295–338. Доступно в Интернете по адресу: Gallica. Теорема Байеса изложена на странице 301.
   • См. также: Лаплас, «Essai philosophique sur les probilités» (Париж, Франция: Mme. Ve. Courcier [Madame veuve (т. е. вдова) Courcier], 1814), стр. 10. Английский перевод: Пьер Симон, маркиз де Лаплас с FW. Траскотт и Ф.Л. Эмори, пер., «Философское эссе о вероятностях» (Нью-Йорк, Нью-Йорк: John Wiley & Sons, 1902), стр. 15.

Рекомендации

1. Джойс, Джеймс (2003), «Теорема Байеса», в Залте, Эдвард Н. (редактор), Стэнфордская энциклопедия философии (изд. Весны 2019 г.), Лаборатория метафизических исследований, Стэнфордский университет , получено 17 января 2020 г.
2. Джеффрис, Гарольд (1973). Научный вывод (3-е изд.). Издательство Кембриджского университета . п. 31. ISBN 978-0521180788.
3. Фрейм, Пол (2015). Апостол Свободы. Уэльс: Издательство Уэльского университета. п. 44. ИСБН 978-1783162161. Проверено 23 февраля 2021 г.
4. Аллен, Ричард (1999). Дэвид Хартли о человеческой природе. СУНИ Пресс. стр. 243–244. ISBN 978-0791494516. Проверено 16 июня 2013 г.
5. Байес, Томас и Прайс, Ричард (1763). «Очерк решения проблемы доктрины случая. Покойный преподобный г-н Байес, переданный г-ном Прайсом в письме Джону Кантону, AMFRS», « Философские труды Лондонского королевского общества ». 53 : 370–418. дои : 10.1098/rstl.1763.0053 .
6. Голландия, стр. 46–7.
7. Прайс, Ричард (1991). Цена: Политические сочинения. Издательство Кембриджского университета. п. XXIII. ISBN 978-0521409698. Проверено 16 июня 2013 г.
8. Митчелл 1911, с. 314.
9. Дастон, Лоррейн (1988). Классическая вероятность в эпоху Просвещения. Принстонский университет Пресс. п. 268. ИСБН 0691084971.
10. Стиглер, Стивен М. (1986). «Обратная вероятность». История статистики: измерение неопределенности до 1900 года . Издательство Гарвардского университета. стр. 99–138. ISBN 978-0674403413.
11. Стиглер, Стивен М. (1983). «Кто открыл теорему Байеса?». Американский статистик . 37 (4): 290–296. дои : 10.1080/00031305.1983.10483122.
12. де Во, Ричард; Веллеман, Пол; Бок, Дэвид (2016). Статистика, данные и модели (4-е изд.). Пирсон. стр. 380–381. ISBN 978-0321986498.
13. Эдвардс, AWF (1986). «Является ли ссылка в Хартли (1749 г.) на байесовский вывод?». Американский статистик . 40 (2): 109–110. дои : 10.1080/00031305.1986.10475370.
14. Хупер, Мартин (2013). «Ричард Прайс, теорема Байеса и Бог». Значение . 10 (1): 36–39. дои : 10.1111/j.1740-9713.2013.00638.x . S2CID  153704746.
15. МакГрейн, SB (2011). Теория, которая не умрет: как правило Байеса взломало код-загадку, выследило российские подводные лодки и одержало победу в двухвековых спорах . Издательство Йельского университета . ISBN 978-0300188226.
16. Стюарт, А.; Орд, К. (1994), Расширенная теория статистики Кендалла: Том I - Теория распределения , Эдвард Арнольд , §8.7
17. Колмогоров, А.Н. (1933) [1956]. Основы теории вероятностей . Издательская компания Челси.
18. Таральдсен, Гуннар; Туфто, Ярле; Линдквист, Бо Х. (24 июля 2021 г.). «Неправильные априорные и неправильные апостериорные». Скандинавский статистический журнал . 49 (3): 969–991. дои : 10.1111/sjos.12550 . hdl : 11250/2984409 . ISSN  0303-6898. S2CID  237736986.
19. Роберт, Кристиан П.; Казелла, Джордж (2004). Статистические методы Монте-Карло. Спрингер. ISBN 978-1475741452. ОСЛК  1159112760.
20. Ли, Питер М. (2012). "Глава 1". Байесовская статистика . Уайли . ISBN 978-1-1183-3257-3.
21. «Теорема Байеса: Введение». Тринити-университет . Архивировано из оригинала 21 августа 2004 года . Проверено 5 августа 2014 г.
22. «Теорема Байеса - формула, утверждение, доказательство | Правило Байеса» . Куемат . Проверено 20 октября 2023 г.
23. Аудун Йосанг, 2016, Субъективная логика; Формализм рассуждений в условиях неопределенности. Спрингер, Чам, ISBN 978-3-319-42337-1 
24. Аудун Йосанг, 2016, Обобщение теоремы Байеса в субъективной логике. Международная конференция IEEE по мультисенсорному слиянию и интеграции интеллектуальных систем (MFI 2016), Баден-Баден, сентябрь 2016 г.
25. Коллер, Д .; Фридман, Н. (2009). Вероятностные графические модели. Массачусетс: MIT Press. п. 1208. ИСБН 978-0-262-01319-2. Архивировано из оригинала 27 апреля 2014 г.
26. Крафт, Стефани А; Дуэнас, Деван; Уилфонд, Бенджамин С; Годдард, Катрина AB (24 сентября 2018 г.). «Развивающаяся среда расширенного скрининга носителей: проблемы и возможности». Генетика в медицине . 21 (4): 790–797. дои : 10.1038/s41436-018-0273-4. ПМК 6752283 . ПМИД  30245516. 
27. Огино, Сюдзи; Уилсон, Роберт Б; Голд, Берт; Хоули, Памела; Гроди, Уэйн В. (октябрь 2004 г.). «Байесовский анализ рисков муковисцидоза при пренатальном скрининге и скрининге носителей». Генетика в медицине . 6 (5): 439–449. дои : 10.1097/01.GIM.0000139511.83336.8F . ПМИД  15371910.
28. «Типы мутаций CFTR». Фонд муковисцидоза, www.cff.org/What-is-CF/Genetics/Types-of-CFTR-Mutations/.
29. «Ген CFTR - Домашний справочник генетики» . Национальная медицинская библиотека США, Национальные институты здравоохранения, ghr.nlm.nih.gov/gene/CFTR#location.

Библиография

•  В эту статью включен текст из публикации, которая сейчас находится в свободном доступе :  Митчелл, Джон Малкольм (1911). «Прайс, Ричард». В Чисхолме, Хью (ред.). Британская энциклопедия . Том. 22 (11-е изд.). Издательство Кембриджского университета. стр. 314–315.

дальнейшее чтение

• Грунау, Ханс-Кристоф (24 января 2014 г.). «Предисловие выпуска 04.03.2013». Jahresbericht der Deutschen Mathematiker-Vereinigung . 115 (3–4): 127–128. дои : 10.1365/s13291-013-0077-z .
• Гельман А., Карлин Дж. Б., Стерн Х. С. и Рубин Д. Б. (2003), «Анализ байесовских данных», второе издание, CRC Press.
• Гринстед, К.М. и Снелл, Дж.Л. (1997), «Введение в вероятность (2-е издание)», Американское математическое общество (доступен бесплатный PDF-файл) [1].
• «Формула Байеса», Математическая энциклопедия , EMS Press , 2001 [1994]
• Макгрейн, С.Б. (2011). Теория, которая не умрет: как правило Байеса взломало код-загадку, выследило российские подводные лодки и одержало победу в двухвековых спорах . Издательство Йельского университета . ISBN 978-0-300-18822-6.
• Лаплас, Пьер Симон (1986). «Воспоминания о вероятности причин событий». Статистическая наука . 1 (3): 364–378. дои : 10.1214/ss/1177013621 . JSTOR  2245476.
• Ли, Питер М. (2012), Байесовская статистика: введение , 4-е издание. Уайли. ISBN 978-1-118-33257-3 . 
• Пуга Дж.Л., Кшивинский М., Альтман Н. (31 марта 2015 г.). «Теорема Байеса». Природные методы . 12 (4): 277–278. дои : 10.1038/nmeth.3335 . ПМИД  26005726.
• Розенталь, Джеффри С. (2005), «Удар молнии: любопытный мир вероятностей». ХарперКоллинз. (Гранта, 2008. ISBN 9781862079960 ). 
• Стиглер, Стивен М. (август 1986 г.). «Мемуары Лапласа об обратной вероятности 1774 года». Статистическая наука . 1 (3): 359–363. дои : 10.1214/ss/1177013620 .
• Стоун, СП (2013), загрузите главу 1 книги «Правило Байеса: учебное пособие по байесовскому анализу», Sebtel Press, Англия.
• Байесовское рассуждение для умных людей . Введение и учебное пособие по использованию теоремы Байеса в статистике и когнитивной науке.
• Моррис, Дэн (2016). Прочтите первые 6 глав бесплатно из книги «Примеры теорем Байеса: наглядное введение для начинающих» Blue Windmill ISBN 978-1549761744 . Краткое руководство о том, как понять проблемные сценарии и найти P(B), P(A) и P(B|A). 

Внешние ссылки

• Учебное пособие по вероятности и теореме Байеса, разработанное для студентов-психологов Оксфордского университета
• Интуитивное объяснение теоремы Байеса Элиезера С. Юдковского
• Байесовская клиническая диагностическая модель