Закон Дарси

Уравнение, описывающее поток жидкости через пористую среду

Закон Дарси — это уравнение, описывающее поток жидкости через пористую среду и через ячейку Хеле-Шоу . Закон был сформулирован Генри Дарси на основе результатов экспериментов ^[1] по потоку воды через слои песка , составляющих основу гидрогеологии , раздела наук о Земле . Он аналогичен закону Ома в электростатике, линейно связывая объемный расход жидкости с разницей гидравлического напора (которая часто просто пропорциональна разнице давлений) через гидравлическую проводимость . Фактически, закон Дарси является частным случаем уравнения Стокса для потока импульса , в свою очередь вытекающего из уравнения Навье-Стокса для импульса .

Фон

Закон Дарси был впервые определён экспериментально Дарси, но с тех пор был выведен из уравнений Навье–Стокса с помощью методов гомогенизации . ^{[2] [3]} Он аналогичен закону Фурье в области теплопроводности , закону Ома в области электрических сетей и закону Фика в теории диффузии .

Одним из применений закона Дарси является анализ потока воды через водоносный горизонт ; закон Дарси вместе с уравнением сохранения массы упрощается до уравнения потока грунтовых вод , одного из основных соотношений гидрогеологии .

Моррис Маскат впервые ^[4] уточнил уравнение Дарси для однофазного потока, включив вязкость в уравнение Дарси для одной (жидкой) фазы. Можно понять, что вязкие жидкости с большей трудностью проникают через пористую среду, чем менее вязкие жидкости. Это изменение сделало его пригодным для исследователей в нефтяной промышленности. Основываясь на экспериментальных результатах своих коллег Вайкоффа и Ботсета, Маскат и Мерес также обобщили закон Дарси, чтобы охватить многофазный поток воды, нефти и газа в пористой среде нефтяного пласта . Обобщенные уравнения многофазного потока Маската и других обеспечивают аналитическую основу для разработки пластов , которая существует и по сей день.

Описание

Диаграмма, показывающая определения и направления для закона Дарси. A — площадь поперечного сечения (м ² ) цилиндра. Q — расход (м ³ /с) жидкости, протекающей через площадь A. Поток жидкости через A равен q = Q/A. L — длина цилиндра. Δp = p _выход - p _вход = p _b - p _a . = Δp/L = гидравлический градиент , приложенный между точками a и b. ${\displaystyle \nabla p}$

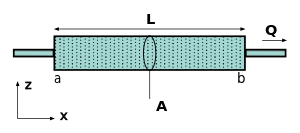
В интегральной форме закон Дарси, уточненный Моррисом Маскатом , при отсутствии гравитационных сил и в однородно проницаемой среде задается простым соотношением пропорциональности между объемным расходом и падением давления через пористую среду . Константа пропорциональности связана с проницаемостью среды, динамической вязкостью жидкости , заданным расстоянием , на котором вычисляется падение давления, и площадью поперечного сечения , в виде: ${\displaystyle Q}$ ${\displaystyle \Delta p}$ ${\displaystyle k}$ ${\displaystyle \mu }$ ${\displaystyle L}$ ${\displaystyle A}$ $${\displaystyle Q={\frac {kA}{\mu L}}\Delta p}$$

Обратите внимание, что соотношение:

$${\displaystyle R={\frac {\mu L}{kA}}}$$

можно определить как гидравлическое сопротивление закона Дарси .

Закон Дарси можно обобщить до локальной формы:

Уравнение состояния Дарси ( изотропная пористая среда )

${\displaystyle \mathbf {q} =-{\frac {k}{\mu }}\nabla p}$

где - гидравлический градиент , а - объемный поток , который здесь также называется поверхностной скоростью . Обратите внимание, что соотношение: ${\displaystyle \nabla p}$ ${\displaystyle \mathbf {q} }$

$${\displaystyle \sigma ={\frac {k}{\mu }}}$$

можно рассматривать как закон Дарси гидравлической проводимости .

В (менее общей) интегральной форме объемный поток и градиент давления соответствуют соотношениям:

${\displaystyle q={\frac {Q}{A}}}$

${\displaystyle \nabla p={\frac {\Delta p}{L}}}$.

В случае анизотропной пористой среды проницаемость является тензором второго порядка , и в тензорной записи можно записать более общий закон:

Уравнение состояния Дарси ( анизотропная пористая среда )

${\displaystyle q_{i}=-{\frac {k_{ij}}{\mu }}\partial _{j}p}$

Обратите внимание, что величина , часто называемая потоком Дарси или скоростью Дарси, не является скоростью, с которой жидкость движется через поры. Это удельный расход или поток на единицу площади. Скорость потока ( u ) связана с потоком ( q ) через пористость ( φ ) следующим уравнением: ${\displaystyle \mathbf {q} }$

${\displaystyle \mathbf {q} =\varphi \,\mathbf {u} .}$

Уравнение состояния Дарси для однофазного (жидкостного) потока является определяющим уравнением для абсолютной проницаемости (однофазной проницаемости).

Что касается диаграммы справа, скорость потока выражена в единицах СИ , а поскольку пористость φ является безразмерным числом , поток Дарси , или расход на единицу площади, также определяется в единицах ; проницаемость в единицах , динамическая вязкость в единицах и гидравлический градиент в единицах . ${\displaystyle \mathrm {(m/s)} }$ ${\displaystyle \mathbf {q} }$ ${\displaystyle \mathrm {(m/s)} }$ ${\displaystyle k}$ ${\displaystyle \mathrm {(m^{2})} }$ ${\displaystyle \mu }$ ${\displaystyle \mathrm {(Pa\cdot s)} }$ ${\displaystyle \mathrm {(Pa/m)} }$

В интегральной форме общее падение давления выражается в единицах , а длина образца — в единицах , объемный расход Дарси или расход также определяется в единицах , а площадь поперечного сечения — в единицах . Некоторые из этих параметров используются в альтернативных определениях ниже. В определении потока используется отрицательный знак в соответствии со стандартным физическим соглашением о том, что жидкости текут из областей высокого давления в области низкого давления. Обратите внимание, что необходимо учитывать напор , если вход и выход находятся на разных высотах. Если изменение давления отрицательное, то поток будет направлен в положительном направлении x . Было несколько предложений относительно уравнения состояния для абсолютной проницаемости, и наиболее известным из них, вероятно, является уравнение Козени (также называемое уравнением Козени–Кармана ). ${\displaystyle \Delta p=p_{b}-p_{a}}$ ${\displaystyle \mathrm {(Pa)} }$ ${\displaystyle L}$ ${\displaystyle \mathrm {(m)} }$ ${\displaystyle Q}$ ${\displaystyle \mathrm {(m^{3}/s)} }$ ${\displaystyle A}$ ${\displaystyle \mathrm {(m^{2})} }$

Рассматривая соотношение для статического давления жидкости ( закон Стевина ):

$${\displaystyle p=\rho gh}$$можно также отказаться от интегральной формы в уравнении: где ν — кинематическая вязкость . Соответствующая гидравлическая проводимость , таким образом, равна: $${\displaystyle Q={\frac {kAg}{\nu L}}\,{\Delta h}}$$

${\displaystyle K={\frac {k\rho g}{\mu }}={\frac {kg}{\nu }}.}$

Закон Дарси — это простое математическое утверждение, которое точно суммирует несколько известных свойств, которые проявляют подземные воды , текущие в водоносных горизонтах , в том числе:

• если градиент давления на расстоянии отсутствует, поток не возникает (это гидростатические условия),
• если есть градиент давления, поток будет происходить от высокого давления к низкому (в направлении, противоположном направлению увеличения градиента — отсюда и отрицательный знак в законе Дарси),
• чем больше градиент давления (через тот же пластовый материал), тем больше скорость разряда и
• скорость истечения жидкости часто будет разной — через разные материалы пласта (или даже через один и тот же материал, в разном направлении) — даже если в обоих случаях существует один и тот же градиент давления.

Графическая иллюстрация использования уравнения установившегося потока грунтовых вод (основанного на законе Дарси и законе сохранения массы) представлена ​​при построении сетей водотоков для количественной оценки объема грунтовых вод, протекающих под плотиной .

Закон Дарси действителен только для медленного, вязкого потока; однако большинство случаев потока грунтовых вод попадают в эту категорию. Обычно любой поток с числом Рейнольдса меньше единицы является явно ламинарным, и было бы допустимо применять закон Дарси. Экспериментальные испытания показали, что режимы потока с числом Рейнольдса до 10 все еще могут быть режимами Дарси, как в случае потока грунтовых вод. Число Рейнольдса (безразмерный параметр) для потока пористой среды обычно выражается как

${\displaystyle \mathrm {Re} ={\frac {qd}{\nu }}\,,}$

где ν — кинематическая вязкость воды , q — удельный расход (не скорость движения пор — с единицами длины на время), d — репрезентативный диаметр зерна для пористой среды (стандартный выбор — math| d ₃₀ , что является 30%-ным размером прохождения из анализа размера зерна с использованием сит — с единицами длины).

Вывод

Для стационарного, ползучего, несжимаемого потока, т.е. ⁠D ( ρu _i )/Дт⁠ ≈ 0 , уравнение Навье–Стокса упрощается до уравнения Стокса , которое, если пренебречь объемным членом, имеет вид:

${\displaystyle \mu \nabla ^{2}u_{i}-\partial _{i}p=0\,,}$

где μ — вязкость, u _i — скорость в направлении i , а p — давление. Предполагая, что сила вязкого сопротивления линейна со скоростью, мы можем записать:

${\displaystyle -\left(k^{-1}\right)_{ij}\mu \varphi u_{j}-\partial _{i}p=0\,,}$

где φ — пористость , а k _ij — тензор проницаемости второго порядка. Это дает скорость в направлении n ,

${\displaystyle k_{ni}\left(k^{-1}\right)_{ij}u_{j}=\delta _{nj}u_{j}=u_{n}=-{\frac {k_{ni}}{\varphi \mu }}\partial _{i}p\,,}$

что дает закон Дарси для объемной плотности потока в направлении n ,

${\displaystyle q_{n}=-{\frac {k_{ni}}{\mu }}\,\partial _{i}p\,.}$

В изотропных пористых средах недиагональные элементы в тензоре проницаемости равны нулю, k _ij = 0 для i ≠ j , а диагональные элементы идентичны, k _ii = k , и получается общая форма, как показано ниже, которая позволяет определить скорость потока жидкости путем решения системы уравнений в заданной области. ^[5]

${\displaystyle {\boldsymbol {q}}=-{\frac {k}{\mu }}\,{\boldsymbol {\nabla }}p\,.}$

Приведенное выше уравнение является основным уравнением для однофазного потока жидкости в пористой среде.

Использование в нефтяной промышленности

Другой вывод закона Дарси широко используется в нефтяной инженерии для определения потока через проницаемые среды — наиболее простой из них предназначен для одномерного однородного пласта горной породы с одной жидкой фазой и постоянной вязкостью жидкости .

Почти все нефтяные пласты имеют водную зону под нефтяной опорой, а некоторые также имеют газовую шапку над нефтяной опорой. Когда давление в пласте падает из-за добычи нефти, вода поступает в нефтяную зону снизу, а газ поступает в нефтяную зону сверху (если газовая шапка существует), и мы получаем одновременный поток и несмешивающееся смешивание всех жидких фаз в нефтяной зоне. Оператор нефтяного месторождения может также закачивать воду (и/или газ) для улучшения добычи нефти. Поэтому нефтяная промышленность использует обобщенное уравнение Дарси для многофазного потока, которое было разработано Маскатом и другими. Поскольку имя Дарси так широко распространено и тесно связано с потоком в пористой среде, многофазное уравнение обозначается законом Дарси для многофазного потока или обобщенным уравнением Дарси (или законом) или просто уравнением Дарси (или законом) или просто уравнением потока, если контекст говорит, что в тексте обсуждается многофазное уравнение Маската и других. Многофазный поток в нефтяных и газовых пластах — это обширная тема, и одна из многочисленных статей на эту тему — закон Дарси для многофазного потока .

Использование при приготовлении кофе

В ряде статей использовался закон Дарси для моделирования физики заваривания в гейзерной кофеварке , в частности, того, как горячая вода просачивается через кофейную гущу под давлением, начиная со статьи Варламова и Балестрино 2001 года ^[6] и продолжая статьей Джанино 2007 года ^[7] , статьей Наварини и др. 2008 года ^[8] и статьей У. Кинга 2008 года ^[9] . В статьях либо будет принято, что проницаемость кофе постоянна, в качестве упрощения, либо будут измеряться изменения в процессе заваривания.

Дополнительные формы

Дифференциальное выражение

Закон Дарси можно выразить в самом общем виде следующим образом:

${\displaystyle \mathbf {q} =-K\nabla h}$

где q — вектор объемного потока жидкости в определенной точке среды, h — полный гидравлический напор , а K — тензор гидравлической проводимости в этой точке. Гидравлическую проводимость часто можно аппроксимировать как скаляр . (Обратите внимание на аналогию с законом Ома в электростатике. Вектор потока аналогичен плотности тока, напор аналогичен напряжению, а гидравлическая проводимость аналогична электропроводности.)

Квадратичный закон

Для потоков в пористых средах с числами Рейнольдса больше, чем примерно от 1 до 10, инерционные эффекты также могут стать значительными. Иногда к уравнению Дарси добавляется инерционный член, известный как член Форхгеймера . Этот член способен учитывать нелинейное поведение разницы давления в зависимости от данных потока. ^[10]

${\displaystyle \nabla p=-{\frac {\mu }{k}}q-{\frac {\rho }{k_{1}}}q^{2}\,,}$

где дополнительный член k ₁ известен как инерционная проницаемость, в единицах длины . ${\displaystyle \mathrm {(m)} }$

Поток в середине песчаного резервуара настолько медленный, что уравнение Форхгеймера обычно не требуется, но поток газа в скважину для добычи газа может быть достаточно высоким, чтобы оправдать его использование. В этом случае расчеты производительности притока для скважины, а не ячейки сетки трехмерной модели, основаны на уравнении Форхгеймера. Эффект этого заключается в том, что в формуле производительности притока появляется дополнительный зависящий от скорости скин.

Некоторые карбонатные резервуары имеют много трещин, и уравнение Дарси для многофазного потока обобщено для того, чтобы управлять как потоком в трещинах, так и потоком в матрице (т.е. традиционной пористой породе). Неровная поверхность стенок трещин и высокая скорость потока в трещинах могут оправдать использование уравнения Форхгеймера.

Поправка на газы в мелкодисперсных средах (диффузия Кнудсена или эффект Клинкенберга)

Для газового потока в малых характерных размерах (например, очень мелкий песок, нанопористые структуры и т. д.) взаимодействие частиц со стенкой становится более частым, что приводит к дополнительному трению стенки (трение Кнудсена). Для потока в этой области, где присутствуют как вязкое , так и трение Кнудсена , необходимо использовать новую формулировку. Кнудсен представил полуэмпирическую модель для потока в переходном режиме, основанную на его экспериментах с малыми капиллярами. ^{[11] [12]} Для пористой среды уравнение Кнудсена можно задать как ^[12]

${\displaystyle N=-\left({\frac {k}{\mu }}{\frac {p_{a}+p_{b}}{2}}+D_{\mathrm {K} }^{\mathrm {eff} }\right){\frac {1}{R_{\mathrm {g} }T}}{\frac {p_{\mathrm {b} }-p_{\mathrm {a} }}{L}}\,,}$

где N — молярный поток, R _g — газовая постоянная, T — температура, D^эфф
_К— эффективный коэффициент диффузии Кнудсена пористой среды. Модель также может быть получена из бинарной модели трения, основанной на первом принципе (BFM). ^{[13] [14]} Дифференциальное уравнение переходного потока в пористой среде, основанное на BFM, задается как ^[13]

${\displaystyle {\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}N\,.}$

Это уравнение справедливо как для капилляров , так и для пористых сред. Терминология эффекта Кнудсена и диффузии Кнудсена более распространена в машиностроении и химической инженерии . В геологической и нефтехимической инженерии этот эффект известен как эффект Клинкенберга . Используя определение молярного потока, приведенное выше уравнение можно переписать как

${\displaystyle {\frac {\partial p}{\partial x}}=-R_{\mathrm {g} }T\left({\frac {kp}{\mu }}+D_{\mathrm {K} }\right)^{-1}{\dfrac {p}{R_{\mathrm {g} }T}}q\,.}$

Это уравнение можно преобразовать в следующее уравнение

${\displaystyle q=-{\frac {k}{\mu }}\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right){\frac {\partial p}{\partial x}}\,.}$

Сравнивая это уравнение с обычным законом Дарси, можно дать новую формулировку:

${\displaystyle q=-{\frac {k^{\mathrm {eff} }}{\mu }}{\frac {\partial p}{\partial x}}\,,}$

где

${\displaystyle k^{\mathrm {eff} }=k\left(1+{\frac {D_{\mathrm {K} }\mu }{k}}{\frac {1}{p}}\right)\,.}$

Это эквивалентно эффективной формуле проницаемости, предложенной Клинкенбергом: ^[15]

${\displaystyle k^{\mathrm {eff} }=k\left(1+{\frac {b}{p}}\right)\,.}$

где b известен как параметр Клинкенберга, который зависит от газа и структуры пористой среды. Это совершенно очевидно, если сравнить приведенные выше формулы. Параметр Клинкенберга b зависит от проницаемости, диффузии Кнудсена и вязкости (т.е. как от свойств газа, так и от свойств пористой среды).

Закон Дарси для коротких временных масштабов

Для очень коротких временных масштабов к закону Дарси можно добавить производную по времени от потока, что приводит к действительным решениям на очень малых временах (в теплопередаче это называется модифицированной формой закона Фурье ).

${\displaystyle \tau {\frac {\partial q}{\partial t}}+q=-k\nabla h\,,}$

где τ — очень малая постоянная времени, которая приводит это уравнение к нормальной форме закона Дарси в «нормальные» времена (> наносекунд ). Основная причина этого заключается в том, что обычное уравнение потока грунтовых вод ( уравнение диффузии ) приводит к сингулярностям на границах постоянного напора в очень малые времена. Эта форма более строга с математической точки зрения, но приводит к гиперболическому уравнению потока грунтовых вод, которое сложнее решить и которое полезно только в очень малые времена, как правило, за пределами сферы практического использования.

Форма закона Дарси по Бринкману

Другим расширением традиционной формы закона Дарси является термин Бринкмана, который используется для учета переходного потока между границами (введенный Бринкманом в 1949 году ^[16] ),

${\displaystyle -\beta \nabla ^{2}q+q=-{\frac {k}{\mu }}\nabla p\,,}$

где β — эффективный член вязкости . Этот поправочный член учитывает поток через среду, где зерна среды сами по себе пористые, но его трудно использовать, и обычно им пренебрегают.

Справедливость закона Дарси

Закон Дарси действителен для ламинарного потока через отложения . В мелкозернистых отложениях размеры промежутков малы; таким образом, поток ламинарный. Крупнозернистые отложения также ведут себя аналогично, но в очень крупнозернистых отложениях поток может быть турбулентным . ^[17] Следовательно, закон Дарси не всегда действителен для таких отложений. Для потока через коммерческие круглые трубы поток ламинарный, когда число Рейнольдса меньше 2000, и турбулентный, когда оно больше 4000, но в некоторых отложениях было обнаружено, что поток ламинарный, когда значение числа Рейнольдса меньше 1. ^[18]

Смотрите также

• Дарси — единица измерения проницаемости жидкости .
• Гидрогеология
• Уравнение потока грунтовых вод
• Математическая модель
• Уравнения черного масла
• Закон Фика
• Уравнение Эргуна

Ссылки

1. Дарси, Х. (1856). Публичные фонтаны города Дижон . Париж: Дальмонт.
2. Уитакер, С. (1986). «Поток в пористых средах I: Теоретический вывод закона Дарси». Транспорт в пористых средах . 1 : 3–25. Bibcode :1986TPMed...1....3W. doi :10.1007/BF01036523. S2CID  121904058.
3. Браун, GO (2002). «Генри Дарси и создание закона». Исследования водных ресурсов . 38 (7). doi :10.1029/2001WR000727. ISSN  0043-1397.
4. Читайте «Памятные почести: Том 14» на NAP.edu. 2011. doi :10.17226/12884. ISBN 978-0-309-15218-1.
5. Адаптация пористой среды для контролируемого капиллярного потока Журнал коллоидной и интерфейсной науки 539 (2019) 379–387
6. А. Варламов и Г. Балестрино, «La fisica di un buon caffè», Il Nuovo Saggiatore 17Ᏸ3-4Ᏸ, 59–66 ???, 2001 г..
7. Джанино, Кончетто. Экспериментальный анализ итальянского кофейника «мокко». Американский журнал физики (2007)
8. "Экспериментальное исследование экстракции кофе под давлением пара в кофеварке, работающей на плите" Л. Наварини, Э. Нобиле, Ф. Пинто, А. Шери, Ф. Сугги-Ливерани
9. Кинг, Уоррен. «Физика кофемашины для приготовления эспрессо на плите». Американский журнал физики (2008)
10. Бежан, А. (1984). Конвекционная теплопередача . John Wiley & Sons.
11. Каннингем, RE; Уильямс, RJJ (1980). Диффузия в газах и пористых средах . Нью-Йорк: Plenum Press.
12. Carrigy, N.; Pant, LM; Mitra, SK; Secanell, M. (2013). «Кнудсеновская диффузия и проницаемость газодиффузионных слоев с микропористым покрытием pemfc для различных загрузок политетрафторэтилена». Журнал электрохимического общества . 160 (2): F81–89. doi :10.1149/2.036302jes.
13. Pant, LM; Mitra, SK; Secanell, M. (2012). «Измерения абсолютной проницаемости и диффузии Кнудсена в слоях диффузии газа PEMFC и микропористых слоях». Journal of Power Sources . 206 : 153–160. doi :10.1016/j.jpowsour.2012.01.099.
14. Керкхоф, П. (1996). «Модифицированная модель Максвелла–Стефана для транспорта через инертные мембраны: бинарная модель трения». Chemical Engineering Journal и Biochemical Engineering Journal . 64 (3): 319–343. doi :10.1016/S0923-0467(96)03134-X.
15. Клинкенберг, Л. Дж. (1941). «Проницаемость пористых сред для жидкостей и газов». Практика бурения и добычи . Американский нефтяной институт. С. 200–213.
16. Бринкман, ХК (1949). «Расчет вязкой силы, оказываемой текущей жидкостью на плотный рой частиц». Прикладные научные исследования . 1 : 27–34. CiteSeerX 10.1.1.454.3769 . doi :10.1007/BF02120313. 
17. Jin, Y.; Uth, M.-F.; Kuznetsov, AV; Herwig, H. (2 февраля 2015 г.). «Численное исследование возможности макроскопической турбулентности в пористых средах: прямое численное моделирование». Journal of Fluid Mechanics . 766 : 76–103. Bibcode :2015JFM...766...76J. doi :10.1017/jfm.2015.9. S2CID  119946306.
18. Арора, К. Р. (1989). Механика грунтов и фундаментостроение . Standard Publishers.