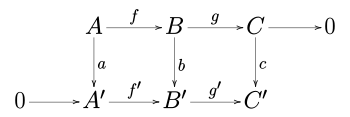
Гомологическая алгебра

Раздел математики

Диаграмма, используемая в лемме о змее , основном результате гомологической алгебры.

Гомологическая алгебра — раздел математики , изучающий гомологию в общем алгебраическом контексте. Это относительно молодая дисциплина, истоки которой можно проследить до исследований в области комбинаторной топологии (предшественницы алгебраической топологии ) и абстрактной алгебры (теории модулей и сизигий ) в конце XIX века, в основном Анри Пуанкаре и Давида Гильберта .

Гомологическая алгебра — это изучение гомологических функторов и сложных алгебраических структур, которые они влекут за собой; ее развитие тесно переплетено с возникновением теории категорий . Центральным понятием являются цепные комплексы , которые можно изучать через их гомологии и когомологии .

Гомологическая алгебра предоставляет средства для извлечения информации, содержащейся в этих комплексах, и представления ее в виде гомологических инвариантов колец , модулей, топологических пространств и других «осязаемых» математических объектов. Спектральная последовательность является мощным инструментом для этого.

Она сыграла огромную роль в алгебраической топологии. Ее влияние постепенно расширялось и в настоящее время включает коммутативную алгебру , алгебраическую геометрию , алгебраическую теорию чисел , теорию представлений , математическую физику , операторные алгебры , комплексный анализ и теорию уравнений с частными производными . K -теория является независимой дисциплиной, которая опирается на методы гомологической алгебры, как и некоммутативная геометрия Алена Конна .

История

Гомологическая алгебра начала изучаться в своей самой базовой форме в 1800-х годах как раздел топологии, а в 1940-х годах стала самостоятельной дисциплиной с изучением таких объектов, как функтор ext и функтор tor , среди прочих. ^[1]

Цепные комплексы и гомология

Понятие цепного комплекса является центральным в гомологической алгебре. Абстрактный цепной комплекс — это последовательность абелевых групп и групповых гомоморфизмов , обладающая тем свойством, что композиция любых двух последовательных отображений равна нулю: ${\displaystyle (C_{\bullet },d_{\bullet })}$

${\displaystyle C_{\bullet }:\cdots \longrightarrow C_{n+1}{\stackrel {d_{n+1}}{\longrightarrow }}C_{n}{\stackrel {d_{n}}{\longrightarrow }}C_{n-1}{\stackrel {d_{n-1}}{\longrightarrow }}\cdots ,\quad d_{n}\circ d_{n+1}=0.}$

Элементы C _n называются n - цепями , а гомоморфизмы d _n называются граничными отображениями или дифференциалами . Цепные группы C _n могут быть наделены дополнительной структурой; например, они могут быть векторными пространствами или модулями над фиксированным кольцом R . Дифференциалы должны сохранять дополнительную структуру, если она существует; например, они должны быть линейными отображениями или гомоморфизмами R -модулей. Для удобства обозначений ограничим внимание абелевыми группами (точнее, категорией Ab абелевых групп); знаменитая теорема Барри Митчелла подразумевает, что результаты будут обобщены на любую абелеву категорию . Каждый цепной комплекс определяет две дополнительные последовательности абелевых групп, циклы Z _n  = Ker d _n и границы B _n  = Im d _{n +1} , где Ker  d и Im  d обозначают ядро ​​и образ d . Поскольку композиция двух последовательных граничных отображений равна нулю, эти группы вложены друг в друга как

${\displaystyle B_{n}\subseteq Z_{n}\subseteq C_{n}.}$

Подгруппы абелевых групп автоматически нормальны ; поэтому мы можем определить n - ю группу гомологий H _n ( C ) как фактор-группу n -циклов по n -границам,

${\displaystyle H_{n}(C)=Z_{n}/B_{n}=\operatorname {Ker} \,d_{n}/\operatorname {Im} \,d_{n+1}.}$

Цепной комплекс называется ациклическим или точной последовательностью, если все его группы гомологии равны нулю.

Цепные комплексы в изобилии возникают в алгебре и алгебраической топологии . Например, если X — топологическое пространство , то сингулярные цепи C _n ( X ) являются формальными линейными комбинациями непрерывных отображений из стандартного n -симплекса в X ; если K — симплициальный комплекс , то симплициальные цепи C _n ( K ) являются формальными линейными комбинациями n -симплексов K ; если A  =  F / R — представление абелевой группы A образующими и соотношениями , где F — свободная абелева группа, натянутая на образующие, а R — подгруппа соотношений, то, положив C ₁ ( A ) =  R , C ₀ ( A ) =  F и C _n ( A ) = 0 для всех остальных n , мы зададим последовательность абелевых групп. Во всех этих случаях имеются естественные дифференциалы d _{n ,} превращающие C _n в цепной комплекс, гомологии которого отражают структуру топологического пространства X , симплициального комплекса K или абелевой группы A . В случае топологических пространств мы приходим к понятию сингулярной гомологии , которая играет фундаментальную роль в исследовании свойств таких пространств, например, многообразий .

На философском уровне гомологическая алгебра учит нас, что определенные цепные комплексы, связанные с алгебраическими или геометрическими объектами (топологические пространства, симплициальные комплексы, R -модули), содержат много ценной алгебраической информации о них, причем гомология является лишь наиболее доступной частью. На техническом уровне гомологическая алгебра предоставляет инструменты для манипулирования комплексами и извлечения этой информации. Вот две общие иллюстрации.

• Два объекта X и Y связаны отображением f между ними. Гомологическая алгебра изучает отношение, индуцированное отображением f , между цепными комплексами, связанными с X и Y , и их гомологиями. Это обобщается на случай нескольких объектов и карт, соединяющих их. Выражаясь на языке теории категорий , гомологическая алгебра изучает функториальные свойства различных конструкций цепных комплексов и гомологии этих комплексов.
• Объект X допускает множественные описания (например, как топологическое пространство и как симплициальный комплекс) или комплекс строится с использованием некоторого «представления» X , которое включает неканонический выбор. Важно знать влияние изменения описания X на цепные комплексы, связанные с X . Обычно комплекс и его гомологии являются функториальными относительно представления; и гомология ( хотя и не сам комплекс) фактически независима от выбранного представления, таким образом, она является инвариантом X . ${\displaystyle C_{\bullet }(X)}$ ${\displaystyle H_{\bullet }(C)}$

Стандартные инструменты

Точные последовательности

В контексте теории групп последовательность

${\displaystyle G_{0}\;{\xrightarrow {f_{1}}}\;G_{1}\;{\xrightarrow {f_{2}}}\;G_{2}\;{\xrightarrow {f_{3}}}\;\cdots \;{\xrightarrow {f_{n}}}\;G_{n}}$

групп и групповых гомоморфизмов называется точным , если образ каждого гомоморфизма равен ядру следующего :

${\displaystyle \mathrm {im} (f_{k})=\mathrm {ker} (f_{k+1}).\!}$

Обратите внимание, что последовательность групп и гомоморфизмов может быть как конечной, так и бесконечной.

Аналогичное определение можно сделать и для некоторых других алгебраических структур . Например, можно иметь точную последовательность векторных пространств и линейных отображений , или модулей и модульных гомоморфизмов . В более общем смысле, понятие точной последовательности имеет смысл в любой категории с ядрами и коядрами .

Короткий

Наиболее распространенным типом точной последовательности является короткая точная последовательность . Это точная последовательность вида

${\displaystyle A\;{\overset {f}{\hookrightarrow }}\;B\;{\overset {g}{\twoheadrightarrow }}\;C}$

где ƒ — мономорфизм , а g — эпиморфизм . В этом случае A — подобъект B , а соответствующий фактор изоморфен C :

${\displaystyle C\cong B/f(A).}$

(где f(A) = im( f )).

Короткую точную последовательность абелевых групп можно также записать в виде точной последовательности с пятью членами:

${\displaystyle 0\;{\xrightarrow {}}\;A\;{\xrightarrow {f}}\;B\;{\xrightarrow {g}}\;C\;{\xrightarrow {}}\;0}$

где 0 представляет нулевой объект , такой как тривиальная группа или нульмерное векторное пространство. Размещение нулей заставляет ƒ быть мономорфизмом, а g — эпиморфизмом (см. ниже).

Длинный

Длинная точная последовательность — это точная последовательность, индексированная натуральными числами .

Пять лемм

Рассмотрим следующую коммутативную диаграмму в любой абелевой категории (например, категории абелевых групп или категории векторных пространств над заданным полем ) или в категории групп .

Пять лемм утверждают, что если строки точны , m и p являются изоморфизмами , l является эпиморфизмом , а q является мономорфизмом , то n также является изоморфизмом.

Лемма змеи

В абелевой категории (такой как категория абелевых групп или категория векторных пространств над заданным полем ) рассмотрим коммутативную диаграмму :

где строки являются точными последовательностями , а 0 — это нулевой объект . Тогда существует точная последовательность, связывающая ядра и коядра a , b и c :

${\displaystyle \ker a\to \ker b\to \ker c{\overset {d}{\to }}\operatorname {coker} a\to \operatorname {coker} b\to \operatorname {coker} c}$

Более того, если морфизм f является мономорфизмом , то таковым является и морфизм ker  a → ker  b , а если g' является эпиморфизмом , то таковым является и морфизм coker  b → coker  c .

Абелевы категории

В математике абелева категория — это категория , в которую можно добавлять морфизмы и объекты, и в которой существуют ядра и коядра , обладающие желаемыми свойствами. Мотивирующим примером прототипа абелевой категории является категория абелевых групп , Ab . Теория возникла в предварительных попытках объединить несколько теорий когомологий Александра Гротендика . Абелевы категории являются очень стабильными категориями, например, они регулярны и удовлетворяют лемме о змее . Класс абелевых категорий замкнут относительно нескольких категориальных конструкций, например, категория цепных комплексов абелевой категории или категория функторов из малой категории в абелеву категорию также являются абелевыми. Эти свойства стабильности делают их неизбежными в гомологической алгебре и за ее пределами; теория имеет основные приложения в алгебраической геометрии , когомологиях и чистой теории категорий . Абелевы категории названы в честь Нильса Хенрика Абеля .

Более конкретно, категория является абелевой , если

• у него есть нулевой объект ,
• он имеет все бинарные продукты и бинарные копродукты , и
• в нем есть все ядра и коядра .
• все мономорфизмы и эпиморфизмы нормальны .​

Производный функтор

Предположим, что нам дан ковариантный левый точный функтор F  : A → B между двумя абелевыми категориями A и B . Если 0 → A → B → C → 0 — короткая точная последовательность в A , то применение F дает точную последовательность 0 → F ( A ) → F ( B ) → F ( C ) и можно спросить, как продолжить эту последовательность вправо, чтобы сформировать длинную точную последовательность. Строго говоря, этот вопрос некорректен, поскольку всегда существует множество различных способов продолжить заданную точную последовательность вправо. Но оказывается, что (если A достаточно «хорошо») существует один канонический способ сделать это, заданный правыми производными функторами F . Для каждого i ≥1 существует функтор R ⁱ F : A → B , и указанная выше последовательность продолжается следующим образом: 0 → F ( A ) → F ( B ) → F ( C ) → R ¹ F ( A ) → R ¹ F ( B ) → R ¹ F ( C ) → R ² F ( A ) → R ² F ( B ) → ... . Отсюда мы видим, что F является точным функтором тогда и только тогда, когда R ¹ F = 0; так что в некотором смысле правые производные функторы F измеряют «насколько далеко» F от точности.

Ext-функтор

Пусть R — кольцо , а Mod _R — категория модулей над R. Пусть B — в Mod _R , и положим T ( B ) = Hom _R ( A,B ) для фиксированного A в Mod _R. Это точный слева функтор , и, таким образом , он имеет производные справа функторы R ⁿ T . Функтор Ext определяется как

${\displaystyle \operatorname {Ext} _{R}^{n}(A,B)=(R^{n}T)(B).}$

Это можно рассчитать, взяв любое инъективное разрешение

${\displaystyle 0\rightarrow B\rightarrow I^{0}\rightarrow I^{1}\rightarrow \cdots ,}$

и вычисления

${\displaystyle 0\rightarrow \operatorname {Hom} _{R}(A,I^{0})\rightarrow \operatorname {Hom} _{R}(A,I^{1})\rightarrow \cdots .}$

Тогда ( R ⁿ T )( B ) — когомологии этого комплекса. Обратите внимание, что Hom _R ( A,B ) исключен из комплекса.

Альтернативное определение дается с использованием функтора G ( A )=Hom _R ( A,B ). Для фиксированного модуля B это контравариантный левый точный функтор , и, таким образом, мы также имеем правые производные функторы R ⁿ G , и можем определить

${\displaystyle \operatorname {Ext} _{R}^{n}(A,B)=(R^{n}G)(A).}$

Это можно рассчитать, выбрав любое проективное разрешение.

${\displaystyle \dots \rightarrow P^{1}\rightarrow P^{0}\rightarrow A\rightarrow 0,}$

и действуя двойственно, вычисляя

${\displaystyle 0\rightarrow \operatorname {Hom} _{R}(P^{0},B)\rightarrow \operatorname {Hom} _{R}(P^{1},B)\rightarrow \cdots .}$

Тогда ( R ⁿ G )( A ) — когомологии этого комплекса. Снова отметим, что Hom _R ( A,B ) исключен.

Оказывается, эти две конструкции дают изоморфные результаты, и поэтому обе могут быть использованы для вычисления функтора Ext.

функтор Tor

Предположим, что R — кольцо , и обозначим через R - Mod категорию левых R -модулей , а через Mod - R — категорию правых R -модулей (если R коммутативно , то эти две категории совпадают). Зафиксируем модуль B в R - Mod . Для A в Mod - R положим T ( A ) = A ⊗ _R B . Тогда T — точный справа функтор из Mod - R в категорию абелевых групп Ab (в случае, когда R коммутативно, это точный справа функтор из Mod - R в Mod - R ) и определены его левые производные функторы L _n T. Положим

${\displaystyle \mathrm {Tor} _{n}^{R}(A,B)=(L_{n}T)(A)}$

т.е. мы берем проективное разрешение

${\displaystyle \cdots \rightarrow P_{2}\rightarrow P_{1}\rightarrow P_{0}\rightarrow A\rightarrow 0}$

затем удалите член A и тензорно умножьте проективное разрешение на B, чтобы получить комплекс

${\displaystyle \cdots \rightarrow P_{2}\otimes _{R}B\rightarrow P_{1}\otimes _{R}B\rightarrow P_{0}\otimes _{R}B\rightarrow 0}$

(обратите внимание, что A ⊗ _R B не отображается, а последняя стрелка — это просто нулевое отображение) и возьмем гомологию этого комплекса.

Спектральная последовательность

Зафиксируем абелеву категорию , например категорию модулей над кольцом. Спектральная последовательность — это выбор неотрицательного целого числа r ₀ и набора из трех последовательностей:

1. Для всех целых чисел r ≥ r ₀ объект E _r , называемый листом (как лист бумаги ), а иногда страницей или термином ,
2. Эндоморфизмы dr  : E _r → E _{r ,} удовлетворяющие d _r o d _r = 0, называемые _{граничными} отображениями или дифференциалами ,
3. Изоморфизмы E _r+1 с H ( E _r ), гомологии E _r относительно d _r .

Лист E ₂ когомологической спектральной последовательности

Спектральная последовательность с двойной градацией имеет огромный объем данных для отслеживания, но существует общая техника визуализации, которая делает структуру спектральной последовательности более ясной. У нас есть три индекса, r , p и q . Для каждого r представьте, что у нас есть лист миллиметровой бумаги. На этом листе мы примем p за горизонтальное направление, а q за вертикальное направление. В каждой точке решетки у нас есть объект . ${\displaystyle E_{r}^{p,q}}$

Очень часто n = p + q является другим естественным индексом в спектральной последовательности. n проходит по диагонали, с северо-запада на юго-восток, через каждый лист. В гомологическом случае дифференциалы имеют бистепень (− r ,  r  − 1), поэтому они уменьшают n на единицу. В когомологическом случае n увеличивается на единицу. Когда r равно нулю, дифференциал перемещает объекты на одну позицию вниз или вверх. Это похоже на дифференциал на цепном комплексе. Когда r равно единице, дифференциал перемещает объекты на одну позицию влево или вправо. Когда r равно двум, дифференциал перемещает объекты так же, как ход коня в шахматах . Для более высоких r дифференциал действует как обобщенный ход коня.

Функториальность

Непрерывное отображение топологических пространств порождает гомоморфизм между их n-ыми группами гомологии для всех n . Этот основной факт алгебраической топологии находит естественное объяснение через некоторые свойства цепных комплексов. Поскольку очень часто приходится изучать несколько топологических пространств одновременно, в гомологической алгебре приходится одновременно рассматривать несколько цепных комплексов.

Морфизм между двумя цепными комплексами — это семейство гомоморфизмов абелевых групп , которые коммутируют с дифференциалами в том смысле, что для всех n . Морфизм цепных комплексов индуцирует морфизм их групп гомологий, состоящий из гомоморфизмов для всех n . Морфизм F называется квазиизоморфизмом, если он индуцирует изоморфизм на n -й гомологии для всех n . ${\displaystyle F:C_{\bullet }\to D_{\bullet },}$ ${\displaystyle F_{n}:C_{n}\to D_{n}}$ ${\displaystyle F_{n-1}\circ d_{n}^{C}=d_{n}^{D}\circ F_{n}}$ ${\displaystyle H_{\bullet }(F)}$ ${\displaystyle H_{n}(F):H_{n}(C)\to H_{n}(D)}$

Многие конструкции цепных комплексов, возникающие в алгебре и геометрии, включая сингулярные гомологии , обладают следующим свойством функториальности : если два объекта X и Y связаны отображением f , то соответствующие цепные комплексы связаны морфизмом , и, более того, композиция отображений f :  X  →  Y и g :  Y  →  Z индуцирует морфизм , совпадающий с композицией Отсюда следует, что группы гомологии также являются функториальными, так что морфизмы между алгебраическими или топологическими объектами приводят к совместимым отображениям между их гомологиями. ${\displaystyle F=C(f):C_{\bullet }(X)\to C_{\bullet }(Y),}$ ${\displaystyle g\circ f}$ ${\displaystyle C(g\circ f):C_{\bullet }(X)\to C_{\bullet }(Z)}$ ${\displaystyle C(g)\circ C(f).}$ ${\displaystyle H_{\bullet }(C)}$

Следующее определение возникает из типичной ситуации в алгебре и топологии. Тройка, состоящая из трех цепных комплексов и двух морфизмов между ними, называется точной тройкой или короткой точной последовательностью комплексов и записывается как ${\displaystyle L_{\bullet },M_{\bullet },N_{\bullet }}$ ${\displaystyle f:L_{\bullet }\to M_{\bullet },g:M_{\bullet }\to N_{\bullet },}$

${\displaystyle 0\longrightarrow L_{\bullet }{\overset {f}{\longrightarrow }}M_{\bullet }{\overset {g}{\longrightarrow }}N_{\bullet }\longrightarrow 0,}$

если для любого n последовательность

${\displaystyle 0\longrightarrow L_{n}{\overset {f_{n}}{\longrightarrow }}M_{n}{\overset {g_{n}}{\longrightarrow }}N_{n}\longrightarrow 0}$

— короткая точная последовательность абелевых групп. По определению это означает, что f _n — инъекция , g n _— сюръекция , и Im f _n  = Ker g _n . Одна из самых основных теорем гомологической алгебры, иногда называемая леммой о зигзаге , утверждает, что в этом случае существует длинная точная последовательность в гомологии

${\displaystyle \cdots \longrightarrow H_{n}(L){\overset {H_{n}(f)}{\longrightarrow }}H_{n}(M){\overset {H_{n}(g)}{\longrightarrow }}H_{n}(N){\overset {\delta _{n}}{\longrightarrow }}H_{n-1}(L){\overset {H_{n-1}(f)}{\longrightarrow }}H_{n-1}(M)\longrightarrow \cdots ,}$

где группы гомологий L , M и N циклически следуют друг за другом, а δ _n — некоторые гомоморфизмы, определяемые f и g , называемые связующими гомоморфизмами . Топологические проявления этой теоремы включают последовательность Майера–Виеториса и длинную точную последовательность для относительной гомологии .

Основополагающие аспекты

Теории когомологий были определены для многих различных объектов, таких как топологические пространства , пучки , группы , кольца , алгебры Ли и C*-алгебры . Изучение современной алгебраической геометрии было бы почти немыслимо без когомологий пучков .

Центральным в гомологической алгебре является понятие точной последовательности ; они могут быть использованы для выполнения реальных вычислений. Классическим инструментом гомологической алгебры является производный функтор ; наиболее простыми примерами являются функторы Ext и Tor .

Имея в виду разнообразный набор приложений, было естественно попытаться привести весь предмет к единообразной основе. Было предпринято несколько попыток, прежде чем предмет устоялся. Приблизительную историю можно изложить следующим образом:

• Картан - Эйленберг : В своей книге 1956 года «Гомологическая алгебра» эти авторы использовали проективные и инъективные модульные резолюции .
• «Тохоку»: подход, описанный в знаменитой статье Александра Гротендика , опубликованной во второй серии журнала Tohoku Mathematical Journal в 1957 году, в котором используется концепция абелевой категории (включая пучки абелевых групп).
• Производная категория Гротендика и Вердье . Производные категории восходят к тезису Вердье 1967 года. Они являются примерами триангулированных категорий, используемых в ряде современных теорий.

Они переходят от вычислимости к общности.

Вычислительная кувалда par excellence — это спектральная последовательность ; они необходимы в подходах Картана-Эйленберга и Тохоку, где они нужны, например, для вычисления производных функторов композиции двух функторов. Спектральные последовательности менее существенны в подходе производных категорий, но все еще играют роль, когда необходимы конкретные вычисления.

Были попытки создания «некоммутативных» теорий, расширяющих первые когомологии до торсоров (важных в когомологиях Галуа ).

Смотрите также

• Абстрактная бессмыслица , термин для гомологической алгебры и теории категорий.
• Дериватор
• Гомотопическая алгебра
• Список тем гомологической алгебры

Ссылки

1. Weibel, Charles A. (1999). «История гомологической алгебры». История топологии . стр. 797–836. doi :10.1016/b978-044482375-5/50029-8. ISBN 9780444823755.

• Анри Картан , Сэмюэль Эйленберг , Гомологическая алгебра . С приложением Дэвида А. Буксбаума. Переиздание оригинала 1956 года. Princeton Landmarks in Mathematics. Princeton University Press, Принстон, Нью-Джерси, 1999. xvi+390 стр. ISBN 0-691-04991-2 
• Гротендик, Александр (1957). «Sur quelques point d'algèbre homologique, I». Математический журнал Тохоку . 9 (2): 119–221. дои : 10.2748/tmj/1178244839 .
• Saunders Mac Lane , Homology . Переиздание издания 1975 года. Classics in Mathematics. Springer-Verlag, Берлин, 1995. x+422 стр. ISBN 3-540-58662-8 
• Питер Хилтон ; Штаммбах, У. Курс гомологической алгебры . Второе издание. Graduate Texts in Mathematics, 4. Springer-Verlag, Нью-Йорк, 1997. xii+364 стр. ISBN 0-387-94823-6 
• Гельфанд, Сергей И.; Юрий Манин , Методы гомологической алгебры . Перевод с русского издания 1988 года. Второе издание. Springer Monographs in Mathematics. Springer-Verlag, Берлин, 2003. xx+372 стр. ISBN 3-540-43583-2 
• Гельфанд, Сергей И.; Юрий Манин, Гомологическая алгебра . Перевод с русского оригинала 1989 года авторами. Перепечатка оригинального английского издания из серии Encyclopaedia of Mathematical Sciences ( Algebra , V, Encyclopaedia Math. Sci., 38, Springer, Berlin, 1994). Springer-Verlag, Berlin, 1999. iv+222 pp. ISBN 3-540-65378-3 
• Weibel, Charles A. (1994). Введение в гомологическую алгебру . Cambridge Studies in Advanced Mathematics. Vol. 38. Cambridge University Press. ISBN 978-0-521-55987-4. MR  1269324. OCLC  36131259.