Спектральный анализ методом наименьших квадратов

Метод расчета периодичности

Результат сопоставления набора точек данных квадратичной функцией

Спектральный анализ наименьших квадратов ( LSSA ) — это метод оценки частотного спектра , основанный на подгонке синусоид к выборкам данных методом наименьших квадратов , аналогичный анализу Фурье . ^{[1] [2]} Анализ Фурье, наиболее используемый спектральный метод в науке, обычно усиливает долгопериодический шум в длинных записях и записях с пропусками; LSSA смягчает такие проблемы. ^[3] В отличие от анализа Фурье, для использования LSSA данные не обязательно должны быть расположены на одинаковом расстоянии друг от друга.

Разработанный в 1969 ^[4] и 1971 годах, ^[5] LSSA также известен как метод Ваничека и метод Гаусса-Ваничека в честь Петра Ваничека , ^{[6] [7]} , а также как метод Ломба ^[3] или периодограмма Ломба-Скаргла. , ^{[2] [8]} на основе упрощений, предложенных сначала Николасом Р. Ломбом ^[9] , а затем Джеффри Д. Скарглом. ^[10]

Историческая справка

Тесная связь между анализом Фурье , периодограммой и аппроксимацией синусоиды методом наименьших квадратов известна уже давно. ^[11] Однако большинство разработок ограничиваются полными наборами данных с равноотстоящими друг от друга выборками. В 1963 году Фрик Дж. М. Барнинг из Математического центра в Амстердаме обрабатывал неравномерно распределенные данные с помощью аналогичных методов, ^[12] включая как анализ периодограммы, эквивалентный тому, что сегодня называется методом Ломба, так и аппроксимацию выбранных частот синусоид, определенных из таких значений, методом наименьших квадратов. периодограммы — и связаны процедурой, известной сегодня как поиск соответствия с обратной подгонкой ^[13] или поиск ортогонального сопоставления. ^[14]

Петр Ваничек , канадский геофизик и геодезист из Университета Нью-Брансуика , предложил в 1969 году также подход сопоставления-преследования для одинаково и неравномерно расположенных данных, который он назвал «последовательным спектральным анализом», а результат - «периодограммой наименьших квадратов». ^[4] Он обобщил этот метод для учета любых систематических компонентов, выходящих за рамки простого среднего значения, таких как «предсказанная линейная (квадратичная, экспоненциальная, ...) вековая тенденция неизвестной величины», и применил его к множеству выборок, в 1971. ^[5]

Строго метод наименьших квадратов Ваничека затем был упрощен в 1976 году Николасом Р. Ломбом из Сиднейского университета , который указал на его тесную связь с анализом периодограммы . ^[9] Впоследствии определение периодограммы неравноотстоящих данных было модифицировано и проанализировано Джеффри Д. Скарглом из Исследовательского центра Эймса НАСА , ^[10] который показал, что при незначительных изменениях оно становится идентичным формуле наименьших квадратов Ломба для подгонка отдельных частот синусоид.

Скаргл заявляет, что его статья «не представляет новую технику обнаружения, а вместо этого изучает надежность и эффективность обнаружения с помощью наиболее часто используемого метода, периодограммы, в случае, когда время наблюдения распределено неравномерно» , и далее указывает на аппроксимация синусоиды методом наименьших квадратов по сравнению с анализом периодограммы, что его статья «по-видимому, впервые устанавливает, что (с предложенными модификациями) эти два метода в точности эквивалентны». ^[10]

Пресс ^[3] резюмирует развитие событий следующим образом:

Совершенно другой метод спектрального анализа данных с неравномерной выборкой, который смягчает эти трудности и обладает некоторыми другими очень желательными свойствами, был разработан Ломбом, частично основанный на более ранних работах Барнинга и Ваничека и дополнительно разработанный Скарглом.

В 1989 году Майкл Дж. Коренберг из Королевского университета в Кингстоне, Онтарио, разработал метод «быстрого ортогонального поиска», позволяющий более быстро найти почти оптимальное разложение спектров или другие задачи ^[15] , аналогичный методу, который позже стал известен как поиск ортогонального соответствия.

Разработка LSSA и вариантов

Метод Ваничека

В линейной регрессии предполагается , что наблюдения ( красный ) являются результатом случайных отклонений ( зеленый ) от основного отношения ( синий ) между зависимой переменной ( y ) и независимой переменной ( x ). Затем при нормированной подгонке, например, по критерию наименьших квадратов , точки данных ( красная ) представлены линией нормативно наилучшего соответствия ( синяя ), от которой всегда остаются «остатки» ( зеленая ).

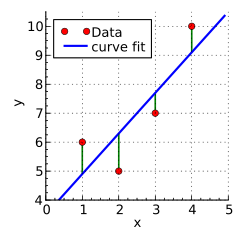
В методе Ваничека дискретный набор данных аппроксимируется взвешенной суммой синусоид постепенно определяемых частот с использованием стандартной линейной регрессии или аппроксимации методом наименьших квадратов . ^[16] Частоты выбираются с использованием метода, аналогичного методу Барнинга, но идя дальше в оптимизации выбора каждой последующей новой частоты путем выбора частоты, которая минимизирует остаток после подбора методом наименьших квадратов (эквивалент метода подбора, теперь известного как поиск соответствия) . с предварительной подгонкой ^[13] ). Количество синусоидов должно быть меньше или равно количеству выборок данных (с учетом синусов и косинусов той же частоты, что и отдельные синусоиды).

Вектор данных Φ представлен как взвешенная сумма синусоидальных базисных функций, сведенных в таблицу в матрице A путем оценки каждой функции в шагах расчета с весовым вектором x :

${\displaystyle \phi \approx {\textbf {A}}x}$,

где вектор весов x выбирается так, чтобы минимизировать сумму квадратов ошибок аппроксимации Φ . Решение для x представляет собой замкнутую форму с использованием стандартной линейной регрессии : ^[17]

${\displaystyle x=({\textbf {A}}^{\mathrm {T} }{\textbf {A}})^{-1}{\textbf {A}}^{\mathrm {T} }\phi .}$

Здесь матрица A может быть основана на любом наборе функций, взаимно независимых (не обязательно ортогональных) при вычислении в шагах расчета; Функции, используемые для спектрального анализа, обычно представляют собой синусы и косинусы, равномерно распределенные по интересующему диапазону частот. Если мы выберем слишком много частот в слишком узком диапазоне частот, функции будут недостаточно независимыми, матрица будет плохо обусловленной, а результирующий спектр будет бессмысленным. ^[17]

Когда базисные функции в A ортогональны (то есть не коррелированы, то есть столбцы имеют нулевое попарное скалярное произведение ), матрица A ^T A является диагональной; когда все столбцы имеют одинаковую степень (сумму квадратов элементов), тогда эта матрица представляет собой единичную матрицу, умноженную на константу, поэтому инверсия тривиальна. Последнее имеет место, когда времена выборки расположены одинаково, а синусоиды выбраны как синусы и косинусы, одинаково разнесенные попарно в частотном интервале от 0 до полупериода на выборку (с интервалом 1/N циклов на выборку, исключая синусоидальные фазы в 0). и максимальную частоту, где они тождественно равны нулю). Этот случай известен как дискретное преобразование Фурье , слегка переписанное с точки зрения измерений и коэффициентов. ^[17]

${\displaystyle x={\textbf {A}}^{\mathrm {T} }\phi }$— Случай ДПФ для N равноотстоящих отсчетов и частот в пределах скалярного коэффициента.

Метод Ломб

Спектр мощности (квадрат величины) двух синусоидальных базисных функций , рассчитанный методом периодограммы

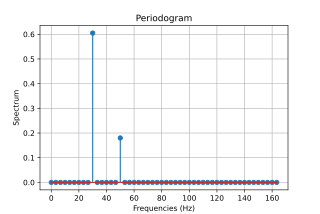
Пытаясь снизить вычислительную нагрузку метода Ваничека в 1976 году ^[9] (уже не проблема), Ломб предложил использовать приведенное выше упрощение в целом, за исключением парных корреляций между синусоидальными и косинусоидными основаниями одной и той же частоты, поскольку корреляции между парами синусоидов часто малы, по крайней мере, когда они не расположены плотно. Эта формулировка по существу аналогична традиционной периодограмме , но адаптирована для использования с неравномерно расположенными выборками. Вектор x является достаточно хорошей оценкой основного спектра, но поскольку мы игнорируем любые корреляции, A x больше не является хорошим приближением к сигналу, и метод больше не является методом наименьших квадратов, хотя в литературе продолжают называться таковым.

Вместо того, чтобы просто брать скалярные произведения данных с синусоидальными и косинусоидальными сигналами напрямую, Скаргл модифицировал стандартную формулу периодограммы так, чтобы сначала найти временную задержку, так что эта пара синусоидов была бы взаимно ортогональна на шагах расчета , а также скорректирована с учетом потенциально неравных мощности этих двух базисных функций, чтобы получить лучшую оценку мощности на частоте. ^{[3] [10]} Эта процедура сделала его модифицированный метод периодограммы точно эквивалентным методу Ломба. Временная задержка по определению равна ${\displaystyle \tau }$ ${\displaystyle t_{j}}$ ${\displaystyle \tau }$

${\displaystyle \tan {2\omega \tau }={\frac {\sum _{j}\sin 2\omega t_{j}}{\sum _{j}\cos 2\omega t_{j}}}.}$

Тогда периодограмма на частоте оценивается как: ${\displaystyle \omega }$

${\displaystyle P_{x}(\omega )={\frac {1}{2}}\left({\frac {\left[\sum _{j}X_{j}\cos \omega (t_{j}-\tau )\right]^{2}}{\sum _{j}\cos ^{2}\omega (t_{j}-\tau )}}+{\frac {\left[\sum _{j}X_{j}\sin \omega (t_{j}-\tau )\right]^{2}}{\sum _{j}\sin ^{2}\omega (t_{j}-\tau )}}\right)}$,

которая, как сообщает Скаргл, имеет то же статистическое распределение, что и периодограмма в случае равномерной выборки. ^[10]

На любой отдельной частоте этот метод дает ту же мощность, что и аппроксимация методом наименьших квадратов синусоид этой частоты и формы: ${\displaystyle \omega }$

${\displaystyle \phi (t)=A\sin \omega t+B\cos \omega t.}$^[18]

На практике всегда трудно судить, является ли данный пик Ломба значимым или нет, особенно когда природа шума неизвестна, поэтому, например, спектральный пик ложной тревоги при анализе периодограммы Ломба зашумленного периодического сигнала может быть результатом шум в данных о турбулентности. ^[19] Методы Фурье также могут сообщать о ложных спектральных пиках при анализе исправленных или отредактированных иным образом данных. ^[7]

Обобщенная периодограмма Ломба – Скаргла

Стандартная периодограмма Ломба – Скаргла действительна только для модели с нулевым средним. Обычно это аппроксимируется путем вычитания среднего значения данных перед расчетом периодограммы. Однако это неточное предположение, когда среднее значение модели (подогнанные синусоиды) не равно нулю. Обобщенная периодограмма Ломба – Скаргла устраняет это предположение и явно определяет среднее значение. В этом случае устанавливается функция

${\displaystyle \phi (t)=A\sin \omega t+B\cos \omega t+C.}$^[20]

Обобщенная периодограмма Ломба – Скаргла также упоминается в литературе как периодограмма с плавающим средним . ^[21]

Метод «быстрого ортогонального поиска» Коренберга.

Майкл Коренберг из Королевского университета в Кингстоне, Онтарио , разработал метод выбора разреженного набора компонентов из чрезмерно полного набора (например, синусоидальных компонентов для спектрального анализа), названный быстрым ортогональным поиском (FOS). Математически FOS использует слегка модифицированное разложение Холецкого в процессе уменьшения среднеквадратических ошибок (MSER), реализованное как инверсия разреженной матрицы . ^{[15] [22]} Как и другие методы LSSA, FOS позволяет избежать основного недостатка дискретного анализа Фурье, поэтому он может точно идентифицировать встроенные периодичности и превосходно работать с неравномерно расположенными данными. Метод быстрого ортогонального поиска применялся и для других задач, таких как идентификация нелинейных систем .

Метод хи-квадрата Палмера

Палмер разработал метод поиска функции, наиболее подходящей для любого выбранного количества гармоник, что дает больше свободы в поиске несинусоидальных гармонических функций. ^[23] Это быстрый ( на основе БПФ ) метод взвешенного анализа наименьших квадратов произвольно расположенных данных с неравномерными стандартными ошибками. Доступен исходный код, реализующий эту технику. ^[24] Поскольку данные часто не отбираются в дискретные промежутки времени с одинаковым интервалом, этот метод «связывает» данные путем редкого заполнения массива временных рядов в моменты выборки. Все промежуточные точки сетки получают нулевой статистический вес, что эквивалентно наличию бесконечных полос ошибок время от времени между выборками.

Приложения

Бета-распределение для разных значений его параметров

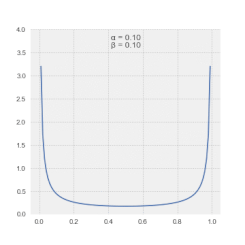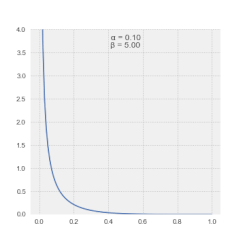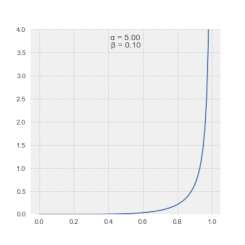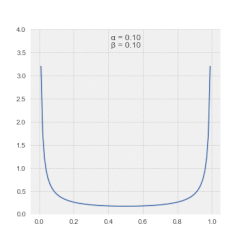
Самая полезная функция LSSA — это возможность спектрального анализа неполных записей без необходимости манипулировать данными или изобретать несуществующие данные.

Величины в спектре LSSA отражают вклад частоты или периода в дисперсию временного ряда . ^{[4] Как правило, определенные таким образом спектральные величины обеспечивают прямой режим} уровня значимости выходного сигнала . ^[25] Альтернативно, спектральные величины в спектре Ваничека также могут быть выражены в дБ . ^[26] Обратите внимание, что спектральные величины в спектре Ваничека следуют β-распределению . ^[27]

Обратное преобразование LSSA Ваничека возможно, в чем легче всего убедиться, записав прямое преобразование в виде матрицы; обратная матрица (когда матрица не является сингулярной) или псевдообратная будет тогда обратным преобразованием; обратное будет точно соответствовать исходным данным, если выбранные синусоиды взаимно независимы в точках выборки и их количество равно количеству точек данных. ^[17] Для метода периодограмм такой обратной процедуры не известно.

Выполнение

LSSA может быть реализован менее чем на одной странице кода MATLAB . ^[28] По сути: ^[16]

«Чтобы вычислить спектр методом наименьших квадратов, мы должны вычислить m спектральных значений… что включает в себя выполнение аппроксимации методом наименьших квадратов m раз, каждый раз, чтобы получить [спектральную мощность] для другой частоты»

Т.е. для каждой частоты в желаемом наборе частот функции синуса и косинуса оцениваются в моменты времени, соответствующие выборкам данных, и скалярные произведения вектора данных с векторами синусоиды берутся и соответствующим образом нормализуются; следуя методу, известному как периодограмма Ломба/Скаргла, временной сдвиг рассчитывается для каждой частоты, чтобы ортогонализировать компоненты синуса и косинуса перед скалярным произведением; ^[17] наконец, мощность вычисляется на основе этих двух амплитудных компонентов. Этот же процесс реализует дискретное преобразование Фурье , когда данные равномерно распределены во времени, а выбранные частоты соответствуют целым числам циклов в конечной записи данных.

Этот метод обрабатывает каждую синусоидальную составляющую независимо или вне контекста, даже если они могут не быть ортогональными точкам данных; это оригинальный метод Ваничека. Кроме того, можно выполнить полную одновременную или контекстную аппроксимацию методом наименьших квадратов, решив матричное уравнение и разделив общую дисперсию данных между указанными частотами синусоиды. ^[17] Такое матричное решение методом наименьших квадратов изначально доступно в MATLAB как оператор обратной косой черты . ^[29]

Кроме того, одновременный или контекстный метод, в отличие от независимой или внеконтекстной версии (а также версии периодограммы, предложенной Ломбом), не может соответствовать большему количеству компонентов (синусов и косинусов), чем имеется выборок данных, поэтому что: ^[17]

«...серьезные последствия могут также возникнуть, если выбранные частоты приведут к тому, что некоторые компоненты Фурье (триггерные функции) станут почти линейно зависимыми друг от друга, тем самым создавая плохо обусловленное или почти сингулярное N. Чтобы избежать такой плохой обусловленности, становится необходимо либо выбрать другой набор частот для оценки (например, равноотстоящие друг от друга частоты), либо просто пренебречь корреляциями в N (т. е. недиагональными блоками) и оценить обратное преобразование наименьших квадратов отдельно для отдельных частот... "

С другой стороны, метод периодограммы Ломба может использовать сколь угодно большое количество или плотность частотных компонентов, как в стандартной периодограмме ; то есть частотная область может быть подвергнута передискретизации с произвольным коэффициентом. ^[3] Однако, как упоминалось выше, следует иметь в виду, что упрощение Ломба и отклонение от критерия наименьших квадратов открыли в его методике серьезные источники ошибок, приводящие даже к ложным спектральным пикам. ^[19]

В анализе Фурье, таком как преобразование Фурье и дискретное преобразование Фурье , все синусоиды, соответствующие данным, взаимно ортогональны, поэтому нет различия между простой проекцией вне контекста, основанной на скалярном произведении, на базисные функции и внутренней проекцией. контекстная одновременная аппроксимация по методу наименьших квадратов; то есть не требуется никакого обращения матрицы для разделения дисперсии между ортогональными синусоидами разных частот по методу наименьших квадратов. ^[30] В прошлом метод Фурье был для многих предпочтительным методом благодаря эффективной реализации быстрого преобразования Фурье , когда доступны полные записи данных с равноотстоящими отсчетами, и они также использовали семейство методов Фурье для анализа записей с пробелами. , который, однако, требовал манипулирования и даже изобретения несуществующих данных только для того, чтобы иметь возможность запускать алгоритм на основе Фурье.

Смотрите также

• Неравномерное дискретное преобразование Фурье
• Ортогональные функции
• СигСпец
• Синусоидальная модель
• Спектральная плотность
• Оценка спектральной плотности для конкурирующих альтернатив

Рекомендации

1. Джафер Ибаноглу (2000). Переменные звезды как важнейшие астрофизические инструменты. Спрингер. ISBN 0-7923-6084-2.
2. Д. Скотт Бирни; Дэвид Оспер; Гильермо Гонсалес (2006). Наблюдательная астрономия. Издательство Кембриджского университета. ISBN 0-521-85370-2.
3. Press (2007). Численные рецепты (3-е изд.). Издательство Кембриджского университета. ISBN 978-0-521-88068-8.
4. П. Ваничек (1 августа 1969 г.). «Приблизительный спектральный анализ методом наименьших квадратов» (PDF) . Астрофизика и космическая наука . 4 (4): 387–391. Бибкод : 1969Ap&SS...4..387В. дои : 10.1007/BF00651344. OCLC  5654872875. S2CID  124921449.
5. П. Ваничек (1 июля 1971 г.). «Дальнейшее развитие и свойства спектрального анализа методом наименьших квадратов» (PDF) . Астрофизика и космическая наука . 12 (1): 10–33. Бибкод : 1971Ap&SS..12...10В. дои : 10.1007/BF00656134. S2CID  109404359.
6. Дж. Тейлор; С. Гамильтон (20 марта 1972 г.). «Некоторые испытания метода спектрального анализа Ваничека». Астрофизика и космическая наука . 17 (2): 357–367. Бибкод : 1972Ap&SS..17..357T. дои : 10.1007/BF00642907. S2CID  123569059.
7. М. Омербашич (26 июня 2006 г.). «Спектральный анализ Гаусса-Ваничека сборника Сепкоски: никаких новых жизненных циклов». Вычисления в науке и технике . 8 (4): 26–30. arXiv : math-ph/0608014 . Бибкод : 2006CSE.....8d..26O. дои : 10.1109/MCSE.2006.68.
8. Ханс П.А. Ван Донген (1999). «Поиск биологических ритмов: обнаружение пиков на периодограмме неравномерно распределенных данных». Журнал биологических ритмов . 14 (6): 617–620. дои : 10.1177/074873099129000984. PMID  10643760. S2CID  14886901.
9. Lomb, NR (1976). «Частотный анализ неравномерно расположенных данных методом наименьших квадратов». Астрофизика и космическая наука . 39 (2): 447–462. Бибкод : 1976Ap&SS..39..447L. дои : 10.1007/BF00648343. S2CID  2671466.
10. Scargle, JD (1982). «Исследования по анализу астрономических временных рядов. II - Статистические аспекты спектрального анализа неравномерно расположенных данных». Астрофизический журнал . 263 : 835. Бибкод : 1982ApJ...263..835S. дои : 10.1086/160554.
11. Дэвид Брант (1931). Комбинация наблюдений (2-е изд.). Издательство Кембриджского университета.
12. Барнинг, FJM (1963). «Численный анализ кривой блеска 12 Lacertae». Бюллетень астрономических институтов Нидерландов . 17 : 22. Бибкод :1963БАН....17...22Б.
13. Паскаль Винсент; Йошуа Бенджио (2002). «Погоня за соответствием ядра» (PDF) . Машинное обучение . 48 : 165–187. дои : 10.1023/А:1013955821559 .
14. Ю. К. Пати, Р. Резайфар и П. С. Кришнапрасад, «Погоня за ортогональным сопоставлением: аппроксимация рекурсивной функции с приложениями к вейвлет-разложению», в Proc. 27-я Асиломарская конференция по сигналам, системам и компьютерам, редактор А. Сингха, Лос-Аламитос, Калифорния, США, IEEE Computer Society Press, 1993 г.
15. Коренберг, MJ (1989). «Надежный ортогональный алгоритм для идентификации системы и анализа временных рядов». Биологическая кибернетика . 60 (4): 267–276. дои : 10.1007/BF00204124. PMID  2706281. S2CID  11712196.
16. Уэллс, Д.Э., П. Ваничек, С. Пагиатакис, 1985. Возвращение к спектральному анализу метода наименьших квадратов. Технический отчет 84 Департамента геодезической инженерии, Университет Нью-Брансуика, Фредериктон, 68 страниц, доступен по адресу [1].
17. Краймер, М.Р., Спектр наименьших квадратов, его обратное преобразование и функция автокорреляции: теория и некоторые приложения в геодезии, доктор философии. Диссертация, Университет Торонто, Канада (1998).
18. Уильям Дж. Эмери; Ричард Э. Томсон (2001). Методы анализа данных в физической океанографии. Эльзевир. ISBN 0-444-50756-6.
19. Чжоу, W.-X.; Сорнетт, Д. (октябрь 2001 г.). «Статистическая значимость периодичности и логарифмической периодичности с коррелированным шумом с тяжелым хвостом». Международный журнал современной физики C . 13 (2): 137–169. arXiv : cond-mat/0110445 . Бибкод : 2002IJMPC..13..137Z. дои : 10.1142/S0129183102003024. S2CID  8256563.
20. М. Цехмайстер; М. Кюрстер (март 2009 г.). «Обобщенная периодограмма Ломба – Скаргла. Новый формализм для периодограмм с плавающим средним и кеплеровских периодограмм». Астрономия и астрофизика . 496 (2): 577–584. arXiv : 0901.2573 . Бибкод : 2009A&A...496..577Z. дои : 10.1051/0004-6361: 200811296. S2CID  10408194.
21. Эндрю Камминг; Джеффри В. Марси; Р. Пол Батлер (декабрь 1999 г.). «Поиск планеты Лик: обнаруживаемость и массовые пороги». Астрофизический журнал . 526 (2): 890–915. arXiv : astro-ph/9906466 . Бибкод : 1999ApJ...526..890C. дои : 10.1086/308020. S2CID  12560512.
22. Коренберг, Майкл Дж.; Бренан, Колин Дж. Х.; Хантер, Ян В. (1997). «Оценка рамановского спектра с помощью быстрого ортогонального поиска». Аналитик . 122 (9): 879–882. Бибкод : 1997Ана...122..879К. дои : 10.1039/a700902j.
23. Палмер, Дэвид М. (2009). «Быстрый метод хи-квадрат для поиска по периоду данных с нерегулярной выборкой». Астрофизический журнал . 695 (1): 496–502. arXiv : 0901.1913 . Бибкод : 2009ApJ...695..496P. дои : 10.1088/0004-637X/695/1/496. S2CID  5991300.
24. «Дэвид Палмер: Быстрый поиск периода хи-квадрат» .
25. Бирд, А.Г., Уильямс, П.Дж.С., Митчелл, Н.Дж. и Мюллер, Х.Г. Специальная климатология планетарных волн и приливной изменчивости, J Atm. Солар-Тер. Физ. 63 (09), с.801–811 (2001).
26. Пагиатакис, С. Стохастическая значимость пиков в спектре метода наименьших квадратов, Журнал Geodesy 73, стр.67-78 (1999).
27. Стивс, Р.Р. Статистический тест значимости пиков в спектре методом наименьших квадратов, Сборник статей Геодезической службы, Министерства энергетики, горнодобывающей промышленности и ресурсов, исследований и картографии, Оттава, Канада, стр. 149-166 (1981).
28. Ричард А. Мюллер ; Гордон Дж. Макдональд (2000). Ледниковые периоды и астрономические причины: данные, спектральный анализ и механизмы (1-е изд.). Шпрингер Берлин Гейдельберг. Бибкод : 2000iaac.book.....M. ISBN 978-3-540-43779-6. ОЛ  20645181М. Викиданные  Q111312009.
29. Тимоти А. Дэвис; Кермит Сигмон (2005). MATLAB Праймер. ЦРК Пресс. ISBN 1-58488-523-8.
30. Даррелл Уильямсон (1999). Дискретная обработка сигналов: алгебраический подход. Спрингер. ISBN 1-85233-161-5.

Внешние ссылки

• Бесплатная загрузка пакета LSSA, FORTRAN, метод спектрального анализа Ваничека наименьших квадратов, из Университета Нью-Брансуика .
• Бесплатная загрузка пакета LSWAVE, MATLAB, включает в себя метод спектрального анализа Ваничека от Национальной геодезической службы США .
• Бесплатная загрузка программного обеспечения LSSA ^{[ постоянная мертвая ссылка ]} (через FTP), FORTRAN, метод Ваничека, из Министерства природных ресурсов Канады .