Окружность Земли — это расстояние вокруг Земли . Измеренная по экватору , она составляет 40 075,017 км (24 901,461 мили). Измеренная через полюса , окружность составляет 40 007,863 км (24 859,734 мили). [1]
Измерение окружности Земли было важно для навигации с древних времен. Первое известное научное измерение и расчет были сделаны Эратосфеном , путем сравнения высот полуденного солнца в двух местах, находящихся на известном расстоянии с севера на юг друг от друга. [2] Он достиг большой степени точности в своих вычислениях. [3] Если рассматривать Землю как сферу , ее окружность была бы ее единственным наиболее важным измерением. [4] Земля отклоняется от сферической формы примерно на 0,3%, что характеризуется сплющиванием .
В наше время окружность Земли использовалась для определения основных единиц измерения длины: морской мили в семнадцатом веке и метра в восемнадцатом. Полярная окружность Земли очень близка к 21 600 морским милям, потому что морская миля была предназначена для выражения одной минуты широты (см. дуга меридиана ), что составляет 21 600 частей полярной окружности (то есть 60 минут × 360 градусов). Полярная окружность также близка к 40 000 километров, потому что метр изначально был определен как одна десятимиллионная (т. е. километр составляет одну десятитысячную) дуги от полюса до экватора ( четверть меридиана ). Точность измерения окружности с тех пор улучшилась, но физическая длина каждой единицы измерения осталась близкой к той, что была определена в то время, поэтому окружность Земли больше не является круглым числом в метрах или морских милях.
Измерение окружности Земли является самым известным из результатов, полученных Эратосфеном , [5] который оценил, что меридиан имеет длину 252 000 стадий , с погрешностью относительно реального значения между −2,4% и +0,8% (предполагая, что значение стадиона составляет от 155 до 160 метров; [3] точное значение стадиона остается предметом споров по сей день; см. стадий ).
Эратосфен описал свою технику в книге под названием «О измерении Земли» , которая не сохранилась; сохранилась лишь упрощенная версия, описанная Клеомедом для популяризации открытия. [6] Клеомед предлагает своему читателю рассмотреть два египетских города, Александрию и Сиену (современный Асуан ):
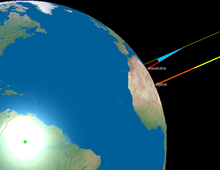
Согласно « О круговых движениях небесных тел » Клеомеда , около 240 г. до н. э. Эратосфен вычислил окружность Земли в Птолемеевом Египте . [8] Используя вертикальный стержень, известный как гномон , и при предыдущих предположениях, он знал, что в местный полдень во время летнего солнцестояния в Сиене (современный Асуан , Египет) Солнце было прямо над головой, так как гномон не отбрасывал тени. Кроме того, тень человека, смотрящего в то время в глубокий колодец в Сиене, блокировала отражение Солнца на воде. Затем Эратосфен измерил угол возвышения Солнца в полдень в Александрии, измерив длину тени другого гномона на земле. [9] Используя длину стержня и длину тени как катеты треугольника, он вычислил угол солнечных лучей. [10] Этот угол был около 7°, или 1/50 окружности круга ; Предположив, что Земля имеет идеальную сферическую форму, он пришел к выводу, что ее окружность в 50 раз больше известного расстояния от Александрии до Сиены (5000 стадий, цифра, которая проверялась ежегодно), т. е. 250 000 стадий . [11] В зависимости от того, использовал ли он «олимпийский стадий» (176,4 м) или итальянский стадий (184,8 м), это означало бы окружность в 44 100 км (погрешность 10%) или 46 100 км, погрешность 15%. [11] Значение для стадиона в 157,7 метров даже было предложено Л. В. Фирсовым, что дало бы еще большую точность, но страдает от ошибок в расчетах и ложных предположений. [12] В 2012 году Энтони Абреу Мора повторил расчет Эратосфена с более точными данными; результат составил 40 074 км, что на 66 км (0,16%) отличается от принятой в настоящее время длины полярной окружности. [10]

Метод Эратосфена был на самом деле более сложным, как утверждает тот же Клеомед, чьей целью было представить упрощенную версию того, что описано в книге Эратосфена. Плиний, например, назвал значение в 252 000 стадий. [13]
Метод был основан на нескольких геодезических поездках, проведенных профессиональными бематистами , чьей работой было точное измерение протяженности территории Египта для сельскохозяйственных и налоговых целей. [3] Более того, тот факт, что мера Эратосфена точно соответствует 252 000 стадий (согласно Плинию), может быть преднамеренным, поскольку это число можно разделить на все натуральные числа от 1 до 10: некоторые историки полагают, что Эратосфен изменил значение 250 000, записанное Клеомедом, на это новое значение для упрощения вычислений; [14] другие историки науки, с другой стороны, полагают, что Эратосфен ввел новую единицу длины, основанную на длине меридиана, как утверждает Плиний, который пишет о стадионе «согласно соотношению Эратосфена». [3] [13]
Посидоний вычислил окружность Земли, ссылаясь на положение звезды Канопус . Как объяснил Клеомед , Посидоний наблюдал Канопус на Родосе , но никогда не поднимался над горизонтом , в то время как в Александрии он видел, как он поднимался до 7+1 ⁄ 2 градуса над горизонтом ( дуга меридиана между широтой двух местностей на самом деле составляет 5 градусов 14 минут). Поскольку он считал, что Родос находится в 5000 стадиях к северу от Александрии, а разница в высоте звезды указывала, что расстояние между двумя местами составляло 1/48 окружности, он умножил 5000 на 48, чтобы получить цифру 240 000 стадий для окружности Земли. [15] Обычно считается [ кем? ] , что стадия, используемая Посидонием, была почти точно 1/10 современной уставной мили. [ нужна цитата ] Таким образом, мера Посидония в 240 000 стадий переводится в 24 000 миль (39 000 км), что не намного меньше фактической окружности в 24 901 милю (40 074 км). [15] Страбон отметил, что расстояние между Родосом и Александрией составляет 3750 стадий, и сообщил, что оценка Посидонием окружности Земли составляет 180 000 стадий или 18 000 миль (29 000 км). [16] Плиний Старший упоминает Посидония среди своих источников и — не называя его имени — сообщает о его методе оценки окружности Земли. Однако он отметил, что Гиппарх добавил около 26 000 стадий к оценке Эратосфена. Меньшее значение, предложенное Страбоном, и разная длина греческих и римских стадий создали постоянную путаницу вокруг результата Посидония. Птолемей использовал меньшее значение Посидония в 180 000 стадий (примерно на 33% меньше) для окружности Земли в своей «Географии» . Это число использовал Христофор Колумб , чтобы занизить расстояние до Индии до 70 000 стадиев. [17]
Около 525 г. н. э. индийский математик и астроном Арьябхата написал «Арьябхатия» , в котором он вычислил диаметр Земли в 1050 йоджан . Длина йоджаны, предполагаемая Арьябхатой, является предметом спора. Одно внимательное прочтение дает эквивалент в 14 200 километров (8 800 миль), что на 11% больше, чем нужно. [18] Другое дает 15 360 км (9 540 миль), что на 20% больше, чем нужно. [19] Еще одно дает 13 440 км (8 350 миль), что на 5% больше, чем нужно. [20]
Около 830 г. н. э. халиф Аль-Мамун поручил группе мусульманских астрономов во главе с Аль-Хорезми измерить расстояние от Тадмура ( Пальмиры ) до Ракки в современной Сирии . Они вычислили окружность Земли, которая оказалась в пределах 15% от современного значения, а возможно, и гораздо ближе. Насколько точным это было на самом деле, неизвестно из-за неопределенности в преобразовании средневековых арабских единиц в современные единицы, но в любом случае технические ограничения методов и инструментов не позволили бы получить точность выше, чем около 5%. [21]

Более удобный способ оценки был предоставлен в Кодексе Масудикус Аль-Бируни ( 1037). В отличие от своих предшественников, которые измеряли окружность Земли, наблюдая за Солнцем одновременно из двух мест, Аль-Бируни разработал новый метод использования тригонометрических вычислений, основанный на угле между равниной и вершиной горы , что позволило измерить его одному человеку из одного места. [21] С вершины горы он наблюдал угол наклона , который вместе с высотой горы (которую он определил заранее) он применил к формуле закона синусов . Это было самое раннее известное использование угла наклона и самое раннее практическое использование закона синусов. [22] Однако этот метод не мог дать более точных результатов, чем предыдущие методы, из-за технических ограничений, и поэтому Аль-Бируни принял значение, вычисленное в предыдущем столетии экспедицией Аль-Мамуна . [21]
Спустя 1700 лет после смерти Эратосфена Христофор Колумб изучил то, что Эратосфен написал о размерах Земли. Тем не менее, основываясь на карте Тосканелли , он решил верить, что окружность Земли была на 25% меньше. Если бы вместо этого Колумб принял большее значение Эратосфена, он бы знал, что место, где он высадился, было не Азией , а Новым Светом . [23]
В 1617 году голландский ученый Виллеброрд Снеллиус оценил окружность Земли в 24 630 римских миль (24 024 статутных мили). Примерно в то же время британский математик Эдмунд Гюнтер усовершенствовал навигационные инструменты, включая новый квадрант для определения широты в море. Он рассудил, что линии широты могут быть использованы в качестве основы для единицы измерения расстояния , и предложил морскую милю как одну минуту или одну шестидесятую ( 1/60 ) одного градуса широты. Поскольку один градус равен 1/360 окружности, одна угловая минута равна 1/21600 окружности – так, чтобы полярная окружность Земли была бы ровно 21 600 миль. Гюнтер использовал окружность Снеллиуса, чтобы определить морскую милю как 6 080 футов, длину одной минуты дуги на широте 48 градусов. [24]
В 1793 году Франция определила метр таким образом, чтобы полярная окружность Земли составляла 40 000 километров. Чтобы точно измерить это расстояние, Французская академия наук поручила Жану Батисту Жозефу Деламбре и Пьеру Мешену возглавить экспедицию , чтобы попытаться точно измерить расстояние между колокольней в Дюнкерке и замком Монжуик в Барселоне , чтобы оценить длину дуги меридиана через Дюнкерк. Длина первого прототипа метровой планки была основана на этих измерениях, но позже было установлено, что ее длина была короче примерно на 0,2 миллиметра из-за неправильного расчета сплющивания Земли , что сделало прототип примерно на 0,02% короче первоначально предложенного определения метра. Независимо от этого, эта длина стала французским стандартом и постепенно была принята другими странами Европы. [25] Вот почему полярная окружность Земли на самом деле составляет 40 008 километров, а не 40 000.