Сумматор (электроника)

Цифровая схема, которая производит суммы из входных данных

Сумматор , или сумматор , ^[1] — это цифровая схема , которая выполняет сложение чисел. Во многих компьютерах и других типах процессоров сумматоры используются в арифметико-логических устройствах (АЛУ). Они также используются в других частях процессора, где они используются для вычисления адресов , индексов таблиц , операторов инкремента и декремента и подобных операций.

Хотя сумматоры могут быть построены для многих числовых представлений , таких как двоично-десятичные или избыточные-3 , наиболее распространенные сумматоры работают с двоичными числами . В случаях, когда для представления отрицательных чисел используется дополнение до двух или дополнение до единиц , тривиально модифицировать сумматор в сумматор-вычитатель . Другие знаковые представления чисел требуют больше логики вокруг базового сумматора.

История

В 1937 году Джордж Штибиц изобрел 2-битный двоичный сумматор ( модель K ).

Двоичные сумматоры

Половина сумматора

Полусумматор складывает две отдельные двоичные цифры и . Он имеет два выхода, сумму ( ) и перенос ( ). Сигнал переноса представляет собой переполнение в следующую цифру многозначного сложения. Значение суммы равно . Простейшая конструкция полусумматора , изображенная справа, включает в себя вентиль XOR для и вентиль AND для . Булева логика для суммы (в данном случае ) будет тогда как для переноса ( ) будет . С добавлением вентиля OR для объединения их выходов переноса два полусумматора можно объединить, чтобы получить полный сумматор. ^[2] Полусумматор складывает два входных бита и генерирует перенос и сумму, которые являются двумя выходами полусумматора. Входные переменные полусумматора называются битами слагаемого и слагаемого. Выходные переменные — это сумма и перенос. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle S}$ ${\displaystyle C}$ ${\displaystyle 2C+S}$ ${\displaystyle S}$ ${\displaystyle C}$ ${\displaystyle S}$ ${\displaystyle A\oplus B}$ ${\displaystyle C}$ ${\displaystyle A\cdot B}$

Таблица истинности для полусумматора следующая:

Различные схемы цифровой логики полусумматора:

• 
  Полусумматор в действии.
• 
  Схема полусумматора, реализованная с одним вентилем XOR и одним вентилем AND .
• 
  Схема полусумматора, реализованная с пятью вентилями И-НЕ .
• 
  Схематическое обозначение однобитного полусумматора.

Полный сумматор

Полный сумматор складывает двоичные числа и учитывает как входящие, так и исходящие значения. Однобитный полный сумматор складывает три однобитных числа, часто записываемых как , , и ; и являются операндами, и бит, перенесенный из предыдущей менее значимой стадии. ^[3] Схема выдает двухбитный выход. Выходной перенос и сумма обычно представлены сигналами и , где сумма равна . Полный сумматор обычно является компонентом в каскаде сумматоров, которые складывают 8-, 16-, 32- и т. д. битные двоичные числа. ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C_{in}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle C_{in}}$ ${\displaystyle C_{out}}$ ${\displaystyle S}$ ${\displaystyle 2C_{out}+S}$

Полный сумматор может быть реализован многими различными способами, например, с помощью пользовательской схемы транзисторного уровня или составлен из других вентилей. Наиболее распространенная реализация — с помощью:

${\displaystyle S=A\oplus B\oplus C_{in}}$

${\displaystyle C_{out}=(A\cdot B)+(C_{in}\cdot (A\oplus B))}$

Приведенные выше выражения для и могут быть получены с помощью карты Карно для упрощения таблицы истинности. ${\displaystyle S}$ ${\displaystyle C_{in}}$

В этой реализации последний вентиль ИЛИ перед выходом переноса может быть заменен вентильом XOR без изменения результирующей логики. Это происходит потому, что когда A и B оба равны 1, термин всегда равен 0, и, следовательно, может быть только 0. Таким образом, входы в последний вентиль ИЛИ никогда не могут быть оба равны 1 (это единственная комбинация, для которой выходы OR и XOR различаются). ${\displaystyle (A\oplus B)}$ ${\displaystyle (C_{in}\cdot (A\oplus B))}$

Благодаря свойству функциональной полноты вентилей NAND и NOR полный сумматор также может быть реализован с использованием девяти вентилей NAND [ ^4] или девяти вентилей NOR .

Использование только двух типов вентилей удобно, если схема реализуется с использованием простых интегральных микросхем, которые содержат только один тип вентилей на микросхему.

Полный сумматор также может быть построен из двух полусумматоров путем подключения и ко входу одного полусумматора, затем взятия его суммирующего выхода в качестве одного из входов для второго полусумматора и в качестве его другого входа, и, наконец, переносящие выходы из двух полусумматоров подключаются к вентилю ИЛИ. Сумма-выход из второго полусумматора является окончательным суммарным выходом ( ) полного сумматора, а выход из вентиля ИЛИ является окончательным переносящим выходом ( ). Критический путь полного сумматора проходит через оба вентиля XOR и заканчивается на бите суммы . Предполагая, что для завершения вентиля XOR требуется 1 задержка, задержка, налагаемая критическим путем полного сумматора, равна: ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle S}$ ${\displaystyle C_{in}}$ ${\displaystyle S}$ ${\displaystyle C_{out}}$ ${\displaystyle S}$

${\displaystyle T_{\text{FA}}=2\cdot T_{\text{XOR}}=2D}$

Критический путь переноса проходит через один вентиль XOR в сумматоре и через 2 вентиля (AND и OR) в блоке переноса, и поэтому, если для завершения вентилей AND или OR требуется 1 задержка, то задержка составит:

${\displaystyle T_{\text{c}}=T_{\text{XOR}}+T_{\text{AND}}+T_{\text{OR}}=D+D+D=3D}$

Таблица истинности для полного сумматора:

Инвертирование всех входов полного сумматора также инвертирует все его выходы, что может быть использовано при проектировании быстрых сумматоров с непрерывным переносом, поскольку нет необходимости инвертировать перенос. ^[5]

Различные схемы цифровой логики полного сумматора:

• 
  Полный сумматор в действии.
• 
  Схема полного сумматора, реализованная с двумя вентилями XOR , двумя вентилями AND и одним вентилем OR .
• 
  Схема полного сумматора, реализованная с девятью вентилями NAND .
• 
  Схема полного сумматора, реализованная с девятью вентилями ИЛИ-НЕ .
• 
  Полный сумматор с инвертированными выходами с однотранзисторной задержкой распространения переноса в КМОП ^[5]
• 
  Схематическое обозначение 1-битного полного сумматора с C _in и C _out, нарисованными по бокам блока, чтобы подчеркнуть их использование в многобитном сумматоре

Сумматоры, поддерживающие несколько бит

Сумматор с непрерывным переносом

Показан 4-битный сумматор с логической структурной схемой

Десятичный 4-разрядный сумматор с последовательным переносом. FA = полный сумматор, HA = полусумматор.

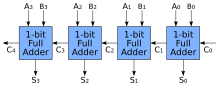
Можно создать логическую схему, используя несколько полных сумматоров для сложения N -битных чисел. Каждый полный сумматор вводит , который является предыдущего сумматора. Этот тип сумматора называется сумматором с непрерывным переносом (RCA), поскольку каждый бит переноса «переносится» на следующий полный сумматор. Первый (и только первый) полный сумматор может быть заменен полусумматором (при условии, что ). ${\displaystyle C_{in}}$ ${\displaystyle C_{out}}$ ${\displaystyle C_{in}=0}$

Схема сумматора с непрерывным переносом проста, что позволяет сократить время проектирования; однако сумматор с непрерывным переносом относительно медленный, поскольку каждый полный сумматор должен ждать вычисления бита переноса из предыдущего полного сумматора. Задержку вентиля можно легко вычислить, проверив схему полного сумматора. Каждому полному сумматору требуется три уровня логики. В 32-битном сумматоре с непрерывным переносом имеется 32 полных сумматора, поэтому задержка критического пути (наихудший случай) составляет 3 (от входа до переноса в первом сумматоре) + 31 × 2 (для распространения переноса в последних сумматорах) = 65 задержек вентиля. ^[6] Общее уравнение для наихудшей задержки для n -битного сумматора с непрерывным переносом, учитывающее как сумму, так и биты переноса, выглядит следующим образом:

${\displaystyle T_{\text{CRA}}(n)=T_{\text{HA}}+(n-1)\cdot T_{\text{c}}+T_{\text{s}}=}$ ${\displaystyle T_{\text{FA}}+(n-1)\cdot T_{c}=}$ ${\displaystyle 3D+(n-1)\cdot 2D=(2n+1)\cdot D}$

Конструкция с чередующимися полярностями переноса и оптимизированными вентилями И-ИЛИ-инвертирования может быть примерно в два раза быстрее. ^{[7] [5]}

Сумматор с переносом и просмотром вперед (Вайнбергер и Смит, 1958)

4-битный сумматор с опережающим переносом

64-битный сумматор с опережающим переносом

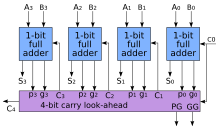
Чтобы сократить время вычислений, Вайнбергер и Смит изобрели более быстрый способ сложения двух двоичных чисел с помощью сумматоров с предпросмотром переноса (CLA). ^[8] Они ввели два сигнала ( и ) для каждой позиции бита, в зависимости от того, распространяется ли перенос из менее значимой позиции бита (по крайней мере один вход равен 1), генерируется в этой позиции бита (оба входа равны 1) или уничтожается в этой позиции бита (оба входа равны 0). В большинстве случаев является просто выходом суммы полусумматора и является выходом переноса того же сумматора. После генерации и создаются переносы для каждой позиции бита. ${\displaystyle P}$ ${\displaystyle G}$ ${\displaystyle P}$ ${\displaystyle G}$ ${\displaystyle P}$ ${\displaystyle G}$

Простым выводом CLA-рекуррентности Вайнбергера-Смита являются: сумматор Брента-Кунга (BKA) ^[9] и сумматор Когге-Стоуна (KSA). ^{[10] [11]} Это было показано в статье Оклобджии и Зейделя в журнале IEEE Journal of Solid-State Circutis. ^[12]

Некоторые другие архитектуры многоразрядных сумматоров разбивают сумматор на блоки. Можно изменять длину этих блоков в зависимости от задержки распространения цепей для оптимизации времени вычислений. Эти блочные сумматоры включают сумматор с пропуском переноса (или обходом переноса) , который определяет значения и для каждого блока, а не для каждого бита, и сумматор с выбором переноса, который предварительно генерирует сумму и значения переноса для любого возможного входа переноса (0 или 1) в блок, используя мультиплексоры для выбора соответствующего результата, когда известен бит переноса. ${\displaystyle P}$ ${\displaystyle G}$

Объединяя несколько сумматоров с переносом и просмотром вперед, можно создавать еще большие сумматоры. Это можно использовать на нескольких уровнях для создания еще больших сумматоров. Например, следующий сумматор — это 64-битный сумматор, который использует четыре 16-битных CLA с двумя уровнями блоков переноса с просмотром вперед .

Другие конструкции сумматоров включают сумматор с выбором переноса , сумматор условной суммы , сумматор с пропуском переноса и сумматор с полным переносом.

Суммирующие устройства с функцией сохранения переноса

Если схема сложения должна вычислить сумму трех или более чисел, может быть выгодно не распространять результат переноса. Вместо этого используются трехвходовые сумматоры, генерирующие два результата: сумму и перенос. Сумма и перенос могут быть поданы на два входа последующего сумматора из трех чисел без необходимости ожидания распространения сигнала переноса. Однако после всех стадий сложения должен использоваться обычный сумматор (такой как ripple-carry или lookahead) для объединения окончательной суммы и результатов переноса.

3:2 компрессоры

Полный сумматор можно рассматривать как компрессор с потерями 3:2 : он суммирует три однобитных входа и возвращает результат в виде одного двухбитного числа; то есть он отображает 8 входных значений в 4 выходных значения. (термин «компрессор» вместо «счетчика» был введен в ^[13] ). Так, например, двоичный вход 101 дает на выходе 1 + 0 + 1 = 10 (десятичное число 2). Перенос представляет собой бит один результата, в то время как сумма представляет собой бит ноль. Аналогично, полусумматор можно использовать как компрессор с потерями 2:2 , сжимая четыре возможных входа в три возможных выхода.

Такие компрессоры можно использовать для ускорения суммирования трех или более слагаемых. Если количество слагаемых равно ровно трем, то схема известна как сумматор с сохранением переноса . Если количество слагаемых равно четырем или более, необходимо более одного слоя компрессоров, и существуют различные возможные конструкции схемы: наиболее распространенными являются деревья Дадда и Уоллеса . Этот тип схемы чаще всего используется в схемах умножителей , поэтому эти схемы также известны как умножители Дадда и Уоллеса.

Квантовые сумматоры

Квантовый полный сумматор, использующий вентили Тоффоли и CNOT . Вентиль CNOT, который на этом рисунке обведен пунктирным квадратом, можно опустить, если не требуется невычисление для восстановления выхода B.

Используя только квантовые логические вентили Тоффоли и CNOT , можно создавать квантовые полные и полусумматоры. ^{[14] [15] [16]} Те же схемы могут быть реализованы и в классических обратимых вычислениях , поскольку и CNOT, и Тоффоли также являются классическими логическими вентилями .

Поскольку квантовое преобразование Фурье имеет низкую сложность схемы , его можно эффективно использовать и для сложения чисел. ^{[17] [18] [19]}

Аналоговые сумматоры

Как и в двоичных сумматорах, объединение двух входных токов эффективно складывает эти токи. В рамках ограничений оборудования недвоичные сигналы (т. е. с основанием выше 2) могут быть сложены вместе для вычисления суммы. Также известный как «суммирующий усилитель», ^[20] этот метод может использоваться для уменьшения количества транзисторов в схеме сложения.

Смотрите также

• Двоичный множитель
• Вычитатель
• Электронный микшер — для добавления аналоговых сигналов

Ссылки

1. Сингх, Аджай Кумар (2010). Цифровое проектирование СБИС. Prentice Hall India. стр. 321. ISBN 9788120341876– через Google Книги.
2. Ланкастер, Джеффри А. (2004). Проектирование и разработка программного обеспечения Excel HSC. Pascal Press. стр. 180. ISBN 978-1-74125175-3.
3. Мано, М. Моррис (1979). Цифровая логика и проектирование компьютеров . Prentice-Hall . С. 119–123. ISBN 978-0-13-214510-7.
4. Teja, Ravi (2021-04-15), Схемы полусумматора и полного сумматора , получено 2021-07-27
5. Фишер, П. "Einfache Schaltungsblöcke" (PDF) . Университет Гейдельберга. Архивировано из оригинала (PDF) 5 сентября 2021 г. Проверено 05 сентября 2021 г.
6. Satpathy, Pinaki (2016). Разработка и реализация сумматора с выбором переноса с использованием T-Spice. Anchor Academic Publishing. стр. 22. ISBN 978-3-96067058-2.
7. Берджесс, Нил (2011). Быстрые сумматоры с последовательным переносом в КМОП-СБИС со стандартными ячейками. 20-й симпозиум IEEE по компьютерной арифметике . С. 103–111.
8. Вайнбергер и Дж. Л. Смит, «Логика для высокоскоростного сложения», Национальное бюро стандартов, циркуляр 591, стр. 3-12, 1958.
9. Брент, Ричард Пирс ; Кунг, Сян Те (март 1982 г.). «Регулярная компоновка параллельных сумматоров». IEEE Transactions on Computers . C-31 (3): 260–264. doi :10.1109/TC.1982.1675982. ISSN  0018-9340. S2CID  17348212. Архивировано из оригинала 24 сентября 2017 г.
10. Когге, Питер Майкл ; Стоун, Гарольд С. (август 1973 г.). «Параллельный алгоритм эффективного решения общего класса рекуррентных уравнений». IEEE Transactions on Computers . C-22 (8): 786–793. doi :10.1109/TC.1973.5009159. S2CID  206619926.
11. Рейндерс, Неле; Дехаене, Вим (2015). Проектирование энергоэффективных цифровых схем с ультранизким напряжением . Аналоговые схемы и обработка сигналов (1-е изд.). Хам, Швейцария: Springer International Publishing AG Switzerland . doi : 10.1007/978-3-319-16136-5. ISBN 978-3-319-16135-8. ISSN  1872-082X. LCCN  2015935431.
12. BR Zeydel, D. Baran, VG Oklobdzija, «Энергоэффективное проектирование высокопроизводительных сумматоров VLSI», IEEE Journal of Solid-State Circuits, том 45, выпуск 6. Июнь 2010 г.
13. В. Г. Оклобджия и Д. Виллегер, «Улучшение конструкции умножителя путем использования улучшенного дерева сжатия столбцов и оптимизированного конечного сумматора в технологии КМОП», IEEE Transactions on VLSI Systems, т. 3, № 2, июнь 1995 г., 10 страниц.
14. Фейнман, Ричард П. (1986). «Квантовые механические компьютеры». Основы физики . 16 (6). Springer Science and Business Media LLC: 507–531. Bibcode : 1986FoPh...16..507F. doi : 10.1007/bf01886518. ISSN  0015-9018. S2CID  122076550.
15. "Пример кода: Квантовый полный сумматор". QuTech (Делфтский технический университет (TU Delft) и Нидерландская организация прикладных научных исследований (TNO)).
16. Дибьенду Чаттерджи, Ариджит Рой (2015). "Квантовая схема полусумматора на основе трансмонов". Progress of Theoretical and Experimental Physics . 2015 (9): 093A02. Bibcode : 2015PTEP.2015i3A02C. doi : 10.1093/ptep/ptv122 .
17. Дрейпер, Томас Г. (7 августа 2000 г.). «Сложение на квантовом компьютере». arXiv : quant-ph/0008033 .
18. Руис-Перес, Лидия; Хуан Карлос, Гарсия-Эскартин (2 мая 2017 г.). «Квантовая арифметика с квантовым преобразованием Фурье». Квантовая обработка информации . 16 (6): 152. arXiv : 1411.5949v2 . Bibcode : 2017QuIP...16..152R. doi : 10.1007/s11128-017-1603-1. S2CID  10948948.
19. Шахин, Энгин (2020). «Квантовые арифметические операции, основанные на квантовом преобразовании Фурье над знаковыми целыми числами». Международный журнал квантовой информации . 18 (6): 2050035. arXiv : 2005.00443v3 . doi : 10.1142/s0219749920500355. ISSN  1793-6918.
20. "Суммирующий усилитель — это сумматор напряжения на операционном усилителе". 22 августа 2013 г.

Дальнейшее чтение

• Liu, Tso-Kai; Hohulin, Keith R.; Shiau, Lih-Er; Muroga, Saburo (январь 1974). «Оптимальные однобитовые полные сумматоры с различными типами вентилей». IEEE Transactions on Computers . C-23 (1). Bell Laboratories: IEEE : 63–70. doi :10.1109/TC.1974.223778. ISSN  0018-9340. S2CID  7746693.
• Lai, Hung Chi; Muroga, Saburo (сентябрь 1979). «Минимальные двоичные параллельные сумматоры с вентилями NOR (NAND)». IEEE Transactions on Computers . C-28 (9). IEEE : 648–659. doi :10.1109/TC.1979.1675433. S2CID  23026844.
• Мид, Карвер; Конвей, Линн (1980) [декабрь 1979]. Введение в системы СБИС (1-е изд.). Рединг, Массачусетс, США: Addison-Wesley . Bibcode :1980aw...book.....M. ISBN 978-0-20104358-7. Получено 2018-05-12 .
• Davio, Marc; Dechamps, Jean-Pierre; Thayse, André (1983). Цифровые системы с реализацией алгоритма (1-е изд.). Philips Research Laboratory , Брюссель, Бельгия: John Wiley & Sons , Wiley-Interscience Publication. ISBN 978-0-471-10413-1. LCCN  82-2710.
• Гослинг, Джон (январь 1971 г.). «Обзор методов высокоскоростного сложения». Proc. IEE . 188 (1): 29–35. doi :10.1049/piee.1971.0004.

Внешние ссылки

• Медиафайлы по теме Сумматоры (цифровые схемы) на Wikimedia Commons
• 8-битный полный сумматор и вычитатель, демонстрация интерактивного полного сумматора, созданного на JavaScript исключительно в учебных целях.
• Интерактивные демонстрации половинных и полных сумматоров в HTML5
• Ширрифф, Кен (ноябрь 2020 г.). «Обратная разработка схемы переноса-просмотра в процессоре Intel 8008».