Функция действительной переменной

Математическая функция

В математическом анализе и приложениях в геометрии , прикладной математике , инженерии и естественных науках функция действительной переменной — это функция , областью определения которой являются действительные числа или подмножество , содержащее интервал положительной длины. Большинство действительных функций, которые рассматриваются и изучаются, дифференцируемы в некотором интервале. Наиболее широко рассматриваемыми такими функциями являются действительные функции , которые являются действительными функциями действительной переменной, то есть функциями действительной переменной, областью определения которых является множество действительных чисел. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

Тем не менее, область значений функции действительной переменной может быть любым множеством. Однако часто предполагается, что она имеет структуру -векторного пространства над действительными числами. То есть область значений может быть евклидовым пространством , координатным вектором , множеством матриц действительных чисел заданного размера или -алгеброй , такой как комплексные числа или кватернионы . Структура -векторного пространства области значений индуцирует структуру -векторного пространства на функциях. Если область значений имеет структуру -алгебры , то же самое верно и для функций. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

Изображение функции действительной переменной — кривая в области значений. В этом контексте функция, определяющая кривую , называется параметрическим уравнением кривой.

Когда область значений функции действительной переменной является конечномерным векторным пространством , функцию можно рассматривать как последовательность действительных функций. Это часто используется в приложениях.

Действительная функция

График действительной функции

Действительная функция — это функция из подмножества в , где обозначает , как обычно, множество действительных чисел . То есть область определения действительной функции является подмножеством , а ее область определения — Обычно предполагается, что область определения содержит интервал положительной длины. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} ,}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} .}$

Простые примеры

Для многих часто используемых действительных функций область определения — это весь набор действительных чисел, а функция непрерывна и дифференцируема в каждой точке области определения. Говорят, что эти функции определены, непрерывны и дифференцируемы всюду. Это случай:

• Все полиномиальные функции , включая постоянные функции и линейные функции
• Функции синуса и косинуса
• Экспоненциальная функция

Некоторые функции определены везде, но не непрерывны в некоторых точках. Например

• Ступенчатая функция Хевисайда определена всюду, но не непрерывна в нуле.

Некоторые функции определены и непрерывны всюду, но не всюду дифференцируемы. Например

• Абсолютное значение определено и непрерывно всюду и дифференцируемо всюду, за исключением нуля.
• Кубический корень определен и непрерывен всюду и дифференцируем всюду, за исключением нуля.

Многие общие функции не определены везде, но непрерывны и дифференцируемы везде, где они определены. Например:

• Рациональная функция представляет собой частное двух полиномиальных функций и не определяется в нулях знаменателя.
• Функция тангенса не определена для случаев, когда k — любое целое число. ${\displaystyle {\frac {\pi }{2}}+k\pi ,}$
• Функция логарифма определена только для положительных значений переменной.

Некоторые функции непрерывны во всей своей области определения и не дифференцируемы в некоторых точках. Это случай:

• Квадратный корень определен только для неотрицательных значений переменной и не дифференцируем в точке 0 (он дифференцируем для всех положительных значений переменной).

Общее определение

Действительная функция действительной переменной — это функция , которая принимает в качестве входных данных действительное число , обычно представленное переменной x , для получения другого действительного числа, значения функции, обычно обозначаемого f ( x ). Для простоты в этой статье действительная функция действительной переменной будет называться просто функцией . Чтобы избежать какой-либо двусмысленности, другие типы функций, которые могут возникнуть, будут явно указаны.

Некоторые функции определены для всех действительных значений переменных (говорят, что они определены везде), но некоторые другие функции определены только если значение переменной берется в подмножестве X , области определения функции, которая всегда должна содержать интервал положительной длины. Другими словами, действительнозначная функция действительной переменной — это функция ${\displaystyle \mathbb {R} }$

${\displaystyle f:X\to \mathbb {R} }$

такой, что его область X является подмножеством , содержащим интервал положительной длины. ${\displaystyle \mathbb {R} }$

Простым примером функции с одной переменной может быть:

${\displaystyle f:X\to \mathbb {R} }$

${\displaystyle X=\{x\in \mathbb {R} \,:\,x\geq 0\}}$

${\displaystyle f(x)={\sqrt {x}}}$

что является квадратным корнем из x .

Изображение

Образ функции — это множество всех значений f , когда переменная x пробегает всю область определения f . Для непрерывной (см. определение ниже) действительной функции со связной областью определения образ — это либо интервал, либо одно значение. В последнем случае функция является постоянной функцией . ${\displaystyle f(x)}$

Прообразом данного действительного числа y является множество решений уравнения y = f ( x ) .

Домен

Область определения функции нескольких действительных переменных — это подмножество , которое иногда определяется явно. Фактически, если ограничить область определения X функции f подмножеством Y ⊂ X , то формально получится другая функция — ограничение f на Y , которое обозначается f _{| Y} . На практике часто не вредно отождествлять f и f _{| Y} , а индекс _{| Y} опускать . ${\displaystyle \mathbb {R} }$

Наоборот, иногда возможно естественным образом расширить область определения данной функции, например, с помощью непрерывности или аналитического продолжения . Это означает, что не стоит явно определять область определения функции действительной переменной.

Алгебраическая структура

Арифметические операции можно применять к функциям следующим образом:

• Для каждого действительного числа r постоянная функция определена всюду. ${\displaystyle (x)\mapsto r}$
• Для каждого действительного числа r и каждой функции f функция имеет ту же область определения, что и f (или определена везде, если r = 0). ${\displaystyle rf:(x)\mapsto rf(x)}$
• Если f и g — две функции соответствующих областей X и Y , такие, что X ∩ Y содержит открытое подмножество , то и — функции, имеющие область определения, содержащую X ∩ Y . ${\displaystyle \mathbb {R} }$ ${\displaystyle f+g:(x)\mapsto f(x)+g(x)}$ ${\displaystyle f\,g:(x)\mapsto f(x)\,g(x)}$

Отсюда следует, что функции n переменных, которые всюду определены, и функции n переменных, которые определены в некоторой окрестности данной точки, образуют коммутативные алгебры над действительными числами ( -алгебры). ${\displaystyle \mathbb {R} }$

Аналогично можно определить , что является функцией только в том случае, если множество точек ( x ) в области определения f такое, что f ( x ) ≠ 0, содержит открытое подмножество . Это ограничение подразумевает, что две указанные выше алгебры не являются полями . ${\displaystyle 1/f:(x)\mapsto 1/f(x),}$ ${\displaystyle \mathbb {R} }$

Непрерывность и предел

Предел действительной функции действительной переменной.

До второй половины 19 века математики рассматривали только непрерывные функции . В то время понятие непрерывности было разработано для функций одной или нескольких действительных переменных задолго до формального определения топологического пространства и непрерывного отображения между топологическими пространствами. Поскольку непрерывные функции действительной переменной повсеместно встречаются в математике, стоит определить это понятие без ссылки на общее понятие непрерывных отображений между топологическими пространствами.

Для определения непрерывности полезно рассмотреть функцию расстояния , которая является всюду определенной функцией двух действительных переменных: ${\displaystyle \mathbb {R} }$ ${\displaystyle d(x,y)=|x-y|}$

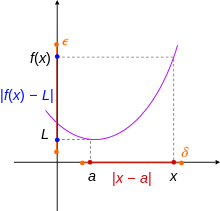
Функция f непрерывна в точке , которая находится внутри ее области определения, если для каждого положительного действительного числа ε существует положительное действительное число φ такое, что для всех таких, что Другими словами, φ можно выбрать достаточно малым, чтобы изображение интервала радиуса φ с центром в точке, отображаемое функцией f , содержалось в интервале длины 2 ε с центром в точке Функция непрерывна, если она непрерывна в каждой точке своей области определения. ${\displaystyle a}$ ${\displaystyle |f(x)-f(a)|<\varepsilon }$ ${\displaystyle x}$ ${\displaystyle d(x,a)<\varphi .}$ ${\displaystyle a}$ ${\displaystyle f(a).}$

Предел действительной функции действительной переменной определяется следующим образом. ^[1] Пусть a — точка топологического замыкания области определения X функции f . Функция f имеет предел L , когда x стремится к a , обозначаемый

${\displaystyle L=\lim _{x\to a}f(x),}$

если выполняется следующее условие: для каждого положительного действительного числа ε > 0 существует положительное действительное число δ > 0 такое, что

${\displaystyle |f(x)-L|<\varepsilon }$

для всех x в области определения, таких что

${\displaystyle d(x,a)<\delta .}$

Если предел существует, то он единственный. Если a находится внутри области, предел существует тогда и только тогда, когда функция непрерывна в точке a . В этом случае мы имеем

${\displaystyle f(a)=\lim _{x\to a}f(x).}$

Когда a находится на границе области определения f , и если f имеет предел в точке a , последняя формула позволяет «расширить по непрерывности» область определения f до a .

Исчисление

Можно собрать ряд функций каждой действительной переменной, скажем

${\displaystyle y_{1}=f_{1}(x)\,,\quad y_{2}=f_{2}(x)\,,\ldots ,y_{n}=f_{n}(x)}$

в вектор, параметризованный x :

${\displaystyle \mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})=[f_{1}(x),f_{2}(x),\ldots ,f_{n}(x)]}$

Производная вектора y — это производные вектора f _i ( x ) для i = 1, 2, ..., n :

${\displaystyle {\frac {d\mathbf {y} }{dx}}=\left({\frac {dy_{1}}{dx}},{\frac {dy_{2}}{dx}},\ldots ,{\frac {dy_{n}}{dx}}\right)}$

Можно также выполнить линейные интегралы вдоль пространственной кривой , параметризованной x , с вектором положения r = r ( x ), путем интегрирования по переменной x :

${\displaystyle \int _{a}^{b}\mathbf {y} (x)\cdot d\mathbf {r} =\int _{a}^{b}\mathbf {y} (x)\cdot {\frac {d\mathbf {r} (x)}{dx}}dx}$

где · — скалярное произведение , а x = a и x = b — начальная и конечная точки кривой.

Теоремы

С помощью определений интегрирования и производных можно сформулировать ключевые теоремы, включая фундаментальную теорему исчисления , интегрирование по частям и теорему Тейлора . Оценку смеси интегралов и производных можно выполнить, используя дифференцирование теоремы под знаком интеграла .

Неявные функции

Действительная неявная функция действительной переменной не записывается в виде " y = f ( x )". Вместо этого отображение происходит из пространства ² в нулевой элемент в (просто обычный ноль 0): ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

${\displaystyle \phi :\mathbb {R} ^{2}\to \{0\}}$

и

${\displaystyle \phi (x,y)=0}$

— это уравнение в переменных. Неявные функции — это более общий способ представления функций, поскольку если:

${\displaystyle y=f(x)}$

то мы всегда можем определить:

${\displaystyle \phi (x,y)=y-f(x)=0}$

Однако обратное не всегда возможно, т.е. не все неявные функции имеют вид этого уравнения.

Одномерные пространственные кривые в R {\displaystyle \mathbb {R} } н

Пространственная кривая в 3d. Вектор положения r параметризуется скаляром t . При r = a красная линия является касательной к кривой, а синяя плоскость является нормалью к кривой.

Формулировка

Даны функции r ₁ = r ₁ ( t ) , r ₂ = r ₂ ( t ) , ..., r _n = r _n ( t ) все от общей переменной t , так что:

${\displaystyle {\begin{aligned}r_{1}:\mathbb {R} \rightarrow \mathbb {R} &\quad r_{2}:\mathbb {R} \rightarrow \mathbb {R} &\cdots &\quad r_{n}:\mathbb {R} \rightarrow \mathbb {R} \\r_{1}=r_{1}(t)&\quad r_{2}=r_{2}(t)&\cdots &\quad r_{n}=r_{n}(t)\\\end{aligned}}}$

или вместе взятые:

${\displaystyle \mathbf {r} :\mathbb {R} \rightarrow \mathbb {R} ^{n}\,,\quad \mathbf {r} =\mathbf {r} (t)}$

затем параметризованный n -кортеж,

${\displaystyle \mathbf {r} (t)=[r_{1}(t),r_{2}(t),\ldots ,r_{n}(t)]}$

описывает одномерную пространственную кривую .

Касательная линия к кривой

В точке r ( t = c ) = a = ( a ₁ , a ₂ , ..., an ) для некоторой константы t = c уравнения одномерной касательной к кривой в этой точке задаются через обычные производные r ₁ ( t ), r ₂ ( _t ), ..., r n ₍ t ) и r по t :

${\displaystyle {\frac {r_{1}(t)-a_{1}}{dr_{1}(t)/dt}}={\frac {r_{2}(t)-a_{2}}{dr_{2}(t)/dt}}=\cdots ={\frac {r_{n}(t)-a_{n}}{dr_{n}(t)/dt}}}$

Нормальная плоскость к кривой

Уравнение n -мерной гиперплоскости, нормальной к касательной в точке r = a , имеет вид:

${\displaystyle (p_{1}-a_{1}){\frac {dr_{1}(t)}{dt}}+(p_{2}-a_{2}){\frac {dr_{2}(t)}{dt}}+\cdots +(p_{n}-a_{n}){\frac {dr_{n}(t)}{dt}}=0}$

или в терминах скалярного произведения :

${\displaystyle (\mathbf {p} -\mathbf {a} )\cdot {\frac {d\mathbf {r} (t)}{dt}}=0}$

где p = ( p ₁ , p ₂ , ..., p _n ) — точки на плоскости , а не на пространственной кривой.

Отношение к кинематике

Кинематические величины классической частицы: масса m , положение r , скорость v , ускорение a .

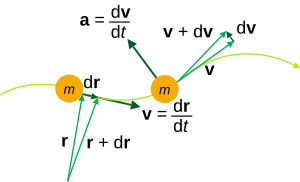
Физическая и геометрическая интерпретация d r ( t )/ dt - это " скорость " точечной частицы, движущейся по пути r ( t ), рассматривая r как пространственные координаты вектора положения , параметризованные временем t , и является вектором, касательным к пространственной кривой для всех t в мгновенном направлении движения. При t = c пространственная кривая имеет касательный вектор d r ( t )/ dt | _{t = c} , а гиперплоскость, нормальная к пространственной кривой при t = c , также нормальна к касательной при t = c . Любой вектор в этой плоскости ( p − a ) должен быть нормален к d r ( t )/ dt | _{t = c} .

Аналогично, d ² r ( t )/ dt ² является « ускорением » частицы и представляет собой вектор, нормальный к кривой, направленный вдоль радиуса кривизны .

Матричнозначные функции

Матрица также может быть функцией одной переменной. Например, матрица вращения в 2d:

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}}$

является матричной функцией угла поворота относительно начала координат. Аналогично, в специальной теории относительности матрица преобразования Лоренца для чистого усиления (без вращений):

${\displaystyle \Lambda (\beta )={\begin{bmatrix}{\frac {1}{\sqrt {1-\beta ^{2}}}}&-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&0&0\\-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&{\frac {1}{\sqrt {1-\beta ^{2}}}}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}}$

является функцией параметра усиления β = v / c , где v — относительная скорость между системами отсчета (непрерывная переменная), а c — скорость света , постоянная.

Банахово и Гильбертово пространства и квантовая механика

Обобщая предыдущий раздел, вывод функции действительной переменной может также лежать в банаховом пространстве или гильбертовом пространстве . В этих пространствах определены деление, умножение и пределы, поэтому такие понятия, как производная и интеграл, по-прежнему применимы. Это происходит особенно часто в квантовой механике, где берется производная кет-функции или оператора . Это происходит, например, в общем зависящем от времени уравнении Шредингера :

${\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi ={\hat {H}}\Psi }$

где берется производная волновой функции, которая может быть элементом нескольких различных гильбертовых пространств.

Комплекснозначная функция действительной переменной

Комплекснозначную функцию действительной переменной можно определить, ослабив в определении действительнозначных функций ограничение области определения действительными числами и допустив комплексные значения.

Если f ( x ) является такой комплекснозначной функцией, ее можно разложить следующим образом:

ж ( Икс ) знак равно г ( Икс ) + яч ( Икс ) ,

где g и h — действительные функции. Другими словами, изучение комплексных функций легко сводится к изучению пар действительных функций.

Мощность множеств функций действительной переменной

Мощность множества вещественных функций вещественной переменной, , равна , что строго больше мощности континуума ( т.е. множества всех вещественных чисел). Этот факт легко проверяется с помощью кардинальной арифметики: ${\displaystyle \mathbb {R} ^{\mathbb {R} }=\{f:\mathbb {R} \to \mathbb {R} \}}$ ${\displaystyle \beth _{2}=2^{\mathfrak {c}}}$

$${\displaystyle \mathrm {card} (\mathbb {R} ^{\mathbb {R} })=\mathrm {card} (\mathbb {R} )^{\mathrm {card} (\mathbb {R} )}={\mathfrak {c}}^{\mathfrak {c}}=(2^{\aleph _{0}})^{\mathfrak {c}}=2^{\aleph _{0}\cdot {\mathfrak {c}}}=2^{\mathfrak {c}}.}$$

Более того, если множество такое, что , то мощность множества также равна , поскольку ${\displaystyle X}$ ${\displaystyle 2\leq \mathrm {card} (X)\leq {\mathfrak {c}}}$ ${\displaystyle X^{\mathbb {R} }=\{f:\mathbb {R} \to X\}}$ ${\displaystyle 2^{\mathfrak {c}}}$

$${\displaystyle 2^{\mathfrak {c}}=\mathrm {card} (2^{\mathbb {R} })\leq \mathrm {card} (X^{\mathbb {R} })\leq \mathrm {card} (\mathbb {R} ^{\mathbb {R} })=2^{\mathfrak {c}}.}$$

Однако множество непрерывных функций имеет строго меньшую мощность, мощность континуума, . Это следует из того факта, что непрерывная функция полностью определяется своим значением на плотном подмножестве своей области определения. ^[2] Таким образом, мощность множества непрерывных вещественных функций на вещественных числах не больше мощности множества вещественных функций рациональной переменной. По кардинальной арифметике: ${\displaystyle C^{0}(\mathbb {R} )=\{f:\mathbb {R} \to \mathbb {R} :f\ \mathrm {continuous} \}}$ ${\displaystyle {\mathfrak {c}}}$

$${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))\leq \mathrm {card} (\mathbb {R} ^{\mathbb {Q} })=(2^{\aleph _{0}})^{\aleph _{0}}=2^{\aleph _{0}\cdot \aleph _{0}}=2^{\aleph _{0}}={\mathfrak {c}}.}$$

С другой стороны, поскольку существует четкая биекция между и множеством постоянных функций , которое образует подмножество , также должно выполняться. Следовательно, . ${\displaystyle \mathbb {R} }$ ${\displaystyle \{f:\mathbb {R} \to \mathbb {R} :f(x)\equiv x_{0}\}}$ ${\displaystyle C^{0}(\mathbb {R} )}$ ${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))\geq {\mathfrak {c}}}$ ${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))={\mathfrak {c}}}$

Смотрите также

• Реальный анализ
• Функция нескольких действительных переменных
• Комплексный анализ
• Функция нескольких комплексных переменных

Ссылки

1. Р. Курант. Дифференциальное и интегральное исчисление . Т. 2. Библиотека Wiley Classics. С. 46–47. ISBN 0-471-60840-8.
2. Рудин, В. (1976). Принципы математического анализа . Нью-Йорк: McGraw-Hill. С. 98–99. ISBN 0-07-054235X.

• Ф. Айрес, Э. Мендельсон (2009). Исчисление . Серия набросков Шаума (5-е изд.). McGraw Hill. ISBN 978-0-07-150861-2.
• R. Wrede, MR Spiegel (2010). Расширенный исчисление . Серия набросков Шаума (3-е изд.). McGraw Hill. ISBN 978-0-07-162366-7.
• Н. Бурбаки (2004). Функции действительной переменной: Элементарная теория. Springer. ISBN 354-065-340-6.

Внешние ссылки

• Многовариантное исчисление
• LA Talman (2007) Дифференцируемость для многомерных функций