Волновой пакет

Короткий «всплеск» или «огибающая» ограниченного волнового воздействия, распространяющегося как единое целое.

Зацикленная анимация волнового пакета, распространяющегося без дисперсии.

В физике волновой пакет (также известный как волновой ряд или группа волн ) представляет собой короткий всплеск локализованного волнового действия, который распространяется как единое целое, очерченное огибающей . Волновой пакет может быть проанализирован или синтезирован из потенциально бесконечного набора составляющих синусоидальных волн с разными волновыми числами , с такими фазами и амплитудами, что они конструктивно интерферируют только в небольшой области пространства и деструктивно в других местах. ^[1] Любой сигнал ограниченной ширины во времени или пространстве требует множества частотных составляющих вокруг центральной частоты в пределах полосы пропускания , обратно пропорциональной этой ширине; даже функция Гаусса считается волновым пакетом, потому что ее преобразование Фурье представляет собой «пакет» волн частот, сгруппированных вокруг центральной частоты. ^[2] Каждая составляющая волновая функция и, следовательно, волновой пакет являются решениями волнового уравнения . В зависимости от волнового уравнения профиль волнового пакета может оставаться постоянным (отсутствие дисперсии) или может меняться (дисперсия) при распространении.

Историческая справка

Идеи, связанные с волновыми пакетами – модуляцией , несущими волнами , фазовой скоростью и групповой скоростью – датируются серединой 1800-х годов. Идея групповой скорости, отличной от фазовой скорости волны, была впервые предложена У. Р. Гамильтоном в 1839 году, а первое полное изложение было сделано Рэлеем в его «Теории звука» в 1877 году. ^[3]

Эрвин Шредингер представил идею волновых пакетов сразу после публикации своего знаменитого волнового уравнения . ^[4] Он решил свое волновое уравнение для квантового гармонического осциллятора , ввел принцип суперпозиции и использовал его, чтобы показать, что компактное состояние может сохраняться. Хотя эта работа и привела к созданию важной концепции когерентных состояний , концепция волнового пакета не сохранилась. Через год после статьи Шредингера Вернер Гейзенберг опубликовал свою статью о принципе неопределенности , показав при этом, что результаты Шредингера применимы только к квантовым гармоническим осцилляторам , а не, например, к кулоновскому потенциалу , характерному для атомов. ^{[4] : 829}

В следующем, 1927 году, Чарльз Гальтон Дарвин исследовал уравнение Шредингера для несвязанного электрона в свободном пространстве, предположив, что исходный волновой пакет имеет гауссовую форму. ^[5] Дарвин показал, что через некоторое время положение пакета, движущегося со скоростью, будет ${\displaystyle t}$ ${\displaystyle x}$ ${\displaystyle v}$

$${\displaystyle x_{0}+vt\pm {\sqrt {\sigma ^{2}+(ht/2\pi \sigma m)^{2}}}}$$

где – неопределенность в начальном положении. ${\displaystyle \sigma }$

Позже, в 1927 году, Пауль Эренфест показал, что время распространения волнового пакета материи шириной и массой в 2 раза составляет Поскольку он настолько мал, волновые пакеты масштаба макроскопических объектов с большой шириной и массой удваиваются только в космических масштабах времени. ^{[4] : 830} ${\displaystyle T}$ ${\displaystyle \Delta x}$ ${\displaystyle m}$ ${\textstyle T\approx \Delta x{\sqrt {m/\hbar }}}$ ${\displaystyle \hbar }$

Значение в квантовой механике

Квантовая механика описывает природу атомных и субатомных систем с помощью волнового уравнения Шрёдингера . Классический предел квантовой механики и многие формулировки квантового рассеяния используют волновые пакеты, образованные из различных решений этого уравнения. Профили квантовых волновых пакетов изменяются по мере распространения; они показывают дисперсию. Физики пришли к выводу, что «волновые пакеты не подходят для представления субатомных частиц». ^{[4] : 829}

Волновые пакеты и классический предел

Шрёдингер разработал волновые пакеты в надежде интерпретировать квантово-волновые решения как локально компактные волновые группы. ^[4] Такие пакеты компромиссной локализации положения для распространения импульса. В координатном представлении волны (например, в декартовой системе координат ) положение локализованной вероятности частицы задается положением пакетного решения. Чем уже пространственный волновой пакет и, следовательно, чем лучше локализовано положение волнового пакета, тем больше разброс импульса волны . Этот компромисс между спредом позиции и спредом импульса является характерной особенностью принципа неопределенности Гейзенберга.

Один из видов оптимального компромисса минимизирует произведение неопределенности позиции и неопределенности импульса . ^{[6] : 60} Если мы поместим такой пакет в покое, он останется в покое: среднее значение положения и импульса соответствует классической частице. Однако он распространяется во всех направлениях со скоростью, определяемой неопределенностью оптимального количества движения . Распространение происходит настолько быстро, что на расстоянии одного круга вокруг атома волновой пакет становится неузнаваемым. ${\displaystyle \Delta x}$ ${\displaystyle \Delta p_{x}}$ ${\displaystyle \Delta p_{x}}$

Волновые пакеты и квантовое рассеяние

Взаимодействие частиц в физике называется рассеянием ; Математика волновых пакетов играет важную роль в подходах к квантовому рассеянию . Монохроматический (одиночный импульс) источник создает трудности сходимости в моделях рассеяния. ^{[7] : 150} Задачи рассеяния также имеют классические пределы. Всякий раз, когда мишень рассеяния (например, атом) имеет размер, намного меньший, чем волновой пакет, центр волнового пакета следует классическим траекториям рассеяния. В других случаях волновой пакет искажается и рассеивается при взаимодействии с целью. ^{[8] : 295}

Основные модели поведения

Недисперсионный

Волновой пакет без дисперсии (действительная или мнимая часть)

Без дисперсии волновой пакет сохраняет свою форму по мере распространения. В качестве примера распространения без дисперсии рассмотрим волновые решения следующего волнового уравнения из классической физики:

$${\displaystyle {\partial ^{2}u \over \partial t^{2}}=c^{2}\,\nabla ^{2}u,}$$

где c — скорость распространения волны в данной среде.

Используя физическое соглашение о времени, e ^{− iωt} , волновое уравнение имеет решения в виде плоских волн .

$${\displaystyle u(\mathbf {x} ,t)=e^{i{(\mathbf {k\cdot x} }-\omega t)},}$$

где

$${\displaystyle \omega ^{2}=|\mathbf {k} |^{2}c^{2},}$$

${\displaystyle |\mathbf {k} |^{2}=k_{x}^{2}+k_{y}^{2}+k_{z}^{2}.}$

Это соотношение между ω и k должно быть справедливым, чтобы плоская волна была решением волнового уравнения. Оно называется дисперсионным соотношением .

Для упрощения рассмотрим только волны, распространяющиеся в одном измерении (распространение на три измерения не вызывает затруднений). Тогда общее решение

$${\displaystyle u(x,t)=Ae^{i(kx-\omega t)}+Be^{-i(kx+\omega t)},}$$

ω = kcнаправлении xx − ct ; x + ctнаправлении x

Волновой пакет — это локализованное возмущение, возникающее в результате суммы множества различных волновых форм . Если пакет сильно локализован, необходимо больше частот, чтобы обеспечить конструктивную суперпозицию в области локализации и деструктивную суперпозицию за ее пределами. Из основных решений в одном измерении общую форму волнового пакета можно выразить как

$${\displaystyle u(x,t)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\,\infty }A(k)~e^{i(kx-\omega (k)t)}\,dk.}$$

Как и в случае плоской волны, волновой пакет движется вправо при ω ( k ) = kc , поскольку u ( x , t ) = F ( x − ct ) , и влево при ω ( k ) = − kc , поскольку ты ( Икс , т ) знак равно F ( Икс + ct ) .

Этот фактор исходит из соглашений о преобразовании Фурье . Амплитуда A ( k ) содержит коэффициенты линейной суперпозиции плосковолновых решений. Эти коэффициенты, в свою очередь, могут быть выражены как функция u ( x , t ) , оцененная при t = 0 путем инвертирования приведенного выше соотношения преобразования Фурье: ${\displaystyle 1/{\sqrt {2\pi }}}$

$${\displaystyle A(k)={\frac {1}{\sqrt {2\pi }}}\int _{-\infty }^{\,\infty }u(x,0)~e^{-ikx}\,dx.}$$

Например, выбирая

$${\displaystyle u(x,0)=e^{-x^{2}+ik_{0}x},}$$

мы получаем

$${\displaystyle A(k)={\frac {1}{\sqrt {2}}}e^{-{\frac {(k-k_{0})^{2}}{4}}},}$$

и наконец

$${\displaystyle {\begin{aligned}u(x,t)&=e^{-(x-ct)^{2}+ik_{0}(x-ct)}\\&=e^{-(x-ct)^{2}}\left[\cos \left(2\pi {\frac {x-ct}{\lambda }}\right)+i\sin \left(2\pi {\frac {x-ct}{\lambda }}\right)\right].\end{aligned}}}$$

Недисперсионное распространение действительной или мнимой части этого волнового пакета представлено на анимации выше.

Дисперсионный

Волновой пакет с дисперсией. Обратите внимание, что волна распространяется, а ее амплитуда уменьшается.

Плотность вероятности в пространстве положений первоначально гауссовского состояния, движущегося в одном измерении с минимально неопределенным постоянным импульсом в свободном пространстве.

Напротив, в качестве примера дисперсии , когда волна меняет форму во время распространения, вместо этого рассмотрим решения уравнения Шредингера (безразмерного с 2Δ x , m и ħ , установленными равными единице),

$${\displaystyle i{\partial \psi \over \partial t}=-{\frac {1}{2}}{\nabla ^{2}\psi },}$$

$${\displaystyle \omega ={\frac {1}{2}}|\mathbf {k} |^{2}.}$$

Еще раз, ограничивая внимание одним измерением, решение уравнения Шредингера, удовлетворяющее начальному условию , представляющее волновой пакет, локализованный в пространстве в начале координат, видится как ${\textstyle \psi (x,0)={\sqrt[{4}]{2/\pi }}\exp \left({-x^{2}+ik_{0}x}\right)}$

$${\displaystyle {\begin{aligned}\psi (x,t)&={\frac {\sqrt[{4}]{2/\pi }}{\sqrt {1+2it}}}e^{-{\frac {1}{4}}k_{0}^{2}}~e^{-{\frac {1}{1+2it}}\left(x-{\frac {ik_{0}}{2}}\right)^{2}}\\&={\frac {\sqrt[{4}]{2/\pi }}{\sqrt {1+2it}}}e^{-{\frac {1}{1+4t^{2}}}(x-k_{0}t)^{2}}~e^{i{\frac {1}{1+4t^{2}}}\left((k_{0}+2tx)x-{\frac {1}{2}}tk_{0}^{2}\right)}~.\end{aligned}}}$$

Впечатление о дисперсионном поведении этого волнового пакета можно получить, взглянув на плотность вероятности:

$${\displaystyle |\psi (x,t)|^{2}={\frac {\sqrt {2/\pi }}{\sqrt {1+4t^{2}}}}~e^{-{\frac {2(x-k_{0}t)^{2}}{1+4t^{2}}}}~.}$$

k _oувеличивается√ 1 + 4 t ² → 2 t^{[номер 1]}

Профиль импульса A ( k ) остается инвариантным. Вероятностный ток​

$${\displaystyle j=\rho v={\frac {1}{2i}}(\psi ^{*}\nabla \psi -\psi \nabla \psi ^{*})=\rho \left(k_{0}+{\frac {4t(x-k_{0}t)}{1+4t^{2}}}\right).}$$

Гауссовы волновые пакеты в квантовой механике

Суперпозиция одномерных плоских волн (синий), которые в сумме образуют пакет гауссовских волн (красный), который распространяется вправо при распространении. Синие точки соответствуют фазовой скорости каждой плоской волны, а красная линия соответствует скорости центральной группы.

Одномерный гауссов волновой пакет, показанный в комплексной плоскости, для a =2 и k =4

Вышеупомянутый дисперсионный гауссовский волновой пакет, ненормированный и просто центрированный в начале координат, вместо этого, при t =0, теперь может быть записан в 3D, теперь в стандартных единицах: ^{[9] [10]}

$${\displaystyle \psi (\mathbf {r} ,0)=e^{-\mathbf {r} \cdot \mathbf {r} /2a},}$$

аквадрат ширины волнового пакета

$${\displaystyle a=2\langle \mathbf {r} \cdot \mathbf {r} \rangle /3\langle 1\rangle =2(\Delta x)^{2}.}$$

Преобразование Фурье также является гауссовым с точки зрения волнового числа, k -вектора (с обратной шириной,

$${\displaystyle 1/a=2\langle \mathbf {k} \cdot \mathbf {k} \rangle /3\langle 1\rangle =2(\Delta p_{x}/\hbar )^{2},}$$

$${\displaystyle \Delta x\Delta p_{x}=\hbar /2,}$$

соотношению неопределенности

$${\displaystyle \psi (\mathbf {k} ,0)=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k} /2}.}$$

Каждая отдельная волна вращается во времени только по фазе, так что зависящее от времени решение с преобразованием Фурье имеет вид

${\displaystyle {\begin{aligned}\Psi (\mathbf {k} ,t)&=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k} /2}e^{-iEt/\hbar }\\&=(2\pi a)^{3/2}e^{-a\mathbf {k} \cdot \mathbf {k} /2-i(\hbar ^{2}\mathbf {k} \cdot \mathbf {k} /2m)t/\hbar }\\&=(2\pi a)^{3/2}e^{-(a+i\hbar t/m)\mathbf {k} \cdot \mathbf {k} /2}.\end{aligned}}}$

Обратное преобразование Фурье по-прежнему является гауссовым, но теперь параметр a стал комплексным, и появился общий коэффициент нормализации. ^[6]

${\displaystyle \Psi (\mathbf {r} ,t)=\left({a \over a+i\hbar t/m}\right)^{3/2}e^{-{\mathbf {r} \cdot \mathbf {r} \over 2(a+i\hbar t/m)}}.}$

Интеграл от Ψ по всему пространству инвариантен, поскольку он является скалярным произведением Ψ с состоянием нулевой энергии, которое представляет собой волну с бесконечной длиной волны, постоянную функцию пространства. Для любого собственного состояния энергии η ( x ) внутренний продукт

$${\displaystyle \langle \eta |\psi \rangle =\int \eta (\mathbf {r} )\psi (\mathbf {r} )d^{3}\mathbf {r} ,}$$

ηη

Интеграл ∫ |Ψ| ² d ³ r также является инвариантом, что является утверждением сохранения вероятности. Явно,

${\displaystyle P(r)=|\Psi |^{2}=\Psi ^{*}\Psi =\left({a \over {\sqrt {a^{2}+(\hbar t/m)^{2}}}}\right)^{3}~e^{-{a\,\mathbf {r} \cdot \mathbf {r} \over a^{2}+(\hbar t/m)^{2}}},}$

в котором √ a — ширина P ( r ) в момент t = 0 ; r — расстояние от начала координат; скорость частицы равна нулю; и начало времени t = 0 может быть выбрано произвольно.

Ширина гауссианы — интересная величина, которую можно определить по плотности вероятности |Ψ| ² ,

$${\displaystyle {\sqrt {a^{2}+(\hbar t/m)^{2} \over a}}.}$$

ħt /( m √ a )распространение волнового пакета^[11]

Например, если электронный волновой пакет изначально локализован в области атомных размеров (т. е. ^10–10 м ), то ширина пакета удваивается примерно за 10–16 ^с . Очевидно, что волновые пакеты частиц действительно распространяются очень быстро (в свободном пространстве): ^[12] Например, через 1 мс ширина вырастет примерно до километра.

Этот линейный рост является отражением (независимой от времени) неопределенности импульса: волновой пакет ограничен узким диапазоном Δ x = √ a /2 и, таким образом, имеет импульс, который неопределенен (согласно принципу неопределенности) на величину ħ / √ 2 a , разброс скорости ħ/m √ 2 a , и, таким образом, в будущем положении на ħt /m √ 2 a . Тогда соотношение неопределенности представляет собой строгое неравенство, действительно очень далекое от насыщения! Первоначальная неопределенность Δ x Δ p = ħ /2 теперь увеличилась в ħt/ma раз (при больших t ).

2D

Двумерный гауссов квантовый волновой пакет. Цвет (желтый зеленый синий) указывает на фазу волновой функции , ее яркость указывает на . , ${\displaystyle \psi }$ ${\displaystyle |\psi |^{2}/|\psi |_{max}^{2}}$ ${\displaystyle k_{0x}=k_{0}}$ ${\displaystyle k_{0y}=0}$

Гауссова двумерная квантовая волновая функция:

${\displaystyle \psi (x,y,t)=\psi (x,t)\psi (y,t)}$

${\displaystyle \psi (x,t)=({\frac {2a^{2}}{\pi }})^{1/4}{\frac {e^{i\phi }}{(a^{4}+{\frac {4\hbar ^{2}t^{2}}{m^{2}}})^{1/4}}}e^{ik_{0}x}exp[-{\frac {(x-{\frac {\hbar k_{0}}{m}}t)^{2}}{a^{2}+{\frac {2i\hbar t}{m}}}}]}$

где

${\displaystyle \phi =-\theta -{\frac {\hbar k_{0}^{2}}{2m}}t}$

${\displaystyle tg(2\theta )={\frac {2\hbar t}{ma^{2}}}}$ ^[13]

Волновой поезд Эйри

В отличие от вышеупомянутого гауссовского волнового пакета, было замечено ^[14] , что определенная волновая функция, основанная на функциях Эйри , распространяется свободно без дисперсии огибающей, сохраняя свою форму. Он ускоряется неискаженно в отсутствие силового поля:

$${\displaystyle \psi =\operatorname {Ai} (B(x-B^{3}t^{2}))\,e^{iB^{3}t\left(x-{\tfrac {2}{3}}B^{3}t^{2}\right)}\,.}$$

ħ = 1m = 1/2Bобезразмеривание

Усеченное представление о развитии времени фронта Эйри в фазовом пространстве. (Нажмите, чтобы анимировать.)

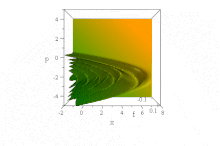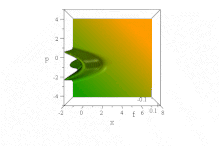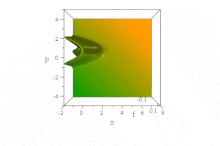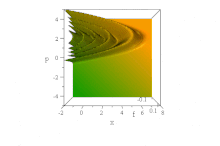
Тем не менее, в этой бессиловой ситуации нет никакого диссонанса с теоремой Эренфеста , поскольку состояние одновременно ненормируемо и имеет неопределенное (бесконечное) ⟨ x ⟩ во все времена. (Насколько это можно было определить, ⟨ p ⟩ = 0 во все времена, несмотря на кажущееся ускорение фронта.)

В фазовом пространстве это очевидно в квазивероятном распределении Вигнера в чистом состоянии этого волнового пакета, форма которого по x и p инвариантна с течением времени, но характеристики которого ускоряются вправо при ускорении парабол B ( x − B ³ t ² ) + ( п / B - tB ² ) ^{2 знак} равно 0 ,

$${\displaystyle W(x,p;t)=W(x-B^{3}t^{2},p-B^{3}t;0)={1 \over 2^{1/3}\pi B}~\mathrm {Ai} \left(2^{2/3}\left(Bx+{p^{2} \over B^{2}}-2Bpt\right)\right).}$$

Обратите внимание, что распределение импульса, полученное путем интегрирования по всем x, является постоянным. Поскольку это плотность вероятности в импульсном пространстве , очевидно, что сама волновая функция не нормируема.

Бесплатный распространитель

Пределом узкой ширины обсуждаемого гауссовского волнового пакета является ядро ​​свободного пропагатора K . Для других дифференциальных уравнений это обычно называют функцией Грина, ^[15] , но в квантовой механике традиционно зарезервировать название функции Грина для временного преобразования Фурье K .

Возвращаясь для простоты к одному измерению, когда m и ħ установлены равными единице, когда a — бесконечно малая величина ε , гауссово начальное условие, масштабированное так, чтобы его интеграл был равен единице,

$${\displaystyle \psi _{0}(x)={1 \over {\sqrt {2\pi \varepsilon }}}e^{-{x^{2} \over 2\varepsilon }}\,}$$

дельта-функциейδ ( x )

$${\displaystyle K_{t}(x)={1 \over {\sqrt {2\pi (it+\varepsilon )}}}e^{-x^{2} \over 2it+\varepsilon }\,}$$

Заметим, что очень узкий начальный волновой пакет мгновенно становится бесконечно широким, но с фазой, которая является более быстроколебательной при больших значениях x . Это может показаться странным — решение переходит от локализации в одной точке к тому, чтобы быть «везде» во все более поздние моменты времени , но это является отражением огромной неопределенности импульса локализованной частицы, как объяснено выше.

Далее заметим, что норма волновой функции бесконечна, что тоже верно, поскольку точно так же расходится квадрат дельта-функции .

Множитель, включающий ε, представляет собой бесконечно малую величину, которая необходима для того, чтобы гарантировать корректность определения интегралов по K. В пределе, когда ε → 0 , K становится чисто осциллирующим, а интегралы от K не сходятся абсолютно. В оставшейся части этого раздела он будет установлен равным нулю, но для того, чтобы все интегрирования по промежуточным состояниям были четко определены, предел ε → 0 следует принимать только после расчета конечного состояния.

Пропагатор — это амплитуда достижения точки x в момент времени t , начиная с начала координат, x = 0. Благодаря трансляционной инвариантности амплитуда достижения точки x при старте из точки y представляет собой одну и ту же функцию, только теперь преобразованную:

$${\displaystyle K_{t}(x,y)=K_{t}(x-y)={1 \over {\sqrt {2\pi it}}}e^{i(x-y)^{2} \over 2t}\,.}$$

В пределе, когда t мало, пропагатор переходит к дельта-функции

$${\displaystyle \lim _{t\to 0}K_{t}(x-y)=\delta (x-y)~,}$$

распределенийпробную функцию

Чтобы убедиться в этом, обратите внимание, что интеграл по всему пространству K всегда равен 1:

$${\displaystyle \int K_{t}(x)dx=1\,,}$$

Kε

Таким образом, ядро ​​распространения — это (будущая) эволюция дельта-функции во времени, и в некотором смысле оно непрерывно: оно переходит к исходной дельта-функции на малых временах. Если исходная волновая функция представляет собой бесконечно узкий пик в положении y ,

$${\displaystyle \psi _{0}(x)=\delta (x-y)\,,}$$

$${\displaystyle \psi _{t}(x)={1 \over {\sqrt {2\pi it}}}e^{i(x-y)^{2}/2t}\,.}$$

Теперь, поскольку каждую функцию можно записать как взвешенную сумму таких узких пиков,

$${\displaystyle \psi _{0}(x)=\int \psi _{0}(y)\delta (x-y)dy\,,}$$

каждой функции ψ ₀K

${\displaystyle \psi _{t}(x)=\int \psi _{0}(y){1 \over {\sqrt {2\pi it}}}e^{i(x-y)^{2}/2t}dy\,.}$

Таким образом, это формальный способ выразить фундаментальное решение или общее решение . Интерпретация этого выражения заключается в том, что амплитуда частицы, находящейся в точке x в момент времени t , равна амплитуде, с которой она стартовала в точке y , умноженной на амплитуду, которую она прошла от y до x , суммированную по всем возможным начальным точкам . Другими словами, это свертка ядра K с произвольным начальным условием ψ ₀ ,

$${\displaystyle \psi _{t}=K*\psi _{0}\,.}$$

Поскольку амплитуду перемещения от x до y за время t + t ' можно рассматривать в два этапа, пропагатор подчиняется тождеству состава:

$${\displaystyle \int K(x-y;t)K(y-z;t')dy=K(x-z;t+t')~,}$$

xzttxytyzt.всем возможным промежуточным состояниям yинтеграла по путям^[16]

Аналитическое продолжение диффузии

Распространение волновых пакетов в квантовой механике напрямую связано с разбросом плотностей вероятности при диффузии . Для частицы, которая беспорядочно ходит , функция плотности вероятности в любой точке удовлетворяет уравнению диффузии (см. также уравнение теплопроводности )

$${\displaystyle {\partial \over \partial t}\rho ={1 \over 2}{\partial ^{2} \over \partial x^{2}}\rho ~,}$$

Решением этого уравнения является расширяющаяся гауссиана,

$${\displaystyle \rho _{t}(x)={1 \over {\sqrt {2\pi t}}}e^{-x^{2} \over 2t}~,}$$

ρ _tt

$${\displaystyle \lim _{t\to 0}\rho _{t}(x)=\delta (x)}$$

$${\displaystyle \lim _{t\to 0}\int _{x}f(x)\rho _{t}(x)=f(0)}$$

пробной функции f

Распространяющийся гауссиан является ядром распространения уравнения диффузии и подчиняется тождеству свертки :

$${\displaystyle K_{t+t'}=K_{t}*K_{t'}\,,}$$

H

$${\displaystyle K_{t}(x)=e^{-tH}\,,}$$

$${\displaystyle H=-{\nabla ^{2} \over 2}\,.}$$

Матрица имеет два индекса, что в непрерывном пространстве делает ее функцией x и x '. В этом случае из-за трансляционной инвариантности матричный элемент K зависит только от разности позиций, и удобным злоупотреблением обозначениями является обращение к оператору, матричным элементам и функции разности под одним и тем же именем:

$${\displaystyle K_{t}(x,x')=K_{t}(x-x')\,.}$$

Трансляционная инвариантность означает, что непрерывное умножение матриц

$${\displaystyle C(x,x'')=\int _{x'}A(x,x')B(x',x'')\,,}$$

$${\displaystyle C(\Delta )=C(x-x'')=\int _{x'}A(x-x')B(x'-x'')=\int _{y}A(\Delta -y)B(y)\,.}$$

Экспонента может быть определена в диапазоне t s, который включает комплексные значения, при условии, что интегралы по ядру распространения остаются сходящимися,

$${\displaystyle K_{z}(x)=e^{-zH}\,.}$$

zx Kдействительно

Пределом этого выражения для z , приближающегося к чисто мнимой оси, является встреченный выше пропагатор Шрёдингера:

$${\displaystyle K_{t}^{\rm {Schr}}=K_{it+\varepsilon }=e^{-(it+\varepsilon )H}\,,}$$

Исходя из фундаментальной идентичности возведения в степень или интеграции путей,

$${\displaystyle K_{z}*K_{z'}=K_{z+z'}\,}$$

z

Таким образом, квантовая эволюция гауссианы, которая представляет собой комплексное диффузионное ядро ​​K ,

$${\displaystyle \psi _{0}(x)=K_{a}(x)=K_{a}*\delta (x)\,}$$

$${\displaystyle \psi _{t}=K_{it}*K_{a}=K_{a+it}\,.}$$

Это иллюстрирует вышеупомянутую диффузионную форму комплексных гауссовских решений:

$${\displaystyle \psi _{t}(x)={1 \over {\sqrt {2\pi (a+it)}}}e^{-{x^{2} \over 2(a+it)}}\,.}$$

Смотрите также

• Волна
• Распространение волн
• Фурье-анализ
• Групповая скорость
• Фазовая скорость
• Свободная частица
• Когерентные состояния
• Форма волны
• Вейвлет
• Волна материи
• Импульсный (обработка сигнала)
• Пульс (физика)
• Уравнение Шрёдингера
• Введение в квантовую механику
• Солитон

Примечания

1. Напротив, введение членов взаимодействия в дисперсионные уравнения, например, для квантового гармонического осциллятора, может привести к появлению недисперсионных решений классического вида - см. когерентные состояния: такие «состояния с минимальной неопределенностью» действительно насыщают. принцип неопределенности навсегда.

Рекомендации

1. Джой Маннерс (2000), Квантовая физика: Введение, CRC Press, стр. 53–56, ISBN 978-0-7503-0720-8
2. Шварц, Мэтью. «Лекция 11: Волновые пакеты и дисперсия» (PDF) . ученый.harvard.edu . Архивировано (PDF) из оригинала 18 марта 2023 г. Проверено 22 июня 2023 г.
3. Бриллюэн, Леон (1960), Распространение волн и групповая скорость , Нью-Йорк: Academic Press Inc., OCLC  537250
4. Kragh, Хельге (2009). «Волновой пакет». В Гринбергере, Дэниел; Хентшель, Клаус; Вайнерт, Фридель (ред.). Сборник квантовой физики . Берлин, Гейдельберг: Springer Berlin Heidelberg. стр. 828–830. дои : 10.1007/978-3-540-70626-7_232. ISBN 978-3-540-70622-9.
5. Дарвин, Чарльз Гальтон. «Свободное движение в волновой механике». Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера 117.776 (1927): 258-293.
6. Шифф, Леонард И. (1995). Квантовая механика . Международная серия по чистой и прикладной физике (3-е изд., 29-е печатное изд.). Нью-Йорк: МакГроу-Хилл. ISBN 978-0-07-055287-6.
7. Ньютон, Роджер Г. (1982). Теория рассеяния волн и частиц . Тексты и монографии по физике (2-е изд.). Нью-Йорк, Гейдельберг, Берлин: Springer. ISBN 978-0-387-10950-3.
8. Сасскинд, Леонард; Фридман, Арт; Сасскинд, Леонард (2014). Квантовая механика: теоретический минимум; [что нужно знать, чтобы начать заниматься физикой] . Теоретический минимум / Леонард Зюскинд и Джордж Грабовский. Нью-Йорк, штат Нью-Йорк: Основные книги. ISBN 978-0-465-08061-8.
9. Паули, Вольфганг (2000), Волновая механика: Том 5 лекций Паули по физике , Книги по физике, Dover Publications , ISBN 978-0-486-41462-1
10. * Аберс, Э.; Пирсон, Эд (2004), Квантовая механика , Аддисон Уэсли , Prentice-Hall Inc. , ISBN 978-0-13-146100-0
11. Дарвин, CG (1927). «Свободное движение в волновой механике», Труды Лондонского королевского общества. Серия А, содержащая статьи математического и физического характера 117 (776), 258-293.
12. Ричард Фицпатрик, Колебания и волны
13. Коэн-Таннуджи, Диу и Лалоэ, Квантовая механика, дополнение G _I , §3-a
14. Берри, М.В.; Балаш, Н.Л. (1979), «Нераспространяющиеся волновые пакеты», Am J Phys , 47 (3): 264–267, Бибкод : 1979AmJPh..47..264B, doi : 10.1119/1.11855
15. Джексон, JD (1975), Классическая электродинамика (2-е изд.), Нью-Йорк: John Wiley & Sons , Inc., ISBN 978-0-471-43132-9
16. Фейнман, Р.П .; Хиббс, AR (1965), Квантовая механика и интегралы по траекториям , Нью-Йорк: McGraw-Hill , ISBN 978-0-07-020650-2

Внешние ссылки

• Учебные материалы, связанные с движением волновых пакетов, в Викиверситете
• Словарное определение волнового пакета в Викисловаре
• График пакета 1d Wave в Google
• Последовательность волн 1d и график плотности вероятности в Google
• График пакетов 2d Wave в Google
• График поезда 2d Wave в Google
• 2D-график плотности вероятности в Google
• Квантовая физика онлайн: Интерактивное моделирование свободного волнового пакета
• Веб-Шрёдингер: Интерактивное двумерное моделирование динамики волновых пакетов
• Моделирование волнового пакета в 2D (По данным ФУРЬЕ-синтеза в 2D)