Дифракция

Явление движения волн

Дифракционная картина красного лазерного луча, проецируемого на пластину после прохождения через небольшое круглое отверстие в другой пластине.

Дифракция — это интерференция или изгиб волн вокруг углов препятствия или через отверстие в область геометрической тени препятствия/отверстия. Дифрагирующий объект или отверстие фактически становится вторичным источником распространяющейся волны. Итальянский ученый Франческо Мария Гримальди придумал слово «дифракция» и был первым, кто записал точные наблюдения этого явления в 1660 году . ^{[1] [2]}

Бесконечное множество точек (показано три) вдоль длины проецируют фазовые вклады от волнового фронта , создавая непрерывно изменяющуюся интенсивность на регистрирующей пластине. ${\displaystyle d}$ ${\displaystyle \theta }$

В классической физике явление дифракции описывается принципом Гюйгенса-Френеля , который рассматривает каждую точку в распространяющемся волновом фронте как набор отдельных сферических вейвлетов . ^[3] Характерный изгибный рисунок наиболее выражен, когда волна от когерентного источника (такого как лазер) сталкивается со щелью/отверстием, сопоставимым по размеру с его длиной волны , как показано на вставленном изображении. Это происходит из-за добавления или интерференции различных точек на волновом фронте (или, что эквивалентно, каждого вейвлета), которые перемещаются по путям разной длины к регистрирующей поверхности. Если имеется несколько близко расположенных отверстий (например, дифракционная решетка ), может возникнуть сложный рисунок различной интенсивности.

Эти эффекты также возникают, когда световая волна проходит через среду с переменным показателем преломления , или когда звуковая волна проходит через среду с переменным акустическим импедансом – все волны дифрагируют, ^[4] включая гравитационные волны , ^[5] волны на воде и другие электромагнитные волны , такие как рентгеновские лучи и радиоволны . Кроме того, квантовая механика также демонстрирует, что материя обладает волнообразными свойствами и, следовательно, подвергается дифракции (которая измеряется на субатомном и молекулярном уровнях). ^[6]

Величина дифракции зависит от размера щели. Дифракция максимальна, когда размер щели близок к длине волны. В этом случае, когда волны проходят через щель, они становятся полукруглыми .

История

Эскиз Томаса Юнга, изображающий двухщелевую дифракцию волн на воде, представленный им Королевскому обществу в 1803 году.

Да Винчи мог наблюдать дифракцию в расширении тени. ^[7] Эффекты дифракции света были впервые тщательно обнаружены и охарактеризованы Франческо Мария Гримальди , который также ввел термин дифракция , от латинского diffringere , «разбивать на части», имея в виду разбиение света в разных направлениях. Результаты наблюдений Гримальди были опубликованы посмертно в 1665 году . ^{[8] [9] [10]} Исаак Ньютон изучал эти эффекты и приписывал их изгибу световых лучей. Джеймс Грегори ( 1638 – 1675 ) наблюдал дифракционные картины, вызванные птичьим пером, что было фактически первой открытой дифракционной решеткой . ^[11] Томас Янг провел знаменитый эксперимент в 1803 году, продемонстрировав интерференцию от двух близко расположенных щелей. ^[12] Объясняя свои результаты интерференцией волн, исходящих из двух разных щелей, он пришел к выводу, что свет должен распространяться как волны. Огюстен-Жан Френель провел более определенные исследования и расчеты дифракции, опубликованные в 1816 ^[13] и 1818 годах ^[14], и тем самым оказал большую поддержку волновой теории света, выдвинутой Христианом Гюйгенсом ^{[15] и обновленной Юнгом, в противовес} корпускулярной теории света Ньютона .

Механизм

Дифракция на одной щели в круглом волновом резервуаре

В классической физике дифракция возникает из-за того, как распространяются волны ; это описывается принципом Гюйгенса-Френеля и принципом суперпозиции волн . Распространение волны можно визуализировать, рассматривая каждую частицу передаваемой среды на волновом фронте как точечный источник вторичной сферической волны . Смещение волны в любой последующей точке является суммой этих вторичных волн. Когда волны складываются, их сумма определяется относительными фазами , а также амплитудами отдельных волн, так что суммированная амплитуда волн может иметь любое значение между нулем и суммой отдельных амплитуд. Следовательно, дифракционные картины обычно имеют ряд максимумов и минимумов.

В современном квантово-механическом понимании распространения света через щель (или щели) каждый фотон описывается своей волновой функцией , которая определяет распределение вероятностей для фотона: светлые и темные полосы — это области, где фотоны с большей или меньшей вероятностью будут обнаружены. Волновая функция определяется физическим окружением, таким как геометрия щели, расстояние до экрана и начальные условия при создании фотона. Волновая природа отдельных фотонов (в отличие от волновых свойств, возникающих только из-за взаимодействия множества фотонов) подразумевалась в эксперименте с низкой интенсивностью и двумя щелями, впервые проведенном GI Taylor в 1909 году . Квантовый подход имеет некоторые поразительные сходства с принципом Гюйгенса-Френеля ; основываясь на этом принципе, когда свет проходит через щели и границы, вторичные точечные источники света создаются вблизи или вдоль этих препятствий, и результирующая дифракционная картина будет профилем интенсивности, основанным на коллективной интерференции всех этих источников света, которые имеют разные оптические пути. В квантовом формализме это похоже на рассмотрение ограниченных областей вокруг щелей и границ, из которых фотоны с большей вероятностью могут возникнуть, и вычисление распределения вероятностей (которое пропорционально результирующей интенсивности классического формализма).

Существуют различные аналитические модели, которые позволяют рассчитать дифрагированное поле, включая уравнение дифракции Кирхгофа (выведенное из волнового уравнения ), ^[16] приближение дифракции Фраунгофера уравнения Кирхгофа (применимое к дальнему полю ), приближение дифракции Френеля (применимое к ближнему полю ) и формулировку интеграла траектории Фейнмана . Большинство конфигураций не могут быть решены аналитически, но могут давать численные решения с помощью методов конечных элементов и граничных элементов .

Можно получить качественное понимание многих явлений дифракции, рассмотрев, как изменяются относительные фазы отдельных источников вторичных волн, и, в частности, условия, при которых разность фаз равна половине цикла, и в этом случае волны будут гасить друг друга.

Простейшими описаниями дифракции являются те, в которых ситуация может быть сведена к двумерной задаче. Для волн на воде это уже так; волны на воде распространяются только по поверхности воды. Для света мы часто можем пренебречь одним направлением, если дифрагирующий объект простирается в этом направлении на расстояние, намного превышающее длину волны. В случае света, проходящего через небольшие круглые отверстия, нам придется учитывать полную трехмерную природу задачи.

• 
  Сгенерированная компьютером картина интенсивности, сформированная на экране путем дифракции от квадратной апертуры
• 
  Генерация интерференционной картины из двухщелевой дифракции
• 
  Вычислительная модель интерференционной картины, полученной при дифракции на двух щелях
• 
  Оптическая дифракционная картина (лазерная, аналог рентгеновской дифракции)
• 
  Согласно некоторым анализам, цвета, видимые в паутине , частично обусловлены дифракцией. ^[17]

Примеры

Эффекты дифракции часто наблюдаются в повседневной жизни. Наиболее яркими примерами дифракции являются те, которые связаны со светом; например, близко расположенные дорожки на CD или DVD действуют как дифракционная решетка , формируя знакомый радужный узор, который можно увидеть, глядя на диск.

Этот принцип можно распространить на создание решетки со структурой, которая будет воспроизводить любую желаемую дифракционную картину; примером может служить голограмма на кредитной карте.

Дифракция в атмосфере на мелких частицах может вызвать корону — яркий диск и кольца вокруг яркого источника света, такого как солнце или луна. В противоположной точке можно также наблюдать глори — яркие кольца вокруг тени наблюдателя. В отличие от короны, глори требует, чтобы частицы были прозрачными сферами (как капельки тумана), поскольку обратное рассеяние света, образующее глорию, включает в себя преломление и внутреннее отражение внутри капли.

При использовании света от компактного источника тень твердого объекта имеет небольшие полосы вблизи его краев.

Яркое пятно ( пятно Араго ), видимое в центре тени круглого препятствия, обусловлено дифракцией.

Дифракционные пики — это дифракционные узоры, возникающие из-за некруглой апертуры в камере или опорных стоек в телескопе. При нормальном зрении дифракция через ресницы может вызывать такие пики.

Вид с конца моста Миллениум; Луна восходит над мостом Саутуарк. Уличные фонари отражаются в Темзе.

Моделирование дифракционных пиков в шестиугольных зеркалах телескопа

Пятнистая картина , которая наблюдается, когда лазерный луч падает на оптически шероховатую поверхность, также является явлением дифракции. Когда мясные деликатесы кажутся радужными , это дифракция от мясных волокон. ^[18] Все эти эффекты являются следствием того, что свет распространяется как волна .

Дифракция может происходить с любым типом волны. Океанские волны дифрагируют вокруг причалов и других препятствий.

Круговые волны, возникающие в результате дифракции от узкого входа в затопленный прибрежный карьер.

Звуковые волны могут рассеиваться вокруг объектов, поэтому можно услышать чей-то крик, даже если спрятаться за деревом. ^[19]

Дифракция также может представлять проблему в некоторых технических приложениях; она устанавливает фундаментальное ограничение на разрешение камеры, телескопа или микроскопа.

Другие примеры дифракции рассмотрены ниже.

Дифракция на одной щели

Двумерная дифракция на одной щели с анимацией изменения ширины

Численная аппроксимация картины дифракции от щели шириной в четыре длины волны с падающей плоской волной. Видны главный центральный луч, нули и инверсии фаз.

График и изображение дифракции на одной щели

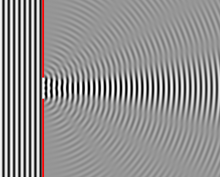
Длинная щель бесконечно малой ширины, освещаемая светом, преломляет его в ряд круговых волн, а волновой фронт, выходящий из щели, представляет собой цилиндрическую волну однородной интенсивности в соответствии с принципом Гюйгенса-Френеля .

Освещенная щель, ширина которой больше длины волны, создает интерференционные эффекты в пространстве ниже щели. Предполагая, что щель ведет себя так, как будто она имеет большое количество точечных источников, равномерно распределенных по ширине щели, можно рассчитать интерференционные эффекты. Анализ этой системы упрощается, если мы рассмотрим свет с одной длиной волны. Если падающий свет когерентен , все эти источники имеют одинаковую фазу. Свет, падающий в заданную точку пространства ниже щели, состоит из вкладов от каждого из этих точечных источников, и если относительные фазы этих вкладов изменяются на или более, мы можем ожидать найти минимумы и максимумы в дифрагированном свете. Такие фазовые различия вызваны различиями в длинах путей, по которым вносящие вклад лучи достигают точки от щели. ${\displaystyle 2\pi }$

Мы можем найти угол, при котором в дифрагированном свете получается первый минимум, с помощью следующих рассуждений. Свет от источника, расположенного на верхнем краю щели, деструктивно интерферирует с источником, расположенным в середине щели, когда разность хода между ними равна . Аналогично, источник, расположенный чуть ниже вершины щели, будет деструктивно интерферировать с источником, расположенным чуть ниже середины щели под тем же углом. Мы можем продолжить эти рассуждения по всей высоте щели, чтобы заключить, что условие деструктивной интерференции для всей щели такое же, как условие деструктивной интерференции между двумя узкими щелями, расстояние между которыми составляет половину ширины щели. Разность хода приблизительно такова, что минимальная интенсивность возникает под углом, заданным выражением, где — ширина щели, — угол падения, при котором возникает минимальная интенсивность, — длина волны света. ${\displaystyle \lambda /2}$ ${\displaystyle {\frac {d\sin(\theta )}{2}}}$ ${\displaystyle \theta _{\text{min}}}$ $${\displaystyle d\,\sin \theta _{\text{min}}=\lambda ,}$$ ${\displaystyle d}$ ${\displaystyle \theta _{\text{min}}}$ ${\displaystyle \lambda }$

Аналогичный аргумент можно использовать, чтобы показать, что если представить, что щель разделена на четыре, шесть, восемь частей и т. д., то минимумы будут получены при углах, определяемых выражением, где — целое число, отличное от нуля. ${\displaystyle \theta _{n}}$ $${\displaystyle d\,\sin \theta _{n}=n\lambda ,}$$ ${\displaystyle n}$

Нет такого простого аргумента, который позволил бы нам найти максимумы дифракционной картины. Профиль интенсивности можно рассчитать с помощью уравнения дифракции Фраунгофера как где — интенсивность под заданным углом, — интенсивность в центральном максимуме ( ), которая также является нормировочным множителем профиля интенсивности, который можно определить путем интегрирования от до и сохранения энергии, и , которая является ненормализованной функцией sinc . $${\displaystyle I(\theta )=I_{0}\,\operatorname {sinc} ^{2}\left({\frac {d\pi }{\lambda }}\sin \theta \right),}$$ ${\displaystyle I(\theta )}$ ${\displaystyle I_{0}}$ ${\displaystyle \theta =0}$ ${\textstyle \theta =-{\frac {\pi }{2}}}$ ${\textstyle \theta ={\frac {\pi }{2}}}$ ${\displaystyle \operatorname {sinc} x={\frac {\sin x}{x}}}$

Этот анализ применим только к дальнему полю ( дифракция Фраунгофера ), то есть на расстоянии, значительно большем ширины щели.

Из приведенного выше профиля интенсивности , если , интенсивность будет мало зависеть от , следовательно, волновой фронт, выходящий из щели, будет напоминать цилиндрическую волну с азимутальной симметрией; Если , только будет иметь заметную интенсивность, следовательно, волновой фронт, выходящий из щели, будет напоминать волновой фронт геометрической оптики . ${\displaystyle d\ll \lambda }$ ${\displaystyle \theta }$ ${\displaystyle d\gg \lambda }$ ${\displaystyle \theta \approx 0}$

Когда угол падения света на щель не равен нулю (что приводит к изменению длины пути ), профиль интенсивности в режиме Фраунгофера (т.е. в дальнем поле) становится следующим: ${\displaystyle \theta _{\text{i}}}$ $${\displaystyle I(\theta )=I_{0}\,\operatorname {sinc} ^{2}\left[{\frac {d\pi }{\lambda }}(\sin \theta \pm \sin \theta _{\text{i}})\right]}$$

Выбор знака плюс/минус зависит от определения угла падения . ${\displaystyle \theta _{\text{i}}}$

Дифракция красного лазерного света на 2-х щелях (вверху) и 5-ти щелях

Дифракция красного лазера с использованием дифракционной решетки

Дифракционная картина лазера с длиной волны 633 нм через сетку из 150 щелей

Дифракционная решетка

Дифракционная решетка

Дифракционная решетка — оптический компонент с регулярным рисунком. Форма света, дифрагированного решеткой, зависит от структуры элементов и количества присутствующих элементов, но все решетки имеют максимумы интенсивности при углах θ _m , которые задаются уравнением решетки , где — угол падения света, — расстояние между элементами решетки, — целое число, которое может быть положительным или отрицательным. $${\displaystyle d\left(\sin {\theta _{m}}\pm \sin {\theta _{i}}\right)=m\lambda ,}$$ ${\displaystyle \theta _{i}}$ ${\displaystyle d}$ ${\displaystyle m}$

Свет, дифрагированный решеткой, определяется путем суммирования света, дифрагированного от каждого из элементов, и по сути представляет собой свертку дифракционных и интерференционных картин.

На рисунке показан свет, дифрагированный решетками из 2 и 5 элементов, где расстояния между решетками одинаковы; видно, что максимумы находятся в одном и том же положении, но детальная структура интенсивностей различна.

Круглая апертура

Компьютерное изображение диска Эйри

Дифракционная картина от круглого отверстия на разных расстояниях

Дифракцию в дальней зоне плоской волны, падающей на круглую апертуру, часто называют диском Эйри . Изменение интенсивности в зависимости от угла определяется выражением, где — радиус круглой апертуры, равно и — функция Бесселя . Чем меньше апертура, тем больше размер пятна на заданном расстоянии и тем больше расхождение дифрагированных лучей. $${\displaystyle I(\theta )=I_{0}\left({\frac {2J_{1}(ka\sin \theta )}{ka\sin \theta }}\right)^{2},}$$ ${\displaystyle a}$ ${\displaystyle k}$ ${\displaystyle 2\pi /\lambda }$ ${\displaystyle J_{1}}$

Общая апертура

Волна, которая исходит из точечного источника, имеет амплитуду в месте , которое задается решением волнового уравнения частотной области для точечного источника ( уравнение Гельмгольца ), где - трехмерная дельта-функция. Дельта-функция имеет только радиальную зависимость, поэтому оператор Лапласа (он же скалярный лапласиан) в сферической системе координат упрощается до ${\displaystyle \psi }$ ${\displaystyle \mathbf {r} }$ $${\displaystyle \nabla ^{2}\psi +k^{2}\psi =\delta (\mathbf {r} ),}$$ ${\displaystyle \delta (\mathbf {r} )}$ $${\displaystyle \nabla ^{2}\psi ={\frac {1}{r}}{\frac {\partial ^{2}}{\partial r^{2}}}(r\psi ).}$$

(См. del в цилиндрических и сферических координатах .) Путем прямой подстановки можно легко показать, что решение этого уравнения представляет собой скалярную функцию Грина , которая в сферической системе координат (и с использованием физического соглашения о времени ) равна ${\displaystyle e^{-i\omega t}}$ $${\displaystyle \psi (r)={\frac {e^{ikr}}{4\pi r}}.}$$

Это решение предполагает, что источник дельта-функции расположен в начале координат. Если источник расположен в произвольной точке источника, обозначенной вектором , а точка поля расположена в точке , то мы можем представить скалярную функцию Грина (для произвольного расположения источника) как ${\displaystyle \mathbf {r} '}$ ${\displaystyle \mathbf {r} }$ $${\displaystyle \psi (\mathbf {r} |\mathbf {r} ')={\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{4\pi |\mathbf {r} -\mathbf {r} '|}}.}$$

Следовательно, если электрическое поле падает на отверстие, то поле, создаваемое этим распределением отверстия, определяется поверхностным интегралом ${\displaystyle E_{\mathrm {inc} }(x,y)}$ $${\displaystyle \Psi (r)\propto \iint \limits _{\mathrm {aperture} }\!\!E_{\mathrm {inc} }(x',y')~{\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{4\pi |\mathbf {r} -\mathbf {r} '|}}\,dx'\,dy',}$$

О расчете полей области Фраунгофера

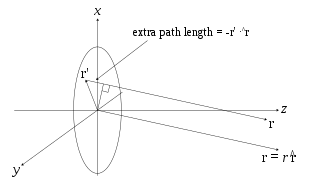
где точка источника в апертуре задается вектором $${\displaystyle \mathbf {r} '=x'\mathbf {\hat {x}} +y'\mathbf {\hat {y}} .}$$

В дальней зоне, где можно использовать приближение параллельных лучей, функция Грина упрощается , как это видно на соседнем рисунке. $${\displaystyle \psi (\mathbf {r} |\mathbf {r} ')={\frac {e^{ik|\mathbf {r} -\mathbf {r} '|}}{4\pi |\mathbf {r} -\mathbf {r} '|}},}$$ $${\displaystyle \psi (\mathbf {r} |\mathbf {r} ')={\frac {e^{ikr}}{4\pi r}}e^{-ik(\mathbf {r} '\cdot \mathbf {\hat {r}} )}}$$

Выражение для поля дальней зоны (области Фраунгофера) становится $${\displaystyle \Psi (r)\propto {\frac {e^{ikr}}{4\pi r}}\iint \limits _{\mathrm {aperture} }\!\!E_{\mathrm {inc} }(x',y')e^{-ik(\mathbf {r} '\cdot \mathbf {\hat {r}} )}\,dx'\,dy'.}$$

Теперь, поскольку и выражение для поля области Фраунгофера от плоской апертуры теперь становится $${\displaystyle \mathbf {r} '=x'\mathbf {\hat {x}} +y'\mathbf {\hat {y}} }$$ $${\displaystyle \mathbf {\hat {r}} =\sin \theta \cos \phi \mathbf {\hat {x}} +\sin \theta ~\sin \phi ~\mathbf {\hat {y}} +\cos \theta \mathbf {\hat {z}} ,}$$ $${\displaystyle \Psi (r)\propto {\frac {e^{ikr}}{4\pi r}}\iint \limits _{\mathrm {aperture} }\!\!E_{\mathrm {inc} }(x',y')e^{-ik\sin \theta (\cos \phi x'+\sin \phi y')}\,dx'\,dy'.}$$

Пусть и поле области Фраунгофера плоской апертуры принимает форму преобразования Фурье $${\displaystyle k_{x}=k\sin \theta \cos \phi }$$ $${\displaystyle k_{y}=k\sin \theta \sin \phi \,,}$$ $${\displaystyle \Psi (r)\propto {\frac {e^{ikr}}{4\pi r}}\iint \limits _{\mathrm {aperture} }\!\!E_{\mathrm {inc} }(x',y')e^{-i(k_{x}x'+k_{y}y')}\,dx'\,dy',}$$

В дальней зоне/области Фраунгофера это становится пространственным преобразованием Фурье распределения апертуры. Принцип Гюйгенса при применении к апертуре просто говорит, что картина дифракции в дальней зоне является пространственным преобразованием Фурье формы апертуры, и это прямой побочный продукт использования приближения параллельных лучей, которое идентично выполнению разложения плоской волны полей плоскости апертуры (см. Фурье-оптика ).

Распространение лазерного луча

Способ, которым профиль лазерного луча изменяется по мере его распространения, определяется дифракцией. Когда весь испускаемый луч имеет плоский, пространственно когерентный волновой фронт, он приближается к гауссовому профилю луча и имеет наименьшую расходимость для данного диаметра. Чем меньше выходной луч, тем быстрее он расходится. Можно уменьшить расходимость лазерного луча, сначала расширив его одной выпуклой линзой , а затем коллимировав его второй выпуклой линзой, фокусная точка которой совпадает с фокусной точкой первой линзы. Результирующий луч имеет больший диаметр и, следовательно, меньшую расходимость. Расходимость лазерного луча может быть уменьшена ниже дифракции гауссова луча или даже обращена в сходимость, если показатель преломления среды распространения увеличивается с интенсивностью света. ^[20] Это может привести к эффекту самофокусировки .

Если волновой фронт излучаемого пучка имеет возмущения, то при определении расходимости лазерного пучка в качестве диаметра гауссова пучка следует рассматривать только поперечную длину когерентности (где возмущение волнового фронта меньше 1/4 длины волны). Если поперечная длина когерентности в вертикальном направлении больше, чем в горизонтальном, то расходимость лазерного пучка в вертикальном направлении будет меньше, чем в горизонтальном.

Дифракционно-ограниченное изображение

На этом удачном изображении двойной звезды дзета Волопаса можно увидеть диск Эйри вокруг каждой из звезд, полученный через апертуру телескопа диаметром 2,56 м .

Способность системы формирования изображения разрешать детали в конечном итоге ограничена дифракцией . Это происходит потому, что плоская волна, падающая на круглую линзу или зеркало, дифрагирует, как описано выше. Свет не фокусируется в точку, а образует диск Эйри с центральным пятном в фокальной плоскости, радиус которого (измеренный до первого нуля) равен , где — длина волны света, а — число f (фокусное расстояние, деленное на диаметр апертуры ) оптики формирования изображения; это строго точно для ( параксиального случая). В пространстве объектов соответствующее угловое разрешение равно , где — диаметр входного зрачка линзы формирования изображения (например, главного зеркала телескопа). $${\displaystyle \Delta x=1.22\lambda N,}$$ ${\displaystyle \lambda }$ ${\displaystyle N}$ ${\displaystyle f}$ ${\displaystyle D}$ ${\displaystyle N\gg 1}$ $${\displaystyle \theta \approx \sin \theta =1.22{\frac {\lambda }{D}},}$$ ${\displaystyle D}$

Два точечных источника будут создавать узор Эйри – см. фотографию двойной звезды. По мере того, как точечные источники будут сближаться, узоры начнут перекрываться, и в конечном итоге они сольются, образуя единый узор, в этом случае два точечных источника не могут быть разрешены на изображении. Критерий Рэлея определяет, что два точечных источника считаются «разрешенными», если разделение двух изображений составляет по крайней мере радиус диска Эйри, т. е. если первый минимум одного совпадает с максимумом другого.

Таким образом, чем больше апертура объектива по сравнению с длиной волны, тем выше разрешение системы формирования изображений. Это одна из причин, по которой астрономическим телескопам требуются большие объективы, и почему объективам микроскопов требуется большая числовая апертура (большой диаметр апертуры по сравнению с рабочим расстоянием) для получения максимально возможного разрешения.

Пятнистые узоры

Пятнистая картина, наблюдаемая при использовании лазерной указки, является еще одним явлением дифракции. Она является результатом наложения множества волн с различными фазами, которые возникают, когда лазерный луч освещает шероховатую поверхность. Они складываются, давая результирующую волну, амплитуда которой, а следовательно, и интенсивность, меняются случайным образом.

Принцип Бабине

Принцип Бабине — полезная теорема, утверждающая, что картина дифракции от непрозрачного тела идентична картине дифракции от отверстия того же размера и формы, но с разной интенсивностью. Это означает, что условия интерференции одного препятствия будут такими же, как и для одной щели.

«Острие ножа»

Эффект ножевого края или дифракция ножевого края — это усечение части падающего излучения , которое ударяется об острое четко определенное препятствие, такое как горный хребет или стена здания. Эффект ножевого края объясняется принципом Гюйгенса-Френеля , который гласит, что четко определенное препятствие для электромагнитной волны действует как вторичный источник и создает новый волновой фронт . Этот новый волновой фронт распространяется в геометрическую область тени препятствия.

Дифракция на острие ножа является результатом « задачи полуплоскости », первоначально решенной Арнольдом Зоммерфельдом с использованием формулировки спектра плоской волны. Обобщением задачи полуплоскости является «задача клина», решаемая как краевая задача в цилиндрических координатах. Решение в цилиндрических координатах было затем распространено на оптический режим Джозефом Б. Келлером , который ввел понятие коэффициентов дифракции через свою геометрическую теорию дифракции (GTD). В 1974 году Прабхакар Патхак и Роберт Куюмджян расширили (сингулярные) коэффициенты Келлера через равномерную теорию дифракции (UTD). ^{[21] [22]}

• Дифракция на острой металлической кромке
• Дифракция на мягкой апертуре с градиентом проводимости по ширине изображения

Узоры

Верхняя половина этого изображения показывает дифракционную картину луча He-Ne лазера на эллиптической апертуре. Нижняя половина — это его двумерное преобразование Фурье, приблизительно восстанавливающее форму апертуры.

Можно сделать несколько качественных наблюдений относительно дифракции в целом:

• Угловое расстояние между элементами дифракционной картины обратно пропорционально размерам объекта, вызывающего дифракцию. Другими словами: чем меньше дифрагирующий объект, тем «шире» результирующая дифракционная картина, и наоборот. (Точнее, это справедливо для синусов углов .)
• Углы дифракции инвариантны относительно масштабирования, то есть они зависят только от отношения длины волны к размеру дифрагирующего объекта.
• Когда дифрагирующий объект имеет периодическую структуру, например, в дифракционной решетке, черты обычно становятся более резкими. Третий рисунок, например, показывает сравнение двухщелевой картины с картиной, образованной пятью щелями, причем оба набора щелей имеют одинаковое расстояние между центром одной щели и следующей.

Дифракция волн материи

Согласно квантовой теории, каждая частица проявляет волновые свойства и, следовательно, может дифрагировать. Дифракция электронов и нейтронов является одним из весомых аргументов в пользу квантовой механики. Длина волны, связанная с частицей, называется длиной волны де Бройля , где — постоянная Планка , а — импульс частицы (масса × скорость для медленно движущихся частиц). Например, атом натрия, движущийся со скоростью около 300 м/с, будет иметь длину волны де Бройля около 50 пикометров. $${\displaystyle \lambda ={\frac {h}{p}}\,,}$$ ${\displaystyle h}$ ${\displaystyle p}$

Дифракция волн материи наблюдалась для малых частиц, таких как электроны, нейтроны, атомы и даже большие молекулы. Короткая длина волны этих волн материи делает их идеально подходящими для изучения атомной кристаллической структуры твердых тел, малых молекул и белков.

дифракция Брэгга

Согласно закону Брэгга , каждая точка (или отражение ) в этой дифракционной картине формируется в результате конструктивной интерференции рентгеновских лучей, проходящих через кристалл. Эти данные могут быть использованы для определения атомной структуры кристалла.

Дифракция от большой трехмерной периодической структуры, такой как многие тысячи атомов в кристалле, называется дифракцией Брэгга . Это похоже на то, что происходит, когда волны рассеиваются на дифракционной решетке . Дифракция Брэгга является следствием интерференции между волнами, отражающимися от многих различных кристаллических плоскостей. Условие конструктивной интерференции задается законом Брэгга : где — длина волны, — расстояние между кристаллическими плоскостями, — угол дифрагированной волны, — целое число, известное как порядок дифрагированного пучка. $${\displaystyle m\lambda =2d\sin \theta ,}$$ ${\displaystyle \lambda }$ ${\displaystyle d}$ ${\displaystyle \theta }$ ${\displaystyle m}$

Дифракцию Брэгга можно проводить с использованием либо электромагнитного излучения с очень короткой длиной волны, например, рентгеновских лучей , либо волн материи, например, нейтронов (и электронов ), длина волны которых порядка (или намного меньше) расстояния между атомами. ^[23] Полученная картина дает информацию о разделении кристаллографических плоскостей , что позволяет сделать вывод о структуре кристалла. ${\displaystyle d}$

Для полноты картины, дифракция Брэгга является пределом для большого числа атомов с рентгеновскими лучами или нейтронами и редко применима для дифракции электронов или с твердыми частицами в диапазоне размеров менее 50 нанометров. ^[23]

Слаженность

Описание дифракции основано на интерференции волн, исходящих из одного и того же источника и идущих разными путями к одной и той же точке на экране. В этом описании разница в фазе между волнами, идущими разными путями, зависит только от эффективной длины пути. Это не учитывает тот факт, что волны, приходящие на экран одновременно, были испущены источником в разное время. Начальная фаза, с которой источник испускает волны, может изменяться со временем непредсказуемым образом. Это означает, что волны, испускаемые источником в моменты времени, которые находятся слишком далеко друг от друга, больше не могут образовывать постоянную интерференционную картину, поскольку соотношение между их фазами больше не является независимым от времени. ^{[24] : 919}

Длина, на которой коррелируется фаза в луче света, называется длиной когерентности . Для того чтобы произошла интерференция, разность длин пути должна быть меньше длины когерентности. Иногда это называют спектральной когерентностью, так как это связано с наличием различных частотных компонентов в волне. В случае света, испускаемого атомным переходом , длина когерентности связана со временем жизни возбужденного состояния, из которого атом совершил переход. ^{[25] : 71–74  [26] : 314–316}

Если волны испускаются из протяженного источника, это может привести к некогерентности в поперечном направлении. При рассмотрении поперечного сечения пучка света длина, на которой коррелируется фаза, называется поперечной длиной когерентности. В случае эксперимента Юнга с двумя щелями это означало бы, что если поперечная длина когерентности меньше расстояния между двумя щелями, то результирующая картина на экране будет выглядеть как две однощелевые дифракционные картины. ^{[25] : 74–79}

В случае таких частиц, как электроны, нейтроны и атомы, длина когерентности связана с пространственной протяженностью волновой функции, описывающей частицу. ^{[27] : 107}

Приложения

Дифракция перед разрушением

Новый способ визуализации отдельных биологических частиц появился в 2010-х годах, используя яркие рентгеновские лучи, генерируемые рентгеновскими лазерами на свободных электронах . Эти фемтосекундные импульсы позволят (потенциально) визуализировать отдельные биологические макромолекулы. Благодаря этим коротким импульсам можно будет избежать радиационного повреждения и получить дифракционные картины отдельных биологических макромолекул. ^{[28] [29]}

Смотрите также

• Угловой чувствительный пиксель
• Атмосферная дифракция
• Призрак Броккена
• Радужность облаков
• Когерентная дифракционная визуализация
• Дифракция от щелей
• Дифракционный пик
• Дифракция против интерференции
• Дифракционный солнечный парус
• Дифрактометр
• Динамическая теория дифракции
• Электронная дифракция
• дифракция Фраунгофера
• Френелевский формирователь изображений
• Число Френеля
• зона Френеля
• Функция рассеяния точки
• Порошковая дифракция
• Квазиоптика
• Рефракция
• Отражение
• Дифракция Шефера–Бергмана
• Проклятие прореженного массива
• Рентгеновская дифракция

Ссылки

1. Франческо Мария Гримальди, Physico mathesis de lumine, coloribus, et iride, aliisque Attachis libri duo (Болонья («Бономия»), Италия: Витторио Бонати, 1665), стр. 2. Архивировано 1 декабря 2016 г. в Wayback Machine :

   Оригинал  : Nobis alius quartus modus illuxit, quem nunc proponimus, vocamusque; дифракция, quia advertimus lumen aliquando diffringi, hoc est partes eius multiplici dissectione separatas per idem tamen medium in diversa ulterius procedere, eo modo, quem mox declarabimus.

   Перевод  : Он осветил нам другой, четвертый путь, который мы теперь открываем и называем «дифракцией» [т. е. дроблением], потому что мы иногда наблюдаем, как свет распадается; то есть части соединения [т. е. луча света], разделенные делением, продвигаются дальше через среду, но в разных [направлениях], как мы вскоре покажем.

2. Каджори, Флориан «История физики в ее элементарных разделах, включая эволюцию физических лабораторий». Архивировано 01.12.2016 в Wayback Machine MacMillan Company, Нью-Йорк, 1899 г.
3. Беспроводная связь: принципы и практика, серия Prentice Hall по технике связи и новым технологиям, TS Rappaport, Prentice Hall, 2002 г., стр. 126
4. Suryanarayana, C.; Norton, M. Grant (29 июня 2013 г.). Рентгеновская дифракция: практический подход. Springer Science & Business Media. стр. 14. ISBN 978-1-4899-0148-4. Получено 7 января 2023 г. .
5. Коккотас, Костас Д. (2003). «Физика гравитационных волн». Энциклопедия физической науки и техники : 67–85. doi :10.1016/B0-12-227410-5/00300-8. ISBN 9780122274107.
6. Юффманн, Томас; Милич, Адриана; Мюлльнерич, Михаэль; Асенбаум, Питер; Цукерник, Александр; Тюксен, Йенс; Мэр Марсель; Чешновский, Ори; Арндт, Маркус (25 марта 2012 г.). «Визуализация квантовой интерференции одиночных молекул в реальном времени». Природные нанотехнологии . 7 (5): 297–300. arXiv : 1402.1867 . Бибкод : 2012NatNa...7..297J. дои : 10.1038/nnano.2012.34. ISSN  1748-3395. PMID  22447163. S2CID  5918772.
7. Комеч, Александр; Мерзон, Анатолий (2019), Комеч, Александр; Мерзон, Анатолий (ред.), «Ранняя теория дифракции», Стационарная дифракция на клиньях: метод автоморфных функций на комплексных характеристиках , Cham: Springer International Publishing, стр. 15–17, doi :10.1007/978-3-030-26699-8_2, ISBN 978-3-030-26699-8, получено 25 апреля 2024 г.
8. Франческо Мария Гримальди, Physico-mathesis de lumine, coloribus, et iride, aliisque adnexis… [Приложена физическая математика света, цвета, радуги и других вещей…] (Болонья («Bonomia»), (Италия): Витторио Бонати, 1665), стр. 1–11. Архивировано 1 декабря 2016 г. в Wayback Machine : «Propositio I. Lumen propagatur seu diffunditur Non solum Directe, Refracte, Ac Reflexe, sed etiam alio quodam Quarto Modo, Diffracte». (Предложение 1. Свет распространяется или распространяется не только прямолинейно, путем преломления и отражения, но и несколько иным четвертым путем: путем дифракции.) На с. 187, Гримальди также обсуждает интерференцию света от двух источников: «Propositio XXII. Lumen aliquando per sui communicationem reddit obscuriorem superficiem corporis aliunde, ac prius illustratam». (Предложение 22. Иногда свет в результате своего прохождения затемняет поверхность тела, [которая была] предварительно освещена другим [источником].)
9. Жан Луи Обер (1760). Мемуары по истории наук и изящных искусств. Париж: Отпечаток. де САС; Чез Э. Гано. стр. 149. Дифракция Гримальди 0–1800.
10. Сэр Дэвид Брюстер (1831). Трактат по оптике. Лондон: Longman, Rees, Orme, Brown & Green и John Taylor. С. 95.
11. Письмо Джеймса Грегори Джону Коллинзу от 13 мая 1673 г. Перепечатано в: Correspondence of Scientific Men of the Seventeenth Century … , под ред. Стивена Джордана Риго (Оксфорд, Англия: Oxford University Press , 1841), т. 2, стр. 251–255, особенно стр. 254 Архивировано 01.12.2016 в Wayback Machine .
12. Томас Янг (1 января 1804 г.). «Бейкерианская лекция: эксперименты и вычисления, относящиеся к физической оптике». Philosophical Transactions of the Royal Society of London . 94 : 1–16. Bibcode : 1804RSPT...94....1Y. doi : 10.1098/rstl.1804.0001 . S2CID  110408369.. (Примечание: эта лекция была прочитана в Королевском обществе 24 ноября 1803 года.)
13. Френель, Огюстен-Жан (1816), «Mémoire sur la diffraction de la lumière» («Мемуары о дифракции света»), Annales de Chimie et de Physique , vol. 1, стр. 239–81 (март 1816 г.); перепечатано как «Deuxième Mémoire…» («Вторые мемуары…») в Oeuvres complètes d'Augustin Fresnel , vol. 1 (Париж: Imprimerie Impériale, 1866), стр. 89–122. (Редакция «Первого мемуара», представленного 15 октября 1815 г.)
14. Френель, Огюстен-Жан (1818 г.), «Mémoire sur la diffraction de la lumière» («Мемуары о дифракции света»), депонированы 29 июля 1818 г., «коронованы» 15 марта 1819 г., опубликованы в Mémoires de l'Académie Royale. des Sciences de l'Institut de France , vol.  V (за 1821 и 1822 гг., напечатано в 1826 г.), стр. 339–475; перепечатано в Oeuvres complètes d'Augustin Fresnel , vol. 1 (Париж: Imprimerie Impériale, 1866), стр. 247–364; частично переведено как «Премия Френеля за воспоминания о дифракции света», в H. Crew (ред.), Волновая теория света: Мемуары Гюйгенса, Юнга и Френеля , American Book Company, 1900, стр. 81–144. ( Впервые опубликовано только в виде отрывков в Annales de Chimie et de Physique , т. 11 (1819), стр. 246–96, 337–78.)
15. Христиан Гюйгенс, Traité de la lumiere … Архивировано 16.06.2016 в Wayback Machine (Лейден, Нидерланды: Питер ван дер Аа, 1690), Глава 1. Со стр. 15 Архивировано 01.12.2016 в Wayback Machine : "J'ay donc monstré de quelle façon l'on peut concevoir que la lumiere s'etend successivement par des ondes spheriques, … " (Таким образом, я показал, каким образом можно представить, что свет распространяется последовательно сферическими волнами, … ) (Примечание: Гюйгенс опубликовал свой Traité в 1690 году; однако в предисловии к своей книге Гюйгенс утверждает, что в 1678 году он впервые передал свою книгу Французской королевской академии наук.)
16. Бейкер, Б. Б. и Копсон, Э. Т. (1939), Математическая теория принципа Гюйгенса , Оксфорд, стр. 36–40.
17. Дитрих Завиша. "Оптические эффекты на паутине" . Получено 21 сентября 2007 г.
18. Арумугам, Надя (9 сентября 2013 г.). «Food Explainer: Why Is Some Deli Meat Iridescent?». Slate . The Slate Group . Архивировано из оригинала 10 сентября 2013 г. Получено 9 сентября 2013 г.
19. Эндрю Нортон (2000). Динамические поля и волны физики. CRC Press. стр. 102. ISBN 978-0-7503-0719-2.
20. Chiao, RY; Garmire, E.; Townes, CH (1964). «Самоудерживание оптических лучей». Physical Review Letters . 13 (15): 479–482. Bibcode : 1964PhRvL..13..479C. doi : 10.1103/PhysRevLett.13.479.
21. Рахмат-Самии, Яхья (июнь 2013 г.). «GTD, UTD, UAT и STD: исторический обзор и личные наблюдения». Журнал IEEE Antennas and Propagation . 55 (3): 29–40. Bibcode : 2013IAPM...55...29R. doi : 10.1109/MAP.2013.6586622.
22. Kouyoumjian, RG; Pathak, PH (ноябрь 1974 г.). «Единообразная геометрическая теория дифракции для края идеально проводящей поверхности». Труды IEEE . 62 (11): 1448–1461. doi :10.1109/PROC.1974.9651.
23. Джон М. Коули (1975) Физика дифракции (Северная Голландия, Амстердам) ISBN 0-444-10791-6 
24. Холлидей, Дэвид; Резник, Роберт; Уокер, Джерл (2005), Основы физики (7-е изд.), США: John Wiley and Sons, Inc., ISBN 978-0-471-23231-5
25. Грант Р. Фаулз (1975). Введение в современную оптику . Courier Corporation. ISBN 978-0-486-65957-2.
26. Хехт, Юджин (2002). Оптика (4-е изд.). Соединенные Штаты Америки: Addison Wesley. ISBN 978-0-8053-8566-3.
27. Аяхико Ичимия; Филип И. Коэн (13 декабря 2004 г.). Дифракция электронов высокой энергии на отражение. Cambridge University Press. ISBN 978-0-521-45373-8. Архивировано из оригинала 16 июля 2017 года.
28. Нойце, Ричард; Ваутс, Ремко; ван дер Спул, Дэвид; Векерт, Эдгар; Хайду, Янош (август 2000 г.). «Потенциал биомолекулярной визуализации с помощью фемтосекундных рентгеновских импульсов». Nature . 406 (6797): 752–757. Bibcode :2000Natur.406..752N. doi :10.1038/35021099. ISSN  1476-4687. PMID  10963603. S2CID  4300920.
29. Чепмен, Генри Н.; Кейлман, Карл; Тимнеану, Никусор (17 июля 2014 г.). «Дифракция перед разрушением». Philosophical Transactions of the Royal Society B: Biological Sciences . 369 (1647): 20130313. doi :10.1098/rstb.2013.0313. PMC 4052855 . PMID  24914146. 

Внешние ссылки

• Фейнмановские лекции по физике, том I, гл. 30: Дифракция
• "Рассеяние и дифракция". Кристаллография . Международный союз кристаллографов .
• Использование компакт-диска в качестве дифракционной решетки на YouTube