Модель свободных электронов

В физике твердого тела модель свободных электронов является квантово-механической моделью поведения носителей заряда в металлическом твердом теле. Она была разработана в 1927 году ^[1] в основном Арнольдом Зоммерфельдом , который объединил классическую модель Друде с квантово-механической статистикой Ферми–Дирака , и поэтому она также известна как модель Друде–Зоммерфельда . ^{[Ashcroft & Mermin 1]}^{[Kittel 1]}

Учитывая его простоту, он удивительно успешно объясняет многие экспериментальные явления, особенно

закон Видемана–Франца, связывающий электропроводность и теплопроводность ;
температурная зависимость электронной теплоемкости ;
форма электронной плотности состояний ;
диапазон значений энергии связи;
электропроводности;
коэффициент термоэлектрического эффекта Зеебека ;
Термоэлектронная эмиссия и автоэлектронная эмиссия из объемных металлов.

Модель свободных электронов разрешила многие несоответствия, связанные с моделью Друде, и дала представление о нескольких других свойствах металлов. Модель свободных электронов предполагает, что металлы состоят из квантового электронного газа, в котором ионы почти не играют никакой роли. Модель может быть очень предсказательной при применении к щелочным и благородным металлам .

Идеи и предположения

В модели свободных электронов учитываются четыре основных предположения: ^{[Эшкрофт и Мермин 2]}

Приближение свободных электронов: Взаимодействие между ионами и валентными электронами в основном игнорируется, за исключением граничных условий. Ионы только сохраняют нейтральность заряда в металле. В отличие от модели Друде, ионы не обязательно являются источником столкновений.
Приближение независимых электронов : Взаимодействия между электронами игнорируются. Электростатические поля в металлах слабы из-за эффекта экранирования .
Приближение времени релаксации: существует некий неизвестный механизм рассеяния, такой, что вероятность столкновения электронов обратно пропорциональна времени релаксации , которое представляет собой среднее время между столкновениями. Столкновения не зависят от электронной конфигурации. $\тау$
Принцип исключения Паули : Каждое квантовое состояние системы может быть занято только одним электроном. Это ограничение доступных электронных состояний учитывается статистикой Ферми–Дирака (см. также Ферми-газ ). Основные предсказания модели свободных электронов выводятся из разложения Зоммерфельда заполнения Ферми–Дирака для энергий около уровня Ферми .

Название модели происходит от первых двух предположений, поскольку каждый электрон можно рассматривать как свободную частицу с соответствующим квадратичным соотношением между энергией и импульсом.

Кристаллическая решетка явно не учитывается в модели свободных электронов, но квантово-механическое обоснование было дано годом позже (1928) теоремой Блоха : несвязанный электрон движется в периодическом потенциале как свободный электрон в вакууме, за исключением того, что масса электрона m _e становится эффективной массой m* , которая может значительно отклоняться от m _e (можно даже использовать отрицательную эффективную массу для описания проводимости электронными дырками ). Эффективные массы могут быть получены из вычислений зонной структуры , которые изначально не учитывались в модели свободных электронов. ^{[ необходима цитата ]}

Из модели Друде

Многие физические свойства напрямую следуют из модели Друде , поскольку некоторые уравнения не зависят от статистического распределения частиц. Принятие классического распределения скоростей идеального газа или распределения скоростей газа Ферми изменяет только результаты, связанные со скоростью электронов. ^{[Ashcroft & Mermin 3]}

В основном, модель свободных электронов и модель Друде предсказывают одинаковую электропроводность постоянного тока σ для закона Ома , то есть ^{[Ashcroft & Mermin 4]}

\mathbf {J} =\сигма \mathbf {E} \quad

\quad \sigma ={\frac {ne^{2}\tau }{m_{e}}},

где — плотность тока , — внешнее электрическое поле, — электронная плотность (число электронов/объем), — среднее время свободного пробега , — электрический заряд электрона . $\mathbf {J}$ $\mathbf {E}$ $n$ $\tau$ $e$

Другие величины, которые остаются такими же в модели свободных электронов, как и в модели Друде, — это восприимчивость переменного тока, плазменная частота , магнитосопротивление и коэффициент Холла, связанный с эффектом Холла . ^{[Эшкрофт и Мермин 3]}

Свойства электронного газа

Многие свойства модели свободных электронов напрямую следуют из уравнений, связанных с газом Ферми, поскольку приближение независимых электронов приводит к ансамблю невзаимодействующих электронов. Для трехмерного электронного газа мы можем определить энергию Ферми как ^{[Ashcroft & Mermin 5]}

E_{\rm {F}}={\frac {\hbar ^{2}}{2m_{e}}}\left(3\pi ^{2}n\right)^{\frac {2}{3}},

где — приведенная постоянная Планка . Энергия Ферми определяет энергию электрона с самой высокой энергией при нулевой температуре. Для металлов энергия Ферми на порядок единиц электронвольт выше минимальной энергии зоны свободных электронов. ^[2] $\hbar$

Плотность состояний

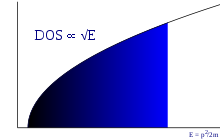
Трехмерная плотность состояний (число энергетических состояний на единицу энергии на объем) невзаимодействующего электронного газа определяется по формуле: ^{[ необходима ссылка ]}

g(E)={\frac {m_{e}}{\pi ^{2}\hbar ^{3}}}{\sqrt {2m_{e}E}}={\frac {3}{2}}{\frac {n}{E_{\rm {F}}}}{\sqrt {\frac {E}{E_{\rm {F}}}}},

где - энергия данного электрона. Эта формула учитывает вырождение спина, но не учитывает возможный сдвиг энергии из-за дна зоны проводимости . Для 2D плотность состояний постоянна, а для 1D обратно пропорциональна квадратному корню из энергии электрона. ${\textstyle E\geq 0}$

Уровень Ферми

Химический потенциал электронов в твердом теле также известен как уровень Ферми и, как и связанная с ним энергия Ферми , часто обозначается . Разложение Зоммерфельда можно использовать для расчета уровня Ферми ( ) при более высоких температурах как: ^{[Ashcroft & Mermin 6]} $\mu$ $E_{\rm {F}}$ $T>0$

E_{\rm {F}}(T)=E_{\rm {F}}(T=0)\left[1-{\frac {\pi ^{2}}{12}}\left({\frac {T}{T_{\rm {F}}}}\right)^{2}-{\frac {\pi ^{4}}{80}}\left({\frac {T}{T_{\rm {F}}}}\right)^{4}+\cdots \right],

где - температура, а мы определяем как температуру Ферми ( - постоянная Больцмана ). Пертурбативный подход оправдан, поскольку температура Ферми обычно составляет около 10 ⁵ К для металла, следовательно, при комнатной температуре или ниже энергия Ферми и химический потенциал практически эквивалентны. $T$ ${\textstyle T_{\rm {F}}=E_{\rm {F}}/k_{\rm {B}}}$ $k_{\rm {B}}$ $E_{\rm {F}}(T=0)$ $E_{\rm {F}}(T>0)$

Сжимаемость металлов и давление вырождения

Полную энергию на единицу объема (при ) можно также рассчитать путем интегрирования по фазовому пространству системы, получим ^{[Ashcroft & Mermin 7]} ${\textstyle T=0}$

u(0)={\frac {3}{5}}nE_{\rm {F}},

которая не зависит от температуры. Сравните с энергией на электрон идеального газа: , которая равна нулю при нулевой температуре. Для того чтобы идеальный газ имел ту же энергию, что и электронный газ, температуры должны быть порядка температуры Ферми. Термодинамически эта энергия электронного газа соответствует давлению при нулевой температуре, заданному ^{[Ashcroft & Mermin 7]} ${\textstyle {\frac {3}{2}}k_{\rm {B}}T}$

P=-\left({\frac {\partial U}{\partial V}}\right)_{T,\mu }={\frac {2}{3}}u(0),

где — объем, а — полная энергия, производная, произведенная при постоянной температуре и химическом потенциале. Это давление называется давлением вырождения электронов и возникает не из-за отталкивания или движения электронов, а из-за ограничения, что не более двух электронов (из-за двух значений спина) могут занимать один и тот же энергетический уровень. Это давление определяет сжимаемость или объемный модуль упругости металла ^{[Ashcroft & Mermin 7]} ${\textstyle V}$ ${\textstyle U(T)=u(T)V}$

B=-V\left({\frac {\partial P}{\partial V}}\right)_{T,\mu }={\frac {5}{3}}P={\frac {2}{3}}nE_{\rm {F}}.

Это выражение дает правильный порядок величины для объемного модуля для щелочных и благородных металлов, которые показывают, что это давление так же важно, как и другие эффекты внутри металла. Для других металлов необходимо учитывать кристаллическую структуру.

Магнитный отклик

Согласно теореме Бора–Ван Лиувена , классическая система в термодинамическом равновесии не может иметь магнитного отклика. Магнитные свойства материи в терминах микроскопической теории являются чисто квантово-механическими. Для электронного газа полный магнитный отклик является парамагнитным , а его магнитная восприимчивость определяется как ^{[ необходима цитата ]}

\chi ={\frac {2}{3}}\mu _{0}\mu _{\mathrm {B} }^{2}g(E_{\mathrm {F} }),

где — диэлектрическая проницаемость вакуума , а — магнетон Бора . Это значение получается в результате конкуренции двух вкладов: диамагнитного вклада (известного как диамагнетизм Ландау ), возникающего из-за орбитального движения электронов в присутствии магнитного поля, и парамагнитного вклада (парамагнетизм Паули). Последний вклад в три раза больше по абсолютной величине, чем диамагнитный вклад, и возникает из-за спина электрона , внутренней квантовой степени свободы, которая может принимать два дискретных значения и связана с магнитным моментом электрона . ${\textstyle \mu _{0}}$ ${\textstyle \mu _{\rm {B}}}$

Поправки к модели Друде

Теплоемкость

Одной из открытых проблем в физике твердого тела до появления квантовой механики было понимание теплоемкости металлов . Хотя большинство твердых тел имели постоянную объемную теплоемкость, заданную законом Дюлонга–Пти , около при больших температурах, он правильно предсказывал ее поведение при низких температурах. В случае металлов, которые являются хорошими проводниками, ожидалось, что электроны также вносят вклад в теплоемкость. $3nk_{\rm {B}}$

Классический расчет с использованием модели Друде, основанной на идеальном газе, дает объемную теплоемкость, определяемую выражением

c_{V}^{\text{Drude}}={\frac {3}{2}}nk_{\rm {B}}

Если бы это было так, то теплоемкость металла должна была бы составлять 1,5 от теплоемкости, полученной по закону Дюлонга–Пти.

Тем не менее, такой большой дополнительный вклад в теплоемкость металлов никогда не измерялся, что вызывает подозрения относительно приведенного выше аргумента. Используя расширение Зоммерфельда, можно получить поправки к плотности энергии при конечной температуре и получить объемную теплоемкость электронного газа, заданную как: ^{[Ashcroft & Mermin 8]}

c_{V}=\left({\frac {\partial u}{\partial T}}\right)_{n}={\frac {\pi ^{2}}{2}}{\frac {T}{T_{\rm {F}}}}nk_{\rm {B}}

где префактор к значительно меньше, чем 3/2, найденный в , примерно в 100 раз меньше при комнатной температуре и намного меньше при более низких . $nk_{B}$ ${\textstyle c_{V}^{\text{Drude}}}$ ${\textstyle T}$

Очевидно, что электронный вклад сам по себе не предсказывает закон Дюлонга-Пти , т.е. наблюдение, что теплоемкость металла остается постоянной при высоких температурах. Модель свободных электронов может быть улучшена в этом смысле путем добавления вклада колебаний кристаллической решетки. Две известные квантовые поправки включают модель твердого тела Эйнштейна и более совершенную модель Дебая . С добавлением последней объемная теплоемкость металла при низких температурах может быть более точно записана в виде, ^{[Ashcroft & Mermin 9]}

c_{V}\approx \gamma T+AT^{3}

где и — константы, связанные с материалом. Линейный член исходит из электронного вклада, а кубический член — из модели Дебая. При высокой температуре это выражение становится неверным, электронной теплоемкостью можно пренебречь, а общая теплоемкость металла стремится к константе, заданной законом Дюлонга–Пти. $\gamma$ $A$

Средняя длина свободного пробега

Обратите внимание, что без приближения времени релаксации нет причин для электронов отклонять свое движение, поскольку нет никаких взаимодействий, поэтому длина свободного пробега должна быть бесконечной. Модель Друде считала, что длина свободного пробега электронов близка к расстоянию между ионами в материале, подразумевая более ранний вывод о том, что диффузионное движение электронов было вызвано столкновениями с ионами. Длина свободного пробега в модели свободных электронов вместо этого задается выражением (где — скорость Ферми) и составляет порядка сотен ангстремов , что по крайней мере на один порядок больше любого возможного классического расчета. ^{[Ashcroft & Mermin 10]} Тогда длина свободного пробега не является результатом столкновений электронов с ионами, а связана с несовершенствами материала, либо из-за дефектов и примесей в металле, либо из-за тепловых флуктуаций. ^[3] ${\textstyle \lambda =v_{\rm {F}}\tau }$ ${\textstyle v_{\rm {F}}={\sqrt {2E_{\rm {F}}/m_{e}}}}$

Теплопроводность и термоЭДС

Хотя модель Друде предсказывает такое же значение электропроводности, как и модель свободных электронов, модели предсказывают несколько иную теплопроводность.

Теплопроводность определяется как для свободных частиц, которая пропорциональна теплоемкости и средней длине свободного пробега, которые зависят от модели ( — средняя (квадратичная) скорость электронов или скорость Ферми в случае модели свободных электронов). ^{[Эшкрофт и Мермин 10]} Это означает, что соотношение между теплопроводностью и электропроводностью определяется законом Видемана–Франца , $\kappa =c_{V}\tau \langle v^{2}\rangle /3$ $\langle v^{2}\rangle ^{1/2}$

{\frac {\kappa }{\sigma }}={\frac {m_{\rm {e}}c_{V}\langle v^{2}\rangle }{3ne^{2}}}=LT

где — число Лоренца, заданное ^{[Ashcroft & Mermin 11]} $L$

L=\left\{{\begin{matrix}\displaystyle {\frac {3}{2}}\left({\frac {k_{\rm {B}}}{e}}\right)^{2}\;,&{\text{Drude}}\\\displaystyle {\frac {\pi ^{2}}{3}}\left({\frac {k_{\rm {B}}}{e}}\right)^{2}\;,&{\text{free electron model.}}\end{matrix}}\right.

Модель свободных электронов ближе к измеренному значению V ² /K ² , тогда как предсказание Друде отклоняется примерно на половину значения, что не является большой разницей. Близкое предсказание к числу Лоренца в модели Друде было результатом того, что классическая кинетическая энергия электрона была примерно на 100 меньше, чем квантовая версия, что компенсирует большое значение классической теплоемкости. $L=2.44\times 10^{-8}$

Однако модель Друде предсказывает неправильный порядок величины для коэффициента Зеебека (термоЭДС), который связывает генерацию разности потенциалов путем приложения градиента температуры к образцу . Можно показать, что этот коэффициент равен , что просто пропорционально теплоемкости, поэтому модель Друде предсказывает константу, которая в сто раз больше значения модели свободных электронов. ^{[Ashcroft & Mermin 12]} В то время как последняя получает коэффициент, который линейен по температуре и обеспечивает гораздо более точные абсолютные значения порядка нескольких десятков мкВ/К при комнатной температуре. ^{[Ashcroft & Mermin 10]}^{[Ashcroft & Mermin 12]} Однако эта модель не может предсказать изменение знака ^{[Ashcroft & Mermin 13]} термоЭДС в литии и благородных металлах, таких как золото и серебро. ^[4] $\nabla V=-S\nabla T$ $S=-{c_{\rm {V}}}/{|ne|}$

Неточности и расширения

Модель свободных электронов имеет несколько недостатков, которые противоречат экспериментальным наблюдениям. Ниже мы перечислим некоторые неточности: ^{[Ashcroft & Mermin 13]}

Температурная зависимость: Модель свободных электронов представляет несколько физических величин, которые имеют неправильную температурную зависимость или вообще не имеют зависимости, как электропроводность. Теплопроводность и удельная теплоемкость хорошо предсказываются для щелочных металлов при низких температурах, но не предсказывают поведение при высоких температурах, возникающее из-за движения ионов и рассеяния фононов .
Эффект Холла и магнитосопротивление: Коэффициент Холла имеет постоянное значение $R H = -1/| ne |$ в модели Друде и в модели свободных электронов. Это значение не зависит от температуры и силы магнитного поля. Коэффициент Холла на самом деле зависит от зонной структуры , и разница с моделью может быть весьма существенной при изучении таких элементов, как магний и алюминий , которые имеют сильную зависимость от магнитного поля. Модель свободных электронов также предсказывает, что поперечное магнитосопротивление, сопротивление в направлении тока, не зависит от силы поля. Почти во всех случаях это так.
Направленный: Проводимость некоторых металлов может зависеть от ориентации образца относительно электрического поля. Иногда даже электрический ток не параллелен полю. Эта возможность не описывается, поскольку модель не учитывает кристалличность металлов, т. е. существование периодической решетки ионов.
Разнообразие проводимости: Не все материалы являются электрическими проводниками , некоторые не проводят электричество очень хорошо ( изоляторы ), некоторые могут проводить при добавлении примесей, как полупроводники . Также существуют полуметаллы с узкими зонами проводимости. Это разнообразие не предсказывается моделью и может быть объяснено только путем анализа валентных и проводящих зон . Кроме того, электроны не являются единственными носителями заряда в металле, электронные вакансии или дырки можно рассматривать как квазичастицы, несущие положительный электрический заряд. Проводимость дырок приводит к противоположному знаку для коэффициентов Холла и Зеебека, предсказываемых моделью.

Другие несоответствия присутствуют в законе Видемана-Франца при промежуточных температурах и частотной зависимости металлов в оптическом спектре. ^{[Эшкрофт и Мермин 13]}

Более точные значения электропроводности и закона Видемана-Франца можно получить, смягчив приближение времени релаксации, обратившись к уравнениям переноса Больцмана . ^{[Ashcroft & Mermin 13]}

Обменное взаимодействие полностью исключено из этой модели, и его включение может привести к другим магнитным реакциям, таким как ферромагнетизм . ^{[ необходима ссылка ]}

Непосредственное продолжение модели свободных электронов можно получить, предположив приближение пустой решетки , которое составляет основу модели зонной структуры, известной как модель почти свободных электронов . ^{[Эшкрофт и Мермин 13]}

Добавление отталкивающих взаимодействий между электронами не сильно меняет представленную здесь картину. Лев Ландау показал, что ферми-газ при отталкивающих взаимодействиях можно рассматривать как газ эквивалентных квазичастиц, которые слегка изменяют свойства металла. Модель Ландау теперь известна как теория ферми-жидкости . Более экзотические явления, такие как сверхпроводимость , где взаимодействия могут быть притягивающими, требуют более точной теории. ^{[ необходима цитата ]}

Смотрите также

Ссылки

Цитаты

^ Эшкрофт и Мермин 1976, Гл. 2 и Гл. 3
^ Эшкрофт и Мермин 1976, стр. 60
^ ab Ashcroft & Mermin 1976, стр. 49–51
^ Эшкрофт и Мермин 1976, стр. 7
↑ Эшкрофт и Мермин 1976, стр. 32–37.
↑ Эшкрофт и Мермин 1976, стр. 45–48.
^ abc Эшкрофт и Мермин 1976, стр. 38–39
^ Эшкрофт и Мермин 1976, стр. 47 (уравнение 2.81)
^ Эшкрофт и Мермин 1976, стр. 49
^ abc Эшкрофт и Мермин 1976, стр. 52
^ Эшкрофт и Мермин 1976, стр. 23 и 52 (уравнение 1.53 и 2.93)
^ ab Ashcroft & Mermin 1976, стр. 23
^ abcde Ashcroft & Mermin 1976, стр. 58–59.

^ Киттель 1972, Гл. 6

Ссылки

^ Зоммерфельд, Арнольд (1 января 1928). «Zur Elektronentheorie der Metalle auf Grund der Fermischen Statistik». Zeitschrift für Physik (на немецком языке). 47 (1–2): 1–32. Бибкод : 1928ZPhy...47....1S. дои : 10.1007/bf01391052. ISSN 0044-3328.
^ Nave, Rod. "Энергии Ферми, температуры Ферми и скорости Ферми". HyperPhysics . Получено 21.03.2018 .
^ Цымбал, Евгений (2008). "Электронный транспорт" (PDF) . Университет Небраски-Линкольн . Получено 21.04.2018 .
^ Xu, Bin; Verstraete, Matthieu J. (2014-05-14). "Первые принципы объяснения положительного коэффициента Зеебека лития". Physical Review Letters . 112 (19): 196603. arXiv : 1311.6805 . doi :10.1103/PhysRevLett.112.196603.

Общий

Киттель, Чарльз (1972). Введение в физику твердого тела . Мичиганский университет: Wiley & Sons. ISBN 978-0-471-49024-1.
Эшкрофт, Нил ; Мермин, Н. Дэвид (1976). Физика твердого тела . Нью-Йорк: Холт, Райнхарт и Уинстон. ISBN 978-0-03-083993-1.
Зоммерфельд, Арнольд ; Бете, Ганс (1933). Электронная теория металлов . Берлин Гейдельберг: Springer Verlag. ISBN 978-3642950025.
Займан, Дж. М. (1972). Принципы теории твердых тел (2-е изд.). Cambridge university press. ISBN 0-521-29733-8.