Анализ дисперсии

Сбор статистических моделей

Дисперсионный анализ ( ANOVA ) представляет собой набор статистических моделей и связанных с ними процедур оценки (таких как «вариация» среди групп и между ними), используемых для анализа различий между средними значениями. ANOVA был разработан статистиком Рональдом Фишером . ANOVA основан на законе общей дисперсии , где наблюдаемая дисперсия в конкретной переменной разбивается на компоненты, приписываемые различным источникам вариации. В своей простейшей форме ANOVA обеспечивает статистический тест того, равны ли два или более средних значения совокупности, и, следовательно, обобщает t -тест за пределы двух средних значений. Другими словами, ANOVA используется для проверки разницы между двумя или более средними значениями.

История

В то время как дисперсионный анализ достиг своего расцвета в 20 веке, предшественники, по словам Стиглера, уходят на столетия в прошлое . ^[1] К ним относятся проверка гипотез, разбиение сумм квадратов, экспериментальные методы и аддитивная модель. Лаплас проводил проверку гипотез в 1770-х годах. ^[2] Около 1800 года Лаплас и Гаусс разработали метод наименьших квадратов для объединения наблюдений, который улучшил методы, использовавшиеся тогда в астрономии и геодезии . Он также инициировал множество исследований вкладов в суммы квадратов. Лаплас знал, как оценить дисперсию из остаточной (а не общей) суммы квадратов. ^[3] К 1827 году Лаплас использовал методы наименьших квадратов для решения проблем ANOVA, касающихся измерений атмосферных приливов. ^[4] До 1800 года астрономы изолировали ошибки наблюдений, возникающие из-за времени реакции (« личное уравнение »), и разработали методы уменьшения ошибок. ^[5] Экспериментальные методы, используемые при изучении личного уравнения, позднее были приняты развивающейся областью психологии ^[6] , которая разработала сильные (полные факторные) экспериментальные методы, к которым вскоре были добавлены рандомизация и ослепление. ^[7] Красноречивое нематематическое объяснение модели аддитивных эффектов было доступно в 1885 году. ^[8]

Рональд Фишер ввел термин «дисперсия» и предложил его формальный анализ в статье 1918 года по теоретической популяционной генетике « Корреляция между родственниками при предположении о менделевском наследовании» . ^[9] Его первое применение дисперсионного анализа к анализу данных было опубликовано в 1921 году в работе «Исследования вариации сельскохозяйственных культур I» . ^[10] В ней вариация временного ряда была разделена на компоненты, представляющие ежегодные причины и медленное ухудшение. Следующая работа Фишера « Исследования вариации сельскохозяйственных культур II» , написанная совместно с Уинифред Маккензи и опубликованная в 1923 году, изучала вариацию урожайности на участках, засеянных разными сортами и подвергнутых разным обработкам удобрениями. ^[11] Дисперсионный анализ стал широко известен после того, как был включен в книгу Фишера 1925 года «Статистические методы для научных работников» .

Модели рандомизации были разработаны несколькими исследователями. Первая была опубликована на польском языке Ежи Нейманом в 1923 году. ^[12]

Пример

Не подходит: молодые против старых, с короткими волосами против длинных.

Справедливое соответствие: питомец против рабочей породы и менее спортивная против более спортивной

Очень хорошо подходит: Вес по породе

Дисперсионный анализ может быть использован для описания сложных взаимосвязей между переменными. Примером может служить выставка собак. Выставка собак не является случайной выборкой породы: она обычно ограничивается взрослыми, чистокровными и образцовыми собаками. Гистограмма веса собак с выставки, вероятно, будет довольно сложной, как желто-оранжевое распределение, показанное на иллюстрациях. Предположим, мы хотим предсказать вес собаки на основе определенного набора характеристик каждой собаки. Один из способов сделать это — объяснить распределение веса, разделив популяцию собак на группы на основе этих характеристик. Успешная группировка разделит собак таким образом, что (a) каждая группа будет иметь низкую дисперсию веса собак (то есть группа будет относительно однородной) и (b) среднее значение каждой группы будет различным (если две группы имеют одинаковое среднее значение, то неразумно делать вывод о том, что группы фактически разделены каким-либо значимым образом).

На иллюстрациях справа группы обозначены как X ₁ , X ₂ и т. д. На первой иллюстрации собаки разделены в соответствии с произведением (взаимодействием) двух бинарных группировок: молодые против старых и короткошерстные против длинношерстных (например, группа 1 — молодые собаки с короткой шерстью, группа 2 — молодые собаки с длинной шерстью и т. д.). Поскольку распределение веса собак внутри каждой из групп (показано синим цветом) имеет относительно большую дисперсию, а средние значения очень похожи по группам, группировка собак по этим характеристикам не дает эффективного способа объяснить вариацию веса собак: знание того, в какой группе находится собака, не позволяет нам предсказать ее вес намного лучше, чем просто знание того, что собака участвует в выставке собак. Таким образом, эта группировка не может объяснить вариацию в общем распределении (желто-оранжевый).

Попытка объяснить распределение веса, сгруппировав собак как домашних животных против рабочих пород и менее спортивных против более спортивных, вероятно, была бы несколько более успешной (справедливое соответствие). Самые тяжелые выставочные собаки, скорее всего, будут крупными, сильными, рабочими породами, в то время как породы, содержащиеся в качестве домашних животных, как правило, меньше и, следовательно, легче. Как показано на второй иллюстрации, распределения имеют дисперсии, которые значительно меньше, чем в первом случае, а средние значения более различимы. Однако значительное перекрытие распределений, например, означает, что мы не можем надежно различить X ₁ и X _2. Группировка собак по подбрасыванию монеты может привести к распределениям, которые выглядят похожими.

Попытка объяснить вес породой, скорее всего, даст очень хорошее соответствие. Все чихуахуа легкие, а все сенбернары тяжелые. Разница в весе между сеттерами и пойнтерами не оправдывает разделение пород. Дисперсионный анализ предоставляет формальные инструменты для обоснования этих интуитивных суждений. Распространенным применением метода является анализ экспериментальных данных или разработка моделей. Метод имеет некоторые преимущества по сравнению с корреляцией: не все данные должны быть числовыми, и одним из результатов метода является суждение о достоверности объясняющей связи.

Классы моделей

В дисперсионном анализе используются три класса моделей, которые описаны здесь.

Модели с фиксированными эффектами

Модель с фиксированными эффектами (класс I) дисперсионного анализа применяется к ситуациям, в которых экспериментатор применяет одно или несколько воздействий к субъектам эксперимента, чтобы увидеть, изменяются ли значения переменной отклика . Это позволяет экспериментатору оценить диапазоны значений переменной отклика, которые воздействие будет генерировать в популяции в целом.

Фиксированные эффекты против случайных эффектов

Модели случайных эффектов

Модель случайных эффектов (класс II) используется, когда обработки не фиксированы. Это происходит, когда различные уровни факторов выбираются из более крупной популяции. Поскольку сами уровни являются случайными величинами , некоторые предположения и метод сопоставления обработок (многовариантное обобщение простых различий) отличаются от модели фиксированных эффектов. ^[13]

Модели смешанных эффектов

Модель со смешанными эффектами (класс III) содержит экспериментальные факторы как фиксированного, так и случайного типов эффектов, с соответственно различными интерпретациями и анализом для двух типов.

Пример

Обучающие эксперименты могут проводиться факультетом колледжа или университета, чтобы найти хороший вводный учебник, при этом каждый текст может считаться лечением. Модель с фиксированными эффектами будет сравнивать список текстов-кандидатов. Модель со случайными эффектами будет определять, существуют ли важные различия в списке случайно выбранных текстов. Модель со смешанными эффектами будет сравнивать (фиксированные) действующие тексты со случайно выбранными альтернативами.

Определение фиксированных и случайных эффектов оказалось неуловимым, поскольку существует множество конкурирующих определений. ^[14]

Предположения

Анализ дисперсии изучался с помощью нескольких подходов, наиболее распространенный из которых использует линейную модель , которая связывает ответ с обработками и блоками. Обратите внимание, что модель линейна по параметрам, но может быть нелинейной по уровням факторов. Интерпретация проста, когда данные сбалансированы по факторам, но для несбалансированных данных требуется гораздо более глубокое понимание.

Анализ учебника с использованием нормального распределения

Дисперсионный анализ можно представить в виде линейной модели , которая делает следующие предположения о распределении вероятностей ответов: ^{[15] [16] [17] [18]}

• Независимость наблюдений – это допущение модели, упрощающее статистический анализ.
• Нормальность – остатки распределены нормально .
• Равенство (или «однородность») дисперсий, называемое гомоскедастичностью — дисперсия данных в группах должна быть одинаковой.

Отдельные предположения модели учебника подразумевают, что ошибки независимы, идентичны и нормально распределены для моделей с фиксированными эффектами, то есть, что ошибки ( ) независимы и ${\displaystyle \varepsilon }$ $${\displaystyle \varepsilon \thicksim N(0,\sigma ^{2}).}$$

Анализ на основе рандомизации

В рандомизированном контролируемом эксперименте воздействия случайным образом назначаются экспериментальным единицам в соответствии с экспериментальным протоколом. Эта рандомизация является объективной и объявляется до проведения эксперимента. Объективное случайное назначение используется для проверки значимости нулевой гипотезы в соответствии с идеями CS Peirce и Ronald Fisher . Этот анализ, основанный на дизайне, обсуждался и разрабатывался Francis J. Anscombe на Rothamsted Experimental Station и Oscar Kempthorne в Iowa State University . ^[19] Kempthorne и его студенты делают предположение об аддитивности воздействия единиц , которое обсуждается в книгах Kempthorne и David R. Cox . ^{[20] [21]}

Аддитивность единичной обработки

В своей простейшей форме предположение об аддитивности единицы воздействия ^{[nb 1]} гласит, что наблюдаемая реакция экспериментальной единицы при получении воздействия может быть записана как сумма реакции единицы и эффекта воздействия , то есть ^{[22] [23] [24]} Предположение об аддитивности единицы воздействия подразумевает, что для каждой обработки й вид воздействия оказывает точно такой же эффект на каждую экспериментальную единицу. ${\displaystyle y_{i,j}}$ ${\displaystyle i}$ ${\displaystyle j}$ ${\displaystyle y_{i}}$ ${\displaystyle t_{j}}$ $${\displaystyle y_{i,j}=y_{i}+t_{j}.}$$ ${\displaystyle j}$ ${\displaystyle j}$ ${\displaystyle t_{j}}$

Предположение об аддитивности единичного лечения обычно не может быть напрямую фальсифицировано , согласно Коксу и Кемпторну. Однако многие следствия аддитивности единичного лечения могут быть фальсифицированы. Для рандомизированного эксперимента предположение об аддитивности единичного лечения подразумевает , что дисперсия постоянна для всех видов лечения. Поэтому, контрапозицией , необходимым условием аддитивности единичного лечения является то, что дисперсия постоянна.

Использование аддитивности единичного воздействия и рандомизации аналогично выводу на основе дизайна, который является стандартным при выборочном обследовании конечной популяции .

Полученная линейная модель

Кемпторн использует рандомизацию-распределение и предположение об аддитивности единичного воздействия для создания производной линейной модели , очень похожей на модель из учебника, обсуждавшуюся ранее. ^[25] Тестовая статистика этой производной линейной модели близко аппроксимируется тестовой статистикой соответствующей нормальной линейной модели, согласно теоремам аппроксимации и исследованиям моделирования. ^[26] Однако есть и различия. Например, анализ на основе рандомизации приводит к небольшой, но (строго) отрицательной корреляции между наблюдениями. ^{[27] [28]} В анализе на основе рандомизации нет предположения о нормальном распределении и, конечно, нет предположения о независимости . Напротив, наблюдения зависимы !

Анализ на основе рандомизации имеет тот недостаток, что его изложение требует утомительной алгебры и большого количества времени. Поскольку анализ на основе рандомизации сложен и близко аппроксимируется подходом с использованием нормальной линейной модели, большинство преподавателей подчеркивают подход с использованием нормальной линейной модели. Мало кто из статистиков возражает против анализа на основе модели сбалансированных рандомизированных экспериментов.

Статистические модели для данных наблюдений

Однако при применении к данным нерандомизированных экспериментов или наблюдательных исследований анализ на основе моделей не имеет гарантии рандомизации. ^[29] Для наблюдательных данных вывод доверительных интервалов должен использовать субъективные модели, как подчеркивали Рональд Фишер и его последователи. На практике оценки эффектов лечения из наблюдательных исследований, как правило, часто непоследовательны. На практике «статистические модели» и наблюдательные данные полезны для предложения гипотез, к которым общественность должна относиться очень осторожно. ^[30]

Резюме предположений

Анализ ANOVA на основе нормальной модели предполагает независимость, нормальность и однородность дисперсий остатков. Анализ на основе рандомизации предполагает только однородность дисперсий остатков (как следствие аддитивности единичного воздействия) и использует процедуру рандомизации эксперимента. Оба эти анализа требуют гомоскедастичности как предположения для анализа нормальной модели и как следствие рандомизации и аддитивности для анализа на основе рандомизации.

Однако исследования процессов, которые изменяют дисперсии, а не средние значения (так называемые эффекты дисперсии), были успешно проведены с использованием ANOVA. ^[31] Для ANOVA в его полной общности нет необходимых предположений, но F - тест , используемый для проверки гипотез ANOVA, имеет предположения и практические ограничения, которые продолжают представлять интерес.

Проблемы, которые не удовлетворяют предположениям ANOVA, часто можно преобразовать, чтобы удовлетворить предположениям. Свойство аддитивности единичной обработки не является инвариантным относительно «изменения масштаба», поэтому статистики часто используют преобразования для достижения аддитивности единичной обработки. Если ожидается, что переменная отклика будет следовать параметрическому семейству распределений вероятностей, то статистик может указать (в протоколе эксперимента или наблюдательного исследования), что отклики должны быть преобразованы для стабилизации дисперсии. ^[32] Кроме того, статистик может указать, что логарифмические преобразования должны применяться к откликам, которые, как полагают, следуют мультипликативной модели. ^{[23] [33]} Согласно теореме Коши о функциональном уравнении , логарифм является единственным непрерывным преобразованием, которое преобразует действительное умножение в сложение. ^{[ необходима ссылка ]}

Характеристики

ANOVA используется при анализе сравнительных экспериментов, в которых интерес представляет только разница в результатах. Статистическая значимость эксперимента определяется отношением двух дисперсий. Это отношение не зависит от нескольких возможных изменений экспериментальных наблюдений: Добавление константы ко всем наблюдениям не меняет значимости. Умножение всех наблюдений на константу не меняет значимости. Таким образом, результат статистической значимости ANOVA не зависит от смещения константы и ошибок масштабирования, а также от единиц, используемых при выражении наблюдений. В эпоху механических вычислений было принято вычитать константу из всех наблюдений (когда это эквивалентно отбрасыванию первых цифр) для упрощения ввода данных. ^{[34] [35]} Это пример кодирования данных .

Алгоритм

Расчеты ANOVA можно охарактеризовать как вычисление ряда средних значений и дисперсий, деление двух дисперсий и сравнение отношения со значением из справочника для определения статистической значимости. Расчет эффекта лечения затем тривиален: «эффект любого лечения оценивается путем взятия разницы между средним значением наблюдений, которые подвергаются лечению, и общим средним значением». ^[36]

текст-середина

Разложение суммы квадратов

Таблица однофакторного дисперсионного анализа, показывающая пример выходных данных

ANOVA использует традиционную стандартизированную терминологию. Уравнение определения дисперсии выборки — , где делитель называется степенями свободы (DF), суммирование называется суммой квадратов (SS), результат называется средним квадратом (MS), а квадраты членов являются отклонениями от среднего выборки. ANOVA оценивает 3 дисперсии выборки: общую дисперсию, основанную на всех отклонениях наблюдений от общего среднего, дисперсию ошибки, основанную на всех отклонениях наблюдений от соответствующих средних значений обработки, и дисперсию обработки. Дисперсия обработки основана на отклонениях средних значений обработки от общего среднего, результат умножается на количество наблюдений в каждой обработке для учета разницы между дисперсией наблюдений и дисперсией средних значений. ${\textstyle s^{2}={\frac {1}{n-1}}\sum _{i}(y_{i}-{\bar {y}})^{2}}$

Фундаментальный метод — это разбиение общей суммы квадратов SS на компоненты, связанные с эффектами, используемыми в модели. Например, модель для упрощенного ANOVA с одним типом лечения на разных уровнях.

$${\displaystyle SS_{\text{Total}}=SS_{\text{Error}}+SS_{\text{Treatments}}}$$

Число степеней свободы DF можно разделить аналогичным образом: один из этих компонентов (для ошибки) определяет распределение хи-квадрат , которое описывает соответствующую сумму квадратов, в то время как то же самое справедливо для «обработок», если эффект обработки отсутствует.

$${\displaystyle DF_{\text{Total}}=DF_{\text{Error}}+DF_{\text{Treatments}}}$$

TheФ-тест

Для проверки статистической значимости однофакторного дисперсионного анализа мы обращаемся к таблице F-вероятности, используя степени свободы на уровне альфа 0,05 . После вычисления F-статистики мы сравниваем значение на пересечении каждой степени свободы, также известное как критическое значение. Если F-статистика больше по величине, чем ее критическое значение, мы можем сказать, что есть статистическая значимость на уровне альфа 0,05 .

F - тест используется для сравнения факторов общего отклонения. Например, в однофакторном ANOVA статистическая значимость проверяется путем сравнения статистики F-теста

$${\displaystyle F={\frac {\text{variance between treatments}}{\text{variance within treatments}}}}$$ $${\displaystyle F={\frac {MS_{\text{Treatments}}}{MS_{\text{Error}}}}={{SS_{\text{Treatments}}/(I-1)} \over {SS_{\text{Error}}/(n_{T}-I)}}}$$

где MS — среднеквадратичное значение, — количество процедур, — общее количество случаев. ${\displaystyle I}$ ${\displaystyle n_{T}}$

к F -распределению , где числитель — это степени свободы, а знаменатель — это степени свободы. Использование F -распределения — естественный кандидат, поскольку тестовая статистика — это отношение двух масштабированных сумм квадратов, каждая из которых следует масштабированному распределению хи-квадрат . ${\displaystyle I-1}$ ${\displaystyle n_{T}-I}$

Ожидаемое значение F равно (где — размер выборки лечения), что равно 1 при отсутствии эффекта лечения. По мере того, как значения F увеличиваются выше 1, доказательства все больше не согласуются с нулевой гипотезой. Два очевидных экспериментальных метода увеличения F — это увеличение размера выборки и уменьшение дисперсии ошибок путем жесткого экспериментального контроля. ${\displaystyle 1+{n\sigma _{\text{Treatment}}^{2}}/{\sigma _{\text{Error}}^{2}}}$ ${\displaystyle n}$

Существует два метода завершения проверки гипотезы ANOVA, оба из которых дают одинаковый результат:

• Метод учебника заключается в сравнении наблюдаемого значения F с критическим значением F, определенным из таблиц. Критическое значение F является функцией степеней свободы числителя и знаменателя и уровня значимости ( α ). Если F ≥ F _Critical , нулевая гипотеза отклоняется.
• Компьютерный метод вычисляет вероятность (p-значение) значения F, большего или равного наблюдаемому значению. Нулевая гипотеза отклоняется, если эта вероятность меньше или равна уровню значимости ( α ).

Известно, что F -тест ANOVA почти оптимален в смысле минимизации ложноотрицательных ошибок для фиксированного уровня ложноположительных ошибок (т. е. максимизации мощности для фиксированного уровня значимости). Например, для проверки гипотезы о том, что различные методы лечения имеют абсолютно одинаковый эффект, p -значения F -теста близко приближаются к p-значениям теста перестановки : приближение особенно близко, когда дизайн сбалансирован. ^{[26] [37]} Такие тесты перестановки характеризуют тесты с максимальной мощностью против всех альтернативных гипотез , как заметил Розенбаум . ^{[nb 2]} F -тест ANOVA (нулевой гипотезы о том, что все методы лечения имеют абсолютно одинаковый эффект) рекомендуется в качестве практического теста из-за его устойчивости против многих альтернативных распределений. ^{[38] [nb 3]}

Расширенный алгоритм

ANOVA состоит из отдельных частей; разделение источников дисперсии и проверка гипотез могут использоваться по отдельности. ANOVA используется для поддержки других статистических инструментов. Регрессия сначала используется для подгонки более сложных моделей к данным, затем ANOVA используется для сравнения моделей с целью выбора простых(r) моделей, которые адекватно описывают данные. «Такие модели могут быть подогнаны без какой-либо ссылки на ANOVA, но инструменты ANOVA затем могут быть использованы для придания некоторого смысла подобранным моделям и для проверки гипотез о пакетах коэффициентов». ^[39] «[М]ы думаем об анализе дисперсии как о способе понимания и структурирования многоуровневых моделей — не как об альтернативе регрессии, а как об инструменте для обобщения сложных многомерных выводов...» ^[39]

Для одного фактора

Самый простой эксперимент, подходящий для анализа ANOVA, — это полностью рандомизированный эксперимент с одним фактором. Более сложные эксперименты с одним фактором включают ограничения на рандомизацию и включают полностью рандомизированные блоки и латинские квадраты (и варианты: греко-латинские квадраты и т. д.). Более сложные эксперименты разделяют многие сложности множественных факторов.

Существуют некоторые альтернативы традиционному однофакторному дисперсионному анализу, например: гетероскедастический F-тест Уэлча, гетероскедастический F-тест Уэлча с усеченными средними и винзоризованными дисперсиями, тест Брауна-Форсайта, тест Александера-Говерна, тест Джеймса второго порядка и тест Краскела-Уоллиса, доступные в однофакторных тестах R.

Полезно представить каждую точку данных в следующей форме, называемой статистической моделью: где $${\displaystyle Y_{ij}=\mu +\tau _{j}+\varepsilon _{ij}}$$

• я = 1, 2, 3, ..., Р
• j = 1, 2, 3, ..., С
• μ = общее среднее (среднее)
• τ _j = дифференциальный эффект (реакция), связанный с уровнем j X;
  это предполагает, что в целом значения τ _j в сумме равны нулю (то есть, ) ${\textstyle \sum _{j=1}^{C}\tau _{j}=0}$
• ε _ij = шум или ошибка, связанная с конкретным значением данных ij

То есть мы представляем себе аддитивную модель, которая утверждает, что каждая точка данных может быть представлена ​​путем суммирования трех величин: истинного среднего значения, усредненного по всем исследуемым уровням факторов, плюс инкрементный компонент, связанный с конкретным столбцом (уровнем факторов), плюс конечный компонент, связанный со всем остальным, что влияет на это конкретное значение данных.

Для нескольких факторов

ANOVA обобщает изучение эффектов множественных факторов. Когда эксперимент включает наблюдения при всех комбинациях уровней каждого фактора, он называется факторным . Факторные эксперименты более эффективны, чем серия экспериментов с одним фактором, и эффективность растет с увеличением числа факторов. ^[40] Следовательно, факторные планы широко используются.

Использование ANOVA для изучения эффектов нескольких факторов имеет сложность. В 3-факторном ANOVA с факторами x, y и z модель ANOVA включает термины для основных эффектов (x, y, z) и термины для взаимодействий (xy, xz, yz, xyz). Все термины требуют проверки гипотез. Распространение терминов взаимодействия увеличивает риск того, что некоторые проверки гипотез дадут ложноположительный результат случайно. К счастью, опыт показывает, что взаимодействия высокого порядка редки. ^{[41] [ требуется проверка ]} Возможность обнаруживать взаимодействия является основным преимуществом многофакторного ANOVA. Проверка одного фактора за раз скрывает взаимодействия, но дает явно непоследовательные экспериментальные результаты. ^[40]

Рекомендуется проявлять осторожность при столкновении со взаимодействиями; Сначала проверьте условия взаимодействия и расширьте анализ за пределы ANOVA, если взаимодействия обнаружены. Тексты различаются в своих рекомендациях относительно продолжения процедуры ANOVA после обнаружения взаимодействия. Взаимодействия усложняют интерпретацию экспериментальных данных. Ни расчеты значимости, ни предполагаемые эффекты лечения не могут быть приняты за чистую монету. «Значительное взаимодействие часто будет маскировать значимость основных эффектов». ^[42] Для улучшения понимания рекомендуются графические методы. Регрессия часто полезна. Подробное обсуждение взаимодействий доступно в Cox (1958). ^[43] Некоторые взаимодействия можно удалить (путем преобразований), а другие — нет.

Для снижения расходов в многофакторном ANOVA используются различные методы. Один из методов, используемых в факторных планах, заключается в минимизации повторений (возможно, без повторений с поддержкой аналитических уловок ) и объединении групп, когда эффекты оказываются статистически (или практически) незначимыми. Эксперимент со многими незначимыми факторами может свестись к эксперименту с несколькими факторами, поддерживаемыми многими повторениями. ^[44]

Ассоциированный анализ

Некоторый анализ требуется для поддержки дизайна эксперимента , в то время как другой анализ выполняется после того, как формально обнаружено, что изменения факторов приводят к статистически значимым изменениям в ответах. Поскольку экспериментирование является итеративным, результаты одного эксперимента изменяют планы для следующих экспериментов.

Подготовительный анализ

Количество экспериментальных единиц

При планировании эксперимента количество экспериментальных единиц планируется для удовлетворения целей эксперимента. Экспериментирование часто является последовательным.

Ранние эксперименты часто разрабатываются для получения несмещенных оценок эффектов лечения и экспериментальной ошибки. Более поздние эксперименты часто разрабатываются для проверки гипотезы о том, что эффект лечения имеет важную величину; в этом случае количество экспериментальных единиц выбирается таким образом, чтобы эксперимент не выходил за рамки бюджета и имел достаточную мощность, среди прочих целей.

Отчетность по анализу размера выборки обычно требуется в психологии. «Предоставьте информацию о размере выборки и процессе, который привел к решениям о размере выборки». ^[45] Анализ, который записывается в экспериментальном протоколе до проведения эксперимента, рассматривается в заявках на гранты и административных наблюдательных советах.

Помимо анализа мощности существуют менее формальные методы выбора числа экспериментальных единиц. К ним относятся графические методы, основанные на ограничении вероятности ложноотрицательных ошибок, графические методы, основанные на ожидаемом увеличении вариации (выше остатков) и методы, основанные на достижении желаемого доверительного интервала. ^[46]

Анализ мощности

Анализ мощности часто применяется в контексте ANOVA для оценки вероятности успешного отклонения нулевой гипотезы, если мы предполагаем определенный дизайн ANOVA, размер эффекта в популяции, размер выборки и уровень значимости. Анализ мощности может помочь в разработке исследования, определяя, какой размер выборки потребуется для того, чтобы иметь разумный шанс отклонения нулевой гипотезы, когда альтернативная гипотеза верна. ^{[47] [48] [49] [50]}

Размер эффекта

Размер эффекта

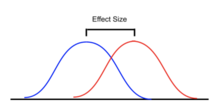
Несколько стандартизированных мер эффекта были предложены для ANOVA, чтобы суммировать силу связи между предиктором(ами) и зависимой переменной или общей стандартизированной разницей полной модели. Стандартизированные оценки размера эффекта облегчают сравнение результатов в разных исследованиях и дисциплинах. Однако, хотя стандартизированные размеры эффекта обычно используются в большей части профессиональной литературы, нестандартизированная мера размера эффекта, которая имеет немедленно «значимые» единицы, может быть предпочтительнее для целей отчетности. ^[51]

Подтверждение модели

Иногда проводятся тесты, чтобы определить, нарушаются ли предположения ANOVA. Остатки проверяются или анализируются для подтверждения гомоскедастичности и общей нормальности. ^[52] Остатки должны иметь вид шума (нормальное распределение с нулевым средним) при построении графика как функции чего-либо, включая время и смоделированные значения данных. Тенденции намекают на взаимодействие между факторами или между наблюдениями.

Последующие тесты

Статистически значимый эффект в ANOVA часто сопровождается дополнительными тестами. Это может быть сделано для того, чтобы оценить, какие группы отличаются от других групп, или для проверки различных других целевых гипотез. Последующие тесты часто различаются с точки зрения того, являются ли они «запланированными» ( a priori ) или «post hoc ». Запланированные тесты определяются до рассмотрения данных, а post hoc тесты задумываются только после рассмотрения данных (хотя термин «post hoc» используется непоследовательно).

Последующие тесты могут быть «простыми» парными сравнениями средних значений отдельных групп или «сложными» сравнениями (например, сравнением среднего объединения по группам A, B и C со средним значением группы D). Сравнения также могут рассматривать тесты тренда, такие как линейные и квадратичные отношения, когда независимая переменная включает упорядоченные уровни. Часто последующие тесты включают метод корректировки для проблемы множественных сравнений .

Последующие тесты для определения того, какие конкретные группы, переменные или факторы имеют статистически разные средние значения, включают тест размаха Тьюки и новый тест множественного размаха Дункана . В свою очередь, эти тесты часто сопровождаются методологией компактного отображения букв (CLD) , чтобы сделать вывод упомянутых тестов более прозрачным для аудитории, не являющейся статистиком.

Проекты исследований

Существует несколько типов ANOVA. Многие статистики основывают ANOVA на дизайне эксперимента , ^[53] особенно на протоколе, который определяет случайное назначение методов лечения субъектам; описание протокола механизма назначения должно включать спецификацию структуры методов лечения и любого блокирования . Также часто применяют ANOVA к данным наблюдений с использованием соответствующей статистической модели. ^[54]

Некоторые популярные разработки используют следующие типы ANOVA:

• Однофакторный дисперсионный анализ (ANOVA) используется для проверки различий между двумя или более независимыми группами (средними значениями), например, различные уровни применения мочевины в культуре или различные уровни воздействия антибиотиков на несколько различных видов бактерий ^[55] или различные уровни воздействия некоторых лекарств на группы пациентов. Однако, если эти группы не являются независимыми, и существует порядок в группах (например, легкое, среднее и тяжелое заболевание) или в дозе лекарства (например, 5 мг/мл, 10 мг/мл, 20 мг/мл), назначаемой одной и той же группе пациентов, то следует использовать оценку линейного тренда . Однако, как правило, однофакторный дисперсионный анализ (ANOVA) используется для проверки различий между по крайней мере тремя группами, поскольку случай с двумя группами может быть охвачен t-тестом . ^[56] Когда есть только два средних значения для сравнения, t-тест и F -тест ANOVA эквивалентны; связь между ANOVA и t задается как F = t ² .
• Факторный дисперсионный анализ применяется при наличии более одного фактора.
• Повторные измерения ANOVA применяются, когда для каждого фактора используются одни и те же субъекты (например, в продольном исследовании ).
• Многомерный дисперсионный анализ (MANOVA) используется, когда имеется более одной переменной отклика .

Предостережения

Сбалансированные эксперименты (с одинаковым размером выборки для каждого лечения) относительно легко интерпретировать; несбалансированные эксперименты предлагают больше сложности. Для однофакторного (одностороннего) ANOVA корректировка для несбалансированных данных проста, но несбалансированному анализу не хватает как надежности, так и мощности. ^[57] Для более сложных планов отсутствие баланса приводит к дальнейшим осложнениям. «Свойство ортогональности основных эффектов и взаимодействий, присутствующих в сбалансированных данных, не переносится на несбалансированный случай. Это означает, что обычные методы дисперсионного анализа неприменимы. Следовательно, анализ несбалансированных факториалов намного сложнее, чем для сбалансированных планов». ^[58] В общем случае «дисперсионный анализ также может быть применен к несбалансированным данным, но тогда суммы квадратов, средние квадраты и F -коэффициенты будут зависеть от порядка, в котором рассматриваются источники вариации». ^[39]

ANOVA (отчасти) является тестом статистической значимости. Американская психологическая ассоциация (и многие другие организации) придерживается мнения, что простое сообщение статистической значимости недостаточно и что предпочтительнее сообщение доверительных границ. ^[51]

Обобщения

ANOVA считается частным случаем линейной регрессии ^{[59] [60]} , которая в свою очередь является частным случаем общей линейной модели . ^[61] Все рассматривают наблюдения как сумму модели (подгонки) и остатка (ошибки), подлежащего минимизации.

Тест Краскела-Уоллиса и тест Фридмана являются непараметрическими тестами, которые не опираются на предположение о нормальности. ^{[62] [63]}

Связь с линейной регрессией

Ниже мы проясним связь между многофакторным дисперсионным анализом и линейной регрессией.

Линейно переупорядочиваем данные так, чтобы -ое наблюдение было связано с ответом и факторами , где обозначает различные факторы, а - общее количество факторов. В однофакторном ANOVA и двухфакторном ANOVA . Кроме того, мы предполагаем, что -ый фактор имеет уровни, а именно . Теперь мы можем закодировать факторы методом one-hot в размерный вектор . ${\displaystyle k}$ ${\displaystyle y_{k}}$ ${\displaystyle Z_{k,b}}$ ${\displaystyle b\in \{1,2,\ldots ,B\}}$ ${\displaystyle B}$ ${\displaystyle B=1}$ ${\displaystyle B=2}$ ${\displaystyle b}$ ${\displaystyle I_{b}}$ ${\displaystyle \{1,2,\ldots ,I_{b}\}}$ ${\textstyle \sum _{b=1}^{B}I_{b}}$ ${\displaystyle v_{k}}$

Функция прямого кодирования определяется таким образом, что -й элемент равен Вектор является конкатенацией всех вышеуказанных векторов для всех . Таким образом, . Чтобы получить полностью общий -way ANOVA взаимодействия, мы должны также конкатенировать каждый дополнительный член взаимодействия в векторе , а затем добавить отсекаемый член. Пусть этот вектор будет . ${\displaystyle g_{b}:\{1,2,\ldots ,I_{b}\}\mapsto \{0,1\}^{I_{b}}}$ ${\displaystyle i}$ ${\displaystyle g_{b}(Z_{k,b})}$ $${\displaystyle g_{b}(Z_{k,b})_{i}={\begin{cases}1&{\text{if }}i=Z_{k,b}\\0&{\text{otherwise}}\end{cases}}}$$ ${\displaystyle v_{k}}$ ${\displaystyle b}$ ${\displaystyle v_{k}=[g_{1}(Z_{k,1}),g_{2}(Z_{k,2}),\ldots ,g_{B}(Z_{k,B})]}$ ${\displaystyle B}$ ${\displaystyle v_{k}}$ ${\displaystyle X_{k}}$

С этой записью у нас теперь есть точная связь с линейной регрессией. Мы просто регрессируем ответ против вектора . Однако есть опасения по поводу идентифицируемости . Чтобы преодолеть такие проблемы, мы предполагаем, что сумма параметров в каждом наборе взаимодействий равна нулю. Отсюда можно использовать F -статистику или другие методы для определения релевантности отдельных факторов. ${\displaystyle y_{k}}$ ${\displaystyle X_{k}}$

Пример

Мы можем рассмотреть пример двухстороннего взаимодействия, где мы предполагаем, что первый фактор имеет 2 уровня, а второй фактор — 3 уровня.

Определим , если и , если , то есть является прямым кодированием первого фактора, а является прямым кодированием второго фактора. ${\displaystyle a_{i}=1}$ ${\displaystyle Z_{k,1}=i}$ ${\displaystyle b_{i}=1}$ ${\displaystyle Z_{k,2}=i}$ ${\displaystyle a}$ ${\displaystyle b}$

При этом, где последний член является термином перехвата. Для более конкретного примера предположим, что Тогда, $${\displaystyle X_{k}=[a_{1},a_{2},b_{1},b_{2},b_{3},a_{1}\times b_{1},a_{1}\times b_{2},a_{1}\times b_{3},a_{2}\times b_{1},a_{2}\times b_{2},a_{2}\times b_{3},1]}$$ $${\displaystyle {\begin{aligned}Z_{k,1}&=2\\Z_{k,2}&=1\end{aligned}}}$$ $${\displaystyle X_{k}=[0,1,1,0,0,0,0,0,1,0,0,1]}$$

Смотрите также

• Математический портал

• ANOVA по рангам
• ANOVA-одновременный компонентный анализ
• Ковариационный анализ ( ANCOVA )
• Анализ молекулярной дисперсии (AMOVA)
• Анализ ритмической дисперсии (ANORVA)
• Ожидаемые средние квадраты
• Объясненное изменение
• Оценка линейного тренда
• Дисперсионный анализ смешанного дизайна
• Многомерный ковариационный анализ ( MANCOVA )
• Пермутационный дисперсионный анализ
• Разложение дисперсии

Сноски

1. Аддитивность единичной обработки в большинстве текстов просто называется аддитивностью. Хинкельманн и Кемпторн добавляют прилагательные и различают аддитивность в строгом и широком смысле. Это позволяет подробно рассмотреть множественные источники ошибок (обработка, состояние, выбор, измерение и выборка) на странице 161.
2. Розенбаум (2002, стр. 40) цитирует раздел 5.7 (Тесты перестановок), теорему 2.3 (на самом деле теорему 3, стр. 184) из книги Лемана «Проверка статистических гипотез» (1959).
3. F -тест для сравнения дисперсий имеет неоднозначную репутацию. Он не рекомендуется в качестве проверки гипотезы для определения того, имеют ли две разные выборки одинаковую дисперсию. Он рекомендуется для ANOVA, где сравниваются две оценки дисперсии одной и той же выборки. Хотя F -тест , как правило, не является устойчивым к отклонениям от нормальности, было обнаружено, что он устойчив в особом случае ANOVA. Цитаты из Moore & McCabe (2003): «Дисперсионный анализ использует F-статистику, но она не то же самое, что F-статистика для сравнения двух стандартных отклонений совокупности». (стр. 554) «F-тест и другие процедуры вывода о дисперсиях настолько не обладают устойчивостью, что малопригодны на практике». (стр. 556) «[ F -тест ANOVA] относительно нечувствителен к умеренной ненормальности и неравным дисперсиям, особенно когда размеры выборок схожи». (стр. 763) ANOVA предполагает гомоскедастичность, но он устойчив. Статистический тест на гомоскедастичность ( F -тест) ненадежен. Мур и МакКейб рекомендуют эмпирическое правило.

Примечания

1. Стиглер (1986)
2. Стиглер (1986, стр. 134)
3. Стиглер (1986, стр. 153)
4. Стиглер (1986, стр. 154–155)
5. Стиглер (1986, стр. 240–242)
6. Стиглер (1986, Глава 7 – Психофизика как контрапункт)
7. Стиглер (1986, стр. 253)
8. Стиглер (1986, стр. 314–315)
9. Корреляция между родственниками на основе предположения о менделевском наследовании . Рональд А. Фишер. Философские труды Королевского общества Эдинбурга . 1918. (том 52, страницы 399–433)
10. Фишер, Рональд А. (1921). ") Исследования по вариации культур. I. Исследование урожайности очищенного зерна из Бродбалка". Журнал сельскохозяйственной науки . 11 (2): 107–135. doi :10.1017/S0021859600003750. hdl : 2440/15170 . S2CID  86029217.
11. Фишер, Рональд А. (1923). ") Исследования по вариации сельскохозяйственных культур. II. Реакция различных сортов картофеля на удобрение". Журнал сельскохозяйственной науки . 13 (3): 311–320. doi :10.1017/S0021859600003592. hdl : 2440/15179 . S2CID  85985907.
12. Шеффе (1959, стр. 291, «Модели рандомизации были впервые сформулированы Нейманом (1923) для полностью рандомизированного плана, Нейманом (1935) для рандомизированных блоков, Уэлчем (1937) и Питманом (1937) для латинского квадрата при определенной нулевой гипотезе и Кемпторном (1952, 1955) и Уилком (1955) для многих других планов».
13. Монтгомери (2001, Глава 12: Эксперименты со случайными факторами)
14. Гельман (2005, стр. 20–21)
15. Снедекор, Джордж У.; Кохран, Уильям Г. (1967). Статистические методы (6-е изд.). стр. 321.
16. Кохран и Кокс (1992, стр. 48)
17. Хауэлл (2002, стр. 323)
18. Андерсон, Дэвид Р.; Суини, Деннис Дж.; Уильямс, Томас А. (1996). Статистика для бизнеса и экономики (6-е изд.). Миннеаполис/Сент-Пол: West Pub. Co. стр. 452–453. ISBN 978-0-314-06378-6.
19. Энскомб (1948)
20. Хинкельманн, Клаус; Кемпторн, Оскар (2005). Планирование и анализ экспериментов, том 2: Расширенный экспериментальный план. John Wiley. стр. 213. ISBN 978-0-471-70993-0.
21. Кокс, DR (1992). Планирование экспериментов . Wiley. ISBN 978-0-471-57429-3.
22. Кемпторн (1979, стр. 30)
23. Cox (1958, Глава 2: Некоторые ключевые предположения)
24. Хинкельманн и Кемпторн (2008, Том 1, На протяжении всего текста. Введено в Разделе 2.3.3: Принципы экспериментального проектирования; Линейная модель; Схема модели)
25. Хинкельманн и Кемпторн (2008, Том 1, Раздел 6.3: Полностью рандомизированный дизайн; Выведенная линейная модель)
26. Hinkelmann и Kempthorne (2008, Том 1, Раздел 6.6: Полностью рандомизированный дизайн; Аппроксимация теста рандомизации)
27. Бейли (2008, Глава 2.14 «Более общая модель» в Бейли, стр. 38–40)
28. Хинкельманн и Кемпторн (2008, Том 1, Глава 7: Сравнение методов лечения)
29. Кемпторн (1979, стр. 125–126, «Экспериментатор должен решить, какие из различных причин, которые, по его мнению, приведут к изменениям в его результатах, должны контролироваться экспериментально. Те причины, которые он не контролирует экспериментально, поскольку он не осознает их, он должен контролировать с помощью метода рандомизации». «Только когда методы лечения в эксперименте применяются экспериментатором с использованием полной процедуры рандомизации, цепочка индуктивных выводов имеет смысл. Только при этих обстоятельствах экспериментатор может приписывать любые наблюдаемые им эффекты лечению и только лечению. При этих обстоятельствах его выводы надежны в статистическом смысле».)
30. Фридман ^{[ необходима полная цитата ]}
31. Монтгомери (2001, Раздел 3.8: Открытие эффектов дисперсии)
32. Хинкельманн и Кемпторн (2008, Том 1, Раздел 6.10: Полностью рандомизированный дизайн; Преобразования)
33. Бейли (2008)
34. Монтгомери (2001, Раздел 3-3: Эксперименты с одним фактором: Дисперсионный анализ; Анализ модели фиксированных эффектов)
35. Cochran & Cox (1992, стр. 2 пример)
36. Кохран и Кокс (1992, стр. 49)
37. Хинкельманн и Кемпторн (2008, Том 1, Раздел 6.7: Полностью рандомизированный дизайн; CRD с неравным числом повторений)
38. Мур и МакКейб (2003, стр. 763)
39. Гельман (2008)
40. Montgomery (2001, Раздел 5-2: Введение в факторные планы; Преимущества факторных расчетов)
41. Belle (2008, Раздел 8.4: Взаимодействия высокого порядка происходят редко)
42. Монтгомери (2001, Раздел 5-1: Введение в факторные планы; Основные определения и принципы)
43. Кокс (1958, Глава 6: Основные идеи о факторных экспериментах)
44. Монтгомери (2001, Раздел 5-3.7: Введение в факторные планы; Двухфакторный факторный план; Одно наблюдение на ячейку)
45. Уилкинсон (1999, стр. 596)
46. Монтгомери (2001, Раздел 3-7: Определение размера выборки)
47. Хауэлл (2002, Глава 8: Власть)
48. Хауэлл (2002, Раздел 11.12: Мощность (в ANOVA))
49. Хауэлл (2002, Раздел 13.7: Анализ мощности для факторных экспериментов)
50. Мур и МакКейб (2003, стр. 778–780)
51. Wilkinson (1999, стр. 599)
52. Монтгомери (2001, Раздел 3-4: Проверка адекватности модели)
53. Кокран и Кокс (1957, стр. 9, «Общее правило заключается в том, что способ проведения эксперимента определяет не только возможность делать выводы, но и необходимые для этого вычисления»).
54. "ANOVA Design". bluebox.creighton.edu . Получено 23 января 2023 г. .
55. "Однофакторный/однофакторный ANOVA". Архивировано из оригинала 7 ноября 2014 г.
56. «Вероятная ошибка среднего» (PDF) . Biometrika . 6 : 1–25. 1908. doi : 10.1093/biomet/6.1.1. hdl : 10338.dmlcz/143545.
57. Монтгомери (2001, Раздел 3-3.4: Несбалансированные данные)
58. Монтгомери (2001, Раздел 14-2: Несбалансированные данные в факторном дизайне)
59. Гельман (2005, стр. 1) (с оговоркой в ​​более позднем тексте)
60. Монтгомери (2001, Раздел 3.9: Регрессионный подход к дисперсионному анализу)
61. Хауэлл (2002, стр. 604)
62. Хауэлл (2002, Глава 18: Повторная выборка и непараметрические подходы к данным)
63. Монтгомери (2001, Раздел 3-10: Непараметрические методы в дисперсионном анализе)

Ссылки

• Anscombe, FJ (1948). «Достоверность сравнительных экспериментов». Журнал Королевского статистического общества. Серия A (общая) . 111 (3): 181–211. doi :10.2307/2984159. JSTOR  2984159. MR  0030181.
• Бейли, РА (2008). Разработка сравнительных экспериментов. Cambridge University Press. ISBN 978-0-521-68357-9.Предварительные главы доступны в Интернете.
• Белль, Джеральд ван (2008). Статистические правила (2-е изд.). Хобокен, Нью-Джерси: Уайли. ISBN 978-0-470-14448-0.
• Кокран, Уильям Г.; Кокс , Гертруда М. (1992). Экспериментальные проекты (2-е изд.). Нью-Йорк: Wiley. ISBN 978-0-471-54567-5.
• Коэн, Якоб (1988). Статистический анализ мощности для поведенческих наук (2-е изд.). Routledge ISBN 978-0-8058-0283-2 
• Коэн, Джейкоб (1992). «Статистика — мощный учебник». Психологический вестник . 112 (1): 155–159. doi :10.1037/0033-2909.112.1.155. PMID  19565683. S2CID  14411587.
• Кокс, Дэвид Р. (1958). Планирование экспериментов . Перепечатано как ISBN 978-0-471-57429-3 
• Кокс, Дэвид Р. (2006). Принципы статистического вывода . Кембридж, Нью-Йорк: Издательство Кембриджского университета. ISBN 978-0-521-68567-2.
• Фридман, Дэвид А. (2005). Статистические модели: теория и практика , Cambridge University Press. ISBN 978-0-521-67105-7 
• Гельман, Эндрю (2005). «Дисперсионный анализ? Почему он важнее, чем когда-либо». Анналы статистики . 33 : 1–53. arXiv : math/0504499 . doi : 10.1214/009053604000001048. S2CID  13529149.
• Гельман, Эндрю (2008). «Дисперсия, анализ». Новый словарь экономики Palgrave (2-е изд.). Бейзингсток, Хэмпшир, Нью-Йорк: Palgrave Macmillan. ISBN 978-0-333-78676-5.
• Хинкельманн, Клаус и Кемпторн, Оскар (2008). Планирование и анализ экспериментов . Том I и II (Второе издание). Wiley. ISBN 978-0-470-38551-7.
• Хауэлл, Дэвид К. (2002). Статистические методы в психологии (5-е изд.). Пасифик-Гроув, Калифорния: Duxbury/Thomson Learning. ISBN 978-0-534-37770-0.
• Кемпторн, Оскар (1979). Планирование и анализ экспериментов (Исправленное переиздание (1952) Wiley ed.). Роберт Э. Кригер. ISBN 978-0-88275-105-4.
• Леманн, Э. Л. (1959) Проверка статистических гипотез. John Wiley & Sons.
• Монтгомери, Дуглас С. (2001). Планирование и анализ экспериментов (5-е изд.). Нью-Йорк: Wiley. ISBN 978-0-471-31649-7.
• Мур, Дэвид С. и МакКейб, Джордж П. (2003). Введение в практику статистики (4e). WH Freeman & Co. ISBN 0-7167-9657-0 
• Розенбаум, Пол Р. (2002). Наблюдательные исследования (2-е изд.). Нью-Йорк: Springer-Verlag. ISBN 978-0-387-98967-9 
• Шеффе, Генри (1959). Анализ дисперсии . Нью-Йорк: Wiley.
• Стиглер, Стивен М. (1986). История статистики: измерение неопределенности до 1900 года . Кембридж, Массачусетс: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.
• Уилкинсон, Леланд (1999). «Статистические методы в психологических журналах; Руководства и пояснения». Американский психолог . 5 (8): 594–604. CiteSeerX  10.1.1.120.4818 . doi :10.1037/0003-066X.54.8.594. S2CID  428023.

Дальнейшее чтение

• Фридман, Дэвид А .; Пизани, Роберт; Первес, Роджер (2007). Статистика (4-е изд.). WW Norton & Company. ISBN 978-0-393-92972-0.
• Табачник, Барбара Г.; Фиделл, Линда С. (2006). Использование многомерной статистики . Pearson International Edition (5-е изд.). Needham, MA: Allyn & Bacon, Inc. ISBN 978-0-205-45938-4.

• Wichura, Michael J. (2006). Координатно-свободный подход к линейным моделям . Cambridge Series in Statistical and Probabilistic Mathematics. Cambridge University Press. стр. xiv+199. ISBN 978-0-521-86842-6. МР  2283455.{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Кристенсен, Рональд (2002). Плоские ответы на сложные вопросы: Теория линейных моделей (третье изд.). Нью-Йорк: Springer. ISBN 978-0-387-95361-8.
• Caliński, Tadeusz; Kageyama, Sanpei (2000). Блочные конструкции: подход рандомизации, том I: Анализ . Lecture Notes in Statistics. Том 150. Нью-Йорк: Springer-Verlag. ISBN 978-0-387-98578-7.
• Кокс, Дэвид Р .; Рид, Нэнси М. (2000).Теория планирования экспериментов. Chapman & Hall/CRC. ISBN 978-1-58488-195-7.
• Хеттманспергер, Т. П.; МакКин, Дж. В. (1998). Надежные непараметрические статистические методы . Библиотека статистики Кендалла. Том 5 (1-е изд.). Нью-Йорк: A Hodder Arnold Publication. С. xiv+467. ISBN 978-0-340-54937-7. МР  1604954.
• Лентнер, Марвин; Бишоп, Томас (1993). Экспериментальный дизайн и анализ (2-е изд.). Блэксбург, Вирджиния: Valley Book Company. ISBN 978-0-9616255-2-8.
• Phadke, Madhav S. (1989). Качественное проектирование с использованием надежной конструкции . Нью-Джерси: Prentice Hall PTR. ISBN 978-0-13-745167-8.
• Бокс, GEP (1954). "Некоторые теоремы о квадратичных формах, применяемые при изучении проблем дисперсионного анализа, II. Эффекты неравенства дисперсий и корреляции между ошибками в двухфакторной классификации". Анналы математической статистики . 25 (3): 484. doi : 10.1214/aoms/1177728717 .
• Бокс, GEP (1954). "Некоторые теоремы о квадратичных формах, применяемые при изучении проблем дисперсионного анализа, I. Влияние неравенства дисперсий на однофакторную классификацию". Анналы математической статистики . 25 (2): 290. doi : 10.1214/aoms/1177728786 .

• Бокс, GEP (1953). «Ненормальность и тесты на дисперсии». Biometrika . 40 (3/4): 318–335. doi :10.1093/biomet/40.3-4.318. JSTOR  2333350.
• Фишер, Рональд (1918). "Исследования вариации культур. I. Исследование урожайности очищенного зерна из Бродбалка" (PDF) . Журнал сельскохозяйственной науки . 11 (2): 107–135. doi :10.1017/S0021859600003750. hdl : 2440/15170 . S2CID  86029217. Архивировано (PDF) из оригинала 22 июня 2023 г. . Получено 5 февраля 2024 г. .

Внешние ссылки

• SOCR : активность ANOVA
• Примеры всех моделей ANOVA и ANCOVA с тремя факторами лечения, включая рандомизированный блок, разделенный график, повторные измерения и латинские квадраты, а также их анализ в R (Университет Саутгемптона)
• Электронный справочник по статистическим методам NIST/SEMATECH, раздел 7.4.3: «Равны ли средние значения?»
• Дисперсионный анализ: Введение