Вейвлет

Функция для интегрального преобразования Фурье

Вейвлет — это волнообразное колебание с амплитудой , которая начинается с нуля, увеличивается или уменьшается, а затем возвращается к нулю один или несколько раз. Вейвлеты называются «краткими колебаниями». Была установлена ​​таксономия вейвлетов на основе количества и направления их импульсов. Вейвлеты наделены определенными свойствами, которые делают их полезными для обработки сигналов .

Сейсмический вейвлет

Например, можно создать вейвлет с частотой до первой октавы и короткой длительностью примерно в одну десятую секунды. Если бы этот вейвлет был свернут с сигналом, созданным из записи мелодии, то полученный сигнал был бы полезен для определения того, когда в песне появилась нота до второй октавы. Математически вейвлет коррелирует с сигналом, если часть сигнала похожа. Корреляция лежит в основе многих практических приложений вейвлетов.

Как математический инструмент, вейвлеты могут использоваться для извлечения информации из многих видов данных, включая аудиосигналы и изображения. Наборы вейвлетов необходимы для полного анализа данных. «Комплементарные» вейвлеты разлагают сигнал без пробелов или наложений, так что процесс разложения является математически обратимым. Таким образом, наборы комплементарных вейвлетов полезны в алгоритмах сжатия/декомпрессии на основе вейвлетов , где желательно восстановить исходную информацию с минимальными потерями.

Формально это представление представляет собой представление вейвлет-ряда квадратично-интегрируемой функции относительно либо полного ортонормированного набора базисных функций , либо сверхполного набора или фрейма векторного пространства для гильбертова пространства квадратично-интегрируемых функций. Это достигается посредством когерентных состояний .

В классической физике явление дифракции описывается принципом Гюйгенса-Френеля , который рассматривает каждую точку в распространяющемся волновом фронте как набор отдельных сферических вейвлетов. ^[1] Характерный изгибный рисунок наиболее выражен, когда волна от когерентного источника (такого как лазер) сталкивается со щелью/отверстием, сопоставимым по размеру с его длиной волны . Это происходит из-за добавления или интерференции различных точек на волновом фронте (или, что эквивалентно, каждого вейвлета), которые перемещаются по путям разной длины к регистрирующей поверхности. Несколько близко расположенных отверстий (например, дифракционная решетка ) могут привести к сложному рисунку различной интенсивности.

Этимология

Слово «вейвлет» десятилетиями использовалось в цифровой обработке сигналов и разведочной геофизике. ^[2] Эквивалентное французское слово ondelette, означающее «маленькая волна», использовалось Жаном Морле и Алексом Гроссманном в начале 1980-х годов.

Теория вейвлетов

Теория вейвлетов применима к нескольким предметам. Все вейвлет-преобразования можно считать формами частотно-временного представления для непрерывных во времени (аналоговых) сигналов и, таким образом, они связаны с гармоническим анализом . Дискретное вейвлет-преобразование (непрерывное во времени) дискретного во времени (выборочного) сигнала с использованием дискретных во времени банков фильтров диадической (октавной полосы) конфигурации является вейвлет-аппроксимацией этого сигнала. Коэффициенты такого банка фильтров называются коэффициентами сдвига и масштабирования в номенклатуре вейвлетов. Эти банки фильтров могут содержать фильтры с конечной импульсной характеристикой (КИХ) или бесконечной импульсной характеристикой (БИХ). Вейвлеты, образующие непрерывное вейвлет-преобразование (НВП), подчиняются принципу неопределенности анализа Фурье соответствующей теории выборки: учитывая сигнал с некоторым событием в нем, нельзя одновременно назначить этому событию точную временную и частотную шкалу отклика. Произведение неопределенностей временной и частотной шкалы отклика имеет нижнюю границу. Таким образом, в скейлограмме непрерывного вейвлет-преобразования этого сигнала такое событие отмечает целую область в плоскости временной шкалы, а не только одну точку. Также дискретные вейвлет-базисы могут рассматриваться в контексте других форм принципа неопределенности. ^{[3] [4] [5] [6]}

Вейвлет-преобразования можно разделить на три класса: непрерывные, дискретные и основанные на множественном разрешении.

Непрерывные вейвлет-преобразования (параметры непрерывного сдвига и масштабирования)

В непрерывных вейвлет-преобразованиях заданный сигнал конечной энергии проецируется на непрерывное семейство частотных диапазонов (или аналогичные подпространства пространства функций L p L ² ( R ) ). Например, сигнал может быть представлен в каждом частотном диапазоне в виде [ f , 2 f ] для всех положительных частот f > 0. Затем исходный сигнал может быть восстановлен с помощью подходящего интегрирования по всем полученным частотным компонентам.

Частотные диапазоны или подпространства (поддиапазоны) являются масштабированными версиями подпространства в масштабе 1. Это подпространство, в свою очередь, в большинстве ситуаций генерируется сдвигами одной генерирующей функции ψ в L ² ( R ), материнского вейвлета . Для примера частотного диапазона масштаба один [1, 2] эта функция с (нормализованной) функцией sinc . Это, Мейера и два других примера материнских вейвлетов: $${\displaystyle \psi (t)=2\,\operatorname {sinc} (2t)-\,\operatorname {sinc} (t)={\frac {\sin(2\pi t)-\sin(\pi t)}{\pi t}}}$$

Подпространство масштаба a или полосы частот [1/ a , 2/ a ] генерируется функциями (иногда называемыми дочерними вейвлетами ) , где a положительно и определяет масштаб, а b — любое действительное число и определяет сдвиг. Пара ( a , b ) определяет точку в правой полуплоскости R ₊ × R . $${\displaystyle \psi _{a,b}(t)={\frac {1}{\sqrt {a}}}\psi \left({\frac {t-b}{a}}\right),}$$

Проекция функции x на подпространство масштаба a тогда имеет вид с вейвлет-коэффициентами $${\displaystyle x_{a}(t)=\int _{\mathbb {R} }WT_{\psi }\{x\}(a,b)\cdot \psi _{a,b}(t)\,db}$$ $${\displaystyle WT_{\psi }\{x\}(a,b)=\langle x,\psi _{a,b}\rangle =\int _{\mathbb {R} }x(t){\psi _{a,b}(t)}\,dt.}$$

Для анализа сигнала x можно собрать вейвлет-коэффициенты в скейлограмму сигнала.

См. список некоторых непрерывных вейвлетов .

Дискретные вейвлет-преобразования (дискретные параметры сдвига и масштабирования, непрерывные во времени)

Вычислительно невозможно проанализировать сигнал, используя все коэффициенты вейвлета, поэтому можно задаться вопросом, достаточно ли выбрать дискретное подмножество верхней полуплоскости, чтобы иметь возможность реконструировать сигнал из соответствующих коэффициентов вейвлета. Одной из таких систем является аффинная система для некоторых действительных параметров a > 1, b > 0. Соответствующее дискретное подмножество полуплоскости состоит из всех точек ( a ^m , nb a ^m ) с m , n в Z . Соответствующие дочерние вейвлеты теперь задаются как $${\displaystyle \psi _{m,n}(t)={\frac {1}{\sqrt {a^{m}}}}\psi \left({\frac {t-nba^{m}}{a^{m}}}\right).}$$

Достаточным условием для восстановления любого сигнала x конечной энергии по формуле является то, что функции образуют ортонормированный базис L ² ( R ). $${\displaystyle x(t)=\sum _{m\in \mathbb {Z} }\sum _{n\in \mathbb {Z} }\langle x,\,\psi _{m,n}\rangle \cdot \psi _{m,n}(t)}$$ ${\displaystyle \{\psi _{m,n}:m,n\in \mathbb {Z} \}}$

Дискретные вейвлет-преобразования на основе мультиразрешения (непрерывные во времени)

D4 вейвлет

В любом дискретизированном вейвлет-преобразовании существует только конечное число вейвлет-коэффициентов для каждой ограниченной прямоугольной области в верхней полуплоскости. Тем не менее, каждый коэффициент требует вычисления интеграла. В особых ситуациях этой числовой сложности можно избежать, если масштабированные и сдвинутые вейвлеты образуют многомасштабный анализ . Это означает, что должна существовать вспомогательная функция , отцовский вейвлет φ в L ² ( R ), и что a является целым числом. Типичный выбор — a = 2 и b = 1. Самая известная пара отцовского и материнского вейвлетов — это вейвлет Добеши с 4 точками. Обратите внимание, что не каждый ортонормированный дискретный базис вейвлетов может быть связан с многомасштабным анализом; например, вейвлет Журна не допускает многомасштабного анализа. ^[7]

Из материнского и отцовского вейвлетов строятся подпространства. Отцовский вейвлет сохраняет свойства временной области, в то время как материнские вейвлеты сохраняют свойства частотной области. $${\displaystyle V_{m}=\operatorname {span} (\phi _{m,n}:n\in \mathbb {Z} ),{\text{ where }}\phi _{m,n}(t)=2^{-m/2}\phi (2^{-m}t-n)}$$ $${\displaystyle W_{m}=\operatorname {span} (\psi _{m,n}:n\in \mathbb {Z} ),{\text{ where }}\psi _{m,n}(t)=2^{-m/2}\psi (2^{-m}t-n).}$$ ${\displaystyle V_{i}}$ ${\displaystyle W_{i}}$

Из этого следует, что последовательность образует многомасштабный анализ L ² и что подпространства являются ортогональными «разностями» указанной выше последовательности, то есть W _m является ортогональным дополнением V _m внутри подпространства V _{m −1} , $${\displaystyle \{0\}\subset \dots \subset V_{1}\subset V_{0}\subset V_{-1}\subset V_{-2}\subset \dots \subset L^{2}(\mathbb {R} )}$$ ${\displaystyle \dots ,W_{1},W_{0},W_{-1},\dots }$ $${\displaystyle V_{m}\oplus W_{m}=V_{m-1}.}$$

По аналогии с теоремой о дискретизации можно заключить, что пространство V _m с расстоянием дискретизации 2 ^м более или менее покрывает полосу частот от 0 до 1/2 ^{m -1} . Как ортогональное дополнение, W _m примерно покрывает полосу [1/2 ^{m −1} , 1/2 ^m ].

Из этих включений и соотношений ортогональности, особенно , следует существование последовательностей и , которые удовлетворяют тождествам так что и так что Второе тождество первой пары является уточняющим уравнением для отцовского вейвлета φ. Обе пары тождеств образуют основу алгоритма быстрого вейвлет- преобразования . ${\displaystyle V_{0}\oplus W_{0}=V_{-1}}$ ${\displaystyle h=\{h_{n}\}_{n\in \mathbb {Z} }}$ ${\displaystyle g=\{g_{n}\}_{n\in \mathbb {Z} }}$ $${\displaystyle g_{n}=\langle \phi _{0,0},\,\phi _{-1,n}\rangle }$$ ${\textstyle \phi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }g_{n}\phi (2t-n),}$ $${\displaystyle h_{n}=\langle \psi _{0,0},\,\phi _{-1,n}\rangle }$$ ${\textstyle \psi (t)={\sqrt {2}}\sum _{n\in \mathbb {Z} }h_{n}\phi (2t-n).}$

Из анализа множественного разрешения выводится ортогональное разложение пространства L ² как Для любого сигнала или функции это дает представление в базисных функциях соответствующих подпространств как где коэффициенты и $${\displaystyle L^{2}=V_{j_{0}}\oplus W_{j_{0}}\oplus W_{j_{0}-1}\oplus W_{j_{0}-2}\oplus W_{j_{0}-3}\oplus \cdots }$$ ${\displaystyle S\in L^{2}}$ $${\displaystyle S=\sum _{k}c_{j_{0},k}\phi _{j_{0},k}+\sum _{j\leq j_{0}}\sum _{k}d_{j,k}\psi _{j,k}}$$ $${\displaystyle c_{j_{0},k}=\langle S,\phi _{j_{0},k}\rangle }$$ $${\displaystyle d_{j,k}=\langle S,\psi _{j,k}\rangle .}$$

Временно-причинные вейвлеты

Для обработки временных сигналов в реальном времени важно, чтобы вейвлет-фильтры не обращались к значениям сигнала из будущего, а также чтобы можно было получить минимальные временные задержки. Временно-каузальные вейвлет-представления были разработаны Сзу и др. ^[8] и Линдебергом ^[9] , причем последний метод также включал в себя эффективную по памяти реализацию рекурсивного времени.

Материнский вейвлет

Для практических приложений и по соображениям эффективности предпочитают непрерывно дифференцируемые функции с компактным носителем в качестве материнских (прототипных) вейвлетов (функций). Однако для удовлетворения аналитических требований (в непрерывном ВТ) и в целом по теоретическим причинам выбирают вейвлет-функции из подпространства пространства Это пространство измеримых по Лебегу функций, которые являются как абсолютно интегрируемыми , так и квадратично интегрируемыми в том смысле, что и ${\displaystyle L^{1}(\mathbb {R} )\cap L^{2}(\mathbb {R} ).}$ $${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|\,dt<\infty }$$ $${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt<\infty .}$$

Нахождение в этом пространстве гарантирует, что можно сформулировать условия нулевого среднего и квадратичной нормы один: — условие для нулевого среднего, а — условие для квадратичной нормы один. $${\displaystyle \int _{-\infty }^{\infty }\psi (t)\,dt=0}$$ $${\displaystyle \int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt=1}$$

Чтобы ψ был вейвлетом для непрерывного вейвлет-преобразования (точную формулировку см. там), материнский вейвлет должен удовлетворять критерию допустимости (грубо говоря, своего рода полудифференцируемости) для получения устойчиво обратимого преобразования.

Для дискретного вейвлет-преобразования необходимо как минимум условие, что ряд вейвлетов является представлением тождества в пространстве L ² ( R ). Большинство конструкций дискретного ВТ используют многомасштабный анализ , который определяет вейвлет с помощью масштабирующей функции. Эта масштабирующая функция сама по себе является решением функционального уравнения.

В большинстве ситуаций полезно ограничить ψ, чтобы она была непрерывной функцией с большим числом M исчезающих моментов, т.е. для всех целых m < M $${\displaystyle \int _{-\infty }^{\infty }t^{m}\,\psi (t)\,dt=0.}$$

Материнский вейвлет масштабируется (или расширяется) в a раз и транслируется (или сдвигается) в b раз, что дает (согласно исходной формулировке Морле):

$${\displaystyle \psi _{a,b}(t)={1 \over {\sqrt {a}}}\psi \left({t-b \over a}\right).}$$

Для непрерывного ВТ пара ( a , b ) изменяется по всей полуплоскости R ₊ × R ; для дискретного ВТ эта пара изменяется по ее дискретному подмножеству, которое также называется аффинной группой .

Эти функции часто неправильно называют базисными функциями (непрерывного) преобразования. Фактически, как и в непрерывном преобразовании Фурье, в непрерывном вейвлет-преобразовании нет базиса. Частотно-временная интерпретация использует слегка отличающуюся формулировку (по Дельпра).

Ограничение：

1. ${\displaystyle {\frac {1}{\sqrt {a}}}\int _{-\infty }^{\infty }\varphi _{a1,b1}(t)\varphi \left({\frac {t-b}{a}}\right)\,dt}$когда а ₁ = а и b ₁ = b ,
2. ${\displaystyle \Psi (t)}$имеет конечный временной интервал

Сравнения с преобразованием Фурье (непрерывное время)

Вейвлет-преобразование часто сравнивают с преобразованием Фурье , в котором сигналы представляются в виде суммы синусоид. Фактически, преобразование Фурье можно рассматривать как частный случай непрерывного вейвлет-преобразования с выбором материнского вейвлета . Основное различие в целом заключается в том, что вейвлеты локализованы как по времени, так и по частоте, тогда как стандартное преобразование Фурье локализовано только по частоте . Кратковременное преобразование Фурье (STFT) похоже на вейвлет-преобразование, в том смысле, что оно также локализовано по времени и частоте, но есть проблемы с компромиссом между частотой и временным разрешением. ${\displaystyle \psi (t)=e^{-2\pi it}}$

В частности, предполагая прямоугольную область окна, можно думать о STFT как о преобразовании с немного другим ядром , где часто можно записать как , где и u соответственно обозначают длину и временное смещение функции окна. Используя теорему Парсеваля , можно определить энергию вейвлета как Из этого квадрат временной поддержки смещения окна по времени u определяется как $${\displaystyle \psi (t)=g(t-u)e^{-2\pi it}}$$ ${\displaystyle g(t-u)}$ ${\textstyle \operatorname {rect} \left({\frac {t-u}{\Delta _{t}}}\right)}$ ${\displaystyle \Delta _{t}}$ $${\displaystyle E=\int _{-\infty }^{\infty }|\psi (t)|^{2}\,dt={\frac {1}{2\pi }}\int _{-\infty }^{\infty }|{\hat {\psi }}(\omega )|^{2}\,d\omega }$$ $${\displaystyle \sigma _{u}^{2}={\frac {1}{E}}\int |t-u|^{2}|\psi (t)|^{2}\,dt}$$

и квадрат спектральной поддержки окна, действующего на частоте ${\displaystyle \xi }$ $${\displaystyle {\hat {\sigma }}_{\xi }^{2}={\frac {1}{2\pi E}}\int |\omega -\xi |^{2}|{\hat {\psi }}(\omega )|^{2}\,d\omega }$$

Умножение с прямоугольным окном во временной области соответствует свертке с функцией в частотной области, что приводит к ложным артефактам звона для коротких/локализованных временных окон. С непрерывным по времени преобразованием Фурье, и эта свертка с дельта-функцией в пространстве Фурье приводит к истинному преобразованию Фурье сигнала . Функция окна может быть некоторым другим аподизирующим фильтром , таким как гауссов . Выбор функции окна повлияет на ошибку аппроксимации относительно истинного преобразования Фурье. ${\displaystyle \operatorname {sinc} (\Delta _{t}\omega )}$ ${\displaystyle \Delta _{t}\to \infty }$ ${\displaystyle x(t)}$

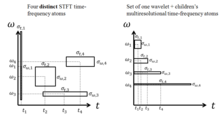
Произведение времени и полосы пропускания заданной разрешающей ячейки не может быть превышено с помощью STFT. Все базисные элементы STFT поддерживают равномерную спектральную и временную поддержку для всех временных сдвигов или смещений, тем самым достигая одинакового разрешения во времени для более низких и более высоких частот. Разрешение определяется исключительно шириной выборки.

Напротив, мультиразрешающие свойства вейвлет-преобразования позволяют большую временную поддержку для более низких частот, сохраняя при этом короткую временную ширину для более высоких частот за счет масштабирующих свойств вейвлет-преобразования. Это свойство расширяет обычный частотно-временной анализ до анализа временной шкалы. ^[10]

Атомы времени-частоты STFT (слева) и атомы шкалы времени DWT (справа). Атомы времени-частоты — это четыре различные базисные функции, используемые для STFT (т. е. требуется четыре отдельных преобразования Фурье ). Атомы шкалы времени DWT достигают малой временной ширины для высоких частот и хорошей временной ширины для низких частот с одним базисным набором преобразования.

Дискретное вейвлет-преобразование менее сложно в вычислительном отношении , занимая O( N ) времени по сравнению с O( N  log  N ) для быстрого преобразования Фурье (БПФ). Это вычислительное преимущество не присуще преобразованию, а отражает выбор логарифмического деления частоты, в отличие от равномерно распределенных частотных делений БПФ, которое использует те же базисные функции, что и дискретное преобразование Фурье (ДПФ). ^[11] Эта сложность применяется только тогда, когда размер фильтра не имеет отношения к размеру сигнала. Вейвлет без компактной поддержки, такой как вейвлет Шеннона, потребовал бы O( N ² ). (Например, логарифмическое преобразование Фурье также существует со сложностью O( N ), но исходный сигнал должен быть дискретизирован логарифмически по времени, что полезно только для определенных типов сигналов. ^[12] )

Определение вейвлета

Вейвлет (или семейство вейвлетов) можно определить различными способами:

Масштабирующий фильтр

Ортогональный вейвлет полностью определяется масштабирующим фильтром — фильтром нижних частот с конечной импульсной характеристикой (КИХ) длиной 2N и суммой 1. В биортогональных вейвлетах определяются отдельные фильтры разложения и реконструкции.

Для анализа с использованием ортогональных вейвлетов фильтр верхних частот рассчитывается как квадратурный зеркальный фильтр нижних частот, а фильтры реконструкции представляют собой обращенные во времени фильтры разложения.

Вейвлеты Добеши и Симлета можно определить с помощью масштабирующего фильтра.

Функция масштабирования

Вейвлеты определяются вейвлет-функцией ψ( t ) (т.е. материнским вейвлетом) и масштабирующей функцией φ( t ) (также называемой отцовским вейвлетом) во временной области.

Функция вейвлета по сути является полосовым фильтром и масштабированием, которое для каждого уровня вдвое уменьшает его полосу пропускания. Это создает проблему, заключающуюся в том, что для покрытия всего спектра потребуется бесконечное число уровней. Функция масштабирования фильтрует самый низкий уровень преобразования и обеспечивает покрытие всего спектра. Подробное объяснение см. в ^{[13] .}

Для вейвлета с компактным носителем φ( t ) можно считать конечной по длине и эквивалентным масштабирующему фильтру g .

Вейвлеты Мейера можно определить с помощью масштабирующих функций

Функция вейвлета

Вейвлет имеет только представление во временной области в виде вейвлет-функции ψ( t ).

Например, мексиканские вейвлеты шляпы могут быть определены функцией вейвлета. См. список нескольких непрерывных вейвлетов .

История

Развитие вейвлетов можно связать с несколькими отдельными направлениями мысли, начиная с работы Альфреда Хаара в начале 20-го века. Более поздняя работа Денниса Габора привела к появлению атомов Габора (1946), которые построены аналогично вейвлетам и применяются для аналогичных целей.

Известный вклад в теорию вейвлетов с тех пор можно отнести к открытию Джорджем Цвейгом непрерывного вейвлет-преобразования (CWT) в 1975 году (первоначально называвшегося кохлеарным преобразованием и обнаруженного при изучении реакции уха на звук), ^[14] формулировке Пьером Гупийо, Алексом Гроссманном и Жаном Морле того, что сейчас известно как CWT (1982), ранней работе Яна-Олова Стрёмберга по дискретным вейвлетам (1983), неортогональному банку фильтров Ле Галля–Табатабаи (LGT) с 5/3 ответвлениями и линейной фазой (1988), ^{[15] [16] [17] ортогональным вейвлетам с компактным носителем} Ингрид Добеши (1988), неортогональной структуре множественного разрешения Стефана Малла (1989), биномиальному QMF Али Акансу ( 1990), Частотно-временная интерпретация НВП Натали Дельпра (1991), гармоническое вейвлет-преобразование Ньюленда (1993) и разбиение множеств в иерархических деревьях (SPIHT), разработанное Амиром Саидом совместно с Уильямом А. Перлманом в 1996 году. ^[18]

Стандарт JPEG 2000 разрабатывался с 1997 по 2000 год комитетом Joint Photographic Experts Group (JPEG) под председательством Тураджа Эбрахими (позже президента JPEG). ^[19] В отличие от алгоритма DCT, используемого исходным форматом JPEG , JPEG 2000 вместо этого использует алгоритмы дискретного вейвлет-преобразования (DWT). Он использует вейвлет-преобразование CDF 9/7 (разработанное Ингрид Добеши в 1992 году) для своего алгоритма сжатия с потерями и банк дискретных временных фильтров Le Gall–Tabatabai (LGT) 5/3 (разработанный Дидье Ле Галлем и Али Дж. Табатабаи в 1988 году) для своего алгоритма сжатия без потерь . ^[20] Технология JPEG 2000 , которая включает расширение Motion JPEG 2000 , была выбрана в качестве стандарта видеокодирования для цифрового кино в 2004 году. ^[21]

Хронология

• Первый вейвлет ( вейвлет Хаара ) Альфреда Хаара (1909)
• С 1970-х годов: Джордж Цвейг , Жан Морле , Алекс Гроссманн
• С 1980-х: Ив Мейер , Дидье Ле Галль, Али Ж. Табатабай, Стефан Малла , Ингрид Добеши , Рональд Койфман , Али Акансу , Виктор Викерхаузер
• С 1990-х годов: Натали Дельпра, Ньюленд, Амир Саид, Уильям А. Перлман, Турадж Эбрахими, JPEG 2000

Вейвлет-преобразования

Вейвлет — это математическая функция, используемая для разделения заданной функции или непрерывного во времени сигнала на различные масштабные компоненты. Обычно можно назначить диапазон частот для каждого масштабного компонента. Каждый масштабный компонент затем может быть изучен с разрешением, соответствующим его масштабу. Вейвлет-преобразование — это представление функции вейвлетами. Вейвлеты — это масштабированные и переведенные копии (известные как «дочерние вейвлеты») конечной длины или быстро затухающей осциллирующей формы волны (известной как «материнский вейвлет»). Вейвлет-преобразования имеют преимущества перед традиционными преобразованиями Фурье для представления функций, которые имеют разрывы и острые пики, а также для точной деконструкции и реконструкции конечных, непериодических и /или нестационарных сигналов .

Вейвлет-преобразования подразделяются на дискретные вейвлет-преобразования (DWT) и непрерывные вейвлет-преобразования (CWT). Обратите внимание, что и DWT, и CWT являются непрерывными во времени (аналоговыми) преобразованиями. Их можно использовать для представления непрерывных во времени (аналоговых) сигналов. CWT работают со всеми возможными масштабами и трансляциями, тогда как DWT используют определенное подмножество значений масштаба и трансляции или сетку представления.

Существует большое количество вейвлет-преобразований, каждое из которых подходит для различных приложений. Полный список см. в списке преобразований, связанных с вейвлетами , но наиболее распространенные из них перечислены ниже:

• Непрерывное вейвлет-преобразование (CWT)
• Дискретное вейвлет-преобразование (ДВП)
• Быстрое вейвлет-преобразование (БВП)
• Схема подъема и обобщенная схема подъема
• Разложение вейвлет-пакета (WPD)
• Стационарное вейвлет-преобразование (СВТ)
• Дробное преобразование Фурье (FRFT)
• Дробное вейвлет-преобразование (FRWT)

Обобщенные преобразования

Существует ряд обобщенных преобразований, частным случаем которых является вейвлет-преобразование. Например, Йозеф Джозеф Сегман ввел масштаб в группу Гейзенберга , что привело к непрерывному пространству преобразований, которое является функцией времени, масштаба и частоты. НВП представляет собой двумерный срез через полученный трехмерный объем времени-масштаба-частоты.

Другим примером обобщенного преобразования является преобразование чирплета , в котором CWT также является двумерным срезом преобразования чирплета.

Важная область применения обобщенных преобразований включает системы, в которых решающее значение имеет высокое разрешение по частоте. Например, электронно-оптические преобразования темного поля, промежуточные между прямым и обратным пространством, широко использовались в гармоническом анализе атомной кластеризации, т. е. в изучении кристаллов и дефектов кристаллов . ^[22] Теперь, когда просвечивающие электронные микроскопы способны предоставлять цифровые изображения с пикометрической информацией об атомной периодичности в наноструктурах всех видов, диапазон приложений распознавания образов ^[23] и деформации ^[24] / метрологии ^[25] для промежуточных преобразований с высоким разрешением по частоте (таких как крушлеты ^[26] и риджлеты ^[27] ) быстро растет.

Дробное вейвлет-преобразование (FRWT) является обобщением классического вейвлет-преобразования в дробных областях преобразования Фурье. Это преобразование способно предоставлять информацию о времени и дробной области одновременно и представлять сигналы в плоскости время-дробная-частота. ^[28]

Приложения

Обычно приближение DWT используется для сжатия данных , если сигнал уже дискретизирован, а CWT — для анализа сигнала . ^{[29] [30]} Таким образом, приближение DWT обычно используется в инженерии и информатике, ^[31] а CWT — в научных исследованиях. ^[32]

Как и некоторые другие преобразования, вейвлет-преобразования могут использоваться для преобразования данных, а затем кодирования преобразованных данных, что приводит к эффективному сжатию. Например, JPEG 2000 — это стандарт сжатия изображений, который использует биортогональные вейвлеты. Это означает, что хотя кадр и является сверхполным, он является плотным кадром (см. типы кадров векторного пространства ), и одни и те же функции кадра (за исключением сопряжения в случае сложных вейвлетов) используются как для анализа, так и для синтеза, т. е. как в прямом, так и в обратном преобразовании. Подробности см. в сжатии вейвлетов .

Связанное применение — сглаживание/шумопонижение данных на основе порогового значения коэффициента вейвлета, также называемого усадкой вейвлета. С помощью адаптивного порогового значения коэффициентов вейвлета, которые соответствуют нежелательным частотным компонентам, можно выполнять операции сглаживания и/или шумоподавления.

Wavelet-преобразования также начинают использоваться для коммуникационных приложений. Wavelet OFDM — это базовая схема модуляции, используемая в HD-PLC ( технология связи по линиям электропередач, разработанная Panasonic ), а также в одном из дополнительных режимов, включенных в стандарт IEEE 1901. Wavelet OFDM может достигать более глубоких вырезов, чем традиционный FFT OFDM, и wavelet OFDM не требует защитного интервала (который обычно представляет собой значительную накладную плату в системах FFT OFDM). ^[33]

Как представление сигнала

Часто сигналы можно хорошо представить в виде суммы синусоид. Однако рассмотрим прерывистый сигнал с резким разрывом; этот сигнал все еще можно представить в виде суммы синусоид, но для этого требуется бесконечное число, что является наблюдением, известным как явление Гиббса . Это, таким образом, требует бесконечного числа коэффициентов Фурье, что непрактично для многих приложений, таких как сжатие. Вейвлеты более полезны для описания этих сигналов с разрывами из-за их локализованного во времени поведения (как преобразования Фурье, так и вейвлет-преобразования локализованы по частоте, но вейвлеты обладают дополнительным свойством локализации во времени). Из-за этого многие типы сигналов на практике могут быть неразреженными в области Фурье, но очень разреженными в области вейвлетов. Это особенно полезно при реконструкции сигналов, особенно в недавно популярной области сжатого зондирования . (Обратите внимание, что кратковременное преобразование Фурье (STFT) также локализовано по времени и частоте, но часто возникают проблемы с компромиссом между разрешением частоты и времени. Вейвлеты являются лучшими представлениями сигнала благодаря многомасштабному анализу .)

Это мотивирует, почему вейвлет-преобразования теперь принимаются для огромного количества приложений, часто заменяя обычное преобразование Фурье . Многие области физики увидели этот сдвиг парадигмы, включая молекулярную динамику , теорию хаоса , ^[34] вычисления ab initio , астрофизику , анализ данных переходных процессов гравитационных волн , ^{[35] [36]} локализацию матрицы плотности , сейсмологию , оптику , турбулентность и квантовую механику . Это изменение также произошло в обработке изображений , ЭЭГ , ЭМГ , ^[37] анализе ЭКГ , ритмах мозга , анализе ДНК , анализе белков , климатологии , анализе сексуальной реакции человека, ^[38] общей обработке сигналов , распознавании речи , акустике, вибрационных сигналах, ^[39] компьютерной графике , мультифрактальном анализе и разреженном кодировании . В компьютерном зрении и обработке изображений понятие представления масштабного пространства и операторов гауссовой производной рассматривается как каноническое многомасштабное представление.

Шумоподавление вейвлетов

Очистка сигнала с помощью порогового значения вейвлет-преобразования

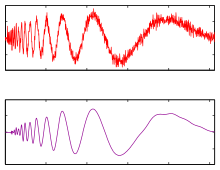
Предположим, что мы измеряем зашумленный сигнал , где представляет сигнал, а представляет шум. Предположим, что имеет разреженное представление в определенном вейвлет-базисе, и ${\displaystyle x=s+v}$ ${\displaystyle s}$ ${\displaystyle v}$ ${\displaystyle s}$ ${\displaystyle v\ \sim \ {\mathcal {N}}(0,\,\sigma ^{2}I)}$

Пусть вейвлет-преобразование будет , где — вейвлет-преобразование сигнальной компоненты, а — вейвлет-преобразование шумовой компоненты. ${\displaystyle x}$ ${\displaystyle y=W^{T}x=W^{T}s+W^{T}v=p+z}$ ${\displaystyle p=W^{T}s}$ ${\displaystyle z=W^{T}v}$

Большинство элементов равны 0 или близки к 0, и ${\displaystyle p}$ ${\displaystyle z\ \sim \ \ {\mathcal {N}}(0,\,\sigma ^{2}I)}$

Поскольку является ортогональным, задача оценки сводится к восстановлению сигнала в iid гауссовском шуме . Поскольку является разреженным, один из методов заключается в применении модели гауссовой смеси для . ${\displaystyle W}$ ${\displaystyle p}$ ${\displaystyle p}$

Предположим, что априорно , где — дисперсия «значимых» коэффициентов, а — дисперсия «незначимых» коэффициентов. ${\displaystyle p\ \sim \ a{\mathcal {N}}(0,\,\sigma _{1}^{2})+(1-a){\mathcal {N}}(0,\,\sigma _{2}^{2})}$ ${\displaystyle \sigma _{1}^{2}}$ ${\displaystyle \sigma _{2}^{2}}$

Тогда , называется коэффициентом сжатия, который зависит от предшествующих дисперсий и . При установке коэффициентов, которые опускаются ниже порога сжатия, на ноль, как только применяется обратное преобразование, ожидаемо небольшое количество сигнала теряется из-за предположения о разреженности. Ожидается, что более крупные коэффициенты в первую очередь представляют сигнал из-за разреженности, и статистически очень малая часть сигнала, хотя и большая часть шума, как ожидается, будет представлена ​​в таких более низких коэффициентах величины... поэтому ожидается, что операция обнуления удалит большую часть шума и не большую часть сигнала. Обычно коэффициенты выше порогового значения не изменяются во время этого процесса. Некоторые алгоритмы шумоподавления на основе вейвлетов могут также ослаблять более крупные коэффициенты на основе статистической оценки количества шума, которое, как ожидается, будет удалено таким ослаблением. ${\displaystyle {\tilde {p}}=E(p/y)=\tau (y)y}$ ${\displaystyle \tau (y)}$ ${\displaystyle \sigma _{1}^{2}}$ ${\displaystyle \sigma _{2}^{2}}$

Наконец, примените обратное вейвлет-преобразование, чтобы получить ${\displaystyle {\tilde {s}}=W{\tilde {p}}}$

Многомасштабная климатическая сеть

Агарвал и др. предложили вейвлет-ориентированные передовые линейные ^[40] и нелинейные ^[41] методы для построения и исследования климата как сложных сетей в разных временных масштабах. Климатические сети, построенные с использованием наборов данных SST в разных временных масштабах, подтвердили, что вейвлет-ориентированный многомасштабный анализ климатических процессов обещает лучшее понимание динамики системы, которая может быть упущена, когда процессы анализируются только в одном временном масштабе ^[42]

Список вейвлетов

Дискретные вейвлеты

• Бейлкин (18)
• Вейвлет Мура Вейвлет Морле
• Биортогональные почти койфлетные (BNC) вейвлеты
• Койфлет (6, 12, 18, 24, 30)
• Вейвлет Коэна-Добеши-Фово (иногда его называют CDF N/P или биортогональными вейвлетами Добеши)
• Вейвлет Добеши (2, 4, 6, 8, 10, 12, 14, 16, 18, 20 и т.д.)
• Биномиальный QMF (также известный как вейвлет Добеши)
• вейвлет Хаара
• Вейвлет Матье
• вейвлет Лежандра
• Вейвлет Вилласенора
• Симлет ^[43]

Непрерывные вейвлеты

Реально значимый

• Бета-вейвлет
• Эрмитов вейвлет
• Вейвлет Мейера
• Мексиканская шляпа вейвлет
• Пуассоновский вейвлет
• Вейвлет Шеннона
• Сплайн-вейвлет
• Вейвлет Стрёмберга

Комплекснозначный

• Сложный мексиканский вейвлет шляпы
• fbsp вейвлет
• Морле вейвлет
• Вейвлет Шеннона
• Модифицированный вейвлет Морле

Смотрите также

• Преобразование Chirplet
• Курвелет
• Цифровое кино
• Уменьшение размеров
• Фильтры банков
• Преобразования, связанные с Фурье
• Фрактальное сжатие
• Дробное преобразование Фурье
• Вейвлет Габора § Пространство вейвлетов ^[44]
• Принцип Гюйгенса–Френеля (физические вейвлеты)
• JPEG2000
• Спектральный анализ методом наименьших квадратов для вычисления периодичности в любых, в том числе неравномерно распределенных данных
• Морле вейвлет
• Многомасштабный анализ
• Шум
• Неразделимый вейвлет
• Масштаб пространства
• Масштабированная корреляция
• Шерлет
• Кратковременное преобразование Фурье
• Спектрограмма
• Сверхширокополосное радио – передает вейвлеты
• Вейвлет для анализа многомерных сигналов

Ссылки

1. Беспроводная связь: принципы и практика, серия Prentice Hall по технике связи и новым технологиям, Т. С. Раппапорт, Prentice Hall, 2002, стр. 126.
2. Рикер, Норман (1953). «Сжатие вейвлетов, расширение вейвлетов и управление сейсмическим разрешением». Geophysics . 18 (4): 769–792. Bibcode : 1953Geop...18..769R. doi : 10.1190/1.1437927.
3. Мейер, Ив (1992), Вейвлеты и операторы, Кембридж, Великобритания: Cambridge University Press, ISBN 0-521-42000-8 
4. Чуй, Чарльз К. (1992), Введение в вейвлеты, Сан-Диего, Калифорния: Academic Press, ISBN 0-12-174584-8 
5. Добеши, Ингрид. (1992), Десять лекций о вейвлетах, SIAM, ISBN 978-0-89871-274-2 
6. Акансу, Али Н.; Хаддад, Ричард А. (1992), Разложение сигнала с множественным разрешением: преобразования, поддиапазоны и вейвлеты, Бостон, Массачусетс: Academic Press, ISBN 978-0-12-047141-6 
7. Ларсон, Дэвид Р. (2007), Анализ вейвлетов и приложения (см.: Унитарные системы и наборы вейвлетов) , Appl. Numer. Harmon. Anal., Birkhäuser, стр. 143–171
8. Szu, Harold H.; Telfer, Brian A.; Lohmann, Adolf W. (1992). "Причинное аналитическое вейвлет-преобразование". Optical Engineering . 31 (9): 1825. Bibcode : 1992OptEn..31.1825S. doi : 10.1117/12.59911.
9. Линдеберг, Т. (23 января 2023 г.). «Причинно-следственное и рекурсивное по времени масштабно-ковариантное масштабно-пространственное представление временных сигналов и прошедшего времени». Биологическая кибернетика . 117 (1–2): 21–59. doi : 10.1007/s00422-022-00953-6 . PMC 10160219. PMID  36689001 . 
10. Маллат, Стефан. «Вейвлет-тур по обработке сигналов. 1998». 250-252.
11. Руководство для ученых и инженеров по цифровой обработке сигналов Стивена У. Смита, доктора философии, глава 8, уравнение 8-1: http://www.dspguide.com/ch8/4.htm
12. Хейнс, В. Г. В.; Джонс, Алан Г. (1988). «Логарифмическое преобразование Фурье» (PDF) . Geophysical Journal (92): 171–178. doi : 10.1111/j.1365-246X.1988.tb01131.x . S2CID  9720759.
13. «Действительно понятное руководство по вейвлетам – PolyValens». www.polyvalens.com .
14. Вайсштейн, Эрик В. «Цвейг, Джордж — из «Мира научной биографии» Эрика Вайсштейна». scienceworld.wolfram.com . Получено 20 октября 2021 г.
15. Салливан, Гэри (8–12 декабря 2003 г.). «Общие характеристики и соображения по проектированию для временного поддиапазонного видеокодирования». ITU-T . Группа экспертов по кодированию видео . Получено 13 сентября 2019 г. .
16. Бовик, Алан С. (2009). Основное руководство по обработке видео. Academic Press . стр. 355. ISBN 9780080922508.
17. Галль, Дидье Ле; Табатабай, Али Дж. (1988). «Кодирование поддиапазонов цифровых изображений с использованием симметричных фильтров с коротким ядром и методов арифметического кодирования». ICASSP-88., Международная конференция по акустике, речи и обработке сигналов . стр. 761–764 т.2. doi :10.1109/ICASSP.1988.196696. S2CID  109186495.
18. Саид, Амир; Перлман, Уильям А. (июнь 1996 г.). «Новый быстрый и эффективный кодек изображений, основанный на разбиении наборов в иерархических деревьях». Труды IEEE по схемам и системам для видеотехнологий . 6 (3): 243–250. doi :10.1109/76.499834. ISSN  1051-8215.
19. Таубман, Дэвид; Марселлин, Майкл (2012). Основы, стандарты и практика сжатия изображений JPEG2000: Основы, стандарты и практика сжатия изображений. Springer Science & Business Media . ISBN 9781461507994.
20. Unser, M.; Blu, T. (2003). «Математические свойства вейвлет-фильтров JPEG2000» (PDF) . IEEE Transactions on Image Processing . 12 (9): 1080–1090. Bibcode :2003ITIP...12.1080U. doi :10.1109/TIP.2003.812329. PMID  18237979. S2CID  2765169. Архивировано из оригинала (PDF) 2019-10-13.
21. Шварц, Чарльз С. (2005). Понимание цифрового кино: профессиональный справочник. Тейлор и Фрэнсис . стр. 147. ISBN 9780240806174.
22. P. Hirsch, A. Howie, R. Nicholson, DW Pashley и MJ Whelan (1965/1977) Электронная микроскопия тонких кристаллов (Butterworths, London/Krieger, Malabar FLA) ISBN 0-88275-376-2 
23. P. Fraundorf, J. Wang, E. Mandell и M. Rose (2006) Цифровые таблицы темного поля, Микроскопия и микроанализ 12 :S2, 1010–1011 (ср. arXiv:cond-mat/0403017)
24. Hÿtch, MJ; Snoeck, E.; Kilaas, R. (1998). «Количественное измерение полей смещения и деформации с помощью микрографий HRTEM». Ультрамикроскопия . 74 (3): 131–146. doi :10.1016/s0304-3991(98)00035-7.
25. Мартин Роуз (2006) Измерение расстояний между полосами решетки на изображении HRTEM с использованием цифрового разложения темного поля (диссертация на степень магистра физики, Университет Миссури – Сент-Луис)
26. Ф. Г. Мейер и Р. Р. Койфман (1997) Прикладной и вычислительный гармонический анализ 4 :147.
27. AG Flesia, H. Hel-Or , A. Averbuch, EJ Candes , RR Coifman и DL Donoho (2001) Цифровая реализация пакетов риджлетов (Academic Press, Нью-Йорк).
28. Ши, Дж.; Чжан, Н.-Т.; Лю, С.-П. (2011). «Новое дробное вейвлет-преобразование и его приложения». Sci. China Inf. Sci . 55 (6): 1270–1279. doi :10.1007/s11432-011-4320-x. S2CID  255201598.
29. AN Akansu, WA Serdijn и IW Selesnick, Новые приложения вейвлетов: обзор, Physical Communication, Elsevier, т. 3, выпуск 1, стр. 1-18, март 2010 г.
30. Томас, Р., Ли, З., Лопес-Санчес, Дж. М., Лю, П. и Синглтон, А. 2016. Использование вейвлет-инструментов для анализа сезонных колебаний на основе данных временных рядов InSAR: пример оползня Хуангтупо. Оползни, 13, 437-450, doi: 10.1007/s10346-015-0589-y.
31. Ляхов, Павел; Семёнова, Наталия; Нагорнов, Николай; Бергерман, Максим; Абдулсалямова, Альбина (2023-11-14). "Высокоскоростная вейвлет-обработка изображений с использованием метода Винограда с понижением частоты дискретизации". Математика . 11 (22): 4644. doi : 10.3390/math11224644 . ISSN  2227-7390. Вейвлеты активно используются для решения широкого круга задач обработки изображений в различных областях науки и техники, например, для шумоподавления изображений, реконструкции, анализа, а также анализа и обработки видео. Методы вейвлет-обработки основаны на дискретном вейвлет-преобразовании с использованием одномерной цифровой фильтрации.
32. Дун, Лян; Чжан, Шаохуа; Гань, Тяньсиюй; Цю, Янь; Сун, Циньфэн; Чжао, Юнтао (2023-12-01). "Анализ частотных характеристик потенциала труба-почва при помехах блуждающего тока метрополитена с использованием метода непрерывного вейвлет-преобразования". Строительство и строительные материалы . 407 : 133453. doi : 10.1016/j.conbuildmat.2023.133453. ISSN  0950-0618. S2CID  263317973.
33. Стефано Галли; О. Логвинов (июль 2008 г.). «Последние разработки в области стандартизации связи по линиям электропередач в IEEE». Журнал IEEE Communications . 46 (7): 64–71. doi :10.1109/MCOM.2008.4557044. S2CID  2650873.Обзор предложения P1901 PHY/MAC.
34. Wotherspoon, T.; et., al. (2009). «Адаптация к краю хаоса с обратной связью случайных вейвлетов». J. Phys. Chem . 113 (1): 19–22. Bibcode :2009JPCA..113...19W. doi :10.1021/jp804420g. PMID  19072712.
35. Эбботт, Бенджамин П. и др. (LIGO Scientific Collaboration и Virgo Collaboration) (2016). «Наблюдение гравитационно-волнового транзиента GW150914 с минимальными предположениями». Phys. Rev. D. 93 ( 12): 122004. arXiv : 1602.03843 . Bibcode : 2016PhRvD..93l2004A. doi : 10.1103/PhysRevD.93.122004. S2CID  119313566.
36. V Necula, S Klimenko и G Mitselmakher (2012). "Анализ переходных процессов с быстрым частотно-временным преобразованием Вильсона-Добеши". Journal of Physics: Conference Series . 363 (1): 012032. Bibcode : 2012JPhCS.363a2032N. doi : 10.1088/1742-6596/363/1/012032 .
37. Дж. Рафи и др. Извлечение признаков сигналов ЭМГ предплечья для протезирования, Expert Systems with Applications 38 (2011) 4058–67.
38. J. Rafiee et al. Женские сексуальные реакции с использованием методов обработки сигналов, Журнал сексуальной медицины 6 (2009) 3086–96. (pdf)
39. Rafiee, J.; Tse, Peter W. (2009). «Использование автокорреляции в вейвлет-коэффициентах для диагностики неисправностей». Механические системы и обработка сигналов . 23 (5): 1554–72. Bibcode : 2009MSSP...23.1554R. doi : 10.1016/j.ymssp.2009.02.008.
40. Агарвал, Анкит; Махесваран, Ратинасами; Марван, Норберт; Цезарь, Левке; Куртс, Юрген (ноябрь 2018 г.). "Многомасштабная мера сходства на основе вейвлетов для сложных сетей" (PDF) . The European Physical Journal B. 91 ( 11): 296. Bibcode : 2018EPJB...91..296A. doi : 10.1140/epjb/e2018-90460-6. eISSN  1434-6036. ISSN  1434-6028. S2CID  125557123.
41. Агарвал, Анкит; Марван, Норберт; Ратинасами, Махешваран; Мерц, Бруно; Куртс, Юрген (13 октября 2017 г.). «Многомасштабный анализ синхронизации событий для раскрытия климатических процессов: подход, основанный на вейвлетах». Нелинейные процессы в геофизике . 24 (4): 599–611. Бибкод : 2017NPGeo..24..599A. дои : 10.5194/npg-24-599-2017 . eISSN  1607-7946. S2CID  28114574.
42. Агарвал, Анкит; Цезарь, Левке; Марван, Норберт; Махешваран, Ратинасами; Мерц, Бруно; Куртс, Юрген (19 июня 2019 г.). «Сетевая идентификация и характеристика телекоммуникационных соединений разных масштабов». Научные отчеты . 9 (1): 8808. Бибкод : 2019NatSR...9.8808A. дои : 10.1038/s41598-019-45423-5. eISSN  2045-2322. ПМК 6584743 . ПМИД  31217490. 
43. Matlab Toolbox – URL: http://matlab.izmiran.ru/help/toolbox/wavelet/ch06_a32.html
44. Эрик Хьельмас (1999-01-21) URL-адрес Gabor Wavelets : http://www.ansatt.hig.no/erikh/papers/scia99/node6.html

Дальнейшее чтение

• Хаар А., Zur Theorie der ortagonalen Funktionensysteme , Mathematische Annalen, 69 , стр. 331–371, 1910.
• Ингрид Добеши , Десять лекций о вейвлетах , Общество промышленной и прикладной математики, 1992, ISBN 0-89871-274-2 . 
• Али Акансу и Ричард Хаддад, Разложение сигнала с множественным разрешением: преобразования, поддиапазоны, вейвлеты , Academic Press, 1992, ISBN 0-12-047140-X . 
• PP Vaidyanathan , Многоскоростные системы и банки фильтров , Prentice Hall, 1993, ISBN 0-13-605718-7 . 
• Джеральд Кайзер, Дружественное руководство по вейвлетам , Биркхаузер, 1994, ISBN 0-8176-3711-7 . 
• Младен Виктор Викерхаузер, Адаптированный вейвлет-анализ от теории к программному обеспечению , AK Peters Ltd, 1994, ISBN 1-56881-041-5 . 
• Мартин Веттерли и Елена Ковачевич, «Вейвлеты и субполосное кодирование», Prentice Hall, 1995, ISBN 0-13-097080-8 . 
• Барбара Берк Хаббард , «Мир глазами вейвлетов: история математической техники в процессе становления», AK Peters Ltd, 1998, ISBN 1-56881-072-5 , ISBN 978-1-56881-072-0 .  
• Стефан Малла , «Вейвлет-тур по обработке сигналов», 2-е издание, Academic Press, 1999, ISBN 0-12-466606-X . 
• Дональд Б. Персиваль и Эндрю Т. Уолден, Методы вейвлет-анализа временных рядов , Cambridge University Press, 2000, ISBN 0-521-68508-7 . 
• Рамазан Генчай, Фарук Сельчук и Брэндон Уитчер, Введение в вейвлеты и другие методы фильтрации в финансах и экономике , Academic Press, 2001, ISBN 0-12-279670-5 . 
• Пол С. Эддисон, Иллюстрированное руководство по вейвлет-преобразованию , Институт физики , 2002, ISBN 0-7503-0692-0 . 
• Б. Боашаш, редактор, «Анализ и обработка частотно-временных сигналов – полный справочник», Elsevier Science, Оксфорд, 2003, ISBN 0-08-044335-4 . 
• Тони Ф. Чан и Джеки (Цзяньхун) Шен, Обработка и анализ изображений – вариационные, дифференциальные уравнения в частных производных, вейвлет-методы и стохастические методы , Общество прикладной математики, ISBN 0-89871-589-X (2005). 
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), «Раздел 13.10. Вейвлет-преобразования», Numerical Recipes: The Art of Scientific Computing (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8, заархивировано из оригинала 2011-08-11 , извлечено 2011-08-13.
• «Как вейвлеты позволяют исследователям преобразовывать — и понимать — данные». Журнал Quanta . 2021-10-13 . Получено 2021-10-20 .

Внешние ссылки

• «Вейвлет-анализ», Энциклопедия математики , EMS Press , 2001 [1994]
• 1-й симпозиум NJIT по вейвлетам (30 апреля 1990 г.) (первая конференция по вейвлетам в США)
• Биномиально-QMF-вейвлеты Добеши
• Вейвлеты Гилберта Стрэнга, American Scientist 82 (1994) 250–255. (Очень короткое и превосходное введение)
• Курс по вейвлетам, прочитанный в Калифорнийском университете в Санта-Барбаре, 2004 г.
• Вейвлеты для детей (файл PDF) (Вводная информация (для очень умных детей!))
• WITS: Где находится Starlet? Словарь десятков вейвлетов и связанных с вейвлетами терминов, оканчивающихся на -let, от activelets до x-lets через bandlets, contourlets, curvellets, noiselets, whiplets.
• Дробное сплайн-вейвлет-преобразование описывает дробное вейвлет-преобразование на основе дробных b-сплайнов.
• Панорама многомасштабных геометрических представлений, переплетение пространственной, направленной и частотной селективности представляет собой учебное пособие по двумерным ориентированным вейвлетам и связанным с ними геометрическим многомасштабным преобразованиям.
• Краткое введение в вейвлеты Рене Пушингера
• Действительно понятное руководство по вейвлетам от Клеменса Валенса
• «Как вейвлеты позволяют исследователям преобразовывать — и понимать — данные». Журнал Quanta . 2021-10-13 . Получено 2021-10-20 .