Гильбертово пространство

Type of topological vector space

Состояние колеблющейся струны можно смоделировать как точку в гильбертовом пространстве. Разложение колеблющейся струны на ее колебания в отдельных обертонах задается проекцией точки на оси координат в пространстве.

В математике гильбертовы пространства (названные в честь Дэвида Гильберта ) позволяют обобщать методы линейной алгебры и исчисления с (конечномерных) евклидовых векторных пространств на пространства, которые могут быть бесконечномерными . Гильбертовы пространства естественным образом и часто возникают в математике и физике , как правило, как функциональные пространства . Формально гильбертово пространство — это векторное пространство, снабженное скалярным произведением , которое индуцирует функцию расстояния , для которой пространство является полным метрическим пространством . Гильбертово пространство — это частный случай банахова пространства .

Самые ранние гильбертовы пространства изучались с этой точки зрения в первом десятилетии 20-го века Дэвидом Гильбертом , Эрхардом Шмидтом и Фридьешем Риссом . Они являются незаменимыми инструментами в теориях уравнений с частными производными , квантовой механике , анализе Фурье (который включает приложения к обработке сигналов и теплопередаче ) и эргодической теории (которая образует математическую основу термодинамики ). Джон фон Нейман ввел термин гильбертово пространство для абстрактной концепции, которая лежит в основе многих из этих разнообразных приложений. Успех методов гильбертова пространства открыл очень плодотворную эру для функционального анализа . Помимо классических евклидовых векторных пространств, примерами гильбертовых пространств являются пространства квадратично-интегрируемых функций , пространства последовательностей , пространства Соболева, состоящие из обобщенных функций , и пространства Харди голоморфных функций .

Геометрическая интуиция играет важную роль во многих аспектах теории гильбертова пространства. Точные аналоги теоремы Пифагора и закона параллелограмма справедливы в гильбертовом пространстве. На более глубоком уровне перпендикулярная проекция на линейное подпространство играет важную роль в задачах оптимизации и других аспектах теории. Элемент гильбертова пространства может быть однозначно задан его координатами относительно ортонормированного базиса , по аналогии с декартовыми координатами в классической геометрии. Когда этот базис счетно бесконечен , он позволяет отождествить гильбертово пространство с пространством бесконечных последовательностей , которые суммируются с квадратом . Последнее пространство часто в старой литературе называют гильбертовым пространством.

Определение и иллюстрация

Мотивирующий пример: Евклидово векторное пространство

Одним из наиболее известных примеров гильбертова пространства является евклидово векторное пространство , состоящее из трехмерных векторов , обозначаемое как R ³ , и снабженное скалярным произведением . Скалярное произведение берет два вектора x и y и производит действительное число x ⋅ y . Если x и y представлены в декартовых координатах , то скалярное произведение определяется как $${\displaystyle {\begin{pmatrix}x_{1}\\x_{2}\\x_{3}\end{pmatrix}}\cdot {\begin{pmatrix}y_{1}\\y_{2}\\y_{3}\end{pmatrix}}=x_{1}y_{1}+x_{2}y_{2}+x_{3}y_{3}\,.}$$

Скалярное произведение удовлетворяет свойствам ^[1]

1. Он симметричен относительно x и y : x ⋅ y = y ⋅ x .
2. Он линеен по своему первому аргументу: ( a x ₁ + b x ₂ ) ⋅ y = a ( x ₁ ⋅ y ) + b ( x ₂ ⋅ y ) для любых скаляров a , b и векторов x ₁ , x ₂ и y .
3. Он положительно определен : для всех векторов x , x ⋅ x ≥ 0 , причем равенство имеет место тогда и только тогда, когда x = 0 .

Операция над парами векторов, которая, подобно скалярному произведению, удовлетворяет этим трем свойствам, известна как (реальное) скалярное произведение . Векторные пространства, снабженные таким скалярным произведением, известны как (реальное) скалярное произведение . Каждое конечномерное скалярное произведение также является гильбертовым пространством. ^[2] Основная особенность скалярного произведения, которая связывает его с евклидовой геометрией, заключается в том, что оно связано как с длиной (или нормой ) вектора, обозначаемого ‖ x ‖ , так и с углом θ между двумя векторами x и y посредством формулы $${\displaystyle \mathbf {x} \cdot \mathbf {y} =\left\|\mathbf {x} \right\|\left\|\mathbf {y} \right\|\,\cos \theta \,.}$$

Полнота означает, что ряд векторов (синего цвета) приводит к четко определенному вектору чистого смещения (оранжевого цвета).

Многомерное исчисление в евклидовом пространстве опирается на способность вычислять пределы и иметь полезные критерии для заключения о существовании пределов. Математический ряд, состоящий из векторов в R ^3, абсолютно сходится при условии, что сумма длин сходится как обычный ряд действительных чисел: ^[3] $${\displaystyle \sum _{n=0}^{\infty }\mathbf {x} _{n}}$$ $${\displaystyle \sum _{k=0}^{\infty }\|\mathbf {x} _{k}\|<\infty \,.}$$

Так же, как и ряд скаляров, ряд векторов, который сходится абсолютно, также сходится к некоторому предельному вектору L в евклидовом пространстве, в том смысле, что $${\displaystyle {\Biggl \|}\mathbf {L} -\sum _{k=0}^{N}\mathbf {x} _{k}{\Biggr \|}\to 0\quad {\text{as }}N\to \infty \,.}$$

Это свойство выражает полноту евклидова пространства: ряд, который сходится абсолютно, сходится и в обычном смысле.

Гильбертовы пространства часто берутся над комплексными числами . Комплексная плоскость , обозначенная C , снабжена понятием величины, комплексным модулем | z | , который определяется как квадратный корень из произведения z на его комплексно сопряженное число : $${\displaystyle |z|^{2}=z{\overline {z}}\,.}$$

Если z = x + iy — разложение z на действительную и мнимую части, то модуль — это обычная евклидова двумерная длина: $${\displaystyle |z|={\sqrt {x^{2}+y^{2}}}\,.}$$

Скалярное произведение пары комплексных чисел z и w — это произведение z на комплексно сопряженное число w : $${\displaystyle \langle z,w\rangle =z{\overline {w}}\,.}$$

Это комплекснозначное. Действительная часть ⟨ z , w ⟩ дает обычное двумерное евклидово скалярное произведение .

Вторым примером является пространство C ^{2 ,} элементами которого являются пары комплексных чисел z = ( z ₁ , z ₂ ) . Тогда скалярное произведение z с другим таким вектором w = ( w ₁ , w ₂ ) задается как $${\displaystyle \langle z,w\rangle =z_{1}{\overline {w_{1}}}+z_{2}{\overline {w_{2}}}\,.}$$

Действительная часть ⟨ z , w ⟩ тогда является двумерным евклидовым скалярным произведением. Это внутреннее произведение является эрмитово симметричным, что означает, что результат перестановки z и w является комплексно сопряженным: $${\displaystyle \langle w,z\rangle ={\overline {\langle z,w\rangle }}\,.}$$

Определение

Гильбертово пространство — это действительное или комплексное пространство скалярного произведения , которое также является полным метрическим пространством относительно функции расстояния, индуцированной скалярным произведением. ^[4]

Сказать, что комплексное векторное пространство H является комплексным пространством скалярного произведения, означает, что существует скалярное произведение, сопоставляющее комплексное число каждой паре элементов H , которое удовлетворяет следующим свойствам: ${\displaystyle \langle x,y\rangle }$ ${\displaystyle x,y}$

1. Скалярное произведение является сопряженно симметричным; то есть скалярное произведение пары элементов равно комплексно сопряженному скалярному произведению поменянных элементов: Важно отметить, что это означает, что является действительным числом. $${\displaystyle \langle y,x\rangle ={\overline {\langle x,y\rangle }}\,.}$$ ${\displaystyle \langle x,x\rangle }$
2. Скалярное произведение линейно по первому ^{[nb 1]} аргументу. Для всех комплексных чисел и ${\displaystyle a}$ ${\displaystyle b,}$ $${\displaystyle \langle ax_{1}+bx_{2},y\rangle =a\langle x_{1},y\rangle +b\langle x_{2},y\rangle \,.}$$
3. Внутреннее произведение элемента на самого себя положительно определено : $${\displaystyle {\begin{alignedat}{4}\langle x,x\rangle >0&\quad {\text{ if }}x\neq 0,\\\langle x,x\rangle =0&\quad {\text{ if }}x=0\,.\end{alignedat}}}$$

Из свойств 1 и 2 следует, что комплексное скалярное произведение является антилинейным , также называемым сопряженно-линейным , по своему второму аргументу, что означает, что $${\displaystyle \langle x,ay_{1}+by_{2}\rangle ={\bar {a}}\langle x,y_{1}\rangle +{\bar {b}}\langle x,y_{2}\rangle \,.}$$

Действительное внутреннее произведение пространства определяется таким же образом, за исключением того, что H является действительным векторным пространством, а внутреннее произведение принимает действительные значения. Такое внутреннее произведение будет билинейным отображением и будет образовывать двойственную систему . ^[5] ${\displaystyle (H,H,\langle \cdot ,\cdot \rangle )}$

Норма — это действительная функция , а расстояние между двумя точками в H определяется через норму следующим образом: $${\displaystyle \|x\|={\sqrt {\langle x,x\rangle }}\,,}$$ ${\displaystyle d}$ ${\displaystyle x,y}$ $${\displaystyle d(x,y)=\|x-y\|={\sqrt {\langle x-y,x-y\rangle }}\,.}$$

То, что эта функция является функцией расстояния, означает, во-первых, что она симметрична относительно , ​​а во-вторых, что расстояние между и само по себе равно нулю, а в противном случае расстояние между и должно быть положительным, и, наконец, что выполняется неравенство треугольника , означающее, что длина одного катета треугольника xyz не может превышать сумму длин двух других катетов: ${\displaystyle x}$ ${\displaystyle y,}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle y}$ $${\displaystyle d(x,z)\leq d(x,y)+d(y,z)\,.}$$

Последнее свойство в конечном итоге является следствием более фундаментального неравенства Коши–Шварца , которое утверждает равенство тогда и только тогда, когда и линейно зависимы . $${\displaystyle \left|\langle x,y\rangle \right|\leq \|x\|\|y\|}$$ ${\displaystyle x}$ ${\displaystyle y}$

При заданной таким образом функции расстояния любое пространство внутреннего произведения является метрическим пространством и иногда называется хаусдорфовым предгильбертовым пространством . ^[6] Любое предгильбертово пространство, которое дополнительно является также полным пространством, является гильбертовым пространством. ^[7]

Полнота H выражается с помощью формы критерия Коши для последовательностей в H : предгильбертово пространство H является полным, если каждая последовательность Коши сходится относительно этой нормы к элементу в пространстве. Полноту можно охарактеризовать следующим эквивалентным условием: если ряд векторов сходится абсолютно в том смысле, что , то ряд сходится в H , в том смысле, что частичные суммы сходятся к элементу H . ^[8] $${\displaystyle \sum _{k=0}^{\infty }u_{k}}$$ $${\displaystyle \sum _{k=0}^{\infty }\|u_{k}\|<\infty \,,}$$

Как полное нормированное пространство, гильбертовы пространства по определению также являются банаховыми пространствами . Как таковые они являются топологическими векторными пространствами , в которых топологические понятия, такие как открытость и замкнутость подмножеств, хорошо определены . Особое значение имеет понятие замкнутого линейного подпространства гильбертова пространства, которое со скалярным произведением, индуцированным ограничением , также является полным (будучи замкнутым множеством в полном метрическом пространстве) и, следовательно, гильбертовым пространством само по себе.

Второй пример: пространства последовательностей

Пространство последовательностей l ² состоит из всех бесконечных последовательностей z = ( z ₁ , z ₂ , …) комплексных чисел, таких, что сходится следующий ряд : ^[9] $${\displaystyle \sum _{n=1}^{\infty }|z_{n}|^{2}}$$

Скалярное произведение на l ² определяется как: $${\displaystyle \langle \mathbf {z} ,\mathbf {w} \rangle =\sum _{n=1}^{\infty }z_{n}{\overline {w_{n}}}\,,}$$

Этот второй ряд сходится вследствие неравенства Коши–Шварца и сходимости предыдущего ряда.

Полнота пространства сохраняется при условии, что всякий раз, когда ряд элементов из l ² сходится абсолютно (по норме), то он сходится к элементу из l ² . Доказательство является базовым в математическом анализе и позволяет манипулировать математическими рядами элементов пространства с той же легкостью, что и рядами комплексных чисел (или векторов в конечномерном евклидовом пространстве). ^[10]

История

Дэвид Гилберт

До разработки пространств Гильберта математикам и физикам были известны другие обобщения евклидовых пространств . В частности, идея абстрактного линейного пространства (векторного пространства) приобрела некоторую популярность к концу 19-го века: ^[11] это пространство, элементы которого можно складывать и умножать на скаляры (такие как действительные или комплексные числа ) без обязательного отождествления этих элементов с «геометрическими» векторами , такими как векторы положения и импульса в физических системах. Другие объекты, изучаемые математиками на рубеже 20-го века, в частности пространства последовательностей (включая ряды ) и пространства функций, ^[12] можно естественным образом рассматривать как линейные пространства. Функции, например, можно складывать или умножать на постоянные скаляры, и эти операции подчиняются алгебраическим законам, которым удовлетворяют сложение и скалярное умножение пространственных векторов.

В первом десятилетии 20-го века параллельные разработки привели к введению пространств Гильберта. Первым из них было наблюдение, возникшее во время изучения интегральных уравнений Дэвидом Гильбертом и Эрхардом Шмидтом ^[13] , что две квадратично интегрируемые действительные функции f и g на интервале [ a , b ] имеют скалярное произведение

${\displaystyle \langle f,g\rangle =\int _{a}^{b}f(x)g(x)\,\mathrm {d} x}$

который имеет много знакомых свойств евклидова скалярного произведения. В частности, идея ортогонального семейства функций имеет смысл. Шмидт использовал сходство этого скалярного произведения с обычным скалярным произведением, чтобы доказать аналог спектрального разложения для оператора вида

${\displaystyle f(x)\mapsto \int _{a}^{b}K(x,y)f(y)\,\mathrm {d} y}$

где K — непрерывная функция, симметричная относительно x и y . Полученное разложение собственных функций выражает функцию K в виде ряда вида

${\displaystyle K(x,y)=\sum _{n}\lambda _{n}\varphi _{n}(x)\varphi _{n}(y)}$

где функции φ _n ортогональны в том смысле, что ⟨ φ _n , φ _m ⟩ = 0 для всех n ≠ m . Отдельные члены в этой серии иногда называют элементарными решениями произведений. Однако существуют разложения собственных функций, которые не сходятся в подходящем смысле к квадратично интегрируемой функции: недостающим ингредиентом, который обеспечивает сходимость, является полнота. ^[14]

Вторым достижением стал интеграл Лебега , альтернатива интегралу Римана, введенному Анри Лебегом в 1904 году . ^[15] Интеграл Лебега позволил интегрировать гораздо более широкий класс функций. В 1907 году Фридьеш Рисс и Эрнст Сигизмунд Фишер независимо доказали, что пространство L2 ^{функций} , интегрируемых по Лебегу с квадратом, является полным метрическим пространством . ^[16] Вследствие взаимодействия геометрии и полноты результаты 19-го века Жозефа Фурье , Фридриха Бесселя и Марка-Антуана Парсеваля по тригонометрическим рядам легко переносились на эти более общие пространства, что привело к геометрическому и аналитическому аппарату, который теперь обычно известен как теорема Рисса–Фишера . ^[17]

Дальнейшие основные результаты были доказаны в начале 20-го века. Например, теорема о представлении Рисса была независимо установлена ​​Морисом Фреше и Фридьесом Риссом в 1907 году. ^[18] Джон фон Нейман ввел термин абстрактное гильбертово пространство в своей работе о неограниченных эрмитовых операторах . ^[19] Хотя другие математики, такие как Герман Вейль и Норберт Винер, уже изучали конкретные гильбертовы пространства очень подробно, часто с физически мотивированной точки зрения, фон Нейман дал первое полное и аксиоматическое их рассмотрение. ^[20] Фон Нейман позже использовал их в своей основополагающей работе по основам квантовой механики, ^[21] и в своей дальнейшей работе с Юджином Вигнером . Название «гильбертово пространство» вскоре было принято другими, например, Германом Вейлем в его книге о квантовой механике и теории групп. ^[22]

Значимость концепции гильбертова пространства была подчеркнута осознанием того, что оно предлагает одну из лучших математических формулировок квантовой механики . ^[23] Короче говоря, состояния квантово-механической системы являются векторами в определенном гильбертовом пространстве, наблюдаемые являются эрмитовыми операторами в этом пространстве, симметрии системы являются унитарными операторами , а измерения являются ортогональными проекциями . Связь между квантово-механическими симметриями и унитарными операторами дала толчок развитию унитарной теории представления групп , начатой ​​в работе Германа Вейля 1928 года. ^[22] С другой стороны, в начале 1930-х годов стало ясно, что классическая механика может быть описана в терминах гильбертова пространства ( классическая механика Купмана–фон Неймана ) и что определенные свойства классических динамических систем могут быть проанализированы с использованием методов гильбертова пространства в рамках эргодической теории . ^[24]

Алгебра наблюдаемых в квантовой механике, естественно, является алгеброй операторов, определенных в гильбертовом пространстве, согласно формулировке квантовой теории в матричной механике Вернера Гейзенберга . ^[25] Фон Нейман начал исследовать операторные алгебры в 1930-х годах как кольца операторов в гильбертовом пространстве. Вид алгебр, изученный фон Нейманом и его современниками, теперь известен как алгебры фон Неймана . ^[26] В 1940-х годах Израиль Гельфанд , Марк Наймарк и Ирвинг Сигал дали определение вида операторных алгебр, называемых C*-алгебрами , которые, с одной стороны, не ссылались на лежащее в основе гильбертово пространство, а с другой стороны, экстраполировали многие полезные особенности операторных алгебр, которые ранее изучались. Спектральная теорема для самосопряженных операторов, в частности, лежащая в основе большей части существующей теории гильбертова пространства, была обобщена на C*-алгебры. ^[27] Эти методы теперь являются основными в абстрактном гармоническом анализе и теории представлений.

Примеры

Пространства Лебега

^{Пространства} Лебега — это функциональные пространства , связанные с пространствами мер ( X , M , μ ) , где X — множество, M — σ-алгебра подмножеств X , а μ — счетно-аддитивная мера на M. Пусть L2 ( X , μ ) — пространство тех комплекснозначных измеримых функций на X, для которых интеграл Лебега квадрата абсолютной величины функции конечен, т. е. для функции f из L2 ( X , μ ) , и где функции идентифицируются тогда и только тогда, когда они различаются только на ^{множестве} меры нуль . $${\displaystyle \int _{X}|f|^{2}\mathrm {d} \mu <\infty \,,}$$

Тогда внутреннее произведение функций f и g в L ² ( X , μ ) определяется как или $${\displaystyle \langle f,g\rangle =\int _{X}f(t){\overline {g(t)}}\,\mathrm {d} \mu (t)}$$ $${\displaystyle \langle f,g\rangle =\int _{X}{\overline {f(t)}}g(t)\,\mathrm {d} \mu (t)\,,}$$

где вторая форма (сопряженность первого элемента) обычно встречается в литературе по теоретической физике . Для f и g в L ² интеграл существует из-за неравенства Коши–Шварца и определяет скалярное произведение на пространстве. Оснащенное этим скалярным произведением, L ² фактически является полным. ^[28] Интеграл Лебега необходим для обеспечения полноты: в областях действительных чисел, например, недостаточно функций, интегрируемых по Риману . ^[29]

Пространства Лебега появляются во многих естественных ситуациях. Пространства L ² ( R ) и L ² ([0,1]) квадратично-интегрируемых функций относительно меры Лебега на действительной прямой и единичном интервале соответственно являются естественными областями, на которых определяются преобразование Фурье и ряд Фурье. В других ситуациях мера может быть чем-то иным, чем обычная мера Лебега на действительной прямой. Например, если w — любая положительная измеримая функция, пространство всех измеримых функций f на интервале [0, 1], удовлетворяющих , называется весовым пространством L 2 L $${\displaystyle \int _{0}^{1}{\bigl |}f(t){\bigr |}^{2}w(t)\,\mathrm {d} t<\infty }$$ ²
_нед.([0, 1]) , а w называется весовой функцией. Внутренний продукт определяется как $${\displaystyle \langle f,g\rangle =\int _{0}^{1}f(t){\overline {g(t)}}w(t)\,\mathrm {d} t\,.}$$

Взвешенное пространство L²
_нед.([0, 1]) идентично гильбертову пространству L ² ([0, 1], μ ) , где мера μ измеримого по Лебегу множества A определяется как $${\displaystyle \mu (A)=\int _{A}w(t)\,\mathrm {d} t\,.}$$

Взвешенные пространства L2 ^, подобные этому, часто используются для изучения ортогональных многочленов , поскольку различные семейства ортогональных многочленов ортогональны относительно различных весовых функций. ^[30]

Соболевские пространства

Пространства Соболева , обозначаемые как H ^s или W ^{s , 2} , являются пространствами Гильберта. Это особый вид функционального пространства , в котором может выполняться дифференциация , но которое (в отличие от других банаховых пространств, таких как пространства Гёльдера ) поддерживает структуру скалярного произведения. Поскольку дифференциация разрешена, пространства Соболева являются удобной средой для теории уравнений с частными производными . ^[31] Они также составляют основу теории прямых методов в вариационном исчислении . ^[32]

Для s — неотрицательного целого числа и Ω ⊂ R ⁿ пространство Соболева H ^s (Ω) содержит L ² функций, слабые производные порядка до s которых также являются L ² . Скалярное произведение в H ^s (Ω) — это где точка обозначает скалярное произведение в евклидовом пространстве частных производных каждого порядка. Пространства Соболева также могут быть определены, когда s — не целое число. $${\displaystyle \langle f,g\rangle =\int _{\Omega }f(x){\bar {g}}(x)\,\mathrm {d} x+\int _{\Omega }Df(x)\cdot D{\bar {g}}(x)\,\mathrm {d} x+\cdots +\int _{\Omega }D^{s}f(x)\cdot D^{s}{\bar {g}}(x)\,\mathrm {d} x}$$

Пространства Соболева также изучаются с точки зрения спектральной теории, опираясь более конкретно на структуру пространства Гильберта. Если Ω является подходящей областью, то можно определить пространство Соболева H ^s (Ω) как пространство потенциалов Бесселя ; ^[33] грубо говоря, $${\displaystyle H^{s}(\Omega )=\left\{(1-\Delta )^{-s/2}f\mathrel {\Big |} f\in L^{2}(\Omega )\right\}\,.}$$

Здесь Δ — лапласиан, а (1 − Δ) ^{− s  / 2} понимается в терминах теоремы о спектральном отображении . Помимо предоставления работоспособного определения пространств Соболева для нецелых s , это определение также имеет особенно желательные свойства относительно преобразования Фурье , которые делают его идеальным для изучения псевдодифференциальных операторов . Используя эти методы на компактном римановом многообразии , можно получить, например, разложение Ходжа , которое является основой теории Ходжа . ^[34]

Пространства голоморфных функций

Харди пространства

Пространства Харди — это функциональные пространства, возникающие в комплексном анализе и гармоническом анализе , элементами которых являются некоторые голоморфные функции в комплексной области. ^[35] Пусть U обозначает единичный круг в комплексной плоскости. Тогда пространство Харди H ² ( U ) определяется как пространство голоморфных функций f на U таких, что средние

$${\displaystyle M_{r}(f)={\frac {1}{2\pi }}\int _{0}^{2\pi }\left|f{\bigl (}re^{i\theta }{\bigr )}\right|^{2}\,\mathrm {d} \theta }$$

остаются ограниченными при r < 1. Норма в этом пространстве Харди определяется как $${\displaystyle \left\|f\right\|_{2}=\lim _{r\to 1}{\sqrt {M_{r}(f)}}\,.}$$

Пространства Харди в круге связаны с рядами Фурье. Функция f принадлежит H ² ( U ) тогда и только тогда, когда , где $${\displaystyle f(z)=\sum _{n=0}^{\infty }a_{n}z^{n}}$$ $${\displaystyle \sum _{n=0}^{\infty }|a_{n}|^{2}<\infty \,.}$$

Таким образом, H ² ( U ) состоит из тех функций, которые являются L ² на окружности, и отрицательные частотные коэффициенты Фурье которых обращаются в нуль.

Пространства Бергмана

Пространства Бергмана — это еще одно семейство гильбертовых пространств голоморфных функций. ^[36] Пусть D — ограниченное открытое множество в комплексной плоскости (или многомерное комплексное пространство), а L ^{2, h} ( D ) — пространство голоморфных функций f в D , которые также находятся в L ² ( D ) в том смысле, что $${\displaystyle \|f\|^{2}=\int _{D}|f(z)|^{2}\,\mathrm {d} \mu (z)<\infty \,,}$$

где интеграл берется относительно меры Лебега в D . Очевидно, что L ^{2, h} ( D ) является подпространством L ² ( D ) ; на самом деле, это замкнутое подпространство, и, следовательно, само по себе гильбертово пространство. Это является следствием оценки, справедливой на компактных подмножествах K из D , которая , в свою очередь, следует из интегральной формулы Коши . Таким образом, сходимость последовательности голоморфных функций в L ² ( D ) влечет также компактную сходимость , и, следовательно, предельная функция также голоморфна. Другим следствием этого неравенства является то, что линейный функционал, который оценивает функцию f в точке D , на самом деле непрерывен на L ^{2, h} ( D ) . Теорема о представлении Рисса подразумевает, что функционал оценки может быть представлен как элемент L ^{2, h} ( D ) . Таким образом, для каждого z ∈ D существует функция η _z ∈ L ^{2, h} ( D ) такая , что для всех f ∈ L ^{2, h} ( D ) . Подынтегральное выражение известно как ядро ​​Бергмана D . Это интегральное ядро ​​удовлетворяет воспроизводящему свойству $${\displaystyle \sup _{z\in K}\left|f(z)\right|\leq C_{K}\left\|f\right\|_{2}\,,}$$ $${\displaystyle f(z)=\int _{D}f(\zeta ){\overline {\eta _{z}(\zeta )}}\,\mathrm {d} \mu (\zeta )}$$ $${\displaystyle K(\zeta ,z)={\overline {\eta _{z}(\zeta )}}}$$ $${\displaystyle f(z)=\int _{D}f(\zeta )K(\zeta ,z)\,\mathrm {d} \mu (\zeta )\,.}$$

Пространство Бергмана является примером воспроизводящего ядра Гильбертова пространства , которое является гильбертовым пространством функций вместе с ядром K ( ζ , z ), которое проверяет свойство воспроизводства, аналогичное этому. Пространство Харди H ² ( D ) также допускает воспроизводящее ядро, известное как ядро ​​Сегё . ^[37] Воспроизводящие ядра распространены и в других областях математики. Например, в гармоническом анализе ядро ​​Пуассона является воспроизводящим ядром для гильбертова пространства квадратично-интегрируемых гармонических функций в единичном шаре . То, что последнее вообще является гильбертовым пространством, является следствием теоремы о среднем значении для гармонических функций.

Приложения

Многие приложения гильбертовых пространств используют тот факт, что гильбертовы пространства поддерживают обобщения простых геометрических понятий, таких как проекция и изменение базиса из их обычной конечномерной установки. В частности, спектральная теория непрерывных самосопряженных линейных операторов в гильбертовом пространстве обобщает обычное спектральное разложение матрицы , и это часто играет важную роль в приложениях теории к другим областям математики и физики.

Теория Штурма–Лиувилля

Обертоны вибрирующей струны. Это собственные функции связанной задачи Штурма–Лиувилля. Собственные значения 1, ⁠1/2⁠ , ⁠1/3⁠ , ... образуют (музыкальный) гармонический ряд .

В теории обыкновенных дифференциальных уравнений спектральные методы на подходящем гильбертовом пространстве используются для изучения поведения собственных значений и собственных функций дифференциальных уравнений. Например, проблема Штурма–Лиувилля возникает при изучении гармоник волн в скрипичной струне или барабане и является центральной проблемой в обыкновенных дифференциальных уравнениях . ^[38] Задача представляет собой дифференциальное уравнение вида для неизвестной функции y на интервале [ a , b ] , удовлетворяющее общим однородным граничным условиям Робина Функции p , q и w заданы заранее, и задача состоит в том, чтобы найти функцию y и константы λ, для которых уравнение имеет решение. Задача имеет решения только для определенных значений λ , называемых собственными значениями системы, и это является следствием спектральной теоремы для компактных операторов , примененной к интегральному оператору, определяемому функцией Грина для системы. Более того, еще одним следствием этого общего результата является то, что собственные значения λ системы могут быть расположены в возрастающей последовательности, стремящейся к бесконечности. ^{[39] [nb 2]} $${\displaystyle -{\frac {\mathrm {d} }{\mathrm {d} x}}\left[p(x){\frac {\mathrm {d} y}{\mathrm {d} x}}\right]+q(x)y=\lambda w(x)y}$$ $${\displaystyle {\begin{cases}\alpha y(a)+\alpha 'y'(a)&=0\\\beta y(b)+\beta 'y'(b)&=0\,.\end{cases}}}$$

Уравнения с частными производными

Гильбертовы пространства образуют основной инструмент в изучении уравнений с частными производными . ^[31] Для многих классов уравнений с частными производными, таких как линейные эллиптические уравнения , можно рассмотреть обобщенное решение (известное как слабое решение) путем расширения класса функций. Многие слабые формулировки включают класс функций Соболева , который является гильбертовым пространством. Подходящая слабая формулировка сводится к геометрической задаче, аналитической задаче нахождения решения или, что часто более важно, демонстрации того, что решение существует и является единственным для заданных граничных данных. Для линейных эллиптических уравнений одним геометрическим результатом, который обеспечивает однозначную разрешимость для большого класса задач, является теорема Лакса–Мильгрэма . Эта стратегия образует рудимент метода Галеркина ( метода конечных элементов ) для численного решения уравнений с частными производными. ^[40]

Типичным примером является уравнение Пуассона −Δ u = g с граничными условиями Дирихле в ограниченной области Ω в R ^2. Слабая формулировка состоит в нахождении функции u такой, что для всех непрерывно дифференцируемых функций v в Ω , обращающихся в нуль на границе: $${\displaystyle \int _{\Omega }\nabla u\cdot \nabla v=\int _{\Omega }gv\,.}$$

Это можно переформулировать в терминах гильбертова пространства H¹
₀(Ω), состоящая из функций u таких, что u , вместе со своими слабыми частными производными, квадратично интегрируемы на Ω и исчезают на границе. Тогда вопрос сводится к нахождению u в этом пространстве, такого, что для всех v в этом пространстве $${\displaystyle a(u,v)=b(v)}$$

где a — непрерывная билинейная форма , а b — непрерывный линейный функционал , заданный соответственно формулами $${\displaystyle a(u,v)=\int _{\Omega }\nabla u\cdot \nabla v,\quad b(v)=\int _{\Omega }gv\,.}$$

Поскольку уравнение Пуассона является эллиптическим , то из неравенства Пуанкаре следует, что билинейная форма a является коэрцитивной . Теорема Лакса–Мильграма тогда гарантирует существование и единственность решений этого уравнения. ^[41]

Гильбертовы пространства позволяют формулировать многие эллиптические уравнения с частными производными аналогичным образом, и теорема Лакса–Милгрэма является тогда основным инструментом в их анализе. С подходящими модификациями подобные методы могут быть применены к параболическим уравнениям с частными производными и некоторым гиперболическим уравнениям с частными производными . ^[42]

Эргодическая теория

Траектория бильярдного шара на стадионе Бунимовича описывается эргодической динамической системой .

Область эргодической теории — это изучение долгосрочного поведения хаотических динамических систем . Типичным случаем области, к которой применяется эргодическая теория, является термодинамика , в которой — хотя микроскопическое состояние системы чрезвычайно сложно (невозможно понять совокупность отдельных столкновений между частицами материи) — среднее поведение на достаточно длительных интервалах времени поддается изучению. Законы термодинамики — это утверждения о таком среднем поведении. В частности, одна из формулировок нулевого закона термодинамики утверждает, что на достаточно длительных временных масштабах единственным функционально независимым измерением, которое можно сделать для термодинамической системы в равновесии, является ее полная энергия в форме температуры . ^[43]

Эргодическая динамическая система — это та, для которой, кроме энергии, измеряемой гамильтонианом , нет других функционально независимых сохраняющихся величин на фазовом пространстве . Более конкретно, предположим, что энергия E фиксирована, и пусть Ω _E — подмножество фазового пространства, состоящее из всех состояний энергии E (энергетическая поверхность), и пусть T _t обозначает оператор эволюции на фазовом пространстве. Динамическая система эргодична, если каждая инвариантная измеримая функция на Ω _E постоянна почти всюду . ^[44] Инвариантная функция f — это та, для которой для всех w на Ω _E и всех времен t . Теорема Лиувилля подразумевает, что существует мера μ на энергетической поверхности, которая инвариантна относительно переноса времени . В результате перенос времени является унитарным преобразованием гильбертова пространства L ² (Ω _E , μ ), состоящего из квадратично интегрируемых функций на энергетической поверхности Ω _E относительно скалярного произведения $${\displaystyle f(T_{t}w)=f(w)}$$ $${\displaystyle \left\langle f,g\right\rangle _{L^{2}\left(\Omega _{E},\mu \right)}=\int _{E}f{\bar {g}}\,\mathrm {d} \mu \,.}$$

Среднеэргодическая теорема фон Неймана ^[24] утверждает следующее:

• Если U _t — (сильно непрерывная) однопараметрическая полугруппа унитарных операторов в гильбертовом пространстве H , а P — ортогональная проекция на пространство общих неподвижных точек U _t , { x ∈ H | U _t x = x , ∀ t > 0} , то $${\displaystyle Px=\lim _{T\to \infty }{\frac {1}{T}}\int _{0}^{T}U_{t}x\,\mathrm {d} t\,.}$$

Для эргодической системы фиксированный набор временной эволюции состоит только из постоянных функций, поэтому эргодическая теорема подразумевает следующее: ^[45] для любой функции f ∈ L ² (Ω _E , μ ) , $${\displaystyle {\underset {T\to \infty }{L^{2}-\lim }}{\frac {1}{T}}\int _{0}^{T}f(T_{t}w)\,\mathrm {d} t=\int _{\Omega _{E}}f(y)\,\mathrm {d} \mu (y)\,.}$$

То есть долгосрочное среднее значение наблюдаемой f равно ее математическому ожиданию на энергетической поверхности.

анализ Фурье

Суперпозиция базисных функций синусоидальной волны (внизу) для формирования пилообразной волны (вверху)

Сферические гармоники , ортонормированный базис для гильбертова пространства квадратично-интегрируемых функций на сфере, изображенный в виде графика вдоль радиального направления.

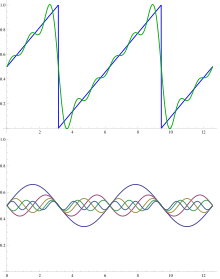
Одной из основных целей анализа Фурье является разложение функции в (возможно, бесконечную) линейную комбинацию заданных базисных функций: ассоциированный ряд Фурье . Классический ряд Фурье, ассоциированный с функцией f, определенной на интервале [0, 1], представляет собой ряд вида , где $${\displaystyle \sum _{n=-\infty }^{\infty }a_{n}e^{2\pi in\theta }}$$ $${\displaystyle a_{n}=\int _{0}^{1}f(\theta )\;\!e^{-2\pi in\theta }\,\mathrm {d} \theta \,.}$$

Пример сложения первых нескольких членов ряда Фурье для пилообразной функции показан на рисунке. Базисные функции — это синусоиды с длинами волн ⁠λ/н⁠ (для целого числа n ) короче длины волны λ самой пилообразной волны (за исключением n = 1 , основной волны).

Существенная проблема в классических рядах Фурье заключается в том, в каком смысле ряд Фурье сходится, если сходится вообще, к функции f . Методы гильбертова пространства дают один из возможных ответов на этот вопрос. ^[46] Функции e _n ( θ ) = e ^{2π inθ} образуют ортогональный базис гильбертова пространства L ² ([0, 1]) . Следовательно, любая квадратично интегрируемая функция может быть выражена в виде ряда $${\displaystyle f(\theta )=\sum _{n}a_{n}e_{n}(\theta )\,,\quad a_{n}=\langle f,e_{n}\rangle }$$

и , более того, этот ряд сходится в смысле гильбертова пространства (то есть в смысле L2 mean ).

Проблему можно также изучать с абстрактной точки зрения: каждое гильбертово пространство имеет ортонормированный базис , и каждый элемент гильбертова пространства может быть записан уникальным образом как сумма кратных этих базисных элементов. Коэффициенты, появляющиеся в этих базисных элементах, иногда абстрактно известны как коэффициенты Фурье элемента пространства. ^[47] Абстракция особенно полезна, когда более естественно использовать различные базисные функции для такого пространства, как L2 ([0, 1]) . Во многих случаях желательно не разлагать функцию на тригонометрические функции, а скорее на ортогональные многочлены или вейвлеты , например, ^{[48] и в более высоких размерностях} на сферические гармоники . ^[49]

Например, если e _n — любые ортонормированные базисные функции L ² [0, 1] , то заданную функцию в L ² [0, 1] можно аппроксимировать как конечную линейную комбинацию ^[50] $${\displaystyle f(x)\approx f_{n}(x)=a_{1}e_{1}(x)+a_{2}e_{2}(x)+\cdots +a_{n}e_{n}(x)\,.}$$

Коэффициенты { a _j } выбираются так, чтобы сделать величину разности ‖ f − f _n ‖ ² как можно меньше. Геометрически наилучшим приближением является ортогональная проекция f на подпространство, состоящее из всех линейных комбинаций { e _j } , и может быть вычислено по формуле ^[51] $${\displaystyle a_{j}=\int _{0}^{1}{\overline {e_{j}(x)}}f(x)\,\mathrm {d} x\,.}$$

То, что эта формула минимизирует разность ‖ f − f _n ‖ ^2, является следствием неравенства Бесселя и формулы Парсеваля.

В различных приложениях к физическим проблемам функция может быть разложена на физически значимые собственные функции дифференциального оператора (обычно оператора Лапласа ): это формирует основу для спектрального изучения функций по отношению к спектру дифференциального оператора. ^[52] Конкретное физическое приложение включает проблему восприятия формы барабана : учитывая основные моды вибрации, которые способна производить мембрана барабана, можно ли вывести форму самого барабана? ^[53] Математическая формулировка этого вопроса включает собственные значения Дирихле уравнения Лапласа на плоскости, которые представляют основные моды вибрации по прямой аналогии с целыми числами, которые представляют основные моды вибрации скрипичной струны.

Спектральная теория также лежит в основе некоторых аспектов преобразования Фурье функции. В то время как анализ Фурье разлагает функцию, определенную на компактном множестве, на дискретный спектр Лапласа (который соответствует колебаниям скрипичной струны или барабана), преобразование Фурье функции является разложением функции, определенной на всем евклидовом пространстве, на ее компоненты в непрерывном спектре Лапласа. Преобразование Фурье также является геометрическим, в некотором смысле, уточненном теоремой Планшереля , которая утверждает, что оно является изометрией одного гильбертова пространства («временной области») с другим («частотной области»). Это свойство изометрии преобразования Фурье является повторяющейся темой в абстрактном гармоническом анализе (поскольку оно отражает сохранение энергии для непрерывного преобразования Фурье), о чем свидетельствует, например, теорема Планшереля для сферических функций, встречающихся в некоммутативном гармоническом анализе .

Квантовая механика

Орбитали электрона в атоме водорода являются собственными функциями энергии .​

В математически строгой формулировке квантовой механики , разработанной Джоном фон Нейманом , ^[54] возможные состояния (точнее, чистые состояния ) квантово-механической системы представлены единичными векторами (называемыми векторами состояния ), находящимися в комплексном сепарабельном гильбертовом пространстве, известном как пространство состояний , хорошо определенное с точностью до комплексного числа нормы 1 ( фазовый множитель ). Другими словами, возможные состояния являются точками в проективизации гильбертова пространства, обычно называемого комплексным проективным пространством . Точная природа этого гильбертова пространства зависит от системы; например, состояния положения и импульса для одной нерелятивистской частицы со спином ноль являются пространством всех квадратично интегрируемых функций, в то время как состояния для спина одного протона являются единичными элементами двумерного комплексного гильбертова пространства спиноров . Каждая наблюдаемая представлена ​​самосопряженным линейным оператором, действующим на пространстве состояний. Каждое собственное состояние наблюдаемой величины соответствует собственному вектору оператора, а соответствующее собственное значение соответствует значению наблюдаемой величины в этом собственном состоянии. ^[55]

Внутренний продукт между двумя векторами состояния — это комплексное число, известное как амплитуда вероятности . Во время идеального измерения квантово-механической системы вероятность того, что система коллапсирует из заданного начального состояния в определенное собственное состояние, задается квадратом абсолютного значения амплитуд вероятности между начальным и конечным состояниями. ^[56] Возможные результаты измерения — это собственные значения оператора, что объясняет выбор самосопряженных операторов, поскольку все собственные значения должны быть действительными. Распределение вероятностей наблюдаемой в заданном состоянии можно найти, вычислив спектральное разложение соответствующего оператора. ^[57]

Для общей системы состояния обычно не являются чистыми, а вместо этого представлены как статистические смеси чистых состояний или смешанные состояния, заданные матрицами плотности : самосопряженные операторы следа один в гильбертовом пространстве. ^[58] Более того, для общих квантово-механических систем эффекты одного измерения могут влиять на другие части системы таким образом, который вместо этого описывается положительной операторно-значной мерой . Таким образом, структура как состояний, так и наблюдаемых в общей теории значительно сложнее, чем идеализация для чистых состояний. ^[59]

Теория вероятностей

В теории вероятностей гильбертовы пространства также имеют разнообразные приложения. Здесь фундаментальное гильбертово пространство — это пространство случайных величин на заданном вероятностном пространстве , имеющее класс (конечные первый и второй моменты ). Распространенной операцией в статистике является операция центрирования случайной величины путем вычитания ее математического ожидания . Таким образом, если — случайная величина, то — ее центрирование. С точки зрения гильбертова пространства это ортогональная проекция на ядро ​​оператора математического ожидания, которое является непрерывным линейным функционалом на гильбертовом пространстве (фактически, скалярным произведением с постоянной случайной величиной 1), и поэтому это ядро ​​является замкнутым подпространством. ${\displaystyle L^{2}}$ ${\displaystyle X}$ ${\displaystyle X-E(X)}$ ${\displaystyle X}$

Условное ожидание имеет естественную интерпретацию в гильбертовом пространстве. ^[60] Предположим, что задано вероятностное пространство , где — сигма-алгебра на множестве , а — вероятностная мера на пространстве мер . Если — сигма-подалгебра , то условное ожидание — это ортогональная проекция на подпространство , состоящее из -измеримых функций. Если случайная величина в независима от сигма-алгебры , то условное ожидание , т. е. ее проекция на -измеримые функции, является константой. Эквивалентно, проекция ее центрирования равна нулю. ${\displaystyle (\Omega ,P,{\mathcal {B}})}$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle \Omega }$ ${\displaystyle P}$ ${\displaystyle (\Omega ,{\mathcal {B}})}$ ${\displaystyle {\mathcal {F}}\leq {\mathcal {B}}}$ ${\displaystyle {\mathcal {B}}}$ ${\displaystyle E[X|{\mathcal {F}}]}$ ${\displaystyle X}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle X}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle {\mathcal {F}}}$ ${\displaystyle E(X|{\mathcal {F}})=E(X)}$ ${\displaystyle {\mathcal {F}}}$

В частности, если две случайные величины и (в ) независимы, то центрированные случайные величины и ортогональны. (Это означает, что две переменные имеют нулевую ковариацию : они некоррелированы .) В этом случае теорема Пифагора в ядре оператора ожидания подразумевает, что дисперсии и удовлетворяют тождеству : иногда называемому теоремой Пифагора статистики, и имеет важное значение в линейной регрессии . ^[61] Как выразился Стэплтон (1995), « дисперсионный анализ можно рассматривать как разложение квадрата длины вектора на сумму квадратов длин нескольких векторов с использованием теоремы Пифагора». ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle L^{2}(\Omega ,P)}$ ${\displaystyle X-E(X)}$ ${\displaystyle Y-E(Y)}$ ${\displaystyle X}$ ${\displaystyle Y}$ $${\displaystyle \operatorname {Var} (X+Y)=\operatorname {Var} (X)+\operatorname {Var} (Y),}$$

Теория мартингалов может быть сформулирована в гильбертовых пространствах. Мартингал в гильбертовом пространстве — это последовательность элементов гильбертова пространства, такая, что для каждого n , является ортогональной проекцией на линейную оболочку . ^[62] Если являются случайными величинами, это воспроизводит обычное определение (дискретного) мартингала: ожидание , обусловленное , равно . ${\displaystyle x_{1},x_{2},\dots }$ ${\displaystyle x_{n}}$ ${\displaystyle x_{n+1}}$ ${\displaystyle x_{1},\dots ,x_{n}}$ ${\displaystyle x_{k}}$ ${\displaystyle x_{n+1}}$ ${\displaystyle x_{1},\dots ,x_{n}}$ ${\displaystyle x_{n}}$

Гильбертовы пространства также используются в основах исчисления Ито . ^[63] Любому квадратично-интегрируемому мартингалу можно связать гильбертову норму на пространстве классов эквивалентности прогрессивно измеримых процессов относительно мартингала (используя квадратичную вариацию мартингала в качестве меры). Интеграл Ито можно построить, сначала определив его для простых процессов, а затем используя их плотность в гильбертовом пространстве. Примечательным результатом является изометрия Ито , которая свидетельствует, что для любого мартингала M, имеющего квадратичную меру вариации , и любого прогрессивно измеримого процесса H : всякий раз, когда ожидание в правой части конечно. ${\displaystyle d\langle M\rangle _{t}}$ $${\displaystyle E\left[\left(\int _{0}^{t}H_{s}dM_{s}\right)^{2}\right]=E\left[\int _{0}^{t}H_{s}^{2}d\langle M\rangle _{s}\right]}$$

Более глубокое применение гильбертовых пространств, которое особенно важно в теории гауссовских процессов , представляет собой попытку, предпринятую Леонардом Гроссом и другими, придать смысл некоторым формальным интегралам по бесконечномерным пространствам, таким как интеграл Фейнмана по траекториям из квантовой теории поля . Проблема с таким интегралом заключается в том, что не существует бесконечномерной меры Лебега . Понятие абстрактного пространства Винера позволяет построить меру на банаховом пространстве B , которое содержит гильбертово пространство H , называемое пространством Камерона–Мартина , как плотное подмножество, из конечно-аддитивной цилиндрической меры множества на H. Результирующая мера на B является счетно-аддитивной и инвариантной относительно переноса элементами H , и это обеспечивает математически строгий способ мышления о мере Винера как о гауссовой мере на пространстве Соболева . ^[64] ${\displaystyle H^{1}([0,\infty ))}$

Восприятие цвета

Любой истинный физический цвет может быть представлен комбинацией чистых спектральных цветов . Поскольку физические цвета могут состоять из любого количества спектральных цветов, пространство физических цветов может быть удачно представлено гильбертовым пространством над спектральными цветами. У людей есть три типа колбочек для восприятия цвета, поэтому воспринимаемые цвета могут быть представлены трехмерным евклидовым пространством. Линейное отображение «многие к одному» из гильбертова пространства физических цветов в евклидово пространство воспринимаемых человеком цветов объясняет, почему многие различные физические цвета могут восприниматься людьми как идентичные (например, чистый желтый свет по сравнению со смесью красного и зеленого света, см. метамерию ). ^{[65] [66]}

Характеристики

Пифагорейская идентичность

Два вектора u и v в гильбертовом пространстве H ортогональны, когда ⟨ u , v ⟩ = 0 . Обозначение для этого — u ⊥ v . В более общем случае, когда S является подмножеством в H , обозначение u ⊥ S означает, что u ортогонален каждому элементу из S .

Когда u и v ортогональны, имеем $${\displaystyle \|u+v\|^{2}=\langle u+v,u+v\rangle =\langle u,u\rangle +2\,\operatorname {Re} \langle u,v\rangle +\langle v,v\rangle =\|u\|^{2}+\|v\|^{2}\,.}$$

Индукцией по n это распространяется на любое семейство u ₁ , ..., u _n из n ортогональных векторов, $${\displaystyle \left\|u_{1}+\cdots +u_{n}\right\|^{2}=\left\|u_{1}\right\|^{2}+\cdots +\left\|u_{n}\right\|^{2}.}$$

В то время как тождество Пифагора, как указано, справедливо в любом пространстве внутреннего произведения, для расширения тождества Пифагора на ряды требуется полнота. ^[67] Ряд Σ u _k ортогональных векторов сходится в H тогда и только тогда, когда сходится ряд квадратов норм, и Более того, сумма ряда ортогональных векторов не зависит от порядка, в котором она берется. $${\displaystyle {\Biggl \|}\sum _{k=0}^{\infty }u_{k}{\Biggr \|}^{2}=\sum _{k=0}^{\infty }\left\|u_{k}\right\|^{2}\,.}$$

Тождество параллелограмма и поляризация

Геометрически тождество параллелограмма утверждает, что AC ² + BD ² = 2(AB ² + AD ² ) . На словах, сумма квадратов диагоналей в два раза больше суммы квадратов любых двух смежных сторон.

По определению, каждое гильбертово пространство также является банаховым пространством . Более того, в каждом гильбертовом пространстве выполняется следующее тождество параллелограмма : ^[68] $${\displaystyle \|u+v\|^{2}+\|u-v\|^{2}=2{\bigl (}\|u\|^{2}+\|v\|^{2}{\bigr )}\,.}$$

Наоборот, каждое банахово пространство, в котором выполняется тождество параллелограмма, является гильбертовым пространством, а скалярное произведение однозначно определяется нормой тождества поляризации . ^[69] Для действительных гильбертовых пространств тождество поляризации равно $${\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}{\bigl (}\|u+v\|^{2}-\|u-v\|^{2}{\bigr )}\,.}$$

Для комплексных гильбертовых пространств это $${\displaystyle \langle u,v\rangle ={\tfrac {1}{4}}{\bigl (}\|u+v\|^{2}-\|u-v\|^{2}+i\|u+iv\|^{2}-i\|u-iv\|^{2}{\bigr )}\,.}$$

Закон параллелограмма подразумевает, что любое гильбертово пространство является равномерно выпуклым банаховым пространством . ^[70]

Наилучшее приближение

В этом подразделе используется теорема о проекции Гильберта . Если C — непустое замкнутое выпуклое подмножество гильбертова пространства H , а x — точка в H , то существует единственная точка y ∈ C , которая минимизирует расстояние между x и точками в C , ^[71] $${\displaystyle y\in C\,,\quad \|x-y\|=\operatorname {dist} (x,C)=\min {\bigl \{}\|x-z\|\mathrel {\big |} z\in C{\bigr \}}\,.}$$

Это эквивалентно утверждению, что существует точка с минимальной нормой в сдвинутом выпуклом множестве D = C − x . Доказательство состоит в демонстрации того, что каждая минимизирующая последовательность ( d _n ) ⊂ D является последовательностью Коши (используя тождество параллелограмма), следовательно, сходится (используя полноту) к точке в D , которая имеет минимальную норму. В более общем случае это справедливо в любом равномерно выпуклом банаховом пространстве. ^[72]

Применяя этот результат к замкнутому подпространству F пространства H , можно показать, что точка y ∈ F, ближайшая к x, характеризуется соотношением ^[73] $${\displaystyle y\in F\,,\quad x-y\perp F\,.}$$

Эта точка y является ортогональной проекцией x на F , а отображение P _F  : x → y является линейным (см . Ортогональные дополнения и проекции). Этот результат особенно важен в прикладной математике , особенно в численном анализе , где он составляет основу методов наименьших квадратов . ^[74]

В частности, когда F не равно H , можно найти ненулевой вектор v ортогональный к F (выберите x ∉ F и v = x − y ). Очень полезный критерий получается путем применения этого наблюдения к замкнутому подпространству F , порожденному подмножеством S из H .

Подмножество S из H охватывает плотное векторное подпространство тогда (и только тогда), когда вектор 0 является единственным вектором v ∈ H, ортогональным к S.

Двойственность

Двойственное пространство H * — это пространство всех непрерывных линейных функций из пространства H в базовое поле. Оно несет естественную норму, определяемую формулой Эта норма удовлетворяет закону параллелограмма , и поэтому двойственное пространство также является пространством скалярного произведения, где это скалярное произведение может быть определено в терминах этой двойственной нормы с помощью тождества поляризации . Двойственное пространство также является полным, поэтому оно является гильбертовым пространством само по себе. Если e _• = ( e _i ) _{i ∈ I} — полный ортонормированный базис для H , то скалярное произведение в двойственном пространстве любых двух равно где все, кроме счетного числа членов в этом ряду, равны нулю. $${\displaystyle \|\varphi \|=\sup _{\|x\|=1,x\in H}|\varphi (x)|\,.}$$ ${\displaystyle f,g\in H^{*}}$ $${\displaystyle \langle f,g\rangle _{H^{*}}=\sum _{i\in I}f(e_{i}){\overline {g(e_{i})}}}$$

Теорема о представлении Рисса дает удобное описание дуального пространства. Каждому элементу u из H соответствует уникальный элемент φ _u из H * , определяемый как , где, кроме того, $${\displaystyle \varphi _{u}(x)=\langle x,u\rangle }$$ ${\displaystyle \left\|\varphi _{u}\right\|=\left\|u\right\|.}$

Теорема Рисса о представлении утверждает, что отображение из H в H *, определенное как u ↦ φ _u, является сюръективным , что делает это отображение изометрическим антилинейным изоморфизмом. ^[75] Таким образом, для каждого элемента φ дуального H * существует один и только один u _φ в H такой, что для всех x ∈ H . Скалярное произведение на дуальном пространстве H * удовлетворяет $${\displaystyle \langle x,u_{\varphi }\rangle =\varphi (x)}$$ $${\displaystyle \langle \varphi ,\psi \rangle =\langle u_{\psi },u_{\varphi }\rangle \,.}$$

Изменение порядка в правой части восстанавливает линейность по φ из антилинейности u _φ . В вещественном случае антилинейный изоморфизм из H в его дуальное на самом деле является изоморфизмом, и поэтому вещественные гильбертовы пространства естественно изоморфны своим собственным дуальным.

Представляющий вектор u _φ получается следующим образом. Когда φ ≠ 0 , ядро ​​F = Ker( φ ) является замкнутым векторным подпространством H , не равным H , следовательно, существует ненулевой вектор v , ортогональный F . Вектор u является подходящим скалярным кратным λv вектора v . Требование, чтобы φ ( v ) = ⟨ v , u ⟩ , дает $${\displaystyle u=\langle v,v\rangle ^{-1}\,{\overline {\varphi (v)}}\,v\,.}$$

Это соответствие φ ↔ u используется в популярной в физике нотации «бра–кет» . ^[76] В физике принято считать, что скалярное произведение, обозначаемое как ⟨ x | y ⟩ , является линейным справа. Результат ⟨ x | y ⟩ можно рассматривать как действие линейного функционала ⟨ x | ( бра ) на вектор | y ⟩ ( кет ). $${\displaystyle \langle x|y\rangle =\langle y,x\rangle \,.}$$

Теорема Рисса о представлении в основе своей опирается не только на наличие скалярного произведения, но и на полноту пространства. Фактически, теорема подразумевает, что топологическое сопряженное пространство любого скалярного произведения может быть отождествлено с его завершением. ^[77] Непосредственным следствием теоремы Рисса о представлении является также то, что гильбертово пространство H является рефлексивным , что означает, что естественное отображение из H в его двойное сопряженное пространство является изоморфизмом.

Слабо сходящиеся последовательности

В гильбертовом пространстве H последовательность { x _n } слабо сходится к вектору x ∈ H , когда для каждого v ∈ H. $${\displaystyle \lim _{n}\langle x_{n},v\rangle =\langle x,v\rangle }$$

Например, любая ортонормированная последовательность { f _n } слабо сходится к 0, как следствие неравенства Бесселя. Каждая слабо сходящаяся последовательность { x _n } ограничена, по принципу равномерной ограниченности .

Наоборот, каждая ограниченная последовательность в гильбертовом пространстве допускает слабо сходящиеся подпоследовательности ( теорема Алаоглу ). ^[78] Этот факт может быть использован для доказательства результатов минимизации для непрерывных выпуклых функционалов , таким же образом, как теорема Больцано–Вейерштрасса используется для непрерывных функций на R ^d . Среди нескольких вариантов одно простое утверждение выглядит следующим образом: ^[79]

Если f  : H → R — выпуклая непрерывная функция, такая что f ( x ) стремится к +∞, когда ‖ x ‖ стремится к ∞ , то f допускает минимум в некоторой точке x ₀ ∈ H .

Этот факт (и его различные обобщения) являются основополагающими для прямых методов в вариационном исчислении . Результаты минимизации для выпуклых функционалов также являются прямым следствием несколько более абстрактного факта, что замкнутые ограниченные выпуклые подмножества в гильбертовом пространстве H являются слабо компактными , поскольку H рефлексивно. Существование слабо сходящихся подпоследовательностей является частным случаем теоремы Эберлейна–Шмульяна .

Свойства банахова пространства

Любое общее свойство банаховых пространств продолжает выполняться для гильбертовых пространств. Теорема об открытом отображении утверждает, что непрерывное сюръективное линейное преобразование из одного банахова пространства в другое является открытым отображением , то есть оно переводит открытые множества в открытые множества. Следствием является ограниченная обратная теорема , что непрерывная и биективная линейная функция из одного банахова пространства в другое является изоморфизмом (то есть непрерывным линейным отображением, обратное которому также непрерывно). Эту теорему значительно проще доказать в случае гильбертовых пространств, чем в общих банаховых пространствах. ^[80] Теорема об открытом отображении эквивалентна теореме о замкнутом графике , которая утверждает, что линейная функция из одного банахова пространства в другое непрерывна тогда и только тогда, когда ее график является замкнутым множеством . ^[81] В случае гильбертовых пространств это является основным при изучении неограниченных операторов (см. замкнутый оператор ).

(Геометрическая) теорема Хана–Банаха утверждает, что замкнутое выпуклое множество может быть отделено от любой точки вне его посредством гиперплоскости гильбертова пространства. Это является непосредственным следствием свойства наилучшего приближения: если y — элемент замкнутого выпуклого множества F, ближайший к x , то разделяющая гиперплоскость — это плоскость, перпендикулярная отрезку xy , проходящему через его середину. ^[82]

Операторы в гильбертовых пространствах

Ограниченные операторы

Непрерывные линейные операторы A  : H ₁ → H ₂ из гильбертова пространства H ₁ во второе гильбертово пространство H ₂ ограничены в том смысле, что они отображают ограниченные множества в ограниченные множества. ^[83] Наоборот, если оператор ограничен, то он непрерывен. Пространство таких ограниченных линейных операторов имеет норму , норму оператора, заданную как $${\displaystyle \lVert A\rVert =\sup {\bigl \{}\|Ax\|\mathrel {\big |} \|x\|\leq 1{\bigr \}}\,.}$$

Сумма и композиция двух ограниченных линейных операторов снова ограничены и линейны. Для y в H ₂ отображение, которое отправляет x ∈ H ₁ в ⟨ Ax , y ⟩, является линейным и непрерывным, и согласно теореме Рисса о представлении, следовательно, может быть представлено в виде для некоторого вектора A * y в H ₁ . Это определяет другой ограниченный линейный оператор A * : H ₂ → H ₁ , сопряженный к A . Сопряжённый удовлетворяет A ** = A . Когда теорема Рисса о представлении используется для идентификации каждого гильбертова пространства с его непрерывным двойственным пространством, можно показать, что  сопряженный к A тождественен транспонированному ^t A : H ₂ * → H ₁ * к A , что по определению отправляет в функционал $${\displaystyle \left\langle x,A^{*}y\right\rangle =\langle Ax,y\rangle }$$ ${\displaystyle \psi \in H_{2}^{*}}$ ${\displaystyle \psi \circ A\in H_{1}^{*}.}$

Множество B( H ) всех ограниченных линейных операторов на H (имеются в виду операторы H → H ) вместе с операциями сложения и композиции, нормой и сопряженной операцией представляет собой C*-алгебру , которая является типом операторной алгебры .

Элемент A из B( H ) называется «самосопряженным» или «эрмитовым», если A * = A . Если A является эрмитовым и ⟨ Ax , x ⟩ ≥ 0 для каждого x , то A называется «неотрицательным», что записывается как A ≥ 0 ; если равенство имеет место только при x = 0 , то A называется «положительным». Множество самосопряженных операторов допускает частичный порядок , в котором A ≥ B , если A − B ≥ 0 . Если A имеет вид B * B для некоторого B , то A неотрицателен; если B обратим, то A положителен. Обратное утверждение также верно в том смысле, что для неотрицательного оператора A существует единственный неотрицательный квадратный корень B такой, что $${\displaystyle A=B^{2}=B^{*}B\,.}$$

В смысле, уточненном спектральной теоремой , самосопряженные операторы можно с пользой рассматривать как операторы, которые являются «действительными». Элемент A из B( H ) называется нормальным, если A * A = AA * . Нормальные операторы распадаются на сумму самосопряженного оператора и мнимого кратного самосопряженного оператора, которые коммутируют друг с другом. Нормальные операторы также можно с пользой рассматривать в терминах их действительных и мнимых частей. $${\displaystyle A={\frac {A+A^{*}}{2}}+i{\frac {A-A^{*}}{2i}}}$$

Элемент U из B( H ) называется унитарным, если U обратим и его обратный элемент задается как U * . Это также можно выразить, потребовав, чтобы U был на и ⟨ Ux , Uy ⟩ = ⟨ x , y ⟩ для всех x , y ∈ H . Унитарные операторы образуют группу относительно композиции, которая является группой изометрий H .

Элемент B( H ) компактен, если он переводит ограниченные множества в относительно компактные множества. Эквивалентно, ограниченный оператор T компактен, если для любой ограниченной последовательности { x _k } последовательность { Tx _k } имеет сходящуюся подпоследовательность. Многие интегральные операторы компактны и фактически определяют специальный класс операторов, известных как операторы Гильберта–Шмидта , которые особенно важны при изучении интегральных уравнений . Операторы Фредгольма отличаются от компактного оператора кратностью тождества и эквивалентно характеризуются как операторы с конечномерным ядром и коядром . Индекс оператора Фредгольма T определяется как $${\displaystyle \operatorname {index} T=\dim \ker T-\dim \operatorname {coker} T\,.}$$

Индекс гомотопически инвариантен и играет важную роль в дифференциальной геометрии благодаря теореме Атьи–Зингера об индексе .

Неограниченные операторы

Неограниченные операторы также поддаются обработке в гильбертовых пространствах и имеют важные приложения в квантовой механике . ^[84] Неограниченный оператор T в гильбертовом пространстве H определяется как линейный оператор, область определения которого D ( T ) является линейным подпространством H . Часто область определения D ( T ) является плотным подпространством H , и в этом случае T известен как плотно определенный оператор .

Сопряженный оператор плотно определенного неограниченного оператора определяется по существу тем же способом, что и для ограниченных операторов. Самосопряженные неограниченные операторы играют роль наблюдаемых в математической формулировке квантовой механики. Примерами самосопряженных неограниченных операторов в гильбертовом пространстве L ² ( R ) являются: ^[85]

• Подходящее расширение дифференциального оператора , где i — мнимая единица, а f — дифференцируемая функция компактного носителя. $${\displaystyle (Af)(x)=-i{\frac {\mathrm {d} }{\mathrm {d} x}}f(x)\,,}$$
• Оператор умножения на x : $${\displaystyle (Bf)(x)=xf(x)\,.}$$

Они соответствуют наблюдаемым импульсу и положению соответственно. Ни A, ни B не определены на всем H , поскольку в случае A производная не обязательно должна существовать, а в случае B функция произведения не обязательно должна быть квадратично интегрируемой. В обоих случаях множество возможных аргументов образуют плотные подпространства L ² ( R ) .

Конструкции

Прямые суммы

Два гильбертовых пространства H ₁ и H ₂ можно объединить в другое гильбертово пространство, называемое (ортогональной) прямой суммой [ ^86] и обозначаемое $${\displaystyle H_{1}\oplus H_{2}\,,}$$

состоящий из множества всех упорядоченных пар ( x ₁ , x ₂ ) , где x _i ∈ H _i , i = 1, 2 , и скалярного произведения, определяемого формулой $${\displaystyle {\bigl \langle }(x_{1},x_{2}),(y_{1},y_{2}){\bigr \rangle }_{H_{1}\oplus H_{2}}=\left\langle x_{1},y_{1}\right\rangle _{H_{1}}+\left\langle x_{2},y_{2}\right\rangle _{H_{2}}\,.}$$

В более общем случае, если H _i — семейство гильбертовых пространств, индексированное i ∈ I , то прямая сумма H _i , обозначаемая как , состоит из множества всех индексированных семейств в декартовом произведении H i _, таких что $${\displaystyle \bigoplus _{i\in I}H_{i}}$$ $${\displaystyle x=(x_{i}\in H_{i}\mid i\in I)\in \prod _{i\in I}H_{i}}$$ $${\displaystyle \sum _{i\in I}\|x_{i}\|^{2}<\infty \,.}$$

Внутренний продукт определяется как $${\displaystyle \langle x,y\rangle =\sum _{i\in I}\left\langle x_{i},y_{i}\right\rangle _{H_{i}}\,.}$$

Каждое из H _i включено как замкнутое подпространство в прямую сумму всех H _i . Более того, H _i попарно ортогональны. Обратно, если в гильбертовом пространстве H существует система замкнутых подпространств V _i , i ∈ I , которые попарно ортогональны и объединение которых плотно в H , то H канонически изоморфно прямой сумме V _i . В этом случае H называется внутренней прямой суммой V _i . Прямая сумма (внутренняя или внешняя) также снабжена семейством ортогональных проекций E _i на i -е прямое слагаемое H _i . Эти проекции являются ограниченными, самосопряженными, идемпотентными операторами, которые удовлетворяют условию ортогональности $${\displaystyle E_{i}E_{j}=0,\quad i\neq j\,.}$$

Спектральная теорема для компактных самосопряженных операторов в гильбертовом пространстве H утверждает, что H распадается в ортогональную прямую сумму собственных подпространств оператора, а также дает явное разложение оператора в виде суммы проекций на собственные подпространства. Прямая сумма гильбертовых пространств также появляется в квантовой механике как пространство Фока системы, содержащей переменное число частиц, где каждое гильбертово пространство в прямой сумме соответствует дополнительной степени свободы для квантово-механической системы. В теории представлений теорема Петера–Вейля гарантирует, что любое унитарное представление компактной группы в гильбертовом пространстве распадается в прямую сумму конечномерных представлений.

Тензорные продукты

Если x ₁ , y ₁ ∊ H ₁ и x ₂ , y ₂ ∊ H ₂ , то можно определить скалярное произведение на (обычном) тензорном произведении следующим образом. На простых тензорах пусть $${\displaystyle \langle x_{1}\otimes x_{2},\,y_{1}\otimes y_{2}\rangle =\langle x_{1},y_{1}\rangle \,\langle x_{2},y_{2}\rangle \,.}$$

Эта формула затем расширяется полуторалинейностью до скалярного произведения на H ₁ ⊗ H ₂ . Гильбертово тензорное произведение H ₁ и H ₂ , иногда обозначаемое как H ₁ H ₂ ${\displaystyle {\widehat {\otimes }}}$ , является гильбертовым пространством, полученным путем дополнения H ₁ ⊗ H ₂ для метрики, связанной с этим скалярным произведением. ^[87]

Примером может служить гильбертово пространство L ² ([0, 1]) . Гильбертово тензорное произведение двух копий L ² ([0, 1]) изометрически и линейно изоморфно пространству L ² ([0, 1] ² ) квадратично-интегрируемых функций на квадрате [0, 1] ² . Этот изоморфизм переводит простой тензор f ₁ ⊗ f ₂ в функцию на квадрате. $${\displaystyle (s,t)\mapsto f_{1}(s)\,f_{2}(t)}$$

Этот пример типичен в следующем смысле. ^[88] Каждому простому тензорному произведению x ₁ ⊗ x ₂ соответствует оператор ранга один из H^∗
₁в H ₂ , который отображает заданный x * ∈ H^∗
₁как $${\displaystyle x^{*}\mapsto x^{*}(x_{1})x_{2}\,.}$$

This mapping defined on simple tensors extends to a linear identification between H₁ ⊗ H₂ and the space of finite rank operators from H^∗
₁ to H₂. This extends to a linear isometry of the Hilbertian tensor product H₁ ${\displaystyle {\widehat {\otimes }}}$ H₂ with the Hilbert space HS(H^∗
₁, H₂) of Hilbert–Schmidt operators from H^∗
₁ to H₂.

Orthonormal bases

The notion of an orthonormal basis from linear algebra generalizes over to the case of Hilbert spaces.^[89] In a Hilbert space H, an orthonormal basis is a family {e_k}_{k ∈ B} of elements of H satisfying the conditions:

1. Orthogonality: Every two different elements of B are orthogonal: ⟨e_k, e_j⟩ = 0 for all k, j ∈ B with k ≠ j.
2. Normalization: Every element of the family has norm 1: ‖e_k‖ = 1 for all k ∈ B.
3. Completeness: The linear span of the family e_k, k ∈ B, is dense in H.

A system of vectors satisfying the first two conditions basis is called an orthonormal system or an orthonormal set (or an orthonormal sequence if B is countable). Such a system is always linearly independent.

Despite the name, an orthonormal basis is not, in general, a basis in the sense of linear algebra (Hamel basis). More precisely, an orthonormal basis is a Hamel basis if and only if the Hilbert space is a finite-dimensional vector space.^[90]

Completeness of an orthonormal system of vectors of a Hilbert space can be equivalently restated as:

for every v ∈ H, if ⟨v, e_k⟩ = 0 for all k ∈ B, then v = 0.

This is related to the fact that the only vector orthogonal to a dense linear subspace is the zero vector, for if S is any orthonormal set and v is orthogonal to S, then v is orthogonal to the closure of the linear span of S, which is the whole space.

Examples of orthonormal bases include:

• the set {(1, 0, 0), (0, 1, 0), (0, 0, 1)} forms an orthonormal basis of R³ with the dot product;
• the sequence { f_n | n ∈ Z} with f_n(x) = exp(2πinx) forms an orthonormal basis of the complex space L²([0, 1]);

In the infinite-dimensional case, an orthonormal basis will not be a basis in the sense of linear algebra; to distinguish the two, the latter basis is also called a Hamel basis. That the span of the basis vectors is dense implies that every vector in the space can be written as the sum of an infinite series, and the orthogonality implies that this decomposition is unique.

Sequence spaces

The space ${\displaystyle \ell _{2}}$ of square-summable sequences of complex numbers is the set of infinite sequences^[9] $${\displaystyle (c_{1},c_{2},c_{3},\dots )}$$of real or complex numbers such that $${\displaystyle \left|c_{1}\right|^{2}+\left|c_{2}\right|^{2}+\left|c_{3}\right|^{2}+\cdots <\infty \,.}$$

This space has an orthonormal basis: $${\displaystyle {\begin{aligned}e_{1}&=(1,0,0,\dots )\\e_{2}&=(0,1,0,\dots )\\&\ \ \vdots \end{aligned}}}$$

This space is the infinite-dimensional generalization of the ${\displaystyle \ell _{2}^{n}}$ space of finite-dimensional vectors. It is usually the first example used to show that in infinite-dimensional spaces, a set that is closed and bounded is not necessarily (sequentially) compact (as is the case in all finite dimensional spaces). Indeed, the set of orthonormal vectors above shows this: It is an infinite sequence of vectors in the unit ball (i.e., the ball of points with norm less than or equal one). This set is clearly bounded and closed; yet, no subsequence of these vectors converges to anything and consequently the unit ball in ${\displaystyle \ell _{2}}$ is not compact. Intuitively, this is because "there is always another coordinate direction" into which the next elements of the sequence can evade.

One can generalize the space ${\displaystyle \ell _{2}}$ in many ways. For example, if B is any set, then one can form a Hilbert space of sequences with index set B, defined by^[91] $${\displaystyle \ell ^{2}(B)={\biggl \{}x:B\xrightarrow {x} \mathbb {C} \mathrel {\bigg |} \sum _{b\in B}\left|x(b)\right|^{2}<\infty {\biggr \}}\,.}$$

The summation over B is here defined by $${\displaystyle \sum _{b\in B}\left|x(b)\right|^{2}=\sup \sum _{n=1}^{N}\left|x(b_{n})\right|^{2}}$$the supremum being taken over all finite subsets of B. It follows that, for this sum to be finite, every element of l²(B) has only countably many nonzero terms. This space becomes a Hilbert space with the inner product $${\displaystyle \langle x,y\rangle =\sum _{b\in B}x(b){\overline {y(b)}}}$$

for all x, y ∈ l²(B). Here the sum also has only countably many nonzero terms, and is unconditionally convergent by the Cauchy–Schwarz inequality.

An orthonormal basis of l²(B) is indexed by the set B, given by

$${\displaystyle e_{b}(b')={\begin{cases}1&{\text{if }}b=b'\\0&{\text{otherwise.}}\end{cases}}}$$

Bessel's inequality and Parseval's formula

Let f₁, …, f_n be a finite orthonormal system in H. For an arbitrary vector x ∈ H, let $${\displaystyle y=\sum _{j=1}^{n}\langle x,f_{j}\rangle \,f_{j}\,.}$$

Then ⟨x, f_k⟩ = ⟨y, f_k⟩ for every k = 1, …, n. It follows that x − y is orthogonal to each f_k, hence x − y is orthogonal to y. Using the Pythagorean identity twice, it follows that $${\displaystyle \|x\|^{2}=\|x-y\|^{2}+\|y\|^{2}\geq \|y\|^{2}=\sum _{j=1}^{n}{\bigl |}\langle x,f_{j}\rangle {\bigr |}^{2}\,.}$$

Let {f_i}, i ∈ I, be an arbitrary orthonormal system in H. Applying the preceding inequality to every finite subset J of I gives Bessel's inequality:^[92] $${\displaystyle \sum _{i\in I}{\bigl |}\langle x,f_{i}\rangle {\bigr |}^{2}\leq \|x\|^{2},\quad x\in H}$$(according to the definition of the sum of an arbitrary family of non-negative real numbers).

Geometrically, Bessel's inequality implies that the orthogonal projection of x onto the linear subspace spanned by the f_i has norm that does not exceed that of x. In two dimensions, this is the assertion that the length of the leg of a right triangle may not exceed the length of the hypotenuse.

Bessel's inequality is a stepping stone to the stronger result called Parseval's identity, which governs the case when Bessel's inequality is actually an equality. By definition, if {e_k}_{k ∈ B} is an orthonormal basis of H, then every element x of H may be written as $${\displaystyle x=\sum _{k\in B}\left\langle x,e_{k}\right\rangle \,e_{k}\,.}$$

Even if B is uncountable, Bessel's inequality guarantees that the expression is well-defined and consists only of countably many nonzero terms. This sum is called the Fourier expansion of x, and the individual coefficients ⟨x, e_k⟩ are the Fourier coefficients of x. Parseval's identity then asserts that^[93] $${\displaystyle \|x\|^{2}=\sum _{k\in B}|\langle x,e_{k}\rangle |^{2}\,.}$$

Conversely,^[93] if {e_k} is an orthonormal set such that Parseval's identity holds for every x, then {e_k} is an orthonormal basis.

Hilbert dimension

As a consequence of Zorn's lemma, every Hilbert space admits an orthonormal basis; furthermore, any two orthonormal bases of the same space have the same cardinality, called the Hilbert dimension of the space.^[94] For instance, since l²(B) has an orthonormal basis indexed by B, its Hilbert dimension is the cardinality of B (which may be a finite integer, or a countable or uncountable cardinal number).

The Hilbert dimension is not greater than the Hamel dimension (the usual dimension of a vector space). The two dimensions are equal if and only if one of them is finite.

As a consequence of Parseval's identity,^[95] if {e_k}_{k ∈ B} is an orthonormal basis of H, then the map Φ : H → l²(B) defined by Φ(x) = ⟨x, e_k⟩_k∈B is an isometric isomorphism of Hilbert spaces: it is a bijective linear mapping such that $${\displaystyle {\bigl \langle }\Phi (x),\Phi (y){\bigr \rangle }_{l^{2}(B)}=\left\langle x,y\right\rangle _{H}}$$for all x, y ∈ H. The cardinal number of B is the Hilbert dimension of H. Thus every Hilbert space is isometrically isomorphic to a sequence space l²(B) for some set B.

Separable spaces

By definition, a Hilbert space is separable provided it contains a dense countable subset. Along with Zorn's lemma, this means a Hilbert space is separable if and only if it admits a countable orthonormal basis. All infinite-dimensional separable Hilbert spaces are therefore isometrically isomorphic to the square-summable sequence space ${\displaystyle \ell ^{2}.}$

In the past, Hilbert spaces were often required to be separable as part of the definition.^[96]

In quantum field theory

Most spaces used in physics are separable, and since these are all isomorphic to each other, one often refers to any infinite-dimensional separable Hilbert space as "the Hilbert space" or just "Hilbert space".^[97] Even in quantum field theory, most of the Hilbert spaces are in fact separable, as stipulated by the Wightman axioms. However, it is sometimes argued that non-separable Hilbert spaces are also important in quantum field theory, roughly because the systems in the theory possess an infinite number of degrees of freedom and any infinite Hilbert tensor product (of spaces of dimension greater than one) is non-separable.^[98] For instance, a bosonic field can be naturally thought of as an element of a tensor product whose factors represent harmonic oscillators at each point of space. From this perspective, the natural state space of a boson might seem to be a non-separable space.^[98] However, it is only a small separable subspace of the full tensor product that can contain physically meaningful fields (on which the observables can be defined). Another non-separable Hilbert space models the state of an infinite collection of particles in an unbounded region of space. An orthonormal basis of the space is indexed by the density of the particles, a continuous parameter, and since the set of possible densities is uncountable, the basis is not countable.^[98]

Orthogonal complements and projections

If S is a subset of a Hilbert space H, the set of vectors orthogonal to S is defined by $${\displaystyle S^{\perp }=\left\{x\in H\mid \langle x,s\rangle =0\ {\text{ for all }}s\in S\right\}\,.}$$

The set S^⊥ is a closed subspace of H (can be proved easily using the linearity and continuity of the inner product) and so forms itself a Hilbert space. If V is a closed subspace of H, then V^⊥ is called the orthogonal complement of V. In fact, every x ∈ H can then be written uniquely as x = v + w, with v ∈ V and w ∈ V^⊥. Therefore, H is the internal Hilbert direct sum of V and V^⊥.

The linear operator P_V : H → H that maps x to v is called the orthogonal projection onto V. There is a natural one-to-one correspondence between the set of all closed subspaces of H and the set of all bounded self-adjoint operators P such that P² = P. Specifically,

Theorem — The orthogonal projection P_V is a self-adjoint linear operator on H of norm ≤ 1 with the property P²
_V = P_V. Moreover, any self-adjoint linear operator E such that E² = E is of the form P_V, where V is the range of E. For every x in H, P_V(x) is the unique element v of V that minimizes the distance ‖x − v‖.

This provides the geometrical interpretation of P_V(x): it is the best approximation to x by elements of V.^[99]

Projections P_U and P_V are called mutually orthogonal if P_UP_V = 0. This is equivalent to U and V being orthogonal as subspaces of H. The sum of the two projections P_U and P_V is a projection only if U and V are orthogonal to each other, and in that case P_U + P_V = P_U+V.^[100] The composite P_UP_V is generally not a projection; in fact, the composite is a projection if and only if the two projections commute, and in that case P_UP_V = P_U∩V.^[101]

By restricting the codomain to the Hilbert space V, the orthogonal projection P_V gives rise to a projection mapping π : H → V; it is the adjoint of the inclusion mapping $${\displaystyle i:V\to H\,,}$$meaning that $${\displaystyle \left\langle ix,y\right\rangle _{H}=\left\langle x,\pi y\right\rangle _{V}}$$for all x ∈ V and y ∈ H.

The operator norm of the orthogonal projection P_V onto a nonzero closed subspace V is equal to 1: $${\displaystyle \|P_{V}\|=\sup _{x\in H,x\neq 0}{\frac {\|P_{V}x\|}{\|x\|}}=1\,.}$$

Every closed subspace V of a Hilbert space is therefore the image of an operator P of norm one such that P² = P. The property of possessing appropriate projection operators characterizes Hilbert spaces:^[102]

• A Banach space of dimension higher than 2 is (isometrically) a Hilbert space if and only if, for every closed subspace V, there is an operator P_V of norm one whose image is V such that P²
  _V = P_V.

While this result characterizes the metric structure of a Hilbert space, the structure of a Hilbert space as a topological vector space can itself be characterized in terms of the presence of complementary subspaces:^[103]

• A Banach space X is topologically and linearly isomorphic to a Hilbert space if and only if, to every closed subspace V, there is a closed subspace W such that X is equal to the internal direct sum V ⊕ W.

The orthogonal complement satisfies some more elementary results. It is a monotone function in the sense that if U ⊂ V, then V^⊥ ⊆ U^⊥ with equality holding if and only if V is contained in the closure of U. This result is a special case of the Hahn–Banach theorem. The closure of a subspace can be completely characterized in terms of the orthogonal complement: if V is a subspace of H, then the closure of V is equal to V^⊥⊥. The orthogonal complement is thus a Galois connection on the partial order of subspaces of a Hilbert space. In general, the orthogonal complement of a sum of subspaces is the intersection of the orthogonal complements:^[104] $${\displaystyle {\biggl (}\sum _{i}V_{i}{\biggr )}^{\perp }=\bigcap _{i}V_{i}^{\perp }\,.}$$

If the V_i are in addition closed, then $${\displaystyle {\overline {\sum _{i}V_{i}^{\perp }{\vphantom {\Big |}}}}={\biggl (}\bigcap _{i}V_{i}{\biggr )}^{\perp }\,.}$$

Spectral theory

There is a well-developed spectral theory for self-adjoint operators in a Hilbert space, that is roughly analogous to the study of symmetric matrices over the reals or self-adjoint matrices over the complex numbers.^[105] In the same sense, one can obtain a "diagonalization" of a self-adjoint operator as a suitable sum (actually an integral) of orthogonal projection operators.

The spectrum of an operator T, denoted σ(T), is the set of complex numbers λ such that T − λ lacks a continuous inverse. If T is bounded, then the spectrum is always a compact set in the complex plane, and lies inside the disc |z| ≤ ‖T‖. If T is self-adjoint, then the spectrum is real. In fact, it is contained in the interval [m, M] where $${\displaystyle m=\inf _{\|x\|=1}\langle Tx,x\rangle \,,\quad M=\sup _{\|x\|=1}\langle Tx,x\rangle \,.}$$

Moreover, m and M are both actually contained within the spectrum.

The eigenspaces of an operator T are given by $${\displaystyle H_{\lambda }=\ker(T-\lambda )\,.}$$

Unlike with finite matrices, not every element of the spectrum of T must be an eigenvalue: the linear operator T − λ may only lack an inverse because it is not surjective. Elements of the spectrum of an operator in the general sense are known as spectral values. Since spectral values need not be eigenvalues, the spectral decomposition is often more subtle than in finite dimensions.

However, the spectral theorem of a self-adjoint operator T takes a particularly simple form if, in addition, T is assumed to be a compact operator. The spectral theorem for compact self-adjoint operators states:^[106]

• A compact self-adjoint operator T has only countably (or finitely) many spectral values. The spectrum of T has no limit point in the complex plane except possibly zero. The eigenspaces of T decompose H into an orthogonal direct sum: $${\displaystyle H=\bigoplus _{\lambda \in \sigma (T)}H_{\lambda }\,.}$$ Moreover, if E_λ denotes the orthogonal projection onto the eigenspace H_λ, then $${\displaystyle T=\sum _{\lambda \in \sigma (T)}\lambda E_{\lambda }\,,}$$ where the sum converges with respect to the norm on B(H).

This theorem plays a fundamental role in the theory of integral equations, as many integral operators are compact, in particular those that arise from Hilbert–Schmidt operators.

The general spectral theorem for self-adjoint operators involves a kind of operator-valued Riemann–Stieltjes integral, rather than an infinite summation.^[107] The spectral family associated to T associates to each real number λ an operator E_λ, which is the projection onto the nullspace of the operator (T − λ)⁺, where the positive part of a self-adjoint operator is defined by $${\displaystyle A^{+}={\tfrac {1}{2}}{\Bigl (}{\sqrt {A^{2}}}+A{\Bigr )}\,.}$$

The operators E_λ are monotone increasing relative to the partial order defined on self-adjoint operators; the eigenvalues correspond precisely to the jump discontinuities. One has the spectral theorem, which asserts $${\displaystyle T=\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{\lambda }\,.}$$

The integral is understood as a Riemann–Stieltjes integral, convergent with respect to the norm on B(H). In particular, one has the ordinary scalar-valued integral representation $${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} \langle E_{\lambda }x,y\rangle \,.}$$

A somewhat similar spectral decomposition holds for normal operators, although because the spectrum may now contain non-real complex numbers, the operator-valued Stieltjes measure dE_λ must instead be replaced by a resolution of the identity.

A major application of spectral methods is the spectral mapping theorem, which allows one to apply to a self-adjoint operator T any continuous complex function f defined on the spectrum of T by forming the integral $${\displaystyle f(T)=\int _{\sigma (T)}f(\lambda )\,\mathrm {d} E_{\lambda }\,.}$$

The resulting continuous functional calculus has applications in particular to pseudodifferential operators.^[108]

The spectral theory of unbounded self-adjoint operators is only marginally more difficult than for bounded operators. The spectrum of an unbounded operator is defined in precisely the same way as for bounded operators: λ is a spectral value if the resolvent operator $${\displaystyle R_{\lambda }=(T-\lambda )^{-1}}$$

fails to be a well-defined continuous operator. The self-adjointness of T still guarantees that the spectrum is real. Thus the essential idea of working with unbounded operators is to look instead at the resolvent R_λ where λ is nonreal. This is a bounded normal operator, which admits a spectral representation that can then be transferred to a spectral representation of T itself. A similar strategy is used, for instance, to study the spectrum of the Laplace operator: rather than address the operator directly, one instead looks as an associated resolvent such as a Riesz potential or Bessel potential.

A precise version of the spectral theorem in this case is:^[109]

Theorem — Given a densely defined self-adjoint operator T on a Hilbert space H, there corresponds a unique resolution of the identity E on the Borel sets of R, such that $${\displaystyle \langle Tx,y\rangle =\int _{\mathbb {R} }\lambda \,\mathrm {d} E_{x,y}(\lambda )}$$ for all x ∈ D(T) and y ∈ H. The spectral measure E is concentrated on the spectrum of T.

There is also a version of the spectral theorem that applies to unbounded normal operators.

In popular culture

In Gravity's Rainbow (1973), a novel by Thomas Pynchon, one of the characters is called "Sammy Hilbert-Spaess", a pun on "Hilbert Space". The novel refers also to Gödel's incompleteness theorems.^[110]

See also

• Mathematics portal

• Banach space – Normed vector space that is complete
• Fock space – Multi particle state space
• Fundamental theorem of Hilbert spaces
• Hadamard space – geodesically complete metric space of non-positive curvaturePages displaying wikidata descriptions as a fallback
• Hausdorff space – Type of topological space
• Hilbert algebra
• Hilbert C*-module – Mathematical objects that generalise the notion of Hilbert spaces
• Hilbert manifold – Manifold modelled on Hilbert spaces
• L-semi-inner product – Generalization of inner products that applies to all normed spaces
• Locally convex topological vector space – A vector space with a topology defined by convex open sets
• Operator theory – Mathematical field of study
• Operator topologies – Topologies on the set of operators on a Hilbert space
• Quantum state space – Mathematical space representing physical quantum systems
• Rigged Hilbert space – Construction linking the study of "bound" and continuous eigenvalues in functional analysis
• Topological vector space – Vector space with a notion of nearness

Remarks

1. In some conventions, inner products are linear in their second arguments instead.
2. The eigenvalues of the Fredholm kernel are ⁠1/λ⁠, which tend to zero.

Notes

1. Axler 2014, p. 164 §6.2
2. However, some sources call finite-dimensional spaces with these properties pre-Hilbert spaces, reserving the term "Hilbert space" for infinite-dimensional spaces; see, e.g., Levitan 2001.
3. Marsden 1974, §2.8
4. The mathematical material in this section can be found in any good textbook on functional analysis, such as Dieudonné (1960), Hewitt & Stromberg (1965), Reed & Simon (1980) or Rudin (1987).
5. Schaefer & Wolff 1999, pp. 122–202.
6. Dieudonné 1960, §6.2
7. Roman 2008, p. 327
8. Roman 2008, p. 330 Theorem 13.8
9. Stein & Shakarchi 2005, p. 163
10. Dieudonné 1960
11. Largely from the work of Hermann Grassmann, at the urging of August Ferdinand Möbius (Boyer & Merzbach 1991, pp. 584–586). The first modern axiomatic account of abstract vector spaces ultimately appeared in Giuseppe Peano's 1888 account (Grattan-Guinness 2000, §5.2.2; O'Connor & Robertson 1996).
12. A detailed account of the history of Hilbert spaces can be found in Bourbaki 1987.
13. Schmidt 1908
14. Titchmarsh 1946, §IX.1
15. Lebesgue 1904. Further details on the history of integration theory can be found in Bourbaki (1987) and Saks (2005).
16. Bourbaki 1987.
17. Dunford & Schwartz 1958, §IV.16
18. In Dunford & Schwartz (1958, §IV.16), the result that every linear functional on L²[0,1] is represented by integration is jointly attributed to Fréchet (1907) and Riesz (1907). The general result, that the dual of a Hilbert space is identified with the Hilbert space itself, can be found in Riesz (1934).
19. von Neumann 1929.
20. Kline 1972, p. 1092
21. Hilbert, Nordheim & von Neumann 1927
22. Weyl 1931.
23. Prugovečki 1981, pp. 1–10.
24. von Neumann 1932
25. Peres 1993, pp. 79–99.
26. Murphy 1990, p. 112
27. Murphy 1990, p. 72
28. Halmos 1957, Section 42.
29. Hewitt & Stromberg 1965.
30. Abramowitz, Milton; Stegun, Irene Ann, eds. (1983) [June 1964]. "Chapter 22". Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. Applied Mathematics Series. Vol. 55 (Ninth reprint with additional corrections of tenth original printing with corrections (December 1972); first ed.). Washington D.C.; New York: United States Department of Commerce, National Bureau of Standards; Dover Publications. p. 773. ISBN 978-0-486-61272-0. LCCN 64-60036. MR 0167642. LCCN 65-12253.
31. Bers, John & Schechter 1981.
32. Giusti 2003.
33. Stein 1970
34. Details can be found in Warner (1983).
35. A general reference on Hardy spaces is the book Duren (1970).
36. Krantz 2002, §1.4
37. Krantz 2002, §1.5
38. Young 1988, Chapter 9.
39. Pedersen 1995, §4.4
40. More detail on finite element methods from this point of view can be found in Brenner & Scott (2005).
41. Brezis 2010, section 9.5
42. Evans 1998
43. Pathria (1996), Chapters 2 and 3
44. Einsiedler & Ward (2011), Proposition 2.14.
45. Reed & Simon 1980
46. A treatment of Fourier series from this point of view is available, for instance, in Rudin (1987) or Folland (2009).
47. Halmos 1957, §5
48. Bachman, Narici & Beckenstein 2000
49. Stein & Weiss 1971, §IV.2.
50. Lanczos 1988, pp. 212–213
51. Lanczos 1988, Equation 4-3.10
52. The classic reference for spectral methods is Courant & Hilbert 1953. A more up-to-date account is Reed & Simon 1975.
53. Kac 1966
54. von Neumann 1955
55. Holevo 2001, p. 17
56. Rieffel & Polak 2011, p. 55
57. Peres 1993, p. 101
58. Peres 1993, pp. 73
59. Nielsen & Chuang 2000, p. 90
60. Billingsley (1986), p. 477, ex. 34.13}}
61. Stapleton 1995
62. Hewitt & Stromberg (1965), Exercise 16.45.
63. Karatzas & Shreve 2019, Chapter 3
64. Stroock (2011), Chapter 8.
65. Hermann Weyl (2009), "Mind and nature", Mind and nature: selected writings on philosophy, mathematics, and physics, Princeton University Press.
66. Berthier, M. (2020), "Geometry of color perception. Part 2: perceived colors from real quantum states and Hering's rebit", The Journal of Mathematical Neuroscience, 10 (1): 14, doi:10.1186/s13408-020-00092-x, PMC 7481323, PMID 32902776.
67. Reed & Simon 1980, Theorem 12.6
68. Reed & Simon 1980, p. 38
69. Young 1988, p. 23.
70. Clarkson 1936.
71. Rudin 1987, Theorem 4.10
72. Dunford & Schwartz 1958, II.4.29
73. Rudin 1987, Theorem 4.11
74. Blanchet, Gérard; Charbit, Maurice (2014). Digital Signal and Image Processing Using MATLAB. Vol. 1 (Second ed.). New Jersey: Wiley. pp. 349–360. ISBN 978-1848216402.
75. Weidmann 1980, Theorem 4.8
76. Peres 1993, pp. 77–78.
77. Weidmann (1980), Exercise 4.11.
78. Weidmann 1980, §4.5
79. Buttazzo, Giaquinta & Hildebrandt 1998, Theorem 5.17
80. Halmos 1982, Problem 52, 58
81. Rudin 1973
82. Trèves 1967, Chapter 18
83. A general reference for this section is Rudin (1973), chapter 12.
84. See Prugovečki (1981), Reed & Simon (1980, Chapter VIII) and Folland (1989).
85. Prugovečki 1981, III, §1.4
86. Dunford & Schwartz 1958, IV.4.17-18
87. Weidmann 1980, §3.4
88. Kadison & Ringrose 1983, Theorem 2.6.4
89. Dunford & Schwartz 1958, §IV.4.
90. Roman 2008, p. 218
91. Rudin 1987, Definition 3.7
92. For the case of finite index sets, see, for instance, Halmos 1957, §5. For infinite index sets, see Weidmann 1980, Theorem 3.6.
93. Hewitt & Stromberg (1965), Theorem 16.26.
94. Levitan 2001. Many authors, such as Dunford & Schwartz (1958, §IV.4), refer to this just as the dimension. Unless the Hilbert space is finite dimensional, this is not the same thing as its dimension as a linear space (the cardinality of a Hamel basis).
95. Hewitt & Stromberg (1965), Theorem 16.29.
96. Prugovečki 1981, I, §4.2
97. von Neumann (1955) defines a Hilbert space via a countable Hilbert basis, which amounts to an isometric isomorphism with l². The convention still persists in most rigorous treatments of quantum mechanics; see for instance Sobrino 1996, Appendix B.
98. Streater & Wightman 1964, pp. 86–87
99. Young 1988, Theorem 15.3
100. von Neumann 1955, Theorem 16
101. von Neumann 1955, Theorem 14
102. Kakutani 1939
103. Lindenstrauss & Tzafriri 1971
104. Halmos 1957, §12
105. A general account of spectral theory in Hilbert spaces can be found in Riesz & Sz.-Nagy (1990). A more sophisticated account in the language of C*-algebras is in Rudin (1973) or Kadison & Ringrose (1997)
106. See, for instance, Riesz & Sz.-Nagy (1990, Chapter VI) or Weidmann 1980, Chapter 7. This result was already known to Schmidt (1908) in the case of operators arising from integral kernels.
107. Riesz & Sz.-Nagy 1990, §§107–108
108. Shubin 1987
109. Rudin 1973, Theorem 13.30.
110. Pynchon, Thomas (1973). Gravity's Rainbow. Viking Press. pp. 217, 275. ISBN 978-0143039945.

References

• Axler, Sheldon (18 December 2014), Linear Algebra Done Right, Undergraduate Texts in Mathematics (3rd ed.), Springer Publishing (published 2015), p. 296, ISBN 978-3-319-11079-0
• Bachman, George; Narici, Lawrence; Beckenstein, Edward (2000), Fourier and wavelet analysis, Universitext, Berlin, New York: Springer-Verlag, ISBN 978-0-387-98899-3, MR 1729490.
• Bers, Lipman; John, Fritz; Schechter, Martin (1981), Partial differential equations, American Mathematical Society, ISBN 978-0-8218-0049-2.
• Billingsley, Patrick (1986), Probability and measure, Wiley.
• Bourbaki, Nicolas (1986), Spectral theories, Elements of mathematics, Berlin: Springer-Verlag, ISBN 978-0-201-00767-1.
• Bourbaki, Nicolas (1987), Topological vector spaces, Elements of mathematics, Berlin: Springer-Verlag, ISBN 978-3-540-13627-9.
• Boyer, Carl Benjamin; Merzbach, Uta C (1991), A History of Mathematics (2nd ed.), John Wiley & Sons, Inc., ISBN 978-0-471-54397-8.
• Brenner, S.; Scott, R. L. (2005), The Mathematical Theory of Finite Element Methods (2nd ed.), Springer, ISBN 978-0-387-95451-6.
• Brezis, Haim (2010), Functional analysis, Sobolev spaces, and partial differential equations, Springer.
• Buttazzo, Giuseppe; Giaquinta, Mariano; Hildebrandt, Stefan (1998), One-dimensional variational problems, Oxford Lecture Series in Mathematics and its Applications, vol. 15, The Clarendon Press Oxford University Press, ISBN 978-0-19-850465-8, MR 1694383.
• Clarkson, J. A. (1936), "Uniformly convex spaces", Trans. Amer. Math. Soc., 40 (3): 396–414, doi:10.2307/1989630, JSTOR 1989630.
• Courant, Richard; Hilbert, David (1953), Methods of Mathematical Physics, Vol. I, Interscience.
• Dieudonné, Jean (1960), Foundations of Modern Analysis, Academic Press.
• Dirac, P.A.M. (1930), The Principles of Quantum Mechanics, Oxford: Clarendon Press.
• Dunford, N.; Schwartz, J.T. (1958), Linear operators, Parts I and II, Wiley-Interscience.
• Duren, P. (1970), Theory of H^p-Spaces, New York: Academic Press.
• Einsiedler, Manfred; Ward, Thomas (2011), Ergodic theory with a view towards number theory, Springer.
• Evans, L. C. (1998), Partial Differential Equations, Providence: American Mathematical Society, ISBN 0-8218-0772-2.
• Folland, Gerald B. (2009), Fourier analysis and its application (Reprint of Wadsworth and Brooks/Cole 1992 ed.), American Mathematical Society Bookstore, ISBN 978-0-8218-4790-9.
• Folland, Gerald B. (1989), Harmonic analysis in phase space, Annals of Mathematics Studies, vol. 122, Princeton University Press, ISBN 978-0-691-08527-2.
• Fréchet, Maurice (1907), "Sur les ensembles de fonctions et les opérations linéaires", C. R. Acad. Sci. Paris, 144: 1414–1416.
• Fréchet, Maurice (1904), "Sur les opérations linéaires", Transactions of the American Mathematical Society, 5 (4): 493–499, doi:10.2307/1986278, JSTOR 1986278.
• Giusti, Enrico (2003), Direct Methods in the Calculus of Variations, World Scientific, ISBN 978-981-238-043-2.
• Grattan-Guinness, Ivor (2000), The search for mathematical roots, 1870–1940, Princeton Paperbacks, Princeton University Press, ISBN 978-0-691-05858-0, MR 1807717.
• Halmos, Paul (1957), Introduction to Hilbert Space and the Theory of Spectral Multiplicity, Chelsea Pub. Co
• Halmos, Paul (1982), A Hilbert Space Problem Book, Springer-Verlag, ISBN 978-0-387-90685-0.
• Hewitt, Edwin; Stromberg, Karl (1965), Real and Abstract Analysis, New York: Springer-Verlag.
• Hilbert, David; Nordheim, Lothar Wolfgang; von Neumann, John (1927), "Über die Grundlagen der Quantenmechanik", Mathematische Annalen, 98: 1–30, doi:10.1007/BF01451579, S2CID 120986758.
• Holevo, Alexander S. (2001), Statistical Structure of Quantum Theory, Lecture Notes in Physics, Springer, ISBN 3-540-42082-7, OCLC 318268606.
• Kac, Mark (1966), "Can one hear the shape of a drum?", American Mathematical Monthly, 73 (4, part 2): 1–23, doi:10.2307/2313748, JSTOR 2313748.
• Kadison, Richard V.; Ringrose, John R. (1997), Fundamentals of the theory of operator algebras. Vol. I, Graduate Studies in Mathematics, vol. 15, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-0819-1, MR 1468229.
• Kadison, Richard V.; Ringrose, John R. (1983), Fundamentals of the Theory of Operator Algebras, Vol. I: Elementary Theory, New York: Academic Press, Inc.
• Karatzas, Ioannis; Shreve, Steven (2019), Brownian Motion and Stochastic Calculus (2nd ed.), Springer, ISBN 978-0-387-97655-6

• Kakutani, Shizuo (1939), "Some characterizations of Euclidean space", Japanese Journal of Mathematics, 16: 93–97, doi:10.4099/jjm1924.16.0_93, MR 0000895.
• Kline, Morris (1972), Mathematical thought from ancient to modern times, Volume 3 (3rd ed.), Oxford University Press (published 1990), ISBN 978-0-19-506137-6.
• Kolmogorov, Andrey; Fomin, Sergei V. (1970), Introductory Real Analysis (Revised English edition, trans. by Richard A. Silverman (1975) ed.), Dover Press, ISBN 978-0-486-61226-3.
• Krantz, Steven G. (2002), Function Theory of Several Complex Variables, Providence, R.I.: American Mathematical Society, ISBN 978-0-8218-2724-6.
• Lanczos, Cornelius (1988), Applied analysis (Reprint of 1956 Prentice-Hall ed.), Dover Publications, ISBN 978-0-486-65656-4.
• Lebesgue, Henri (1904), Leçons sur l'intégration et la recherche des fonctions primitives, Gauthier-Villars.
• Levitan, B.M. (2001) [1994], "Hilbert space", Encyclopedia of Mathematics, EMS Press.
• Lindenstrauss, J.; Tzafriri, L. (1971), "On the complemented subspaces problem", Israel Journal of Mathematics, 9 (2): 263–269, doi:10.1007/BF02771592, ISSN 0021-2172, MR 0276734, S2CID 119575718.
• Marsden, Jerrold E. (1974), Elementary classical analysis, W. H. Freeman and Co., MR 0357693.
• Murphy, Gerald J. (1990), C*-algebras and Operator Theory, Academic Press, ISBN 0-12-511360-9.
• von Neumann, John (1929), "Allgemeine Eigenwerttheorie Hermitescher Funktionaloperatoren", Mathematische Annalen, 102: 49–131, doi:10.1007/BF01782338, S2CID 121249803.
• von Neumann, John (1932), "Physical Applications of the Ergodic Hypothesis", Proc Natl Acad Sci USA, 18 (3): 263–266, Bibcode:1932PNAS...18..263N, doi:10.1073/pnas.18.3.263, JSTOR 86260, PMC 1076204, PMID 16587674.
• von Neumann, John (1955), Mathematical Foundations of Quantum Mechanics, Princeton Landmarks in Mathematics, translated by Beyer, Robert T., Princeton University Press (published 1996), ISBN 978-0-691-02893-4, MR 1435976.
• Nielsen, Michael A.; Chuang, Isaac L. (2000), Quantum Computation and Quantum Information (1st ed.), Cambridge: Cambridge University Press, ISBN 978-0-521-63503-5, OCLC 634735192.
• O'Connor, John J.; Robertson, Edmund F. (1996), "Abstract linear spaces", MacTutor History of Mathematics Archive, University of St Andrews
• Pathria, RK (1996), Statistical mechanics (2 ed.), Academic Press.
• Pedersen, Gert (1995), Analysis Now, Graduate Texts in Mathematics, vol. 118, Berlin, New York: Springer-Verlag, ISBN 978-1-4612-6981-6, MR 0971256
• Peres, Asher (1993), Quantum Theory: Concepts and Methods, Kluwer, ISBN 0-7923-2549-4, OCLC 28854083
• Prugovečki, Eduard (1981), Quantum mechanics in Hilbert space (2nd ed.), Dover (published 2006), ISBN 978-0-486-45327-9.
• Reed, Michael; Simon, Barry (1980), Functional Analysis (vol I of 4 vols), Methods of Modern Mathematical Physics, Academic Press, ISBN 978-0-12-585050-6.
• Reed, Michael; Simon, Barry (1975), Fourier Analysis, Self-Adjointness (vol II of 4 vols), Methods of Modern Mathematical Physics, Academic Press, ISBN 9780125850025.
• Rieffel, Eleanor G.; Polak, Wolfgang H. (2011-03-04), Quantum Computing: A Gentle Introduction, MIT Press, ISBN 978-0-262-01506-6.
• Riesz, Frigyes (1907), "Sur une espèce de Géométrie analytique des systèmes de fonctions sommables", C. R. Acad. Sci. Paris, 144: 1409–1411.
• Riesz, Frigyes (1934), "Zur Theorie des Hilbertschen Raumes", Acta Sci. Math. Szeged, 7: 34–38.
• Riesz, Frigyes; Sz.-Nagy, Béla (1990), Functional analysis, Dover, ISBN 978-0-486-66289-3.
• Roman, Stephen (2008), Advanced Linear Algebra, Graduate Texts in Mathematics (Third ed.), Springer, ISBN 978-0-387-72828-5
• Rudin, Walter (1973). Functional Analysis. International Series in Pure and Applied Mathematics. Vol. 25 (First ed.). New York, NY: McGraw-Hill Science/Engineering/Math. ISBN 9780070542259.
• Rudin, Walter (1987), Real and Complex Analysis, McGraw-Hill, ISBN 978-0-07-100276-9.
• Saks, Stanisław (2005), Theory of the integral (2nd Dover ed.), Dover, ISBN 978-0-486-44648-6; originally published Monografje Matematyczne, vol. 7, Warszawa, 1937.
• Schaefer, Helmut H.; Wolff, Manfred P. (1999). Topological Vector Spaces. GTM. Vol. 8 (Second ed.). New York, NY: Springer New York Imprint Springer. ISBN 978-1-4612-7155-0. OCLC 840278135.
• Schmidt, Erhard (1908), "Über die Auflösung linearer Gleichungen mit unendlich vielen Unbekannten", Rend. Circ. Mat. Palermo, 25: 63–77, doi:10.1007/BF03029116, S2CID 120666844.
• Shubin, M. A. (1987), Pseudodifferential operators and spectral theory, Springer Series in Soviet Mathematics, Berlin, New York: Springer-Verlag, ISBN 978-3-540-13621-7, MR 0883081.
• Sobrino, Luis (1996), Elements of non-relativistic quantum mechanics, River Edge, New Jersey: World Scientific Publishing Co. Inc., Bibcode:1996lnrq.book.....S, doi:10.1142/2865, ISBN 978-981-02-2386-1, MR 1626401.
• Stapleton, James (1995), Linear statistical models, John Wiley and Sons.
• Stewart, James (2006), Calculus: Concepts and Contexts (3rd ed.), Thomson/Brooks/Cole.
• Stein, E (1970), Singular Integrals and Differentiability Properties of Functions, Princeton Univ. Press, ISBN 978-0-691-08079-6.
• Stein, Elias; Weiss, Guido (1971), Introduction to Fourier Analysis on Euclidean Spaces, Princeton, N.J.: Princeton University Press, ISBN 978-0-691-08078-9.
• Stein, E; Shakarchi, R (2005), Real analysis, measure theory, integration, and Hilbert spaces, Princeton University Press.
• Streater, Ray; Wightman, Arthur (1964), PCT, Spin and Statistics and All That, W. A. Benjamin, Inc.
• Stroock, Daniel (2011), Probability theory: an analytic view (2 ed.), Cambridge University Press.
• Teschl, Gerald (2009). Mathematical Methods in Quantum Mechanics; With Applications to Schrödinger Operators. Providence: American Mathematical Society. ISBN 978-0-8218-4660-5..
• Titchmarsh, Edward Charles (1946), Eigenfunction expansions, part 1, Oxford University: Clarendon Press.
• Trèves, François (1967), Topological Vector Spaces, Distributions and Kernels, Academic Press.
• Warner, Frank (1983), Foundations of Differentiable Manifolds and Lie Groups, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90894-6.
• Weidmann, Joachim (1980), Linear operators in Hilbert spaces, Graduate Texts in Mathematics, vol. 68, Berlin, New York: Springer-Verlag, ISBN 978-0-387-90427-6, MR 0566954.
• Weyl, Hermann (1931), The Theory of Groups and Quantum Mechanics (English 1950 ed.), Dover Press, ISBN 978-0-486-60269-1.
• Young, Nicholas (1988), An introduction to Hilbert space, Cambridge University Press, ISBN 978-0-521-33071-8, Zbl 0645.46024.

External links

• "Hilbert space", Encyclopedia of Mathematics, EMS Press, 2001 [1994]
• Hilbert space at Mathworld
• 245B, notes 5: Hilbert spaces by Terence Tao