
В математике концепция проективного пространства возникла из визуального эффекта перспективы , где параллельные линии кажутся пересекающимися в бесконечности . Таким образом, проективное пространство можно рассматривать как расширение евклидова пространства или, в более общем смысле, аффинного пространства с точками в бесконечности , таким образом, что существует одна точка в бесконечности каждого направления параллельных линий .
Это определение проективного пространства имеет недостаток, заключающийся в том, что оно не изотропно , имеет два разных вида точек, которые должны рассматриваться отдельно в доказательствах. Поэтому обычно предпочитают другие определения. Существует два класса определений. В синтетической геометрии точка и линия являются примитивными сущностями, которые связаны отношением инцидентности «точка находится на прямой» или «прямая проходит через точку», которое подчиняется аксиомам проективной геометрии . Для некоторого такого набора аксиом было показано, что проективные пространства, которые определяются, эквивалентны тем, которые вытекают из следующего определения, которое чаще встречается в современных учебниках.
Используя линейную алгебру , проективное пространство размерности n определяется как множество векторных прямых (то есть векторных подпространств размерности один) в векторном пространстве V размерности n + 1. Эквивалентно, это фактор- множество V \ {0} по отношению эквивалентности «находиться на одной векторной прямой». Поскольку векторная прямая пересекает единичную сферу V в двух антиподальных точках , проективные пространства могут быть эквивалентно определены как сферы, в которых идентифицированы антиподальные точки. Проективное пространство размерности 1 является проективной прямой , а проективное пространство размерности 2 является проективной плоскостью .
Проективные пространства широко используются в геометрии , поскольку допускают более простые утверждения и более простые доказательства. Например, в аффинной геометрии две различные прямые на плоскости пересекаются не более чем в одной точке, тогда как в проективной геометрии они пересекаются ровно в одной точке. Кроме того, существует только один класс конических сечений , которые можно различить только по их пересечениям с прямой на бесконечности: две точки пересечения для гипербол ; одна для параболы , которая касается прямой на бесконечности; и ни одной реальной точки пересечения эллипсов .
В топологии , и, более конкретно, в теории многообразий , проективные пространства играют фундаментальную роль, являясь типичными примерами неориентируемых многообразий .
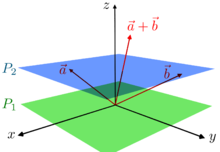
Как было отмечено выше, проективные пространства были введены для формализации утверждений типа «две копланарные прямые пересекаются ровно в одной точке, и эта точка находится на бесконечности, если прямые параллельны ». Такие утверждения подсказаны изучением перспективы , которую можно рассматривать как центральную проекцию трехмерного пространства на плоскость (см. Модель камеры-обскуры ). Точнее, входной зрачок камеры или глаза наблюдателя является центром проекции , а изображение формируется на плоскости проекции .
Математически, центр проекции — это точка O пространства (пересечение осей на рисунке); плоскость проекции ( P 2 , на рисунке синего цвета) — это плоскость, не проходящая через O , которую часто выбирают в качестве плоскости уравнения z = 1 , когда рассматриваются декартовы координаты . Тогда центральная проекция отображает точку P в пересечение прямой OP с плоскостью проекции. Такое пересечение существует тогда и только тогда, когда точка P не принадлежит плоскости ( P 1 , на рисунке зеленого цвета), которая проходит через O и параллельна P 2 .
Отсюда следует, что прямые, проходящие через O, распадаются на два непересекающихся подмножества: прямые, не содержащиеся в P 1 , которые находятся во взаимно однозначном соответствии с точками P 2 , и прямые, содержащиеся в P 1 , которые находятся во взаимно однозначном соответствии с направлениями параллельных прямых в P 2 . Это предполагает определение точек (называемых здесь проективными точками для ясности) проективной плоскости как прямых, проходящих через O . Проективная прямая в этой плоскости состоит из всех проективных точек (которые являются прямыми), содержащихся в плоскости, проходящей через O . Поскольку пересечение двух плоскостей, проходящих через O , является прямой, проходящей через O , пересечение двух различных проективных прямых состоит из одной проективной точки. Плоскость P 1 определяет проективную прямую, которая называется прямой на бесконечности P 2 . Отождествляя каждую точку P 2 с соответствующей проективной точкой , можно таким образом сказать , что проективная плоскость является несвязным объединением P 2 и (проективной) прямой на бесконечности.
Так как аффинное пространство с выделенной точкой O может быть отождествлено с его связанным векторным пространством (см. Аффинное пространство § Векторные пространства как аффинные пространства ), предыдущее построение обычно выполняется, начиная с векторного пространства и называется проективизацией . Кроме того, построение может быть выполнено, начиная с векторного пространства любой положительной размерности.
Итак, проективное пространство размерности n можно определить как множество векторных прямых (векторных подпространств размерности один) в векторном пространстве размерности n + 1. Проективное пространство можно также определить как элементы любого множества, которое находится в естественном соответствии с этим множеством векторных прямых.
Этот набор может быть набором классов эквивалентности при отношении эквивалентности между векторами, определяемом как «один вектор является произведением другого на ненулевой скаляр». Другими словами, это равносильно определению проективного пространства как набора векторных линий, в которых удален нулевой вектор.
Третье эквивалентное определение состоит в определении проективного пространства размерности n как множества пар антиподальных точек в сфере размерности n (в пространстве размерности n + 1 ).
Если задано векторное пространство V над полем K , то проективное пространство P ( V ) представляет собой множество классов эквивалентности V \ {0} при отношении эквивалентности ~, определяемом соотношением x ~ y , если существует ненулевой элемент λ из K, такой что x = λy . Если V является топологическим векторным пространством , фактор-пространство P ( V ) является топологическим пространством, наделенным фактор-топологией топологии подпространства V \ {0} . Это имеет место , когда K является полем R действительных чисел или полем C комплексных чисел . Если V конечномерно , размерность P ( V ) равна размерности V минус один.
В общем случае, когда V = K n +1 , проективное пространство P ( V ) обозначается P n ( K ) (а также K P n или P n ( K ) , хотя это обозначение можно спутать с возведением в степень). Пространство P n ( K ) часто называют проективным пространством размерности n над K , или проективным n -пространством , поскольку все проективные пространства размерности n ему изоморфны (потому что каждое векторное пространство K размерности n + 1 изоморфно K n +1 ).
Элементы проективного пространства P ( V ) обычно называются точками . Если выбран базис V и, в частности, если V = K n +1 , проективные координаты точки P являются координатами на основе любого элемента соответствующего класса эквивалентности. Эти координаты обычно обозначаются [ x 0 : ... : x n ] , двоеточия и скобки используются для отличия от обычных координат и подчеркивания того, что это класс эквивалентности, который определен с точностью до умножения на ненулевую константу. То есть, если [ x 0 : ... : x n ] являются проективными координатами точки, то [ λx 0 : ... : λx n ] также являются проективными координатами той же точки для любого ненулевого λ в K . Кроме того, из приведенного выше определения следует, что [ x 0 : ... : x n ] являются проективными координатами точки тогда и только тогда, когда хотя бы одна из координат отлична от нуля.
Если K — поле действительных или комплексных чисел, проективное пространство называется действительным проективным пространством или комплексным проективным пространством соответственно. Если n равно одному или двум, проективное пространство размерности n называется проективной прямой или проективной плоскостью соответственно. Комплексная проективная прямая также называется сферой Римана .
Все эти определения естественным образом распространяются на случай, когда K — тело ; см., например, Кватернионное проективное пространство . Обозначение PG( n , K ) иногда используется для P n ( K ) . [1] Если K — конечное поле с q элементами, P n ( K ) часто обозначается PG( n , q ) (см. PG(3,2) ). [a]
Пусть P ( V ) — проективное пространство, где V — векторное пространство над полем K , а — каноническое отображение , которое отображает ненулевой вектор v в его класс эквивалентности, который представляет собой векторную прямую, содержащую v, с удаленным нулевым вектором.
Каждое линейное подпространство W пространства V является объединением прямых. Отсюда следует, что p ( W ) является проективным пространством, которое можно отождествить с P ( W ) .
Таким образом, проективное подпространство — это проективное пространство, которое получается путем ограничения отношения эквивалентности, определяющего P ( V ), линейным подпространством .
Если p ( v ) и p ( w ) — две различные точки P ( V ) , то векторы v и w линейно независимы . Отсюда следует, что:
В синтетической геометрии , где проективные прямые являются примитивными объектами, первое свойство является аксиомой, а второе — определением проективного подпространства.
Каждое пересечение проективных подпространств является проективным подпространством. Отсюда следует, что для каждого подмножества S проективного пространства существует наименьшее проективное подпространство, содержащее S , пересечение всех проективных подпространств, содержащих S . Это проективное подпространство называется проективной оболочкой S , а S является охватывающим множеством для него.
Множество точек S проективно независимо, если его охват не является охватом никакого собственного подмножества S. Если S является охватывающим множеством проективного пространства P , то существует подмножество S , охватывающее P и являющееся проективно независимым (это следует из аналогичной теоремы для векторных пространств). Если размерность P равна n , такое независимое охватывающее множество имеет n + 1 элемент.
В отличие от случаев векторных пространств и аффинных пространств , независимого охватывающего множества недостаточно для определения координат. Нужна еще одна точка, см. следующий раздел.
Проективный фрейм или проективный базис — это упорядоченный набор точек в проективном пространстве, позволяющий определять координаты. [2] Точнее, в n -мерном проективном пространстве проективный фрейм — это кортеж из n + 2 точек, такой, что любые n + 1 из них независимы; то есть они не содержатся в гиперплоскости .
Если V — векторное пространство размерности ( n + 1) , а p — каноническая проекция из V в P ( V ) , то ( p ( e 0 ), ..., p ( e n +1 )) является проективным фреймом тогда и только тогда, когда ( e 0 , ..., e n ) является базисом V и все коэффициенты e n +1 на этом базисе не равны нулю. Изменяя масштаб первых n векторов, любой фрейм можно переписать как ( p ( e ′ 0 ), ..., p( e ′ n +1 )) таким образом, что e ′ n +1 = e ′ 0 + ... + e ′ n ; это представление уникально с точностью до умножения всех e ′ i на общий ненулевой множитель.
Проективные координаты или однородные координаты точки p ( v ) на системе отсчета ( p ( e 0 ), ..., p ( e n +1 )) с e n +1 = e 0 + ... + e n являются координатами v на основе ( e 0 , ..., e n ) . Они определены только с точностью до масштабирования с общим ненулевым множителем.
Канонический фрейм проективного пространства P n ( K ) состоит из образов по p элементов канонического базиса K n +1 (то есть кортежей , имеющих только один ненулевой элемент, равный 1), и образа по p их суммы.
В математике проективная геометрия — это изучение геометрических свойств , которые инвариантны относительно проективных преобразований . Это означает, что по сравнению с элементарной евклидовой геометрией проективная геометрия имеет другую настройку, проективное пространство , и выборочный набор основных геометрических понятий. Основные интуиции состоят в том, что проективное пространство имеет больше точек, чем евклидово пространство , для заданного измерения, и что разрешены геометрические преобразования , которые преобразуют дополнительные точки (называемые « точками на бесконечности ») в евклидовы точки, и наоборот.
Свойства, значимые для проективной геометрии, соблюдаются этой новой идеей преобразования, которая более радикальна по своим эффектам, чем может быть выражена матрицей преобразования и переносами ( аффинными преобразованиями ). Первый вопрос для геометров заключается в том, какой вид геометрии подходит для новой ситуации. В отличие от евклидовой геометрии , понятие угла не применяется в проективной геометрии, потому что никакая мера углов не является инвариантной относительно проективных преобразований, как это видно на перспективном рисунке с изменяющейся точки зрения. Одним из источников проективной геометрии действительно была теория перспективы. Еще одним отличием от элементарной геометрии является способ, которым параллельные линии можно сказать, что они встречаются в точке на бесконечности , как только концепция переводится в термины проективной геометрии. Опять же, это понятие имеет интуитивную основу, такую как железнодорожные пути, встречающиеся на горизонте на перспективном рисунке. См. Проективная плоскость для основ проективной геометрии в двух измерениях.
Хотя идеи были доступны и раньше, проективная геометрия была в основном развитием 19-го века. Она включала теорию комплексного проективного пространства , в которой координаты ( однородные координаты ) были комплексными числами. Несколько основных типов более абстрактной математики (включая теорию инвариантов , итальянскую школу алгебраической геометрии и Эрлангенскую программу Феликса Клейна , приведшую к изучению классических групп ) были мотивированы проективной геометрией. Она также была предметом многих практиков сама по себе, как синтетическая геометрия . Другая тема, которая развилась из аксиоматических исследований проективной геометрии, — это конечная геометрия .
Тема проективной геометрии в настоящее время разделена на множество исследовательских подтем, двумя примерами которых являются проективная алгебраическая геометрия (изучение проективных многообразий ) и проективная дифференциальная геометрия (изучение дифференциальных инвариантов проективных преобразований).В проективной геометрии гомография — это изоморфизм проективных пространств, индуцированный изоморфизмом векторных пространств, из которых выводятся проективные пространства. [3] Это биекция , которая отображает прямые в прямые, и, таким образом, коллинеация . В общем случае некоторые коллинеации не являются гомографиями, но основная теорема проективной геометрии утверждает, что это не так в случае действительных проективных пространств размерности не менее двух. Синонимы включают проективность, проективное преобразование и проективную коллинеацию.
Исторически гомографии (и проективные пространства) были введены для изучения перспективы и проекций в евклидовой геометрии , и термин гомография , который этимологически примерно означает «подобный рисунок», датируется этим временем. В конце 19-го века были введены формальные определения проективных пространств, которые расширили евклидовы и аффинные пространства путем добавления новых точек, называемых точками на бесконечности . Термин «проективное преобразование» возник в этих абстрактных конструкциях. Эти конструкции делятся на два класса, которые, как было показано, эквивалентны. Проективное пространство может быть построено как множество линий векторного пространства над заданным полем (приведенное выше определение основано на этой версии); эта конструкция облегчает определение проективных координат и позволяет использовать инструменты линейной алгебры для изучения гомографии. Альтернативный подход состоит в определении проективного пространства через набор аксиом, которые явно не включают в себя какое-либо поле ( геометрия инцидентности , см. также синтетическую геометрию ); В этом контексте коллинеации определить проще, чем омографии, а омографии определяются как особые коллинеации, поэтому их называют «проективными коллинеациями».
Для простоты, если не указано иное, проективные пространства, рассматриваемые в этой статье, предполагаются определенными над (коммутативным) полем . Эквивалентно теорема Паппуса о шестиугольнике и теорема Дезарга предполагаются верными. Большая часть результатов остается верной или может быть обобщена на проективные геометрии, для которых эти теоремы не верны.Проективное пространство — это топологическое пространство , наделенное фактор-топологией топологии конечномерного действительного векторного пространства.
Пусть S — единичная сфера в нормированном векторном пространстве V , и рассмотрим функцию , которая отображает точку S в векторную прямую, проходящую через нее. Эта функция непрерывна и сюръективна. Обратный образ каждой точки P ( V ) состоит из двух антиподальных точек . Поскольку сферы являются компактными пространствами , отсюда следует, что:
Для каждой точки P из S ограничение π на окрестность P является гомеоморфизмом на ее образ, при условии, что окрестность достаточно мала, чтобы не содержать ни одной пары антиподальных точек. Это показывает, что проективное пространство является многообразием. Простой атлас может быть предоставлен следующим образом.
Как только базис выбран для V , любой вектор может быть отождествлен с его координатами на базисе, а любая точка P ( V ) может быть отождествлена с ее однородными координатами . Для i = 0, ..., n множество является открытым подмножеством P ( V ) , и поскольку каждая точка P ( V ) имеет по крайней мере одну ненулевую координату.
Каждому U i сопоставлена карта , представляющая собой гомеоморфизмы, такие, что символ «шляпка» означает, что соответствующий термин отсутствует.

Эти карты образуют атлас , и поскольку отображения перехода являются аналитическими функциями , получается, что проективные пространства являются аналитическими многообразиями .
Например, в случае n = 1 , то есть проективной прямой, есть только два U i , каждый из которых может быть идентифицирован как копия действительной прямой . В обеих прямых пересечение двух диаграмм является множеством ненулевых действительных чисел, а отображение перехода происходит в обоих направлениях. Изображение представляет проективную прямую как окружность, в которой идентифицированы антиподальные точки, и показывает два гомеоморфизма действительной прямой на проективную прямую; поскольку антиподальные точки идентифицированы, изображение каждой прямой представляется как открытый полукруг, который может быть идентифицирован с проективной прямой с одной удаленной точкой.
Действительные проективные пространства имеют простую комплексную структуру CW , так как P n ( R ) может быть получено из P n −1 ( R ) путем присоединения n -клетки с факторпроекцией S n −1 → P n −1 ( R ) в качестве присоединения отображения.
Первоначально алгебраическая геометрия была изучением общих нулей множеств многомерных многочленов . Эти общие нули, называемые алгебраическими многообразиями , принадлежат аффинному пространству . Вскоре выяснилось, что в случае действительных коэффициентов необходимо учитывать все комплексные нули для получения точных результатов. Например, основная теорема алгебры утверждает, что одномерный свободный от квадратов многочлен степени n имеет ровно n комплексных корней. В многомерном случае рассмотрение комплексных нулей также необходимо, но недостаточно: необходимо также учитывать нули на бесконечности . Например, теорема Безу утверждает, что пересечение двух плоских алгебраических кривых соответствующих степеней d и e состоит ровно из de точек, если рассматривать комплексные точки в проективной плоскости и если подсчитывать точки с их кратностью. [b] Другим примером является формула род-степень , которая позволяет вычислить род плоской алгебраической кривой по ее особенностям в комплексной проективной плоскости .
Таким образом, проективное многообразие — это множество точек в проективном пространстве, однородные координаты которых являются общими нулями множества однородных многочленов . [c]
Любое аффинное многообразие может быть единственным образом дополнено до проективного многообразия путем добавления его точек на бесконечности , что состоит в гомогенизации определяющих многочленов и удалении компонентов, содержащихся в гиперплоскости на бесконечности, путем насыщения относительно гомогенизирующей переменной.
Важным свойством проективных пространств и проективных многообразий является то, что образ проективного многообразия при морфизме алгебраических многообразий замкнут для топологии Зарисского (то есть является алгебраическим множеством ). Это является обобщением на каждое основное поле компактности действительного и комплексного проективного пространства.
Проективное пространство само является проективным многообразием, представляя собой множество нулей нулевого многочлена.
Теория схем , введенная Александром Гротендиком во второй половине 20-го века, позволяет определить обобщение алгебраических многообразий, называемых схемами , путем склеивания меньших частей, называемых аффинными схемами , аналогично тому, как многообразия могут быть построены путем склеивания открытых множеств R n . Конструкция Proj — это построение схемы проективного пространства и, в более общем смысле, любого проективного многообразия путем склеивания аффинных схем. В случае проективных пространств можно взять в качестве этих аффинных схем аффинные схемы, связанные с картами (аффинными пространствами) приведенного выше описания проективного пространства как многообразия.
В синтетической геометрии проективное пространство S может быть аксиоматически определено как множество P (множество точек) вместе с множеством L подмножеств P (множество прямых), удовлетворяющих следующим аксиомам: [4]
Последняя аксиома устраняет сводимые случаи, которые могут быть записаны как несвязное объединение проективных пространств вместе с 2-точечными прямыми, соединяющими любые две точки в различных проективных пространствах. Более абстрактно, ее можно определить как структуру инцидентности ( P , L , I ), состоящую из множества точек P , множества линий L и отношения инцидентности I , которое устанавливает, какие точки лежат на каких линиях.
Структуры, определяемые этими аксиомами, более общие, чем те, которые получены из конструкции векторного пространства, приведенной выше. Если (проективная) размерность равна по крайней мере трем, то по теореме Веблена–Янга разницы нет. Однако для размерности два существуют примеры, удовлетворяющие этим аксиомам, которые не могут быть построены из векторных пространств (или даже модулей над телами). Эти примеры не удовлетворяют теореме Дезарга и известны как недезарговы плоскости . В размерности один любое множество с по крайней мере тремя элементами удовлетворяет аксиомам, поэтому обычно предполагается дополнительная структура для проективных прямых, определенных аксиоматически. [5]
Можно избежать проблемных случаев в низких размерностях, добавляя или изменяя аксиомы, которые определяют проективное пространство. Коксетер (1969, стр. 231) дает такое расширение, основанное на Бахмане. [6] Чтобы гарантировать, что размерность равна по крайней мере двум, замените аксиому трех точек на линию выше на:
Чтобы избежать недезарговых плоскостей, включите теорему Паппуса в качестве аксиомы; [e]
И, чтобы гарантировать, что векторное пространство определено над полем, которое не имеет четной характеристики , включите аксиому Фано ; [f]
Подпространство проективного пространства — это подмножество X , такое, что любая линия, содержащая две точки X, является подмножеством X (то есть полностью содержится в X ). Полное пространство и пустое пространство всегда являются подпространствами.
Геометрическая размерность пространства называется равной n, если это наибольшее число, для которого существует строго возрастающая цепочка подпространств такого вида:
Говорят, что подпространство X i в такой цепи имеет (геометрическую) размерность i . Подпространства размерности 0 называются точками , размерности 1 называются прямыми и т. д. Если полное пространство имеет размерность n , то любое подпространство размерности n − 1 называется гиперплоскостью .
Проективные пространства допускают эквивалентную формулировку в терминах теории решеток . Существует биективное соответствие между проективными пространствами и геомодулярными решетками, а именно, подпрямо неприводимыми , компактно порожденными , дополненными , модулярными решетками . [7]

Конечное проективное пространство — это проективное пространство, где P — конечное множество точек. В любом конечном проективном пространстве каждая прямая содержит одинаковое количество точек, а порядок пространства определяется как на единицу меньше этого общего числа. Для конечных проективных пространств размерности не менее трех теорема Веддерберна подразумевает, что тело, над которым определено проективное пространство, должно быть конечным полем GF( q ) , порядок (то есть количество элементов) которого равен q (степень простого числа). Конечное проективное пространство, определенное над таким конечным полем, имеет q + 1 точек на прямой, поэтому два понятия порядка совпадают. Обозначительно PG( n , GF( q )) обычно записывается как PG( n , q ) .
Все конечные поля одного и того же порядка изоморфны, поэтому с точностью до изоморфизма существует только одно конечное проективное пространство для каждой размерности, большей или равной трем, над заданным конечным полем. Однако в размерности два существуют недезарговы плоскости. С точностью до изоморфизма существуют
конечные проективные плоскости порядков 2, 3, 4, ..., 10 соответственно. Числа за пределами этого очень трудно вычислить и они не определены, за исключением некоторых нулевых значений из-за теоремы Брука–Райзера .
Наименьшая проективная плоскость — это плоскость Фано , PG(2, 2) с 7 точками и 7 прямыми. Наименьшим 3-мерным проективным пространством является PG(3, 2) с 15 точками, 35 прямыми и 15 плоскостями.
Инъективные линейные отображения T ∈ L ( V , W ) между двумя векторными пространствами V и W над одним и тем же полем K индуцируют отображения соответствующих проективных пространств P ( V ) → P ( W ) посредством:
где v — ненулевой элемент V , а [...] обозначает классы эквивалентности вектора при определяющей идентификации соответствующих проективных пространств. Поскольку члены класса эквивалентности отличаются скалярным множителем, а линейные отображения сохраняют скалярные множители, это индуцированное отображение является корректно определенным . (Если T не является инъективным, то оно имеет нулевое пространство больше {0} ; в этом случае значение класса T ( v ) проблематично, если v не равно нулю и находится в нулевом пространстве. В этом случае получается так называемое рациональное отображение , см. также Бирациональная геометрия .)
Два линейных отображения S и T в L ( V , W ) индуцируют одно и то же отображение между P ( V ) и P ( W ) тогда и только тогда, когда они отличаются скалярным множителем, то есть если T = λS для некоторого λ ≠ 0. Таким образом, если отождествить скалярные множители тождественного отображения с базовым полем K , то множество K -линейных морфизмов из P ( V ) в P ( W ) будет просто P ( L ( V , W ) ) .
Автоморфизмы P ( V ) → P ( V ) можно описать более конкретно. (Мы имеем дело только с автоморфизмами, сохраняющими базовое поле K ) . Используя понятие пучков, порожденных глобальными сечениями , можно показать, что любой алгебраический (не обязательно линейный) автоморфизм должен быть линейным, т. е. исходить из (линейного) автоморфизма векторного пространства V . Последние образуют группу GL( V ) . Определив отображения, которые отличаются скаляром, можно заключить, что
факторгруппа GL ( V ) по модулю матриц, которые являются скалярными кратными единицы. (Эти матрицы образуют центр Aut ( V ) . ) Группы PGL называются проективными линейными группами . Автоморфизмы комплексной проективной прямой P 1 ( C ) называются преобразованиями Мёбиуса .
Если применить приведенную выше конструкцию к двойственному пространству V ∗ вместо V , то получится двойственное проективное пространство, которое можно канонически отождествить с пространством гиперплоскостей через начало координат V . То есть, если V n -мерно , то P ( V ∗ ) является грассманианом n − 1 плоскостей в V .
В алгебраической геометрии эта конструкция допускает большую гибкость в построении проективных расслоений. Хотелось бы иметь возможность связать проективное пространство с каждым квазикогерентным пучком E над схемой Y , а не только с локально свободными. [ необходимо разъяснение ] Подробнее см. EGA II , гл. II, пар. 4.
Многообразия Севери–Брауэра — это алгебраические многообразия над полем K , которые становятся изоморфными проективным пространствам после расширения базового поля K.
Другим обобщением проективных пространств являются взвешенные проективные пространства ; они сами по себе являются частными случаями торических многообразий . [8]