Векторный пакет

Математическая параметризация векторных пространств другим пространством

(Бесконечно протяженная) Лента Мёбиуса представляет собой линейное расслоение над 1-сферой S ¹ . Локально вокруг каждой точки в S ¹ он выглядит как U  ×  R (где U — открытая дуга , включающая точку), но общий расслоение отличается от S ¹  ×  R (который вместо этого представляет собой цилиндр ).

В математике векторное расслоение — это топологическая конструкция, которая уточняет идею семейства векторных пространств , параметризованных другим пространством (например, топологическим пространством , многообразием или алгебраическим многообразием ): в каждой точке пространства мы связать (или «присоединить») векторное пространство таким образом, чтобы эти векторные пространства сочетались друг с другом, образуя другое пространство того же типа (например, топологическое пространство, многообразие или алгебраическое многообразие), которое затем называется векторным расслоением над . ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle x}$ ${\displaystyle X}$ ${\displaystyle V(x)}$ ${\displaystyle X}$ ${\displaystyle X}$

Простейшим примером является случай, когда семейство векторных пространств является постоянным, т. е. существует фиксированное векторное пространство такое, что для всех in : в этом случае существует копия для каждого in , и эти копии подходят друг к другу, образуя векторное расслоение. над . Такие векторные расслоения называются тривиальными . Более сложный (и прототипический) класс примеров — это касательные расслоения гладких (или дифференцируемых) многообразий : к каждой точке такого многообразия мы присоединяем касательное пространство к многообразию в этой точке. Касательные расслоения, вообще говоря, не являются тривиальными расслоениями. Например, касательное расслоение сферы нетривиально по теореме о волосатом шаре . В общем, многообразие называется параллелизуемым тогда и только тогда, когда его касательное расслоение тривиально. ${\displaystyle V}$ ${\displaystyle V(x)=V}$ ${\displaystyle x}$ ${\displaystyle X}$ ${\displaystyle V}$ ${\displaystyle x}$ ${\displaystyle X}$ ${\displaystyle X\times V}$ ${\displaystyle X}$

Векторные расслоения почти всегда должны быть локально тривиальными , что означает, что они являются примерами расслоений . Кроме того, векторные пространства обычно должны быть над действительными или комплексными числами , и в этом случае векторное расслоение называется действительным или комплексным векторным расслоением (соответственно). Комплексные векторные расслоения можно рассматривать как вещественные векторные расслоения с дополнительной структурой. Далее мы сосредоточимся на вещественных векторных расслоениях в категории топологических пространств .

Определение и первые последствия

Векторное расслоение над базой . Точка соответствует началу координат в слое векторного расслоения , и этот слой отображается в точку с помощью проекции . ${\displaystyle E}$ ${\displaystyle M}$ ${\displaystyle m_{1}}$ ${\displaystyle M}$ ${\displaystyle E_{m_{1}}}$ ${\displaystyle E}$ ${\displaystyle m_{1}}$ ${\displaystyle \pi :E\to M}$

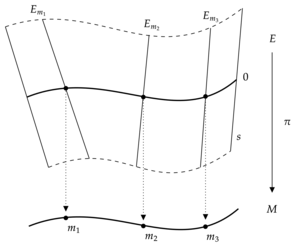
Реальное векторное расслоение состоит из:

1. топологические пространства ( базовое пространство ) и ( общее пространство ) ${\displaystyle X}$ ${\displaystyle E}$
2. непрерывная сюръекция ( проекция расслоения ) ${\displaystyle \pi :E\to X}$
3. для каждого in структура конечномерного вещественного векторного пространства на слое ${\displaystyle x}$ ${\displaystyle X}$ ${\displaystyle \pi ^{-1}(\{x\})}$

где выполняется следующее условие совместимости: для каждой точки в существует открытая окрестность , натуральное число и гомеоморфизм ${\displaystyle p}$ ${\displaystyle X}$ ${\displaystyle U\subseteq X}$ ${\displaystyle p}$ ${\displaystyle k}$

${\displaystyle \varphi \colon U\times \mathbb {R} ^{k}\to \pi ^{-1}(U)}$

такой, что для всех в , ${\displaystyle x}$ ${\displaystyle U}$

• ${\displaystyle (\pi \circ \varphi )(x,v)=x}$для всех векторов в и ${\displaystyle v}$ ${\displaystyle \mathbb {R} ^{k}}$
• отображение является линейным изоморфизмом между векторными пространствами и . ${\displaystyle v\mapsto \varphi (x,v)}$ ${\displaystyle \mathbb {R} ^{k}}$ ${\displaystyle \pi ^{-1}(\{x\})}$

Открытая окрестность вместе с гомеоморфизмом называется локальной тривиализацией векторного расслоения. Локальная тривиализация показывает, что локально карта «выглядит» как проекция на . ${\displaystyle U}$ ${\displaystyle \varphi }$ ${\displaystyle \pi }$ ${\displaystyle U\times \mathbb {R} ^{k}}$ ${\displaystyle U}$

Каждый слой представляет собой конечномерное вещественное векторное пространство и, следовательно, имеет размерность . Локальные тривиализации показывают, что функция локально постоянна и , следовательно, постоянна на каждом компоненте связности . Если равно константе на всех , то называется рангом векторного расслоения и называется векторным расслоением ранга . Часто определение векторного расслоения включает в себя то, что ранг четко определен, поэтому он постоянен. Векторные расслоения ранга 1 называются линейными расслоениями , а расслоения ранга 2 реже называются плоскими расслоениями. ${\displaystyle \pi ^{-1}(\{x\})}$ ${\displaystyle k_{x}}$ ${\displaystyle x\to k_{x}}$ ${\displaystyle X}$ ${\displaystyle k_{x}}$ ${\displaystyle k}$ ${\displaystyle X}$ ${\displaystyle k}$ ${\displaystyle E}$ ${\displaystyle k}$ ${\displaystyle k_{x}}$

Декартово произведение , снабженное проекцией , называется тривиальным расслоением ранга над . ${\displaystyle X\times \mathbb {R} ^{k}}$ ${\displaystyle X\times \mathbb {R} ^{k}\to X}$ ${\displaystyle k}$ ${\displaystyle X}$

Функции перехода

Два тривиальных векторных расслоения над открытыми множествами могут быть склеены над пересечением с помощью функций перехода , которые служат для склеивания заштрихованных серых областей после применения линейного преобразования к слоям (обратите внимание на преобразование синего четырехугольника под действием ). Разный выбор функций перехода может привести к образованию разных векторных расслоений, которые после завершения склейки станут нетривиальными. ${\displaystyle U_{\alpha }}$ ${\displaystyle U_{\beta }}$ ${\displaystyle U_{\alpha \beta }}$ ${\displaystyle g_{\alpha \beta }}$ ${\displaystyle g_{\alpha \beta }}$

Ленту Мёбиуса можно построить нетривиальной склейкой двух тривиальных расслоений на ^{открытых} подмножествах U и V окружности S1 . При тривиальной склейке (с g _UV =1 ) получается тривиальный пучок, а при нетривиальной склейке g _UV =1 на одном перекрытии и g _UV =-1 на втором перекрытии получается нетривиальный пучок E , лента Мёбиуса. Это можно представить как «подкручивание» одного из локальных графиков .

Учитывая векторное расслоение ранга и пару окрестностей и , над которыми расслоение тривиализуется через ${\displaystyle E\to X}$ ${\displaystyle k}$ ${\displaystyle U}$ ${\displaystyle V}$

${\displaystyle {\begin{aligned}\varphi _{U}\colon U\times \mathbb {R} ^{k}&\mathrel {\xrightarrow {\cong } } \pi ^{-1}(U),\\\varphi _{V}\colon V\times \mathbb {R} ^{k}&\mathrel {\xrightarrow {\cong } } \pi ^{-1}(V)\end{aligned}}}$

составная функция

${\displaystyle \varphi _{U}^{-1}\circ \varphi _{V}\colon (U\cap V)\times \mathbb {R} ^{k}\to (U\cap V)\times \mathbb {R} ^{k}}$

четко определен на перекрытии и удовлетворяет

${\displaystyle \varphi _{U}^{-1}\circ \varphi _{V}(x,v)=\left(x,g_{UV}(x)v\right)}$

для некоторой -значной функции ${\displaystyle {\text{GL}}(k)}$

${\displaystyle g_{UV}\colon U\cap V\to \operatorname {GL} (k).}$

Они называются функциями перехода (или преобразованиями координат ) векторного расслоения.

Набор функций перехода образует коцикл Чеха в том смысле, что

${\displaystyle g_{UU}(x)=I,\quad g_{UV}(x)g_{VW}(x)g_{WU}(x)=I}$

для всех , над которыми расслоение упрощается, удовлетворяя . Таким образом, данные определяют пучок волокон ; дополнительные данные указывают структурную группу, в которой действие на волокно является стандартным действием . ${\displaystyle U,V,W}$ ${\displaystyle U\cap V\cap W\neq \emptyset }$ ${\displaystyle (E,X,\pi ,\mathbb {R} ^{k})}$ ${\displaystyle g_{UV}}$ ${\displaystyle {\text{GL}}(k)}$ ${\displaystyle {\text{GL}}(k)}$

Обратно, данному расслоению с коциклом , действующим на слое стандартным образом , соответствует векторное расслоение. Это пример теоремы о построении расслоений для векторных расслоений, и его можно рассматривать как альтернативное определение векторного расслоения. ${\displaystyle (E,X,\pi ,\mathbb {R} ^{k})}$ ${\displaystyle {\text{GL}}(k)}$ ${\displaystyle \mathbb {R} ^{k}}$

Подпакеты

Линейное подрасслоение тривиального векторного расслоения ранга 2 над одномерным многообразием . ${\displaystyle L}$ ${\displaystyle E}$ ${\displaystyle M}$

Один простой метод построения векторных расслоений — это взятие подрасслоений других векторных расслоений. Учитывая векторное расслоение над топологическим пространством, подрасслоение — это просто подпространство , для которого ограничение на также дает структуру векторного расслоения. В этом случае слой является векторным подпространством для каждого . ${\displaystyle \pi :E\to X}$ ${\displaystyle F\subset E}$ ${\displaystyle \left.\pi \right|_{F}}$ ${\displaystyle \pi }$ ${\displaystyle F}$ ${\displaystyle \left.\pi \right|_{F}:F\to X}$ ${\displaystyle F_{x}\subset E_{x}}$ ${\displaystyle x\in X}$

Подрасслоение тривиального расслоения не обязательно должно быть тривиальным, и действительно, каждое вещественное векторное расслоение над компактом можно рассматривать как подрасслоение тривиального расслоения достаточно высокого ранга. Например, полосу Мёбиуса , нетривиальное линейное расслоение над окружностью, можно рассматривать как подрасслоение тривиального расслоения ранга 2 над окружностью.

Морфизмы векторных расслоений

Морфизм векторного расслоения π ₁ : E ₁ → X ₁ в векторное расслоение π ₂ : E ₂ → X ₂ задается парой непрерывных отображений f : E ₁ → E ₂ и g : X ₁ → X ₂ , таких что

г  ∘  π ₁ знак равно π ₂  ∘  ж

для каждого x в X ₁ отображение π ₁ ⁻¹ ({ x }) → π ₂ ⁻¹ ({ g ( x )}), индуцированное f, является линейным отображением векторных пространств.

Обратите внимание, что g определяется f (поскольку π ₁ сюръективно), и тогда говорят, что f покрывает g .

Класс всех векторных расслоений вместе с морфизмами расслоений образует категорию . Ограничиваясь векторными расслоениями, для которых пространства являются многообразиями (а проекции расслоений являются гладкими отображениями) и гладкими морфизмами расслоений, мы получаем категорию гладких векторных расслоений. Морфизмы векторных расслоений являются частным случаем понятия отображения расслоений между расслоениями и иногда называются гомоморфизмами (векторных) расслоений .

Гомоморфизм расслоения из E ₁ в E ₂ с обратным, который также является гомоморфизмом расслоения (из E ₂ в E ₁ ), называется (векторным) изоморфизмом расслоения , и тогда E ₁ и E ₂ называются изоморфными векторными расслоениями. Изоморфизм векторного расслоения E (ранга k ) над X с тривиальным расслоением (ранга k над X ) называется тривиализацией E , и тогда E называется тривиальным (или тривиализируемым ). Определение векторного расслоения показывает, что любое векторное расслоение локально тривиально .

Мы также можем рассмотреть категорию всех векторных расслоений над фиксированным базовым пространством X . В качестве морфизмов этой категории мы возьмем те морфизмы векторных расслоений, отображение которых на базовом пространстве является тождественным отображением на X . То есть морфизмы расслоений, для которых коммутирует следующая диаграмма :

(Обратите внимание, что эта категория не абелева ; ядро ​​морфизма векторных расслоений, вообще говоря, не является векторным расслоением каким-либо естественным образом.)

Морфизм векторного расслоения между векторными расслоениями π ₁ : E ₁ → X ₁ и π ₂ : E ₂ → X ₂ , покрывающий отображение g из X ₁ в X ₂ , также можно рассматривать как морфизм векторного расслоения над X ₁ из E ₁ в X 2. расслоение обратных связей g * E ₂ .

Сечения и локально свободные пучки

Векторное расслоение над базой сечения . ${\displaystyle E}$ ${\displaystyle M}$ ${\displaystyle s}$

Карту, связывающую нормаль с каждой точкой поверхности, можно рассматривать как сечение. Поверхность — это пространство X , и в каждой точке x есть вектор векторного пространства, прикрепленный к точке x .

Учитывая векторное расслоение π : E → X и открытое подмножество U в X , мы можем рассматривать сечения π на U , т.е. непрерывные функции s : U → E , где композиция π  ∘  s такова, что ( π ∘ s )( u ) = ты для всех ты в U . По сути, секция непрерывно присваивает каждой точке U вектор из присоединенного векторного пространства. Например, сечения касательного расслоения дифференциального многообразия представляют собой не что иное, как векторные поля на этом многообразии.

Пусть F ( U ) — множество всех сечений на U. F ( U ) всегда содержит хотя бы один элемент, а именно нулевое сечение : функцию s , которая отображает каждый элемент x из U в нулевой элемент векторного пространства π ⁻¹ ({ x }). При поточечном сложении и скалярном умножении секций F ( U ) само становится реальным векторным пространством. Коллекция этих векторных пространств представляет собой пучок векторных пространств на X .

Если s — элемент F ( U ) и α: U → R — непрерывное отображение, то α s (поточечное скалярное умножение) находится в F ( U ). Мы видим, что F ( U ) — модуль над кольцом непрерывных вещественных функций на U. Более того, если O _X обозначает структурный пучок непрерывных вещественных функций на X , то F становится пучком O _X -модулей.

Не каждый пучок O _X -модулей возникает таким образом из векторного расслоения: возникают только локально свободные . (Причина: локально мы ищем сечения проекции ^U × Rk → U ; это как раз непрерывные функции U → Rk ^, а такая функция представляет собой k - кортеж непрерывных функций U → R. )

Более того: категория вещественных векторных расслоений на X эквивалентна категории локально свободных и конечно порожденных пучков O _X -модулей.

Таким образом, мы можем думать о категории вещественных векторных расслоений на X как о находящейся внутри категории пучков O _X -модулей ; эта последняя категория абелева, поэтому именно здесь мы можем вычислить ядра и коядра морфизмов векторных расслоений.

Векторное расслоение ранга n тривиально тогда и только тогда, когда оно имеет n линейно независимых глобальных секций.

Операции над векторными расслоениями

Большинство операций над векторными пространствами можно расширить до векторных расслоений, выполняя операции с векторным пространством послойно .

Например, если E — векторное расслоение над X , то существует расслоение E* над X , называемое двойственным расслоением , слой которого в точке x ∈ X является двойственным векторным пространством ( E _x )*. Формально E* можно определить как множество пар ( x , φ), где x ∈ X и φ ∈ ( E _x )*. Двойственное расслоение локально тривиально, поскольку двойственное пространство к обратному локальному тривиализации E является локальной тривиализацией E* : ключевым моментом здесь является то, что операция взятия двойственного векторного пространства является функториальной .

Существует множество функториальных операций, которые можно выполнять над парами векторных пространств (над одним и тем же полем), и они непосредственно распространяются на пары векторных расслоений E , F на X (над данным полем). Далее следует несколько примеров.

• Сумма Уитни (названная в честь Хасслера Уитни ) или расслоение прямой суммы E и F — это векторное расслоение E ⊕ F над X , слой которого над x является прямой суммой E _x ⊕ F _x векторных пространств E _x и F _x .
• Расслоение тензорных произведений E ⊗ F определяется аналогичным образом с использованием послойного тензорного произведения векторных пространств.
• Hom -расслоение Hom( E , F ) — это векторное расслоение, слой которого в точке x представляет собой пространство линейных отображений из E _x в F _x (которое часто обозначается Hom ( E _x , F _x ) или L ( E _x , F _Икс )). Hom-расслоение так называется (и полезно), потому что существует взаимно однозначное соответствие между гомоморфизмами векторного расслоения из E в F над X и сечениями Hom( E , F ) над X .
• Основываясь на предыдущем примере, учитывая сечение s расслоения эндоморфизмов Hom ( E , E ) и функцию f : X → R , можно построить собственное расслоение , взяв слой над точкой x ∈ X в качестве f ( x )- собственное пространство линейного отображения s ( x ): E _x → E _x . Хотя эта конструкция является естественной, если не принять меры, результирующий объект не будет иметь локальных тривиализаций. Рассмотрим случай, когда s является нулевой секцией, а f имеет изолированные нули. Слой над этими нулями в полученном «собственном расслоении» будет изоморфен слою над ними в E , тогда как везде слой представляет собой тривиальное 0-мерное векторное пространство.
• Двойственное векторное расслоение E* — это расслоение Hom( E , R × X ) гомоморфизмов расслоения E и тривиальное расслоение R × X. Существует канонический изоморфизм векторных расслоений Hom( E , F ) = E* ⊗ F.

Каждая из этих операций является частным примером общей особенности расслоений: многие операции, которые можно выполнить над категорией векторных пространств, также можно выполнить и над категорией векторных расслоений функториальным образом. Это уточняется на языке гладких функторов . Операцией иного характера является построение обратных связок . Учитывая векторное расслоение E → Y и непрерывное отображение f : X → Y , можно «вернуть» E к векторному расслоению f*E над X . Слой над точкой x ∈ X — это , по сути, просто слой над f ( x ) ∈ Y. Следовательно, суммирование Уитни E ⊕ F можно определить как расслоение обратного образа диагонального отображения из X в X × X , где расслоение над X × X есть E  ×  F .

Замечание : Пусть X — компакт . Любое векторное расслоение E над X является прямым слагаемым тривиального расслоения; т. е. существует расслоение E ' такое, что E ⊕ E ' тривиально. Это не работает, если X не компактно: например, тавтологическое линейное расслоение над бесконечным вещественным проективным пространством не обладает этим свойством. ^[1]

Дополнительные структуры и обобщения

Векторным расслоениям часто придается больше структуры. Например, векторные расслоения могут быть оснащены метрикой векторного расслоения . Обычно эта метрика должна быть положительно определенной , и в этом случае каждый слой E становится евклидовым пространством . Векторному расслоению с комплексной структурой соответствует комплексное векторное расслоение , которое также можно получить, заменив в определении вещественные векторные пространства на комплексные и потребовав, чтобы все отображения были комплексно-линейными в слоях. В более общем смысле, дополнительную структуру, налагаемую на векторное расслоение, обычно можно понять с точки зрения результирующего сокращения структурной группы расслоения . Также могут использоваться векторные расслоения над более общими топологическими полями .

Если вместо конечномерного векторного пространства взять слой F банаховым пространством , то получится банахово расслоение ^{. [2]} В частности, необходимо потребовать, чтобы локальные тривиализации были изоморфизмами банахова пространства (а не просто линейными изоморфизмами) на каждом из слоев и чтобы, кроме того, переходы

${\displaystyle g_{UV}\colon U\cap V\to \operatorname {GL} (F)}$

являются непрерывными отображениями банаховых многообразий . В соответствующей теории расслоений C ^p все отображения должны быть C ^p .

Векторные расслоения — это специальные расслоения , слои которых представляют собой векторные пространства и чей коцикл соблюдает структуру векторного пространства. Можно построить более общие пучки волокон, в которых волокно может иметь другую структуру; например, пучки сфер расслоены сферами.

Гладкие векторные расслоения

Регулярность функций перехода, описывающих векторное расслоение, определяет тип векторного расслоения. Если используются функции непрерывного перехода g _UV , результирующее векторное расслоение E будет только непрерывным, но не гладким. Если используются функции плавного перехода h _UV , то результирующее векторное расслоение F является гладким векторным расслоением.

Векторное расслоение ( E , p , M ) является гладким , если E и M — гладкие многообразия , p: E → M — гладкое отображение, а локальные тривиализации являются диффеоморфизмами . В зависимости от требуемой степени гладкости существуют различные соответствующие понятия C p -расслоений, бесконечно дифференцируемых C ^∞ -расслоений и вещественных аналитических C ^ω -расслоений. В этом разделе мы сосредоточимся на C ∞ -расслоениях. Наиболее важным примером C∞ - ^{векторного} расслоения является касательное расслоение ( TM , πTM , M ) C∞ ^- _{многообразия} M.

Гладкое векторное расслоение можно охарактеризовать тем, что оно допускает описанные выше функции перехода, которые являются гладкими функциями на перекрытиях тривиализирующих карт U и V . То есть векторное расслоение E является гладким, если оно допускает покрытие тривиализацией открытых множеств такое, что для любых двух таких множеств U и V функция перехода

${\displaystyle g_{UV}:U\cap V\to \operatorname {GL} (k,\mathbb {R} )}$

— гладкая функция в матричную группу GL(k, R ), которая является группой Ли .

Аналогично, если функции перехода:

• C ^r тогда векторное расслоение является векторным расслоением C ^r ,
• вещественно -аналитическое , то векторное расслоение является вещественно-аналитическим векторным расслоением (для этого требуется, чтобы группа матриц имела вещественную аналитическую структуру),
• голоморфно , то векторное расслоение является голоморфным векторным расслоением (для этого требуется, чтобы группа матриц была комплексной группой Ли ),
• алгебраические функции , то векторное расслоение является алгебраическим векторным расслоением (для этого требуется, чтобы группа матриц была алгебраической группой ).

C∞ ^- векторные расслоения ( E , p , M ) обладают очень важным свойством, которого нет у более общих C∞ - ^{расслоений} . А именно, касательное пространство T _v ( E _x ) в любой точке _v ∈ E x _{естественным} образом отождествляется с самим слоем Ex . Эта идентификация достигается с помощью вертикального подъема vl _v : E _x → T _v ( E _x ), определяемого как

${\displaystyle \operatorname {vl} _{v}w[f]:=\left.{\frac {d}{dt}}\right|_{t=0}f(v+tw),\quad f\in C^{\infty }(E_{x}).}$

Вертикальный лифт также можно рассматривать как естественный изоморфизм C ^∞ -векторного расслоения p*E → VE , где ( p*E , p*p , E ) — расслоение обратного образа ( E , p , M ) над E через p : E → M и VE  := Ker( p _* ) ⊂ TE — вертикальное касательное расслоение , естественное векторное подрасслоение касательного расслоения ( TE , π _TE , E ) полного пространства E.

Полное пространство E любого гладкого векторного расслоения содержит естественное векторное поле V _v  := vl _v v , известное как каноническое векторное поле . Более формально, V является гладким сечением ( TE , π _TE , E ), и его также можно определить как бесконечно малый генератор действия группы Ли , заданный послойным скалярным умножением. Каноническое векторное поле V полностью характеризует гладкую структуру векторного расслоения следующим образом. Для подготовки отметим, что когда X — гладкое векторное поле на гладком многообразии M и x ∈ M такое, что X _x = 0, линейное отображение ${\displaystyle (t,v)\mapsto e^{tv}}$

${\displaystyle C_{x}(X):T_{x}M\to T_{x}M;\quad C_{x}(X)Y=(\nabla _{Y}X)_{x}}$

не зависит от выбора линейной ковариантной производной ∇ на M . Каноническое векторное поле V на E удовлетворяет аксиомам

1. Поток ( t , v ) → Φ ^t _V ( v ) V определен глобально.
2. Для каждого v ∈ V существует единственный lim _t→∞ Φ ^t _V ( v ) ∈ V .
3. C _v ( V )∘ C _v ( V ) = C _v ( V ) всякий раз, когда V _v = 0.
4. Нулевое множество V — это гладкое подмногообразие E , коразмерность которого равна рангу C _v ( V ).

И наоборот, если E — любое гладкое многообразие, а V — гладкое векторное поле на E , удовлетворяющее условиям 1–4, то на E существует уникальная структура векторного расслоения, каноническим векторным полем которого является V .

Для любого гладкого векторного расслоения ( E , p , M ) общее пространство TE его касательного расслоения ( TE , π _TE , E ) имеет естественную вторичную структуру векторного расслоения ( TE , p _* , TM ), где p _* - это толчок -вперед канонической проекции p : E → M . Операции с векторным расслоением в этой вторичной структуре векторного расслоения — это продвижение вперед + _* : T ( E × E ) → TE и λ _* : TE → TE исходного сложения +: E × E → E и скалярное умножение λ: E → Э.​

К-теория

Группа K-теории K ( X ) компактного топологического пространства Хаусдорфа определяется как абелева группа , порожденная классами изоморфизма [ E ] комплексных векторных расслоений по модулю отношения , которое всякий раз, когда у нас есть точная последовательность

$${\displaystyle 0\to A\to B\to C\to 0,}$$

$${\displaystyle [B]=[A]+[C]}$$

топологической К-теорииКО-теориякомпактными носителями

Знаменитая теорема периодичности Рауля Ботта утверждает , что K-теория любого пространства X изоморфна теории S ² X , двойной надстройки X.

В алгебраической геометрии рассматриваются группы К-теории, состоящие из когерентных пучков на схеме X , а также группы К-теории векторных расслоений на схеме с указанным выше отношением эквивалентности . Эти две конструкции одинаковы при условии, что лежащая в их основе схема является гладкой .

Смотрите также

Общие понятия

• Грассманиан : классифицирующие пространства для векторных расслоений, среди которых проективные пространства для линейных расслоений.
• Класс характеристики
• Принцип разделения
• Стабильный пакет

Топология и дифференциальная геометрия

• Соединение : понятие, необходимое для дифференциации участков векторных расслоений.
• Калибровочная теория : общее исследование связей векторных расслоений и главных расслоений и их связи с физикой.

Алгебраическая и аналитическая геометрия

• Алгебраическое векторное расслоение
• Группа Пикарда
• Голоморфное векторное расслоение

Примечания

1. Хэтчер 2003, пример 3.6.
2. Ланг 1995.

Источники

• Авраам, Ральф Х .; Марсден, Джерролд Э. (1978), Основы механики , Лондон: Бенджамин-Каммингс, см. раздел 1.5, ISBN. 978-0-8053-0102-1.
• Хэтчер, Аллен (2003), Векторные расслоения и K-теория (изд. 2.0).
• Йост, Юрген (2002), Риманова геометрия и геометрический анализ (3-е изд.), Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-3-540-42627-1, см. раздел 1.5.
• Ланг, Серж (1995), Дифференциальные и римановы многообразия , Берлин, Нью-Йорк: Springer-Verlag , ISBN 978-0-387-94338-1.
• Ли, Джеффри М. (2009), Многообразия и дифференциальная геометрия, Аспирантура по математике , том. 107, Провиденс: Американское математическое общество, ISBN. 978-0-8218-4815-9.
• Ли, Джон М. (2003), Введение в гладкие многообразия, Нью-Йорк: Springer, ISBN 0-387-95448-1см. гл.5
• Рубей, Елена (2014), Алгебраическая геометрия, краткий словарь , Берлин/Бостон: Уолтер Де Грюйтер, ISBN 978-3-11-031622-3.

Внешние ссылки

• «Векторное расслоение», Математическая энциклопедия , EMS Press , 2001 [1994]
• Почему полезно изучать векторные расслоения? на MathOverflow
• Почему полезно классифицировать векторные расслоения пространства?