Полное внутреннее отражение

В физике полное внутреннее отражение ( ПВО ) — это явление, при котором волны , приходящие на границу раздела (из одной среды в другую) (например, из воды в воздух), не преломляются во вторую («внешнюю») среду, а полностью отражаются обратно в первую («внутреннюю») среду. Это происходит, когда вторая среда имеет более высокую скорость волны (т. е. более низкий показатель преломления ), чем первая, и волны падают под достаточно косым углом на границу раздела. Например, поверхность вода-воздух в типичном аквариуме, если смотреть на нее наклонно снизу, отражает подводную сцену как зеркало без потери яркости (рис. 1).

Полное внутреннее отражение происходит не только с электромагнитными волнами, такими как свет и микроволны , но и с другими типами волн, включая звуковые и водные волны . Если волны способны образовывать узкий пучок (рис. 2), отражение, как правило, описывается в терминах « лучей », а не волн; в среде, свойства которой не зависят от направления, такой как воздух, вода или стекло , «лучи» перпендикулярны связанным волновым фронтам . Полное внутреннее отражение происходит, когда превышается критический угол.

Преломление обычно сопровождается частичным отражением. Когда волны преломляются из среды с меньшей скоростью распространения (с большим показателем преломления ) в среду с большей скоростью распространения (с меньшим показателем преломления) — например, из воды в воздух — угол преломления (между исходящим лучом и нормалью к поверхности ) больше угла падения (между входящим лучом и нормалью). Когда угол падения приближается к определенному порогу, называемому критическим углом , угол преломления приближается к 90°, при котором преломленный луч становится параллельным граничной поверхности. Когда угол падения увеличивается сверх критического угла, условия преломления больше не могут быть выполнены, поэтому преломленный луч отсутствует, и частичное отражение становится полным. Для видимого света критический угол составляет около 49° для падения из воды в воздух и около 42° для падения из обычного стекла в воздух.

Детали механизма ПВО порождают более тонкие явления. В то время как полное отражение, по определению, не подразумевает непрерывного потока мощности через границу раздела между двумя средами, внешняя среда переносит так называемую затухающую волну , которая распространяется вдоль границы раздела с амплитудой, которая экспоненциально убывает с расстоянием от границы раздела. «Полное» отражение действительно является полным, если внешняя среда без потерь (совершенно прозрачна), непрерывна и имеет бесконечную протяженность, но может быть заметно меньше полного, если затухающая волна поглощается внешней средой с потерями (« ослабленное полное отражение ») или отклоняется внешней границей внешней среды или объектами, встроенными в эту среду («разбитое» ПВО). В отличие от частичного отражения между прозрачными средами, полное внутреннее отражение сопровождается нетривиальным сдвигом фазы (не просто нулем или 180°) для каждого компонента поляризации (перпендикулярного или параллельного плоскости падения ), и сдвиги изменяются в зависимости от угла падения. Объяснение этого эффекта Огюстеном Жаном Френелем в 1823 году пополнило ряд доказательств в пользу волновой теории света .

Фазовые сдвиги используются изобретением Френеля, ромбом Френеля , для изменения поляризации. Эффективность полного внутреннего отражения используется оптическими волокнами (используемыми в телекоммуникационных кабелях и в фиброскопах, формирующих изображения ), а также отражающими призмами , такими как призмы Порро / крыши, восстанавливающие изображение для монокуляров и биноклей .

Оптическое описание

Хотя полное внутреннее отражение может происходить с любым типом волны, о котором можно сказать, что оно падает под углом, включая (например) микроволны ^[1] и звуковые волны ^[2] , оно наиболее известно в случае световых волн.

Полное внутреннее отражение света можно продемонстрировать с помощью полукругло-цилиндрического блока обычного стекла или акрилового стекла. На рис. 3 «лучевой ящик» проецирует узкий луч света (« луч ») радиально внутрь. Полукруглое поперечное сечение стекла позволяет входящему лучу оставаться перпендикулярным к изогнутой части поверхности воздух/стекло, а затем продолжать движение по прямой линии к плоской части поверхности, хотя его угол с плоской частью меняется.

Там, где луч встречает плоскую границу раздела стекло-воздух, угол между лучом и нормалью (перпендикуляром) к границе раздела называется углом падения . ^[3] Если этот угол достаточно мал, луч частично отражается, но в основном передается, а переданная часть преломляется от нормали, так что угол преломления (между преломленным лучом и нормалью к границе раздела) больше угла падения. На данный момент обозначим угол падения θ _i , а угол преломления θ _t (где t обозначает переданный , оставляя r для отраженного ). По мере того, как θ _i увеличивается и приближается к определенному «критическому углу», обозначаемому θ _c (или иногда θ _cr ), угол преломления приближается к 90° (то есть преломленный луч приближается к касательной к границе раздела), и преломленный луч становится слабее, в то время как отраженный луч становится ярче. ^[4] Когда θ _i превышает θ _c , преломленный луч исчезает и остается только отраженный луч, так что вся энергия падающего луча отражается; это полное внутреннее отражение (ПВО). Вкратце:

Если θ _i < θ _c ‍ , падающий луч расщепляется, частично отражаясь и частично преломляясь;
Если θ _i > θ _c ‍ , падающий луч испытывает полное внутреннее отражение (ПВО); никакая его часть не пропускается.

Критический угол

Критический угол — это наименьший угол падения, который дает полное отражение, или, что эквивалентно, наибольший угол, для которого существует преломленный луч. ^[5] Для световых волн, падающих из «внутренней» среды с одним показателем преломления $n 1$ , ‍ во «внешнюю» среду с одним показателем преломления $n 2$ , ‍ критический угол задается как ‍ и определяется, если $‍ n$ $2$ $\leq$ $n$ $1$ . Для некоторых других типов волн удобнее мыслить в терминах скоростей распространения, а не показателей преломления. Объяснение критического угла в терминах скоростей является более общим и поэтому будет рассмотрено в первую очередь. $\theta _{{\text{c}}\!}=\arcsin(n_{2}/n_{1})\,,$

Когда волновой фронт преломляется из одной среды в другую, падающая (входящая) и преломленная (исходящая) части волнового фронта встречаются на общей линии на преломляющей поверхности (интерфейсе). Пусть эта линия, обозначенная L , движется со скоростью $u$ по поверхности, ^[6]^[7] где $u$ измеряется перпендикулярно L ‍ ( рис. 4). Пусть падающий и преломленный волновые фронты распространяются с нормальными скоростями и (соответственно), и пусть они образуют двугранные углы θ ₁ и θ ₂ (соответственно) с интерфейсом. Из геометрии ‍ является компонентой $u$ в направлении, нормальном к падающей волне, так что ‍ Аналогично , ‍ Решая каждое уравнение относительно $1/$ $u$ и приравнивая результаты, получаем общий закон преломления волн: $v_{1}$ $v_{2}$ $v_{1}$ $v_{1\!}=u\sin \theta _{1}\,.$ $v_{2}=u\sin \theta _{2}\,.$

Но двугранный угол между двумя плоскостями также является углом между их нормалями. Таким образом, θ ₁ — это угол между нормалью к падающему волновому фронту и нормалью к границе раздела, в то время как θ ₂ — это угол между нормалью к преломленному волновому фронту и нормалью к границе раздела; и уравнение ( 1 ) говорит нам, что синусы этих углов находятся в том же отношении, что и соответствующие скорости. ^[8]

Этот результат имеет форму « закона Снеллиуса », за исключением того, что мы еще не сказали, что отношение скоростей постоянно, и не отождествили θ ₁ и θ ₂ с углами падения и преломления (названными выше θ _i и θ _t ). Однако, если мы теперь предположим, что свойства среды изотропны (независимы от направления), то отсюда следуют два дополнительных вывода: во-первых, две скорости, а следовательно, и их отношение, не зависят от их направлений; и, во-вторых, направления нормали волны совпадают с направлениями лучей , так что θ ₁ и θ ₂ совпадают с углами падения и преломления, как определено выше. ^{[Примечание 1]}

Очевидно, что угол преломления не может превышать 90°. В предельном случае мы положим $‍ θ$ $2$ $= 90°$ и $‍ θ$ $1$ $=$ $θ$ $c$ ‍ в уравнении ( 1 ) и решим для критического угла:

При выводе этого результата мы сохраняем предположение об изотропности среды, чтобы отождествить θ ₁ и θ ₂ с углами падения и преломления. ^{[Примечание 3]}

Для электромагнитных волн , и особенно для света, принято выражать вышеприведенные результаты в терминах показателей преломления . Показатель преломления среды с нормальной скоростью определяется как ‍ где c — скорость света в вакууме. ^[9] Следовательно ‍ Аналогично , ‍ Сделав эти замены в уравнениях ( 1 ) и ( 2 ), получаем $v_{1}$ $n_{1\!}=c/v_{1}\,,$ $v_{1\!}=c/n_{1}\,.$ $v_{2}=c/n_{2}\,.$

Уравнение ( 3 ) представляет собой закон преломления для обычных сред в терминах показателей преломления, при условии, что θ ₁ и θ ₂ берутся как двугранные углы; но если среды изотропны , то $n 1$ и $n 2$ становятся независимыми от направления, в то время как θ ₁ и θ ₂ могут быть приняты как углы падения и преломления для лучей, и уравнение (4 ) следует. Таким образом, для изотропных сред уравнения ( 3 ) и ( 4 ) вместе описывают поведение на рис. 5.

Согласно уравнению ( 4 ), для падения из воды ( $n 1 \approx 1,333$ ) в воздух ( $n 2 \approx 1$ ) имеем $θ$ $c$ $\approx 48,6°$ , тогда как для падения из обычного стекла или акрила ( $n$ $1$ $\approx 1,50$ ) в воздух ( $n$ $2$ $\approx 1$ ) имеем $θ$ $c$ $\approx 41,8°$ .

Функция arcsin, дающая θ _c, определена только если $‍ n$ $2$ $\leq$ $n$ $1$ Следовательно, для изотропных сред полное внутреннее отражение не может произойти, если вторая среда имеет более высокий показатель преломления (меньшую нормальную скорость), чем первая. Например, не может быть TIR для падения из воздуха в воду; вместо этого критический угол для падения из воды в воздух ‍ является углом преломления при скользящем падении из воздуха в воду (рис. 6). ^[10] $(v_{2}\geq v_{1})\,.$

Среду с более высоким показателем преломления обычно называют оптически более плотной , а среду с более низким показателем преломления — оптически более разреженной . ^[11] Поэтому говорят, что полное внутреннее отражение возможно при падении «от плотной к редкой», но не при падении «от редкой к плотной».

Примеры из повседневной жизни

Если стоять около аквариума, опустив глаза ниже уровня воды, можно увидеть рыбу или подводные предметы, отраженные на поверхности воды и воздуха (рис. 1). Яркость отраженного изображения — такая же яркая, как и «прямой» вид — может быть поразительной.

Похожий эффект можно наблюдать, открыв глаза во время плавания прямо под поверхностью воды. Если вода спокойна, поверхность за пределами критического угла (измеренного от вертикали) кажется зеркальной, отражающей объекты ниже. Область над водой не может быть видна, кроме как сверху, где полусферическое поле зрения сжимается в коническое поле, известное как окно Снеллиуса , угловой диаметр которого в два раза больше критического угла (ср. рис. 6). ^[12] Поле зрения над водой теоретически составляет 180° по ширине, но кажется меньше, потому что по мере приближения к горизонту вертикальное измерение сильнее сжимается рефракцией; например, по уравнению. ( 3 ), для углов падения воздуха на воду 90°, 80° и 70° соответствующие углы преломления составляют 48,6° ( θ _cr на рис. 6), 47,6° и 44,8°, что указывает на то, что изображение точки, расположенной на 20° выше горизонта, находится на расстоянии 3,8° от края окна Снеллиуса, тогда как изображение точки, расположенной на 10° выше горизонта, находится всего в 1° от края. ^[13]

Рис. 7, например, представляет собой фотографию, сделанную около дна мелководного конца бассейна. То, что выглядит как широкая горизонтальная полоса на правой стене, состоит из нижних краев ряда оранжевых плиток и их отражений; это отмечает уровень воды, который затем можно проследить по другой стене. Пловец потревожил поверхность над собой, задев нижнюю половину своего отражения и исказив отражение лестницы (справа). Но большая часть поверхности все еще спокойна, давая четкое отражение плиточного дна бассейна. Пространство над водой не видно, за исключением верхней части кадра, где ручки лестницы едва различимы над краем окна Снелла — внутри которого отражение дна бассейна лишь частичное, но все же заметно на фотографии. Можно даже различить цветную окантовку края окна Снелла из-за изменения показателя преломления, следовательно, критического угла, с длиной волны (см. Дисперсия ).

Рис. 8 : Круглый бриллиант огранки «бриллиант »

Критический угол влияет на углы, под которыми ограняются драгоценные камни . Круглая « бриллиантовая » огранка, например, предназначена для преломления света, падающего на передние грани, отражения его дважды с помощью ПВО от задних граней и передачи его снова через передние грани, так что камень выглядит ярким. Алмаз (рис. 8) особенно подходит для этой обработки, поскольку его высокий показатель преломления (около 2,42) и, следовательно, малый критический угол (около 24,5°) обеспечивают желаемое поведение в широком диапазоне углов обзора. ^[14] Более дешевые материалы, которые также поддаются этой обработке, включают кубический цирконий (показатель ≈ 2,15) и муассанит (неизотропный, следовательно, дважды преломляющий , с показателем в диапазоне от около 2,65 до 2,69, ^{[Примечание 4]} в зависимости от направления и поляризации); поэтому оба они популярны в качестве имитаторов алмаза .

Мимолетная волна

Математически волны описываются в терминах изменяющихся во времени полей , где «поле» является функцией местоположения в пространстве. Распространяющаяся волна требует поля «усилия» и поля «потока», причем последнее является вектором ( если мы работаем в двух или трех измерениях). Произведение усилия и потока связано с мощностью (см. Эквивалентность систем ). Например, для звуковых волн в невязкой жидкости мы могли бы взять поле усилия как давление (скаляр), а поле потока как скорость жидкости (вектор). Произведение этих двух величин есть интенсивность (мощность на единицу площади). ^[15]^{[Примечание 5]} Для электромагнитных волн мы будем брать поле усилия как электрическое поле $E,$ а поле потока как намагничивающее поле $H.$ Оба они являются векторами, и их векторное произведение снова есть интенсивность (см. Вектор Пойнтинга ). ^[16]

Когда волна в (скажем) среде 1 отражается от границы раздела между средой 1 и средой 2, поле потока в среде 1 представляет собой векторную сумму полей потока, обусловленных падающей и отраженной волнами. ^{[Примечание 6]} Если отражение наклонное, падающее и отраженное поля не находятся в противоположных направлениях и, следовательно, не могут компенсироваться на границе раздела; даже если отражение полное, либо нормальная составляющая, либо тангенциальная составляющая объединенного поля (как функция местоположения и времени) должны быть ненулевыми рядом с границей раздела. Более того, физические законы, управляющие полями, обычно подразумевают, что одна из двух компонент непрерывна поперек границы раздела (то есть она не меняется внезапно, когда мы пересекаем границу); например, для электромагнитных волн одним из условий границы раздела является то, что тангенциальная составляющая $H$ непрерывна, если нет поверхностного тока. ^[17] Следовательно, даже если отражение полное, должно быть некоторое проникновение поля потока в среду 2; и это, в сочетании с законами, связывающими поля усилия и потока, подразумевает, что также будет некоторое проникновение поля усилия. То же самое условие непрерывности подразумевает, что изменение («волнистость») поля в среде 2 будет синхронизировано с изменением падающих и отраженных волн в среде 1.

Но если отражение полное, то пространственное проникновение полей в среду 2 должно быть каким-то образом ограничено, иначе общая протяженность и, следовательно, общая энергия этих полей будут продолжать увеличиваться, высасывая энергию из среды 1. Полное отражение продолжающегося волнового поезда позволяет сохранять некоторую энергию в среде 2, но не позволяет осуществлять непрерывную передачу энергии из среды 1 в среду 2.

Таким образом, используя в основном качественные рассуждения, можно заключить, что полное внутреннее отражение должно сопровождаться волнообразным полем во «внешней» среде, распространяющимся вдоль границы синхронно с падающей и отраженной волнами, но с некоторым ограниченным пространственным проникновением во «внешнюю» среду; такое поле можно назвать затухающей волной .

Рис. 9 показывает основную идею. Предполагается, что падающая волна плоская и синусоидальная . Отраженная волна для простоты не показана. Затухающая волна движется вправо в ногу с падающей и отраженной волнами, но ее амплитуда падает с увеличением расстояния от интерфейса.

(Две особенности затухающей волны на рис. 9 будут объяснены позже: во-первых, гребни затухающей волны перпендикулярны границе раздела; и, во-вторых, затухающая волна немного опережает падающую волну.)

Нарушенное полное внутреннее отражение (FTIR)

Если внутреннее отражение должно быть полным, не должно быть никакого отклонения затухающей волны. Предположим, например, что электромагнитные волны, падающие из стекла (с более высоким показателем преломления) в воздух (с более низким показателем преломления) под определенным углом падения, подвергаются ПВО. И предположим, что у нас есть третья среда (часто идентичная первой), показатель преломления которой достаточно высок, чтобы, если бы третья среда заменила вторую, мы получили стандартный переданный волновой поезд для того же угла падения. Затем, если третья среда находится на расстоянии нескольких длин волн от поверхности первой среды, где затухающая волна имеет значительную амплитуду во второй среде, то затухающая волна эффективно преломляется в третью среду, давая ненулевую передачу в третью среду и, следовательно, меньшее, чем полное отражение обратно в первую среду. ^[18] Поскольку амплитуда затухающей волны затухает через воздушный зазор, переданные волны ослабляются , так что передача меньше, а следовательно, больше отражение, чем было бы без зазора; но пока есть некоторая передача, отражение меньше полного. Это явление называется нарушенным полным внутренним отражением (где «не нарушенное» отрицает «полное»), сокращенно «не нарушенное ПВО» или «FTIR».

Разочарованное ПВО можно наблюдать, глядя на верхнюю часть стакана с водой, который держат в руке (рис. 10). Если стакан держать свободно, контакт может быть недостаточно близким и широким, чтобы произвести заметный эффект. Но если держать его более плотно, гребни отпечатков пальцев будут сильно взаимодействовать с исчезающими волнами, позволяя гребням быть видимыми через в противном случае полностью отражающую поверхность стекло-воздух. ^[19]

Тот же эффект можно продемонстрировать с помощью микроволн, используя парафин в качестве «внутренней» среды (где существуют падающие и отраженные волны). В этом случае допустимая ширина зазора может быть (например) 1 см или несколько см, что легко наблюдать и регулировать. ^[1]^[20]

Термин фрустрированное ПВО также применяется к случаю, когда затухающая волна рассеивается объектом, достаточно близким к отражающему интерфейсу. Этот эффект, вместе с сильной зависимостью количества рассеянного света от расстояния от интерфейса, используется в микроскопии полного внутреннего отражения . ^[21]

Механизм FTIR называется связью затухающих волн и является хорошим аналогом для визуализации квантового туннелирования . ^[22] Из-за волновой природы материи электрон имеет ненулевую вероятность «туннелирования» через барьер, даже если классическая механика скажет, что его энергии недостаточно. ^[18]^[19] Аналогично, из-за волновой природы света фотон имеет ненулевую вероятность пересечения щели, даже если лучевая оптика скажет, что его приближение слишком наклонное.

Другая причина, по которой внутреннее отражение может быть меньше полного, даже за пределами критического угла, заключается в том, что внешняя среда может быть «потеряющей» (менее идеально прозрачной), в этом случае внешняя среда будет поглощать энергию из затухающей волны, так что поддержание затухающей волны будет черпать энергию из падающей волны. Последующее отражение меньше полного называется ослабленным полным отражением (НПВО). Этот эффект, и особенно зависимость поглощения от частоты, можно использовать для изучения состава неизвестной внешней среды. ^[23]

Вывод затухающей волны

В однородной плоской синусоидальной электромагнитной волне электрическое поле $E$ имеет вид

где $E k$ — (постоянный) комплексный амплитудный вектор, $i$ — мнимая единица , $k$ — волновой вектор (величина которого $k$ — угловое волновое число ), $r$ — вектор положения , ω — угловая частота , $t$ — время, и подразумевается, что действительная часть выражения — это физическое поле. ^{[Примечание 7]} Намагничивающее поле $H$ имеет ту же форму с теми же $k$ и ω . Значение выражения не меняется, если положение $r$ изменяется в направлении, нормальном к $k$ ; следовательно, $k$ перпендикулярно волновым фронтам .

Если ℓ — компонент $r$ в направлении $k ‍ ,$ ‍ поле ( 5 ) можно записать Если аргумент должен быть постоянным, ℓ должен увеличиваться со скоростью ‍ , известной как фазовая скорость . ^[24] Это, в свою очередь, равно где $c$ — фазовая скорость в эталонной среде (принятой за вакуум), а $n$ — локальный показатель преломления относительно эталонной среды. Решение относительно $k$ дает ‍ , т.е. $\mathbf {E_{k}} e^{i(k\ell -\omega t)}\,.$ $e^{i(\cdots )}$ $\omega /k\,,\,$ $c/n\,,\,$ $k=n\omega /c\,,\,$

где - волновое число в вакууме. ^[25]^{[Примечание 8]} $\,k_{0}=\omega /c\,$

Из ( 5 ) электрическое поле во «внешней» среде имеет вид

где $k t$ — волновой вектор для прошедшей волны (мы предполагаем изотропную среду, но прошедшая волна пока не считается затухающей).

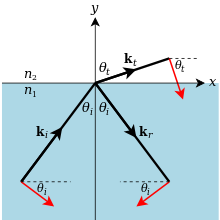
В декартовых координатах $(x, y, z)$ пусть область $y$ $< 0$ имеет показатель преломления $n$ $1$ $,$ , а область $y$ $> 0$ имеет показатель преломления $n$ $2$ . Тогда плоскость $xz$ является границей раздела, а ось $y$ перпендикулярна границе раздела (рис. 11). Пусть $i$ и $j$ (жирным римским шрифтом ) будут единичными векторами в направлениях $x$ и $y$ соответственно. Пусть плоскость падения (содержащая нормаль падающей волны и нормаль к границе раздела) будет плоскостью $xy$ (плоскостью страницы) с углом падения θ _{i ,} измеренным от $j$ к $i$ . Пусть угол преломления, измеренный в том же направлении, будет θ _t ( t для прошедшего , оставляя r для отраженного ).

Из ( 6 ) переданный волновой вектор $k t$ имеет величину $n 2 k 0$ . Следовательно, из геометрии, где последний шаг использует закон Снеллиуса. Взяв скалярное произведение с вектором положения, мы получаем так, что уравнение ( 7 ) становится $\mathbf {k} _{\text{t}}=n_{2}k_{0}(\mathbf {i} \sin \theta _{\text{t}}+\mathbf {j} \cos \theta _{\text{t}})=k_{0}(\mathbf {i} \,n_{1}\sin \theta _{\text{i}}+\mathbf {j} \,n_{2}\cos \theta _{\text{t}})\,,$ $\mathbf {k} _{\text{t}}\mathbf {\cdot r} =k_{0}(n_{1}x\sin \theta _{\text{i}}+n_{2}y\cos \theta _{\text{t}})\,,$

В случае ПВО угол θ _t не существует в обычном смысле. Но мы все еще можем интерпретировать ( 8 ) для переданной (затухающей) волны, допуская, чтобы $cos θ t$ был комплексным . Это становится необходимым, когда мы записываем $cos θ t$ через $sin θ t ‍ ,$ ‍ и, следовательно, через $sin θ i ,$ используя закон Снеллиуса: Для θ _i больше критического угла значение под символом квадратного корня отрицательно, так что ^[26] $\cos \theta _{\text{t}}={\sqrt {1-\sin ^{2}\theta _{\text{t}}}}={\sqrt {1-(n_{1}/n_{2})^{2}\sin ^{2}\theta _{\text{i}}}}\,.$

Чтобы определить, какой знак применим, подставим ( 9 ) в ( 8 ), получив

где неопределенный знак противоположен знаку в ( 9 ). Для затухающей прошедшей волны – то есть той, амплитуда которой затухает с ростом $y$ – неопределенный знак в ( 10 ) должен быть минусом , поэтому неопределенный знак в ( 9 ) должен быть плюсом . ^{[Примечание 9]}

При правильном знаке результат ( 10 ) можно сократить

где

а $k 0$ — волновое число в вакууме, т.е. $\,\omega /c\,.$

Таким образом, затухающая волна представляет собой плоскую синусоиду, движущуюся в направлении $x$ , с амплитудой, которая экспоненциально затухает в направлении $y$ (ср. рис. 9). Очевидно, что энергия, запасенная в этой волне, также движется в направлении $x$ и не пересекает границу раздела. Следовательно, вектор Пойнтинга обычно имеет компонент в направлении $x$ , но его компонент $y$ в среднем равен нулю (хотя его мгновенный компонент $y$ не является тождественно нулем). ^[27]^[28]

Уравнение ( 11 ) показывает, что амплитуда затухающей волны падает в $e$ раз по мере того, как координата $y$ (измеренная от интерфейса) увеличивается на расстояние, обычно называемое «глубиной проникновения» затухающей волны. ^[29] Взяв обратные величины первого уравнения ( 12 ), мы находим, что глубина проникновения равна ^[28] где λ ₀ — длина волны в вакууме, т.е. ^[30] Разделив числитель и знаменатель на $n$ $2$ , получаем где — длина волны во второй (внешней) среде. Следовательно, мы можем построить график $d$ в единицах λ ₂ , как функцию угла падения, для различных значений (рис. 12). Когда θ _i уменьшается в направлении критического угла, знаменатель приближается к нулю, так что $d$ неограниченно увеличивается — как и следовало ожидать, потому что как только θ _i становится меньше критического, во внешней среде допускаются однородные плоские волны. Когда θ _i приближается к 90° (скользящее падение), $d$ приближается к минимуму. При падении из воды в воздух или из обычного стекла в воздух $d$ $min$ не сильно отличается от ⁠ $d=1/\kappa \,,\,$ $d={\frac {\lambda _{0}}{2\pi \,{\sqrt {n_{1}^{2}\sin ^{2}\theta _{\text{i}}\,-\,n_{2}^{2}}}}}~,$ $\,2\pi /k_{0}\,.$ $d={\frac {\lambda _{2}}{2\pi \,{\sqrt {(n_{1}/n_{2})^{2}\sin ^{2}\theta _{\text{i}}\,-\,1}}}}~,$ $\,\lambda _{2}=\lambda _{0}/n_{2}\,$ $n_{1}/n_{2\,}$ $d_{\text{min}}={\frac {\lambda _{2}}{2\pi \,{\sqrt {(n_{1}/n_{2})^{2}-1}}}}~.$ λ2/2π⁠ . Но $d$ больше при меньших углах падения (рис. 12), и амплитуда все еще может быть значительной на расстояниях в несколько раз больше $d$ ; например, поскольку $e -4,6$ чуть больше 0,01, амплитуда затухающей волны на расстоянии $4,6 ‍ d$ от интерфейса составляет по крайней мере 1% от ее значения на интерфейсе. Поэтому, говоря вольно, мы склонны говорить, что амплитуда затухающей волны значительна в пределах «нескольких длин волн» от интерфейса.

Фазовые сдвиги

Между 1817 и 1823 годами Огюстен-Жан Френель обнаружил, что полное внутреннее отражение сопровождается нетривиальным сдвигом фазы (то есть сдвигом фазы, который не ограничивается 0° или 180°), поскольку коэффициент отражения Френеля приобретает ненулевую мнимую часть . ^[31] Теперь мы объясним этот эффект для электромагнитных волн в случае линейных , однородных , изотропных, немагнитных сред. Сдвиг фазы оказывается опережением , которое растет с увеличением угла падения за пределами критического угла, но которое зависит от поляризации падающей волны.

В уравнениях ( 5 ), ( 7 ), ( 8 ), ( 10 ) и ( 11 ) мы сдвигаем фазу на угол ϕ, если заменяем $ωt$ на $ωt+ϕ$ (то есть, если заменяем $-ωt$ на $-ωt-ϕ$ ), в результате чего (комплексное) поле умножается на $e -iϕ$ . Таким образом, сдвиг фазы эквивалентен умножению на комплексную константу с отрицательным аргументом . Это становится более очевидным, когда (например) поле ( 5 ) факторизуется как , где последний множитель содержит зависимость от времени. ^{[Примечание 10]} $\mathbf {E_{k}} e^{i\mathbf {k\cdot r} }e^{-i\omega t},\,$

Чтобы представить поляризацию падающей, отраженной или прошедшей волны, электрическое поле, прилегающее к интерфейсу, можно разложить на две перпендикулярные компоненты, известные как компоненты s и p , которые параллельны поверхности и плоскости падения соответственно; другими словами, компоненты s и p соответственно квадратны и параллельны плоскости падения. ^{[Примечание 11]}

Для каждого компонента поляризации падающее, отраженное или прошедшее электрическое поле ( $E$ в уравнении ( 5 ) ) имеет определенное направление и может быть представлено его (комплексным) скалярным компонентом в этом направлении. Коэффициент отражения или прохождения затем может быть определен как отношение комплексных компонентов в одной и той же точке или в бесконечно малых точках по разные стороны интерфейса. Но для того, чтобы зафиксировать знаки коэффициентов, мы должны выбрать положительные значения для «направлений». Для компонентов s очевидным выбором является утверждение, что положительные направления падающего, отраженного и прошедшего полей все одинаковы (например, направление $z$ на рис. 11). Для компонентов p в этой статье принято соглашение, что положительные направления падающего, отраженного и прошедшего полей наклонены к одной и той же среде (то есть к одной и той же стороне интерфейса, например, как красные стрелки на рис. 11). ^{[Примечание 12]} Но читатель должен быть предупрежден, что в некоторых книгах используются разные соглашения для компонентов p , что приводит к разным знакам в результирующей формуле для коэффициента отражения. ^[32]

Для s -поляризации пусть коэффициенты отражения и пропускания будут $r s$ и $t s$ соответственно. Для p -поляризации пусть соответствующие коэффициенты будут $r p$ и $t p$ . Тогда для линейных , однородных , изотропных, немагнитных сред коэффициенты будут иметь вид: ^[33]

(Для вывода вышеизложенного см. уравнения Френеля § Теория .)

Теперь предположим, что прошедшая волна является эванесцентной. С правильным знаком (+), подстановка ( 9 ) в ( 13 ) дает где то есть, $n$ - индекс "внутренней" среды относительно "внешней" или индекс внутренней среды, если внешняя - вакуум. ^{[Примечание 13]} Таким образом, величина $r$ $s$ равна 1, а аргумент r $s$ равен $что дает$ сдвиг фазы на ‍ [^34] $r_{s}=\,{\frac {n\cos \theta _{\text{i}}-i{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{n\cos \theta _{\text{i}}+i{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}}\,,$ $n=n_{1}/n_{2}\,;$ $-2\arctan {\frac {\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}{n\cos \theta _{\text{i}}}}\,,$

Сделав ту же замену в ( 14 ), мы находим, что $t s$ имеет тот же знаменатель, что и $r s ,$ с положительным действительным числителем (вместо комплексно-сопряженного числителя) и, следовательно, имеет половину аргумента $r s ‍ ,$ ‍ так что фазовый сдвиг затухающей волны вдвое меньше, чем у отраженной волны .

При том же выборе знака ^{[Примечание 14]} подстановка ( 9 ) в ( 15 ) дает величину , равную 1, а аргумент которой равен , что дает сдвиг фазы на ‍ [^34] $r_{p}=\,{\frac {\cos \theta _{\text{i}}-in{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{\cos \theta _{\text{i}}+in{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}}\,,$ $-2\arctan {\frac {\,n{\sqrt {n^{2}\sin ^{2}\theta _{\text{i}}-1}}}{\cos \theta _{\text{i}}}}\,,$

Сделав ту же замену в ( 16 ), мы снова обнаруживаем, что фазовый сдвиг затухающей волны составляет половину от такового у отраженной волны.

Уравнения ( 17 ) и ( 18 ) применяются, когда $‍ θ$ $c$ $\leq$ $θ$ $i$ $< 90°,$ где θ _i — угол падения, а θ _c — критический угол ‍ arcsin $(1/$ $n$ $)$ . Эти уравнения показывают, что

каждое опережение фазы равно нулю при критическом угле (для которого числитель равен нулю);
каждое фазовое продвижение приближается к 180°, когда $‍ θ$ $i$ $\to 90°$ ; и
$δ p > δ s$ ‍ при промежуточных значениях θ _i ( потому что множитель $n$ находится в числителе ( 18 ) и знаменателе ( 17 ) ) .^[35]

При $θ i \leq θ c$ коэффициенты отражения определяются уравнениями ( 13 ) и ( 15 ) и являются действительными , так что сдвиг фаз $составляет$ либо 0° (если коэффициент положительный), либо 180° (если коэффициент отрицательный).

В ( 13 ), если мы подставим ‍ ( закон Снеллиуса) и умножим числитель и знаменатель на $‍ ⁠$ $n_{2}=n_{1}\sin \theta _{\text{i}}/\sin \theta _{\text{t}}$ $1 / н 1 ⁠ sin θ t$ ‍ , ‍ получаем ^[36]^[37]

что положительно для всех углов падения проходящего луча (поскольку $‍ θ$ $t$ $>$ $θ$ $i$ ), давая фазовый сдвиг $δ$ $s ,$ равный нулю.

Если мы сделаем то же самое с ( 15 ), то легко показать, что результат эквивалентен ^[38]^[39]

который отрицателен для малых углов (то есть, вблизи нормального падения), но меняет знак под углом Брюстера , где θ _i и θ _t являются дополнительными. Таким образом, сдвиг фазы $δ p$ составляет 180° для малых θ _i, но переключается на 0° под углом Брюстера. Объединение дополнительности с законом Снеллиуса дает $‍ θ$ $i$ $= arctan (1/$ $n$ $)$ ‍ как угол Брюстера для падения от плотного к редкому. ^{[Примечание 15]}

( Уравнения ( 19 ) и ( 20 ) известны как закон синусов Френеля и закон касательных Френеля . ^[40] Оба сводятся к 0/0 при нормальном падении, но дают правильные результаты в пределе , когда $‍ θ$ $i$ $\to 0.$ То, что они имеют противоположные знаки по мере приближения к нормальному падению, является очевидным недостатком соглашения о знаках, используемого в этой статье; соответствующее преимущество состоит в том, что они имеют одинаковые знаки при скользящем падении. )

Это завершает информацию, необходимую для построения графика $δ s$ и $δ p$ для всех углов падения. Это сделано на рис. 13, ^[34] с $δ p$ красным и $δ s$ синим, для трех показателей преломления. На шкале угла падения (горизонтальная ось) угол Брюстера находится там, где $δ p$ (красный) падает от 180° до 0°, а критический угол находится там, где и $δ p$ , и $δ s$ (красный и синий) снова начинают расти. Слева от критического угла находится область частичного отражения, где оба коэффициента отражения являются действительными (фаза 0° или 180°) с величинами меньше 1. Справа от критического угла находится область полного отражения, где оба коэффициента отражения являются комплексными с величинами, равными 1. В этой области черные кривые показывают фазовый сдвиг p- компоненты относительно s- компоненты: ^[41] Видно, что показатель преломления 1,45 недостаточен для получения разности фаз 45°, тогда как показатель преломления 1,5 достаточен (с небольшим запасом) для получения разности фаз 45° при двух углах падения: около 50,2° и 53,3°. $\delta =\delta _{p\!}-\delta _{s}\,.$

Этот относительный сдвиг в 45° используется в изобретении Френеля, теперь известном как ромб Френеля, в котором углы падения выбраны таким образом, что два внутренних отражения вызывают общий относительный сдвиг фаз в 90° между двумя поляризациями падающей волны. Это устройство выполняет ту же функцию, что и двулучепреломляющая четвертьволновая пластина , но является более ахроматичным (то есть фазовый сдвиг ромба менее чувствителен к длине волны ). Любое из устройств может быть использовано, например, для преобразования линейной поляризации в круговую поляризацию (которую также открыл Френель) и наоборот.

На рис. 13 $δ$ вычисляется путем окончательного вычитания; но есть и другие способы его выражения. Сам Френель в 1823 году ^[42] дал формулу для $cos δ$ . Борн и Вольф (1970, стр. 50) выводят выражение для ‍ tan $(δ /2)$ и находят его максимум аналитически.

Для ПВО пучка с конечной шириной изменение фазового сдвига с углом падения приводит к эффекту Гуса-Хенхен , который представляет собой боковой сдвиг отраженного пучка в плоскости падения. ^[28]^[43] Этот эффект применим к линейной поляризации в направлении s или p . Эффект Имберта-Федорова является аналогичным эффектом для круговой или эллиптической поляризации и производит сдвиг, перпендикулярный плоскости падения. ^[44]

Приложения

Оптические волокна используют полное внутреннее отражение для передачи сигналов на большие расстояния с небольшим затуханием.^[45] Они используются в телекоммуникационных кабелях и в фиброскопах, формирующих изображения, таких как колоноскопы .^[46]

В катадиоптрической линзе Френеля , изобретенной Огюстеном-Жаном Френелем для использования в маяках , внешние призмы используют полное внутреннее отражение для отклонения света от лампы на больший угол, чем это было бы возможно с чисто преломляющими призмами, но с меньшим поглощением света (и меньшим риском потускнения), чем с обычными зеркалами. ^[47]

Другие отражающие призмы , использующие ПВО, включают следующие (с некоторым совпадением между категориями): ^[48]

Призмы , восстанавливающие изображение, для биноклей и зрительных труб включают парные призмы Порро 45°-90°-45° (рис. 14), призму Порро–Аббе , встроенные призмы Кёнига^[49] и Аббе–Кёнига , а также компактную встроенную призму Шмидта–Пехана . (Последняя состоит из двух компонентов, один из которых является разновидностью призмы Бауэрнфайнда , которая требует отражающего покрытия на одной из двух своих отражающих граней из-за субкритического угла падения.) Эти призмы имеют дополнительную функцию сгибания оптического пути от объективной линзы до главного фокуса , уменьшая общую длину для заданного основного фокусного расстояния .
Призматическая звездная диагональ для астрономического телескопа может состоять из одной призмы Порро (настроенной на однократное отражение , дающей зеркально перевернутое изображение) или призмы Амичи (дающей неперевернутое изображение).
Крышные призмы используют TIR на двух гранях, встречающихся под острым углом 90°. Эта категория включает типы Koenig, Abbe–Koenig, Schmidt–Pechan и Amici (уже упомянутые), а также крышную пентапризму, используемую в зеркальных камерах ; последняя из них требует отражающего покрытия на одной не-TIR грани.
Призматический уголковый отражатель использует три полных внутренних отражения для изменения направления входящего света.
Призма Дове обеспечивает прямоугольное изображение с зеркальным отражением.

Поляризационные призмы : Хотя ромб Френеля, который преобразует между линейной и эллиптической поляризацией, не является двулучепреломляющим (двойным преломлением), существуют другие виды призм, которые сочетают двулучепреломление с TIR таким образом, что свет определенной поляризации полностью отражается, в то время как свет ортогональной поляризации по крайней мере частично передается. Примерами являются призма Николя , ^[50] призма Глана–Томпсона , призма Глана–Фуко (или «призма Фуко»), ^[51]^[52] и призма Глана–Тейлора . ^[53]

Рефрактометры , измеряющие показатели преломления, часто используют критический угол.^[54]^[55]

Датчики дождя для автоматических стеклоочистителей/дворников ветрового стекла были реализованы с использованием принципа, согласно которому полное внутреннее отражение будет направлять инфракрасный луч от источника к детектору, если внешняя поверхность ветрового стекла сухая, но любые капли воды на поверхности будут отражать часть света.^[56]

Светодиодные панели с торцевой подсветкой , используемые (например) для подсветки ЖК - мониторов компьютеров, используют полное инфракрасное излучение для ограничения света светодиода акриловой стеклянной панелью, за исключением того, что часть света рассеивается травлением на одной стороне панели, что обеспечивает приблизительно равномерную световую эмиссию . ^[57]

Микроскопия полного внутреннего отражения (TIRM) использует затухающую волну для освещения небольших объектов вблизи отражающего интерфейса. Последующее рассеяние затухающей волны (форма нарушенного TIR) заставляет объекты казаться яркими при просмотре с «внешней» стороны. ^[21] В микроскопе флуоресценции полного внутреннего отражения (TIRFM) вместо того, чтобы полагаться на простое рассеяние, мы выбираем затухающую длину волны, достаточно короткую, чтобы вызвать флуоресценцию (рис. 15). ^[58] Высокая чувствительность освещения к расстоянию от интерфейса позволяет измерять чрезвычайно малые смещения и силы. ^[59]

Светоделительный куб использует нарушенное ПВО для разделения мощности входящего луча между переданным и отраженным лучами. ^{[18] Ширину воздушного зазора (или зазора с низким показателем преломления) между двумя призмами можно сделать регулируемой, что обеспечивает более}высокую передачу и более низкое отражение для более узкого зазора или более высокое отражение и более низкую передачу для более широкого зазора. ^[60]

Оптическая модуляция может быть достигнута посредством фрустрированного ПВО с быстро изменяющимся зазором.^[61] Поскольку коэффициент пропускания очень чувствителен к ширине зазора (функция является приблизительно экспоненциальной до тех пор, пока зазор почти не закроется), этот метод может обеспечить большой динамический диапазон .

Оптические дактилоскопические устройства использовали нарушенную технологию ПИР для записи изображений отпечатков пальцев людей без использования чернил (см. рис. 11). ^[62]

Анализ походки можно выполнить, используя расстроенный TIR с высокоскоростной камерой, чтобы захватить и проанализировать следы.^[63]

Гониоскоп , используемый в оптометрии и офтальмологии для диагностики глаукомы , подавляет TIR, чтобы заглянуть в угол между радужной оболочкой и роговицей . Этот вид обычно блокируется TIR на границе роговицы и воздуха. Гониоскоп заменяет воздух средой с более высоким индексом , позволяя пропускать свет при косом падении, обычно с последующим отражением в «зеркале», которое само по себе может быть реализовано с использованием TIR. ^[64]^[65]

Некоторые интерактивные столы и доски с функцией multi-touch используют FTIR для обнаружения касания экрана пальцами. Инфракрасная камера размещается за поверхностью экрана, которая подсвечивается инфракрасными светодиодами по краям; при касании поверхности FTIR заставляет часть инфракрасного света выходить за пределы плоскости экрана, и камера видит это как яркие области. Затем программное обеспечение компьютерного зрения используется для перевода этого в ряд координат и жестов.

История

Открытие

Удивительно всеобъемлющие и в значительной степени правильные объяснения радуги Теодориха Фрайбергского ( написанные между 1304 и 1310 годами) ^[66] и Камала ад-Дина аль-Фариси (завершенные к 1309 году) ^[67] , хотя иногда упоминаются в связи с полным внутренним отражением (ПВО), имеют сомнительную актуальность, поскольку внутреннее отражение солнечного света в сферической капле дождя не является полным. ^{[Примечание 16]} Но, по словам Карла Бенджамина Бойера , трактат Теодориха о радуге также классифицировал оптические явления по пяти причинам, последней из которых было «полное отражение на границе двух прозрачных сред». ^[68] Работа Теодориха была забыта, пока ее не открыл заново Джованни Баттиста Вентури в 1814 году. ^[69]

Теодорих впал в безвестность, открытие ПВО обычно приписывалось Иоганну Кеплеру , который опубликовал свои выводы в своей работе «Диоптрице» в 1611 году. Хотя Кеплеру не удалось найти истинный закон преломления, он экспериментально показал, что при падении из воздуха в стекло падающие и преломленные лучи вращаются в одном и том же направлении вокруг точки падения, и что при изменении угла падения на ±90° угол преломления (как мы его теперь называем) изменяется на ±42°. Он также знал, что падающие и преломленные лучи взаимозаменяемы. Но эти наблюдения не охватывали случай падения луча из стекла в воздух под углом более 42°, и Кеплер быстро пришел к выводу, что такой луч может быть только отраженным . ^[70]

Рене Декарт заново открыл закон преломления и опубликовал его в своей «Диоптрике» 1637 года. В той же работе он упомянул о смысле вращения падающих и преломленных лучей и условии полного внутреннего отражения. Но он пренебрег обсуждением предельного случая и, следовательно, не смог дать выражение для критического угла, хотя он мог бы легко это сделать. ^[71]

Гюйгенс и Ньютон: конкурирующие объяснения

Христиан Гюйгенс в своем «Трактате о свете » (1690) уделил большое внимание порогу, при котором падающий луч «не способен проникнуть в другое прозрачное вещество». ^[72] Хотя он не дал ни названия, ни алгебраического выражения для критического угла, он привел численные примеры для падения стекла в воздух и воды в воздух, отметил большое изменение угла преломления при небольшом изменении угла падения вблизи критического угла и назвал это причиной быстрого увеличения яркости отраженного луча по мере того, как преломленный луч приближается к касательной к границе раздела. ^[73] Понимание Гюйгенса подтверждается современной теорией: в уравнениях ( 13 ) и ( 15 ) выше нет ничего, что говорило бы о том, что коэффициенты отражения возрастают исключительно круто, когда θ _t приближается к 90°, за исключением того, что, согласно закону Снеллиуса, θ _t сам по себе является все более крутой функцией θ _i .

Гюйгенс предложил объяснение ПВО в рамках той же структуры, что и его объяснения законов прямолинейного распространения, отражения, обычного преломления и даже необычного преломления « исландского кристалла » (кальцита). Эта структура основывалась на двух предпосылках: во-первых, каждая точка, пересекаемая распространяющимся волновым фронтом, становится источником вторичных волновых фронтов («принцип Гюйгенса»); и, во-вторых, при наличии начального волнового фронта любое последующее положение волнового фронта является огибающей ( общей касательной поверхностью) всех вторичных волновых фронтов, испускаемых из начального положения. Все случаи отражения или преломления поверхностью затем объясняются просто путем рассмотрения вторичных волн, испускаемых этой поверхностью. В случае преломления из среды с более медленным распространением в среду с более быстрым распространением существует определенная наклонность падения, за пределами которой вторичные волновые фронты не могут образовать общую касательную во второй среде; ^[74] это то, что мы теперь называем критическим углом. Когда фронт падающей волны приближается к этому критическому наклону, преломленный волновой фронт концентрируется на преломляющей поверхности, усиливая вторичные волны, которые создают отражение обратно в первую среду. ^[75]

Система Гюйгенса даже учитывала частичное отражение на границе раздела различных сред, хотя и смутно, по аналогии с законами столкновений частиц разных размеров. ^[76] Однако до тех пор, пока волновая теория продолжала предполагать продольные волны , у нее не было никаких шансов учесть поляризацию, а следовательно, и никаких шансов объяснить зависимость от поляризации необычной рефракции, ^[77] или коэффициента частичного отражения, или фазового сдвига в ПВО.

Исаак Ньютон отверг волновое объяснение прямолинейного распространения, полагая, что если бы свет состоял из волн, он бы «изгибался и распространялся во все стороны» в тени. ^[78] Его корпускулярная теория света объясняла прямолинейное распространение более просто, и она учитывала обычные законы преломления и отражения, включая полное внутреннее отражение, на основе гипотезы о том, что корпускулы света подвергаются воздействию силы, действующей перпендикулярно границе раздела. ^[79] В этой модели при падении от плотного к редкому сила была притяжением обратно к более плотной среде, а критический угол был углом падения, при котором нормальная скорость приближающейся корпускулы была как раз достаточной, чтобы достичь дальней стороны силового поля; при более наклонном падении корпускула поворачивала бы обратно. ^[80] Ньютон дал то, что можно назвать формулой для критического угла, хотя и в словах: «как синусы, измеряющие преломление, так и синус угла падения, при котором начинается полное отражение, относится к радиусу окружности». ^[81]

Ньютон пошел дальше Гюйгенса двумя путями. Во-первых, неудивительно, что Ньютон указал на связь между ПВО и дисперсией : когда луч белого света приближается к границе раздела стекло-воздух с увеличивающимся наклоном, наиболее сильно преломленные лучи (фиолетовые) первыми «выводятся» «полным отражением», а за ними следуют менее преломленные лучи. ^[82] Во-вторых, он заметил, что полное отражение может быть нарушено (как мы теперь говорим), если положить вместе две призмы, одну плоскую, а другую слегка выпуклую; и он объяснил это просто, заметив, что корпускулы будут притягиваться не только к первой призме, но и ко второй. ^[83]

Однако в двух других отношениях система Ньютона была менее последовательной. Во-первых, его объяснение частичного отражения зависело не только от предполагаемых сил притяжения между корпускулами и средой, но и от более туманной гипотезы «Приступов легкого отражения» и «Приступов легкого прохождения». ^[84] Во-вторых, хотя его корпускулы могли предположительно иметь «стороны» или «полюса», ориентация которых могла предположительно определять, испытывают ли корпускулы обычную или необычную рефракцию в «Островном кристалле», ^[85] его геометрическое описание необычной рефракции ^[86] было теоретически неподтвержденным ^[87] и эмпирически неточным. ^[88]

Лаплас, Малюс и нарушенное полное внутреннее отражение (НПВО)

Уильям Хайд Волластон в первой из двух статей, прочитанных в Королевском обществе Лондона в 1802 году, ^[55] сообщил о своем изобретении рефрактометра, основанного на критическом угле падения от внутренней среды с известной «преломляющей способностью» (показателем преломления) к внешней среде, показатель которой должен был быть измерен. ^[89] С помощью этого устройства Волластон измерил «преломляющую способность» многочисленных материалов, некоторые из которых были слишком непрозрачны, чтобы допустить прямое измерение угла преломления. Переводы его статей были опубликованы во Франции в 1803 году и, по-видимому, привлекли внимание Пьера-Симона Лапласа . ^[90]

Согласно разработке Лапласом теории преломления Ньютона, корпускула, падающая на плоскую границу раздела между двумя однородными изотропными средами, подвергалась силовому полю, которое было симметрично относительно границы. Если бы обе среды были прозрачными, полное отражение произошло бы, если бы корпускула была повернута назад до того, как она вышла из поля во второй среде. Но если бы вторая среда была непрозрачной, отражение не было бы полным, если бы корпускула не была повернута назад до того, как она покинула первую среду ; это требовало большего критического угла, чем тот, который дается законом Снеллиуса, и, следовательно, оспаривало бы справедливость метода Волластона для непрозрачных сред. ^[91] Лаплас объединил два случая в одну формулу для относительного показателя преломления в терминах критического угла (минимальный угол падения для ПВО). Формула содержала параметр, который принимал одно значение для прозрачной внешней среды и другое значение для непрозрачной внешней среды. Теория Лапласа далее предсказала связь между показателем преломления и плотностью для данного вещества. ^[92]

В 1807 году теория Лапласа была экспериментально проверена его учеником Этьеном-Луи Малусом . Взяв формулу Лапласа для показателя преломления как данность и используя ее для измерения показателя преломления пчелиного воска в жидком (прозрачном) состоянии и твердом (непрозрачном) состоянии при различных температурах (следовательно, и при различных плотностях), Малус проверил соотношение Лапласа между показателем преломления и плотностью. ^[93]^[94]

Но теория Лапласа подразумевала, что если угол падения превышает его модифицированный критический угол, отражение будет полным, даже если внешняя среда поглощает. Очевидно, что это было неправильно: в уравнениях ( 12 ) выше не существует порогового значения угла θ _i, за пределами которого κ становится бесконечным; поэтому глубина проникновения затухающей волны (1/ κ ) всегда не равна нулю, и внешняя среда, если она вообще имеет потери, ослабит отражение. Что касается того, почему Малюс, по-видимому, наблюдал такой угол для непрозрачного воска, мы должны сделать вывод, что существовал определенный угол, за пределами которого ослабление отражения было настолько малым, что НПВО было визуально неотличимо от ПВО. ^[95]

Френель и фазовый сдвиг

Френель пришел к изучению полного внутреннего отражения через свои исследования поляризации. В 1811 году Франсуа Араго обнаружил, что поляризованный свет, по-видимому, «деполяризуется» в зависимости от ориентации и цвета при прохождении через срез двупреломляющего кристалла: возникающий свет проявлял цвета при просмотре через анализатор (второй поляризатор). Хроматическая поляризация , как стало называться это явление, была более тщательно исследована в 1812 году Жаном-Батистом Био . В 1813 году Био установил, что один случай, изученный Араго, а именно кварц, разрезанный перпендикулярно своей оптической оси , на самом деле был постепенным вращением плоскости поляризации с расстоянием. ^[96]

В 1816 году Френель предложил свою первую попытку волновой теории хроматической поляризации. Без (пока) явного привлечения поперечных волн его теория трактовала свет как состоящий из двух перпендикулярно поляризованных компонентов. ^[97] В 1817 году он заметил, что плоскополяризованный свет, по-видимому, частично деполяризуется полным внутренним отражением, если изначально поляризован под острым углом к плоскости падения. ^[98] Включив полное внутреннее отражение в эксперимент по хроматической поляризации, он обнаружил, что явно деполяризованный свет представляет собой смесь компонентов, поляризованных параллельно и перпендикулярно плоскости падения, и что полное отражение вносит разность фаз между ними. ^[99] Выбор подходящего угла падения (еще точно не определенного) дал разность фаз в 1/8 цикла. Два таких отражения от «параллельных граней» «двух связанных призм» дали разность фаз в 1/4 цикла. В этом случае, если свет изначально был поляризован под углом 45° к плоскости падения и отражения, он, по-видимому, полностью деполяризовался после двух отражений. Эти результаты были изложены в мемуаре, представленном и зачитанном Французской академии наук в ноябре 1817 года. ^[100]

В 1821 году Френель вывел формулы, эквивалентные его законам синуса и тангенса ( уравнения ( 19 ) и ( 20 ), выше ), моделируя световые волны как поперечные упругие волны с колебаниями, перпендикулярными тому, что ранее называлось плоскостью поляризации . ^[101]^{[Примечание 17]} Используя старые экспериментальные данные, он быстро подтвердил, что уравнения правильно предсказывают направление поляризации отраженного луча, когда падающий луч был поляризован под углом 45° к плоскости падения, для света, падающего из воздуха на стекло или воду. ^[102] Экспериментальное подтверждение было сообщено в «постскриптуме» к работе, в которой Френель изложил свою зрелую теорию хроматической поляризации, введя поперечные волны. ^[103] Подробности вывода были даны позже, в мемуарах, зачитанных в академии в январе 1823 года. ^[104] Вывод сочетал сохранение энергии с непрерывностью тангенциальной вибрации на границе раздела, но не учитывал никаких условий для нормальной составляющей вибрации. ^[105]

Между тем, в мемуарах, представленных в декабре 1822 года, ^[106] Френель ввел термины «линейная поляризация» , «круговая поляризация» и «эллиптическая поляризация» . ^[107] Для круговой поляризации два перпендикулярных компонента были сдвинуты по фазе на четверть цикла (±90°).

Новая терминология оказалась полезной в мемуарах января 1823 года ^[104], содержащих подробные выводы законов синуса и тангенса: в том же мемуаре Френель обнаружил, что для углов падения, больших критического угла, результирующие коэффициенты отражения были комплексными с единичной величиной. Отметив, что величина представляла отношение амплитуд, как обычно, он предположил, что аргумент представлял фазовый сдвиг, и проверил гипотезу экспериментально. ^[108] Проверка включала

вычисление угла падения, который внес бы общую разность фаз 90° между компонентами s и p , для различного числа полных внутренних отражений под этим углом (обычно имелось два решения),
подвергая свет этому числу полных внутренних отражений под этим углом падения, с начальной линейной поляризацией под углом 45° к плоскости падения, и
проверка того, что конечная поляризация была круговой. ^[109]

Эта процедура была необходима, поскольку с технологией того времени нельзя было измерить сдвиги фаз s и p напрямую, и нельзя было измерить произвольную степень эллиптичности поляризации, например, которая могла быть вызвана разницей между сдвигами фаз. Но можно было проверить, что поляризация была круговой , поскольку яркость света тогда была нечувствительна к ориентации анализатора.

Для стекла с показателем преломления 1,51 Френель подсчитал, что разность фаз в 45° между двумя коэффициентами отражения (следовательно, разность в 90° после двух отражений) требует угла падения 48°37' или 54°37'. Он вырезал ромб под последним углом и обнаружил, что он работает так, как и ожидалось. ^[110] Таким образом, спецификация ромба Френеля была завершена. Аналогичным образом Френель подсчитал и проверил угол падения, который даст разность фаз в 90° после трех отражений под тем же углом и четырех отражений под тем же углом. В каждом случае было два решения, и в каждом случае он сообщал, что больший угол падения давал точную круговую поляризацию (для начальной линейной поляризации под углом 45° к плоскости отражения). Для случая трех отражений он также проверил меньший угол, но обнаружил, что он дает некоторую окраску из-за близости критического угла и его небольшой зависимости от длины волны. (Сравните рис. 13 выше, на котором показано, что разность фаз $δ$ более чувствительна к показателю преломления при меньших углах падения.)

Для большей уверенности Френель предсказал и подтвердил, что четыре полных внутренних отражения при 68°27' дадут точную круговую поляризацию, если два из отражений будут иметь воду в качестве внешней среды, а два других — воздух, но не если отражающие поверхности будут полностью влажными или полностью сухими. ^[111]

Вывод Френеля о сдвиге фазы в ПВО, как полагают, был первым случаем, когда физический смысл был придан аргументу комплексного числа. Хотя это рассуждение было применено без преимущества знания того, что световые волны являются электромагнитными, оно прошло проверку экспериментом и выжило в удивительной целости после того, как Джеймс Клерк Максвелл изменил предполагаемую природу волн. ^[112] Между тем, успех Френеля вдохновил Джеймса МакКуллага и Огюстена-Луи Коши , начиная с 1836 года, на анализ отражения от металлов с использованием уравнений Френеля с комплексным показателем преломления . ^[113] Мнимая часть комплексного показателя представляет собой поглощение. ^[114]

Термин «критический угол» , используемый для удобства в приведенном выше повествовании, является анахронизмом: по-видимому, он датируется 1873 годом. ^[115]

В 20 веке квантовая электродинамика переосмыслила амплитуду электромагнитной волны в терминах вероятности обнаружения фотона. ^[116] В этой структуре частичное пропускание и нарушенное полное внутреннее отражение касаются вероятности пересечения фотоном границы, а ослабленное полное отражение касается вероятности поглощения фотона на другой стороне.

Исследования более тонких аспектов фазового сдвига в ПВО, включая эффекты Гуса-Хэнхен и Имберта-Федорова и их квантовые интерпретации, продолжались и в 21 веке. ^[44]

Галерея

Индийский спинорог и его полное отражение на поверхности воды.
Полное отражение кисти от поверхности вода-воздух в стакане
Полное внутреннее отражение зеленого лазера в ножке бокала для вина

Смотрите также

Примечания

^ Двулучепреломляющие среды, такие как кальцит , являются неизотропными (анизотропными). Когда мы говорим, что необыкновенное преломление кристалла кальцита «нарушает закон Снеллиуса», мы имеем в виду, что закон Снеллиуса не применим к необыкновенному лучу , поскольку направление этого луча внутри кристалла обычно отличается от направления соответствующей волновой нормали (Гюйгенс, 1690, tr. Thompson, стр. 65, ст. 24), и поскольку скорость волновой нормали сама по себе зависит от направления. (Обратите внимание, что цитируемый отрывок содержит ошибку перевода: во фразе «сопряженный относительно диаметров, которые не находятся на прямой линии AB» слово «не» не поддерживается оригинальным французским текстом Гюйгенса и является геометрически неверным.)
^ Согласно уравнениям ( 13 ) и ( 15 ), отражение является полным для падения под критическим углом. На этом основании рис. 5 должен показывать полностью отраженный луч и никакого тангенциального луча для падения под θ _c . Но из-за дифракции падающий луч конечной ширины не может иметь единственный угол падения; должно быть некоторое расхождение луча. Более того, график коэффициента отражения в зависимости от угла падения становится вертикальным при θ _c (Jenkins & White, 1976, стр. 527), так что небольшое расхождение луча вызывает большую потерю отражения. Аналогично, вблизи критического угла небольшое расхождение в угле падения вызывает большое расхождение в угле преломления (ср. Huygens, 1690, tr. Thompson, стр. 41); поэтому тангенциальный преломленный луч следует рассматривать только как предельный случай.
^ Для неизотропных сред уравнение ( 1 ) по-прежнему описывает закон преломления в терминах направлений и скоростей нормали волны , но область применимости этого закона определяется ограничениями на направления лучей (ср. Бухвальд, 1989, стр. 29).
^ Указанный диапазон варьируется из-за различных политипов кристаллов .
^ Мощность «на единицу площади» подходит для полей в трех измерениях. В двух измерениях мы можем захотеть, чтобы произведение усилия и потока было мощностью на единицу длины . В одном измерении или в модели с сосредоточенными элементами мы можем захотеть, чтобы это была просто мощность.
^ Мы предполагаем, что уравнения, описывающие поля, линейны .
^ Вышеуказанная форма ( 5 ) обычно используется физиками. Инженеры-электрики обычно предпочитают форму , то есть они не только используют $j$ вместо $i$ для мнимой единицы, но и меняют знак показателя степени, в результате чего все выражение заменяется его комплексно сопряженным , оставляя действительную часть неизменной. Форма инженеров-электриков и формулы, выведенные из нее, могут быть преобразованы в общепринятую форму физиков путем замены $-i$ на $j$ (Stratton, 1941, стр. vii–viii). $\mathbf {E_{k}} e^{j(\omega t-\mathbf {k\cdot r} )};$
^ Мы предполагаем, что доплеровские сдвиги отсутствуют , так что ω не изменяется на границах раздела сред.
^ Если мы правильно преобразуем это в электротехнические соглашения, то получим $-j ‍ \sqrt \dots$ в правой части ( 9 ), что не является главным квадратным корнем. Поэтому недопустимо предполагать, априори , что то, что математики называют « главным квадратным корнем », является физически применимым.
^ В электротехнической конвенции зависящий от времени фактор — это $e ‍ jωt,$ так что сдвиг фазы соответствует умножению на комплексную константу с положительным аргументом. Однако в этой статье используется физическая конвенция с зависящим от времени фактором $e -iωt$ .
^ Первоначально s происходит от немецкого senkrecht , что означает «перпендикулярный» (к плоскости падения). Альтернативные мнемоники в тексте, возможно, больше подходят для носителей английского языка .
^ Другими словами, для обеих поляризаций в данной статье используется соглашение о том, что положительные направления падающего, отраженного и прошедшего полей одинаковы для любого поля, которое перпендикулярно плоскости падения; это поле $E$ для s- поляризации и поле $H$ для p- поляризации.
^ Эта номенклатура следует Jenkins & White, 1976, стр. 526–9. Некоторые авторы, однако, используют обратный показатель преломления и поэтому получают разные формы для наших уравнений ( 17 ) и ( 18 ). Примерами являются Born & Wolf [1970, стр. 49, уравнения (60)] ‍ и Stratton [1941, стр. 499, уравнения (43)]. Кроме того, Born & Wolf определяют $δ ⊥$ и $δ ∥$ как аргументы, а не как фазовые сдвиги, вызывающие смену знака.
^ Просто случайно, что главный квадратный корень оказывается правильным в данной ситуации, и только потому, что мы используем зависящий от времени фактор $e -iωt$ . Если бы мы вместо этого использовали зависящий от времени фактор инженеров-электриков $e ‍ jωt$ , выбор главного квадратного корня дал бы тот же аргумент для коэффициента отражения, но это было бы интерпретировано как противоположный фазовый сдвиг, что было бы неправильно. Но если мы выберем квадратный корень так, чтобы передаваемое поле было мимолетным, мы получим правильный фазовый сдвиг с любым зависящим от времени фактором.
^ Более знакомая формула $arctan n$ ‍ относится к падению от редкой к плотной среде. В обоих случаях $n$ — показатель преломления более плотной среды относительно более редкой среды.
^ Для внешнего луча, падающего на сферическую каплю дождя, преломленный луч находится в плоскости падающего луча и центра капли, а угол преломления меньше критического угла для падения вода-воздух; но этот угол преломления, в силу сферической симметрии, также является углом падения для внутреннего отражения, которое, следовательно, меньше полного. Более того, если бы это отражение было полным, все последующие внутренние отражения имели бы тот же угол падения (из-за симметрии) и также были бы полными, так что свет никогда не вышел бы наружу, чтобы создать видимую радугу.
^ Следовательно, когда Френель говорит, что после полного внутреннего отражения при соответствующем падении волна, поляризованная параллельно плоскости падения, «отстает» на 1/8 цикла (цитата из Бухвальда, 1989, стр. 381), он имеет в виду волну, плоскость поляризации которой параллельна плоскости падения, т. е. волну, колебания которой перпендикулярны этой плоскости, т. е. то, что мы теперь называем s- компонентой.

Ссылки

^ ab RP Feynman, RB Leighton и M. Sands, 1963–2013, Фейнмановские лекции по физике , Калифорнийский технологический институт, том II , § 33-6.
^ Антич, Питер П.; Андерсон, Джон А.; Эшман, Ричард Б.; Дауди, Джеймс Э.; Гонсалес, Джером; Мюрри, Роберт К.; Зервех, Джозеф Э.; Пак, Чарльз Й.К. (2009). «Измерение механических свойств костного материала in vitro с помощью отражения ультразвука: Методология и сравнение с передачей ультразвука». Журнал исследований костей и минералов . 6 (4): 417–426. doi :10.1002/jbmr.5650060414. PMID 1858525. S2CID 6914223..
↑ Дженкинс и Уайт, 1976, стр. 11.
^ Дженкинс и Уайт, 1976, стр. 527. (Преломленный луч становится слабее с точки зрения общей мощности, но не обязательно с точки зрения видимости, поскольку луч также становится уже, поскольку он становится более близким к тангенциальному.)
↑ Дженкинс и Уайт, 1976, стр. 26.
↑ См. Thomas Young в Quarterly Review , апрель 1814 г., перепечатано в T. Young (ред. G. Peacock), Miscellaneous Works of the late Thomas Young , Лондон: J. Murray, 1855, т. 1, на стр. 263.
↑ См. Born & Wolf, 1970, стр. 12–13.
↑ См. Гюйгенс, 1690, пер. Томпсона, стр. 38.
^ Born & Wolf, 1970, стр. 13; Jenkins & White, 1976, стр. 9–10. Это определение использует вакуум в качестве «референтной среды». В принципе, любая изотропная среда может быть выбрана в качестве референтной. Для некоторых целей удобно выбрать воздух, в котором скорость света примерно на 0,03% ниже, чем в вакууме (ср. Rutten and van Venrooij, 2002, стр. 10, 352). Однако в настоящей статье выбран вакуум.
↑ См. Дженкинс и Уайт, 1976, стр. 25.
↑ Дженкинс и Уайт, 1976, стр. 10, 25.
↑ См. DK Lynch (1 февраля 2015 г.), «Окно Снелла в волнистой воде», Applied Optics , 54 (4): B8–B11, doi :10.1364/AO.54.0000B8.
^ Гюйгенс (1690, tr. Thompson, стр. 41) для падения стекла в воздух отметил, что если наклон падающего луча всего на 1° меньше критического, то преломленный луч отклоняется от касательной более чем на 11°. Примечание: Определение Гюйгенса «угла падения» является дополнением к современному определению.
^ JR Graham, «Можно ли огранить дизайн драгоценного камня для придания ему наклонной яркости?», International Gem Society, дата обращения 21 марта 2019 г.; архивировано 14 декабря 2018 г.
^ 'PJS' (автор), «Звуковое давление, звуковая мощность и интенсивность звука: в чем разница?» Сообщество Siemens PLM , доступ 10 апреля 2019 г.; архив 10 апреля 2019 г.
↑ Страттон, 1941, стр. 131–137.
↑ Страттон, 1941, стр. 37.
^ abc См. Harvard Natural Sciences Lecture Demonstrations, «Frustrated Total Internal Reflection», дата обращения 9 апреля 2019 г.; архивировано 2 августа 2018 г.
^ ab R. Ehrlich, 1997, Почему тост падает желеобразной стороной вниз: Дзен и искусство физических демонстраций , Princeton University Press, ISBN 978-0-691-02891-0 , стр. 182, по состоянию на 26 марта 2019 г.
↑ Р. Боули, 2009, «Полное внутреннее отражение» (4-минутное видео), Sixty Symbols , Брэди Харан для Ноттингемского университета , с 1:25.
^ ab EJ Ambrose (24 ноября 1956 г.), "Поверхностный контактный микроскоп для изучения движений клеток", Nature , 178 (4543): 1194, Bibcode : 1956Natur.178.1194A, doi : 10.1038/1781194a0 , PMID 13387666, S2CID 4290898.
^ Ван Розум, Аэрноут; Ван Ден Берг, Эд (май 2021 г.). «Использование фрустрированного внутреннего отражения как аналога квантового туннелирования». Journal of Physics: Conference Series . 1929 (1): 012050. Bibcode : 2021JPhCS1929a2050V. doi : 10.1088/1742-6596/1929/1/012050 . S2CID 235591328.
^ Thermo Fisher Scientific, «Технологии образцов FTIR: ослабленное полное внутреннее отражение (ATR)», дата обращения 9 апреля 2019 г.
^ Дженкинс и Уайт, 1976, стр. 228.
^ Борн и Вольф, 1970, стр. 16–17, уравнения (20), (21).
^ Борн и Вольф, 1970, стр. 47, уравнение (54), где их $n$ — наше ( не наше ). $n_{2}/n_{1}$ $n_{1}/n_{2}$
↑ Страттон, 1941, стр. 499; Борн и Вольф, 1970, стр. 48.
^ abc Laboratory of Cold Atoms Near Surfaces (Ягеллонский университет), "Свойства затухающих волн", доступ 11 апреля 2019 г.; архив 28 апреля 2018 г. ( Примечание: на этой странице $z$ используется для координаты, нормальной к интерфейсу, а верхние индексы ⊥ и ∥ для s ("TE") и p поляризаций соответственно. На страницах этого сайта используется зависящий от времени фактор $e + iωt$ — то есть зависящий от времени фактор инженеров-электриков с символом физиков для мнимой единицы.)
^ Хехт, 2017, стр. 136.
↑ Борн и Вольф, 1970, стр. 16.
↑ Уиттекер, 1910, стр. 132, 135–136.
^ Одним из известных авторитетов, использующих «другое» соглашение (но не заходя слишком далеко), являются «Фейнмановские лекции по физике» , том I , уравнение (33.8) (для $B$ ), и том II , рис. 33-6 и 33-7.
^ Борн и Вольф, 1970, стр. 40, уравнения (20), (21), где нижний индекс ⊥ соответствует s , а ∥ — p .
^ abc См. Jenkins & White, 1976, стр. 529.
^ «Фаза поляризации, в которой магнитное поле параллельно интерфейсу, опережает фазу другой поляризации». — Фицпатрик, 2013, стр. 140; Фицпатрик, 2013a; выделено автором.
↑ Френель, 1866, стр. 773, 789n.
^ Борн и Вольф, 1970, стр. 40, уравнения (21a); Хехт, 2017, стр. 125, уравнения (4.42); Дженкинс и Уайт, 1976, стр. 524, уравнения (25a).
↑ Френель, 1866, стр. 757, 789n.
^ Борн и Вольф, 1970, стр. 40, уравнения (21a); Хехт, 2017, стр. 125, уравнения (4.43); Дженкинс и Уайт, 1976, стр. 524, уравнения (25a).
^ Уиттакер, 1910, с. 134; Дарригол, 2012, с. 213 .
^ Stratton, 1941, стр. 500, уравнение (44). Соответствующее выражение в Born & Wolf (1970, стр. 50) наоборот, поскольку члены представляют аргументы, а не фазовые сдвиги.
^ Бухвальд, 1989, стр. 394, ‍ 453 ; Френель, 1866, стр. 759, 786–7, 790.
^ PR Berman, 2012, "Эффект Гуса-Хенхен", Scholarpedia 7 (3): 11584, § 2.1, особенно уравнения (1) - (3). Обратите внимание, что $n$ Бермана является обратной величиной $n$ в настоящей статье.
^ ab Bliokh, KY; Aiello, A. (2013). "Сдвиги пучка Goos–Hänchen и Imbert–Fedorov: обзор". Journal of Optics . 15 (1): 014001. arXiv : 1210.8236 . Bibcode :2013JOpt...15a4001B. doi :10.1088/2040-8978/15/1/014001. S2CID 118380597.
↑ Дженкинс и Уайт, 1976, стр. 40–42.
^ Rudd, WW (1971). «Фиброоптическая колоноскопия: впечатляющий прогресс в хирургии толстой кишки». Canadian Family Physician . 17 (12): 42–45. PMC 2370306. PMID 20468707 .
^ Левитт, 2013, стр. 79–80.
^ Дженкинс и Уайт, 1976, стр. 26–7 (Порро, Дав, 90 ° Амичи, угловой отражатель, Люммер-Бродхун); Born & Wolf, 1970, стр. 240–41 (Порро, Кениг), 243–4 (Голубь).
↑ Борн и Вольф, 1970, стр. 241.
↑ Борн и Вольф, 1970, стр. 690–91.
^ R. Nave, «Prisms for Polarization» (Nicol, Glan–Foucault), Georgia State University, дата обращения 27 марта 2019 г.; архивировано 25 марта 2019 г.
↑ Дженкинс и Уайт, 1976, стр. 510–511 (Николь, Глан–Томпсон, «Фуко»).
^ JF Archard; AM Taylor (декабрь 1948), «Улучшенная призма Глана-Фуко», Journal of Scientific Instruments , 25 (12): 407–9, Bibcode : 1948JScI...25..407A, doi : 10.1088/0950-7671/25/12/304.
^ Бухвальд, 1989, стр. 19–21; Дженкинс и Уайт, 1976, стр. 27–8.
^ ab "XII. Метод исследования преломляющих и рассеивающих способностей с помощью призматического отражения". Philosophical Transactions of the Royal Society of London . 92 : 365–380. 1802. doi :10.1098/rstl.1802.0014. S2CID 110328209.
^ HELLA GmbH & Co. KGaA, «Проверка датчика дождя и датчика фар – Инструкции по ремонту и диагностика неисправностей», дата обращения 9 апреля 2019 г.; архивировано 8 апреля 2019 г.
^ J. Gourlay, «Making Light Work – Light Sources for Modern Lighting Requirements», LED Professional , дата обращения 29 марта 2019 г.; архивировано 12 апреля 2016 г.
^ Д. Аксельрод (апрель 1981 г.), «Контакты клетка-субстрат, освещенные флуоресценцией полного внутреннего отражения», Журнал клеточной биологии , 89 (1): 141–5, doi :10.1083/jcb.89.1.141, PMC 2111781 , PMID 7014571 .
^ Д. Аксельрод (ноябрь 2001 г.), «Флуоресцентная микроскопия полного внутреннего отражения в клеточной биологии» (PDF) , Traffic , 2 (11): 764–74, doi : 10.1034/j.1600-0854.2001.21104.x, hdl : 2027.42/72779 , PMID 11733042, S2CID 15202097.
^ Хехт, 2017, стр. 138.
^ RW Astheimer; G. Falbel; S. Minkowitz (январь 1966), «Инфракрасная модуляция с помощью нарушенного полного внутреннего отражения», Applied Optics , 5 (1): 87–91, Bibcode : 1966ApOpt...5...87A, doi : 10.1364/AO.5.000087, PMID 20048791.
^ NJ Harrick (1962-3), «Дактилоскопия с помощью полного внутреннего отражения» ^{[ постоянная неработающая ссылка ]} , Philips Technical Review , 24 (9): 271–4; архивировано в январе 2024 г.
^ Noldus Information Technology, «CatWalk™ XT», доступ 29 марта 2019 г.; архив 25 марта 2019 г.
^ Э. Брюс, Р. Бендуре, С. Крейн и Н. Лайтхайзер, «Подробнее о гониоскопии», Review of Оптометрия , 21 сентября 2016 г.
^ Glaucoma Associates of Texas, «Гониоскопия», дата обращения 29 марта 2019 г.; архивировано 22 августа 2018 г.
↑ Бойер, 1959, стр. 110.
^ Камаль ад-Дин аль-Фариси, Танких аль-Маназир (рукопись с автографом, 708 г. хиджры / 1309 г. н.э. ), Коллекция Адилнора.
^ Boyer, 1959, стр. 113, 114, 335. Бойер цитирует издание Дж. Вюршмидта книги Теодориха De iride et radiusibus Impressionibus в Beiträge zur Geschichte der Philosophie des Mittelalters , vol. 12, нет. 5–6 (1914), с. 47.
↑ Бойер, 1959, стр. 307, 335.
↑ E. Mach (пер. ‍ JS Anderson & AFA Young), Принципы физической оптики: историческое и философское рассмотрение (Лондон: Methuen & Co, 1926), перепечатано Mineola, NY: Dover, 2003, стр. 30–32.
↑ AI Sabra, Theories of Light: From Descartes to Newton (Лондон: Oldbourne Book Co., 1967), перепечатано Cambridge University Press, 1981, стр. 111–112.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 39.
^ Гюйгенс, 1690, tr. Томпсон, стр. 40–41. Обратите внимание, что определение Гюйгенсом «угла падения» является дополнением к современному определению.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 39–40.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 40–41.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 16, 42.
↑ Гюйгенс, 1690, пер. Томпсона, стр. 92–94.
↑ Ньютон, 1730, стр. 362.
^ Дарригол, 2012, стр. 93–4, 103.
↑ Ньютон, 1730, стр. 370–71.
↑ Ньютон, 1730, стр. 246. Обратите внимание, что «синус» означал длину стороны для определенного «радиуса» (гипотенузы), тогда как в настоящее время мы принимаем радиус за единицу или выражаем синус как отношение.
↑ Ньютон, 1730, стр. 56–62, 264.
↑ Ньютон, 1730, стр. 371–32.
↑ Ньютон, 1730, стр. 281.
↑ Ньютон, 1730, стр. 373.
↑ Ньютон, 1730, стр. 356.
^ Бухвальд, 1980, стр. 327, 331–2.
^ Бухвальд, 1980, стр. 335–6, 364; Бухвальд, 1989, стр. 9–10, 13.
^ Бухвальд, 1989, стр. 19–21.
^ Бухвальд, 1989, стр. 28.
^ Дарригол, 2012, стр. 187–8.
^ Бухвальд, 1989, стр. 30.
^ Бухвальд, 1980, стр. 29–31.
↑ Э. Франкель (май 1976 г.), «Корпускулярная оптика и волновая теория света: наука и политика революции в физике», Социальные исследования науки , 6 (2): 141–84, на стр. 145.
↑ См. Бухвальд, 1989, стр. 30 (цитируя Малуса)
^ Дарригол, 2012, стр. 193–6, 290.
^ Дарригол, 2012, стр. 206.
^ Этот эффект был ранее обнаружен Брюстером , но пока не был должным образом описан. См.: "On a new species of moving polarization", [Quarterly] Journal of Science and the Arts , т. 2, № 3, 1817, стр. 213; T. Young , "Chromatics", Приложение к четвертому, пятому и шестому изданиям Encyclopaedia Britannica , т. 3 (первая половина, выпущена в феврале 1818 г.), стр. 141–63, на стр. 157; Lloyd, 1834, стр. 368.
^ Дарригол, 2012, стр. 207.
↑ A. Fresnel, «Mémoire sur les modifications que la réflexion imprime à la lumière polarisée» («Воспоминания об изменениях, которые отражение производит на поляризованный свет»), подписано и представлено 10 ноября 1817 г., прочитано 24 ноября 1817 г.; напечатано в Fresnel, 1866, стр. 441–485, включая стр. 452 (повторное открытие деполяризации полным внутренним отражением), 455 (два отражения, «связанные призмы», «параллелепипед в стекле»), 467–48 (разность фаз на отражение); см. также стр. 487, примечание 1, для даты прочтения.
^ Дарригол, 2012, стр. 212.
^ Бухвальд, 1989, стр. 390–91; Френель, 1866, стр. 646–68.
^ А. Френель, «Примечание к расчётам teintes que la поляризации, развивающейся в кристаллических пластинках» и далее, Annales de Chimie et de Physique , Ser. 2, том. 17, стр. 102–11 (май 1821 г.), 167–96 (июнь 1821 г.), 312–15 («Постскриптум», июль 1821 г.); перепечатано Френелем, 1866 г., стр. 609–48; переведено как «О расчете оттенков, возникающих в кристаллических пластинках, и постскриптум», Зенодо : 4058004 , 2021.
^ ab A. Fresnel, "Mémoire sur la loi des modifications que la réflexion imprime à la lumière polarisée" ("Mémoire on the law of the modifications that reflectation imprime on polarized light"), прочитано 7 января 1823 г.; перепечатано в Fresnel, 1866 г., стр. 767–99 (полный текст, опубликован в 1831 г.), стр. 753–62 (выдержка, опубликована в 1823 г.). См. особенно стр. 773 (закон синусов), 757 (закон тангенса), 760–61 и 792–6 (углы полного внутреннего отражения для заданных разностей фаз).
^ Бухвальд, 1989, стр. 391–3; Дарригол, 2012, стр. 212–13; Уиттакер, 1910, стр. 133–5.
^ А. Френель, «Mémoire sur la double refraction que les lumineux éprouvent en traversant les aiguilles de cristal de roche suivant les parts parallèles à l'axe», прочитано 9 декабря 1822 года; напечатано во Френеле, 1866 г., стр. 731–51 (полный текст), стр. 719–29 ( выдержка , впервые опубликованная в Bulletin de la Société philomathique за 1822 г., стр. 191–8); полный текст переведен как «Мемуары о двойном преломлении, которому подвергаются световые лучи при прохождении кварцевых игл в направлениях, параллельных оси», Зенодо : 4745976 , 2021.
^ Бухвальд, 1989, стр. 230–31; Френель, 1866, стр. 744.
^ Ллойд, 1834, стр. 369–70; Бухвальд, 1989, стр. 393–4, 453; Френель, 1866, стр. 781–96.
↑ Френель, 1866, стр. 760–61, 792–6; Уэвелл, 1857, стр. 359.
↑ Френель, 1866, стр. 760–61, 792–3.
↑ Френель, 1866, стр. 761, 793–6; Уэвелл, 1857, стр. 359.
^ Бохнер, 1963, стр. 198–200.
↑ Уиттекер, 1910, стр. 177–179.
^ Бохнер, 1963, стр. 200; Борн и Вольф, 1970, стр. 613.
^ Merriam-Webster, Inc., «critical angle», дата обращения 21 апреля 2019 г. (Первоисточник не указан.)
^ RP Feynman, 1985 (седьмое издание, 1988), QED: Странная теория света и материи , Princeton University Press, в частности, стр. 33, 109–110.

Библиография

С. Бохнер (июнь 1963 г.), «Значение некоторых основных математических концепций для физики», Isis , 54 (2): 179–205; JSTOR 228537.
М. Борн и Э. Вольф, 1970, Основы оптики , 4-е изд., Оксфорд: Pergamon Press.
CB Boyer, 1959, Радуга: от мифа к математике , Нью-Йорк: Томас Йоселофф.
JZ Buchwald (декабрь 1980 г.), «Экспериментальные исследования двойного преломления от Гюйгенса до Малуса», Архив истории точных наук , 21 (4): 311–373.
JZ Buchwald, 1989, Возникновение волновой теории света: оптическая теория и эксперимент в начале девятнадцатого века , Издательство Чикагского университета, ISBN 0-226-07886-8 .
О. Дарригол, 2012, История оптики: от греческой античности до девятнадцатого века , Оксфорд, ISBN 978-0-19-964437-7 .
Р. Фицпатрик, 2013, Колебания и волны: Введение , Бока-Ратон, Флорида: CRC Press, ISBN 978-1-4665-6608-8 .
Р. Фицпатрик, 2013а, «Полное внутреннее отражение», Техасский университет в Остине, дата обращения 14 марта 2018 г.
А. Френель, 1866 (изд. Х. де Сенармон, Э. Верде и Л. Френель), Oeuvres complètes d'Augustin Fresnel , Париж: Imprimerie Impériale (3 тома, 1866–70), том. 1 (1866 г.).
Э. Хехт, 2017, Оптика , 5-е изд., Pearson Education, ISBN 978-1-292-09693-3 .
C. Huygens, 1690, Traité de la Lumière (Лейден: Van der Aa), переведено SP Thompson как Treatise on Light , University of Chicago Press, 1912; Project Gutenberg, 2005. (Указанные номера страниц соответствуют изданию 1912 года и HTML-изданию Gutenberg.)
FA Jenkins и HE White, 1976, Основы оптики , 4-е изд., Нью-Йорк: McGraw-Hill, ISBN 0-07-032330-5 .
TH Levitt, 2013, Короткая яркая вспышка: Огюстен Френель и рождение современного маяка , Нью-Йорк: WW Norton, ISBN 978-0-393-35089-0 .
H. Lloyd, 1834, «Отчет о прогрессе и современном состоянии физической оптики», Отчет Четвертого заседания Британской ассоциации содействия развитию науки (состоявшегося в Эдинбурге в 1834 году), Лондон: J. Murray, 1835, стр. 295–413.
I. Newton, 1730, Opticks: or, a Treatise of the Reflections, Refractions, Inflections, and Colours of Light, 4-е изд. (Лондон: William Innys, 1730; Project Gutenberg, 2010); переиздано с предисловием А. Эйнштейна и введением Э. Т. Уиттекера (Лондон: George Bell & Sons, 1931); переиздано с дополнительным предисловием И. Б. Коэна и аналитическим оглавлением Д. Х. Д. Роллера, Минеола, Нью-Йорк: Дувр, 1952, 1979 (с пересмотренным предисловием), 2012. (Указанные номера страниц соответствуют HTML-изданию Gutenberg и изданиям Дувра.)
HGJ Rutten и MAM van Venrooij, 1988 (пятое издание, 2002), Telescope Optics: A Comprehensive Manual for Amateur Astronomers , Richmond, VA: Willmann-Bell, ISBN 978-0-943396-18-7 .
JA Stratton, 1941, Электромагнитная теория , Нью-Йорк: McGraw-Hill.
У. Уэвелл, 1857, История индуктивных наук: от самых ранних до наших дней , 3-е изд., Лондон: JW Parker & Son, т. 2.
ET Whittaker , 1910, [https://archive.org/details/historyoftheorie00whitrich История теорий эфира и электричества: от эпохи Декарта до конца девятнадцатого века , Лондон: Longmans, Green, & Co.

Внешние ссылки

На Викискладе есть медиафайлы по теме Полное внутреннее отражение.

Г-н Манджиакапре, «Флуоресценция в жидкости» (видео, 1 мин ‍ 28 сек ), загружено 13 марта 2012 г. (Флуоресценция и полное инфракрасное излучение фиолетового лазерного луча в хининовой воде.)
PhysicsatUVM, «Нарушенное полное внутреннее отражение» (видео, 37 сек.), загружено 21 ноября 2011 г. («Лазерный луч испытывает полное внутреннее отражение в запотевшем куске оргстекла...»)
SMUPhysics, «Внутреннее отражение» (видео, 12 с), загружено 20 мая 2010 г. (Переход от преломления через критический угол к ПВО в призме 45°-90°-45°.)