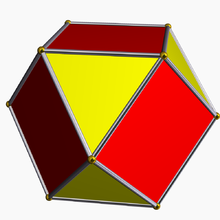
В евклидовой геометрии выпрямление , также известное как критическое усечение или полное усечение , представляет собой процесс усечения многогранника путем маркировки средних точек всех его ребер и отрезания его вершин в этих точках. [1] Полученный многогранник будет ограничен гранями вершинной фигуры и выпрямленными гранями исходного многогранника.
Оператор выпрямления иногда обозначается буквой r с символом Шлефли . Например, r {4,3} — это выпрямленный куб , также называемый кубооктаэдром и также изображаемый как . А выпрямленный кубооктаэдр rr{4,3} представляет собой ромбокубооктаэдр и также обозначается как .
В нотации многогранника Конвея в качестве этого оператора используется for ambo . В теории графов эта операция создает медиальный граф .
Исправление любого правильного самодвойственного многогранника или мозаики приведет к созданию другого правильного многогранника или мозаики с порядком мозаики 4, например, тетраэдр { 3,3} станет октаэдром {3,4}. В частном случае квадратная мозаика {4,4} превратится в другую квадратную мозаику {4,4} в результате операции выпрямления.
Исправление — это финальная точка процесса усечения. Например, на кубе эта последовательность показывает четыре шага континуума усечений между правильной и исправленной формой:
Исправление более высокой степени может быть выполнено на правильных многогранниках более высокой размерности. Высшая степень выпрямления создает двойственный многогранник . Исправление усекает края до точек. Биректификация усекает грани до точек. Трехисправление усекает ячейки до точек и так далее.
Эта последовательность показывает биректифицированный куб как окончательную последовательность перехода от куба к двойственному, где исходные грани усекаются до одной точки:
Двойная форма многоугольника аналогична его выпрямленной форме. Новые вершины размещаются в центре ребер исходного многоугольника.
Каждое платоново тело и его двойник имеют один и тот же выпрямленный многогранник. (Это не относится к многогранникам более высоких размерностей.)
Выпрямленный многогранник оказывается выраженным как пересечение исходного платонового тела с соответствующим масштабом концентрической версией его двойственного тела. По этой причине его название представляет собой сочетание имен оригинала и двойника:
Примеры
Если многогранник неправильный, то средние точки ребер, окружающие вершину, могут быть некомпланарными. Однако в этом случае все еще возможна форма исправления: каждый многогранник имеет многогранный граф в качестве своего 1-скелета , и из этого графа можно сформировать медианный граф , поместив вершину в каждую среднюю точку ребра исходного графа и соединив две из этих новых вершин ребром, если они принадлежат последовательным ребрам вдоль общей грани. Полученный медиальный граф остается многогранником, поэтому по теореме Стейница его можно представить в виде многогранника.
Обозначение многогранника Конвея, эквивалентное выпрямлению , — это ambo , представленное . Двойное применение aa (исправление исправления) — это операция расширения Конвея e , которая аналогична операции кантелляции Джонсона t 0,2 , созданной из правильных многогранников и мозаик.
Каждый выпуклый правильный 4-многогранник имеет выпрямленный вид как равномерный 4-многогранник .
Правильный 4-многогранник {p,q,r} имеет ячейки {p,q}. Его выпрямление будет иметь два типа ячеек: выпрямленный многогранник {p,q}, оставшийся от исходных ячеек, и многогранник {q,r} как новые ячейки, образованные каждой усеченной вершиной.
Однако исправленный {p,q,r} — это не то же самое, что исправленный {r,q,p}. Дальнейшее усечение, называемое битусечением , симметрично между 4-многогранником и его двойственным. См. Равномерный 4-многогранник # Геометрические выводы .
Примеры
Первое исправление усекает ребра до точек. Если многогранник правильный , эта форма представлена расширенным обозначением символа Шлефли t 1 {p,q,...} или r {p,q,...}.
Второе исправление, или биректификация , усекает грани до точек. Если он регулярный, он имеет обозначение t 2 {p,q,...} или 2 r {p,q,...}. Для многогранников биректификация создает двойственный многогранник .
Исправления более высокой степени могут быть построены для многогранников более высокой размерности. В общем случае n-выпрямление усекает n-граней до точек.
Если n-многогранник (n-1)-выпрямлен, его грани сводятся к точкам и многогранник становится ему двойственным .
Для каждой степени ректификации существуют разные эквивалентные обозначения. В этих таблицах показаны имена по измерениям и два типа фасетов для каждого.
Фасеты — это ребра, представленные как {}.
Фасеты — это правильные многоугольники.
Фасеты – это правильные или выпрямленные многогранники.
Фасеты — это правильные или выпрямленные 4-многогранники.
