Горизонт

Видимая кривая, отделяющая землю от неба

На этой фотографии 2008 года, сделанной с борта космического челнока на высоте 226 км (140 миль), хорошо видна кривизна горизонта .

Горизонт — это видимая кривая, которая отделяет поверхность небесного тела от его неба , если смотреть с точки зрения наблюдателя, находящегося на поверхности соответствующего тела или вблизи нее. Эта кривая разделяет все направления наблюдения в зависимости от того, пересекает ли она поверхность соответствующего тела или нет.

Истинный горизонт — это теоретическая линия, которую можно наблюдать с любой степенью точности только тогда, когда она лежит вдоль относительно гладкой поверхности, такой как поверхность океанов Земли . Во многих местах эта линия скрыта рельефом , а на Земле она также может быть скрыта формами жизни, такими как деревья и/или человеческими конструкциями, такими как здания. Полученное пересечение таких препятствий с небом называется видимым горизонтом . На Земле, если смотреть на море с берега, часть моря, ближайшая к горизонту, называется offing . [ ^1]

Истинный горизонт окружает наблюдателя, и обычно предполагается, что это круг, нарисованный на поверхности идеально сферической модели соответствующего небесного тела, т. е. небольшой круг местной соприкасающейся сферы . По отношению к Земле центр истинного горизонта находится ниже наблюдателя и ниже уровня моря . Его радиус или горизонтальное расстояние от наблюдателя немного меняется изо дня в день из-за атмосферной рефракции, на которую сильно влияют погодные условия. Кроме того, чем выше глаза наблюдателя находятся от уровня моря, тем дальше от него горизонт. Например, в стандартных атмосферных условиях для наблюдателя с уровнем глаз выше уровня моря на 1,8 метра (6 футов) горизонт находится на расстоянии около 4,8 километра (3 мили). ^[2] При наблюдении с очень высоких точек, таких как космическая станция , горизонт находится намного дальше и охватывает гораздо большую площадь поверхности Земли. В этом случае горизонт уже не будет представлять собой идеальный круг и даже не будет плоской кривой , такой как эллипс, особенно когда наблюдатель находится над экватором, поскольку поверхность Земли лучше моделировать как сплющенный эллипсоид, чем как сферу.

Этимология

Слово горизонт происходит от греческого ὁρίζων κύκλος ( horízōn kýklos ) «разделяющий круг» ^[3] , где ὁρίζων происходит от глагола ὁρίζω ( horízō ) «разделять, отделять» ^[4] , который в свою очередь происходит от ὅρος ( hóros ) «граница, ориентир» ^{[5] .}

Внешний вид и использование

Вид на океан с двумя кораблями: один на переднем плане и один слева от него на горизонте.

Исторически расстояние до видимого горизонта долгое время было жизненно важным для выживания и успешной навигации, особенно на море, поскольку оно определяло максимальный диапазон зрения наблюдателя и, следовательно, общения , со всеми очевидными последствиями для безопасности и передачи информации, которые подразумевал этот диапазон. Эта важность уменьшилась с развитием радио и телеграфа , но даже сегодня, при полете самолета по визуальным правилам полета , для управления самолетом используется техника, называемая attitude flying , при которой пилот использует визуальную связь между носом самолета и горизонтом для управления самолетом. Пилоты также могут сохранять свою пространственную ориентацию, ссылаясь на горизонт.

Во многих контекстах, особенно в перспективном рисовании , кривизна Земли игнорируется, а горизонт считается теоретической линией, к которой сходятся точки на любой горизонтальной плоскости (при проекции на плоскость изображения) по мере увеличения их расстояния от наблюдателя. Для наблюдателей, находящихся вблизи уровня моря, разница между этим геометрическим горизонтом (который предполагает совершенно плоскую, бесконечную плоскость земли) и истинным горизонтом (который предполагает сферическую поверхность Земли ) незаметна невооруженным глазом. Однако для человека, находящегося на холме высотой 1000 м (3300 футов) и смотрящего на море, истинный горизонт будет примерно на градус ниже горизонтальной линии.

В астрономии горизонт — это горизонтальная плоскость через глаза наблюдателя. Это фундаментальная плоскость горизонтальной системы координат , геометрическое место точек, имеющих высоту в ноль градусов. Хотя в некоторых отношениях он похож на геометрический горизонт, в этом контексте горизонт можно рассматривать как плоскость в пространстве, а не как линию на картинной плоскости.

Расстояние до горизонта

Если не учитывать эффект атмосферной рефракции, расстояние до истинного горизонта от наблюдателя, находящегося близко к поверхности Земли, составляет около ^[2]

${\displaystyle d\approx {\sqrt {2\,h\,R}}\,,}$

где h — высота над уровнем моря, а R — радиус Земли .

Выражение можно упростить следующим образом:

${\displaystyle d\approx k{\sqrt {h}}\,,}$

где константа равна k =3,57 км/м ^½ =1,22 мили/фут ^½ . В этом уравнении предполагается, что поверхность Земли имеет идеально сферическую форму, а R равен примерно 6371 километру (3959 миль).

Примеры

Предположим, что атмосферная рефракция отсутствует, а Земля имеет сферическую форму с радиусом R=6371 километр (3959 миль):

• Для наблюдателя, стоящего на земле на высоте h = 1,70 метра (5 футов 7 дюймов), горизонт находится на расстоянии 4,7 километра (2,9 мили).
• Для наблюдателя, стоящего на земле на высоте h = 2 метра (6 футов 7 дюймов), горизонт находится на расстоянии 5 километров (3,1 мили).
• Для наблюдателя, стоящего на холме или башне на высоте 30 метров (98 футов) над уровнем моря, горизонт находится на расстоянии 19,6 километра (12,2 мили).
• Для наблюдателя, стоящего на холме или башне на высоте 100 метров (330 футов) над уровнем моря, горизонт находится на расстоянии 36 километров (22 мили).
• Для наблюдателя, стоящего на крыше Бурдж-Халифа , на высоте 828 метров (2717 футов) от земли и примерно 834 метра (2736 футов) над уровнем моря, горизонт находится на расстоянии 103 километров (64 мили).
• Для наблюдателя на вершине горы Эверест (высота 8848 метров (29 029 футов)) горизонт находится на расстоянии 336 километров (209 миль).
• Для наблюдателя на борту коммерческого пассажирского самолета, летящего на типичной высоте 35 000 футов (11 000 м), горизонт находится на расстоянии 369 километров (229 миль).
• Для пилота U-2 при полете на высоте 21 000 метров (69 000 футов) горизонт находится на расстоянии 517 километров (321 миля).

Другие планеты

На планетах земной группы и других твердых небесных телах с незначительным влиянием атмосферы расстояние до горизонта для «стандартного наблюдателя» меняется как квадратный корень из радиуса планеты. Так, горизонт на Меркурии находится на 62% дальше от наблюдателя, чем на Земле, на Марсе — на 73%, на Луне — на 52%, на Мимасе — на 18% и т. д.

Вывод

Геометрическая основа расчета расстояния до горизонта, теорема о касательной и секущей

Геометрическое расстояние до горизонта, теорема Пифагора

Три типа горизонта

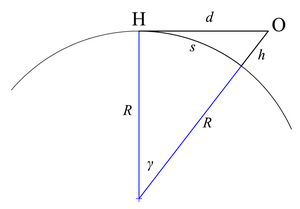
Если предположить, что Земля представляет собой сферу без особенностей (а не сплющенный сфероид ) без атмосферной рефракции, то расстояние до горизонта можно легко рассчитать. ^[6]

Теорема о касательной и секущей утверждает, что

${\displaystyle \mathrm {OC} ^{2}=\mathrm {OA} \times \mathrm {OB} \,.}$

Сделайте следующие замены:

• d = OC = расстояние до горизонта
• D = AB = диаметр Земли
• h = OB = высота наблюдателя над уровнем моря
• D+h = OA = диаметр Земли плюс высота наблюдателя над уровнем моря,

где d, D и h измеряются в тех же единицах. Формула теперь становится

${\displaystyle d^{2}=h(D+h)\,\!}$

или

${\displaystyle d={\sqrt {h(D+h)}}={\sqrt {h(2R+h)}}\,,}$

где R — радиус Земли.

Это же уравнение можно вывести с помощью теоремы Пифагора . На горизонте линия визирования является касательной к Земле и также перпендикулярна радиусу Земли. Это создает прямоугольный треугольник с суммой радиуса и высоты в качестве гипотенузы. С

• d = расстояние до горизонта
• h = высота наблюдателя над уровнем моря
• R = радиус Земли

Обращение ко второму рисунку справа приводит к следующему:

${\displaystyle (R+h)^{2}=R^{2}+d^{2}\,\!}$

${\displaystyle R^{2}+2Rh+h^{2}=R^{2}+d^{2}\,\!}$

${\displaystyle d={\sqrt {h(2R+h)}}\,.}$

Точную формулу выше можно разложить следующим образом:

${\displaystyle d={\sqrt {2Rh+h^{2}}}\,,}$

где R — радиус Земли ( R и h должны быть в одинаковых единицах). Например, если спутник находится на высоте 2000 км, расстояние до горизонта составляет 5430 километров (3370 миль); пренебрежение вторым членом в скобках даст расстояние 5048 километров (3137 миль), ошибка 7%.

Приближение

Графики расстояний до истинного горизонта на Земле для заданной высоты h . s — вдоль поверхности Земли, d — расстояние по прямой, а ~d — приблизительное расстояние по прямой, предполагая, что h << радиус Земли, 6371 км. На изображении SVG наведите курсор на график, чтобы выделить его.

Если наблюдатель находится близко к поверхности Земли, то можно пренебречь h в члене (2 R + h ) , и формула примет вид:

${\displaystyle d={\sqrt {2Rh}}\,.}$

Используя километры для d и R , и метры для h , и принимая радиус Земли равным 6371 км, расстояние до горизонта равно

${\displaystyle d\approx {\sqrt {2\cdot 6371\cdot {h/1000}}}\approx 3.570{\sqrt {h}}\,}$.

Используя имперские единицы измерения , где d и R указаны в уставных милях (обычно используемых на суше), а h — в футах, расстояние до горизонта составляет

${\displaystyle d\approx {\sqrt {2\cdot 3963\cdot {h/5280}}}\approx {\sqrt {1.5h}}\approx 1.22{\sqrt {h}}}$.

Если d выражено в морских милях , а h в футах, постоянный коэффициент составляет около 1,06, что достаточно близко к 1, поэтому его часто игнорируют, что дает:

${\displaystyle d\approx {\sqrt {h}}}$

Эти формулы могут использоваться, когда h намного меньше радиуса Земли (6371 км или 3959 миль), включая все виды с любых горных вершин, самолетов или высотных аэростатов. При заданных константах как метрическая, так и имперская формулы точны с точностью до 1% (см. следующий раздел о том, как получить большую точность). Если h имеет значение по отношению к R , как в случае большинства спутников, то приближение больше недействительно, и требуется точная формула.

Сопутствующие меры

Расстояние дуги

Другое соотношение касается расстояния по дуге большого круга s вдоль изогнутой поверхности Земли до горизонта; это более прямо сопоставимо с географическим расстоянием на карте.

Его можно сформулировать в терминах γ в радианах ,

${\displaystyle s=R\gamma \,;}$

затем

${\displaystyle \cos \gamma =\cos {\frac {s}{R}}={\frac {R}{R+h}}\,.}$

Решение для s дает

${\displaystyle s=R\cos ^{-1}{\frac {R}{R+h}}\,.}$

Расстояние s также можно выразить через расстояние прямой видимости d ; из второго рисунка справа,

${\displaystyle \tan \gamma ={\frac {d}{R}}\,;}$

замена на γ и перестановка дает

${\displaystyle s=R\tan ^{-1}{\frac {d}{R}}\,.}$

Расстояния d и s почти одинаковы, когда высота объекта пренебрежимо мала по сравнению с радиусом (то есть h  ≪  R ).

Зенитный угол

Максимальный зенитный угол для возвышенного наблюдателя в однородной сферической атмосфере

Когда наблюдатель находится на возвышении, зенитный угол горизонта может быть больше 90°. Максимальный видимый зенитный угол достигается, когда луч касается поверхности Земли; из треугольника OCG на рисунке справа,

${\displaystyle \cos \gamma ={\frac {R}{R+h}}}$

где - высота наблюдателя над поверхностью, а - угловое падение горизонта. Он связан с зенитным углом горизонта соотношением: ${\displaystyle h}$ ${\displaystyle \gamma }$ ${\displaystyle z}$

${\displaystyle z=\gamma +90{}^{\circ }}$

Для неотрицательной высоты угол всегда ≥ 90°. ${\displaystyle h}$ ${\displaystyle z}$

Объекты над горизонтом

Геометрическое расстояние до горизонта

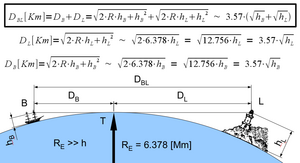
Чтобы вычислить наибольшее расстояние D _BL, на котором наблюдатель B может видеть верхнюю часть объекта L над горизонтом, просто сложите расстояния до горизонта от каждой из двух точек:

ДБЛ = ДБ + ДЛ_​​​

Например, для наблюдателя B высотой h _B =1,70 м, стоящего на земле, расстояние до горизонта составляет D _B =4,65 км. Для башни высотой h _L =100 м расстояние до горизонта составляет D _L =35,7 км. Таким образом, наблюдатель на пляже может видеть вершину башни, пока она находится на расстоянии не более D _BL =40,35 км. И наоборот, если наблюдатель на лодке ( h _B =1,7  м) может видеть только верхушки деревьев на близлежащем берегу ( h _L =10  м), то деревья, вероятно, находятся на расстоянии D _BL =16 км.

Обращаясь к рисунку справа и используя приведенное выше приближение, можно сказать, что вершина маяка будет видна впередсмотрящему в вороньем гнезде на вершине мачты судна, если

${\displaystyle D_{\mathrm {BL} }<3.57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,,}$

где D _BL измеряется в километрах, а h _B и h _L измеряются в метрах.

Вид на залив шириной 20 километров (12 миль) на побережье Испании. Обратите внимание на кривизну Земли, скрывающую основания зданий на дальнем берегу.

Корабль уходит за горизонт.

В качестве другого примера предположим, что наблюдатель, чьи глаза находятся на высоте двух метров над уровнем земли, использует бинокль, чтобы посмотреть на далекое здание, которое, как он знает, состоит из тридцати этажей , каждый высотой 3,5 метра. Он подсчитывает этажи, которые он может видеть, и обнаруживает, что их всего десять. Таким образом, двадцать этажей или 70 метров здания скрыты от него кривизной Земли. Из этого он может рассчитать свое расстояние до здания:

${\displaystyle D\approx 3.57({\sqrt {2}}+{\sqrt {70}})}$

что составляет около 35 километров.

Аналогичным образом можно вычислить, какая часть удаленного объекта видна над горизонтом. Предположим, что глаз наблюдателя находится на высоте 10 метров над уровнем моря, и он наблюдает за судном, находящимся на расстоянии 20 км. Его горизонт:

${\displaystyle 3.57{\sqrt {10}}}$

километров от него, что составляет около 11,3 километров. Корабль находится еще на 8,7 км дальше. Высота точки на корабле, которая едва видна наблюдателю, определяется по формуле:

${\displaystyle h\approx \left({\frac {8.7}{3.57}}\right)^{2}}$

что составляет почти ровно шесть метров. Таким образом, наблюдатель может видеть ту часть корабля, которая находится более чем на шесть метров выше уровня воды. Часть корабля, которая находится ниже этой высоты, скрыта от него кривизной Земли. В этой ситуации говорят, что корабль находится в положении « корпус вниз» .

Эффект атмосферной рефракции

Из-за атмосферной рефракции расстояние до видимого горизонта больше расстояния, основанного на простом геометрическом расчете. Если поверхность земли (или воды) холоднее воздуха над ней, холодный, плотный слой воздуха образуется близко к поверхности, заставляя свет преломляться вниз по мере его перемещения и, следовательно, в некоторой степени огибать кривизну Земли. Обратное происходит, если земля горячее воздуха над ней, как это часто случается в пустынях, создавая миражи . В качестве приблизительной компенсации рефракции геодезисты, измеряющие расстояния более 100 метров, вычитают 14% из вычисленной погрешности кривизны и обеспечивают, чтобы линии визирования находились на расстоянии не менее 1,5 метра от земли, чтобы уменьшить случайные ошибки, создаваемые рефракцией.

Типичный пустынный горизонт

Если бы Земля была безвоздушным миром, как Луна, приведенные выше расчеты были бы точными. Однако у Земли есть атмосфера из воздуха , плотность и показатель преломления которого значительно изменяются в зависимости от температуры и давления. Это заставляет воздух преломлять свет в разной степени, влияя на внешний вид горизонта. Обычно плотность воздуха непосредственно над поверхностью Земли больше, чем его плотность на больших высотах. Это делает его показатель преломления больше вблизи поверхности, чем на больших высотах, что приводит к тому, что свет, распространяющийся примерно горизонтально, преломляется вниз. ^[7] Это делает фактическое расстояние до горизонта больше, чем расстояние, рассчитанное с помощью геометрических формул. При стандартных атмосферных условиях разница составляет около 8%. Это изменяет коэффициент 3,57 в метрических формулах, использованных выше, примерно на 3,86. ^[2] Например, если наблюдатель стоит на берегу моря, его глаза находятся на высоте 1,70 м над уровнем моря, то согласно простым геометрическим формулам, приведенным выше, расстояние до горизонта должно быть 4,7 км. На самом деле атмосферная рефракция позволяет наблюдателю видеть на 300 метров дальше, отодвигая истинный горизонт на 5 км от наблюдателя.

Эта поправка может быть и часто применяется как довольно хорошее приближение, когда атмосферные условия близки к стандартным . Когда условия необычны, это приближение не работает. На рефракцию сильно влияют температурные градиенты, которые могут значительно меняться изо дня в день, особенно над водой. В экстремальных случаях, обычно весной, когда теплый воздух покрывает холодную воду, рефракция может позволить свету следовать за поверхностью Земли на сотни километров. Противоположные условия возникают, например, в пустынях, где поверхность очень горячая, поэтому горячий воздух низкой плотности находится под более холодным воздухом. Это заставляет свет преломляться вверх, вызывая эффекты миража , которые делают концепцию горизонта несколько бессмысленной. Поэтому расчетные значения эффектов рефракции в необычных условиях являются лишь приблизительными. ^[2] Тем не менее, были предприняты попытки рассчитать их более точно, чем простое приближение, описанное выше.

За пределами визуального диапазона длин волн рефракция будет иной. Для радара (например, для длин волн от 300 до 3 мм, т.е. частот от 1 до 100 ГГц) радиус Земли можно умножить на 4/3, чтобы получить эффективный радиус, что даст коэффициент 4,12 в метрической формуле, т.е. горизонт радара будет на 15% за пределами геометрического горизонта или на 7% за пределами визуального. Коэффициент 4/3 не является точным, так как в визуальном случае рефракция зависит от атмосферных условий.

Метод интеграции — Sweer

Если профиль плотности атмосферы известен, расстояние d до горизонта определяется по формуле ^[8]

${\displaystyle d={{R}_{\text{E}}}\left(\psi +\delta \right)\,,}$

где R _E — радиус Земли, ψ — наклон горизонта, а δ — рефракция горизонта. Наклон определяется довольно просто из

${\displaystyle \cos \psi ={\frac {{R}_{\text{E}}{\mu }_{0}}{\left({{R}_{\text{E}}}+h\right)\mu }}\,,}$

где h — высота наблюдателя над Землей, μ — показатель преломления воздуха на высоте наблюдателя, а μ ₀ — показатель преломления воздуха у поверхности Земли.

Рефракцию необходимо найти путем интегрирования

${\displaystyle \delta =-\int _{0}^{h}{\tan \phi {\frac {{\text{d}}\mu }{\mu }}}\,,}$

где - угол между лучом и линией, проходящей через центр Земли. Углы ψ и связаны соотношением ${\displaystyle \phi \,\!}$ ${\displaystyle \phi \,\!}$

${\displaystyle \phi =90{}^{\circ }-\psi \,.}$

Простой метод — Янг

_{Гораздо более простой подход, который дает по сути те же результаты, что и} описанное выше приближение первого порядка, использует геометрическую модель, но использует радиус R′ = 7/6 RE . Расстояние до горизонта тогда равно ^[2]

${\displaystyle d={\sqrt {2R^{\prime }h}}\,.}$

Принимая радиус Земли равным 6371 км, где d в км, а h в м,

${\displaystyle d\approx 3.86{\sqrt {h}}\,;}$

с d в милях и h в футах,

${\displaystyle d\approx 1.32{\sqrt {h}}\,.}$

В случае радара обычно R′ = 4/3 R _E , что приводит (где d в км и h в м) к

${\displaystyle d\approx 4.12{\sqrt {h}}\,;}$

Результаты метода Янга довольно близки к результатам метода Свира и достаточно точны для многих целей.

Точки схода

Две точки на горизонте находятся на пересечениях линий, продолжающих сегменты, представляющие края здания на переднем плане. Линия горизонта здесь совпадает с линией в верхней части дверей и окон.

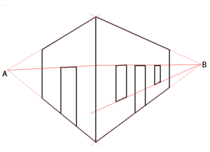
Горизонт является ключевой особенностью плоскости изображения в науке графической перспективы . Предполагая, что плоскость изображения расположена вертикально к земле, а P является перпендикулярной проекцией точки глаза O на плоскость изображения, горизонт определяется как горизонтальная линия, проходящая через P. Точка P является точкой схода линий, перпендикулярных изображению. Если S является другой точкой на горизонте, то это точка схода для всех линий, параллельных OS . Но Брук Тейлор (1719) указал, что плоскость горизонта определяется точкой O , а горизонт был подобен любой другой плоскости :

Термин «горизонтальная линия», например, склонен ограничивать понятия учащегося плоскостью горизонта и заставлять его воображать, что эта плоскость обладает некоторыми особыми привилегиями, которые делают фигуры на ней более легкими и удобными для описания с помощью этой горизонтальной линии, чем фигуры на любой другой плоскости;… Но в этой книге я не делаю никакого различия между плоскостью горизонта и любой другой плоскостью... ^{[9] [10]}

Своеобразная геометрия перспективы, где параллельные линии сходятся на расстоянии, стимулировала развитие проективной геометрии , которая постулирует точку в бесконечности , где параллельные линии встречаются. В своей книге «Геометрия искусства » (2007) Кирсти Андерсен описала эволюцию перспективного рисунка и науки до 1800 года, отметив, что точки схода не обязательно должны быть на горизонте. В главе под названием «Горизонт» Джон Стиллвелл рассказал, как проективная геометрия привела к геометрии инцидентности , современному абстрактному изучению пересечения линий. Стиллвелл также рискнул заняться основами математики в разделе под названием «Каковы законы алгебры?» «Алгебра точек», первоначально данная Карлом фон Штаудтом, выводящим аксиомы поля , была деконструирована в двадцатом веке, что дало широкий спектр математических возможностей. Стиллвелл утверждает

Это открытие 100-летней давности, кажется, способно перевернуть математику с ног на голову, хотя оно еще не полностью усвоено математическим сообществом. Оно не только бросает вызов тенденции превращения геометрии в алгебру, но и предполагает, что и геометрия, и алгебра имеют более простую основу, чем считалось ранее. ^[11]

Смотрите также

• Воздушное ландшафтное искусство
• Рефракция атмосферы
• Рассвет
• Сумерки
• Горизонтальные и вертикальные
• Пейзаж
  • Ландшафтное искусство
• Конечность
  • Потемнение конечностей
  • Лунный лимб
• Радарный горизонт
• Радиогоризонт
• секстант
• Горизонт

Ссылки

1. "Offing". Третий новый международный словарь Вебстера (несокращенное издание).Произносится как «Хор-И-зон».
2. Янг, Эндрю Т. "Расстояние до горизонта". Веб-сайт Green Flash (Разделы: Астрономическая рефракция, Группировка горизонта) . Кафедра астрономии Университета штата Сан-Диего. Архивировано из оригинала 18 октября 2003 г. Получено 16 апреля 2011 г.
3. Лидделл, Генри Джордж; Скотт, Роберт. "ὁρίζων". Греко-английский лексикон . Perseus Digital Library . Архивировано из оригинала 5 июня 2011 г. Получено 19 апреля 2011 г.
4. Лидделл, Генри Джордж; Скотт, Роберт. "ὁρίζω". Греко-английский лексикон . Perseus Digital Library . Архивировано из оригинала 5 июня 2011 г. Получено 19 апреля 2011 г.
5. Лидделл, Генри Джордж; Скотт, Роберт. "ὅρος". Греко-английский лексикон . Perseus Digital Library. Архивировано из оригинала 5 июня 2011 г. Получено 19 апреля 2011 г.
6. Plait, Phil (15 января 2009 г.). «Как далеко находится горизонт?». Discover . Bad Astronomy. Kalmbach Publishing Co. Архивировано из оригинала 29 марта 2017 г. Получено 28.03.2017 .
7. Проктор, Ричард Энтони; Раньярд, Артур Каупер (1892). Старая и новая астрономия. Longmans, Green and Company. С. 73.
8. Свир, Джон (1938). «Путь луча света, касательного к поверхности Земли». Журнал оптического общества Америки . 28 (9): 327–329. Bibcode : 1938JOSA...28..327S. doi : 10.1364/JOSA.28.000327.
9. Тейлор, Брук. Новые принципы перспективы . стр. 1719.
10. Андерсон, Кирсти (1991). «Работа Брука Тейлора о линейной перспективе». Springer. стр. 151. ISBN 0-387-97486-5.
11. Стиллвелл, Джон (2006). «Тоска по невозможному» . Горизонт . AK Peters, Ltd. стр. 47–76. ISBN 1-56881-254-X.

Дальнейшее чтение

• Янг, Эндрю Т. "Dip of the Horizon". Веб-сайт Green Flash (Разделы: Астрономическая рефракция, Группировка горизонта) . Кафедра астрономии Университета штата Сан-Диего . Получено 16 апреля 2011 г.