Изопериметрическое неравенство

Геометрическое неравенство, устанавливающее нижнюю границу площади поверхности множества по его объему.

В математике изопериметрическое неравенство — это геометрическое неравенство, включающее периметр множества и его объем. В -мерном пространстве неравенство ограничивает снизу площадь поверхности или периметр множества его объемом , ${\displaystyle n}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \operatorname {per} (S)}$ ${\displaystyle S\subset \mathbb {R} ^{n}}$ ${\displaystyle \operatorname {vol} (S)}$

${\displaystyle \operatorname {per} (S)\geq n\operatorname {vol} (S)^{(n-1)/n}\,\operatorname {vol} (B_{1})^{1/n}}$,

где — единичная сфера . Равенство выполняется только тогда, когда — сфера в . ${\displaystyle B_{1}\subset \mathbb {R} ^{n}}$ ${\displaystyle S}$ ${\displaystyle \mathbb {R} ^{n}}$

На плоскости, т.е. когда , изопериметрическое неравенство связывает квадрат окружности замкнутой кривой и площадь плоской области, которую она охватывает. Изопериметрическое буквально означает «имеющий тот же периметр ». В частности , в изопериметрическое неравенство устанавливает для длины L замкнутой кривой и площади A плоской области, которую она охватывает, что ${\displaystyle n=2}$ ${\displaystyle \mathbb {R} ^{2}}$

${\displaystyle L^{2}\geq 4\pi A,}$

и это равенство выполняется тогда и только тогда, когда кривая является окружностью.

Изопериметрическая задача заключается в определении плоской фигуры наибольшей возможной площади, граница которой имеет указанную длину. ^[1] Близкая к ней задача Дидоны требует область максимальной площади, ограниченную прямой линией и криволинейной дугой , концы которой принадлежат этой линии. Она названа в честь Дидоны , легендарной основательницы и первой царицы Карфагена . Решение изопериметрической задачи дается окружностью и было известно уже в Древней Греции . Однако первое математически строгое доказательство этого факта было получено только в 19 веке. С тех пор было найдено много других доказательств.

Изопериметрическая задача была расширена несколькими способами, например, на кривые на поверхностях и на области в многомерных пространствах. Возможно, наиболее знакомым физическим проявлением трехмерного изопериметрического неравенства является форма капли воды. А именно, капля обычно принимает симметричную круглую форму. Поскольку количество воды в капле фиксировано, поверхностное натяжение заставляет каплю принимать форму, которая минимизирует площадь поверхности капли, а именно круглую сферу.

Изопериметрическая задача на плоскости

Если область не является выпуклой, «вмятину» на ее границе можно «перевернуть», чтобы увеличить площадь области, сохранив при этом периметр неизменным.

Вытянутую форму можно сделать более круглой, сохранив ее периметр и увеличив площадь.

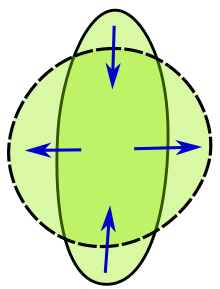
Классическая изопериметрическая задача восходит к античности. ^[2] Задача может быть сформулирована следующим образом: Среди всех замкнутых кривых на плоскости фиксированного периметра, какая кривая (если таковая имеется) максимизирует площадь своей замкнутой области? Можно показать, что этот вопрос эквивалентен следующей задаче: Среди всех замкнутых кривых на плоскости, охватывающей фиксированную область, какая кривая (если таковая имеется) минимизирует периметр?

Эта проблема концептуально связана с принципом наименьшего действия в физике , поскольку ее можно переформулировать: каков принцип действия, который охватывает наибольшую площадь с наибольшей экономией усилий? ^{[ требуется ссылка ]} Философ и ученый XV века кардинал Николай Кузанский считал вращательное действие, процесс, посредством которого образуется круг , наиболее прямым отражением, в сфере чувственных впечатлений, процесса, посредством которого создается Вселенная. Немецкий астроном и астролог Иоганн Кеплер применил изопериметрический принцип при обсуждении морфологии Солнечной системы в Mysterium Cosmographicum ( Священная тайна космоса , 1596).

Хотя окружность кажется очевидным решением проблемы, доказать этот факт довольно сложно. Первый прогресс в решении был достигнут швейцарским геометром Якобом Штейнером в 1838 году с помощью геометрического метода, позже названного симметризацией Штейнера . ^[3] Штейнер показал, что если решение существует, то это должна быть окружность. Доказательство Штейнера было позже завершено несколькими другими математиками.

Штейнер начинает с некоторых геометрических конструкций, которые легко понять; например, можно показать, что любая замкнутая кривая, охватывающая область, которая не является полностью выпуклой, может быть изменена для охвата большей площади путем «переворачивания» вогнутых областей так, чтобы они стали выпуклыми. Можно также показать, что любая замкнутая кривая, которая не является полностью симметричной, может быть «наклонена» так, чтобы она охватывала большую площадь. Единственная фигура, которая является идеально выпуклой и симметричной, — это круг, хотя это само по себе не представляет строгого доказательства изопериметрической теоремы (см. внешние ссылки).

В самолете

Решение изопериметрической задачи обычно выражается в виде неравенства , связывающего длину L замкнутой кривой и площадь A плоской области, которую она охватывает. Изопериметрическое неравенство утверждает, что

${\displaystyle 4\pi A\leq L^{2},}$

и что равенство выполняется тогда и только тогда, когда кривая является окружностью. Площадь диска радиусом R равна πR ² , а длина окружности равна 2 πR , поэтому обе стороны неравенства равны 4 π ² R ² в этом случае.

Были найдены десятки доказательств изопериметрического неравенства. В 1902 году Гурвиц опубликовал короткое доказательство с использованием ряда Фурье , которое применяется к произвольным спрямляемым кривым (не предполагая, что они гладкие). Элегантное прямое доказательство, основанное на сравнении гладкой простой замкнутой кривой с подходящей окружностью, было дано Э. Шмидтом в 1938 году. Оно использует только формулу длины дуги , выражение для площади плоской области из теоремы Грина и неравенство Коши–Шварца .

Для данной замкнутой кривой изопериметрический коэффициент определяется как отношение ее площади к площади круга с тем же периметром. Это равно

${\displaystyle Q={\frac {4\pi A}{L^{2}}}}$

а изопериметрическое неравенство гласит, что Q ≤ 1. Эквивалентно, изопериметрическое отношение L ² / A составляет не менее 4 π для каждой кривой.

Изопериметрическое отношение правильного n -угольника равно

${\displaystyle Q_{n}={\frac {\pi }{n\tan(\pi /n)}}.}$

Пусть — гладкая регулярная выпуклая замкнутая кривая. Тогда улучшенное изопериметрическое неравенство утверждает следующее ${\displaystyle C}$

${\displaystyle L^{2}\geqslant 4\pi A+8\pi \left|{\widetilde {A}}_{0.5}\right|,}$

где обозначают длину , площадь области, ограниченной , и ориентированную площадь каустики Вигнера , соответственно, и равенство выполняется тогда и только тогда, когда является кривой постоянной ширины . ^[4] ${\displaystyle L,A,{\widetilde {A}}_{0.5}}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle C}$ ${\displaystyle C}$

На сфере

Пусть C — простая замкнутая кривая на сфере радиуса 1. Обозначим через L длину C , а через A — площадь, ограниченную C. Сферическое изопериметрическое неравенство утверждает, что

${\displaystyle L^{2}\geq A(4\pi -A),}$

и что равенство выполняется тогда и только тогда, когда кривая является окружностью. На самом деле, есть два способа измерить сферическую площадь, заключенную в простую замкнутую кривую, но неравенство симметрично относительно взятия дополнения.

Это неравенство было обнаружено Полем Леви (1919), который также распространил его на более высокие измерения и общие поверхности. ^[5]

В более общем случае произвольного радиуса R известно ^[6] , что

${\displaystyle L^{2}\geq 4\pi A-{\frac {A^{2}}{R^{2}}}.}$

В евклидовом пространстве

Изопериметрическое неравенство утверждает, что сфера имеет наименьшую площадь поверхности на заданный объем. При наличии ограниченного множества с площадью поверхности и объемом изопериметрическое неравенство утверждает ${\displaystyle S\subset \mathbb {R} ^{n}}$ ${\displaystyle \operatorname {per} (S)}$ ${\displaystyle \operatorname {vol} (S)}$

${\displaystyle \operatorname {per} (S)\geq n\operatorname {vol} (S)^{(n-1)/n}\,\operatorname {vol} (B_{1})^{1/n},}$

где — единичный шар . Равенство выполняется, когда — шар в . При дополнительных ограничениях на множество (таких как выпуклость , регулярность , гладкая граница ) равенство выполняется только для шара. Но в полной общности ситуация более сложная. Соответствующий результат Шмидта (1949, раздел 20.7) (более простое доказательство см. у Бэблера (1957)) поясняется в работе Хадвигера (1957, раздел 5.2.5) следующим образом. Экстремальное множество состоит из шара и «короны», которая не вносит вклад ни в объем, ни в площадь поверхности. То есть равенство выполняется для компактного множества тогда и только тогда, когда содержит замкнутый шар такой, что и Например, «корона» может быть кривой. ${\displaystyle B_{1}\subset \mathbb {R} ^{n}}$ ${\displaystyle S}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle S}$ ${\displaystyle S}$ ${\displaystyle B}$ ${\displaystyle \operatorname {vol} (B)=\operatorname {vol} (S)}$ ${\displaystyle \operatorname {per} (B)=\operatorname {per} (S).}$

Доказательство неравенства следует непосредственно из неравенства Брунна–Минковского между множеством и шаром радиуса , т. е . Возводя неравенство Брунна–Минковского в степень , вычитая из обеих частей, разделяя их на и взяв предел как (Оссерман (1978); Федерер (1969, §3.2.43)). ${\displaystyle S}$ ${\displaystyle \epsilon }$ ${\displaystyle B_{\epsilon }=\epsilon B_{1}}$ ${\displaystyle n}$ ${\displaystyle \operatorname {vol} (S)}$ ${\displaystyle \epsilon }$ ${\displaystyle \epsilon \to 0.}$

В полной общности (Федерер 1969, §3.2.43) изопериметрическое неравенство утверждает, что для любого множества , замыкание которого имеет конечную меру Лебега ${\displaystyle S\subset \mathbb {R} ^{n}}$

${\displaystyle n\,\omega _{n}^{1/n}L^{n}({\bar {S}})^{(n-1)/n}\leq M_{*}^{n-1}(\partial S)}$

где — ( n -1)-мерное содержание Минковского , L ⁿ — n -мерная мера Лебега, а ω n — объем единичного шара в . Если граница S спрямляема , _то содержание Минковского — это ( n -1 ) -мерная мера Хаусдорфа . ${\displaystyle M_{*}^{n-1}}$ ${\displaystyle \mathbb {R} ^{n}}$

n -мерное изопериметрическое неравенство эквивалентно (для достаточно гладких областей) неравенству Соболева на с оптимальной константой: ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle \left(\int _{\mathbb {R} ^{n}}|u|^{n/(n-1)}\right)^{(n-1)/n}\leq n^{-1}\omega _{n}^{-1/n}\int _{\mathbb {R} ^{n}}|\nabla u|}$

для всех . ${\displaystyle u\in W^{1,1}(\mathbb {R} ^{n})}$

В многообразиях Адамара

Адамаровы многообразия являются полными односвязными многообразиями с неположительной кривизной. Таким образом, они обобщают евклидово пространство , которое является адамаровым многообразием с нулевой кривизной. В 1970-х и начале 80-х годов Тьерри Обен , Миша Громов , Юрий Бураго и Виктор Залгаллер выдвинули гипотезу, что евклидово изопериметрическое неравенство ${\displaystyle \mathbb {R} ^{n}}$

${\displaystyle \operatorname {per} (S)\geq n\operatorname {vol} (S)^{(n-1)/n}\operatorname {vol} (B_{1})^{1/n}}$

справедливо для ограниченных множеств в многообразиях Адамара, что стало известно как гипотеза Картана–Адамара . В размерности 2 это уже было установлено в 1926 году Андре Вейлем , который в то время был учеником Адамара . В размерностях 3 и 4 гипотеза была доказана Брюсом Кляйнером в 1992 году и Крисом Кроуком в 1984 году соответственно. ${\displaystyle S}$

В метрическом пространстве мер

Большая часть работы по изопериметрической проблеме была проделана в контексте гладких областей в евклидовых пространствах или, в более общем смысле, в римановых многообразиях . Однако изопериметрическую проблему можно сформулировать в гораздо большей общности, используя понятие содержания Минковского . Пусть будет метрическим мерным пространством : X — метрическое пространство с метрикой d , а μ — борелевская мера на X. Граничная мера , или содержание Минковского , измеримого подмножества A из X определяется как lim inf ${\displaystyle (X,\mu ,d)}$

${\displaystyle \mu ^{+}(A)=\liminf _{\varepsilon \to 0+}{\frac {\mu (A_{\varepsilon })-\mu (A)}{\varepsilon }},}$

где

${\displaystyle A_{\varepsilon }=\{x\in X|d(x,A)\leq \varepsilon \}}$

является ε - расширением A.

Изопериметрическая задача в X спрашивает, насколько малым может быть заданное μ ( A ). Если X — это евклидова плоскость с обычным расстоянием и мерой Лебега , то этот вопрос обобщает классическую изопериметрическую задачу на плоские области, граница которых не обязательно гладкая, хотя ответ оказывается тем же самым. ${\displaystyle \mu ^{+}(A)}$

Функция

${\displaystyle I(a)=\inf\{\mu ^{+}(A)|\mu (A)=a\}}$

называется изопериметрическим профилем метрического мерного пространства . Изопериметрические профили изучались для графов Кэли дискретных групп и для специальных классов римановых многообразий (где обычно рассматриваются только области A с регулярной границей). ${\displaystyle (X,\mu ,d)}$

Для графиков

В теории графов изопериметрические неравенства лежат в основе изучения графов-расширителей , которые являются разреженными графами , обладающими сильными связными свойствами. Конструкции-расширители породили исследования в области чистой и прикладной математики, с несколькими приложениями к теории сложности , проектированию надежных компьютерных сетей и теории кодов с исправлением ошибок . ^[7]

Изопериметрические неравенства для графов связывают размер подмножеств вершин с размером их границы, который обычно измеряется числом ребер, выходящих из подмножества (расширение ребер) или числом соседних вершин (расширение вершин). Для графа и числа ниже приведены два стандартных изопериметрических параметра для графов. ^[8] ${\displaystyle G}$ ${\displaystyle k}$

• Изопериметрический параметр края: $${\displaystyle \Phi _{E}(G,k)=\min _{S\subseteq V}\left\{|E(S,{\overline {S}})|:|S|=k\right\}}$$
• Изопериметрический параметр вершины: $${\displaystyle \Phi _{V}(G,k)=\min _{S\subseteq V}\left\{|\Gamma (S)\setminus S|:|S|=k\right\}}$$

Здесь обозначает множество ребер, выходящих из , а обозначает множество вершин, имеющих соседа в . Изопериметрическая задача состоит в понимании того, как ведут себя параметры и для естественных семейств графов. ${\displaystyle E(S,{\overline {S}})}$ ${\displaystyle S}$ ${\displaystyle \Gamma (S)}$ ${\displaystyle S}$ ${\displaystyle \Phi _{E}}$ ${\displaystyle \Phi _{V}}$

Пример: Изопериметрические неравенства для гиперкубов

-мерный гиперкуб — ​​это граф, вершинами которого являются все булевы векторы длины , то есть множество . Два таких вектора соединены ребром в , если они равны с точностью до одного битового переворота, то есть их расстояние Хэмминга равно единице. Ниже приведены изопериметрические неравенства для булева гиперкуба. [ ^9] ${\displaystyle d}$ ${\displaystyle Q_{d}}$ ${\displaystyle d}$ ${\displaystyle \{0,1\}^{d}}$ ${\displaystyle Q_{d}}$

Изопериметрическое неравенство края

Изопериметрическое неравенство ребра гиперкуба равно . Эта граница точная, о чем свидетельствует каждый набор , который является набором вершин любого подкуба . ${\displaystyle \Phi _{E}(Q_{d},k)\geq k(d-\log _{2}k)}$ ${\displaystyle S}$ ${\displaystyle Q_{d}}$

Вершинное изопериметрическое неравенство

Теорема Харпера ^[10] гласит, что шары Хэмминга имеют наименьшую вершинную границу среди всех множеств заданного размера. Шары Хэмминга — это множества, которые содержат все точки веса Хэмминга не более и не содержат точек веса Хэмминга больше, чем для некоторого целого числа . Эта теорема подразумевает, что любое множество с ${\displaystyle r}$ ${\displaystyle r+1}$ ${\displaystyle r}$ ${\displaystyle S\subseteq V}$

${\displaystyle |S|\geq \sum _{i=0}^{r}{d \choose i}}$

удовлетворяет

${\displaystyle |S\cup \Gamma (S)|\geq \sum _{i=0}^{r+1}{d \choose i}.}$^[11]

В качестве особого случая рассмотрим набор размеров вида ${\displaystyle k=|S|}$

${\displaystyle k={d \choose 0}+{d \choose 1}+\dots +{d \choose r}}$

для некоторого целого числа . Тогда вышеизложенное подразумевает, что точный вершинный изопериметрический параметр равен ${\displaystyle r}$

${\displaystyle \Phi _{V}(Q_{d},k)={d \choose r+1}.}$^[12]

Изопериметрическое неравенство для треугольников

Изопериметрическое неравенство для треугольников относительно периметра p и площади T гласит, что ^[13]

${\displaystyle p^{2}\geq 12{\sqrt {3}}\cdot T,}$

с равенством для равностороннего треугольника . Это подразумевается через неравенство AM–GM , более сильным неравенством, которое также называется изопериметрическим неравенством для треугольников: ^[14]

${\displaystyle T\leq {\frac {\sqrt {3}}{4}}(abc)^{2/3}.}$

Смотрите также

• Математический портал

• Теорема Бляшке–Лебега
• Задача Чаплыгина : изопериметрическая задача — случай задачи Чаплыгина при нулевой скорости ветра.
• Поток, сокращающий кривую
• Расширяющий график
• Гауссово изопериметрическое неравенство
• Изопериметрическое измерение
• Изопериметрическая точка
• Список неравенств треугольника
• Теорема о плоском сепараторе
• Смешанный объем

Примечания

1. Blåsjö, Viktor (2005). «Эволюция изопериметрической проблемы». Amer. Math. Monthly . 112 (6): 526–566. doi :10.2307/30037526. JSTOR  30037526.
2. Олмо, Карлос Бельтран, Ирен (4 января 2021 г.). «Собре товарищи и митос». Эль Паис (на испанском языке) . Проверено 14 января 2021 г.{{cite web}}: CS1 maint: multiple names: authors list (link)
3. Дж. Штайнер, Einfacher Beweis der isoperimetrischen Hauptsätze , J. Reine Angew Math. 18 , (1838), стр. 281–296; и Gesammelte Werke Vol. 2, стр. 77–91, Раймер, Берлин (1882).
4. Звежинский, Михал (2016). «Улучшенное изопериметрическое неравенство и каустика Вигнера плоских овалов». J. Math. Anal. Appl . 442 (2): 726–739. arXiv : 1512.06684 . doi :10.1016/j.jmaa.2016.05.016. S2CID  119708226.
5. Громов, Михаил; Пансу, Пьер (2006). "Приложение C. Изопериметрическое неравенство Пола Леви". Метрические структуры для римановых и неримановых пространств . Современная классика Биркхойзера. Дордрехт: Springer. стр. 519. ISBN 9780817645830.
6. Оссерман, Роберт . «Изопериметрическое неравенство». Бюллетень Американского математического общества. 84.6 (1978) http://www.ams.org/journals/bull/1978-84-06/S0002-9904-1978-14553-4/S0002-9904-1978-14553-4.pdf
7. Хори, Линиал и Виджерсон (2006)
8. Определения 4.2 и 4.3 Hoory, Linial & Widgerson (2006)
9. См. Bollobás (1986) и раздел 4 в Hoory, Linial & Widgerson (2006)
10. См. Калабро (2004) или Боллобас (1986)
11. см. Лидер (1991)
12. Также указано в Hoory, Linial & Widgerson (2006)
13. Чакериан, ГД «Искаженный взгляд на геометрию». Гл. 7 в Mathematical Plums (редактор Р. Хонсбергер). Вашингтон, округ Колумбия: Математическая ассоциация Америки, 1979: 147.
14. Драгутин Свртан и Дарко Велян, «Неевклидовы версии некоторых классических неравенств треугольника», Forum Geometricorum 12, 2012, 197–209. http://forumgeom.fau.edu/FG2012volume12/FG201217.pdf

Ссылки

• Блашке и Лейхтвайс, Elementare Differentialgeometrie (на немецком языке), 5-е издание, полностью переработанное К. Лейхтвайсом. Die Grundlehren der mathematischen Wissenschaften, Band 1. Springer-Verlag , Нью-Йорк, Гейдельберг, Берлин, 1973, ISBN 0-387-05889-3 
• Bollobás, Béla (1986). Комбинаторика: системы множеств, гиперграфы, семейства векторов и комбинаторная вероятность . Cambridge University Press. ISBN 978-0-521-33703-8.
• Бураго (2001) [1994], "Изопериметрическое неравенство", Энциклопедия математики , EMS Press
• Калабро, Крис (2004). "Теорема Харпера" (PDF) . Получено 8 февраля 2011 .
• Капогна, Лука; Донателла Даниэлли; Скотт Полс; Джереми Тайсон (2007). Введение в группу Гейзенберга и субриманову изопериметрическую задачу . Birkhäuser Verlag . ISBN 978-3-7643-8132-5.
• Фенхель, Вернер ; Боннесен, Томми (1934). Теория выпуклости Корпера . Ergebnisse der Mathematik und ihrer Grenzgebiete. Том. 3. Берлин: 1. Верлаг фон Юлиуса Шпрингера.
• Фенхель, Вернер ; Боннесен, Томми (1987). Теория выпуклых тел . Москва, Айдахо: Л. Борон, К. Кристенсон и Б. Смит. BCS Associates. ISBN 9780914351023.
• Федерер, Герберт (1969). Геометрическая теория меры . Springer-Verlag. ISBN 3-540-60656-4..
• Громов, М .: "Изопериметрическое неравенство Пола Леви". Приложение C в Metric structures for Riemannian and non-Riemannian spaces . Основано на французском оригинале 1981 года. С приложениями М. Каца, П. Пансу и С. Семмеса. Перевод с французского Шона Майкла Бейтса. Progress in Mathematics, 152. Birkhäuser Boston, Inc., Бостон, Массачусетс, 1999.
• Хадвигер, Хьюго (1957). Vorlesungen über Inhalt, Oberfläche und Isoperimetrie . Спрингер-Верлаг..
• Hoory, Shlomo; Linial, Nathan ; Widgerson, Avi (2006). "Expander graphs and their applications" (PDF) . Bulletin of the American Mathematical Society . New Series. 43 (4): 439–561. doi : 10.1090/S0273-0979-06-01126-8 .
• Лидер, Имре (1991). «Дискретные изопериметрические неравенства». Труды симпозиумов по прикладной математике . Т. 44. С. 57–80.
• Оссерман, Роберт (1978). «Изопериметрическое неравенство». Bull. Amer. Math. Soc . 84 (6): 1182–1238. doi : 10.1090/S0002-9904-1978-14553-4 ..
• Звежинский, Михал (2016). «Улучшенное изопериметрическое неравенство и каустика Вигнера плоских овалов». J. Math. Anal. Appl . 442 (2): 726–739. arXiv : 1512.06684 . doi :10.1016/j.jmaa.2016.05.016. S2CID  119708226.
• Шмидт, Эрхард (1949). «Die Brunn-Minkowskische Ungleichung und ihr Spiegelbild sowie die isoperimetrische Eigenschaft der Hugel in der euklidischen und nichteuklidischen Geometry. II». Математика. Нахр . 2 (3–4): 171–244. дои : 10.1002/мана.19490020308..
• Бэблер, Ф. (1957). «Цум изопериметрическая проблема». Арх. Математика. (Базель) . 8 : 52–65. дои : 10.1007/BF01898439. S2CID  123704157..

Внешние ссылки

• История изопериметрической задачи при сходимости
• Трейберг: Несколько доказательств изопериметрического неравенства
• Изопериметрическая теорема в разрубании узла