Касательное пространство

Присвоение векторных полей многообразиям

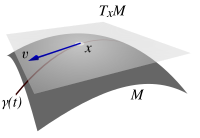
В математике касательное пространство многообразия является обобщением касательных линий к кривым в двумерном пространстве и касательных плоскостей к поверхностям в трехмерном пространстве в высших измерениях. В контексте физики касательное пространство к многообразию в точке можно рассматривать как пространство возможных скоростей для частицы, движущейся по многообразию .

Неформальное описание

Графическое представление касательного пространства одной точки на сфере . Вектор в этом касательном пространстве представляет возможную скорость (чего-либо, движущегося по сфере) в . После перемещения в этом направлении в близлежащую точку скорость будет задана вектором в касательном пространстве этой точки — другом касательном пространстве, которое не показано. ${\displaystyle x}$ ${\displaystyle x}$

В дифференциальной геометрии можно связать с каждой точкой дифференцируемого многообразия касательное пространство — действительное векторное пространство , которое интуитивно содержит возможные направления, в которых можно касательно пройти через . Элементы касательного пространства в точке называются касательными векторами в точке . Это обобщение понятия вектора , основанного на заданной начальной точке, в евклидовом пространстве . Размерность касательного пространства в каждой точке связного многообразия такая же, как и у самого многообразия . ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$

Например, если заданное многообразие является -сферой , то можно изобразить касательное пространство в точке как плоскость, которая касается сферы в этой точке и перпендикулярна радиусу сферы через точку. В более общем смысле, если заданное многообразие рассматривается как вложенное подмногообразие евклидова пространства , то можно изобразить касательное пространство таким буквальным образом. Это был традиционный подход к определению параллельного переноса . Многие авторы в дифференциальной геометрии и общей теории относительности используют его. ^{[1] [2]} Более строго, это определяет аффинное касательное пространство, которое отличается от пространства касательных векторов, описываемых современной терминологией. ${\displaystyle 2}$

В алгебраической геометрии , напротив, существует внутреннее определение касательного пространства в точке алгебраического многообразия , которое дает векторное пространство с размерностью, по крайней мере, такой же, как у него самого. Точки , в которых размерность касательного пространства в точности равна размерности , называются неособыми точками; остальные называются особыми точками. Например, кривая, которая пересекает сама себя, не имеет единственной касательной линии в этой точке. Особые точки — это те, где «тест на многообразие» не выполняется. См. касательное пространство Зарисского . ${\displaystyle V}$ ${\displaystyle V}$ ${\displaystyle p}$ ${\displaystyle V}$ ${\displaystyle V}$

После того, как были введены касательные пространства многообразия, можно определить векторные поля , которые являются абстракциями поля скоростей частиц, движущихся в пространстве. Векторное поле присоединяет к каждой точке многообразия вектор из касательного пространства в этой точке гладким образом. Такое векторное поле служит для определения обобщенного обыкновенного дифференциального уравнения на многообразии: Решение такого дифференциального уравнения представляет собой дифференцируемую кривую на многообразии, производная которой в любой точке равна касательному вектору, присоединенному к этой точке векторным полем.

Все касательные пространства многообразия могут быть «склеены» вместе, образуя новое дифференцируемое многообразие с удвоенной размерностью исходного многообразия, называемое касательным расслоением многообразия.

Формальные определения

Неформальное описание выше опирается на способность многообразия быть встроенным в окружающее векторное пространство, так что касательные векторы могут «высовываться» из многообразия в окружающее пространство. Однако удобнее определить понятие касательного пространства, основываясь исключительно на самом многообразии. ^[3] ${\displaystyle \mathbb {R} ^{m}}$

Существуют различные эквивалентные способы определения касательных пространств многообразия. Хотя определение через скорость кривых интуитивно является самым простым, оно также является самым громоздким для работы. Более элегантные и абстрактные подходы описаны ниже.

Определение через касательные кривые

В картине вложенного многообразия касательный вектор в точке рассматривается как скорость кривой , проходящей через точку . Поэтому мы можем определить касательный вектор как класс эквивалентности кривых, проходящих через , будучи касательными друг к другу в точке . ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$ ${\displaystyle x}$

Предположим, что является дифференцируемым многообразием (с гладкостью ) и что . Выберите координатную карту , где является открытым подмножеством , содержащим . Предположим далее, что даны две кривые с , такие, что обе являются дифференцируемыми в обычном смысле (мы называем эти дифференцируемые кривые инициализированными в ). Тогда и называются эквивалентными в тогда и только тогда, когда производные и в совпадают. Это определяет отношение эквивалентности на множестве всех дифференцируемых кривых, инициализированных в , и классы эквивалентности таких кривых известны как касательные векторы в . Класс эквивалентности любой такой кривой обозначается как . Касательное пространство в , обозначаемое как , тогда определяется как множество всех касательных векторов в ; оно не зависит от выбора координатной карты . ${\displaystyle M}$ ${\displaystyle C^{k}}$ ${\displaystyle k\geq 1}$ ${\displaystyle x\in M}$ ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$ ${\displaystyle U}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle \gamma _{1},\gamma _{2}:(-1,1)\to M}$ ${\displaystyle {\gamma _{1}}(0)=x={\gamma _{2}}(0)}$ ${\displaystyle \varphi \circ \gamma _{1},\varphi \circ \gamma _{2}:(-1,1)\to \mathbb {R} ^{n}}$ ${\displaystyle x}$ ${\displaystyle \gamma _{1}}$ ${\displaystyle \gamma _{2}}$ ${\displaystyle 0}$ ${\displaystyle \varphi \circ \gamma _{1}}$ ${\displaystyle \varphi \circ \gamma _{2}}$ ${\displaystyle 0}$ ${\displaystyle x}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle \gamma }$ ${\displaystyle \gamma '(0)}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle T_{x}M}$ ${\displaystyle x}$ ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$

Касательное пространство и касательный вектор вдоль кривой, проходящей через . ${\displaystyle T_{x}M}$ ${\displaystyle v\in T_{x}M}$ ${\displaystyle x\in M}$

Чтобы определить операции векторного пространства на , мы используем диаграмму и определяем отображение с помощью , где . Отображение оказывается биективным и может использоваться для переноса операций векторного пространства на на , тем самым превращая последний набор в -мерное действительное векторное пространство. Опять же, нужно проверить, что эта конструкция не зависит от конкретной диаграммы и используемой кривой , и на самом деле это не так. ${\displaystyle T_{x}M}$ ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$ ${\displaystyle \mathrm {d} {\varphi }_{x}:T_{x}M\to \mathbb {R} ^{n}}$ ${\textstyle {\mathrm {d} {\varphi }_{x}}(\gamma '(0)):=\left.{\frac {\mathrm {d} }{\mathrm {d} {t}}}[(\varphi \circ \gamma )(t)]\right|_{t=0},}$ ${\displaystyle \gamma \in \gamma '(0)}$ ${\displaystyle \mathrm {d} {\varphi }_{x}}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle T_{x}M}$ ${\displaystyle n}$ ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$ ${\displaystyle \gamma }$

Определение через производные

Предположим теперь, что является многообразием. Действительная функция считается принадлежащей тогда и только тогда, когда для каждой координатной карты отображение бесконечно дифференцируемо. Обратите внимание, что является действительной ассоциативной алгеброй относительно поточечного произведения и суммы функций и скалярного умножения. ${\displaystyle M}$ ${\displaystyle C^{\infty }}$ ${\displaystyle f:M\to \mathbb {R} }$ ${\displaystyle {C^{\infty }}(M)}$ ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$ ${\displaystyle f\circ \varphi ^{-1}:\varphi [U]\subseteq \mathbb {R} ^{n}\to \mathbb {R} }$ ${\displaystyle {C^{\infty }}(M)}$

Вывод в определяется как линейное отображение , удовлетворяющее тождеству Лейбница , которое смоделировано на основе правила произведения исчисления. ${\displaystyle x\in M}$ ${\displaystyle D:{C^{\infty }}(M)\to \mathbb {R} }$ $${\displaystyle \forall f,g\in {C^{\infty }}(M):\qquad D(fg)=D(f)\cdot g(x)+f(x)\cdot D(g),}$$

(Для каждой тождественно постоянной функции следует, что ). ${\displaystyle f={\text{const}},}$ ${\displaystyle D(f)=0}$

Обозначим множество всех выводов в Задание ${\displaystyle T_{x}M}$ ${\displaystyle x.}$

• ${\displaystyle (D_{1}+D_{2})(f):={D}_{1}(f)+{D}_{2}(f)}$и
• ${\displaystyle (\lambda \cdot D)(f):=\lambda \cdot D(f)}$

превращается в векторное пространство. ${\displaystyle T_{x}M}$

Обобщения

Обобщения этого определения возможны, например, на комплексные многообразия и алгебраические многообразия . Однако вместо того, чтобы изучать вывод из полной алгебры функций, вместо этого нужно работать на уровне ростков функций. Причина этого в том, что структурный пучок может не подходить для таких структур. Например, пусть будет алгебраическим многообразием со структурным пучком . Тогда касательное пространство Зарисского в точке является совокупностью всех -выводов , где - основное поле , а - стебель в точке . ${\displaystyle D}$ ${\displaystyle X}$ ${\displaystyle {\mathcal {O}}_{X}}$ ${\displaystyle p\in X}$ ${\displaystyle \mathbb {k} }$ ${\displaystyle D:{\mathcal {O}}_{X,p}\to \mathbb {k} }$ ${\displaystyle \mathbb {k} }$ ${\displaystyle {\mathcal {O}}_{X,p}}$ ${\displaystyle {\mathcal {O}}_{X}}$ ${\displaystyle p}$

Эквивалентность определений

Для и дифференцируемой кривой такой, что определяют (где производная берется в обычном смысле, поскольку является функцией от до ). Можно убедиться, что является выводом в точке и что эквивалентные кривые дают тот же вывод. Таким образом, для класса эквивалентности мы можем определить, где кривая была выбрана произвольно. Отображение является изоморфизмом векторного пространства между пространством классов эквивалентности и пространством выводов в точке ${\displaystyle x\in M}$ ${\displaystyle \gamma :(-1,1)\to M}$ ${\displaystyle \gamma (0)=x,}$ ${\displaystyle {D_{\gamma }}(f):=(f\circ \gamma )'(0)}$ ${\displaystyle f\circ \gamma }$ ${\displaystyle (-1,1)}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle D_{\gamma }(f)}$ ${\displaystyle x,}$ ${\displaystyle \gamma '(0),}$ ${\displaystyle {D_{\gamma '(0)}}(f):=(f\circ \gamma )'(0),}$ ${\displaystyle \gamma \in \gamma '(0)}$ ${\displaystyle \gamma '(0)\mapsto D_{\gamma '(0)}}$ ${\displaystyle \gamma '(0)}$ ${\displaystyle x.}$

Определение через кокасательные пространства

Снова начнем с многообразия и точки . Рассмотрим идеал , состоящий из всех гладких функций, обращающихся в нуль в , т.е. . Тогда и являются действительными векторными пространствами, и можно показать, что фактор-пространство изоморфно кокасательному пространству с помощью теоремы Тейлора . Касательное пространство тогда можно определить как двойственное пространство к . ${\displaystyle C^{\infty }}$ ${\displaystyle M}$ ${\displaystyle x\in M}$ ${\displaystyle I}$ ${\displaystyle C^{\infty }(M)}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle f(x)=0}$ ${\displaystyle I}$ ${\displaystyle I^{2}}$ ${\displaystyle I/I^{2}}$ ${\displaystyle T_{x}^{*}M}$ ${\displaystyle T_{x}M}$ ${\displaystyle I/I^{2}}$

Хотя это определение является наиболее абстрактным, оно также наиболее легко переносится на другие ситуации, например, на многообразия, рассматриваемые в алгебраической геометрии .

Если — вывод в , то для каждого , что означает, что приводит к линейному отображению . Наоборот, если — линейный вывод, то определяет вывод в . Это дает эквивалентность между касательными пространствами, определенными через вывод, и касательными пространствами, определенными через кокасательные пространства. ${\displaystyle D}$ ${\displaystyle x}$ ${\displaystyle D(f)=0}$ ${\displaystyle f\in I^{2}}$ ${\displaystyle D}$ ${\displaystyle I/I^{2}\to \mathbb {R} }$ ${\displaystyle r:I/I^{2}\to \mathbb {R} }$ ${\displaystyle D(f):=r\left((f-f(x))+I^{2}\right)}$ ${\displaystyle x}$

Характеристики

Если является открытым подмножеством , то является многообразием естественным образом (возьмем координатные карты в качестве тождественных отображений на открытых подмножествах ), и все касательные пространства естественным образом отождествляются с . ${\displaystyle M}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle M}$ ${\displaystyle C^{\infty }}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle \mathbb {R} ^{n}}$

Касательные векторы как производные по направлению

Другой способ думать о касательных векторах — как о производных по направлению . Если задан вектор в , то можно определить соответствующую производную по направлению в точке как ${\displaystyle v}$ ${\displaystyle \mathbb {R} ^{n}}$ ${\displaystyle x\in \mathbb {R} ^{n}}$

${\displaystyle \forall f\in {C^{\infty }}(\mathbb {R} ^{n}):\qquad (D_{v}f)(x):=\left.{\frac {\mathrm {d} }{\mathrm {d} {t}}}[f(x+tv)]\right|_{t=0}=\sum _{i=1}^{n}v^{i}{\frac {\partial f}{\partial x^{i}}}(x).}$

Эта карта естественным образом является выводом в . Более того, каждый вывод в точке в имеет эту форму. Следовательно, существует взаимно-однозначное соответствие между векторами (рассматриваемыми как касательные векторы в точке) и выводами в точке. ${\displaystyle x}$ ${\displaystyle \mathbb {R} ^{n}}$

Поскольку касательные векторы к общему многообразию в точке могут быть определены как производные в этой точке, естественно думать о них как о направленных производных. В частности, если является касательным вектором к в точке (рассматриваемой как производная), то определим направленную производную в направлении как ${\displaystyle v}$ ${\displaystyle M}$ ${\displaystyle x}$ ${\displaystyle D_{v}}$ ${\displaystyle v}$

${\displaystyle \forall f\in {C^{\infty }}(M):\qquad {D_{v}}(f):=v(f).}$

Если мы думаем о начальной скорости дифференцируемой кривой, инициализированной при , т.е. , то вместо этого определим как ${\displaystyle v}$ ${\displaystyle \gamma }$ ${\displaystyle x}$ ${\displaystyle v=\gamma '(0)}$ ${\displaystyle D_{v}}$

${\displaystyle \forall f\in {C^{\infty }}(M):\qquad {D_{v}}(f):=(f\circ \gamma )'(0).}$

Базис касательного пространства в точке

Для многообразия , если задана карта с , то можно определить упорядоченный базис с помощью ${\displaystyle C^{\infty }}$ ${\displaystyle M}$ ${\displaystyle \varphi =(x^{1},\ldots ,x^{n}):U\to \mathbb {R} ^{n}}$ ${\displaystyle p\in U}$ ${\textstyle \left\{\left.{\frac {\partial }{\partial x^{1}}}\right|_{p},\dots ,\left.{\frac {\partial }{\partial x^{n}}}\right|_{p}\right\}}$ ${\displaystyle T_{p}M}$

${\displaystyle \forall i\in \{1,\ldots ,n\},~\forall f\in {C^{\infty }}(M):\qquad {\left.{\frac {\partial }{\partial x^{i}}}\right|_{p}}(f):=\left({\frac {\partial }{\partial x^{i}}}{\Big (}f\circ \varphi ^{-1}{\Big )}\right){\Big (}\varphi (p){\Big )}.}$

Тогда для каждого касательного вектора имеем ${\displaystyle v\in T_{p}M}$

${\displaystyle v=\sum _{i=1}^{n}v^{i}\left.{\frac {\partial }{\partial x^{i}}}\right|_{p}.}$

Следовательно, эта формула выражает линейную комбинацию базисных касательных векторов, определенных координатной диаграммой . ^[4] ${\displaystyle v}$ ${\textstyle \left.{\frac {\partial }{\partial x^{i}}}\right|_{p}\in T_{p}M}$ ${\displaystyle \varphi :U\to \mathbb {R} ^{n}}$

Производная карты

Каждое гладкое (или дифференцируемое) отображение между гладкими (или дифференцируемыми) многообразиями индуцирует естественные линейные отображения между их соответствующими касательными пространствами: ${\displaystyle \varphi :M\to N}$

${\displaystyle \mathrm {d} {\varphi }_{x}:T_{x}M\to T_{\varphi (x)}N.}$

Если касательное пространство определяется через дифференцируемые кривые, то это отображение определяется как

${\displaystyle {\mathrm {d} {\varphi }_{x}}(\gamma '(0)):=(\varphi \circ \gamma )'(0).}$

Если же, вместо этого, касательное пространство определяется через производные, то эта карта определяется как

${\displaystyle [\mathrm {d} {\varphi }_{x}(D)](f):=D(f\circ \varphi ).}$

Линейное отображение называется по-разному: производная, полная производная, дифференциал или прямой перенос в . Его часто выражают с помощью множества других обозначений: ${\displaystyle \mathrm {d} {\varphi }_{x}}$ ${\displaystyle \varphi }$ ${\displaystyle x}$

${\displaystyle D\varphi _{x},\qquad (\varphi _{*})_{x},\qquad \varphi '(x).}$

В некотором смысле производная является наилучшим линейным приближением к близкой к . Заметим, что когда , то отображение совпадает с обычным понятием дифференциала функции . В локальных координатах производная от задается якобианом . ${\displaystyle \varphi }$ ${\displaystyle x}$ ${\displaystyle N=\mathbb {R} }$ ${\displaystyle \mathrm {d} {\varphi }_{x}:T_{x}M\to \mathbb {R} }$ ${\displaystyle \varphi }$ ${\displaystyle \varphi }$

Важным результатом, касающимся производной карты, является следующее:

Теорема  —  Если — локальный диффеоморфизм в в , то — линейный изоморфизм . Обратно, если непрерывно дифференцируемо и — изоморфизм, то существует открытая окрестность такая, что диффеоморфно отображается на свой образ. ${\displaystyle \varphi :M\to N}$ ${\displaystyle x}$ ${\displaystyle M}$ ${\displaystyle \mathrm {d} {\varphi }_{x}:T_{x}M\to T_{\varphi (x)}N}$ ${\displaystyle \varphi :M\to N}$ ${\displaystyle \mathrm {d} {\varphi }_{x}}$ ${\displaystyle U}$ ${\displaystyle x}$ ${\displaystyle \varphi }$ ${\displaystyle U}$

Это обобщение теоремы об обратной функции на отображения между многообразиями.

Смотрите также

• Координатно-индуцированный базис
• Котангенсивное пространство
• Дифференциальная геометрия кривых
• Экспоненциальная карта
• Вектор пространства

Примечания

1. до Кармо, Манфредо П. (1976). Дифференциальная геометрия кривых и поверхностей . Prentice-Hall.:
2. Дирак, Пол AM (1996) [1975]. Общая теория относительности . Princeton University Press. ISBN 0-691-01146-X.
3. Крис Дж. Ишем (1 января 2002 г.). Современная дифференциальная геометрия для физиков. Allied Publishers. стр. 70–72. ISBN 978-81-7764-316-9.
4. Лерман, Юджин. «Введение в дифференциальную геометрию» (PDF) . стр. 12.

Ссылки

• Ли, Джеффри М. (2009), Многообразия и дифференциальная геометрия , аспирантура по математике , т. 107, Провиденс: Американское математическое общество.
• Michor, Peter W. (2008), Темы дифференциальной геометрии , аспирантура по математике, т. 93, Провиденс: Американское математическое общество.
• Спивак, Майкл (1965), Исчисление на многообразиях: современный подход к классическим теоремам продвинутого исчисления, WA Benjamin, Inc., ISBN 978-0-8053-9021-6.

Внешние ссылки

• Касательные плоскости в MathWorld