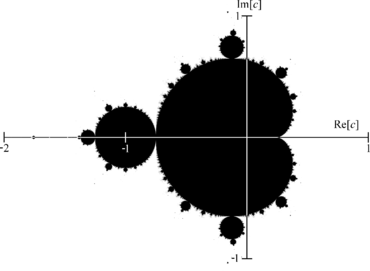
В математике комплексная плоскость — это плоскость , образованная комплексными числами , с декартовой системой координат , в которой ось X , называемая действительной осью , образована действительными числами , а ось Y , называемая мнимой осью . образуется мнимыми числами .
Комплексная плоскость позволяет геометрическую интерпретацию комплексных чисел. При сложении они складывают подобные векторы . Умножение двух комплексных чисел проще выразить в полярных координатах : величина или модуль произведения представляет собой произведение двух абсолютных значений или модулей, а угол или аргумент произведения представляет собой сумму двух углов. или аргументы. В частности, умножение на комплексное число по модулю 1 действует как вращение.
Комплексную плоскость иногда называют плоскостью Аргана или плоскостью Гаусса .
В комплексном анализе комплексные числа обычно обозначаются символом z , который можно разделить на действительную ( x ) и мнимую ( y ) части:
например: z = 4 + 5 i , где x и y — действительные числа, а i — мнимая единица . В этих общепринятых обозначениях комплексное число z соответствует точке ( x , y ) на декартовой плоскости .
В декартовой плоскости точка ( x , y ) также может быть представлена в полярных координатах как
В декартовой плоскости можно предположить, что арктангенс принимает значения от − π /2 до π /2 (в радианах ), и необходимо позаботиться о том, чтобы определить более полную функцию арктангенса для точек ( x , y ), когда x ≤ 0. [примечание 1] В комплексной плоскости эти полярные координаты принимают вид
где [примечание 2]
Здесь | г | — абсолютное значение или модуль комплексного числа z ; θ , аргумент z , обычно берется в интервале 0 ≤ θ < 2 π ; а последнее равенство (to | z | e iθ ) взято из формулы Эйлера . Без ограничения на диапазон θ аргумент z является многозначным, поскольку комплексная показательная функция является периодической с периодом 2 π i . Таким образом, если θ является одним из значений arg( z ), остальные значения задаются формулой arg( z ) = θ + 2 nπ , где n — любое ненулевое целое число. [2]
Хотя геометрическое представление комплексных чисел редко используется явно, оно неявно основано на его структуре евклидова векторного пространства размерности 2, где скалярное произведение комплексных чисел w и z определяется выражением ; тогда для комплексного числа z его абсолютное значение | г | совпадает с его евклидовой нормой, а его аргумент arg( z ) с углом поворота от 1 до z .
Теория контурного интегрирования составляет большую часть комплексного анализа. В этом контексте важно направление движения по замкнутой кривой: изменение направления движения кривой на противоположное умножает значение интеграла на −1. По соглашению положительное направление — против часовой стрелки. Например, единичная окружность проходится в положительном направлении, когда мы начинаем с точки z = 1, затем двигаемся вверх и влево через точку z = i , затем вниз и влево через −1, затем вниз и до направо через − i и, наконец, вверх и вправо до z = 1, откуда мы начали.
Почти весь комплексный анализ связан со сложными функциями , то есть с функциями, которые отображают некоторое подмножество комплексной плоскости в какое-то другое (возможно, перекрывающееся или даже идентичное) подмножество комплексной плоскости. Здесь принято говорить о области определения f ( z ) как о лежащей в z -плоскости, а область значений f ( z ) — как о наборе точек в w -плоскости. Символами мы пишем
и часто думайте о функции f как о преобразовании из z -плоскости (с координатами ( x , y )) в w -плоскость (с координатами ( u , v )).
Комплексная плоскость обозначается как .
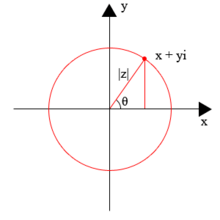
Диаграмма Аргана представляет собой геометрический график комплексных чисел в виде точек z = x + iy , где ось x используется как действительная ось, а ось y – как мнимая ось. [3] Такие участки названы в честь Жана-Робера Аргана (1768–1822), хотя впервые они были описаны норвежско-датским землемером и математиком Каспаром Весселем (1745–1818). [примечание 3] Диаграммы Аргана часто используются для построения положений нулей и полюсов функции на комплексной плоскости.

Может оказаться полезным представить комплексную плоскость так, как если бы она занимала поверхность сферы. Дана сфера единичного радиуса, поместим ее центр в начало комплексной плоскости, ориентированный так, чтобы экватор на сфере совпадал с единичным кругом в плоскости, а северный полюс находился «над» плоскостью.
Мы можем установить взаимно однозначное соответствие между точками на поверхности сферы за вычетом северного полюса и точками на комплексной плоскости следующим образом. Дана точка на плоскости и нарисуйте прямую линию, соединяющую ее с северным полюсом сферы. Эта линия пересечет поверхность сферы ровно в одной точке. Точка z = 0 будет спроецирована на южный полюс сферы. Поскольку внутренняя часть единичного круга находится внутри сферы, вся эта область ( | z | < 1 ) будет отображена на южном полушарии. Сам единичный круг ( | z | = 1 ) будет отображен на экваторе, а внешняя часть единичного круга ( | z | > 1 ) будет отображена на северном полушарии, за вычетом северного полюса. Очевидно, что эта процедура обратима: если взять любую точку на поверхности сферы, не являющуюся северным полюсом, мы можем провести прямую линию, соединяющую эту точку с северным полюсом и пересекающую плоскую плоскость ровно в одной точке.
В этой стереографической проекции сам северный полюс не связан ни с одной точкой комплексной плоскости. Мы совершенствуем взаимно-однозначное соответствие, добавляя к комплексной плоскости еще одну точку – так называемую точку на бесконечности – и отождествляя ее с северным полюсом сферы. Это топологическое пространство, комплексная плоскость плюс бесконечная точка, известно как расширенная комплексная плоскость . Когда мы обсуждаем комплексный анализ, мы говорим об одной «точке бесконечности». На прямой действительной числовой линии есть две точки на бесконечности (положительная и отрицательная) , но на расширенной комплексной плоскости есть только одна точка на бесконечности (северный полюс). [5]
Представьте себе на минутку, что произойдет с линиями широты и долготы, если их спроецировать со сферы на плоскую плоскость. Все линии широты параллельны экватору, поэтому они станут идеальными кругами с центром в начале координат z = 0 . А линии долготы станут прямыми, проходящим через начало координат (а также через «точку в бесконечности», поскольку они проходят как через северный, так и через южный полюс сферы).
Это не единственная возможная, но правдоподобная стереографическая ситуация проекции сферы на плоскость, состоящую из двух и более величин. Например, северный полюс сферы можно поместить поверх начала координат z = −1 в плоскости, касательной к окружности. Детали не имеют особого значения. Любая стереографическая проекция сферы на плоскость создаст одну «точку в бесконечности» и отобразит линии широты и долготы на сфере в круги и прямые линии соответственно на плоскости.
При обсуждении функций комплексной переменной часто удобно думать о разрезе на комплексной плоскости. Эта идея естественным образом возникает в нескольких различных контекстах.
Рассмотрим простое двузначное отношение
Прежде чем мы сможем рассматривать эту связь как однозначную функцию , необходимо каким-то образом ограничить диапазон результирующего значения. Когда речь идет о квадратных корнях неотрицательных действительных чисел, это легко сделать. Например, мы можем просто определить
быть неотрицательным действительным числом y таким, что y 2 = x . Эта идея не так хорошо работает в двумерной комплексной плоскости. Чтобы понять почему, давайте подумаем о том, как значение f ( z ) меняется при движении точки z по единичному кругу. Мы можем написать
Очевидно, что когда z движется по всему кругу, w очерчивает только половину круга. Таким образом, одно непрерывное движение в комплексной плоскости превратило положительный квадратный корень e 0 = 1 в отрицательный квадратный корень e iπ = −1 .
Эта проблема возникает потому, что точка z = 0 имеет только один квадратный корень, а любое другое комплексное число z ≠ 0 имеет ровно два квадратных корня. На прямой числовой линии мы могли бы обойти эту проблему, установив «барьер» в единственной точке x = 0. В комплексной плоскости необходим барьер большего размера, чтобы предотвратить полное окружение любым замкнутым контуром точки ветвления z = 0. Это обычно делается путем обрезки ветвей ; в этом случае «разрез» может простираться от точки z = 0 вдоль положительной вещественной оси до точки, находящейся на бесконечности, так что аргумент переменной z в плоскости разреза ограничивается диапазоном 0 ≤ arg( z ) < 2 π .
Теперь мы можем дать полное описание w знак равно z 1 ⁄ 2 . Для этого нам нужны две копии плоскости z , каждая из которых разрезана по действительной оси. На одном экземпляре мы определяем квадратный корень из 1 как e 0 = 1 , а на другом мы определяем квадратный корень из 1 как e iπ = −1. Мы называем эти две копии полных разрезанных плоских листов . Приведя аргумент непрерывности, мы видим, что (теперь однозначная) функция w = z 1 ⁄ 2 отображает первый лист в верхнюю половину w -плоскости , где 0 ≤ arg( w ) < π , отображая при этом второй лист лист в нижнюю половину w -плоскости (где π ≤ arg( w ) < 2 π ). [6]
Разрез ветки в этом примере не обязательно должен лежать вдоль действительной оси. Это даже не обязательно должна быть прямая линия. Подойдет любая непрерывная кривая, соединяющая начало координат z = 0 с точкой на бесконечности. В некоторых случаях срез ветки даже не обязательно должен проходить через точку, находящуюся на бесконечности. Например, рассмотрим отношения
Здесь многочлен z 2 − 1 обращается в нуль при z = ±1 , поэтому очевидно, что g имеет две точки ветвления. Мы можем «разрезать» плоскость по вещественной оси, от −1 до 1, и получить лист, на котором g ( z ) является однозначной функцией. Альтернативно, разрез может проходить от z = 1 вдоль положительной действительной оси через точку на бесконечности, а затем продолжить «вверх» по отрицательной действительной оси до другой точки ветвления, z = -1.
Эту ситуацию легче всего визуализировать с помощью описанной выше стереографической проекции. На сфере один из этих разрезов проходит через южное полушарие в продольном направлении, соединяя точку на экваторе ( z = −1) с другой точкой на экваторе ( z = 1) и проходя через южный полюс (начало координат z = 0) в пути. Второй вариант разреза проходит в продольном направлении через северное полушарие и соединяет те же две экваториальные точки, проходя через северный полюс (то есть точку, находящуюся на бесконечности).
Мероморфная функция — это комплексная функция, которая голоморфна и, следовательно, аналитична всюду в своей области определения, за исключением конечного или счетного числа точек. [примечание 4] Точки, в которых такая функция не может быть определена, называются полюсами мероморфной функции. Иногда все эти полюса лежат на одной прямой. В этом случае математики могут сказать, что функция «голоморфна на плоскости сечения». Вот простой пример.
Гамма - функция , определяемая формулой
где γ — постоянная Эйлера–Машерони и имеет простые полюса в точках 0, −1, −2, −3, ... потому что ровно один знаменатель в бесконечном произведении обращается в нуль, когда z равно нулю или отрицательному целому числу. [примечание 5] Поскольку все ее полюса лежат на отрицательной вещественной оси, от z = 0 до точки, находящейся на бесконечности, эту функцию можно описать как «голоморфную на плоскости сечения, разрез простирается вдоль отрицательной вещественной оси, от 0 ( включительно) до бесконечности».
Альтернативно, Γ( z ) можно было бы описать как «голоморфную в плоскости сечения с − π < arg( z ) < π и исключающую точку z = 0».
Этот разрез немного отличается от разреза ветвления, с которым мы уже столкнулись, поскольку он фактически исключает отрицательную действительную ось из плоскости разреза. Разрез ветки оставил действительную ось, соединенную с плоскостью сечения с одной стороны (0 ≤ θ ), но отделил ее от плоскости сечения с другой стороны ( θ < 2 π ).
Конечно, на самом деле нет необходимости исключать весь отрезок от z = 0 до −∞, чтобы построить область, в которой Γ( z ) голоморфна. Все, что нам действительно нужно сделать, это проколоть плоскость в счетном множестве точек {0, −1, −2, −3, ...}. Но замкнутый контур в проколотой плоскости может окружать один или несколько полюсов Γ( z ), давая контурный интеграл , который не обязательно равен нулю, согласно теореме о вычетах . Разрезая комплексную плоскость, мы обеспечиваем не только голоморфность Γ( z ) в этой ограниченной области, но и то, что контурный интеграл Γ по любой замкнутой кривой, лежащей в плоскости сечения, тождественно равен нулю.
Многие сложные функции определяются бесконечными рядами или цепными дробями . Фундаментальным соображением при анализе этих бесконечно длинных выражений является определение части комплексной плоскости, в которой они сходятся к конечному значению. Разрез в плоскости может облегчить этот процесс, как показывают следующие примеры.
Рассмотрим функцию, определяемую бесконечным рядом
Поскольку z 2 = (− z ) 2 для любого комплексного числа z , ясно, что f ( z ) является четной функцией от z , поэтому анализ можно ограничить одной половиной комплексной плоскости. И поскольку ряд не определен, когда
имеет смысл разрезать плоскость вдоль всей мнимой оси и установить сходимость этого ряда, где действительная часть z не равна нулю, прежде чем приступить к более трудной задаче исследования f ( z ), когда z — чисто мнимое число. [примечание 6]
В этом примере разрез является просто удобством, поскольку точки, в которых бесконечная сумма не определена, изолированы, и плоскость разреза можно заменить подходящей проколотой плоскостью. В некоторых случаях сокращение необходимо, а не просто удобно. Рассмотрим бесконечную периодическую цепную дробь
Можно показать , что f ( z ) сходится к конечному значению тогда и только тогда, когда z не является отрицательным действительным числом таким, что z < − 1 ⁄ 4 . Другими словами, областью сходимости этой цепной дроби является плоскость разреза, где разрез проходит вдоль отрицательной действительной оси, от − 1 ⁄ 4 до точки на бесконечности. [8]
Мы уже видели, как связаны отношения
можно превратить в однозначную функцию, разбив область определения f на два несвязанных листа. Также возможно «склеить» эти два листа обратно вместе, чтобы сформировать единую риманову поверхность , на которой f ( z ) = z 1/2 может быть определена как голоморфная функция, образом которой является вся w -плоскость (за исключением точки ш = 0 ). Вот как это работает.
Представьте себе две копии разрезаемой комплексной плоскости, разрезы простираются вдоль положительной действительной оси от z = 0 до точки на бесконечности. На одном листе определим 0 ≤ arg( z ) < 2 π , так что 1 1/2 = e 0 = 1 по определению. На втором листе определите 2 π ≤ arg( z ) < 4 π , так что 1 1/2 = e iπ = −1 , опять же по определению. Теперь переверните второй лист вверх дном так, чтобы воображаемая ось указывала в направлении, противоположном воображаемой оси первого листа, причем обе реальные оси были направлены в одном направлении, и «склейте» два листа вместе (так, чтобы край на первый лист с меткой « θ = 0 » соединен с ребром с меткой « θ < 4 π » на втором листе, а ребро на втором листе с меткой « θ = 2 π » соединено с ребром с меткой « θ < 2». π » на первом листе). Результатом является область римановой поверхности, на которой f ( z ) = z 1/2 является однозначным и голоморфным (кроме случаев, когда z = 0 ). [6]
Чтобы понять, почему f является однозначным в этой области, представьте себе контур вокруг единичной окружности, начиная с z = 1 на первом листе. Когда 0 ≤ θ < 2 π, мы все еще находимся на первом листе. Когда θ = 2 π , мы перешли на второй лист и должны сделать второй полный обход вокруг точки ветвления z = 0 , прежде чем вернуться в нашу исходную точку, где θ = 4 π эквивалентно θ = 0 , потому что о том, как мы склеили два листа вместе. Другими словами, поскольку переменная z делает два полных оборота вокруг точки ветвления, образ z в w -плоскости очерчивает только одну полную окружность.
Формальное дифференцирование показывает, что
откуда мы можем заключить, что производная f существует и конечна всюду на римановой поверхности, кроме случаев, когда z = 0 (т. е. f голоморфна, за исключением случаев, когда z = 0 ).
Как можно определить риманову поверхность для функции
также обсуждалось выше, быть построенным? Мы снова начинаем с двух копий z -плоскости, но на этот раз каждая из них разрезается по реальному отрезку, простирающемуся от z = −1 до z = 1 – это две точки ветвления g ( z ). Мы переворачиваем один из них вверх дном так, чтобы две воображаемые оси были направлены в противоположные стороны, и склеиваем соответствующие края двух разрезанных листов вместе. Мы можем убедиться, что g является однозначной функцией на этой поверхности, проследив контур вокруг круга единичного радиуса с центром в точке z = 1 . Начиная с точки z = 2 на первом листе, мы поворачиваем половину круга, прежде чем встретить разрез в точке z = 0 . Разрез заставляет нас оказаться на втором листе, так что, когда z совершил один полный оборот вокруг точки ветвления z = 1 , w сделал только половину полного оборота, знак w поменялся на противоположный (поскольку e iπ = −1 ), и наш путь привел нас к точке z = 2 на втором листе поверхности. Продолжая еще пол-оборота, мы встречаем другую сторону разреза, где z = 0 , и, наконец, достигаем нашей начальной точки ( z = 2 на первом листе), сделав два полных оборота вокруг точки ветвления.
Естественный способ обозначить θ = arg( z ) в этом примере — установить − π < θ ≤ π на первом листе, при этом π < θ ≤ 3 π на втором. Воображаемые оси на двух листах направлены в противоположные стороны, так что направление положительного вращения против часовой стрелки сохраняется при перемещении замкнутого контура с одного листа на другой (помните, второй лист перевернут ) . Представьте себе эту поверхность, встроенную в трехмерное пространство, причем оба листа параллельны плоскости xy . Затем на поверхности появляется вертикальное отверстие, где два разреза соединяются вместе. Что, если разрез будет сделан от z = −1 вниз по действительной оси до точки, находящейся на бесконечности, и от z = 1 вверх по действительной оси, пока разрез не встретится сам с собой? Снова можно построить риманову поверхность, но на этот раз «дырка» горизонтальна. С топологической точки зрения обе версии этой римановой поверхности эквивалентны — они представляют собой ориентируемые двумерные поверхности рода один.
В теории управления одно из применений комплексной плоскости известно как s-плоскость . Он используется для графической визуализации корней уравнения, описывающего поведение системы (характеристическое уравнение). Уравнение обычно выражается в виде многочлена от параметра «s» преобразования Лапласа , отсюда и название «плоскость». Точки на s-плоскости принимают форму , где вместо обычного «i » используется «j» для обозначения мнимого компонента.
Другое связанное использование комплексной плоскости связано с критерием устойчивости Найквиста . Это геометрический принцип, который позволяет определять стабильность системы с обратной связью с обратной связью путем проверки графика Найквиста ее величины и фазовой характеристики в разомкнутом контуре как функции частоты (или передаточной функции контура ) в комплексной плоскости.
Z -плоскость — это версия s-плоскости с дискретным временем , где вместо преобразования Лапласа используются z-преобразования .
Комплексная плоскость связана с двумя различными квадратичными пространствами . Для точки z = x + iy на комплексной плоскости квадратичная функция z 2 и квадрат нормы являются квадратичными формами . Первым часто пренебрегают после использования второго для задания метрики на комплексной плоскости. Эти отдельные грани комплексной плоскости как квадратичного пространства возникают при построении алгебр над полем с процессом Кэли-Диксона . Эту процедуру можно применить к любому полю , и для полей R и C получаются разные результаты : когда R является взлетным полем, тогда C строится с квадратичной формой , но процесс также может начинаться с C и z 2 , и в этом случае порождаются алгебры, отличные от алгебр, полученных из R . В любом случае генерируемые алгебры являются композиционными алгебрами ; в этом случае комплексная плоскость является множеством точек для двух различных композиционных алгебр.
Предыдущие разделы этой статьи посвящены комплексной плоскости с точки зрения геометрического представления комплексных чисел. Хотя использование термина «комплексная плоскость» имеет долгую и богатую с математической точки зрения историю, это ни в коем случае не единственное математическое понятие, которое можно охарактеризовать как «комплексная плоскость». Есть как минимум три дополнительных возможности.