Ориентируемость

Возможность непротиворечивого определения «по часовой стрелке» в математическом пространстве.

Тор – это ориентируемая поверхность .

Лента Мёбиуса является неориентируемой поверхностью. Обратите внимание, как диск переворачивается при каждом цикле.

Римская поверхность неориентируема.

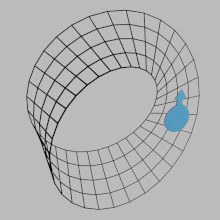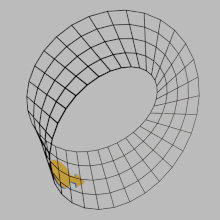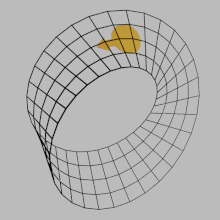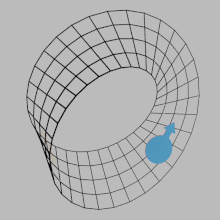
В математике ориентируемость — это свойство некоторых топологических пространств, таких как вещественные векторные пространства , евклидовы пространства , поверхности и, в более общем смысле, многообразия , которое позволяет последовательно определять понятия «по часовой стрелке» и «против часовой стрелки». ^[1] Пространство является ориентируемым, если такое непротиворечивое определение существует. В этом случае возможны два определения, и выбор между ними — это ориентация пространства. Вещественные векторные пространства, евклидовы пространства и сферы ориентируемы. Пространство является неориентируемым, если «по часовой стрелке» меняется на «против часовой стрелки» после прохождения в нем некоторых циклов и возвращения в исходную точку. Это означает, что геометрическая фигура , например, который непрерывно движется по такой петле, превращается в свое зеркальное отражение . Лента Мёбиуса является примером неориентируемого пространства.

Могут быть даны различные эквивалентные формулировки ориентируемости в зависимости от желаемого применения и уровня общности. В формулировках, применимых к общим топологическим многообразиям, часто используются методы теории гомологии , тогда как для дифференцируемых многообразий присутствует больше структуры, что позволяет формулировать их в терминах дифференциальных форм . Обобщением понятия ориентируемости пространства является понятие ориентируемости семейства пространств, параметризованного каким-либо другим пространством (расслоением ) , для которого в каждом из пространств необходимо выбрать ориентацию, непрерывно меняющуюся по отношению к изменениям в пространстве. значения параметров.

Ориентируемые поверхности

В этой анимации представлена ​​простая аналогия с использованием шестерни, которая вращается по правилу правой руки относительно вектора нормали поверхности. Ориентация кривых, заданных границами, определяется направлением, в котором движутся точки, когда их толкает движущееся колесо. На неориентируемой поверхности, такой как лента Мёбиуса, граница должна была бы двигаться в обоих направлениях одновременно, что невозможно.

Поверхность S в евклидовом пространстве R3 ориентируема ^, если киральная двумерная фигура (например ,) нельзя перемещать по поверхности и обратно туда, где он начался, чтобы он выглядел как собственное зеркальное отражение (). В противном случае поверхность неориентируема . Абстрактная поверхность (т. е. двумерное многообразие ) является ориентируемой, если на поверхности можно определить непротиворечивую концепцию вращения по часовой стрелке непрерывным образом. То есть петля, идущая по поверхности в одном направлении, никогда не может непрерывно деформироваться (без перекрытия себя) в петлю, идущую в противоположном направлении. Это оказывается эквивалентным вопросу о том, не содержит ли поверхность подмножества, гомеоморфного ленте Мёбиуса . Таким образом, для поверхностей ленту Мёбиуса можно считать источником всей неориентируемости.

Для ориентируемой поверхности последовательный выбор «по часовой стрелке» (в отличие от против часовой стрелки) называется ориентацией , а поверхность называется ориентированной . Для поверхностей, включенных в евклидово пространство, ориентация задается выбором непрерывно меняющейся нормали к поверхности n в каждой точке. Если такая нормаль вообще существует, то всегда есть два способа ее выбора: n или − n . В более общем смысле, ориентируемая поверхность допускает ровно две ориентации, а различие между ориентированной поверхностью и ориентируемой поверхностью тонкое и часто размытое. Ориентируемая поверхность — это абстрактная поверхность, допускающая ориентацию, тогда как ориентированная поверхность — это поверхность, которая является абстрактно ориентируемой и имеет дополнительные данные выбора одной из двух возможных ориентаций.

Примеры

Большинство поверхностей, встречающихся в физическом мире, являются ориентируемыми. Например, сферы , плоскости и торы являются ориентируемыми. Но ленты Мёбиуса , реальные проективные плоскости и бутылки Клейна неориентируемы. Все они, если их представить в трех измерениях, имеют только одну сторону. Настоящая проективная плоскость и бутылка Клейна не могут быть вложены в ^R3 , а только погружены с хорошими пересечениями.

Обратите внимание, что локально встроенная поверхность всегда имеет две стороны, поэтому близорукий муравей, ползающий по односторонней поверхности, будет думать, что существует «другая сторона». Сущность односторонности состоит в том, что муравей может переползать с одной стороны поверхности на «другую», не проходя поверхность и не переворачиваясь через край, а просто проползая достаточно далеко.

В общем, свойство ориентироваться не эквивалентно двусторонности; однако это справедливо, когда окружающее пространство (например, R ³ выше) ориентируемо. Например, тор, вложенный в

${\displaystyle K^{2}\times S^{1}}$

может быть односторонним, а бутылка Клейна в том же пространстве — двусторонней; здесь имеется в виду бутылка Клейна. ${\displaystyle K^{2}}$

Ориентация по триангуляции

Любая поверхность имеет триангуляцию : разложение на треугольники, при котором каждое ребро треугольника приклеено не более чем к одному другому ребру. Каждый треугольник ориентируется путем выбора направления по периметру треугольника, связывая направление с каждым краем треугольника. Если это сделать так, что при склеивании соседние края смотрят в противоположную сторону, то это определяет ориентацию поверхности. Такой выбор возможен только в том случае, если поверхность ориентируема, а в этом случае существует ровно две разные ориентации.

Если фигураможно последовательно расположить во всех точках поверхности, не превращаясь в ее зеркальное отражение, то это вызовет ориентацию в указанном выше смысле на каждом из треугольников триангуляции путем выбора направления каждого из треугольников исходя из порядка крас- зелено-синий цветов любой из фигур внутри треугольника.

Этот подход распространяется на любое n -многообразие, имеющее триангуляцию. Однако некоторые 4-многообразия не имеют триангуляции, и вообще при n > 4 некоторые n -многообразия имеют неэквивалентные триангуляции.

Ориентируемость и гомология

Если H ₁ ( S ) обозначает первую группу гомологий поверхности S , то S ориентируема тогда и только тогда, когда H ₁ ( S ) имеет тривиальную крученую подгруппу . Точнее, если S ориентируемо, то H ₁ ( S ) — свободная абелева группа , а если нет, то H ₁ ( S ) = F + Z /2 Z , где F — свободная абелева группа, и образуется Z /2 Z -фактор. средней кривой в ленте Мёбиуса , вложенной в S .

Ориентируемость многообразий

Пусть M — связное топологическое n - многообразие . Существует несколько возможных определений того, что значит, что M является ориентируемым. Некоторые из этих определений требуют, чтобы M имело дополнительную структуру, например, было дифференцируемым. Иногда n = 0 необходимо рассматривать как особый случай. Когда к M применимо более одного из этих определений , тогда M ориентируемо согласно одному определению тогда и только тогда, когда оно ориентируемо согласно другим определениям. ^{[2] [3]}

Ориентируемость дифференцируемых многообразий

Наиболее интуитивные определения требуют, чтобы M было дифференцируемым многообразием. Это означает, что функции перехода в атласе M являются C ¹ -функциями. Такая функция допускает определитель Якобиана . Когда определитель Якобиана положителен, функция перехода называется сохраняющей ориентацию . Ориентированный атлас на M — это атлас, все функции перехода которого сохраняют ориентацию. M ориентируемо , если оно допускает ориентированный атлас. Когда n > 0 , ориентация M представляет собой максимально ориентированный атлас. (Когда n = 0 , ориентация M является функцией M → {±1} .)

Ориентируемость и ориентации также можно выразить через касательное расслоение. Касательное расслоение является векторным расслоением , поэтому это расслоение со структурной группой GL( n , R ) . То есть функции перехода многообразия индуцируют функции перехода на касательном расслоении, которые являются послойными линейными преобразованиями. Если структурную группу можно свести к группе GL ⁺ ( n , R ) матриц с положительным детерминантом или, что то же самое, если существует атлас, функции перехода которого определяют сохраняющее ориентацию линейное преобразование в каждом касательном пространстве, то многообразие M ориентируемо. Наоборот, M ориентируем тогда и только тогда, когда структурную группу касательного расслоения можно сократить таким образом. Аналогичные наблюдения можно сделать и для пакета кадров.

Другой способ определения ориентации на дифференцируемом многообразии — через формы объёма . Форма объема — это никуда не исчезающее сечение ω ⋀ n T ^∗ M , верхней внешней ^{степени} кокасательного расслоения к M. Например, R ⁿ имеет стандартную форму объема, заданную выражением dx ¹ ∧ ⋯ ∧ dx ⁿ . Учитывая форму объема на M , совокупность всех карт U → R ⁿ , для которых стандартная форма объема возвращается к положительному кратному ω , является ориентированным атласом. Таким образом, существование формы объема эквивалентно ориентируемости многообразия.

Формы объема и касательные векторы можно комбинировать, чтобы дать еще одно описание ориентируемости. Если X ₁ , …, X _n является базисом касательных векторов в точке p , то базис называется правым, если ω( X ₁ , …, X _n ) > 0 . Функция перехода сохраняет ориентацию тогда и только тогда, когда она переводит правые основания в правые. Существование объемной формы влечет за собой редукцию структурной группы касательного расслоения или реперного расслоения к GL ⁺ ( n , R ) . Как и раньше, отсюда следует ориентируемость M . И наоборот, если M ориентируемо, то формы локального объема можно соединить вместе, чтобы создать форму глобального объема, при этом ориентируемость необходима для обеспечения того, чтобы глобальная форма никуда не исчезала.

Гомологии и ориентируемость общих многообразий

В основе всех приведенных выше определений ориентируемости дифференцируемого многообразия лежит понятие сохраняющей ориентацию переходной функции. Возникает вопрос, что именно сохраняют такие функции перехода. Они не могут сохранять ориентацию многообразия, поскольку ориентация многообразия является атласом, и нет смысла говорить, что функция перехода сохраняет или не сохраняет атлас, членом которого она является.

Этот вопрос можно решить, определив локальные ориентации. На одномерном многообразии локальная ориентация вокруг точки p соответствует выбору левого и правого положения вблизи этой точки. На двумерном многообразии это соответствует выбору движения по часовой стрелке или против часовой стрелки. Эти две ситуации имеют общую черту: они описываются в терминах поведения верхнего измерения вблизи p , но не при p . В общем случае пусть M — топологическое n -многообразие. Локальная ориентация M вокруг точки p — это выбор генератора группы

${\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right).}$

Чтобы увидеть геометрическое значение этой группы, выберите диаграмму вокруг p . В этой карте есть окрестность точки p , представляющая собой открытый шар B вокруг начала координат O. По теореме вырезания изоморфен . Шар B стягиваем, поэтому его группы гомологии исчезают, за исключением нулевой степени, а пространство B \ O является ( n - 1) -сферой, поэтому его группы гомологий исчезают, за исключением степеней n - 1 и 0 . Вычисление с длинной точной последовательностью в относительной гомологии показывает, что указанная выше группа гомологий изоморфна . Таким образом, выбор генератора соответствует решению о том, является ли в данной карте сфера вокруг p положительной или отрицательной. Отражение R ⁿ через начало координат действует отрицанием на , поэтому геометрическая значимость выбора генератора состоит в том, что он отличает карты от их отражений. ${\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}$ ${\displaystyle H_{n}\left(B,B\setminus \{O\};\mathbf {Z} \right)}$ ${\displaystyle H_{n-1}\left(S^{n-1};\mathbf {Z} \right)\cong \mathbf {Z} }$ ${\displaystyle H_{n-1}\left(S^{n-1};\mathbf {Z} \right)}$

На топологическом многообразии функция перехода сохраняет ориентацию , если в каждой точке p в своей области определения она фиксирует генераторы . Отсюда соответствующие определения такие же, как и в дифференцируемом случае. Ориентированный атлас - это тот , для которого все функции перехода сохраняют ориентацию, M является ориентируемым, если он допускает ориентированный атлас, а когда n > 0 , ориентация M является максимальным ориентированным атласом. ${\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}$

Интуитивно понятно, что ориентация M должна определять уникальную локальную ориентацию M в каждой точке. Это уточняется, если отметить, что любая карта в ориентированном атласе вокруг p может использоваться для определения сферы вокруг p , и эта сфера определяет генератор . Более того, любая другая карта вокруг p связана с первой картой с помощью функции перехода, сохраняющей ориентацию, и это означает, что две карты дают один и тот же генератор, следовательно, генератор уникален. ${\displaystyle H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}$

Возможны также чисто гомологические определения. Предполагая, что M замкнуто и связно, M ориентируем тогда и только тогда, когда n- я группа гомологий изоморфна целым числам Z . Ориентация M — это выбор генератора α этой группы . Этот генератор определяет ориентированный атлас, фиксируя генератор бесконечной циклической группы и беря в качестве ориентированных карт те, для которых α перемещается вперед к фиксированному генератору. И наоборот, ориентированный атлас определяет такой генератор, поскольку совместимые локальные ориентации могут быть склеены вместе, чтобы дать генератор группы гомологий . ^[4] ${\displaystyle H_{n}(M;\mathbf {Z} )}$ ${\displaystyle H_{n}(M;\mathbf {Z} )}$ ${\displaystyle H_{n}(M;\mathbf {Z} )}$

Ориентация и когомологии

Многообразие M ориентируемо тогда и только тогда, когда первый класс Стифеля–Уитни обращается в нуль. В частности, если первая группа когомологий с коэффициентами Z /2 равна нулю, то многообразие ориентируемо. Более того, если M ориентируемо и w ₁ обращается в нуль, то параметризует выбор ориентаций. ^[5] Эта характеристика ориентируемости распространяется на ориентируемость общих векторных расслоений над M , а не только касательного расслоения. ${\displaystyle w_{1}(M)\in H^{1}(M;\mathbf {Z} /2)}$ ${\displaystyle H^{0}(M;\mathbf {Z} /2)}$

Двойная обложка ориентации

Вокруг каждой точки М существуют две локальные ориентации. Интуитивно понятно, что существует способ перейти от локальной ориентации в точке p к локальной ориентации в соседней точке p ′ : когда две точки лежат на одной и той же карте координат U → R ⁿ , эта карта координат определяет совместимые локальные ориентации в точке п и п ' . Таким образом, множеству локальных ориентаций можно придать топологию, и эта топология превращает его в многообразие.

Точнее, пусть O — множество всех локальных ориентаций M . Чтобы топологизировать O, мы укажем подбазу для его топологии. Пусть U — открытое подмножество M , выбранное так, что изоморфно Z . Предположим, что α — генератор этой группы. Для каждого p в U существует функция продвижения вперед . Кодомен этой группы имеет два образующих, и α отображается в один из них. Топология на O определена так, что ${\displaystyle H_{n}(M,M\setminus U;\mathbf {Z} )}$ ${\displaystyle H_{n}(M,M\setminus U;\mathbf {Z} )\to H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)}$

${\displaystyle \{{\text{Image of }}\alpha {\text{ in }}H_{n}\left(M,M\setminus \{p\};\mathbf {Z} \right)\colon p\in U\}}$

открыт.

Существует каноническое отображение π: O → M , которое переводит локальную ориентацию из точки p в точку p . Ясно, что каждая точка M имеет ровно два прообраза относительно π . Фактически, π является даже локальным гомеоморфизмом, поскольку прообразы упомянутых выше открытых множеств U гомеоморфны дизъюнктному объединению двух копий U . Если M ориентируемо, то M само является одним из этих открытых множеств, поэтому O — непересекающееся объединение двух копий M . Однако если M неориентируемо, то O связно и ориентируемо. Многообразие O называется ориентационным двойным накрытием .

Многообразия с границей

Если M — многообразие с краем, то ориентация M определяется как ориентация его внутренней части. Такая ориентация индуцирует ориентацию ∂ M . Действительно, предположим, что ориентация M фиксирована. Пусть U → Rn ⁺ _— карта в граничной точке M , которая, будучи ограничена внутренней частью M , находится в выбранном ориентированном атласе. Ограничение этой карты на ∂ M является картой ∂ M . Такие карты образуют ориентированный атлас для ∂ M .

Когда M гладкое, в каждой точке p ∂ M ограничение касательного расслоения M на ∂ M изоморфно T _p ∂ M ⊕ R , где фактор R описывается вектором нормали, указывающим внутрь. Ориентация T _p ∂ M определяется условием, что базис T _p ∂ M положительно ориентирован тогда и только тогда, когда он в сочетании с вектором нормали, указывающим внутрь, определяет положительно ориентированный базис T _p M .

Ориентируемая двойная крышка

Анимация ориентируемой двойной накладки ленты Мёбиуса .

Близкое к этому понятие использует идею покрытия пространства . Для связного многообразия M возьмем M ^∗ , набор пар ( x , o), где x — точка M , а o — ориентация в x ; здесь мы предполагаем, что M либо гладкое, поэтому мы можем выбрать ориентацию в касательном пространстве в точке, либо мы используем сингулярные гомологии для определения ориентации. Затем для каждого открытого ориентированного подмножества M мы рассматриваем соответствующий набор пар и определяем его как открытое множество M ^∗ . Это дает M ^∗ топологию, и проекция, отправляющая ( x , o) в x , становится покрывающим отображением 2 к 1. Это накрывающее пространство называется ориентируемым двойным накрытием , так как оно ориентируемо. M ^∗ связно тогда и только тогда, когда M неориентируемо.

Другой способ построить это покрытие — разделить петли, основанные на базовой точке, на петли, сохраняющие или меняющие ориентацию. Петли, сохраняющие ориентацию, порождают подгруппу фундаментальной группы, которая представляет собой либо всю группу, либо индекс два. В последнем случае (что означает наличие пути, меняющего ориентацию) подгруппа соответствует связному двойному накрытию; это покрытие является ориентируемым по конструкции. В первом случае можно просто взять две копии M , каждая из которых соответствует разной ориентации.

Ориентация векторных расслоений

Вещественное векторное расслоение , которое априори имеет структурную группу GL(n) , называется ориентируемым, если структурную группу можно свести к группе матриц с положительным определителем . Для касательного расслоения это сокращение всегда возможно, если основное базовое многообразие ориентируемо, и фактически это обеспечивает удобный способ определения ориентируемости гладкого вещественного многообразия : гладкое многообразие считается ориентируемым, если его касательное расслоение ориентируемо ( как векторное расслоение). Обратите внимание, что как многообразие само по себе касательное расслоение всегда ориентируемо, даже над неориентируемыми многообразиями. ${\displaystyle GL^{+}(n)}$

Связанные понятия

Лоренцева геометрия

В лоренцевой геометрии существует два вида ориентируемости: ориентация в пространстве и ориентация во времени. Они играют роль в причинной структуре пространства-времени. ^[6] В контексте общей теории относительности пространственно -временное многообразие является пространственно-ориентируемым, если всякий раз, когда два наблюдателя-правши отправляются на ракетных кораблях, стартующих в одной и той же точке пространства-времени, а затем снова встречаются в другой точке, они остаются правшами с уважение друг к другу. Если пространство-время ориентировано во времени, то два наблюдателя всегда будут договариваться о направлении времени в обеих точках их встречи. Фактически, пространство-время ориентировано во времени тогда и только тогда, когда любые два наблюдателя могут договориться, какая из двух встреч предшествовала другой. ^[7]

Формально псевдоортогональная группа O( p , q ) имеет пару характеров : характер пространственной ориентации σ ₊ и характер ориентации времени σ ₋ ,

${\displaystyle \sigma _{\pm }:\operatorname {O} (p,q)\to \{-1,+1\}.}$

Их произведение σ = σ ₊ σ ₋ является определителем, придающим характер ориентации. Пространственная ориентация псевдориманова многообразия отождествляется с сечением соответствующего расслоения

${\displaystyle \operatorname {O} (M)\times _{\sigma _{+}}\{-1,+1\}}$

где O( M ) — пучок псевдоортогональных кадров. Аналогично, временная ориентация — это часть соответствующего пакета.

${\displaystyle \operatorname {O} (M)\times _{\sigma _{-}}\{-1,+1\}.}$

Смотрите также

• Ориентация кривой
• Ориентировочная связка

Рекомендации

1. Манро, Маршалл Эванс (1963). Современное многомерное исчисление. Аддисон-Уэсли. п. 263.
2. Спивак, Майкл (1965). Исчисление на многообразиях . ХарперКоллинз . ISBN 978-0-8053-9021-6.
3. Хэтчер, Аллен (2001). Алгебраическая топология . Издательство Кембриджского университета . ISBN 978-0521795401.
4. Хэтчер 2001, с. 236 Теорема 3.26(а)
5. Лоусон, Х. Блейн ; Мишельсон, Мария-Луиза (1989). Спиновая геометрия . Издательство Принстонского университета . п. 79 Теорема 1.2. ISBN 0-691-08542-0.
6. Хокинг, Юго-Запад ; Эллис, СКФ (1973). Крупномасштабная структура пространства-времени . Издательство Кембриджского университета. ISBN 0-521-20016-4.
7. Хэдли, Марк Дж. (2002). «Ориентируемость пространства-времени» (PDF) . Классическая и квантовая гравитация . 19 (17): 4565–71. arXiv : gr-qc/0202031v4 . CiteSeerX 10.1.1.340.8125 . дои : 10.1088/0264-9381/19/17/308. 

Внешние ссылки

• Ориентация многообразий в Атласе многообразий.
• Ориентационное покрытие в Атласе многообразия.
• Ориентация многообразий в теориях обобщенных когомологий в Атласе многообразий.
• Статья в математической энциклопедии об ориентации.