Плитка Пенроуза

Непериодическое замощение плоскости

Мозаика Пенроуза с ромбами, обладающая пятикратной симметрией.

Разбиение Пенроуза является примером апериодического разбиения . Здесь замощение — это покрытие плоскости непересекающимися многоугольниками или другими фигурами, а замощение является апериодическим, если оно не содержит сколь угодно больших периодических областей или участков. Однако, несмотря на отсутствие трансляционной симметрии , плитки Пенроуза могут обладать как отражательной симметрией , так и пятикратной вращательной симметрией . Плитки Пенроуза названы в честь математика и физика Роджера Пенроуза , который исследовал их в 1970-х годах.

Существует несколько вариантов плиток Пенроуза разной формы. В первоначальной форме плитки Пенроуза использовались плитки четырех разных форм, но позже она была сокращена до двух форм: либо двух разных ромбов , либо двух разных четырехугольников , называемых воздушными змеями и дротиками. Плитки Пенроуза получаются путем ограничения способов совмещения этих фигур таким образом, чтобы избежать периодического замощения. Это можно сделать несколькими различными способами, включая правила сопоставления, правила мозаики замены или правила конечного подразделения , схемы разреза и проекта, а также покрытия. Даже при таком ограничении каждая вариация дает бесконечное множество различных мозаик Пенроуза.

Роджер Пенроуз в фойе Института фундаментальной физики и астрономии Митчелла Техасского университета A&M стоит на полу, выложенном плиткой Пенроуза.

Плитки Пенроуза самоподобны : их можно преобразовать в эквивалентные плитки Пенроуза с плитками разных размеров, используя процессы, называемые инфляцией и дефляцией . Узор, представленный каждым конечным участком плитки в мозаике Пенроуза, встречается в мозаике бесконечное число раз. Это квазикристаллы : реализованная в виде физической структуры мозаика Пенроуза будет создавать дифракционные картины с пиками Брэгга и пятикратной симметрией, раскрывая повторяющиеся узоры и фиксированную ориентацию ее плиток. ^[1] Изучение этих мозаик сыграло важную роль в понимании физических материалов, которые также образуют квазикристаллы. ^[2] Плитка Пенроуза также применялась в архитектуре и отделке, как показано на напольной плитке.

Предыстория и история

Периодические и апериодические мозаики

Рисунок 1. Часть периодического мозаики с двумя прототипами

Покрытие плоской поверхности («плоскости») каким-либо узором из геометрических фигур («плитки») без нахлестов и зазоров называется черепицей . Наиболее известные мозаики, такие как покрытие пола квадратами, сходящимися от края до края, являются примерами периодических мозаик . Если квадратную плитку сместить на ширину плитки параллельно ее сторонам, в результате получится тот же узор плиток, что и до сдвига. Сдвиг (формально — трансляция ), сохраняющий замощение таким образом, называется периодом замощения. Замощение называется периодическим, если оно имеет периоды, которые сдвигают замощение в двух разных направлениях. ^[3]

Плитки в квадратной мозаике имеют только одну форму, а другие плитки обычно имеют только конечное число форм. Эти формы называются прототипами , и говорят, что набор прототипов допускает замощение мозаики или замощение плоскости , если существует мозаика плоскости с использованием только этих форм. То есть каждая плитка в мозаике должна быть конгруэнтна одному из этих прототипов. ^[4]

Мозаика, не имеющая периодов, является непериодической . Набор прототайлов называется апериодическим, если все его мозаики непериодичны, и в этом случае его мозаики также называются апериодическими мозаиками . ^[5] Разбиения Пенроуза являются одними из простейших известных примеров апериодических разбиений плоскости конечными наборами протоплиток. ^[3]

Самые ранние апериодические мозаики

Апериодический набор домино Ванга . ^[6]

Тема апериодических мозаик получила новый интерес в 1960-х годах, когда логик Хао Ван заметил связь между задачами принятия решений и мозаикой. ^[7] В частности, он ввел мозаику из квадратных пластинок с цветными краями, теперь известную как домино Ванга или плитки , и сформулировал « проблему домино »: определить, может ли данный набор домино Ванга замостить плоскость с совпадающими цветами на соседних края домино. Он заметил, что если бы эта проблема была неразрешимой , то должен был бы существовать апериодический набор домино Ванга. В то время это казалось неправдоподобным, поэтому Ван предположил, что такого набора не может существовать.

Шесть прототипов Робинсона

Ученик Вана Роберт Бергер доказал, что проблема домино неразрешима (поэтому гипотеза Ванга неверна) в своей диссертации 1964 года ^[8] и получил апериодический набор из 20 426 домино Ванга. ^[9] Он также описал сокращение до 104 таких прототипов; последний не появился в его опубликованной монографии ^[10] , но в 1968 году Дональд Кнут подробно описал модификацию набора Бергера, требующую всего 92 домино. ^[11]

Согласования цветов, требуемого при укладке плитки домино Ванга, можно легко добиться, изменяя края плиток, как части головоломки, так, чтобы они могли сочетаться друг с другом только так, как предписано раскраской краев. ^[12] Рафаэль Робинсон в статье 1971 года ^[13] , которая упростила методы Бергера и доказательство неразрешимости, использовал этот метод для получения апериодического набора всего из шести прототайлов. ^[14]

Разработка разбиений Пенроуза

Рисунок 2. Пятиугольная мозаика Пенроуза (P1), нарисованная черным цветом на цветной ромбовидной мозаике (P3) с желтыми краями. ^[15]

Первая мозаика Пенроуза (плитка P1 ниже) представляет собой апериодический набор из шести прототипов, введенный Роджером Пенроузом в статье 1974 года ^[16] и основанный на пятиугольниках, а не на квадратах. Любая попытка замостить плоскость правильными пятиугольниками обязательно оставляет пробелы, но Иоганн Кеплер в своей работе 1619 года «Harmonices Mundi» показал, что эти пробелы можно заполнить с помощью пентаграмм ( звездных многоугольников ), десятиугольников и родственных им фигур. ^[17] Кеплер расширил это разбиение на пять многоугольников и не обнаружил никаких периодических закономерностей, а также предположил, что каждое расширение будет привносить новую особенность ^[18], создавая, таким образом, апериодическое разбиение. Следы этих идей можно найти и в творчестве Альбрехта Дюрера . ^[19] Признавая вдохновение Кеплера, Пенроуз нашел правила сопоставления для этих форм, получив апериодический набор. Эти правила соответствия могут быть заданы украшением краев, как в случае с плитками Ванга. Мозаику Пенроуза можно рассматривать как завершение конечного шаблона Аа Кеплера . ^[20]

Плитка не Пенроуза пятиугольниками и тонкими ромбами в паломнической церкви Святого Иоанна Непомуцкого начала XVIII века в Зеленой горе, Чехия.

Впоследствии Пенроуз сократил количество прототипов до двух, открыв мозаику воздушного змея и дротика (плитка P2 ниже) и мозаику ромба (плитка P3 ниже). ^[21] Ромбическая мозаика была независимо открыта Робертом Амманном в 1976 году. ^[22] Пенроуз и Джон Х. Конвей исследовали свойства мозаик Пенроуза и обнаружили, что свойство замены объясняет их иерархическую природу; их результаты были опубликованы Мартином Гарднером в его колонке « Математические игры » в журнале Scientific American в январе 1977 года . ^[23]

В 1981 году Н.Г. де Брейн предложил два разных метода построения мозаик Пенроуза. «Многосеточный метод » Де Брёйна позволяет получить мозаику Пенроуза как двойственный граф расположения пяти семейств параллельных прямых. В его «методе разрезания и проектирования» плитки Пенроуза получаются как двумерные проекции пятимерной кубической структуры. В этих подходах мозаика Пенроуза рассматривается как набор точек, ее вершин, а плитки — это геометрические фигуры, полученные соединением вершин ребрами. ^[24]

Мозаика Пенроуза

Мозаика P1 с использованием оригинального набора из шести прототипов Пенроуза.

Плитки Penrose P1 с наложенными дугами и узлами для обеспечения соблюдения правил мозаики.

Три типа мозаики Пенроуза, P1–P3, описаны отдельно ниже. ^[25] У них есть много общих черт: в каждом случае плитки построены из форм, связанных с пятиугольником (и, следовательно, с золотым сечением ), но основные формы плиток должны быть дополнены правилами сопоставления , чтобы плитка была апериодической. Эти правила можно описать с помощью помеченных вершин или ребер или узоров на гранях плитки; альтернативно, профиль края может быть изменен (например, с помощью углублений и выступов) для получения апериодического набора прототайлов. ^{[9] [26]}

Оригинальная пятиугольная мозаика Пенроуза (P1)

Первая мозаика Пенроуза использует пятиугольники и три другие формы: пятиконечную «звезду» (пентаграмму), «лодку» (примерно 3/5 звезды) и «ромб» (тонкий ромб). ^[27] Чтобы все мозаики были непериодическими, существуютправила сопоставления , которые определяют, как плитки могут встречаться друг с другом, а для пятиугольных плиток существует три различных типа правил сопоставления. Если рассматривать эти три типа как разные прототипы, то в целом получится набор из шести прототипов. Обычно три разных типа пятиугольных плиток обозначаются тремя разными цветами, как на рисунке выше справа. ^[28]

Укладка воздушных змеев и дротиков (P2)

Часть плоскости покрыта плиткой Пенроуза типа P2 (воздушный змей и дротик). Создано путем применения нескольких дефляций, см. раздел ниже.

Во второй мозаике Пенроуза используются четырехугольники, называемые «воздушный змей» и «дротик», которые можно объединить в ромб. Однако правила сопоставления запрещают такое сочетание. ^[29] И воздушный змей, и дротик состоят из двух треугольников, названных треугольниками Робинсона , по заметкам Робинсона 1975 года. ^[30]

Плитки с воздушным змеем и дротиками (вверху) и семь возможных фигур вершин в плитке P2, каждая из которых имеет следующие прозвища: Первый ряд: звезда, туз, солнце. Второй ряд: король, валет, дама, двойка.

• Воздушный змей представляет собой четырехугольник, четыре внутренних угла которого составляют 72, 72, 72 и 144 градуса. Воздушный змей можно разделить пополам вдоль оси симметрии, чтобы образовать пару острых треугольников Робинсона (с углами 36, 72 и 72 градуса).
• Дротик представляет собой невыпуклый четырехугольник, четыре внутренних угла которого равны 36, 72, 36 и 216 градусов . Дротик можно разделить пополам вдоль оси симметрии, чтобы образовать пару тупых треугольников Робинсона (с углами 36, 36 и 108 градусов), которые меньше острых треугольников.

Правила сопоставления можно описать несколькими способами. Один из подходов состоит в том, чтобы раскрасить вершины (в два цвета, например, черный и белый) и потребовать, чтобы соседние плитки имели совпадающие вершины. ^[31] Другой способ — использовать узор из дуг окружностей (как показано выше слева зеленым и красным цветом) для ограничения размещения плиток: когда две плитки имеют общий край в плитке, узоры должны совпадать на этих краях. ^[21]

Эти правила часто требуют размещения определенных плиток: например, вогнутая вершина любого дротика обязательно заполняется двумя воздушными змеями. Соответствующая фигура (центр верхнего ряда на нижнем изображении слева) Конвей называет «тузом»; хотя он выглядит как увеличенный воздушный змей, он не выглядит таким же образом. ^[32] Точно так же вогнутая вершина, образующаяся при встрече двух воздушных змеев вдоль короткого края, обязательно заполняется двумя дротиками (внизу справа). Фактически, существует только семь возможных способов пересечения плиток в вершине; две из этих фигур – а именно, «звезда» (вверху слева) и «солнце» (вверху справа) – имеют 5-кратную двугранную симметрию (за счет вращения и отражения), а остальные имеют единственную ось отражения (вертикальную в Изображение). ^[33] За исключением туза (вверху посередине) и солнца, все эти вершинные фигуры требуют размещения дополнительных плиток. ^[34]

Укладка ромба (P3)

Правило сопоставления для ромбов Пенроуза с использованием дуг окружностей или модификаций ребер для соблюдения правил мозаики.

Правило сопоставления для ромбов Пенроуза с использованием параболических ребер для соблюдения правил замощения.

Плитка Пенроуза типа P3 с использованием ромбов Пенроуза с параболическими краями.

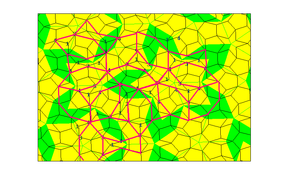
Третья мозаика использует пару ромбов (часто называемых в этом контексте «ромбами») с равными сторонами, но разными углами. ^[9] Обычные плитки в форме ромба можно использовать для периодического замощения плоскости, поэтому необходимо ввести ограничения на то, как можно собирать плитки: никакие две плитки не могут образовывать параллелограмм, так как это позволило бы периодическое замощение мозаикой, но это ограничение не является достаточно, чтобы вызвать апериодичность, как показано на рисунке 1 выше.

Существует два вида плиток, оба из которых можно разложить на треугольники Робинсона. ^[30]

• Тонкий ромб t имеет четыре угла с углами 36, 144, 36 и 144 градуса. Тромб можно разделить пополам по короткой диагонали , образуя пару острых треугольников Робинсона.
• Толстый ромб Т имеет углы 72, 108, 72 и 108 градусов. Тромб можно разделить пополам по длинной диагонали , чтобы образовать пару тупых треугольников Робинсона; в отличие от мозаики P2, они больше острых треугольников.

Правила сопоставления различают стороны плиток и предполагают, что плитки могут располагаться рядом определенными способами, но не другими. Два способа описания этих правил сопоставления показаны на изображении справа. В одной из форм плитки должны быть собраны так, чтобы кривые на гранях совпадали по цвету и положению по краю. В другом плитки необходимо собирать так, чтобы неровности на их краях совпадали. ^[9]

Существует 54 циклически упорядоченных комбинации таких углов, сумма которых в вершине составляет 360 градусов, но правила замощения допускают появление только семи таких комбинаций (хотя одна из них возникает двумя способами). ^[35]

Различные комбинации углов и лицевой кривизны позволяют создавать плитки произвольной сложности, такие как цыплята Пенроуза . ^[36]

Особенности и конструкции

Золотое сечение и локальная пятиугольная симметрия

Некоторые свойства и общие черты мозаик Пенроуза связаны с золотым сечением (приблизительно 1,618). ^{[30] [31]} Это отношение длин хорд к длинам сторон в правильном пятиугольнике и удовлетворяет условию φ = 1 + 1/ φ . ${\displaystyle \varphi ={\frac {1+{\sqrt {5}}}{2}}}$

Пятиугольник с вписанным толстым ромбом (светлый), острыми треугольниками Робинсона (слегка заштрихованными) и маленьким тупым треугольником Робинсона (более темным). Пунктирные линии дают дополнительные края для воздушных змеев и дротиков с надписями.

Следовательно, отношение длин длинных сторон к коротким сторонам в ( равнобедренных ) треугольниках Робинсона равно φ :1. Отсюда следует, что отношение длин длинных сторон к коротким как в плитках для змея, так и в дротиках также равно φ :1, как и отношение длин сторон к короткой диагонали в тонком ромбе t и длинной диагонали к сторонам в толстом ромбе. Т. _ Как в мозаике P2, так и в P3 отношение площадей большего треугольника Робинсона к меньшему составляет φ :1, следовательно, такими же являются отношения площадей воздушного змея к дротику и толстого ромба к тонкому. ромб. (Как большие, так и меньшие тупоугольные треугольники Робинсона можно найти в пятиугольнике слева: большие треугольники наверху – половинки толстого ромба – имеют линейные размеры, увеличенные на φ по сравнению с маленьким заштрихованным треугольником в основании, и поэтому соотношение площадей равно φ ² :1.)

Любая мозаика Пенроуза обладает локальной пятиугольной симметрией в том смысле, что в мозаике есть точки, окруженные симметричной конфигурацией плиток: такие конфигурации имеют пятикратную вращательную симметрию относительно центральной точки, а также пять зеркальных линий симметрии отражения, проходящих через точку. , группа диэдральной симметрии . ^[9] Эта симметрия обычно сохраняет только участок плитки вокруг центральной точки, но этот участок может быть очень большим: Конвей и Пенроуз доказали, что всякий раз, когда цветные кривые на мозаиках P2 или P3 замыкаются в петлю, область внутри петля имеет пятиугольную симметрию, причем в любом замощении найдется не более двух таких кривых каждого цвета, которые не смыкаются. ^[37]

Может быть не более одной центральной точки глобальной пятикратной симметрии: если бы их было больше одной, то вращение друг друга привело бы к двум более близким центрам пятикратной симметрии, что приводит к математическому противоречию. ^[38] Существует только две мозаики Пенроуза (каждого типа) с глобальной пятиугольной симметрией: для мозаики P2 с помощью воздушных змеев и дротиков центральной точкой является либо вершина «солнце», либо «звезда». ^[39]

Инфляция и дефляция

Пятиугольник, разложенный на шесть пятиугольников меньшего размера (половина додекаэдрической сетки) с промежутками.

Многие общие черты плиток Пенроуза вытекают из иерархической пятиугольной структуры, заданной правилами замены : это часто называют инфляцией и дефляцией или композицией и разложением плиток или (коллекций) плиток. ^{[9] [23] [40]} Правила замены разлагают каждую плитку на более мелкие плитки той же формы, что и те, которые используются в мозаике (и, таким образом, позволяют «составлять» большие плитки из меньших). Это показывает, что мозаика Пенроуза обладает масштабным самоподобием, и поэтому ее можно рассматривать как фрактал , использующий тот же процесс, что и пентачешуйку . ^[41]

Первоначально Пенроуз открыл мозаику P1 таким способом, разложив пятиугольник на шесть меньших пятиугольников (половина сетки додекаэдра ) и пять полуромбов; Затем он заметил, что, когда он повторяет этот процесс, все промежутки между пятиугольниками могут быть заполнены звездами, ромбами, лодками и другими пятиугольниками. ^[27] Повторяя этот процесс бесконечно, он получил один из двух мозаик P1 с пятиугольной симметрией. ^{[9] [20]}

Разложения треугольника Робинсона

Треугольники Робинсона и их разложения

Метод замены для мозаик P2 и P3 можно описать с помощью треугольников Робинсона разных размеров. Треугольники Робинсона, возникающие в мозаике P2 (путем деления змеев и дротиков пополам), называются A-плитами, а треугольники, возникающие в мозаике P3 (путем разделения ромбов пополам), называются B-плитками. ^[30] Меньшая плитка A, обозначенная A _S , представляет собой тупоугольный треугольник Робинсона, а большая плитка A, AL _, является остроугольной ; Напротив, меньшая B-плитка, обозначенная _BS , представляет собой остроугольный треугольник Робинсона, а большая B-плитка, BL _, тупая.

Конкретно, если A _S имеет длины сторон (1, 1, φ ), то _AL имеет длины сторон ( φ , φ , 1). B-плитки могут быть связаны с такими A-тайлами двумя способами:

• Если BS _имеет тот же размер, что и _AL , то BL _— это увеличенная версия φ A _S из _AS с длинами сторон ( φ , φ , φ ²  = 1 +  φ ) — это разлагается на плитку _AL и A _S. плитка, соединенная по общей стороне длиной 1.
• Если вместо этого BL _{отождествляется} с _{AS , то BS представляет собой уменьшенную версию (1/ φ )AL A L с} длинами _сторон ( 1 / φ _, 1 / φ , 1 ) – соединение плитки BS _и B Тогда плитка _L вдоль общей стороны длиной 1 дает (разложение) плитку _AL .

В этих разложениях, по-видимому, существует двусмысленность: треугольники Робинсона можно разложить двумя способами, которые являются зеркальными отражениями друг друга на (равнобедренной) оси симметрии треугольника. В мозаике Пенроуза этот выбор фиксируется правилами сопоставления. Кроме того, правила сопоставления также определяют, как меньшие треугольники в мозаике образуют более крупные. ^[30]

Частичное надувание звезды для получения ромбов и набора ромбов для получения туза.

Отсюда следует, что мозаики P2 и P3 взаимно локально выводимы : мозаика одним набором плиток может использоваться для генерации мозаики другим набором плиток. Например, замощение воздушными змеями и дротиками можно разделить на A-плитки, и их можно скомпоновать каноническим способом, образуя B-плитки и, следовательно, ромбы. ^[15] Мозаики P2 и P3 также являются взаимно локально выводимыми с мозаикой P1 (см. рисунок 2 выше). ^[42]

Разложение B-плиток на A-плитки можно записать

BS _знак равно А _L , BL знак _равно А _L + А _S

(при условии, что B-плитки имеют больший размер), что можно резюмировать в уравнении матрицы замены : ^[43]

${\displaystyle {\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.}$

Объединение этого с разложением увеличенных φ A-плиток на B-плитки дает замену

${\displaystyle {\begin{pmatrix}\varphi A_{L}\\\varphi A_{S}\end{pmatrix}}={\begin{pmatrix}1&1\\1&0\end{pmatrix}}{\begin{pmatrix}B_{L}\\B_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,,}$

так что увеличенная плитка φ A _L распадается на две плитки _AL и одну плитку A _S. Правила сопоставления требуют особой замены: две плитки _AL в плитке φ AL _L должны образовывать воздушный змей, и, таким образом, воздушный змей распадается на два воздушных змея и два полудротика, а дротик распадается на воздушный змей и два полудротика. дартс. ^{[44] [45]} Увеличенные φ B-плитки разлагаются на B-плитки аналогичным образом (через φ A-плитки).

Композицию и декомпозицию можно повторять, так что, например,

${\displaystyle \varphi ^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}={\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}{\begin{pmatrix}A_{L}\\A_{S}\end{pmatrix}}\,.}$

Количество воздушных змеев и дротиков на n- й итерации построения определяется n- й степенью матрицы подстановки:

${\displaystyle {\begin{pmatrix}2&1\\1&1\end{pmatrix}}^{n}={\begin{pmatrix}F_{2n+1}&F_{2n}\\F_{2n}&F_{2n-1}\end{pmatrix}}\,,}$

где F _n — n -е число Фибоначчи . Таким образом, отношение количества воздушных змеев к дротикам в любом достаточно большом узоре мозаики Пенроуза P2 приближается к золотому сечению φ . ^[46] Аналогичный результат верен и для отношения числа толстых и тонких ромбов в мозаике Пенроуза P3. ^[44]

Дефляция для мозаик P2 и P3

Последовательные дефляции вершины «солнце» в мозаике Пенроуза типа P2

Последовательные дефляции набора плиток в мозаике Пенроуза типа P3

8-я дефляция вершины «солнце» в мозаике Пенроуза типа P2.

Начиная с набора плиток из заданной мозаики (которая может быть отдельной плиткой, мозаикой плоскости или любой другой коллекцией), дефляция происходит с помощью последовательности шагов, называемых поколениями. В одном поколении дефляции каждая плитка заменяется двумя или более новыми плитками, которые представляют собой уменьшенные версии плиток, использованных в исходной плитке. Правила замены гарантируют, что новые плитки будут расположены в соответствии с правилами сопоставления. ^[44] Повторные поколения дефляции создают мозаику исходной формы аксиомы с все меньшими и меньшими плитками.

Это правило разделения плиток является правилом подразделения .

Приведенную выше таблицу следует использовать с осторожностью. Сдувание полукайта и полудротика полезно только в контексте сдувания более крупного объекта, как показано на примере сдувания солнца и звезды. Они дают неправильные результаты при применении к одиночным воздушным змеям и дротикам.

Кроме того, простое правило подразделения создает дыры возле краев мозаики, которые едва заметны на верхнем и нижнем рисунках справа. Дополнительные правила принуждения могут оказаться полезными.

Последствия и применение

Инфляция и дефляция дают метод построения мозаики воздушного змея и дротика (P2) или ромба (P3), известный как генерация вверх-вниз . ^{[32] [44] [45]}

Мозаики Пенроуза, будучи непериодическими, не обладают трансляционной симметрией – узор нельзя сдвинуть так, чтобы он совпадал с самим собой по всей плоскости. Однако любая ограниченная область, независимо от ее размера, будет повторяться внутри мозаики бесконечное число раз. Следовательно, ни один конечный фрагмент не может однозначно определить полную мозаику Пенроуза и даже не определить, какая позиция внутри мозаики отображается. ^[47]

Это показывает, в частности, что число различных мозаик Пенроуза (любого типа) несчетно . Генерация сверху вниз дает один метод параметризации мозаики, но другие методы используют стержни Аммана, пентагриды или схемы разреза и проецирования. ^[44]

Связанные тайлы и темы

Декагональные покрытия и квазикристаллы.

Декагон Гаммельта (слева) с разложением на коршуны и дротики, обозначенные пунктирными линиями; более толстые темные линии ограничивали вписанный туз и толстый ромб; возможные совпадения (справа) - на один или два красных туза. ^[48]

В 1996 году немецкий математик Петра Гуммельт продемонстрировала, что покрытие (так называемое, чтобы отличить его от непересекающихся мозаик), эквивалентное мозаике Пенроуза, может быть построено с использованием одной десятиугольной плитки, если разрешены два типа перекрывающихся областей. ^[49] Десятиугольная плитка украшена цветными пятнами, а правило покрытия допускает только те перекрытия, которые совместимы с окраской. Подходящее разложение десятиугольной плитки на воздушных змеев и дротики превращает такое покрытие в плитку Пенроуза (P2). Аналогично, мозаику P3 можно получить, вписав в каждый декагон толстый ромб; оставшееся пространство заполнено тонкими ромбами.

Эти покрытия рассматривались как реалистичная модель роста квазикристаллов : перекрывающиеся декагоны представляют собой «квазиэлементарные ячейки», аналогичные элементарным ячейкам , из которых построены кристаллы, а правила сопоставления максимизируют плотность определенных атомных кластеров. ^{[48] ​​[50]} Апериодический характер покрытий может затруднить теоретические исследования физических свойств, таких как электронная структура, из-за отсутствия теоремы Блоха . Однако спектры квазикристаллов все еще можно рассчитать с контролем ошибок. ^[51]

Связанные мозаики

Плитка Tie и Navette (красного цвета на фоне Пенроуза)

Три варианта мозаики Пенроуза взаимно локально выводимы. Выбор некоторых подмножеств из вершин мозаики P1 позволяет создать другие непериодические мозаики. Если углы одного пятиугольника в P1 помечены последовательно цифрами 1,3,5,2,4 , то устанавливается однозначная маркировка во всех пятиугольниках в порядке либо по часовой стрелке, либо против часовой стрелки. Точки с одинаковой меткой определяют замощение треугольниками Робинсона, а точки с номерами 3 и 4 на них определяют вершины замощения Тай-и-Наветта. ^[52]

Вариант мозаики, не являющийся квазикристаллом. Это не мозаика Пенроуза, поскольку она не соответствует правилам выравнивания плиток.

Существуют также другие родственные неэквивалентные мозаики, такие как мозаика шестиугольник-лодка-звезда и мозаика Микуллы-Рота. Например, если правила сопоставления для ромбовидной мозаики свести к определенному ограничению на углы, разрешенные в каждой вершине, получится бинарная мозаика. ^[53] Его основная симметрия также пятикратная, но это не квазикристалл. Его можно получить либо украшая ромбы исходной мозаики меньшими, либо применяя правила замены, но не методом разрезания и проецирования де Брейна. ^[54]

Искусство и архитектура

• 
  Пятиугольный и десятиугольный узор плитки Гирих на перемычке из храма Дарб-и Имам , Исфахан , Иран (1453 г. н.э.)
• 
  Транзитный центр Salesforce в Сан-Франциско. Внешняя «кожа» из белого алюминия перфорирована в виде плитки Пенроуза.
• 
  Плитка Пенроуза на полу в Компьютерном центре 3 (CC-3), IIIT Аллахабад

Эстетическая ценность черепицы уже давно оценена по достоинству и остается источником интереса к ней; следовательно, внимание привлек внешний вид (а не формальные определяющие свойства) мозаик Пенроуза. Отмечено сходство с некоторыми декоративными узорами, используемыми в Северной Африке и на Ближнем Востоке; ^{[55] [56]} физики Питер Дж. Лу и Пол Стейнхардт представили доказательства того, что плитка Пенроуза лежит в основе примеров средневековых исламских геометрических узоров , таких как плитки гирих (ремни) в храме Дарб-э Имам в Исфахане . ^[57]

Художник Drop City Кларк Ричерт использовал ромбы Пенроуза в своих произведениях искусства в 1970 году, полученные путем проецирования тени ромботриаконтаэдра на плоскость, наблюдая за встроенными «толстыми» и «тонкими» ромбами, которые складываются вместе, образуя непериодическую мозаику. Историк искусства Мартин Кемп заметил, что Альбрехт Дюрер нарисовал похожие мотивы ромбовидной плитки. ^[58]

В 1979 году Университет Майами использовал плитку Пенроуза, выполненную из терраццо , для украшения двора бакалавриата на своем факультете математики и статистики. ^[59]

В Индийском институте информационных технологий в Аллахабаде с момента первой фазы строительства в 2001 году учебные корпуса проектировались на основе «геометрии Пенроуза», стилизованной под мозаику , разработанную Роджером Пенроузом. Во многих местах этих зданий пол покрыт геометрическими узорами, выложенными плиткой Пенроуза. ^[60]

Пол атриума здания Бейлисс Университета Западной Австралии выложен плиткой Пенроуза. ^[61]

Здание Эндрю Уайлса , где по состоянию на октябрь 2013 года располагался математический факультет Оксфордского университета , ^[62] включает в себя участок плитки Пенроуза в качестве мощения входа. ^[63]

Пешеходная часть улицы Кескускату в центре Хельсинки вымощена плиткой Пенроуза. Работы были завершены в 2014 году. ^[64]

Транзитный центр Transbay в Сан-Франциско, построенный в 2018 году, имеет перфорацию на волнистой белой металлической обшивке внешней поверхности с узором Пенроуза. ^[65]

Смотрите также

• Плитка Гирих
• Список апериодических наборов плиток
• Укладка вертушки
• Пятиугольная плитка
• Квакваверсальная мозаика

Примечания

1. Сенешаль 1996, стр. 241–244.
2. Радин 1996.
3. Общие ссылки на эту статью включают Gardner 1997, стр. 1–30, Grünbaum & Shephard 1987, стр. 520–548 и amp, 558–579 и Senechal 1996, стр. 170–206.
4. Гарднер 1997, стр. 20, 23.
5. Грюнбаум и Шепард 1987, с. 520
6. Чулик и Кари, 1997 г.
7. Ван 1961
8. Роберт Бергер в проекте «Математическая генеалогия»
9. Остин 2005a
10. Бергер 1966
11. Грюнбаум и Шепард 1987, с. 584
12. Гарднер 1997, с. 5
13. Робинсон 1971
14. Грюнбаум и Шепард 1987, с. 525
15. Сенешаль 1996, стр. 173–174.
16. Пенроуз 1974
17. Грюнбаум и Шепард 1987, раздел 2.5.
18. Кеплер, Йоханнес (1997). Гармония мира. Американское философское общество. п. 108. ИСБН 0871692090.
19. Удача 2000
20. Сенешаль 1996, с. 171
21. Гарднер 1997, с. 6
22. Гарднер 1997, с. 19
23. Гарднер 1997, глава 1
24. де Брейн 1981
25. Обозначения P1–P3 взяты из Grünbaum & Shephard 1987, раздел 10.3.
26. Грюнбаум и Шепард 1987, раздел 10.3.
27. Пенроуз 1978, с. 32
28. «Однако, как будет вскоре объяснено, пятиугольники разного цвета будут считаться разными типами плиток». Остин, 2005а; Grünbaum & Shephard 1987, рисунок 10.3.1, показывает модификации ребер, необходимые для получения апериодического набора прототипов.
29. «Конечно, ромб периодически выкладывается плиткой, но нам не разрешено соединять части таким образом». Гарднер 1997, стр. 6–7.
30. Grünbaum & Shephard 1987, стр. 537–547.
31. Сенешаль 1996, с. 173
32. Гарднер 1997, с. 8
33. Гарднер 1997, стр. 10–11.
34. Гарднер 1997, с. 12
35. Сенешаль 1996, с. 178
36. "Плитки Пенроуза". Убийственная математика . Проверено 20 января 2020 г.
37. Гарднер 1997, с. 9
38. Гарднер 1997, с. 27
39. Грюнбаум и Шепард 1987, с. 543
40. В Grünbaum & Shephard 1987 термин «инфляция» используется там, где другие авторы использовали бы «дефляцию» (с последующим изменением масштаба). Менее двусмысленными являются термины «композиция» и «декомпозиция», которые также используют многие авторы.
41. Рамачандрарао, П. (2000). «О фрактальной природе мозаики Пенроуза» (PDF) . Современная наука . 79 : 364.
42. Грюнбаум и Шепард 1987, с. 546
43. Сенешаль 1996, стр. 157–158.
44. Остин 2005b
45. Сенешаль 1996, с. 183
46. Гарднер 1997, с. 7
47. «... любой конечный участок, который мы выбираем в мозаике, будет лежать внутри одной раздутой плитки, если мы продолжим двигаться достаточно далеко вверх по инфляционной иерархии. Это означает, что везде, где эта плитка находится на этом уровне иерархии, наш исходный участок должно также встречаться в исходном тайлинге. Следовательно, исправление будет встречаться бесконечно часто в исходном тайлинге, а также, по сути, и в каждом другом тайлинге». Остин 2005а
48. Лорд и Ранганатан, 2001 г.
49. Гаммелт 1996
50. Стейнхардт и Чонг 1996; см. также Стейнхардт, Пол Дж. «Новая парадигма структуры квазикристаллов».
51. Колбрук; Римский; Хансен (2019). «Как вычислить спектры с контролем ошибок». Письма о физических отзывах . 122 (25): 250201. Бибкод : 2019PhRvL.122y0201C. doi : 10.1103/PhysRevLett.122.250201. PMID  31347861. S2CID  198463498.
52. Удача, Р. (1990). «Подрешетки Пенроуза». Журнал некристаллических твердых тел . 117–8 (90): 832–5. Бибкод : 1990JNCS..117..832L. дои : 10.1016/0022-3093(90)90657-8.
53. Лансон и Биллард, 1988 г.
54. Годреш и Лансон 1992; см. также Дирка Фреттло; Ф. Гелер и Эдмунд Харрисс . «Двоичный». Энциклопедия плитки . Кафедра математики Билефельдского университета.
55. Заславский и др. 1988 год; Маковицкий 1992 г.
56. Прейндж, Себастьян Р.; Питер Дж. Лу (1 сентября 2009 г.). «Плитки бесконечности». Саудовская Арамко Мир . Сервисная компания Арамко. стр. 24–31 . Проверено 22 февраля 2010 г.
57. Лу и Стейнхардт, 2007 г.
58. Кемп 2005 г.
59. Плитка Пенроуза в Университете Майами. Архивировано 14 августа 2017 года в Wayback Machine Дэвидом Куллманом, представлено на заседании секции Математической ассоциации Америки в Огайо, Государственный университет Шони , 24 октября 1997 года.
60. «Индийский институт информационных технологий, Аллахабад». АрхНет .
61. «Столетие: Университет Западной Австралии». www.treasures.uwa.edu.au .
62. «Проект нового строительства». Архивировано из оригинала 22 ноября 2012 года . Проверено 30 ноября 2013 г.
63. «Роджер Пенроуз объясняет математику тротуарной плитки Пенроуза» . Математический институт Оксфордского университета .
64. "Keskuskadun kävelykadusta voi tulla matemaattisen hämmästelyn kohde" . Хельсингин Саномат . 6 августа 2014 г.
65. Кучар, Салли (11 июля 2013 г.). «Ознакомьтесь с предлагаемым скином для транзитного центра Transbay». Обузданный .

Рекомендации

Основные источники

• Бергер, Р. (1966). Неразрешимость задачи домино. Мемуары Американского математического общества. Том. 66. ИСБН 9780821812662..
• де Брейн, Н.Г. (1981). «Алгебраическая теория непериодических разбиений Пенроуза плоскости I, II» (PDF) . Indagationes Mathematicae . 43 (1): 39–66. дои : 10.1016/1385-7258(81)90017-2 ..
• Гаммелт, Петра (1996). «Мозаики Пенроуза как покрытия конгруэнтных десятиугольников». Геометрии посвященные . 62 (1): 1–17. дои : 10.1007/BF00239998. МР  1400977. Збл  0893.52011.
• Пенроуз, Роджер (1974). «Роль эстетики в чистых и прикладных математических исследованиях». Вестник Института математики и ее приложений . 10 : 266 и далее..
• США 4133152, Пенроуз, Роджер , «Набор плиток для покрытия поверхности», опубликовано 9 января 1979  г.
• Робинсон, Р.М. (1971). «Неразрешимость и непериодичность разбиений плоскости». Математические изобретения . 12 (3): 177–190. Бибкод : 1971InMat..12..177R. дои : 10.1007/BF01418780. S2CID  14259496..
• Шехтман, Д.; Блех, И.; Гратиас, Д.; Кан, JW (1984). «Металлическая фаза с дальним ориентационным порядком и отсутствием трансляционной симметрии». Письма о физических отзывах . 53 (20): 1951–1953. Бибкод : 1984PhRvL..53.1951S. doi : 10.1103/PhysRevLett.53.1951 .
• Ван, Х. (1961). «Доказательство теорем методом распознавания образов II». Технический журнал Bell System . 40 : 1–42. doi :10.1002/j.1538-7305.1961.tb03975.x..

Вторичные источники

• Остин, Дэвид (2005a). «Плитки Пенроуза говорят на многие мили». Провиденс: Американское математическое общество..
• Остин, Дэвид (2005b). «Плитки Пенроуза, перевязанные лентами». Провиденс: Американское математическое общество..
• Колбрук, Мэтью; Роман, Богдан; Хансен, Андерс (2019). «Как вычислить спектры с контролем ошибок». Письма о физических отзывах . 122 (25): 250201. Бибкод : 2019PhRvL.122y0201C. doi : 10.1103/PhysRevLett.122.250201. PMID  31347861. S2CID  198463498.
• Чулик, Карел; Кари, Яркко (1997). «Об апериодических множествах плиток Ванга». Основы информатики . Конспекты лекций по информатике. Том. 1337. стр. 153–162. дои : 10.1007/BFb0052084. ISBN 978-3-540-63746-2.
• Гарднер, Мартин (1997). Плитки Пенроуза к шифрам с люком . Издательство Кембриджского университета. ISBN 978-0-88385-521-8.. (Впервые опубликовано WH Freeman, Нью-Йорк (1989), ISBN 978-0-7167-1986-1 .)  
  • Глава 1 (стр. 1–18) представляет собой переиздание Гарднера, Мартина (январь 1977 г.). «Необычайная непериодическая мозаика, обогащающая теорию плиток». Научный американец . Том. 236, нет. 1. С. 110–121. Бибкод : 1977SciAm.236a.110G. doi : 10.1038/scientificamerican0177-110..
• Годреш, К; Лансон, Ф. (1992). «Простой пример мозаики неПизо с пятикратной симметрией» (PDF) . Журнал де Физика I. 2 (2): 207–220. Бибкод : 1992JPhy1...2..207G. дои : 10.1051/jp1: 1992134. S2CID  120168483..
• Грюнбаум, Бранко ; Шепард, GC (1987). Плитки и узоры . Нью-Йорк: WH Freeman. ISBN 978-0-7167-1193-3..
• Кемп, Мартин (2005). «Наука в культуре: трюк с плиткой». Природа . 436 (7049): 332. Бибкод : 2005Natur.436..332K. дои : 10.1038/436332а ..
• Лансон, Фредерик; Биллард, Люк (1988). «Двумерная система с квазикристаллическим основным состоянием» (PDF) . Журнал де Физический . 49 (2): 249–256. CiteSeerX  10.1.1.700.3611 . doi : 10.1051/jphys: 01988004902024900..
• Лорд, Э.А.; Ранганатан, С. (2001). «Декагон Гаммельта как« квазиэлементарная ячейка »» (PDF) . Акта Кристаллографика . А57 (5): 531–539. CiteSeerX  10.1.1.614.3786 . дои : 10.1107/S0108767301007504. ПМИД  11526302.
• Лу, Питер Дж.; Стейнхардт, Пол Дж. (2007). «Декагональные и квазикристаллические плитки в средневековой исламской архитектуре» (PDF) . Наука . 315 (5815): 1106–1110. Бибкод : 2007Sci...315.1106L. дои : 10.1126/science.1135491. PMID  17322056. S2CID  10374218..
• Удача, Р. (2000). «Дюрер-Кеплер-Пенроуз: развитие пятиугольных мозаик». Материаловедение и инженерия . 294 (6): 263–267. дои : 10.1016/S0921-5093(00)01302-2..
• Маковицкий, Э. (1992). «800-летняя пятиугольная плитка из Мараги, Иран, и вдохновленные ею новые разновидности апериодической плитки». В И. Харгиттай (ред.). Пятикратная симметрия . Сингапур – Лондон: World Scientific. стр. 67–86. ISBN 9789810206000..
• Пенроуз, Роджер (1978). «Пентаплексити» (PDF) . Эврика . Том. 39. стр. 16–22.. (Номера страниц, цитируемые здесь, взяты из репродукции Пенроуза, Р. (1979–80). «Пентаплексия: класс непериодических мозаик плоскости». The Mathematical Intelligencer . 2 : 32–37. doi : 10.1007/BF03024384 S2CID 120305260  ..)
• Радин, Чарльз (апрель 1996 г.). «Рецензия на книгу: Квазикристаллы и геометрия» (PDF) . Уведомления Американского математического общества . 43 (4): 416–421.
• Сенешаль, Марджори (1996). Квазикристаллы и геометрия . Издательство Кембриджского университета. ISBN 978-0-521-57541-6..
• Стейнхардт, Пол Дж.; Чон, Хён-Чай (1996). «Более простой подход к мозаике Пенроуза с последствиями для формирования квазикристаллов». Природа . 382 (1 августа): 431–433. Бибкод : 1996Natur.382..431S. дои : 10.1038/382431a0. S2CID  4354819..
• Заславский, ГМ; Сагдеев, Роальд З.; Усиков Д.А.; Черников, А.А. (1988). «Минимальный хаос, стохастическая паутина и структуры квазикристаллической симметрии». Успехи советской физики . 31 (10): 887–915. Бибкод : 1988SvPhU..31..887Z. doi : 10.1070/PU1988v031n10ABEH005632..

Внешние ссылки

• Вайсштейн, Эрик В. «Плитки Пенроуза». Математический мир .
• Джон Савард. «Плитки Пенроуза». quadibloc.com . Проверено 28 ноября 2009 г.
• Эрик Хван. «Плитка Пенроуза». намерение.нет . Проверено 28 ноября 2009 г.
• Ф. Гелер; Э. Харрисс и Д. Фреттло. «Ромб Пенроуза». Энциклопедия плитки . Кафедра математики Билефельдского университета . Проверено 28 ноября 2009 г.
• Кевин Браун. «О сетках и мозаиках де Брёйна». mathpages.com . Проверено 28 ноября 2009 г.
• Дэвид Эппштейн . «Плитки Пенроуза». Свалка геометрии . ics.uci.edu/~eppstein . Проверено 28 ноября 2009 г.Здесь есть список дополнительных ресурсов.
• Уильям Чоу. «Плитка Пенроуза в архитектуре» . Проверено 28 декабря 2009 г.
• «Просмотр плиток Пенроуза».