В математике действительная проективная плоскость — это двумерное проективное пространство , во многих отношениях похожее на знакомую евклидову плоскость, но без понятий расстояния , окружности , меры угла или параллельности . Это среда для плоской проективной геометрии , в которой отношения между объектами не считаются изменяющимися при проективных преобразованиях . Название проективный происходит от перспективного рисунка : проецирование изображения с одной плоскости на другую, если смотреть из точки вне любой из плоскостей, например, фотографируя плоскую картину под косым углом, является проективным преобразованием.
Основными объектами в проективной плоскости являются точки и прямые линии , и, как и в евклидовой геометрии , каждая пара точек определяет уникальную прямую, проходящую через обе, но в отличие от евклидовой геометрии в проективной геометрии каждая пара прямых также определяет уникальную точку на своем пересечении (в евклидовой геометрии параллельные прямые никогда не пересекаются). В контекстах, где нет двусмысленности, ее просто называют проективной плоскостью ; квалификатор «реальный» добавляется, чтобы отличить ее от других проективных плоскостей, таких как комплексная проективная плоскость и конечные проективные плоскости .
Одной из распространенных моделей реальной проективной плоскости является пространство линий в трехмерном евклидовом пространстве , которые проходят через определенную исходную точку ; в этой модели линии, проходящие через исходную точку, считаются «точками» проективной плоскости, а плоскости, проходящие через исходную точку, считаются «линиями» в проективной плоскости. Эти проективные точки и линии можно изобразить в двух измерениях, пересекая их любой произвольной плоскостью, не проходящей через исходную точку; тогда параллельная плоскость, которая проходит через исходную точку (проективная «линия»), называется линией на бесконечности . (См. § Однородные координаты ниже.)
В топологии название « реальная проективная плоскость» применяется к любой поверхности , которая топологически эквивалентна реальной проективной плоскости. Топологически реальная проективная плоскость компактна и неориентируема ( односторонняя). Она не может быть вложена в трехмерное евклидово пространство без пересечения с собой. Она имеет эйлерову характеристику 1, следовательно, полурод (неориентируемый род, род Эйлера) равен 1.
Топологическую действительную проективную плоскость можно построить, взяв (единственный) край ленты Мёбиуса и приклеив его к себе в правильном направлении, или приклеив край к диску . С другой стороны, действительную проективную плоскость можно построить, отождествив каждую пару противоположных сторон квадрата, но в противоположных направлениях, как показано на схеме. (Выполнение любой из этих операций в трехмерном пространстве заставляет поверхность пересекать саму себя.)
Проективная геометрия не обязательно связана с кривизной, и действительная проективная плоскость может быть скручена и помещена в евклидову плоскость или трехмерное пространство многими различными способами. [1] Некоторые из наиболее важных примеров описаны ниже.
Проективная плоскость не может быть вложена (то есть без пересечения) в трехмерное евклидово пространство . Доказательство того, что проективная плоскость не вкладывается в трехмерное евклидово пространство, выглядит следующим образом: Предполагая, что она вкладывается, она ограничила бы компактную область в трехмерном евклидовом пространстве обобщенной теоремой о кривой Жордана . Тогда направленное наружу единичное нормальное векторное поле дало бы ориентацию граничного многообразия, но граничное многообразие было бы проективной плоскостью , которая не является ориентируемой. Это противоречие, и поэтому наше предположение о том, что она вкладывается, должно быть ложным.
Рассмотрим сферу , и пусть большие окружности сферы будут "линиями", а пары антиподальных точек будут "точками". Легко проверить, что эта система подчиняется аксиомам, требуемым для проективной плоскости :
Если мы отождествим каждую точку на сфере с ее антиподальной точкой, то получим представление действительной проективной плоскости, в которой «точки» проективной плоскости действительно являются точками. Это означает, что проективная плоскость является факторпространством сферы, полученным путем разбиения сферы на классы эквивалентности по отношению эквивалентности ~, где x ~ y , если y = x или y = − x . Это факторпространство сферы гомеоморфно совокупности всех прямых, проходящих через начало координат в R 3 .
Факторное отображение сферы на действительную проективную плоскость на самом деле является двулистным (т.е. два к одному) накрывающим отображением . Из этого следует, что фундаментальная группа действительной проективной плоскости является циклической группой порядка 2; т.е. целые числа по модулю 2. Можно взять петлю AB из рисунка выше в качестве генератора.

Поскольку сфера покрывает действительную проективную плоскость дважды, плоскость можно представить в виде замкнутой полусферы, по краю которой обозначены противоположные точки. [2]
Проективная плоскость может быть погружена (локальные окрестности исходного пространства не имеют самопересечений) в 3-мерное пространство. Поверхность Боя является примером погружения.
Примеры многогранников должны иметь не менее девяти граней. [3]

Римская поверхность Штейнера представляет собой более вырожденное отображение проективной плоскости в трехмерное пространство, содержащее крестообразную шапку .

Многогранным представлением является тетрагемигексаэдр [4] , который имеет ту же общую форму , что и римская поверхность Штейнера, показанная здесь.
Рассматривая в противоположном направлении, некоторые абстрактные правильные многогранники — полукуб , полудодекаэдр и полуикосаэдр — могут быть построены как правильные фигуры в проективной плоскости; см. также проективные многогранники .
Были описаны различные планарные (плоские) проекции или отображения проективной плоскости. В 1874 году Клейн описал отображение: [1]
Центральная проекция проективной полусферы на плоскость дает обычную бесконечную проективную плоскость, описанную ниже.
Замкнутая поверхность получается путем приклеивания диска к крестообразной крышке . Эта поверхность может быть параметрически представлена следующими уравнениями:
где u и v находятся в диапазоне от 0 до 2π .
Эти уравнения аналогичны уравнениям тора . На рисунке 1 показан замкнутый диск с крестообразной крышкой.
Диск с крестообразной шапкой имеет плоскость симметрии , которая проходит через его отрезок линии двойных точек. На рисунке 1 диск с крестообразной шапкой виден сверху его плоскости симметрии z = 0, но он выглядел бы так же, если бы был виден снизу.
Диск с крестообразной крышкой можно разрезать вдоль его плоскости симметрии, при этом следя за тем, чтобы не разрезать ни одну из его двойных точек. Результат показан на рисунке 2.
После того, как это исключение будет сделано, станет видно, что нарезанный крестообразно покрытый диск гомеоморфен самопересекающемуся диску, как показано на рисунке 3.
Самопересекающийся диск гомеоморфен обычному диску. Параметрические уравнения самопересекающегося диска:
где u изменяется от 0 до 2π , а v изменяется от 0 до 1.
Проецируя самопересекающийся диск на плоскость симметрии ( z = 0 в параметризации, приведенной ранее), которая проходит только через двойные точки, мы получаем обычный диск, который повторяет себя (складывается сам на себя).
Плоскость z = 0 разрезает самопересекающийся диск на пару дисков, являющихся зеркальными отражениями друг друга. Центры дисков находятся в начале координат .
Теперь рассмотрим ободки дисков (при v = 1). Точки на ободе самопересекающегося диска располагаются парами, которые являются отражениями друг друга относительно плоскости z = 0.
Диск с крестообразной крышкой образуется путем идентификации этих пар точек, делая их эквивалентными друг другу. Это означает, что точка с параметрами ( u , 1) и координатами отождествляется с точкой ( u + π, 1), координаты которой равны . Но это означает, что пары противоположных точек на ободе (эквивалентного) обычного диска отождествляются друг с другом; так из диска образуется действительная проективная плоскость. Следовательно, поверхность, показанная на рисунке 1 (крестообразная крышка с диском), топологически эквивалентна действительной проективной плоскости RP 2 .
Точки на плоскости могут быть представлены однородными координатами . Точка имеет однородные координаты [ x : y : z ], где координаты [ x : y : z ] и [ tx : ty : tz ] считаются представляющими одну и ту же точку для всех ненулевых значений t . Точки с координатами [ x : y :1] являются обычной действительной плоскостью , называемой конечной частью проективной плоскости, а точки с координатами [ x : y :0], называемые точками на бесконечности или идеальными точками , составляют линию, называемую линией на бесконечности . (Однородные координаты [0:0:0] не представляют никакой точки.)
Прямые на плоскости также могут быть представлены однородными координатами. Проективная прямая, соответствующая плоскости ax + by + cz = 0 в R3 , имеет однородные координаты ( a : b : c ). Таким образом, эти координаты имеют отношение эквивалентности ( a : b : c ) = ( da : db : dc ) для всех ненулевых значений d . Следовательно, другое уравнение той же прямой dax + dby + dcz = 0 дает те же однородные координаты. Точка [ x : y : z ] лежит на прямой ( a : b : c ), если ax + by + cz = 0. Следовательно, прямые с координатами ( a : b : c ), где a , b не равны оба 0, соответствуют прямым в обычной действительной плоскости , поскольку они содержат точки, которые не находятся на бесконечности. Прямая с координатами (0 : 0 : 1) является бесконечно удаленной прямой, поскольку на ней расположены только те точки, у которых z = 0.
Линия в P 2 может быть представлена уравнением ax + by + cz = 0. Если мы будем рассматривать a , b , и c как вектор-столбец ℓ , а x , y , z как вектор-столбец x , то приведенное выше уравнение можно записать в матричной форме как:
Используя векторную запись, мы можем вместо этого записать x ⋅ ℓ = 0 или ℓ ⋅ x = 0.
Уравнение k ( x T ℓ ) = 0 (где k — ненулевой скаляр) выметает плоскость, которая проходит через ноль в R 3 , а k ( x ) выметает прямую, снова проходящую через ноль. Плоскость и прямая являются линейными подпространствами в R 3 , которые всегда проходят через ноль.
В P2 уравнение прямой имеет вид ax + by + cz = 0, и это уравнение может представлять прямую на любой плоскости, параллельной плоскости x , y , путем умножения уравнения на k .
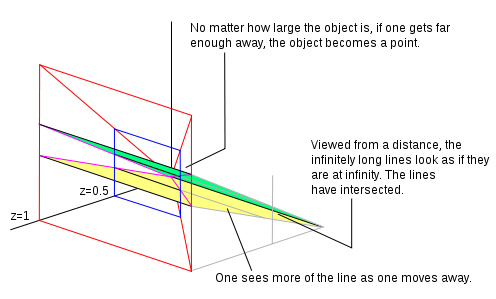
Если z = 1, то у нас есть нормализованная однородная координата. Все точки, у которых z = 1, создают плоскость. Давайте представим, что мы смотрим на эту плоскость (с позиции, расположенной дальше по оси z и оглядываясь назад к началу координат), и на плоскости нарисованы две параллельные линии. С того места, где мы стоим (учитывая наши зрительные возможности), мы можем видеть только определенную часть плоскости, которую мы представляем как область, выделенную красным на диаграмме. Если мы отойдем от плоскости по оси z (все еще глядя назад к началу координат), мы увидим большую часть плоскости. В нашем поле зрения исходные точки сместились. Мы можем отразить это движение, разделив однородную координату на константу. На соседнем изображении мы разделили на 2, поэтому значение z теперь становится равным 0,5. Если мы отойдем достаточно далеко, то, на что мы смотрим, станет точкой на расстоянии. По мере того, как мы отходим, мы видим все больше и больше параллельных линий. Линии встретятся на линии в бесконечности (линии, которая проходит через ноль на плоскости при z = 0 ). Прямые на плоскости при z = 0 являются идеальными точками. Плоскость при z = 0 является прямой на бесконечности.
Однородная точка (0, 0, 0) — это точка, в которой находятся все действительные точки, если смотреть на плоскость с бесконечного расстояния; линия на плоскости z = 0 — это точка пересечения параллельных прямых.
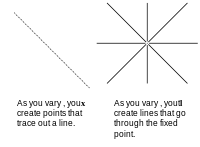
В уравнении x T ℓ = 0 есть два вектора-столбца . Вы можете оставить один из них постоянным и изменить другой. Если мы оставим точку x постоянной и изменим коэффициенты ℓ, мы создадим новые линии, проходящие через точку. Если мы оставим коэффициенты постоянными и изменим точки, удовлетворяющие уравнению, мы создадим линию. Мы рассматриваем x как точку, потому что оси, которые мы используем, это x , y и z . Если бы мы вместо этого нанесли коэффициенты на график, используя оси, обозначенные a , b , c , точки стали бы линиями, а линии стали бы точками. Если вы доказываете что-то с помощью данных, нанесенных на оси, обозначенные x , y и z, тот же аргумент можно использовать для данных, нанесенных на оси, обозначенные a , b и c . Это двойственность.
Уравнение x T ℓ = 0 вычисляет скалярное произведение двух векторов-столбцов. Скалярное произведение двух векторов равно нулю, если векторы ортогональны . В P 2 линия между точками x 1 и x 2 может быть представлена как вектор-столбец ℓ , который удовлетворяет уравнениям x 1 T ℓ = 0 и x 2 T ℓ = 0 , или, другими словами, вектор-столбец ℓ, который ортогонален x 1 и x 2. Перекрестное произведение найдет такой вектор: линия, соединяющая две точки, имеет однородные координаты, заданные уравнением x 1 × x 2 . Пересечение двух линий может быть найдено таким же образом, используя двойственность, как перекрестное произведение векторов, представляющих линии, ℓ 1 × ℓ 2 .
Проективная плоскость вкладывается в 4-мерное евклидово пространство. Действительная проективная плоскость P 2 ( R ) является фактором двумерной сферы
антиподальным отношением ( x , y , z ) ~ (− x , − y , − z ) . Рассмотрим функцию R 3 → R 4 , заданную как ( x , y , z ) ↦ ( xy , xz , y 2 − z 2 , 2 yz ) . Это отображение ограничивается отображением, областью определения которого является S 2 , и, поскольку каждый компонент является однородным многочленом четной степени, он принимает одинаковые значения в R 4 в каждой из любых двух антиподальных точек на S 2 . Это дает отображение P 2 ( R ) → R 4 . Более того, это отображение является вложением. Обратите внимание, что это вложение допускает проекцию в R 3 , которая является римской поверхностью .
Склеивая проективные плоскости последовательно, мы получаем неориентируемые поверхности более высокого полурода . Процесс склеивания состоит в вырезании небольшого диска из каждой поверхности и идентификации ( склеивании ) их граничных окружностей. Склеивание двух проективных плоскостей создает бутылку Клейна .
В статье о фундаментальном многоугольнике описываются высшие неориентируемые поверхности.