Площадь круга

В геометрии площадь, ограниченная кругом радиусом r $,$ равна π $r$ $2.$ $Здесь$ греческая буква π представляет собой постоянное отношение длины окружности к ее диаметру , приблизительно равное 3,14159.

Один из методов вывода этой формулы, который возник у Архимеда , заключается в рассмотрении круга как предела последовательности правильных многоугольников с увеличивающимся числом сторон. Площадь правильного многоугольника равна половине его периметра , умноженного на расстояние от его центра до его сторон , и поскольку последовательность стремится к кругу, соответствующая формула — что площадь равна половине длины окружности , умноженной на радиус, — а именно, $A = .mw-parser-output .sfrac{white-space:nowrap}.mw-parser-output .sfrac.tion,.mw-parser-output .sfrac .tion{display:inline-block;vertical-align:-0.5em;font-size:85%;text-align:center}.mw-parser-output .sfrac .num{display:block;line-height:1em;margin:0.0em 0.1em;border-bottom:1px solid}.mw-parser-output .sfrac .den{display:block;line-height:1em;margin:0.1em 0.1em}.mw-parser-output .sr-only{border:0;clip:rect(0,0,0,0);clip-path:polygon(0px 0px,0px 0px,0px 0px);height:1px;margin:-1px;overflow:hidden;padding:0;position:absolute;width:1px}⁠1/2⁠ × 2π r × r$ , справедливо для окружности.

Терминология

Хотя в неформальном контексте его часто называют площадью круга , строго говоря, термин «диск» относится к внутренней области круга, тогда как «круг» зарезервирован только для границы, которая является кривой и сама по себе не охватывает никакой площади. Поэтому площадь диска — более точное выражение для площади, заключенной в круг.

История

Современная математика может получить площадь, используя методы интегрального исчисления или его более сложного потомка, вещественного анализа . Однако площадь диска изучалась древними греками . Евдокс Книдский в пятом веке до нашей эры обнаружил, что площадь диска пропорциональна его радиусу в квадрате. ^[1] Архимед использовал инструменты евклидовой геометрии , чтобы показать, что площадь внутри круга равна площади прямоугольного треугольника , основание которого имеет длину окружности круга, а высота равна радиусу круга, в своей книге Измерение круга . Окружность равна 2πr $,$ а площадь треугольника равна половине основания, умноженного на высоту, что дает площадь $πr2$ для диска. До Архимеда Гиппократ Хиосский был первым, кто показал, что площадь диска пропорциональна квадрату его диаметра, как часть его квадратуры луночки Гиппократа , ^[2 ^], но не определил константу пропорциональности .

Исторические аргументы

Исторически было выдвинуто множество аргументов для установления уравнения с различной степенью математической строгости. Самым известным из них является метод исчерпывания Архимеда , одно из самых ранних применений математической концепции предела , а также происхождение аксиомы Архимеда , которая остается частью стандартной аналитической обработки действительной числовой системы . Первоначальное доказательство Архимеда не является строгим по современным стандартам, поскольку оно предполагает, что мы можем сравнить длину дуги окружности с длиной секущей и касательной, а также аналогичные утверждения о площади, как геометрически очевидно. $A=\pi r^{2}$

Использование полигонов

Площадь правильного многоугольника равна половине его периметра, умноженного на апофему . По мере увеличения числа сторон правильного многоугольника, многоугольник стремится к окружности, а апофема стремится к радиусу. Это говорит о том, что площадь диска равна половине длины окружности его ограничивающего круга, умноженной на радиус. ^[3]

Доказательство Архимеда

Следуя аргументу Архимеда в «Измерении круга» (ок. 260 г. до н. э.), сравните площадь, ограниченную кругом, с прямоугольным треугольником, основание которого имеет длину окружности круга, а высота равна радиусу круга. Если площадь круга не равна площади треугольника, то она должна быть либо больше, либо меньше. Мы исключаем каждый из них от противного, оставляя равенство как единственную возможность. Мы используем правильные многоугольники таким же образом.

Не больше

Предположим, что площадь C, заключенная в круг, больше площади T = ¹ ⁄ ₂cr треугольника. Пусть E обозначает избыточную величину. Впишите квадрат в круг так, чтобы его четыре угла лежали на круге. Между квадратом и кругом находятся четыре сегмента. Если общая площадь этих зазоров, G ₄ , больше E , разделите каждую дугу пополам. Это превращает вписанный квадрат во вписанный восьмиугольник и производит восемь сегментов с меньшим общим зазором, G ₈ . Продолжайте разделение, пока общая площадь зазора, G _n , не станет меньше E . Теперь площадь вписанного многоугольника, P _n = C − G _n , должна быть больше площади треугольника.

{\begin{aligned}E&{}=C-T\\&{}>G_{n}\\P_{n}&{}=C-G_{n}\\&{}>C-E\\P_{n}&{}>T\end{aligned}}

Но это приводит к противоречию, как следует. Проведите перпендикуляр из центра к середине стороны многоугольника; его длина, h , меньше радиуса окружности. Также пусть каждая сторона многоугольника имеет длину s ; тогда сумма сторон, ns , меньше длины окружности. Площадь многоугольника состоит из n равных треугольников с высотой h и основанием s , таким образом, равна ¹ ⁄ ₂nhs . Но поскольку h < r и ns < c , площадь многоугольника должна быть меньше площади треугольника, ¹ ⁄ ₂cr , противоречие. Следовательно, наше предположение о том, что C может быть больше T, должно быть неверным.

Не менее

Предположим, что площадь, ограниченная кругом, меньше площади треугольника T. Пусть D обозначает величину дефицита. Опишите квадрат так, чтобы середина каждого ребра лежала на круге. Если общий зазор между квадратом и кругом, G ₄ , больше D , срежьте углы касательными к окружности, чтобы получился описанный восьмиугольник, и продолжайте срезать, пока площадь зазора не станет меньше D . Площадь многоугольника, P _n , должна быть меньше T .

{\begin{aligned}D&{}=T-C\\&{}>G_{n}\\P_{n}&{}=C+G_{n}\\&{}<C+D\\P_{n}&{}<T\end{aligned}}

Это также приводит к противоречию. Так как перпендикуляр к середине каждой стороны многоугольника является радиусом длины r . И поскольку общая длина стороны больше окружности, многоугольник состоит из n одинаковых треугольников с общей площадью больше T. Снова мы получаем противоречие, поэтому наше предположение о том, что C может быть меньше T, также должно быть неверным.

Следовательно, должно быть так, что площадь, ограниченная кругом, в точности равна площади треугольника. Это завершает доказательство.

Доказательство перестановки

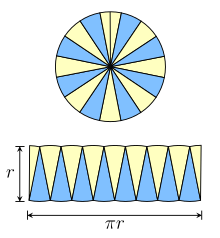
Следуя Сато Мошуну (Smith & Mikami 1914, стр. 130–132), Николаю Кузанскому ^[4] и Леонардо да Винчи (Beckmann 1976, стр. 19), мы можем использовать вписанные правильные многоугольники другим способом. Предположим, мы вписываем шестиугольник . Разрежем шестиугольник на шесть треугольников, разделив его от центра. Два противоположных треугольника оба касаются двух общих диаметров; сдвиньте их вдоль одного так, чтобы радиальные ребра были смежными. Теперь они образуют параллелограмм , при этом стороны шестиугольника образуют два противоположных ребра, одно из которых является основанием, s . Два радиальных ребра образуют наклонные стороны, а высота, h , равна его апофеме (как в доказательстве Архимеда). Фактически, мы также можем собрать все треугольники в один большой параллелограмм, поместив последовательные пары рядом друг с другом. То же самое верно, если мы увеличим его до восьми сторон и так далее. Для многоугольника с 2 n сторонами параллелограмм будет иметь основание длиной ns и высоту h . По мере увеличения числа сторон длина основания параллелограмма приближается к половине длины окружности, а его высота приближается к радиусу окружности. В пределе параллелограмм становится прямоугольником с шириной $π$ r и высотой r .

Современные доказательства

Существуют различные эквивалентные определения константы π. Традиционное определение в доисчисленной геометрии — это отношение длины окружности к ее диаметру:

\pi ={\frac {C}{D}}.

Однако, поскольку длина окружности не является примитивным аналитическим понятием, это определение не подходит для современных строгих трактовок. Стандартное современное определение состоит в том, что $π$ равно удвоенному наименьшему положительному корню функции косинуса или, что эквивалентно, полупериоду функции синуса (или косинуса). Функция косинуса может быть определена либо как степенной ряд , либо как решение определенного дифференциального уравнения . Это позволяет избежать любой ссылки на окружности в определении $π$ , так что утверждения об отношении $π$ к окружности и площади кругов на самом деле являются теоремами, а не определениями, которые вытекают из аналитических определений таких понятий, как «площадь» и «окружность».

Аналитические определения считаются эквивалентными, если согласиться, что окружность круга измеряется как спрямляемая кривая с помощью интеграла

C=2\int _{-R}^{R}{\frac {R\,dx}{\sqrt {R^{2}-x^{2}}}}=2R\int _{-1}^{1}{\frac {dx}{\sqrt {1-x^{2}}}}.

Интеграл, стоящий справа, является абелевым интегралом , значение которого равно полупериоду синусоидальной функции , равному $π$ . Таким образом, это справедливо как теорема. $C=2\pi R=\pi D$

Несколько из следующих аргументов используют только концепции из элементарного исчисления для воспроизведения формулы , но во многих случаях, чтобы рассматривать их как фактические доказательства, они неявно полагаются на тот факт, что можно разработать тригонометрические функции и фундаментальную константу $π$ таким образом, который полностью независим от их связи с геометрией. Мы указали, где это уместно, как каждое из этих доказательств может быть сделано полностью независимым от всей тригонометрии, но в некоторых случаях это требует более сложных математических идей, чем те, которые предоставляет элементарное исчисление. $A=\pi r^{2}$

Лук устойчив

Используя исчисление, мы можем суммировать площадь пошагово, разбивая диск на тонкие концентрические кольца, подобные слоям луковицы . Это метод интегрирования оболочки в двух измерениях. Для бесконечно тонкого кольца «луковицы» радиусом t накопленная площадь равна 2 $π$ t dt , окружной длине кольца, умноженной на его бесконечно малую ширину (можно аппроксимировать это кольцо прямоугольником с шириной = 2 $π$ t и высотой = dt ). Это дает элементарный интеграл для диска радиусом r .

{\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{r}2\pi t\,dt\\&{}=2\pi \left[{\frac {t^{2}}{2}}\right]_{0}^{r}\\&{}=\pi r^{2}.\end{aligned}}

Это строго обосновано правилом многомерной подстановки в полярных координатах. А именно, площадь задается двойным интегралом постоянной функции 1 по самому диску. Если D обозначает диск, то двойной интеграл можно вычислить в полярных координатах следующим образом:

{\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{r}\int _{0}^{2\pi }t\ d\theta \ dt\\&{}=\int _{0}^{r}\left[t\theta \right]_{0}^{2\pi }dt\\&{}=\int _{0}^{r}2\pi t\,dt\\\end{aligned}}

что является тем же результатом, что получен выше.

Эквивалентное строгое обоснование, не полагаясь на специальные координаты тригонометрии, использует формулу коплощади . Определим функцию как . Обратите внимание, что ρ — функция Липшица , градиент которой является единичным вектором ( почти всюду ). Пусть D — круг в . Мы покажем, что , где — двумерная мера Лебега в . Мы будем считать, что одномерная мера Хаусдорфа окружности — это , длина окружности радиуса r . (Это можно принять за определение окружности.) Тогда по формуле коплощади $\rho :\mathbb {R} ^{2}\to \mathbb {R}$ ${\textstyle \rho (x,y)={\sqrt {x^{2}+y^{2}}}}$ $|\nabla \rho |=1$ $\rho <1$ $\mathbb {R} ^{2}$ ${\mathcal {L}}^{2}(D)=\pi$ ${\mathcal {L}}^{2}$ $\mathbb {R} ^{2}$ $\rho =r$ $2\pi r$

{\begin{aligned}{\mathcal {L}}^{2}(D)&=\iint _{D}|\nabla \rho |\,d{\mathcal {L}}^{2}\\&=\int _{\mathbb {R} }{\mathcal {H}}^{1}(\rho ^{-1}(r)\cap D)\,dr\\&=\int _{0}^{1}{\mathcal {H}}^{1}(\rho ^{-1}(r))\,dr\\&=\int _{0}^{1}2\pi r\,dr=\pi .\end{aligned}}

Треугольное доказательство

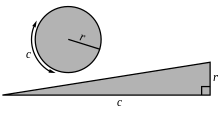
Подобно доказательству лука, описанному выше, мы могли бы использовать исчисление другим способом, чтобы прийти к формуле для площади диска. Рассмотрим развертывание концентрических окружностей в прямые полосы. Это сформирует прямоугольный треугольник с r в качестве высоты и 2 $π$ r (являющийся внешним ломтиком лука) в качестве основания.

Нахождение площади этого треугольника даст площадь диска.

{\begin{aligned}{\text{Area}}&{}={\frac {1}{2}}\cdot {\text{base}}\cdot {\text{height}}\\&{}={\frac {1}{2}}\cdot 2\pi r\cdot r\\&{}=\pi r^{2}\end{aligned}}

Противоположный и прилежащий углы для этого треугольника составляют соответственно в градусах 9,0430611..., 80,956939... и в радианах 0,1578311... OEIS : A233527 , 1,4129651... OEIS : A233528 .

Явно, мы представляем себе деление круга на треугольники, каждый с высотой, равной радиусу круга, и основанием, которое бесконечно мало. Площадь каждого из этих треугольников равна . Суммируя (интегрируя) все площади этих треугольников, мы приходим к формуле для площади круга: $1/2\cdot r\cdot du$

{\begin{aligned}\mathrm {Area} (r)&{}=\int _{0}^{2\pi r}{\frac {1}{2}}r\,du\\&{}=\left[{\frac {1}{2}}ru\right]_{0}^{2\pi r}\\&{}=\pi r^{2}.\end{aligned}}

Его также можно обосновать с помощью двойного интеграла постоянной функции 1 по кругу, изменив порядок интегрирования и использовав замену переменных в приведенном выше повторном интеграле:

{\begin{aligned}\mathrm {Area} (r)&{}=\iint _{D}1\ d(x,y)\\&{}=\iint _{D}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }\int _{0}^{r}t\ dt\ d\theta \\&{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\ d\theta \\\end{aligned}}

Выполнение замены преобразует интеграл в $u=r\theta ,\ du=r\ d\theta$

\int _{0}^{2\pi r}{\frac {1}{2}}{\frac {r^{2}}{r}}du=\int _{0}^{2\pi r}{\frac {1}{2}}r\ du

что совпадает с результатом выше.

Доказательство треугольника можно переформулировать как применение теоремы Грина в форме потока-дивергенции (т.е. двумерной версии теоремы о дивергенции ), таким образом, чтобы избежать всякого упоминания тригонометрии и константы π. Рассмотрим векторное поле на плоскости. Так что дивергенция r $равна$ двум , и , следовательно , площадь диска D равна $\mathbf {r} =x\mathbf {i} +y\mathbf {j}$

A={\frac {1}{2}}\iint _{D}\operatorname {div} \mathbf {r} \,dA.

По теореме Грина это то же самое, что и внешний поток r через окружность, ограничивающую D :

A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot \mathbf {n} \,ds

где n — единичная нормаль, а ds — мера длины дуги. Для окружности радиуса R с центром в начале координат имеем и , поэтому приведенное выше равенство имеет вид $|\mathbf {r} |=R$ $\mathbf {n} =\mathbf {r} /R$

A={\frac {1}{2}}\oint _{\partial D}\mathbf {r} \cdot {\frac {\mathbf {r} }{R}}\,ds={\frac {R}{2}}\oint _{\partial D}\,ds.

Интеграл от ds по всему кругу равен просто длине дуги, которая является его окружностью, поэтому это показывает, что площадь A , заключенная в круг, равна длине окружности, умноженной на ее длину. $\partial D$ $R/2$

Другое доказательство, использующее треугольники, рассматривает область, ограниченную кругом, как состоящую из бесконечного числа треугольников (т. е. каждый треугольник имеет угол $d𝜃$ в центре круга), каждый с площадью $⁠$ $1 / 2 ⁠ \cdot r 2 \cdot d𝜃$ (выведено из выражения для площади треугольника: $⁠$ $1 / 2 ⁠ \cdot а \cdot б \cdot грех 𝜃 = ⁠ 1 / 2 ⁠ \cdot р \cdot р \cdot грех(d𝜃) = ⁠ 1 / 2 ⁠ \cdot r 2 \cdot d𝜃$ ). Обратите внимание, что $sin(d𝜃) \approx d𝜃$ из-за приближения малых углов . Таким образом, суммируя площади треугольников, можно найти выражение для площади круга: ${\begin{aligned}\mathrm {Area} &{}=\int _{0}^{2\pi }{\frac {1}{2}}r^{2}\,d\theta \\&{}=\left[{\frac {1}{2}}r^{2}\theta \right]_{0}^{2\pi }\\&{}=\pi r^{2}.\end{aligned}}$

Полукруглое доказательство

Обратите внимание, что площадь полукруга радиуса r можно вычислить с помощью интеграла . ${\textstyle \int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx}$

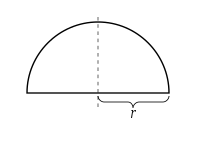
С помощью тригонометрической подстановки мы подставляем , следовательно $x=r\sin \theta$ $dx=r\cos \theta \,d\theta .$ ${\begin{aligned}\int _{-r}^{r}{\sqrt {r^{2}-x^{2}}}\,dx&=\int _{-{\frac {\pi }{2}}}^{\frac {\pi }{2}}{\sqrt {r^{2}\left(1-\sin ^{2}\theta \right)}}\cdot r\cos \theta \,d\theta \\&=2r^{2}\int _{0}^{\frac {\pi }{2}}\cos ^{2}\theta \,d\theta \\&={\frac {\pi r^{2}}{2}}.\end{aligned}}$

Последний шаг следует, поскольку тригонометрическое тождество подразумевает, что и имеют равные интегралы по интервалу , используя интегрирование путем подстановки . Но с другой стороны, поскольку , сумма двух интегралов равна длине этого интервала, которая равна . Следовательно, интеграл от равен половине длины этого интервала, которая равна . $\cos(\theta )=\sin(\pi /2-\theta )$ $\cos ^{2}\theta$ $\sin ^{2}\theta$ $[0,\pi /2]$ $\cos ^{2}\theta +\sin ^{2}\theta =1$ $\pi /2$ $\cos ^{2}\theta$ $\pi /4$

Следовательно, площадь круга радиусом r , который в два раза больше площади полукруга, равна . $2\cdot {\frac {\pi r^{2}}{2}}=\pi r^{2}$

Это конкретное доказательство может показаться предрешающим вопрос, если функции синуса и косинуса, участвующие в тригонометрической подстановке, рассматриваются как определенные относительно окружностей. Однако, как отмечалось ранее, можно определить синус, косинус и $π$ таким образом, который полностью независим от тригонометрии, и в этом случае доказательство справедливо по формуле замены переменных и теореме Фубини , предполагая основные свойства синуса и косинуса (которые также можно доказать, не предполагая ничего об их отношении к окружностям).

Изопериметрическое неравенство

Окружность — это замкнутая кривая наименьшего периметра, которая охватывает максимальную площадь. Это известно как изопериметрическое неравенство , которое гласит, что если спрямляемая жорданова кривая в евклидовой плоскости имеет периметр C и охватывает площадь A (по теореме о жордановой кривой ), то

4\pi A\leq C^{2}.

Более того, равенство в этом неравенстве выполняется тогда и только тогда, когда кривая является окружностью, в этом случае и . $A=\pi r^{2}$ $C=2\pi r$

Быстрое приближение

Расчеты, которые Архимед использовал для численного приближения площади, были трудоемкими, и он остановился на многоугольнике с 96 сторонами. Более быстрый метод использует идеи Виллеброрда Снеллиуса ( Cyclometricus , 1621), далее развитые Христианом Гюйгенсом ( De Circuli Magnitudine Inventa , 1654), описанные в Gerretsen & Verdenduin (1983, стр. 243–250).

Метод удвоения Архимеда

Дана окружность, пусть u _n будет периметром вписанного правильного n- угольника, и пусть U _n будет периметром описанного правильного n- угольника. Тогда u _n и U _n являются нижней и верхней границами окружности окружности, которые становятся все более и более острыми с ростом n , и их среднее значение ( u _n + U _n )/2 является особенно хорошим приближением к окружности. Чтобы вычислить u _n и U _n для больших n , Архимед вывел следующие формулы удвоения:

u_{2n}={\sqrt {U_{2n}u_{n}}}

( геометрическое среднее ), и

U_{2n}={\frac {2U_{n}u_{n}}{U_{n}+u_{n}}}

( среднее гармоническое ).

Начав с шестиугольника, Архимед удвоил n четыре раза, чтобы получить 96-угольник, что дало ему хорошее приближение к длине окружности.

В современной нотации мы можем воспроизвести его вычисления (и пойти дальше) следующим образом. Для единичной окружности вписанный шестиугольник имеет u ₆ = 6, а описанный шестиугольник имеет U ₆ = 4 √ 3 . Удвоение семь раз дает

(Здесь ⁠у _н + У _н/2⁠ приближается к длине окружности единичного круга, которая равна 2π $,$ поэтому ⁠у _н + У _н/4⁠ приближается к $π$ .)

Последняя запись таблицы содержит ³⁵⁵ ⁄ ₁₁₃ в качестве одного из лучших рациональных приближений ; т. е. нет лучшего приближения среди рациональных чисел со знаменателем до 113. Число ³⁵⁵ ⁄ ₁₁₃ также является отличным приближением к $π$ , приписываемым китайскому математику Цзу Чунчжи , который назвал его Милю . ^[5] Это приближение лучше, чем любое другое рациональное число со знаменателем меньше 16 604. ^[6]

Уточнение Снеллиуса-Гюйгенса

Снелл предложил (а Гюйгенс доказал) более точную границу, чем у Архимеда:

n{\frac {3\sin {\frac {\pi }{n}}}{2+\cos {\frac {\pi }{n}}}}<\pi <n\left(2\sin {\frac {\pi }{3n}}+\tan {\frac {\pi }{3n}}\right).

Это для n = 48 дает лучшее приближение (около 3,14159292), чем метод Архимеда для n = 768.

Вывод формулы удвоения Архимеда

Пусть одна сторона вписанного правильного n- угольника имеет длину s _n и касается окружности в точках A и B. Пусть A′ будет точкой, противоположной A на окружности, так что A′A является диаметром, а A′AB — вписанным треугольником на диаметре. По теореме Фалеса это прямоугольный треугольник с прямым углом в точке B. Пусть длина A′B будет c _n , которую мы называем дополнением s _n ; таким образом, c _n² + s _n² = (2 r ) ² . Пусть C делит дугу от A до B пополам, и пусть C′ будет точкой, противоположной C на окружности. Таким образом, длина CA равна s _{2 n} , длина C′A равна c _{2 n} , а C′CA сам по себе является прямоугольным треугольником на диаметре C′C. Так как C делит пополам дугу от A до B, C′C перпендикулярно делит пополам хорду от A до B, скажем, в точке P. Таким образом, треугольник C′AP является прямоугольным треугольником и подобен C′CA, поскольку они разделяют угол в точке C′. Таким образом, все три соответствующие стороны находятся в одинаковой пропорции; в частности, мы имеем C′A : C′C = C′P : C′A и AP : C′A = CA : C′C. Центр окружности, O, делит пополам A′A, поэтому мы также имеем треугольник OAP, подобный A′AB, с OP, в два раза меньшей длины A′B. С точки зрения длин сторон это дает нам

{\begin{aligned}c_{2n}^{2}&{}=\left(r+{\frac {1}{2}}c_{n}\right)2r\\c_{2n}&{}={\frac {s_{n}}{s_{2n}}}.\end{aligned}}

В первом уравнении C′P есть C′O+OP, длина r + ¹ ⁄ ₂c _n , а C′C — диаметр, 2 r . Для единичной окружности мы имеем знаменитое уравнение удвоения Людольфа ван Кейлена ,

c_{2n}={\sqrt {2+c_{n}}}.

Если мы теперь опишем правильный n- угольник со стороной A″B″, параллельной AB, то OAB и OA″B″ будут подобными треугольниками, причем A″B″ : AB = OC : OP. Назовем описанную сторону S _n ; тогда это S _n : s _n = 1 : ¹ ⁄ ₂c _n . (Мы снова использовали, что OP составляет половину длины A′B.) Таким образом, мы получаем

c_{n}=2{\frac {s_{n}}{S_{n}}}.

Назовем вписанный периметр u _n = ns _n , а описанный периметр U _n = nS _n . Тогда, объединяя уравнения, имеем

c_{2n}={\frac {s_{n}}{s_{2n}}}=2{\frac {s_{2n}}{S_{2n}}},

так что

u_{2n}^{2}=u_{n}U_{2n}.

Это дает уравнение среднего геометрического .

Мы также можем сделать вывод

2{\frac {s_{2n}}{S_{2n}}}{\frac {s_{n}}{s_{2n}}}=2+2{\frac {s_{n}}{S_{n}}},

или

{\frac {2}{U_{2n}}}={\frac {1}{u_{n}}}+{\frac {1}{U_{n}}}.

Это дает уравнение гармонического среднего .

приближение Дарта

Когда более эффективные методы нахождения площадей недоступны, мы можем прибегнуть к «метанию дротиков». Этот метод Монте-Карло использует тот факт, что если случайные образцы берутся равномерно разбросанными по поверхности квадрата, в котором находится диск, то доля образцов, которые попадают на диск, приближается к отношению площади диска к площади квадрата. Это следует считать методом крайней меры для вычисления площади диска (или любой формы), поскольку он требует огромного количества образцов для получения полезной точности; оценка, хорошая до 10 ^{− n,} требует около 100 ⁿ случайных образцов (Thijssen 2006, стр. 273).

Конечная перестановка

Мы видели, что, разделив диск на бесконечное число частей, мы можем собрать их обратно в прямоугольник. Замечательный факт, обнаруженный сравнительно недавно (Лачкович 1990), заключается в том, что мы можем разрезать диск на большое, но конечное число частей, а затем собрать их обратно в квадрат равной площади. Это называется проблемой квадратуры круга Тарского . Природа доказательства Лачковича такова, что оно доказывает существование такого разбиения (фактически, многих таких разбиений), но не демонстрирует какого-либо конкретного разбиения.

Неевклидовы окружности

Окружности можно определить в неевклидовой геометрии , в частности в гиперболической и эллиптической плоскостях.

Например, единичная сфера является моделью для двумерной эллиптической плоскости. Она несет внутреннюю метрику , которая возникает при измерении геодезической длины. Геодезические окружности являются параллелями в геодезической системе координат . $S^{2}(1)$

Точнее, фиксируем точку , которую помещаем в зенит. С этим зенитом связана геодезическая полярная система координат , , , где z — точка . В этих координатах геодезическое расстояние от z до любой другой точки, имеющей координаты , равно значению в точке x . Сферическая окружность — это множество точек, находящихся на геодезическом расстоянии R от точки зенита z . Эквивалентно, при фиксированном вложении в сферическая окружность радиуса с центром в точке z — это множество x в , такое что . $\mathbf {z} \in S^{2}(1)$ $(\phi ,\theta )$ $0\leq \phi \leq \pi$ $0\leq \theta <2\pi$ $\phi =0$ $\mathbf {x} \in S^{2}(1)$ $(\phi ,\theta )$ $\phi$ $\mathbb {R} ^{3}$ $R\leq \pi$ $S^{2}(1)$ $\mathbf {x} \cdot \mathbf {z} =\cos R$

Мы также можем измерить площадь сферического диска, заключенного внутри сферического круга, используя внутреннюю меру площади поверхности на сфере. Площадь диска радиусом R тогда определяется как

A=\int _{0}^{2\pi }\int _{0}^{R}\sin(\phi )d\phi \,d\theta =2\pi (1-\cos R).

В более общем случае, если сфера имеет радиус кривизны , то площадь диска радиусом R определяется как $S^{2}(\rho )$ $\rho$

A=2\pi \rho ^{2}(1-\cos(R/\rho )).

Обратите внимание, что, как применение правила Лопиталя , это стремится к евклидовой площади в плоском пределе . $\pi R^{2}$ $\rho \to \infty$

Гиперболический случай аналогичен, при этом площадь диска с внутренним радиусом R в гиперболической плоскости (постоянной кривизны) определяется выражением $-1$

A=2\pi (1-\cosh R)

где cosh — гиперболический косинус . В более общем случае для гиперболической плоскости постоянной кривизны ответ будет таким: $-k$

A=2\pi k^{-2}(1-\cosh(kR)).

Эти тождества важны для сравнительных неравенств в геометрии. Например, площадь, ограниченная кругом радиуса R в плоском пространстве, всегда больше площади сферического круга и меньше гиперболического круга, при условии, что все три круга имеют одинаковый (внутренний) радиус. То есть,

2\pi (1-\cos R)<\pi R^{2}<2\pi (1-\cosh R)

для всех . Интуитивно это происходит потому, что сфера имеет тенденцию изгибаться назад на себя, давая круги меньшей площади, чем те, что на плоскости, в то время как гиперболическая плоскость, будучи погруженной в пространство, развивает полосы, которые производят дополнительную площадь. В более общем смысле верно, что площадь круга фиксированного радиуса R является строго убывающей функцией кривизны. $R>0$

Во всех случаях, если — кривизна (постоянная, положительная или отрицательная), то изопериметрическое неравенство для области с площадью A и периметром L имеет вид $k$

L^{2}\geq 4\pi A-kA^{2}

где равенство достигается именно для круга. ^[7]

Обобщения

Мы можем растянуть диск, чтобы сформировать эллипс . Поскольку это растяжение является линейным преобразованием плоскости, оно имеет коэффициент искажения, который изменит площадь, но сохранит соотношения площадей. Это наблюдение можно использовать для вычисления площади произвольного эллипса из площади единичного круга.

Рассмотрим единичную окружность, описанную квадратом со стороной 2. Преобразование преобразует окружность в эллипс, растягивая или сжимая горизонтальный и вертикальный диаметры до большой и малой осей эллипса. Квадрат преобразуется в прямоугольник, описанный вокруг эллипса. Отношение площади круга к площади квадрата равно $π$ /4, что означает, что отношение эллипса к прямоугольнику также равно $π$ /4. Предположим, что a и b — длины большой и малой осей эллипса. Поскольку площадь прямоугольника равна ab , площадь эллипса равна $π$ ab /4.

Мы также можем рассмотреть аналогичные измерения в более высоких измерениях. Например, мы можем захотеть найти объем внутри сферы. Когда у нас есть формула для площади поверхности, мы можем использовать тот же самый подход «луковицы», который мы использовали для диска.

Смотрите также

Ссылки

^ Стюарт, Джеймс (2003). Ранние трансцендентальные исчисления с одной переменной (5-е изд.). Торонто, Онтарио: Brook/Cole. С. 3. ISBN 0-534-39330-6. Однако, косвенным путем, Евдокс (пятый век до н. э.) использовал исчерпание, чтобы доказать известную формулу для площади диска: $A=\pi r^{2}.$
^ Хит, Томас Л. (2003), Руководство по греческой математике, Courier Dover Publications, стр. 121–132, ISBN 0-486-43231-9.
↑ Хилл, Джордж. Уроки геометрии: для начинающих , стр. 124 (1894).
^ Клегг, Брайан (2012). Знакомство с Infinity . Icon Books. стр. 69. ISBN 978-1-84831-406-1.
^ Марцлофф, Жан-Клод (2006). История китайской математики . Springer. стр. 281. ISBN 9783540337829.
^ Не все наилучшие рациональные приближения являются конечными дробями цепной дроби!
^ Айзек Шавель (2001), Изопериметрические неравенства , Cambridge University Press

Библиография

Архимед (1897), «Измерение окружности», в Heath, TL (ред.), Труды Архимеда, Cambridge University Press
(Первоначально опубликовано издательством Кембриджского университета в 1897 году на основе греческой версии Дж. Л. Хейберга.)
Бекман, Петр (1976), История числа Пи , Гриффин Св. Мартина , ISBN 978-0-312-38185-1
Gerretsen, J.; Verdenduin, P. (1983), «Глава 8: Многоугольники и многогранники», в H. Behnke; F. Bachmann; K. Fladt; H. Kunle (ред.), Основы математики, том II: Геометрия , перевод SH Gould, MIT Press , стр. 243–250, ISBN 978-0-262-52094-2
(Первоначально Grundzüge der Mathematik , Vandenhoeck & Ruprecht, Göttingen, 1971.)
Лачкович, Миклош (1990), «Равноразложимость и несоответствие: решение задачи Тарского о квадратуре круга», Journal für die reine und angewandte Mathematik , 1990 (404): 77–117, doi : 10.1515/crll.1990.404.77, MR 1037431 , S2CID 117762563
Ланг, Серж (1985), «Длина окружности», Математика!: Встречи со старшеклассниками , Springer-Verlag , ISBN 978-0-387-96129-3
Смит, Дэвид Юджин ; Миками, Ёсио (1914), История японской математики, Чикаго: Open Court Publishing , стр. 130–132, ISBN 978-0-87548-170-8
Тийссен, Дж. М. (2006), Вычислительная физика , Cambridge University Press, стр. 273, ISBN 978-0-521-57588-1

Внешние ссылки

Новости науки о проблеме Тарского Архивировано 13 апреля 2008 г. на Wayback Machine