Джон Уоллис

Английский математик (1616–1703).

Джон Уоллис ( / ˈ w ɒ l ɪ s / ; ^[2] латынь : Wallisius ; 3 декабря [ OS 23 ноября] 1616 - 8 ноября [ OS 28 октября] 1703) был английским священнослужителем и математиком , которому частично приписывают развитие исчисления бесконечно малых .

Между 1643 и 1689 годами он служил главным криптографом парламента , а затем и королевского двора. ^[3] Ему приписывают введение символа ∞ для обозначения понятия бесконечности . ^[4] Он аналогичным образом использовал 1/∞ для бесконечно малого . Джон Уоллис был современником Ньютона и одним из величайших интеллектуалов раннего Возрождения математики . ^[5]

биография

Образование

• Кембридж, Массачусетс, Оксфорд, Д.Д.
• Гимназия в Тентердене, Кент, 1625–1631 гг.
• Школа Мартина Холбича в Фельстеде, Эссекс, 1631–1632 гг.
• Кембриджский университет, Эммануэль-колледж, 1632–1640 гг.; БА, 1637; Массачусетс, 1640 год.
• DD в Оксфорде в 1654 году.

Семья

14 марта 1645 года он женился на Сюзанне Глайнд ( ок.  1600 – 16 марта 1687). У них было трое детей:

1. Энн Бленко (4 июня 1656 г. - 5 апреля 1718 г.) вышла замуж за сэра Джона Бленкоу (30 ноября 1642 г. - 6 мая 1726 г.) в 1675 г. с проблемой ^[6]
2. Джон Уоллис (26 декабря 1650 - 14 марта 1717), ^[7] член парламента от Уоллингфорда 1690–1695, женился на Элизабет Харрис (ум. 1693) 1 февраля 1682 года, имел детей: один сын и две дочери.
3. Элизабет Уоллис (1658–1703 ^[8] ), вышла замуж за Уильяма Бенсона (1649–1691) из Таустера, умерла без проблем.

Жизнь

Джон Уоллис родился в Эшфорде, Кент . Он был третьим из пяти детей преподобного Джона Уоллиса и Джоанны Чепмен. Первоначально он получил образование в школе в Эшфорде, но в 1625 году после вспышки чумы перешёл в школу Джеймса Мовата в Тентердене . Уоллис впервые познакомился с математикой в ​​1631 году в школе Фельстеда (тогда известной как школа Мартина Холбича в Фельстеде); ему нравилась математика, но его учеба была неустойчивой, поскольку «в то время у нас математику рассматривали не как академические исследования, а скорее как механические» (Scriba 1970). В школе в Фельстеде Уоллис научилась говорить и писать по-латыни . К этому времени он также владел французским , греческим и ивритом . ^[9] Поскольку предполагалось, что он станет врачом, в 1632 году его отправили в Эммануэль-колледж в Кембридже . ^[10] Находясь там, он составил акт по учению о кровообращении ; Говорят, что это был первый случай в Европе, когда эта теория была публично поддержана в ходе диспутов. Однако его интересы были сосредоточены на математике. Он получил степень бакалавра гуманитарных наук в 1637 году и степень магистра в 1640 году, после чего принял сан священника. С 1643 по 1649 год он служил писцом без права голоса на Вестминстерской ассамблее . Он был избран в стипендию Куинс-колледжа в Кембридже в 1644 году, из которой ему пришлось уйти в отставку после женитьбы.

Все это время Уоллис был близок к парламентской партии, возможно, из-за знакомства с Холбичем в школе Фельстед. Он оказывал им большую практическую помощь в расшифровке донесений роялистов. Качество криптографии в то время было неоднозначным; несмотря на отдельные успехи таких математиков, как Франсуа Вьет , принципы, лежащие в основе разработки и анализа шифров, были очень плохо поняты. Большинство шифров представляли собой специальные методы, основанные на секретном алгоритме , в отличие от систем, основанных на переменном ключе . Уоллис понял, что последние гораздо более безопасны, даже назвав их «невзламываемыми», хотя он не был достаточно уверен в этом утверждении, чтобы поощрять раскрытие криптографических алгоритмов. Он также был обеспокоен использованием шифров иностранными державами, отклонив, например, просьбу Готфрида Лейбница в 1697 году обучать ганноверских студентов криптографии. ^[11]

Вернувшись в Лондон – он был назначен капелланом церкви Святого Габриэля Фенчерча в 1643 году – Уоллис присоединился к группе ученых, которая позже превратилась в Королевское общество . Наконец он смог удовлетворить свои математические интересы, освоив «Clavis Mathematicae » Уильяма Отреда за несколько недель в 1647 году. Вскоре он начал писать свои собственные трактаты, затрагивающие широкий круг тем, которые он продолжал до конца своей жизни. . Уоллис написал первый обзор математических концепций в Англии, в котором обсуждал индуистско-арабскую систему. ^[12]

Уоллис присоединился к умеренным пресвитерианцам, подписав протест против казни Карла I , чем навлек на себя длительную враждебность независимых. Несмотря на их сопротивление, в 1649 году он был назначен на савильскую кафедру геометрии в Оксфордском университете, где прожил до своей смерти 8 ноября [ OS 28 октября] 1703 года. В 1650 году Уоллис был рукоположен в сан министра. После этого он провел два года у сэра Ричарда Дарли и леди Вир в качестве частного капеллана . В 1661 году он был одним из двенадцати представителей пресвитерианской церкви на Савойской конференции .

Помимо своих математических работ, он писал по теологии , логике , английской грамматике и философии, а также участвовал в разработке системы обучения глухого мальчика речи в Литтлкот-Хаусе . ^[13] Уильям Холдер ранее научил глухого Александра Пофэма говорить «ясно и отчетливо, хорошим и изящным тоном». ^[14] Позже Уоллис взял на себя ответственность за это, в результате чего Холдер обвинил Уоллиса в том, что он «нарезал своих соседей и украшал себя их добычей». ^[15]

Назначение Уоллиса савилианским профессором геометрии в Оксфордском университете.

Парламентский визит в Оксфорд , начавшийся в 1647 году, отстранил от своих должностей многих старших ученых, в том числе в ноябре 1648 года савильских профессоров геометрии и астрономии. В 1649 году Уоллис был назначен савильским профессором геометрии. Уоллис, похоже, был выбран в основном по политическим мотивам (как, возможно, и его предшественник-роялист Питер Тернер , который, несмотря на свое назначение на две профессорские должности, никогда не публиковал никаких математических работ); Хотя Уоллис был, пожалуй, ведущим криптографом страны и входил в неформальную группу ученых, которая позже стала Королевским обществом , у него не было особой репутации математика. Тем не менее, назначение Уоллиса оказалось полностью оправданным его последующей работой в течение 54 лет, когда он служил профессором Савилиана. ^[16]

Вклад в математику

Математическая опера , 1699 г.

Уоллис внес значительный вклад в тригонометрию , исчисление , геометрию и анализ бесконечных рядов . В своей «Математической опере I» (1695 г.) он ввел термин « непрерывная дробь ».

Аналитическая геометрия

В 1655 году Уоллис опубликовал трактат о конических сечениях , в котором они были определены аналитически. Это была самая ранняя книга, в которой эти кривые рассматриваются и определяются как кривые второй степени . Это помогло устранить некоторые кажущиеся трудности и неясность работ Рене Декарта по аналитической геометрии . В «Трактате о конических сечениях» Уоллис популяризировал символ бесконечности ∞. Он писал: «Я предполагаю, что любая плоскость (в соответствии с Геометрией неделимых Кавальери) состоит из бесконечного числа параллельных линий или, как я предпочитаю, из бесконечного числа параллелограммов одной и той же высоты; (пусть высота каждого из них представляет собой бесконечно малую часть 1/∞ всей высоты, и пусть символ ∞ обозначает Бесконечность), а высота всей фигуры составляет высоту фигуры». ^[17]

Интегральное исчисление

Arithmetica Infinitorum , важнейшая из работ Уоллиса, была опубликована в 1656 году. В этом трактате методы анализа Декарта и Кавальери были систематизированы и расширены, но некоторые идеи были открыты для критики. После краткого трактата о конических сечениях он начал с разработки стандартных обозначений степеней, расширив их от целых положительных чисел до рациональных чисел :

${\displaystyle x^{0}=1}$

${\displaystyle x^{-1}={\frac {1}{x}}}$

${\displaystyle x^{-n}={\frac {1}{x^{n}}}{\text{ etc.}}}$

${\displaystyle x^{1/2}={\sqrt {x}}}$

${\displaystyle x^{2/3}={\sqrt[{3}]{x^{2}}}{\text{ etc.}}}$

${\displaystyle x^{1/n}={\sqrt[{n}]{x}}}$

${\displaystyle x^{p/q}={\sqrt[{q}]{x^{p}}}}$

Оставив многочисленные алгебраические приложения этого открытия, он затем приступил к нахождению путем интегрирования площади , заключенной между кривой y = xm , осью x и любой ординатой x = h , и доказал, что ^{отношение} этой площади к для параллелограмма на том же основании и той же высоты равна 1/( m  + 1), что является продолжением квадратурной формулы Кавальери . Он, по-видимому, предполагал, ^что тот же результат будет верен и для кривой y = axm , где a — любая константа, а m — любое положительное или отрицательное число, но он рассмотрел только случай параболы, в которой m = 2, и гиперболы. в котором m = −1. В последнем случае его интерпретация результата неверна. Затем он показал, что аналогичные результаты можно записать для любой кривой вида

${\displaystyle y=\sum _{m}^{}ax^{m}}$

и, следовательно, если ординату y кривой можно разложить по степеням x , можно определить ее площадь: таким образом, он говорит, что если уравнение кривой равно y = x ⁰ + x ¹ + x ² + ... , его площадь будет равна x + x ^2/2 + x ^3/3 + ... . Затем он применил это к квадратуре кривых y = ( x − x ² ) ⁰ , y = ( x − x ² ) ¹ , y = ( x − x ² ) ² и т. д., взятых между пределами x  = 0. и x  = 1. Он показывает, что площади равны соответственно 1, 1/6, 1/30, 1/140 и т. д. Затем он рассмотрел кривые вида y = x ^{1/ m} и установил теорему о том, что площадь ограниченный этой кривой и линиями x  = 0 и x  = 1, равен площади прямоугольника на том же основании и той же высоте, что и m  : m  + 1. Это эквивалентно вычислению

${\displaystyle \int _{0}^{1}x^{1/m}\,dx.}$

Он проиллюстрировал это параболой, в этом случае m = 2. Он сформулировал, но не доказал соответствующий результат для кривой вида y = x ^{p / q} .

Уоллис проявил значительную изобретательность в приведении уравнений кривых к приведенным выше формам, но, так как он не был знаком с биномиальной теоремой , он не смог произвести квадратуру круга , уравнением которой является , так как он не смог разложить его по степеням из х . Однако он сформулировал принцип интерполяции . Таким образом, поскольку ордината круга является средним геометрическим ординат кривых и , можно предположить, что в качестве приближения площадь полукруга можно принять как среднее геометрическое значений ${\displaystyle y={\sqrt {1-x^{2}}}}$ ${\displaystyle y={\sqrt {1-x^{2}}}}$ ${\displaystyle y=(1-x^{2})^{0}}$ ${\displaystyle y=(1-x^{2})^{1}}$ ${\displaystyle \int _{0}^{1}\!{\sqrt {1-x^{2}}}\,dx}$ ${\displaystyle {\tfrac {1}{4}}\pi }$

${\displaystyle \int _{0}^{1}(1-x^{2})^{0}\,dx\ {\text{ and }}\int _{0}^{1}(1-x^{2})^{1}\,dx,}$

то есть и ; это эквивалентно принятию или 3,26... в качестве значения π. Но, утверждал Уоллис, на самом деле мы имеем ряд ... и поэтому член, вставленный между ними, должен быть выбран так, чтобы подчиняться закону этого ряда. ^{[ необходимо разъяснение ]} Это с помощью сложного метода, который здесь подробно не описан, приводит к значению интерполированного члена, которое эквивалентно взятию ${\displaystyle 1}$ ${\displaystyle {\tfrac {2}{3}}}$ ${\displaystyle 4{\sqrt {\tfrac {2}{3}}}}$ ${\displaystyle 1,{\tfrac {1}{6}},{\tfrac {1}{30}},{\tfrac {1}{140}},}$ ${\displaystyle 1}$ ${\displaystyle {\tfrac {1}{6}}}$

${\displaystyle {\frac {\pi }{2}}={\frac {2}{1}}\cdot {\frac {2}{3}}\cdot {\frac {4}{3}}\cdot {\frac {4}{5}}\cdot {\frac {6}{5}}\cdot {\frac {6}{7}}\cdots }$

(которое теперь известно как произведение Уоллиса ).

В этой работе также обсуждаются образование и свойства цепных дробей , причем эта тема стала выдающейся благодаря использованию этих дробей Брункером .

Несколько лет спустя, в 1659 году, Уоллис опубликовал трактат, содержащий решение задач о циклоиде , предложенное Блезом Паскалем . При этом он попутно объяснил, как можно использовать принципы, изложенные в его «Арифметике бесконечности» , для выпрямления алгебраических кривых, и дал решение задачи выпрямления (т. е. нахождения длины) полукубической параболы x ³ = ay ² , которая был открыт в 1657 году его учеником Уильямом Нилом . Поскольку все попытки выпрямить эллипс и гиперболу были (неизбежно) безрезультатными, предполагалось, что никакие кривые не могут быть выпрямлены, как это действительно утверждал Декарт. Логарифмическая спираль была выпрямлена Евангелистой Торричелли и стала первой изогнутой линией (кроме круга), длина которой была определена, но расширение Нила и Уоллиса до алгебраической кривой было новым. Следующей исправленной кривой была циклоида; это сделал Кристофер Рен в 1658 году.

В начале 1658 года аналогичное открытие, независимое от открытия Нейла, было сделано ван Эраэтом , и оно было опубликовано ван Скутеном в его издании «Геометрии» Декарта в 1659 году. Метод Ван Эрайте заключается в следующем. Он полагает, что кривая относится к прямоугольным осям; если это так, и если ( x , y ) — координаты любой точки на ней, а n — длина нормали, ^{[ необходимы пояснения ]} и если другая точка с координатами ( x , η ) взята такая, что η  : h = n  : y , где h — константа; тогда, если ds — элемент длины искомой кривой, то по подобным треугольникам имеем ds  : dx = n  : y . Следовательно, h ds = η dx . Следовательно, если можно найти площадь сечения точки ( x , η ), первую кривую можно выпрямить. Таким способом ван Хёраэ осуществил выпрямление кривой y ³ = ax ² , но добавил, что выпрямление параболы y ² = ax невозможно, так как оно требует квадратуры гиперболы. Решения, предложенные Нилом и Уоллисом, в чем-то похожи на решения, предложенные ван Хёраэтом, хотя общего правила не сформулировано, а анализ неуклюж. Третий метод был предложен Ферма в 1660 году, но он неэлегантен и трудоемок.

Столкновение тел

Теория столкновения тел была выдвинута Королевским обществом в 1668 году на рассмотрение математиков. Уоллис, Кристофер Рен и Христиан Гюйгенс предложили правильные и похожие решения, все в зависимости от того, что сейчас называется сохранением импульса ; но, в то время как Рен и Гюйгенс ограничили свою теорию идеально упругими телами ( упругое столкновение ), Уоллис рассматривал также и несовершенно упругие тела ( неупругое столкновение ). За этим в 1669 году последовала работа по статике (центрам тяжести), а в 1670 году — по динамике : они представляют собой удобный обзор того, что тогда было известно по этому вопросу.

Алгебра

В 1685 году Уоллис опубликовал книгу «Алгебра» , которой предшествовал исторический отчет о развитии этого предмета, содержащий много ценной информации. Второе издание, вышедшее в 1693 году и составившее второй том его оперы , было значительно расширено. Эта алгебра примечательна тем, что содержит первое систематическое использование формул. Здесь данная величина представлена ​​числовым отношением, которое она имеет к единице величины того же вида: таким образом, когда Уоллис хочет сравнить две длины, он считает, что каждая содержит столько-то единиц длины. Возможно, это станет яснее, если отметить, что связь между пространством, описываемым в любой момент времени частицей, движущейся с равномерной скоростью, Уоллис обозначает формулой

s = vt ,

где s — число, обозначающее отношение описываемого пространства к единице длины; в то время как предыдущие авторы обозначали бы то же самое отношение, утверждая, что эквивалентно предложению

s ₁  : s ₂ знак равно v ₁ т ₁  : v ₂ т ₂ .

Числовая линия

Говоря о продвижении и отступлении от точки , Уоллис написал в «Трактате по алгебре» , что «… действительно проектирует Точку ; как проектировал Точку … И каждый проектирует (по крайней мере, в одной и той же Бесконечной Линии) одну Единую Точку: И только один». ${\displaystyle A}$ ${\displaystyle -3}$ ${\displaystyle D}$ ${\displaystyle +3}$ ${\displaystyle C}$ 

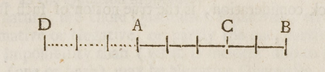
Уоллис считается создателем числовой прямой «для отрицательных величин» ^[18] и «для оперативных целей». ^[19] Это основано на отрывке из его трактата по алгебре 1685 года, в котором он ввел числовую прямую, чтобы проиллюстрировать законность отрицательных величин: ^[20]

Однако не является ли это предположение (отрицательных величин) бесполезным или абсурдным; когда правильно поняли. И хотя, что касается простой алгебраической нотации, она подразумевает количество меньше, чем ничего: тем не менее, когда дело доходит до физического применения, она обозначает как реальную величину, как если бы был знак ; но быть истолковано в противоположном смысле... означает "Ярды вперед"; и , означает ярды назад. ${\displaystyle +}$ ${\displaystyle +3}$ ${\displaystyle 3}$ ${\displaystyle -3}$ ${\displaystyle 3}$

Также было отмечено, что в более ранней работе Уоллис пришел к выводу, что отношение положительного числа к отрицательному больше бесконечности. Аргумент включает в себя частное и рассмотрение того, что происходит по мере приближения, а затем пересечения точки с положительной стороны. ^[21] Уоллис был не одинок в этом мышлении: Леонард Эйлер пришел к такому же выводу, рассмотрев геометрическую серию , оцененную при , а затем рассуждения, аналогичные рассуждениям Уоллиса (он разрешил парадокс, различая различные виды отрицательных чисел). ^[18] ${\displaystyle {\tfrac {1}{x}}}$ ${\displaystyle x}$ ${\displaystyle x=0}$ ${\displaystyle {\tfrac {1}{1-x}}=1+x+x^{2}+\cdots }$ ${\displaystyle x=2}$

Геометрия

Ему обычно приписывают доказательство теоремы Пифагора с использованием подобных треугольников . Однако шесть столетий назад арабский математик Сабит ибн Курра (901 г. н.э.) обобщил теорему Пифагора, применимую ко всем треугольникам. Разумно предположить, что Уоллис знал о работе Табита. ^[22]

Уоллис также был вдохновлен работами исламского математика Садра ат-Туси, сына Насир ад-Дина ат-Туси , в частности написанной в 1298 году книгой ат-Туси о постулате параллельности . Книга была основана на мыслях его отца и представила один из самых ранних аргументов в пользу неевклидовой гипотезы, эквивалентной постулату параллельности. Прочитав это, Уоллис затем написал о своих идеях, развивая собственные мысли по поводу постулата, пытаясь доказать его также с помощью подобных треугольников. ^[23]

Он обнаружил, что пятый постулат Евклида эквивалентен постулату, который в настоящее время называется в его честь «постулатом Уоллиса». Этот постулат гласит: «На данной конечной прямой всегда можно построить треугольник, подобный данному треугольнику». Этот результат был заключен в тенденции попытаться вывести пятый постулат Евклида из четырех других постулатов, что сегодня, как известно, невозможно. В отличие от других авторов, он осознавал, что неограниченный рост треугольника не гарантируется четырьмя первыми постулатами. ^[24]

Калькулятор

Еще одним аспектом математических способностей Уоллиса была его способность производить мысленные вычисления. Он плохо спал и часто делал мысленные расчеты, лежа без сна в своей постели. Однажды ночью он вычислил в уме квадратный корень из 53-значного числа. Утром он продиктовал 27-значный квадратный корень из числа, все еще полностью по памяти. Это был подвиг, который считался выдающимся, и Генри Ольденбург , секретарь Королевского общества, послал коллегу выяснить, как Уоллис это сделал. Это считалось достаточно важным, чтобы заслуживать обсуждения в «Философских трудах Королевского общества» 1685 года. ^{[25] [26]}

Музыкальная теория

Уоллис перевел на латынь произведения Птолемея и Вриенния, а также комментарий Порфирия к Птолемею. Он также опубликовал три письма Генри Ольденбургу по поводу настройки. Он одобрял принцип равного темперамента , который использовался в органах Англии. ^[27]

Другие работы

Математическая опера , 1657 г.

Его «Institutio Logicae» , опубликованный в 1687 году, пользовался большой популярностью. ^[4] Grammatica linguae Anglicanae — это работа по грамматике английского языка , которая печаталась вплоть до восемнадцатого века. Он также опубликовал публикации по теологии. ^[4]

Уоллис как криптограф

Во время работы капелланом леди Вир в 1642 году Уоллис получил зашифрованное письмо о падении Чичестера , которое ему удалось расшифровать в течение двух часов. Так началась его карьера криптографа. Он был умеренным сторонником парламентской стороны во время Первой гражданской войны в Англии и поэтому работал расшифровщиком перехваченной корреспонденции для парламентских лидеров. За свои услуги он был награжден житиями Святого Гавриила и Святого Мартина в Лондоне . ^[28]

Из-за своих парламентских симпатий Уоллис не был нанят криптографом после Реставрации Стюартов , ^[29] но после Славной революции его разыскивал лорд Ноттингем и часто нанимал для расшифровки зашифрованной перехваченной корреспонденции, хотя он считал, что он не всегда был адекватно вознагражден за свою работу. ^[a] Король Вильгельм III с 1689 года также нанимал Уоллиса в качестве криптографа, иногда почти ежедневно. Курьеры приносили ему письма для расшифровки и ждали продукта перед его кабинетом. Король лично интересовался работой и благополучием Уоллиса, о чем свидетельствует письмо, которое он отправил голландскому великому пенсионеру Антони Хейнсиусу в 1689 году ^.

В те первые дни правления Вильгельма прямое получение перехваченных иностранных писем было проблемой для англичан, поскольку у них еще не было ресурсов иностранных Черных палат , но союзники, такие как курфюрст Бранденбурга, не имея собственных Черных палат, иногда дарили такая перехваченная корреспонденция, как письмо короля Франции Людовика XIV королю Польши Яну III Собескому , которое король Вильгельм в 1689 году использовал, вызвало кризис во французско-польских дипломатических отношениях. Он открыто говорил об этом, и Уоллис была вознаграждена за свою роль. ^[31] Но Уоллис начал нервничать, что французы могут принять меры против него. ^[32]

Отношения Уоллиса с немецким математиком Готфридом Вильгельмом Лейбницем были теплыми. Но у Лейбница также были криптографические интересы, и он пытался заставить Уоллиса раскрыть некоторые из своих коммерческих тайн, от чего Уоллис отказался сделать это из патриотических принципов. ^[33]

Смит приводит пример кропотливой работы, которую выполнил Уоллис, как он сам описал это в письме Ричарду Хэмпдену от 3 августа 1689 года. В нем он дает подробный отчет о своей работе над конкретным письмом и о тех частях, с которыми у него возникли трудности. ^[34]

Переписка Уоллиса также показывает подробности того, как он постоял за себя, когда считал, что его недооценивают, финансово или по другим причинам. Он с энтузиазмом лоббировал как от своего имени, так и от имени своих родственников, о чем свидетельствуют письма лорду Ноттингему, Ричарду Хэмпдену и члену парламента Харборду Харборду , которые цитирует Смит. ^[35] В письме английскому посланнику в Пруссии Джеймс Джонстон Уоллис горько жалуется, что придворный прусского курфюрста по имени Сметто поступил с ним неправильно в вопросе справедливой компенсации за услуги, оказанные курфюрсту. В письме он подробно рассказывает о том, что он сделал, и дает совет по простому шифру замены , который мог бы использовать сам Джонстон. ^[36]

Вклад Уоллиса в искусство криптографии носил не только «технологический» характер. Де Леу указывает, что даже «чисто научный» вклад Уоллиса в лингвистику в области «рациональности» естественного языка , развивавшегося с течением времени, сыграл роль в развитии криптологии как науки. Разработка Уоллисом модели английской грамматики, независимой от более ранних моделей, основанных на латинской грамматике, является, по его мнению, примером того, как другие науки помогли развитию криптологии. ^[37]

Уоллис пытался научить своего сына Джона и внука от дочери Анны, Уильяма Бленкоу, премудростям ремесла. С Уильямом он добился такого успеха, что смог убедить правительство позволить внуку получить остаток годовой пенсии в размере 100 фунтов стерлингов, которую Уоллис получал в качестве компенсации за свою криптографическую работу. ^[38]

Уильям Бленкоу в конечном итоге сменил Уоллиса на посту официального криптографа королевы Анны после смерти Уоллиса в 1703 году ^.

Смотрите также

• 31982 Джонваллис , астероид, названный в его честь
• Невидимый колледж
• Академия Джона Уоллиса - бывшая школа Крайстчерч в Эшфорде, переименованная в 2010 году.
• Коническое ребро Уоллиса
• Интегралы Уоллиса

Примечания

1. Смит цитирует свои иногда резкие письма Ноттингему и другим. ^[30]

Рекомендации

1. Джозеф Фредерик Скотт, Математическая работа Джона Уоллиса (1616-1703) , Тейлора и Фрэнсиса, 1938, стр. 109.
2. Словарь случайного дома.
3. Смит, Дэвид Юджин (1917). «Джон Уоллис как криптограф». Бюллетень Американского математического общества . 24 (2): 82–96. дои : 10.1090/s0002-9904-1917-03015-7 . МР  1560009.
4. Чисхолм, Хью , изд. (1911). «Уоллис, Джон»  . Британская энциклопедия . Том. 28 (11-е изд.). Издательство Кембриджского университета. п. 284–285.
5. Кернс, Д.А. (1958). «Джон Уоллис и комплексные числа». Учитель математики . 51 (5): 373–374. JSTOR  27955680.
6. Джоан Тирск (2005). «Бленкоу, Энн, леди Бленкоу (1656–1718)». Оксфордский национальный биографический словарь . Оксфордский национальный биографический словарь (онлайн-изд.). Издательство Оксфордского университета. doi : 10.1093/ref: odnb/41326 . Проверено 21 августа 2023 г. (Требуется подписка или членство в публичной библиотеке Великобритании.)
7. "УОЛЛИС, Джон (1650-1717) из Здоровья, Неттлбед, Оксон" . История парламента онлайн . Проверено 21 августа 2023 г.
8. "Элизабет Уоллис". Ранние современные письма в Интернете: Человек . Проверено 21 августа 2023 г.
9. Юл, Г. Удный (1939). «Джон Уоллис, доктор медицинских наук, ФРС». Заметки и отчеты Лондонского королевского общества . 2 (1): 74–82. дои : 10.1098/rsnr.1939.0012. JSTOR  3087253.
10. "Уоллис, Джон (WLS632J)" . База данных выпускников Кембриджа . Кембриджский университет.
11. Кан, Дэвид (1967), Взломщики кодов: История тайного письма , Нью-Йорк: Macmillan, стр. 169, ЛЦН  63016109
12. 4
13. «Находка может положить конец 350-летнему научному спору» . Би-би-си. 26 июля 2008 года . Проверено 5 мая 2018 г.
14. В. Холдер, В. (1668). «Об эксперименте по поводу глухоты». Философские труды Королевского общества 3, стр. 665–668.
15. Холдер, «Философские труды Королевского общества» , приложение, 10.
16. Джон Уоллис: Хронология
17. Скотт, Дж. Ф. 1981. Математическая работа Джона Уоллиса, DD, FRS (1616–1703) . Chelsea Publishing Co. Нью-Йорк, штат Нью-Йорк. п. 18.
18. Хеффер, Альбрехт (10 марта 2011 г.). «Исторические возражения против числовой линии». Научное образование . 20 (9): 863–880 [872–876]. Бибкод : 2011Sc&Ed..20..863H. doi : 10.1007/s11191-011-9349-0. hdl : 1854/LU-1891046 . S2CID  120058064.
19. Нуньес, Рафаэль (2017). «Насколько математика «зашита», если она вообще есть: биологическая эволюция, развитие и важная роль культуры» (PDF) . В Сере, Мария Д.; Карлсон, Стефани М.; Маратсос, Майкл (ред.). Симпозиум Миннесоты по детской психологии: культура и системы развития, том 38 . John Wiley & Sons, Inc., стр. 83–124 [96]. дои : 10.1002/9781119301981.ch3.
20. Уоллис, Джон (1685). Трактат по алгебре, как исторический, так и практический. Лондон: Ричард Дэвис. п. 265. МПИРГ:GK8U243K.
21. Мартинес, Альберто А. (2006). Негативная математика: как можно изменить математические правила в положительную сторону. Издательство Принстонского университета. п. 22. ISBN 978-0-691-12309-7. Проверено 9 июня 2013 г.
22. Джозеф, Г.Г. (2000). Герб павлина: неевропейские корни математики (2-е изд.). Пингвин. п. 337. ИСБН 978-0-14-027778-4.
23. Математика Египта, Месопотамии, Китая, Индии и ислама: справочник Виктора Дж. Каца, издательство Принстонского университета. Архивировано 1 октября 2016 г. в Wayback Machine.
24. Бертон, Дэвид М. (2011), История математики / Введение (7-е изд.), McGraw-Hill, p. 566, ISBN 978-0-07-338315-6
25. Доктор Уоллис (1685 г.) «Два отрывка из журнала Филологического общества Оксфорда; один содержит статью, опубликованную 31 марта 1685 г. преподобным доктором Уоллисом, президентом этого общества, о силе памяти. при применении с должным вниманием;…», Philosophical Transactions of the Royal Society of London , 15  : 1269-1271. Доступно в Интернете по адресу: Лондонское королевское общество ^{[ постоянная мертвая ссылка ]}
26. Хоппен, К. Теодор (2013), Обычный учёный семнадцатого века: исследование Дублинского философского общества, 1683–1708, Издания библиотеки Рутледжа: История и философия науки, том. 15, Рутледж, с. 157, ISBN 9781135028541
27. Дэвид Дамшодер и Дэвид Рассел Уильямс, Теория музыки от Зарлино до Шенкера: библиография и руководство (Ститвесант, Нью-Йорк: Pendragon Press, 1990), стр. 374.
28. Смит, с. 83
29. Де Леу (1999), с. 138
30. Смит, стр. 83-86.
31. Смит, с. 87
32. Де Леу (1999), с. 139
33. Смит, стр. 83-84.
34. Смит, стр. 85-87.
35. Смит, стр. 89-93.
36. Смит, стр. 94-96.
37. Де Леу (2000), с. 9
38. Кейв, Э., изд. (1788). «Оригинальное письмо доктора Уоллиса с некоторыми подробностями его пенсии». Журнал Джентльмена . 63 (июнь 1788 г.): 479–480 . Проверено 20 августа 2023 г.
39. Де Леу (1999), стр.143

Источники

• Исходный текст данной статьи взят с общедоступного ресурса:
• WW Роуз Бал (1908). «Краткий обзор истории математики» (4-е изд.).
• Леу, К. де (1999). «Черная палата в Голландской республике во время войны за испанское наследство и ее последствий, 1707-1715 гг.» (PDF) . Исторический журнал . 42 (1): 133–156. дои : 10.1017/S0018246X98008292. S2CID  162387765 . Проверено 3 августа 2023 г.
• Леув, К. де (2000). «Использование кодов и шифров в Голландской республике, в основном в 18 веке». Криптология и государственное управление в Голландской Республике (PDF) . Амстердам. стр. 6–51 . Проверено 4 августа 2023 г.{{cite book}}: CS1 maint: отсутствует местоположение издателя ( ссылка )
• Смит, Дэвид Юджин (1917). «Джон Уоллис как криптограф». Бюллетень Американского математического общества . 24 (2): 82–96. дои : 10.1090/s0002-9904-1917-03015-7 . МР  1560009.
• Скриба, CJ (1970). «Автобиография Джона Уоллиса, ФРС». Заметки и отчеты Лондонского королевского общества . 25 : 17–46. дои : 10.1098/rsnr.1970.0003. S2CID  145393357.
• Стедалл, Жаклин, 2005, «Arithmetica Infinitorum» в книге Айвора Граттана-Гиннесса , изд., «Важные произведения в западной математике ». Эльзевир: 23–32.
• Гвиччардини, Никколо (2012) «Джон Уоллис как редактор математической работы Ньютона», Заметки и отчеты Лондонского королевского общества 66 (1): 3–17. Ссылка на JSTOR
• Стедалл, Жаклин А. (2001) «Нашей собственной нации: отчет Джона Уоллиса о математическом обучении в средневековой Англии», Historia Mathematica 28: 73.
• Уоллис, Дж. (1691). Седьмое письмо о священной Троице, вызванное вторым письмом от WJ / Джона Уоллиса ... (Ранние английские книги онлайн). Лондон: Напечатано для Тхо. Паркхерст...

Внешние ссылки

• Переписка Джона Уоллиса в EMLO
• «Уоллис, Джон (1616–1703)»  . Словарь национальной биографии . Лондон: Смит, Элдер и компания 1885–1900.
• О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Джон Уоллис», Архив истории математики MacTutor , Университет Сент-Эндрюс
• Страница проекта Галилео
• «Архивные материалы, касающиеся Джона Уоллиса». Национальный архив Великобритании .
• Портреты Джона Уоллиса в Национальной портретной галерее, Лондон
• Работы Джона Уоллиса в цифровой библиотеке постреформации
• Джон Уоллис (1685) Трактат по алгебре - цифровое факсимиле, Библиотека Линды Холл
• Уоллис, Джон (1685). Трактат по алгебре, как исторической, так и практической. Время от времени показывая его Исходное состояние, прогресс и продвижение, а также то, какими шагами оно достигло той высоты, на которой находится сейчас. Оксфорд: Ричард Дэвис. doi : 10.3931/e-rara-8842.
• Хатчинсон, Джон (1892). «Джон Уоллис»  . Мужчины Кента и Кентишмены (подписная ред.). Кентербери: Кросс и Джекман. стр. 139–140.