Пространство-время

Математическая модель, объединяющая пространство и время

В физике пространство-время , также называемое пространственно-временным континуумом , представляет собой математическую модель , которая объединяет три измерения пространства и одно измерение времени в единый четырехмерный континуум . Диаграммы пространства-времени полезны для визуализации и понимания релятивистских эффектов, таких как то, как различные наблюдатели воспринимают, где и когда происходят события.

До начала 20-го века предполагалось, что трехмерная геометрия вселенной (ее описание в терминах местоположений, форм, расстояний и направлений) отличается от времени (измерения того, когда события происходят во вселенной). Однако пространство и время приобрели новые значения с преобразованием Лоренца и специальной теорией относительности .

В 1908 году Герман Минковский представил геометрическую интерпретацию специальной теории относительности, которая объединила время и три пространственных измерения пространства в единый четырехмерный континуум, ныне известный как пространство Минковского . Эта интерпретация оказалась жизненно важной для общей теории относительности , в которой пространство-время искривляется массой и энергией .

Основы

Определения

Нерелятивистская классическая механика рассматривает время как универсальную величину измерения, которая является однородной во всем, отделена от пространства и согласована всеми наблюдателями. Классическая механика предполагает, что время имеет постоянную скорость течения, независимую от состояния движения наблюдателя или чего-либо внешнего. ^[1] Она предполагает, что пространство является евклидовым : она предполагает, что пространство следует геометрии здравого смысла. ^[2]

В контексте специальной теории относительности время нельзя отделить от трех измерений пространства, поскольку наблюдаемая скорость течения времени для объекта зависит от скорости объекта относительно наблюдателя. ^{[3] : 214–217} Общая теория относительности дает объяснение того, как гравитационные поля могут замедлять течение времени для объекта, видимого наблюдателем вне поля.

В обычном пространстве положение определяется тремя числами, известными как измерения . В декартовой системе координат их часто называют x , y и z . Точка в пространстве-времени называется событием и требует указания четырех чисел: трехмерного местоположения в пространстве и положения во времени (рис. 1). Событие представляется набором координат x , y , z и t . ^[4] Таким образом, пространство-время является четырехмерным .

В отличие от аналогий, используемых в популярных трудах для объяснения событий, таких как петарды или искры, математические события имеют нулевую продолжительность и представляют собой одну точку в пространстве-времени. ^[5] Хотя возможно находиться в движении относительно взрыва петарды или искры, наблюдатель не может находиться в движении относительно события.

Путь частицы через пространство-время можно рассматривать как последовательность событий. Последовательность событий можно связать вместе, чтобы сформировать кривую, которая представляет собой движение частицы через пространство-время. Этот путь называется мировой линией частицы . ^{[6] : 105}

Математически пространство-время является многообразием , то есть оно кажется локально «плоским» вблизи каждой точки таким же образом, как в достаточно малых масштабах поверхность земного шара кажется плоской. ^[7] Масштабный фактор (обычно называемый скоростью света ) связывает расстояния, измеренные в пространстве, с расстояниями, измеренными во времени. Величина этого масштабного фактора (почти 300 000 километров или 190 000 миль в пространстве эквивалентны одной секунде во времени), наряду с тем фактом, что пространство-время является многообразием, подразумевает, что при обычных, нерелятивистских скоростях и на обычных, человеческих масштабах, расстояниях мало что из того, что люди могли бы наблюдать, заметно отличается от того, что они могли бы наблюдать, если бы мир был евклидовым. Только с появлением чувствительных научных измерений в середине 1800-х годов, таких как эксперимент Физо и эксперимент Майкельсона-Морли , стали отмечаться загадочные расхождения между наблюдениями и предсказаниями, основанными на неявном предположении о евклидовом пространстве. ^[8] ${\displaystyle c}$

Рисунок 1-1. Каждое местоположение в пространстве-времени отмечено четырьмя числами, определяемыми системой отсчета : положением в пространстве и временем, которое можно визуализировать как показания часов, расположенных в каждом положении в пространстве. «Наблюдатель» синхронизирует часы в соответствии со своей собственной системой отсчета.

В специальной теории относительности наблюдатель в большинстве случаев будет означать систему отсчета, из которой измеряется набор объектов или событий. Такое использование существенно отличается от обычного английского значения термина. Системы отсчета по своей сути являются нелокальными конструкциями, и согласно такому использованию термина, не имеет смысла говорить о наблюдателе как имеющем местоположение. ^[9]

На рис. 1-1 представьте, что рассматриваемая система отсчета снабжена плотной решеткой часов, синхронизированных в этой системе отсчета, которая простирается бесконечно по всем трем измерениям пространства. Любое конкретное местоположение в пределах решетки не имеет значения. Решетка часов используется для определения времени и положения событий, происходящих в пределах всей системы отсчета. Термин наблюдатель относится ко всему ансамблю часов, связанных с одной инерциальной системой отсчета. ^{[9] : 17–22}

В этом идеализированном случае каждая точка пространства имеет часы, связанные с ней, и, таким образом, часы регистрируют каждое событие мгновенно, без задержки по времени между событием и его записью. Реальный наблюдатель увидит задержку между испусканием сигнала и его обнаружением из-за скорости света. Чтобы синхронизировать часы, при редукции данных после эксперимента время получения сигнала будет скорректировано, чтобы отразить его фактическое время, если бы оно было записано идеализированной решеткой часов. ^{[9] : 17–22}

Во многих книгах по специальной теории относительности, особенно старых, слово «наблюдатель» употребляется в более обычном смысле этого слова. Обычно из контекста ясно, какое значение было принято.

Физики различают то, что измеряют или наблюдают , после того, как вычли задержки распространения сигнала, и то, что видят визуально без таких поправок. Неспособность понять разницу между тем, что измеряют, и тем, что видят, является источником большой путаницы среди студентов теории относительности. ^[10]

История

К середине 1800-х годов различные эксперименты, такие как наблюдение пятна Араго и дифференциальные измерения скорости света в воздухе по сравнению с водой, считались доказывающими волновую природу света в отличие от корпускулярной теории . ^[11] Тогда предполагалось, что распространение волн требует существования волнообразной среды ; в случае световых волн это считалось гипотетическим светоносным эфиром . ^{[примечание 1]} Различные попытки установить свойства этой гипотетической среды дали противоречивые результаты. Например, эксперимент Физо 1851 года, проведенный французским физиком Ипполитом Физо , продемонстрировал, что скорость света в текущей воде была меньше суммы скорости света в воздухе плюс скорость воды на величину, зависящую от показателя преломления воды. ^[12]

Среди прочих вопросов, зависимость частичного увлечения эфиром, подразумеваемая этим экспериментом, от показателя преломления (который зависит от длины волны) привела к неприятному выводу о том, что эфир одновременно течет с разной скоростью для разных цветов света. ^[13] Эксперимент Майкельсона-Морли 1887 года (рис. 1-2) не показал дифференциального влияния движений Земли через гипотетический эфир на скорость света, и наиболее вероятное объяснение, полное увлечение эфиром, противоречило наблюдению за звездной аберрацией . ^[8]

Джордж Фрэнсис Фицджеральд в 1889 году ^[14] и Хендрик Лоренц в 1892 году независимо друг от друга предположили, что материальные тела, движущиеся через неподвижный эфир, подвергаются физическому воздействию при своем прохождении, сжимаясь в направлении движения на величину, которая была как раз необходима для объяснения отрицательных результатов эксперимента Майкельсона-Морли. Никаких изменений длины не происходит в направлениях, поперечных направлению движения.

К 1904 году Лоренц расширил свою теорию таким образом, что пришёл к уравнениям, формально идентичным тем, которые Эйнштейн вывел позже, то есть к преобразованиям Лоренца . ^[15] Как теория динамики (изучение сил и моментов и их влияния на движение), его теория предполагала реальные физические деформации физических составляющих материи. ^{[16] : 163–174} Уравнения Лоренца предсказывали величину, которую он назвал локальным временем , с помощью которой он мог объяснить аберрацию света , эксперимент Физо и другие явления.

Рисунок 1-3.

Анри Пуанкаре был первым, кто объединил пространство и время в пространство-время. ^{[17] [18] : 73–80, 93–95} В 1898 году он утверждал, что одновременность двух событий является вопросом соглашения. ^{[19] [примечание 2]} В 1900 году он признал, что «локальное время» Лоренца на самом деле является тем, что указывается движущимися часами, применив явное операциональное определение синхронизации часов, предполагающее постоянную скорость света. ^{[примечание 3]} В 1900 и 1904 годах он предположил присущую эфиру необнаружимость, подчеркнув справедливость того, что он назвал принципом относительности . В 1905/1906 годах ^[20] он математически усовершенствовал теорию электронов Лоренца, чтобы привести ее в соответствие с постулатом относительности.

Обсуждая различные гипотезы о лоренц-инвариантной гравитации, он ввел новаторскую концепцию 4-мерного пространства-времени, определив различные четыре вектора , а именно четыре положения , четыре скорости и четыре силы . ^{[21] [22]} Однако в последующих работах он не стал развивать 4-мерный формализм, заявив, что эта линия исследований, по-видимому, «влечет за собой большие трудности ради ограниченной выгоды», в конечном итоге придя к выводу, что «трехмерный язык, по-видимому, лучше всего подходит для описания нашего мира». ^[22] Даже в 1909 году Пуанкаре продолжал описывать динамическую интерпретацию преобразования Лоренца. ^{[16] : 163–174}

В 1905 году Альберт Эйнштейн проанализировал специальную теорию относительности с точки зрения кинематики (изучение движущихся тел без учета сил), а не динамики. Его результаты были математически эквивалентны результатам Лоренца и Пуанкаре. Он получил их, признав, что вся теория может быть построена на двух постулатах: принципе относительности и принципе постоянства скорости света. Его работа была наполнена яркими образами, включающими обмен световыми сигналами между движущимися часами, тщательные измерения длин движущихся стержней и другие подобные примеры. ^{[23] [примечание 4]}

В 1905 году Эйнштейн превзошел предыдущие попытки электромагнитного соотношения массы и энергии, введя общую эквивалентность массы и энергии , что сыграло важную роль в его последующей формулировке принципа эквивалентности в 1907 году, который провозглашает эквивалентность инертной и гравитационной массы. Используя эквивалентность массы и энергии, Эйнштейн показал, что гравитационная масса тела пропорциональна его энергетическому содержанию, что стало одним из ранних результатов в развитии общей теории относительности . Хотя, по-видимому, он сначала не думал геометрически о пространстве-времени, ^{[3] : 219} в дальнейшем развитии общей теории относительности Эйнштейн полностью включил формализм пространства-времени.

Когда Эйнштейн опубликовал свою работу в 1905 году, другой его конкурент, его бывший профессор математики Герман Минковский , также пришел к большинству основных элементов специальной теории относительности. Макс Борн рассказал о встрече, которую он провел с Минковским, стремясь стать его учеником/сотрудником: ^[25]

Я отправился в Кельн, встретился с Минковским и прослушал его знаменитую лекцию «Пространство и время», прочитанную 2 сентября 1908 года. [...] Позже он рассказал мне, что для него стало большим потрясением, когда Эйнштейн опубликовал свою статью, в которой была заявлена ​​эквивалентность различных локальных времен наблюдателей, движущихся относительно друг друга; поскольку он пришел к тем же выводам независимо, но не опубликовал их, поскольку хотел сначала разработать математическую структуру во всем ее великолепии. Он никогда не претендовал на приоритет и всегда отдавал Эйнштейну полную долю в великом открытии.

Минковский интересовался состоянием электродинамики после разрушительных экспериментов Майкельсона по крайней мере с лета 1905 года, когда Минковский и Дэвид Гильберт провели продвинутый семинар, на котором присутствовали известные физики того времени, чтобы изучить работы Лоренца, Пуанкаре и др. Минковский считал работу Эйнштейна продолжением работы Лоренца и находился под самым непосредственным влиянием Пуанкаре. ^[26]

Рисунок 1–4. Раскрашенная вручную прозрачность, представленная Минковским в его лекции Raum und Zeit 1908 года.

5 ноября 1907 года (чуть больше, чем за год до своей смерти) Минковский представил свою геометрическую интерпретацию пространства-времени в лекции в Гёттингенском математическом обществе под названием « Принцип относительности» ( Das Relativitätsprinzip ). ^{[примечание 5]} 21 сентября 1908 года Минковский представил свой доклад « Пространство и время » ( Raum und Zeit ) ^[27] Немецкому обществу учёных и врачей. Вступительные слова к «Пространству и времени» включают утверждение Минковского о том, что «Отныне пространство само по себе и время само по себе должны полностью свестись к простой тени, и только некое подобие союза этих двух должно сохранить независимость». В книге «Пространство и время» впервые были представлены публичные диаграммы пространства-времени (рис. 1-4), а также представлена ​​замечательная демонстрация того, что концепция инвариантного интервала (обсуждаемая ниже) вместе с эмпирическим наблюдением конечности скорости света позволяет вывести всю специальную теорию относительности. ^{[примечание 6]}

Концепция пространства-времени и группа Лоренца тесно связаны с определенными типами сферической , гиперболической или конформной геометрий и их группами преобразований, разработанными еще в 19 веке, в которых используются инвариантные интервалы, аналогичные интервалу пространства-времени . ^{[примечание 7]}

Эйнштейн, со своей стороны, изначально пренебрежительно относился к геометрической интерпретации специальной теории относительности Минковского, считая ее überflüssige Gelehrsamkeit (излишней ученостью). Однако для завершения его поиска общей теории относительности, начатого в 1907 году, геометрическая интерпретация относительности оказалась жизненно важной. В 1916 году Эйнштейн полностью признал свою обязанность Минковскому, чья интерпретация значительно облегчила переход к общей теории относительности. ^{[16] : 151–152} Поскольку существуют и другие типы пространства-времени, такие как искривленное пространство-время общей теории относительности, пространство-время специальной теории относительности сегодня известно как пространство-время Минковского.

Пространство-время в специальной теории относительности

Пространственно-временной интервал

В трех измерениях расстояние между двумя точками можно определить с помощью теоремы Пифагора : ${\displaystyle \Delta {d}}$

${\displaystyle (\Delta {d})^{2}=(\Delta {x})^{2}+(\Delta {y})^{2}+(\Delta {z})^{2}}$

Хотя два наблюдателя могут измерять положение x , y и z двух точек, используя разные системы координат, расстояние между точками будет одинаковым для обоих, предполагая, что они измеряют, используя одни и те же единицы. Расстояние является «инвариантным».

Однако в специальной теории относительности расстояние между двумя точками больше не является тем же самым, если оно измеряется двумя разными наблюдателями, когда один из наблюдателей движется, из-за сокращения Лоренца . Ситуация еще более усложняется, если две точки разделены как во времени, так и в пространстве. Например, если один наблюдатель видит, что два события происходят в одном и том же месте, но в разное время, человек, движущийся относительно первого наблюдателя, увидит два события, происходящих в разных местах, потому что движущаяся точка зрения видит себя неподвижной, а положение события — удаляющимся или приближающимся. Таким образом, для измерения эффективного «расстояния» между двумя событиями должна использоваться другая мера. ^{[31] : 48–50, 100–102}

В четырехмерном пространстве-времени аналогом расстояния является интервал. Хотя время входит в качестве четвертого измерения, оно рассматривается иначе, чем пространственные измерения. Таким образом, пространство Минковского отличается в важных отношениях от четырехмерного евклидова пространства . Основная причина слияния пространства и времени в пространство-время заключается в том, что пространство и время по отдельности не являются инвариантными, то есть при соответствующих условиях разные наблюдатели будут расходиться во мнениях относительно продолжительности времени между двумя событиями (из-за замедления времени ) или расстояния между двумя событиями (из-за сокращения длины ). Специальная теория относительности предоставляет новый инвариант, называемый интервалом пространства-времени , который объединяет расстояния в пространстве и во времени. Все наблюдатели, которые измеряют время и расстояние между любыми двумя событиями, в конечном итоге вычислят один и тот же интервал пространства-времени. Предположим, что наблюдатель измеряет два события как разделенные во времени и пространственным расстоянием Тогда квадрат интервала пространства-времени между двумя событиями, разделенными расстоянием в пространстве и по -координате , равен: ^[32] ${\displaystyle \Delta t}$ ${\displaystyle \Delta x.}$ ${\displaystyle (\Delta {s})^{2}}$ ${\displaystyle \Delta {x}}$ ${\displaystyle \Delta {ct}=c\Delta t}$ ${\displaystyle ct}$

${\displaystyle (\Delta s)^{2}=(\Delta ct)^{2}-(\Delta x)^{2},}$

или для трех пространственных измерений,

${\displaystyle (\Delta s)^{2}=(\Delta ct)^{2}-(\Delta x)^{2}-(\Delta y)^{2}-(\Delta z)^{2}.}$

Константа скорости света преобразует единицы времени (например, секунды) в единицы пространства (например, метры). Квадрат интервала является мерой разделения между событиями A и B, которые разделены во времени и, кроме того, разделены пространством либо потому, что есть два отдельных объекта, претерпевающих события, либо потому, что один объект в пространстве движется по инерции между своими событиями. Интервал разделения является разностью между квадратом пространственного расстояния, разделяющего событие B и событие A, и квадратом пространственного расстояния, пройденного световым сигналом за тот же интервал времени . Если разделение событий вызвано световым сигналом, то эта разность исчезает и . ${\displaystyle c,}$ ${\displaystyle t}$ ${\displaystyle \Delta s^{2}}$ ${\displaystyle \Delta t}$ ${\displaystyle \Delta s=0}$

Когда рассматриваемые события находятся бесконечно близко друг к другу, то мы можем записать

${\displaystyle ds^{2}=c^{2}dt^{2}-dx^{2}-dy^{2}-dz^{2}.}$

В другой инерциальной системе отсчета, скажем, с координатами , интервал пространства-времени можно записать в той же форме, что и выше. В силу постоянства скорости света световые события во всех инерциальных системах отсчета принадлежат нулевому интервалу, . Для любого другого бесконечно малого события, где , можно доказать, что что в свою очередь при интегрировании приводит к . ^{[33] : 2} Инвариантность интервала пространства-времени между одними и теми же событиями для всех инерциальных систем отсчета является одним из фундаментальных результатов специальной теории относительности. ${\displaystyle (t',x',y',z')}$ ${\displaystyle ds'}$ ${\displaystyle ds=ds'=0}$ ${\displaystyle ds\neq 0}$ ${\displaystyle ds^{2}=ds'^{2}}$ ${\displaystyle s=s'}$

Хотя для краткости часто можно увидеть интервальные выражения, выраженные без дельт, в том числе в большинстве последующих обсуждений, следует понимать, что в общем случае означает и т. д. Мы всегда имеем дело с различиями пространственных или временных значений координат, принадлежащих двум событиям, и поскольку не существует предпочтительного начала, отдельные значения координат не имеют существенного значения. ${\displaystyle x}$ ${\displaystyle \Delta {x}}$

Рисунок 2–1. Диаграмма пространства-времени, иллюстрирующая два фотона, A и B, возникающие в одном и том же событии, и объект, движущийся медленнее скорости света, C.

Уравнение выше похоже на теорему Пифагора, за исключением знака минус между и членами. Интервал пространства-времени — это величина, а не она сама. Причина в том, что в отличие от расстояний в евклидовой геометрии, интервалы в пространстве-времени Минковского могут быть отрицательными. Вместо того чтобы иметь дело с квадратными корнями из отрицательных чисел, физики обычно рассматривают его как отдельный символ сам по себе, а не как квадрат чего-либо. ^{[3] : 217} ${\displaystyle (ct)^{2}}$ ${\displaystyle x^{2}}$ ${\displaystyle s^{2},}$ ${\displaystyle s}$ ${\displaystyle s^{2}}$

Примечание: В литературе по теории относительности используются два соглашения о знаках:

${\displaystyle s^{2}=(ct)^{2}-x^{2}-y^{2}-z^{2}}$

и

${\displaystyle s^{2}=-(ct)^{2}+x^{2}+y^{2}+z^{2}}$

Эти соглашения о знаках связаны с метрическими сигнатурами (+−−−) и (−+++). Незначительное изменение заключается в том, чтобы разместить временную координату последней, а не первой. Оба соглашения широко используются в области изучения. ^[34]

В дальнейшем обсуждении мы будем использовать первое соглашение.

В общем случае может принимать любое действительное числовое значение. Если положительно, то пространственно-временной интервал называется времениподобным . Поскольку пространственное расстояние, пройденное любым массивным объектом, всегда меньше расстояния, пройденного светом за тот же интервал времени, положительные интервалы всегда времениподобны. Если отрицательно, то пространственно-временной интервал называется пространстваподобным . Пространственно-временные интервалы равны нулю, когда Другими словами, пространственно-временной интервал между двумя событиями на мировой линии чего-либо, движущегося со скоростью света, равен нулю. Такой интервал называется светоподобным или нулевым . Фотон, прибывающий в наш глаз от далекой звезды, не состарится, несмотря на то, что (с нашей точки зрения) потратил годы на свое прохождение. ^{[31] : 48–50} ${\displaystyle s^{2}}$ ${\displaystyle s^{2}}$ ${\displaystyle s^{2}}$ ${\displaystyle x=\pm ct.}$

Пространственно-временная диаграмма обычно рисуется только с одной пространственной и одной временной координатой. Рис. 2-1 представляет пространственно-временную диаграмму, иллюстрирующую мировые линии (т. е. пути в пространстве-времени) двух фотонов, A и B, происходящих из одного и того же события и идущих в противоположных направлениях. Кроме того, C иллюстрирует мировую линию объекта со скоростью ниже скорости света. Вертикальная временная координата масштабируется таким образом, чтобы она имела те же единицы (метры), что и горизонтальная пространственная координата. Поскольку фотоны движутся со скоростью света, их мировые линии имеют наклон ±1. ^{[31] : 23–25} Другими словами, каждый метр, который фотон проходит влево или вправо, требует приблизительно 3,3 наносекунды времени. ${\displaystyle c}$

Системы отсчета

Рисунок 2-2. Диаграмма Галилея двух систем отсчета в стандартной конфигурации.

Рисунок 2–3. (a) Диаграмма Галилея двух систем отсчета в стандартной конфигурации, (b) пространственно-временная диаграмма двух систем отсчета, (c) пространственно-временная диаграмма, показывающая путь отраженного светового импульса.

Чтобы получить представление о том, как пространственно-временные координаты, измеренные наблюдателями в разных системах отсчета, сравниваются друг с другом, полезно работать с упрощенной установкой с системами в стандартной конфигурации. При осторожности это позволяет упростить математику без потери общности в полученных выводах. На рис. 2-2 показаны две галилеевы системы отсчета (т. е. обычные трехмерные системы отсчета) в относительном движении. Система S принадлежит первому наблюдателю O, а система S′ (произносится как «S prime») принадлежит второму наблюдателю O′.

• Оси x , y , z кадра S ориентированы параллельно соответствующим штрихованным осям кадра S′.
• Кадр S′ движется в направлении x кадра S с постоянной скоростью v , измеренной в кадре S.
• Начало координат кадров S и S′ совпадает, когда время t = 0 для кадра S и t ′ = 0 для кадра S′. ^{[6] : 107}

Рис. 2-3a перерисовывает рис. 2-2 в другой ориентации. Рис. 2-3b иллюстрирует релятивистскую диаграмму пространства-времени с точки зрения наблюдателя O. Поскольку S и S′ находятся в стандартной конфигурации, их начала совпадают в моменты времени t  = 0 в системе S и t ′ = 0 в системе S′. Ось ct ′ проходит через события в системе S′, которые имеют x ′ = 0. Но точки с x ′ = 0 движутся в направлении x системы S со скоростью v , так что они не совпадают с осью ct в любой момент времени, отличный от нуля. Следовательно, ось ct ′ наклонена относительно оси ct на угол θ , заданный ^{[31] : 23–31}

${\displaystyle \tan(\theta )=v/c.}$

Ось x ′ также наклонена относительно оси x . Чтобы определить угол этого наклона, вспомним, что наклон мировой линии светового импульса всегда равен ±1. На рис. 2-3c представлена ​​пространственно-временная диаграмма с точки зрения наблюдателя O′. Событие P представляет собой испускание светового импульса при x ′ = 0, ct ′ = − a . Импульс отражается от зеркала, расположенного на расстоянии a от источника света (событие Q), и возвращается к источнику света при x ′ = 0,  ct ′ =  a (событие R).

Те же события P, Q, R изображены на рис. 2-3b в системе координат наблюдателя O. Пути света имеют наклоны = 1 и −1, так что △PQR образует прямоугольный треугольник с PQ и QR, оба под углом 45 градусов к осям x и ct . Поскольку OP = OQ = OR, угол между x ′ и x также должен быть θ . ^{[6] : 113–118}

В то время как неподвижная система имеет пространственные и временные оси, которые встречаются под прямым углом, движущаяся система рисуется с осями, которые встречаются под острым углом. Рамки фактически эквивалентны. ^{[31] : 23–31} Асимметрия возникает из-за неизбежных искажений в том, как пространственно-временные координаты могут отображаться на декартовой плоскости , и ее следует считать не более странной, чем способ, которым на проекции Меркатора Земли относительные размеры массивов суши вблизи полюсов (Гренландия и Антарктида) сильно преувеличены по сравнению с массивами суши вблизи экватора.

Световой конус

Рисунок 2–4. Световой конус, центрированный на событии, делит остальное пространство-время на будущее, прошлое и «в другом месте».

На рис. 2–4 событие O находится в начале пространственно-временной диаграммы, а две диагональные линии представляют все события, которые имеют нулевой пространственно-временной интервал относительно исходного события. Эти две линии образуют то, что называется световым конусом события O, поскольку добавление второго пространственного измерения (рис. 2-5) создает видимость двух прямых круговых конусов , встречающихся вершинами в точке O. Один конус простирается в будущее (t>0), другой — в прошлое (t<0).

Рисунок 2–5. Световой конус в двумерном пространстве плюс временное измерение.

Световой (двойной) конус делит пространство-время на отдельные области относительно его вершины. Внутренняя часть будущего светового конуса состоит из всех событий, которые отделены от вершины большим временем (временным расстоянием), чем необходимо для пересечения их пространственного расстояния со скоростью света; эти события составляют времяподобное будущее события O. Аналогично, времениподобное прошлое состоит из внутренних событий прошлого светового конуса. Таким образом, во времениподобных интервалах Δ ct больше Δ x , что делает времениподобные интервалы положительными. ^{[3] : 220}

Область, внешняя по отношению к световому конусу, состоит из событий, которые отделены от события O большим пространством , чем может быть пересечено со скоростью света за данное время . Эти события составляют так называемую пространственноподобную область события O, обозначенную «В другом месте» на рис. 2-4. События на самом световом конусе называются светоподобными (или нуль-отделенными ) от O. Из-за инвариантности интервала пространства-времени все наблюдатели будут назначать один и тот же световой конус любому данному событию и, таким образом, будут соглашаться с этим разделением пространства-времени. ^{[3] : 220}

Световой конус играет важную роль в концепции причинности . Сигнал, не превышающий скорость света, может перемещаться из положения и времени O в положение и время D (рис. 2-4). Следовательно, событие O может иметь причинное влияние на событие D. Будущий световой конус содержит все события, на которые может оказать причинное влияние O. Аналогично, сигнал, не превышающий скорость света, может перемещаться из положения и времени A в положение и время O. Прошлый световой конус содержит все события, которые могут оказать причинное влияние на O. Напротив, если предположить, что сигналы не могут перемещаться быстрее скорости света, любое событие, например, B или C, в пространственноподобной области (В другом месте), не может ни повлиять на событие O, ни быть затронутым событием O, использующим такую ​​сигнализацию. При этом предположении любая причинная связь между событием O и любыми событиями в пространственноподобной области светового конуса исключается. ^[35]

Относительность одновременности

Рисунок 2–6. Анимация, иллюстрирующая относительность одновременности.

Все наблюдатели согласятся, что для любого данного события событие в пределах будущего светового конуса данного события происходит после данного события. Аналогично, для любого данного события событие в пределах прошлого светового конуса данного события происходит до данного события. Соотношение до-после, наблюдаемое для событий, разделенных по времени, остается неизменным независимо от того, в какой системе отсчета находится наблюдатель, т. е. независимо от того, как движется наблюдатель. Ситуация совершенно иная для событий, разделенных по пространству. Рис. 2-4 был нарисован из системы отсчета наблюдателя, движущегося со скоростью v = 0. Из этой системы отсчета событие C наблюдается после события O, а событие B наблюдается до события O. ^[36]

Из другой системы отсчета упорядочение этих не связанных причинно событий может быть изменено на противоположное. В частности, можно заметить, что если два события происходят одновременно в определенной системе отсчета, они обязательно разделены пространственноподобным интервалом и, таким образом, не связаны причинно. Наблюдение, что одновременность не абсолютна, а зависит от системы отсчета наблюдателя, называется относительностью одновременности . ^[36]

Рис. 2-6 иллюстрирует использование диаграмм пространства-времени в анализе относительности одновременности. События в пространстве-времени инвариантны, но системы координат преобразуются, как обсуждалось выше для рис. 2-3. Три события (A, B, C) являются одновременными из системы отсчета наблюдателя, движущегося со скоростью v = 0. Из системы отсчета наблюдателя, движущегося со скоростью v = 0,3 c , события кажутся происходящими в порядке C, B, A. Из системы отсчета наблюдателя, движущегося со скоростью v = −0,5 c , события кажутся происходящими в порядке A, B, C . Белая линия представляет собой плоскость одновременности, перемещаемую из прошлого наблюдателя в будущее наблюдателя, выделяя события, находящиеся на ней. Серая область — это световой конус наблюдателя, который остается инвариантным.

Пространственноподобный интервал пространства-времени дает то же расстояние, которое наблюдатель измерил бы, если бы измеряемые события были одновременны для наблюдателя. Пространственноподобный интервал пространства-времени, следовательно, дает меру надлежащего расстояния , т. е. истинного расстояния = Аналогично, времениподобный интервал пространства-времени дает ту же меру времени, которая была бы представлена ​​кумулятивным тиканьем часов, движущихся вдоль данной мировой линии. Времениподобный интервал пространства-времени, следовательно, дает меру надлежащего времени = ^{[3] : 220–221} ${\displaystyle {\sqrt {-s^{2}}}.}$ ${\displaystyle {\sqrt {s^{2}}}.}$

Инвариантная гипербола

Рисунок 2–7. (а) Семейства инвариантных гипербол, (б) Двуполостные и однополостные гиперболоиды.

В евклидовом пространстве (имеющем только пространственные измерения) множество точек, равноудаленных (используя евклидову метрику) от некоторой точки, образуют окружность (в двух измерениях) или сферу (в трех измерениях). В (1+1)-мерном пространстве-времени Минковского (имеющем одно временное и одно пространственное измерение) точки на некотором постоянном пространственно-временном интервале от начала координат (используя метрику Минковского) образуют кривые, заданные двумя уравнениями

${\displaystyle (ct)^{2}-x^{2}=\pm s^{2},}$

с некоторой положительной действительной константой. Эти уравнения описывают два семейства гипербол в пространственно-временной диаграмме x – ct , которые называются инвариантными гиперболами . ${\displaystyle s^{2}}$

На рис. 2-7а каждая пурпурная гипербола соединяет все события, имеющие некоторое фиксированное пространственное разделение от начала координат, тогда как зеленые гиперболы соединяют события, имеющие одинаковое времяподобное разделение.

Пурпурные гиперболы, пересекающие ось x , являются времениподобными кривыми, то есть эти гиперболы представляют собой реальные пути, которые могут быть пройдены (постоянно ускоряющимися) частицами в пространстве-времени: Между любыми двумя событиями на одной гиперболе возможна причинно-следственная связь, поскольку обратный наклон — представляющий необходимую скорость — для всех секущих меньше . С другой стороны, зеленые гиперболы, пересекающие ось ct , являются пространственноподобными кривыми, поскольку все интервалы вдоль этих гипербол являются пространственноподобными интервалами: Между любыми двумя точками на одной из этих гипербол причинно-следственная связь невозможна, поскольку все секущие представляют скорости, большие . ${\displaystyle c}$ ${\displaystyle c}$

Рис. 2-7b отражает ситуацию в (1+2)-мерном пространстве-времени Минковского (одно временное и два пространственных измерения) с соответствующими гиперболоидами. Инвариантные гиперболы, смещенные на пространственноподобные интервалы от начала координат, порождают гиперболоиды с одной полосой, тогда как инвариантные гиперболы, смещенные на времениподобные интервалы от начала координат, порождают гиперболоиды с двумя полосами.

(1+2)-мерная граница между пространственно- и времяподобными гиперболоидами, установленная событиями, образующими нулевой пространственно-временной интервал до начала координат, образована вырождением гиперболоидов в световой конус. В (1+1)-мерностях гиперболы вырождаются в две серые 45°-линии, изображенные на рис. 2-7а.

Замедление времени и сокращение длины

Рисунок 2–8. Инвариантная гипербола состоит из точек, которые могут быть достигнуты из начала координат за фиксированное собственное время часами, движущимися с разной скоростью.

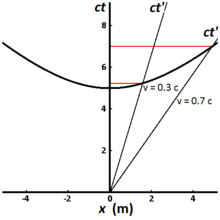
На рис. 2-8 показана инвариантная гипербола для всех событий, которые могут быть достигнуты из начала координат за собственное время 5 метров (приблизительно1,67 × 10−8 ^с ). Различные мировые линии представляют часы, движущиеся с разной скоростью. Часы  , неподвижные относительно наблюдателя, имеют вертикальную мировую линию, и прошедшее время, измеренное наблюдателем, совпадает с собственным временем. Для часов, движущихся со скоростью 0,3  с , прошедшее время, измеренное наблюдателем, составляет 5,24 метра (1,75 × 10−8  с ), в то время как для часов, движущихся со скоростью 0,7  с , прошедшее время ^, измеренное наблюдателем, составляет 7,00 метров (2,34 × 10−8  с ). ^{[3] : 220–221}

Это иллюстрирует явление, известное как замедление времени . Часы, которые движутся быстрее, тратят больше времени (в системе наблюдателя), чтобы отсчитать то же самое количество собственного времени, и они движутся дальше по оси x в пределах этого собственного времени, чем они бы двигались без замедления времени. ^{[3] : 220–221} Измерение замедления времени двумя наблюдателями в разных инерциальных системах отсчета является взаимным. Если наблюдатель O измеряет часы наблюдателя O′ как идущие медленнее в своей системе, наблюдатель O′ в свою очередь будет измерять часы наблюдателя O как идущие медленнее.

Рисунок 2–9. На этой пространственно-временной диаграмме длина движущегося стержня в 1 м, измеренная в штрихованной системе отсчета, представляет собой укороченное расстояние OC при проецировании на нештрихованную систему отсчета.

Сокращение длины , как и замедление времени, является проявлением относительности одновременности. Измерение длины требует измерения пространственно-временного интервала между двумя событиями, которые являются одновременными в вашей системе отсчета. Но события, которые являются одновременными в одной системе отсчета, в общем случае не являются одновременными в других системах отсчета.

Рис. 2-9 иллюстрирует движения стержня длиной 1 м, который движется со скоростью 0,5  с вдоль оси x . Края синей полосы представляют мировые линии двух конечных точек стержня. Инвариантная гипербола иллюстрирует события, отделенные от начала координат пространственноподобным интервалом в 1 м. Конечные точки O и B, измеренные при t ′  = 0, являются одновременными событиями в системе S′. Но для наблюдателя в системе S события O и B не являются одновременными. Чтобы измерить длину, наблюдатель в системе S измеряет конечные точки стержня, спроецированные на ось x вдоль их мировых линий. Проекция мирового листа стержня на ось x дает укороченную длину OC. ^{[6] : 125}

(не показано) Проведение вертикальной линии через A так, чтобы она пересекала ось x ′, показывает, что, даже если OB укорочена с точки зрения наблюдателя O, OA также укорочена с точки зрения наблюдателя O′. Точно так же, как каждый наблюдатель измеряет часы другого как идущие медленнее, каждый наблюдатель измеряет линейки другого как сокращающиеся.

Что касается взаимного сокращения длины, рис. 2-9 иллюстрирует, что штрихованная и нештрихованная рамки взаимно повернуты на гиперболический угол (аналогичный обычным углам в евклидовой геометрии). ^{[примечание 8]} Из-за этого поворота проекция штрихованной метровой линейки на нештрихованную ось x укорачивается, в то время как проекция нештрихованной метровой линейки на штрихованную ось x′ также укорачивается.

Взаимное замедление времени и парадокс близнецов

Взаимное замедление времени

Взаимное замедление времени и сокращение длины, как правило, кажутся новичкам внутренне противоречивыми концепциями. Если наблюдатель в системе S измеряет часы, находящиеся в покое в системе S', как идущие медленнее, чем его', в то время как S' движется со скоростью v в S, то принцип относительности требует, чтобы наблюдатель в системе S' также измерял часы в системе S, движущиеся со скоростью − v в S', как идущие медленнее, чем ее. Как двое часов могут идти медленнее друг друга, является важным вопросом, который «затрагивает суть понимания специальной теории относительности». ^{[3] : 198}

Это кажущееся противоречие возникает из-за неправильного учета различных настроек необходимых, связанных измерений. Эти настройки позволяют дать последовательное объяснение единственному кажущемуся противоречию. Речь идет не об абстрактном тиканье двух одинаковых часов, а о том, как измерить в одном кадре временное расстояние двух тиков движущихся часов. Оказывается, при взаимном наблюдении за длительностью между тиками часов, каждые из которых движутся в соответствующем кадре, должны быть задействованы различные наборы часов. Для того чтобы измерить в кадре S длительность тика движущихся часов W′ (покоящихся в S′), используются двое дополнительных синхронизированных часов W ₁ и W _2, находящихся в покое в двух произвольно фиксированных точках в S с пространственным расстоянием d .

Два события можно определить условием «двое часов находятся одновременно в одном месте», т. е. когда W′ проходит каждый через W ₁ и W ₂ . Для обоих событий регистрируются два показания совмещенных часов. Разность двух показаний W ₁ и W ₂ является временным расстоянием двух событий в S, а их пространственное расстояние равно d . Разность двух показаний W′ является временным расстоянием двух событий в S′. В S′ эти события разделены только во времени, они происходят в одном и том же месте в S′. Из-за инвариантности пространственно-временного интервала, охватываемого этими двумя событиями, и ненулевого пространственного разделения d в S временное расстояние в S′ должно быть меньше, чем в S: меньшее временное расстояние между двумя событиями, полученное в результате показаний движущихся часов W′, принадлежит более медленно идущим часам W′.

И наоборот, для оценки в системе отсчета S′ временного расстояния между двумя событиями на движущихся часах W (покоящихся в системе отсчета S) необходимы двое часов, покоящихся в системе отсчета S′.

В этом сравнении часы W движутся со скоростью − v . Повторная запись четырех показаний для событий, определяемых как «два часа одновременно в одном месте», приводит к аналогичным временным расстояниям двух событий, теперь разделенных во времени и пространстве в S′, и разделенных только во времени, но совмещенных в S. Чтобы сохранить инвариантность интервала пространства-времени, временное расстояние в S должно быть меньше, чем в S′, из-за пространственного разделения событий в S′: теперь часы W, как наблюдается, идут медленнее.

Необходимые записи для двух суждений, с «одними движущимися часами» и «двумя покоящимися часами» в S или S′ соответственно, включают два разных набора, каждый с тремя часами. Поскольку в измерениях участвуют разные наборы часов, нет необходимости, чтобы измерения были взаимно «согласованными», так что если один наблюдатель измеряет движущиеся часы как отстающие, другой наблюдатель измеряет часы одного из них как быстрые. ^{[3] : 198–199}

Рисунок 2-10. Взаимное замедление времени.

Рис. 2-10 иллюстрирует предыдущее обсуждение взаимного замедления времени с помощью диаграмм Минковского. Верхняя картинка отражает измерения, наблюдаемые из кадра S "в состоянии покоя" с нештрихованными прямоугольными осями и кадра S′ "движущийся с v  > 0", координируемого штрихованными косыми осями, наклоненными вправо; нижняя картинка показывает кадр S′ "в состоянии покоя" со штрихованными прямоугольными координатами и кадр S "движущийся с − v  < 0", с нештрихованными косыми осями, наклоненными влево.

Каждая линия, проведенная параллельно пространственной оси ( x , x ′), представляет собой линию одновременности. Все события на такой линии имеют одинаковое значение времени ( ct , ct ′). Аналогично, каждая линия, проведенная параллельно временной оси ( ct , ct′ ), представляет собой линию равных значений пространственных координат ( x , x ′).

Можно обозначить на обеих картинках начало координат O (= O ′ ) как событие, где соответствующие «движущиеся часы» совмещены с «первыми покоящимися часами» в обоих сравнениях. Очевидно, что для этого события показания на обоих часах в обоих сравнениях равны нулю. Как следствие, мировые линии движущихся часов представляют собой наклоненную вправо ось ct ′ (верхние картинки, часы W′) и наклоненную влево ось ct (нижние картинки, часы W). Мировые линии W ₁ и W′ ₁ представляют собой соответствующие вертикальные оси времени ( ct на верхних картинках и ct ′ на нижних картинках).

На верхнем рисунке местом для W ₂ принято значение A _x > 0, и, таким образом, мировая линия (не показанная на рисунках) этих часов пересекает мировую линию движущихся часов ( ось ct ′) в событии, обозначенном A , где «двое часов одновременно находятся в одном месте». На нижнем рисунке местом для W′ ₂ принято значение C _{x ′}  < 0, и, таким образом, в этом измерении движущиеся часы W проходят мимо W′ ₂ в событии C .

На верхнем рисунке ct -координата A _t события A (показание W ₂ ) обозначена как B , что дает прошедшее время между двумя событиями, измеренное с помощью W ₁ и W ₂ , как OB . Для сравнения длина временного интервала OA , измеренная с помощью W′, должна быть преобразована в масштаб оси ct . Это делается с помощью инвариантной гиперболы (см. также рис. 2-8) через A , соединяющей все события с тем же пространственно-временным интервалом от начала координат, что и A . Это дает событие C на оси ct , и очевидно: OC  <  OB , «движущиеся» часы W′ идут медленнее.

Чтобы показать взаимное замедление времени непосредственно на верхнем рисунке, событие D может быть построено как событие при x ′ = 0 (местоположение часов W′ в S′), которое одновременно с C ( OC имеет такой же пространственно-временной интервал, как OA ) в S′. Это показывает, что временной интервал OD длиннее, чем OA , показывая, что «движущиеся» часы идут медленнее. ^{[6] : 124}

На нижнем рисунке система S движется со скоростью − v в системе S′, находящейся в состоянии покоя. Мировая линия часов W — это ось ct (наклоненная влево), мировая линия W′ ₁ — это вертикальная ось ct ′, а мировая линия W′ ₂ — это вертикальная ось, проходящая через событие C , с координатой ct ′ D. Инвариантная гипербола, проходящая через событие C, масштабирует временной интервал OC до OA , который короче OD ; также B строится (аналогично D на верхних рисунках) как одновременный с A в S, при x  = 0. Результат OB  >  OC снова соответствует вышесказанному.

Слово «мера» имеет важное значение. В классической физике наблюдатель не может влиять на наблюдаемый объект, но состояние движения объекта может влиять на наблюдения наблюдателя за объектом.

Парадокс близнецов

Многие введения в специальную теорию относительности иллюстрируют различия между галилеевской относительностью и специальной теорией относительности, предлагая ряд «парадоксов». Эти парадоксы, по сути, являются некорректно поставленными проблемами, возникающими из-за нашего незнания скоростей, сравнимых со скоростью света. Лекарство состоит в том, чтобы решить множество проблем в специальной теории относительности и ознакомиться с ее так называемыми контринтуитивными предсказаниями. Геометрический подход к изучению пространства-времени считается одним из лучших методов развития современной интуиции. ^[37]

Парадокс близнецов — это мысленный эксперимент с участием идентичных близнецов, один из которых совершает путешествие в космос на высокоскоростной ракете, возвращается домой и обнаруживает, что близнец, оставшийся на Земле, постарел больше. Этот результат кажется загадочным, поскольку каждый близнец наблюдает, как другой близнец движется, и поэтому на первый взгляд может показаться, что каждый должен обнаружить, что другой постарел меньше. Парадокс близнецов обходит представленное выше обоснование взаимного замедления времени, избегая требования третьих часов. ^{[3] : 207} Тем не менее, парадокс близнецов не является истинным парадоксом, поскольку его легко понять в контексте специальной теории относительности.

Впечатление о существовании парадокса возникает из-за непонимания положений специальной теории относительности. Специальная теория относительности не объявляет все системы отсчета эквивалентными, а только инерциальные. Система отсчета путешествующего близнеца не является инерциальной в периоды, когда он ускоряется. Более того, разница между близнецами обнаруживается наблюдательно: путешествующему близнецу нужно запускать свои ракеты, чтобы вернуться домой, в то время как близнецу, остающемуся дома, этого делать не нужно. ^{[38] [примечание 9]}

Рисунок 2–11. Пространственно-временное объяснение парадокса близнецов.

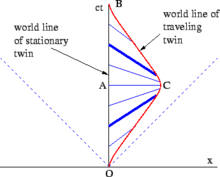
Эти различия должны привести к разнице в возрасте близнецов. Пространственно-временная диаграмма на рис. 2-11 представляет собой простой случай близнеца, идущего прямо вдоль оси x и немедленно поворачивающего обратно. С точки зрения близнеца-домоседа, в парадоксе близнецов нет ничего загадочного. Собственное время, измеренное вдоль мировой линии путешествующего близнеца от O до C, плюс собственное время, измеренное от C до B, меньше собственного времени близнеца-домоседа, измеренного от O до A до B. Более сложные траектории требуют интегрирования собственного времени между соответствующими событиями вдоль кривой (т. е. интеграла пути ), чтобы вычислить общее количество собственного времени, испытанного путешествующим близнецом. ^[38]

Сложности возникают, если парадокс близнецов анализировать с точки зрения путешествующего близнеца.

В дальнейшем используется номенклатура Вайса, в которой близнец-домосед обозначен как Теренс, а близнец-путешественник — как Стелла. ^[38]

Стелла не находится в инерциальной системе отсчета. Учитывая этот факт, иногда неверно утверждается, что полное разрешение парадокса близнецов требует общей теории относительности: ^[38]

Чистый анализ SR будет выглядеть следующим образом: Анализ в системе покоя Стеллы показывает, что она неподвижна в течение всего путешествия. Когда она запускает свои ракеты для разворота, она испытывает псевдосилу, которая напоминает силу тяготения. ^{[38] Рис. 2-6 и 2-11 иллюстрируют концепцию линий (плоскостей) одновременности: линии, параллельные оси} x наблюдателя ( плоскость xy ), представляют собой наборы событий, которые одновременны в системе наблюдателя. На рис. 2-11 синие линии соединяют события на мировой линии Теренса, которые, с точки зрения Стеллы , одновременны с событиями на ее мировой линии. (Теренс, в свою очередь, наблюдал бы набор горизонтальных линий одновременности.) На протяжении как исходящего, так и входящего этапов путешествия Стеллы она измеряет часы Теренса как идущие медленнее, чем ее собственные. Но во время поворота (т. е. между жирными синими линиями на рисунке) происходит сдвиг угла ее линий одновременности, соответствующий быстрому перескакиванию событий в мировой линии Теренса, которые Стелла считает одновременными с ее собственными. Поэтому в конце своего путешествия Стелла обнаруживает, что Теренс постарел больше, чем она. ^[38]

Хотя общая теория относительности не требуется для анализа парадокса близнецов, применение принципа эквивалентности общей теории относительности действительно дает некоторое дополнительное понимание предмета. Стелла не неподвижна в инерциальной системе отсчета. Анализ в системе покоя Стеллы показывает, что она неподвижна в течение всего путешествия. Когда она движется по инерции, ее система покоя инерциальна, и часы Теренса будут казаться идущими медленнее. Но когда она запускает свои ракеты для разворота, ее система покоя является ускоренной системой, и она испытывает силу, которая толкает ее, как если бы она находилась в гравитационном поле. Теренс будет казаться высоко в этом поле, и из-за гравитационного замедления времени его часы будут казаться идущими быстрее, настолько, что в конечном итоге Теренс постарел больше, чем Стелла, когда они снова будут вместе. ^[38] Теоретические аргументы, предсказывающие гравитационное замедление времени, не являются исключительными для общей теории относительности. Любая теория гравитации предскажет гравитационное замедление времени, если она соблюдает принцип эквивалентности, включая теорию Ньютона. ^{[3] : 16}

Гравитация

В этом вводном разделе основное внимание уделено пространству-времени специальной теории относительности, поскольку его проще всего описать. Пространство-время Минковского плоское, не учитывает гравитацию, однородно во всем и служит не более чем статическим фоном для событий, которые в нем происходят. Наличие гравитации значительно усложняет описание пространства-времени. В общей теории относительности пространство-время больше не является статическим фоном, а активно взаимодействует с физическими системами, которые оно содержит. Пространство-время искривляется в присутствии материи, может распространять волны, искривлять свет и демонстрирует множество других явлений. ^{[3] : 221} Некоторые из этих явлений описаны в последующих разделах этой статьи.

Базовая математика пространства-времени

Галилеевы преобразования

Основная цель — иметь возможность сравнивать измерения, сделанные наблюдателями в относительном движении. Если есть наблюдатель O в системе S, который измерил временные и пространственные координаты события, назначая этому событию три декартовых координаты и время, измеренное на его решетке синхронизированных часов ( x , y , z , t ) (см. рис. 1-1). Второй наблюдатель O′ в другой системе S′ измеряет то же самое событие в своей системе координат и своей решетке синхронизированных часов ( x ′ , y ′ , z ′ , t ′ ) . В инерциальных системах ни один из наблюдателей не находится под ускорением, и простой набор уравнений позволяет нам связать координаты ( x , y , z , t ) с ( x ′ , y ′ , z ′ , t ′ ) . Учитывая, что две системы координат находятся в стандартной конфигурации, то есть они выровнены с параллельными ( x , y , z ) координатами, и что t = 0 , когда t ′ = 0 , преобразование координат выглядит следующим образом: ^{[39] [40]}

${\displaystyle x'=x-vt}$

${\displaystyle y'=y}$

${\displaystyle z'=z}$

${\displaystyle t'=t.}$

Рисунок 3–1. Галилеевское пространство-время и композиция скоростей.

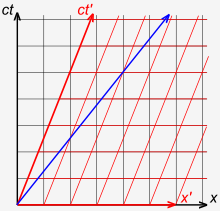
Рис. 3-1 иллюстрирует, что в теории Ньютона универсально время, а не скорость света. ^{[41] : 36–37} Рассмотрим следующий мысленный эксперимент: Красная стрелка иллюстрирует поезд, движущийся со скоростью 0,4 с относительно платформы. Внутри поезда пассажир стреляет пулей со скоростью 0,4 с в кадре поезда. Синяя стрелка иллюстрирует, что человек, стоящий на железнодорожных путях, измеряет пулю как движущуюся со скоростью 0,8 с. Это соответствует нашим наивным ожиданиям.

В более общем случае, если предположить, что система отсчета S′ движется со скоростью v относительно системы отсчета S, то в системе отсчета S′ наблюдатель O′ измеряет объект, движущийся со скоростью u ′ . Скорость u относительно системы отсчета S, поскольку x = ut , x ′ = x − vt и t = t ′ , можно записать как x ′ = ut − vt = ( u − v ) t = ( u − v ) t ′ . Это приводит к u ′ = x ′ / t ′ и в конечном итоге

${\displaystyle u'=u-v}$  или   ${\displaystyle u=u'+v,}$

что является здравым смыслом закона Галилея для сложения скоростей .

Релятивистское сложение скоростей

Рисунок 3–2. Релятивистский состав скоростей

Состав скоростей совершенно иной в релятивистском пространстве-времени. Чтобы немного уменьшить сложность уравнений, мы вводим общее сокращение для отношения скорости объекта относительно света,

${\displaystyle \beta =v/c}$

Рис. 3-2a иллюстрирует красный поезд, который движется вперед со скоростью, заданной v / c = β = s / a . Из заштрихованной рамки поезда пассажир стреляет пулей со скоростью, заданной u ′ / c = β ′ = n / m , где расстояние измеряется вдоль линии, параллельной красной оси x ′ , а не параллельной черной оси x . Какова составная скорость u пули относительно платформы, представленной синей стрелкой? Ссылаясь на рис. 3-2b:

1. С точки зрения платформы составная скорость пули определяется по формуле u = c ( s + r )/( a + b ) .
2. Два желтых треугольника подобны, потому что они прямоугольные треугольники, которые имеют общий угол α . В большом желтом треугольнике соотношение s / a = v / c = β .
3. Отношения соответствующих сторон двух желтых треугольников постоянны, так что r / a = b / s = n / m = β ′ . Таким образом, b = u ′ s / c и r = u ′ a / c .
4. Подставим выражения для b и r в выражение для u на шаге 1, чтобы получить формулу Эйнштейна для сложения скоростей: ^{[41] : 42–48}

   ${\displaystyle u={v+u' \over 1+(vu'/c^{2})}.}$

Представленная выше релятивистская формула сложения скоростей демонстрирует несколько важных особенностей:

• Если u ′ и v оба очень малы по сравнению со скоростью света, то произведение vu ′ / c ² становится исчезающе малым, и общий результат становится неотличим от формулы Галилея (формулы Ньютона) для сложения скоростей: u  =  u ′  +  v . Формула Галилея является частным случаем релятивистской формулы, применимой к малым скоростям.
• Если u ′ приравнять к c , то формула дает u  =  c независимо от начального значения v . Скорость света одинакова для всех наблюдателей независимо от их движения относительно источника излучения. ^{[41] : 49}

Повторное рассмотрение замедления времени и сокращения длины

Рисунок 3-3. Диаграммы пространства-времени, иллюстрирующие замедление времени и сокращение длины.

Легко получить количественные выражения для замедления времени и сокращения длины. Рис. 3-3 представляет собой составное изображение, содержащее отдельные кадры, взятые из двух предыдущих анимаций, упрощенные и переименованные для целей этого раздела.

Чтобы немного уменьшить сложность уравнений, существует множество различных сокращенных обозначений для ct :

${\displaystyle \mathrm {T} =ct}$и являются обычным явлением. ${\displaystyle w=ct}$

Также очень часто можно увидеть использование условности ${\displaystyle c=1.}$

Рисунок 3–4. Фактор Лоренца как функция скорости.

На рис. 3-3a сегменты OA и OK представляют равные интервалы пространства-времени. Замедление времени представлено отношением OB / OK . Инвариантная гипербола имеет уравнение w = √ x ² + k ² , где k  =  OK , а красная линия, представляющая мировую линию движущейся частицы, имеет уравнение w  =  x / β  =  xc / v . Немного алгебраических преобразований дает ${\textstyle OB=OK/{\sqrt {1-v^{2}/c^{2}}}.}$

Выражение, включающее символ квадратного корня, очень часто встречается в теории относительности, и единица над выражением называется фактором Лоренца, обозначаемым греческой буквой гамма : ^[42] ${\displaystyle \gamma }$

${\displaystyle \gamma ={\frac {1}{\sqrt {1-v^{2}/c^{2}}}}={\frac {1}{\sqrt {1-\beta ^{2}}}}}$

Если v больше или равно c , выражение для становится физически бессмысленным, подразумевая, что c — это максимально возможная скорость в природе. Для любого v больше нуля фактор Лоренца будет больше единицы, хотя форма кривой такова, что для низких скоростей фактор Лоренца чрезвычайно близок к единице. ${\displaystyle \gamma }$

На рис. 3-3b сегменты OA и OK представляют собой равные интервалы пространства-времени. Сокращение длины представлено отношением OB / OK . Инвариантная гипербола имеет уравнение x = √ w ² + k ² , где k  =  OK , а края синей полосы, представляющей мировые линии концов движущегося стержня, имеют наклон 1/ β  =  c / v . Событие A имеет координаты ( x ,  w ) = ( γk ,  γβk ). Поскольку касательная через A и B имеет уравнение w  = ( x  −  OB )/ β , мы имеем γβk  = ( γk  −  OB )/ β и

${\displaystyle OB/OK=\gamma (1-\beta ^{2})={\frac {1}{\gamma }}}$

Преобразования Лоренца

Преобразования Галилея и вытекающий из них закон здравого смысла сложения скоростей хорошо работают в нашем обычном низкоскоростном мире самолетов, автомобилей и мячей. Однако начиная с середины 1800-х годов чувствительная научная аппаратура начала обнаруживать аномалии, которые не очень хорошо укладывались в обычное сложение скоростей.

Преобразования Лоренца используются для преобразования координат события из одной системы отсчета в другую в специальной теории относительности.

Фактор Лоренца появляется в преобразованиях Лоренца:

${\displaystyle {\begin{aligned}t'&=\gamma \left(t-{\frac {vx}{c^{2}}}\right)\\x'&=\gamma \left(x-vt\right)\\y'&=y\\z'&=z\end{aligned}}}$

Обратные преобразования Лоренца:

${\displaystyle {\begin{aligned}t&=\gamma \left(t'+{\frac {vx'}{c^{2}}}\right)\\x&=\gamma \left(x'+vt'\right)\\y&=y'\\z&=z'\end{aligned}}}$

Когда v  ≪  c и x достаточно мал, члены v ² / c ² и vx / c ² стремятся к нулю, а преобразования Лоренца приближаются к преобразованиям Галилея.

${\displaystyle t'=\gamma (t-vx/c^{2}),}$ ${\displaystyle x'=\gamma (x-vt)}$и т. д., чаще всего на самом деле означают и т. д. Хотя для краткости уравнения преобразования Лоренца записаны без дельт, x означает Δ x и т. д. Мы, как правило, всегда имеем дело с пространственными и временными различиями между событиями. ${\displaystyle \Delta t'=\gamma (\Delta t-v\Delta x/c^{2}),}$ ${\displaystyle \Delta x'=\gamma (\Delta x-v\Delta t)}$

Называть один набор преобразований нормальными преобразованиями Лоренца, а другой — обратными преобразованиями, вводит в заблуждение, поскольку между системами отсчета нет внутренней разницы. Разные авторы называют один или другой набор преобразований «обратным» набором. Прямые и обратные преобразования тривиально связаны друг с другом, поскольку система отсчета S может двигаться только вперед или назад относительно S ′ . Таким образом, инвертирование уравнений просто влечет за собой переключение штрихованных и нештрихованных переменных и замену v на − v . ^{[43] : 71–79}

Пример: Теренс и Стелла участвуют в космической гонке Земля-Марс. Теренс — официальное лицо на стартовой линии, а Стелла — участник. В момент времени t = t ′ = 0 космический корабль Стеллы мгновенно разгоняется до скорости 0,5  c . Расстояние от Земли до Марса составляет 300 световых секунд (около90,0 × 10 ⁶  км ). Теренс наблюдает, как Стелла пересекает финишную черту в момент t  = 600,00 с . Но Стелла наблюдает, как время на ее корабельном хронометре становится ⁠ ⁠, ${\displaystyle t^{\prime }=\gamma \left(t-vx/c^{2}\right)=519.62\ {\text{s}}}$ когда она пересекает финишную черту, и она вычисляет расстояние между стартовой и финишной линиями, измеренное в ее системе отсчета, которое составляет 259,81 световых секунд (около77,9 × 10 ⁶  км ). 1).

Вывод преобразований Лоренца

Рисунок 3–5. Вывод преобразования Лоренца.

С момента выхода оригинальной работы Эйнштейна в 1905 году было много десятков выводов преобразований Лоренца , каждый из которых имел свою особую направленность. Хотя вывод Эйнштейна был основан на инвариантности скорости света, существуют и другие физические принципы, которые могут служить отправными точками. В конечном счете, эти альтернативные отправные точки можно считать различными выражениями основополагающего принципа локальности , который гласит, что влияние, которое одна частица оказывает на другую, не может передаваться мгновенно. ^[44]

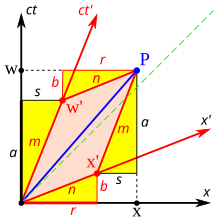
Вывод, представленный здесь и проиллюстрированный на рис. 3-5, основан на выводе, представленном Бэйсом ^{[41] : 64–66} , и использует предыдущие результаты из разделов «Релятивистская композиция скоростей», «Замедление времени» и «Сокращение длины». Событие P имеет координаты ( w ,  x ) в черной «системе покоя» и координаты ( w ′ ,  x ′ ) в красной системе отсчета, которая движется со скоростью β  =  v / c . Чтобы определить w ′ и x ′ через w и x (или наоборот), проще сначала вывести обратное преобразование Лоренца.

1. Не может быть такого явления, как расширение/сокращение длины в поперечных направлениях. y ' должен быть равен y, а z ′ должен быть равен z , в противном случае то, сможет ли быстро движущийся 1-метровый шар пройти через 1-метровое круглое отверстие, зависело бы от наблюдателя. Первый постулат относительности гласит, что все инерциальные системы отсчета эквивалентны, и поперечное расширение/сокращение нарушило бы этот закон. ^{[43] : 27–28}
2. Из рисунка следует, что w = a + b и x  =  r  +  s.
3. Из предыдущих результатов с использованием подобия треугольников мы знаем, что s / a  =  b / r = v / c  =  β .
4. Из-за замедления времени a  =  γw ′
5. Подставляя уравнение (4) в s / a  =  β, получаем s  =  γw ′ β .
6. Сокращение длины и подобные треугольники дают нам r  =  γx ′ и b  =  βr = βγx ′
7. Подстановка выражений для s , a , r и b в уравнения на шаге 2 немедленно дает

   ${\displaystyle w=\gamma w'+\beta \gamma x'}$

   ${\displaystyle x=\gamma x'+\beta \gamma w'}$

Приведенные выше уравнения являются альтернативными выражениями для уравнений t и x обратного преобразования Лоренца, как можно увидеть, подставив ct вместо w , ct ′ вместо w ′ и v / c вместо β . Из обратного преобразования уравнения прямого преобразования могут быть выведены путем решения относительно t ′ и x ′ .

Линейность преобразований Лоренца

Преобразования Лоренца обладают математическим свойством, называемым линейностью, поскольку x ′ и t ′ получаются как линейные комбинации x и t без привлечения высших степеней. Линейность преобразования отражает фундаментальное свойство пространства-времени, которое молчаливо предполагалось при выводе, а именно, что свойства инерциальных систем отсчета не зависят от местоположения и времени. При отсутствии гравитации пространство-время выглядит одинаково везде. ^{[41] : 67} Все инерциальные наблюдатели согласятся с тем, что составляет ускоряющееся и неускоряющееся движение. ^{[43] : 72–73} Любой наблюдатель может использовать свои собственные измерения пространства и времени, но в них нет ничего абсолютного. Соглашения другого наблюдателя будут работать так же хорошо. ^{[3] : 190}

Результатом линейности является то, что если последовательно применить два преобразования Лоренца, результатом также будет преобразование Лоренца.

Пример: Теренс наблюдает, как Стелла удаляется от него со скоростью 0,500  c , и он может использовать преобразования Лоренца с β  = 0,500 , чтобы связать измерения Стеллы со своими собственными. Стелла в своей системе отсчета наблюдает, как Урсула удаляется от нее со скоростью 0,250  c , и она может использовать преобразования Лоренца с β  = 0,250, чтобы связать измерения Урсулы со своими собственными. Из-за линейности преобразований и релятивистского состава скоростей Теренс может использовать преобразования Лоренца с β  = 0,666, чтобы связать измерения Урсулы со своими собственными.

эффект Доплера

Эффект Доплера — это изменение частоты или длины волны для приемника и источника, находящихся в относительном движении. Для простоты мы рассмотрим здесь два основных сценария: (1) движение источника и/или приемника происходит точно вдоль линии, соединяющей их (продольный эффект Доплера), и (2) движение происходит под прямым углом к ​​указанной линии ( поперечный эффект Доплера ). Мы игнорируем сценарии, в которых они движутся вдоль промежуточных углов.

Продольный эффект Доплера

Классический доплеровский анализ имеет дело с волнами, которые распространяются в среде, такими как звуковые волны или водная рябь, и которые передаются между источниками и приемниками, которые движутся друг к другу или друг от друга. Анализ таких волн зависит от того, движутся ли источник, приемник или оба относительно среды. Учитывая сценарий, в котором приемник неподвижен относительно среды, а источник движется прямо от приемника со скоростью v _s для параметра скорости β _s , длина волны увеличивается, а наблюдаемая частота f определяется как

${\displaystyle f={\frac {1}{1+\beta _{s}}}f_{0}}$

С другой стороны, если рассматривать сценарий, в котором источник неподвижен, а приемник движется прямо от источника со скоростью v _r при параметре скорости β _r , длина волны не изменяется, но скорость передачи волн относительно приемника уменьшается, а наблюдаемая частота f определяется выражением

${\displaystyle f=(1-\beta _{r})f_{0}}$

Рисунок 3–6. Пространственно-временная диаграмма релятивистского эффекта Доплера.

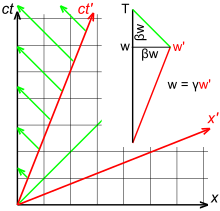
Свет, в отличие от звука или ряби на воде, не распространяется через среду, и нет различия между источником, удаляющимся от приемника, и приемником, удаляющимся от источника. Рис. 3-6 иллюстрирует релятивистскую пространственно-временную диаграмму, показывающую источник, отделяющийся от приемника с параметром скорости , так что разделение между источником и приемником во времени равно . Из-за замедления времени, Поскольку наклон зеленого светового луча равен −1, Следовательно, релятивистский эффект Доплера определяется как ^{[41] : 58–59} ${\displaystyle \beta ,}$ ${\displaystyle w}$ ${\displaystyle \beta w}$ ${\displaystyle w=\gamma w'.}$ ${\displaystyle T=w+\beta w=\gamma w'(1+\beta ).}$

${\displaystyle f={\sqrt {\frac {1-\beta }{1+\beta }}}\,f_{0}.}$

Поперечный эффект Доплера

Рисунок 3–7. Сценарии поперечного эффекта Доплера

Предположим, что источник и приемник, оба приближающиеся друг к другу в равномерном инерционном движении вдоль непересекающихся линий, находятся на максимальном расстоянии друг от друга. Казалось бы, классический анализ предсказывает, что приемник не обнаруживает доплеровского сдвига. Из-за тонкостей в анализе это ожидание не обязательно верно. Тем не менее, при правильном определении, поперечный доплеровский сдвиг является релятивистским эффектом, не имеющим классического аналога. Тонкости таковы: ^{[45] : 541–543}

• Рис. 3-7а. Каково измерение частоты, когда приемник геометрически находится на самом близком расстоянии от источника? Этот сценарий легче всего анализировать из кадра S′ источника. ^{[примечание 10]}
• Рис. 3-7b. Каково измерение частоты, когда приемник видит источник как находящийся ближе всего к нему? Этот сценарий проще всего проанализировать из кадра S приемника.

При обсуждении поперечного доплеровского сдвига обычно рассматриваются два других сценария:

• Рис. 3-7c. Если приемник движется по окружности вокруг источника, какую частоту измеряет приемник?
• Рис. 3-7d. Если источник движется по окружности вокруг приемника, какую частоту измеряет приемник?

<!—конец списка—>

В сценарии (a) точка наибольшего сближения не зависит от кадра и представляет собой момент, когда нет изменения расстояния по сравнению со временем (т. е. dr/dt = 0, где r — расстояние между приемником и источником) и, следовательно, нет продольного доплеровского сдвига. Источник наблюдает, как приемник освещается светом с частотой f ′ , но также наблюдает, как приемник имеет растянутые во времени часы. В кадре S приемник, таким образом, освещается сине-смещенным светом с частотой

${\displaystyle f=f'\gamma =f'/{\sqrt {1-\beta ^{2}}}}$

В сценарии (b) на иллюстрации показано, что приемник освещается светом, когда источник был ближе всего к приемнику, даже если источник переместился. Поскольку часы источника замедлены во времени, как измерено в кадре S, и поскольку dr/dt в этой точке было равно нулю, свет от источника, испускаемый из этой ближайшей точки, смещается в красную область с частотой

${\displaystyle f=f'/\gamma =f'{\sqrt {1-\beta ^{2}}}}$

Сценарии (c) и (d) можно проанализировать с помощью простых аргументов замедления времени. В (c) приемник наблюдает свет от источника как смещенный в синюю сторону в , а в (d) свет смещен в красную сторону. Единственное кажущееся осложнение заключается в том, что орбитальные объекты находятся в ускоренном движении. Однако, если инерциальный наблюдатель смотрит на ускоряющиеся часы, то при вычислении замедления времени важна только мгновенная скорость часов. (Однако обратное неверно.) ^{[45] : 541–543} Большинство отчетов о поперечном доплеровском сдвиге называют эффект красным смещением и анализируют эффект в терминах сценариев (b) или (d). ^{[примечание 11]} ${\displaystyle \gamma }$

Энергия и импульс

Распространение импульса на четыре измерения

Рисунок 3–8. Вектор импульса релятивистского пространства-времени. Оси координат покоящейся системы: импульс, p, и масса * c. Для сравнения мы наложили систему координат пространства-времени с осями: положение и время * c.

В классической механике состояние движения частицы характеризуется ее массой и скоростью. Линейный импульс , произведение массы частицы на скорость, является векторной величиной, имеющей то же направление, что и скорость: p  =  m v . Это сохраняющаяся величина , означающая, что если на замкнутую систему не действуют внешние силы, ее полный линейный импульс не может измениться.

В релятивистской механике вектор импульса расширен до четырех измерений. К вектору импульса добавляется временная составляющая, которая позволяет вектору импульса пространства-времени преобразовываться подобно вектору положения пространства-времени ⁠ ⁠ ${\displaystyle (x,t)}$ . При изучении свойств импульса пространства-времени мы начинаем, на рис. 3-8a, с изучения того, как выглядит частица в состоянии покоя. В системе покоя пространственная составляющая импульса равна нулю, т. е. p  = 0 , но временная составляющая равна mc .

Мы можем получить преобразованные компоненты этого вектора в движущейся системе, используя преобразования Лоренца, или мы можем прочитать его непосредственно из рисунка, поскольку мы знаем, что ⁠ ⁠ ${\displaystyle (mc)^{\prime }=\gamma mc}$ и ⁠ ⁠ ${\displaystyle p^{\prime }=-\beta \gamma mc}$ , поскольку красные оси масштабируются с помощью гаммы. Рис. 3-8b иллюстрирует ситуацию, как она выглядит в движущейся системе. Очевидно, что пространственные и временные компоненты 4-импульса стремятся к бесконечности, когда скорость движущейся системы приближается к c . ^{[41] : 84–87}

Мы вскоре воспользуемся этой информацией, чтобы получить выражение для четырехимпульса .

Импульс света

Рисунок 3–9. Энергия и импульс света в различных инерциальных системах отсчета.

Частицы света, или фотоны, движутся со скоростью c , константой, которая обычно известна как скорость света . Это утверждение не является тавтологией, поскольку многие современные формулировки относительности не начинаются с постоянной скорости света как постулата. Поэтому фотоны распространяются вдоль светоподобной мировой линии и, в соответствующих единицах, имеют равные пространственные и временные компоненты для каждого наблюдателя.

Следствием теории электромагнетизма Максвелла является то, что свет переносит энергию и импульс, и что их отношение является константой: ⁠ ⁠ ${\displaystyle E/p=c}$ . Переставляя, ⁠ ⁠ ${\displaystyle E/c=p}$ , и поскольку для фотонов компоненты пространства и времени равны, E / c , следовательно, должно быть приравнено к компоненте времени вектора импульса пространства-времени.

Фотоны движутся со скоростью света, но имеют конечный импульс и энергию. Чтобы это было так, массовый член в γmc должен быть равен нулю, что означает, что фотоны являются безмассовыми частицами . Бесконечность, умноженная на ноль, — это плохо определенная величина, но E / c определена хорошо.

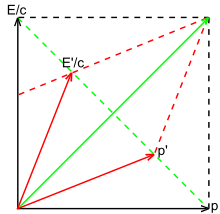
Согласно этому анализу, если энергия фотона равна E в системе покоя, она равна ⁠ ⁠ ${\displaystyle E^{\prime }=(1-\beta )\gamma E}$ в движущейся системе. Этот результат может быть получен путем изучения рис. 3-9 или путем применения преобразований Лоренца, и он согласуется с анализом эффекта Доплера, данным ранее. ^{[41] : 88}

Соотношение массы и энергии

Рассмотрение взаимосвязей между различными компонентами вектора релятивистского импульса привело Эйнштейна к нескольким важным выводам.

• В пределе низкой скорости, когда β = v / c приближается к нулю, γ приближается к 1, поэтому пространственная составляющая релятивистского импульса ⁠ ⁠ ${\displaystyle \beta \gamma mc=\gamma mv}$ приближается к mv , классическому термину для импульса. Следуя этой точке зрения, γm можно интерпретировать как релятивистское обобщение m . Эйнштейн предположил, что релятивистская масса объекта увеличивается со скоростью в соответствии с формулой ⁠ ⁠ ${\displaystyle m_{\text{rel}}=\gamma m}$ .
• Аналогично, сравнивая временную составляющую релятивистского импульса с таковой у фотона, ⁠ ⁠ ${\displaystyle \gamma mc=m_{\text{rel}}c=E/c}$ , Эйнштейн пришел к соотношению ⁠ ⁠ ${\displaystyle E=m_{\text{rel}}c^{2}}$ . Упрощенное до случая нулевой скорости, это уравнение Эйнштейна, связывающее энергию и массу.

Другой способ взглянуть на связь между массой и энергией — рассмотреть рядное расширение γmc ² при низкой скорости:

${\displaystyle E=\gamma mc^{2}={\frac {mc^{2}}{\sqrt {1-\beta ^{2}}}}}$ ${\displaystyle \approx mc^{2}+{\frac {1}{2}}mv^{2}...}$

Второй член — это просто выражение для кинетической энергии частицы. Масса действительно кажется другой формой энергии. ^{[41] : 90–92  [43] : 129–130, 180}

Концепция релятивистской массы, введенная Эйнштейном в 1905 году, m _rel , хотя и многократно подтверждалась ежедневно в ускорителях частиц по всему миру (или в любых приборах, использование которых зависит от высокоскоростных частиц, таких как электронные микроскопы, ^[46] старомодные цветные телевизоры и т. д.), тем не менее не оказалась плодотворной концепцией в физике в том смысле, что она не послужила основой для других теоретических разработок. Например, релятивистская масса не играет никакой роли в общей теории относительности.

По этой причине, а также по педагогическим соображениям, большинство физиков в настоящее время предпочитают другую терминологию, когда речь идет о связи между массой и энергией. ^[47] «Релятивистская масса» — устаревший термин. Термин «масса» сам по себе относится к массе покоя или инвариантной массе и равен инвариантной длине вектора релятивистского импульса. Выражаясь в виде формулы,

${\displaystyle E^{2}-p^{2}c^{2}=m_{\text{rest}}^{2}c^{4}}$

Эта формула применима ко всем частицам, как безмассовым, так и массивным. Для фотонов, где m _rest равен нулю, она дает, ⁠ ⁠ ${\displaystyle E=\pm pc}$ . ^{[41] : 90–92}

Четырех-импульс

Из-за тесной связи между массой и энергией, 4-импульс (также называемый 4-импульсом) также называется 4-вектором энергии-импульса. Используя заглавную букву P для обозначения 4-импульса и строчную букву p для обозначения пространственного импульса, 4-импульс можно записать как

${\displaystyle P\equiv (E/c,{\vec {p}})=(E/c,p_{x},p_{y},p_{z})}$или альтернативно,

${\displaystyle P\equiv (E,{\vec {p}})=(E,p_{x},p_{y},p_{z})}$используя соглашение, что ^{[43] : 129–130, 180} ${\displaystyle c=1.}$

Законы сохранения

В физике законы сохранения утверждают, что некоторые конкретные измеримые свойства изолированной физической системы не изменяются по мере развития системы с течением времени. В 1915 году Эмми Нётер обнаружила, что в основе каждого закона сохранения лежит фундаментальная симметрия природы. ^[48] Тот факт, что физическим процессам все равно, где в пространстве они происходят ( симметрия пространственного переноса ), приводит к сохранению импульса , тот факт, что таким процессам все равно, когда они происходят ( симметрия временного переноса ), приводит к сохранению энергии и так далее. В этом разделе мы рассмотрим ньютоновские взгляды на сохранение массы, импульса и энергии с релятивистской точки зрения.

Общий импульс

Рисунок 3–10. Релятивистское сохранение импульса.

Чтобы понять, как ньютоновский взгляд на сохранение импульса необходимо модифицировать в релятивистском контексте, мы рассмотрим задачу двух сталкивающихся тел, ограниченных одним измерением.

В ньютоновской механике можно выделить два крайних случая этой проблемы, дающих математику минимальной сложности:

(1) Два тела отскакивают друг от друга в абсолютно упругом столкновении.

(2) Два тела слипаются и продолжают двигаться как одна частица. Этот второй случай является случаем полностью неупругого столкновения.

Для обоих случаев (1) и (2) импульс, масса и полная энергия сохраняются. Однако кинетическая энергия не сохраняется в случаях неупругого столкновения. Определенная доля начальной кинетической энергии преобразуется в тепло.

В случае (2) две массы с импульсами ⁠ ⁠ ${\displaystyle {\boldsymbol {p}}_{\boldsymbol {1}}=m_{1}{\boldsymbol {v}}_{\boldsymbol {1}}}$ и ⁠ ⁠ ${\displaystyle {\boldsymbol {p}}_{\boldsymbol {2}}=m_{2}{\boldsymbol {v}}_{\boldsymbol {2}}}$ сталкиваются, образуя одну частицу сохраняющейся массы ⁠ ⁠ , ${\displaystyle m=m_{1}+m_{2}}$ движущуюся со скоростью центра масс исходной системы, . Полный импульс ⁠ ⁠ сохраняется. ${\displaystyle {\boldsymbol {v_{cm}}}=\left(m_{1}{\boldsymbol {v_{1}}}+m_{2}{\boldsymbol {v_{2}}}\right)/\left(m_{1}+m_{2}\right)}$ ${\displaystyle {\boldsymbol {p=p_{1}+p_{2}}}}$

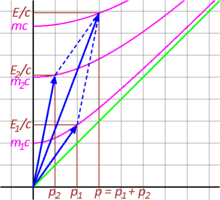
Рис. 3-10 иллюстрирует неупругое столкновение двух частиц с релятивистской точки зрения. Временные компоненты ⁠ ⁠ ${\displaystyle E_{1}/c}$ и ⁠ ⁠ ${\displaystyle E_{2}/c}$ складываются в общую величину E/c результирующего вектора, что означает, что энергия сохраняется. Аналогично, пространственные компоненты ⁠ ⁠ ${\displaystyle {\boldsymbol {p_{1}}}}$ и ⁠ ⁠ ${\displaystyle {\boldsymbol {p_{2}}}}$ складываются в p результирующего вектора. Четырехимпульс, как и ожидалось, является сохраняющейся величиной. Однако инвариантная масса слитой частицы, заданная точкой, где инвариантная гипербола полного импульса пересекает ось энергии, не равна сумме инвариантных масс отдельных столкнувшихся частиц. Действительно, она больше суммы отдельных масс: ⁠ ⁠ ${\displaystyle m>m_{1}+m_{2}}$ . ^{[41] : 94–97}

Рассматривая события этого сценария в обратной последовательности, мы видим, что несохранение массы является обычным явлением: когда нестабильная элементарная частица спонтанно распадается на две более легкие частицы, полная энергия сохраняется, но масса — нет. Часть массы преобразуется в кинетическую энергию. ^{[43] : 134–138}

Выбор систем отсчета

Свобода выбора любой системы отсчета для проведения анализа позволяет нам выбрать ту, которая может быть особенно удобной. Для анализа проблем импульса и энергии наиболее удобной системой отсчета обычно является « система отсчета центра импульса » (также называемая системой отсчета нулевого импульса, или системой отсчета COM). Это система отсчета, в которой пространственная составляющая полного импульса системы равна нулю. Рис. 3-11 иллюстрирует распад высокоскоростной частицы на две дочерние частицы. В лабораторной системе отсчета дочерние частицы преимущественно испускаются в направлении, ориентированном вдоль траектории исходной частицы. Однако в системе отсчета COM две дочерние частицы испускаются в противоположных направлениях, хотя их массы и величины их скоростей, как правило, не одинаковы. ^[49]

Сохранение энергии и импульса

В ньютоновском анализе взаимодействующих частиц преобразование между системами отсчета просто, поскольку все, что необходимо, это применить преобразование Галилея ко всем скоростям. Поскольку ⁠ ⁠ ${\displaystyle v'=v-u}$ , импульс ⁠ ⁠ ${\displaystyle p'=p-mu}$ . Если наблюдается сохранение полного импульса взаимодействующей системы частиц в одной системе отсчета, то будет наблюдаться его сохранение и в любой другой системе отсчета. ^{[43] : 241–245}

Сохранение импульса в системе отсчета COM сводится к требованию, чтобы p  = 0 как до, так и после столкновения. В ньютоновском анализе сохранение массы диктует, что ⁠ ⁠ ${\displaystyle m=m_{1}+m_{2}}$ . В упрощенных одномерных сценариях, которые мы рассматривали, необходимо только одно дополнительное ограничение, прежде чем можно будет определить исходящие импульсы частиц — энергетическое условие. В одномерном случае полностью упругого столкновения без потери кинетической энергии исходящие скорости отскакивающих частиц в системе отсчета COM будут точно равны и противоположны их входящим скоростям. В случае полностью неупругого столкновения с полной потерей кинетической энергии исходящие скорости отскакивающих частиц будут равны нулю. ^{[43] : 241–245}

Ньютоновские импульсы, вычисленные как ⁠ ⁠ ${\displaystyle p=mv}$ , не ведут себя должным образом при лоренцевском преобразовании. Линейное преобразование скоростей ⁠ ⁠ ${\displaystyle v'=v-u}$ заменяется на крайне нелинейное ⁠ ⁠ , ${\displaystyle v^{\prime }=(v-u)/(1-{vu}/{c^{2}})}$ так что расчет, демонстрирующий сохранение импульса в одной системе отсчета, будет недействительным в других системах отсчета. Эйнштейн столкнулся с необходимостью либо отказаться от сохранения импульса, либо изменить определение импульса. Этот второй вариант был тем, что он выбрал. ^{[41] : 104}

Релятивистский закон сохранения энергии и импульса заменяет три классических закона сохранения энергии, импульса и массы. Масса больше не сохраняется независимо, поскольку она включена в общую релятивистскую энергию. Это делает релятивистское сохранение энергии более простой концепцией, чем в нерелятивистской механике, поскольку общая энергия сохраняется без каких-либо оговорок. Кинетическая энергия, преобразованная в тепло или внутреннюю потенциальную энергию, проявляется как увеличение массы. ^{[43] : 127}

Пример: Из-за эквивалентности массы и энергии массы элементарных частиц обычно указываются в единицах энергии, где 1 МэВ = 10 ⁶ электрон-вольт. Заряженный пион — это частица с массой 139,57 МэВ (примерно в 273 раза больше массы электрона). Он нестабилен и распадается на мюон с массой 105,66 МэВ (примерно в 207 раз больше массы электрона) и антинейтрино, масса которого практически незначительна. Разница между массой пиона и массой мюона составляет 33,91 МэВ.

π⁻
→μ−+νμ

Рис. 3-12а иллюстрирует диаграмму энергия-импульс для этой реакции распада в системе покоя пиона. Из-за своей незначительной массы нейтрино движется со скоростью, очень близкой к скорости света. Релятивистское выражение для его энергии, как и для фотона, равно ⁠ ⁠ ${\displaystyle E_{v}=pc,}$ что также является значением пространственной компоненты его импульса. Для сохранения импульса мюон имеет то же значение пространственной компоненты импульса нейтрино, но в противоположном направлении.

Алгебраический анализ энергетики этой реакции распада доступен в сети, ^[50], поэтому на рис. 3-12b представлено графическое решение калькулятора. Энергия нейтрино составляет 29,79 МэВ, а энергия мюона составляет 33,91 МэВ − 29,79 МэВ = 4,12 МэВ . Большая часть энергии уносится нейтрино с массой, близкой к нулевой.

Введение в искривленное пространство-время

Теории Ньютона предполагали, что движение происходит на фоне жесткой евклидовой системы отсчета , которая простирается по всему пространству и всему времени. Гравитация опосредована таинственной силой, действующей мгновенно на расстоянии, чьи действия не зависят от промежуточного пространства. ^{[примечание 12]} Напротив, Эйнштейн отрицал, что существует какая-либо фоновая евклидова система отсчета, которая простирается по всему пространству. Не существует также такой вещи, как сила гравитации, есть только структура самого пространства-времени. ^{[51] : 175–190}

Рисунок 5–1. Приливные эффекты.

В терминах пространства-времени путь спутника, вращающегося вокруг Земли, не диктуется отдаленными влияниями Земли, Луны и Солнца. Вместо этого спутник движется в пространстве только в ответ на локальные условия. Поскольку пространство-время везде локально плоское, если рассматривать его в достаточно малых масштабах, спутник всегда следует прямой линии в своей локальной инерциальной системе отсчета. Мы говорим, что спутник всегда следует по пути геодезической . Никаких доказательств гравитации не может быть обнаружено, следуя вместе с движениями одной частицы. ^{[51] : 175–190}

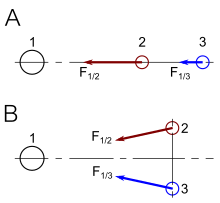
В любом анализе пространства-времени доказательство гравитации требует наблюдения относительных ускорений двух тел или двух отдельных частиц. На рис. 5-1 две отдельные частицы, свободно падающие в гравитационном поле Земли, демонстрируют приливные ускорения из-за локальных неоднородностей в гравитационном поле, так что каждая частица следует по разному пути через пространство-время. Приливные ускорения, которые эти частицы демонстрируют по отношению друг к другу, не требуют сил для своего объяснения. Скорее, Эйнштейн описал их в терминах геометрии пространства-времени, т. е. кривизны пространства-времени. Эти приливные ускорения строго локальны. Это кумулятивный общий эффект многих локальных проявлений кривизны, которые приводят к появлению гравитационной силы, действующей на большом расстоянии от Земли. ^{[51] : 175–190}

Разные наблюдатели, рассматривающие сценарии, представленные на этом рисунке, интерпретируют сценарии по-разному в зависимости от своего знания ситуации. (i) Первый наблюдатель, находящийся в центре масс частиц 2 и 3, но не знающий о большой массе 1, приходит к выводу, что между частицами в сценарии A существует сила отталкивания, в то время как между частицами в сценарии B существует сила притяжения. (ii) Второй наблюдатель, знающий о большой массе 1, улыбается наивности первого репортера. Этот второй наблюдатель знает, что на самом деле кажущиеся силы между частицами 2 и 3 на самом деле представляют собой приливные эффекты, возникающие в результате их дифференциального притяжения массой 1. (iii) Третий наблюдатель, обученный общей теории относительности, знает, что на самом деле нет никаких сил, действующих между тремя объектами. Вместо этого все три объекта движутся по геодезическим в пространстве-времени.

В основе общей теории относительности лежат два центральных положения.

• Первая важная концепция — независимость координат: законы физики не могут зависеть от используемой системы координат. Это важное расширение принципа относительности по сравнению с версией, используемой в специальной теории относительности, которая гласит, что законы физики должны быть одинаковы для каждого наблюдателя, движущегося в неускоренных (инерциальных) системах отсчета. В общей теории относительности, если использовать собственные (переведенные) слова Эйнштейна, «законы физики должны иметь такую ​​природу, чтобы они применялись к системам отсчета в любом виде движения». ^{[52] : 113} Это приводит к немедленной проблеме: в ускоренных системах отсчета человек ощущает силы, которые, по-видимому, позволили бы ему оценить свое состояние ускорения в абсолютном смысле. Эйнштейн решил эту проблему с помощью принципа эквивалентности. ^{[53] : 137–149}

Рисунок 5–2. Принцип эквивалентности

• Принцип эквивалентности гласит, что в любой достаточно малой области пространства эффекты гравитации такие же, как и эффекты ускорения.
  На рис. 5-2 человек A находится в космическом корабле, вдали от любых массивных объектов, который подвергается равномерному ускорению g . Человек B находится в коробке, покоящейся на Земле. При условии, что космический корабль достаточно мал, чтобы приливные эффекты были неизмеримы (учитывая чувствительность современных приборов для измерения гравитации, A и B предположительно должны быть лилипутами ), нет никаких экспериментов, которые A и B могли бы провести, чтобы определить, в какой обстановке они находятся. ^{[53] : 141–149}
  Альтернативное выражение принципа эквивалентности заключается в том, чтобы отметить, что в законе всемирного тяготения Ньютона F = GMm _g /r ² = m _g g и во втором законе Ньютона F = m _i a , нет априорной причины, по которой гравитационная масса m _g должна быть равна инертной массе m _i . Принцип эквивалентности утверждает, что эти две массы идентичны. ^{[53] : 141–149}

Чтобы перейти от элементарного описания искривленного пространства-времени выше к полному описанию гравитации, требуются тензорное исчисление и дифференциальная геометрия, темы, требующие значительного изучения. Без этих математических инструментов можно писать об общей теории относительности, но невозможно продемонстрировать какие-либо нетривиальные выводы.

Технические темы

Действительно ли пространство-время искривлено?

В конвенционалистских взглядах Пуанкаре основными критериями, по которым следует выбирать евклидову или неевклидову геометрию, были бы экономия и простота. Реалист сказал бы, что Эйнштейн открыл, что пространство-время неевклидово. Конвенционалист сказал бы, что Эйнштейн просто посчитал более удобным использовать неевклидову геометрию. Конвенционалист утверждал бы, что анализ Эйнштейна ничего не сказал о том, какова на самом деле геометрия пространства-времени . ^[54]

При этом, как говорится,

1. Можно ли представить общую теорию относительности в терминах плоского пространства-времени?
2. Существуют ли ситуации, в которых интерпретация общей теории относительности в рамках плоского пространства-времени может оказаться более удобной, чем обычная интерпретация искривленного пространства-времени?

В ответ на первый вопрос ряд авторов, включая Дезера, Грищука, Розена, Вайнберга и т. д., представили различные формулировки гравитации как поля в плоском многообразии. Эти теории по-разному называются « биметрической гравитацией », «теоретико-полевым подходом к общей теории относительности» и т. д. ^{[55] [56] [57] [58]} Кип Торн представил популярный обзор этих теорий. ^{[59] : 397–403}

Плоская парадигма пространства-времени утверждает, что материя создает гравитационное поле, которое заставляет линейки сжиматься, когда они поворачиваются из окружной ориентации в радиальную, и это заставляет тикающие часы замедляться. Плоская парадигма пространства-времени полностью эквивалентна парадигме искривленного пространства-времени в том, что они обе представляют одни и те же физические явления. Однако их математические формулировки совершенно различны. Работающие физики обычно переключаются между использованием искривленных и плоских методов пространства-времени в зависимости от требований задачи. Плоская парадигма пространства-времени удобна при выполнении приблизительных вычислений в слабых полях. Следовательно, методы плоского пространства-времени, как правило, используются при решении задач гравитационных волн, в то время как методы искривленного пространства-времени, как правило, используются при анализе черных дыр. ^{[59] : 397–403}

Асимптотические симметрии

Группа симметрии пространства-времени для специальной теории относительности — это группа Пуанкаре , которая является десятимерной группой из трех лоренцевских бустов, трех вращений и четырех пространственно-временных трансляций. Логично спросить, какие симметрии, если таковые имеются, могут применяться в общей теории относительности . Поддающимся решению случаем может быть рассмотрение симметрий пространства-времени, как их видят наблюдатели, находящиеся далеко от всех источников гравитационного поля. Наивное ожидание асимптотически плоских симметрий пространства-времени может заключаться в простом расширении и воспроизведении симметрий плоского пространства-времени специальной теории относительности, а именно группы Пуанкаре.

В 1962 году Герман Бонди , М. Г. ван дер Бург, А. В. Метцнер ^[60] и Райнер К. Сакс ^[61] обратились к этой проблеме асимптотической симметрии , чтобы исследовать поток энергии на бесконечности из-за распространяющихся гравитационных волн . Их первым шагом было принятие решения о некоторых физически разумных граничных условиях, которые можно было бы наложить на гравитационное поле на светоподобной бесконечности, чтобы охарактеризовать, что значит сказать, что метрика является асимптотически плоской, не делая никаких априорных предположений о природе группы асимптотической симметрии — даже предположения, что такая группа существует. Затем, после разработки того, что они считали наиболее разумными граничными условиями, они исследовали природу результирующих преобразований асимптотической симметрии, которые оставляют инвариантной форму граничных условий, соответствующих асимптотически плоским гравитационным полям. ^{[62] : 35}

Они обнаружили, что асимптотические преобразования симметрии на самом деле образуют группу, и структура этой группы не зависит от конкретного гравитационного поля, которое случайно присутствует. Это означает, что, как и ожидалось, можно отделить кинематику пространства-времени от динамики гравитационного поля, по крайней мере, на пространственной бесконечности. Озадачивающим сюрпризом в 1962 году стало их открытие богатой бесконечномерной группы (так называемой группы BMS) в качестве асимптотической группы симметрии вместо конечномерной группы Пуанкаре, которая является подгруппой группы BMS. Преобразования Лоренца являются не только асимптотическими преобразованиями симметрии, но существуют также дополнительные преобразования, которые не являются преобразованиями Лоренца, но являются асимптотическими преобразованиями симметрии. Фактически, они обнаружили дополнительную бесконечность генераторов преобразований, известных как супертрансляции . Это подразумевает вывод о том, что общая теория относительности (ОТО) не сводится к специальной теории относительности в случае слабых полей на больших расстояниях. ^{[62] : 35}

Риманова геометрия

Риманова геометрия — это раздел дифференциальной геометрии , изучающий римановы многообразия , определяемые как гладкие многообразия с римановой метрикой ( внутренним произведением на касательном пространстве в каждой точке, которое плавно меняется от точки к точке). Это дает, в частности, локальные понятия угла , длины кривых , площади поверхности и объема . Из них можно вывести некоторые другие глобальные величины путем интегрирования локальных вкладов.

Риманова геометрия возникла из видения Бернхарда Римана, выраженного в его вступительной лекции « Ueber die Hypothesen, welche der Geometrie zu Grunde liegen » («О гипотезах, на которых основана геометрия»). ^[63] Это очень широкое и абстрактное обобщение дифференциальной геометрии поверхностей в R 3 . Развитие римановой геометрии привело к синтезу разнообразных результатов, касающихся геометрии поверхностей и поведения геодезических на них, с методами, которые могут быть применены к изучению дифференцируемых многообразий более высоких размерностей. Это позволило сформулировать общую теорию относительности Эйнштейна , оказало глубокое влияние на теорию групп и теорию представлений , а также на анализ и стимулировало развитие алгебраической и дифференциальной топологии .

Изогнутые коллекторы

По физическим причинам пространственно-временной континуум математически определяется как четырехмерное, гладкое, связное лоренцево многообразие . Это означает, что гладкая метрика Лоренца имеет сигнатуру . Метрика определяет ${\displaystyle (M,g)}$ ${\displaystyle g}$ ${\displaystyle (3,1)}$геометрия пространства-времени , а также определениегеодезическихчастиц и световых лучей. Для каждой точки (события) на этом многообразиииспользуютсякоординатные картыиспользуются декартовы координаты. Более того, для простоты единицы измерения обычно выбираются такими, чтобы скорость светабыла равна 1.^[64] ${\displaystyle (x,y,z,t)}$ ${\displaystyle c}$

Система отсчета (наблюдатель) может быть идентифицирована с помощью одной из этих координатных карт; любой такой наблюдатель может описать любое событие . Другая система отсчета может быть идентифицирована с помощью второй координатной карты около . Два наблюдателя (по одному в каждой системе отсчета) могут описать одно и то же событие , но получить разные описания. ^[64] ${\displaystyle p}$ ${\displaystyle p}$ ${\displaystyle p}$

Обычно для покрытия многообразия требуется много перекрывающихся координатных карт. При наличии двух координатных карт, одна из которых содержит (представляющая наблюдателя), а другая содержит (представляющая другого наблюдателя), пересечение карт представляет собой область пространства-времени, в которой оба наблюдателя могут измерять физические величины и, следовательно, сравнивать результаты. Связь между двумя наборами измерений задается несингулярным преобразованием координат на этом пересечении. Идея координатных карт как локальных наблюдателей, которые могут выполнять измерения в своей окрестности, также имеет хороший физический смысл, поскольку именно так фактически собираются физические данные — локально. ^[64] ${\displaystyle p}$ ${\displaystyle q}$

Например, два наблюдателя, один из которых находится на Земле, а другой — на быстрой ракете к Юпитеру, могут наблюдать, как комета врезается в Юпитер (это событие ). В общем случае они будут не согласны относительно точного места и времени этого удара, т. е. у них будут разные 4-кортежи (поскольку они используют разные системы координат). Хотя их кинематические описания будут различаться, динамические (физические) законы, такие как закон сохранения импульса и первый закон термодинамики, по-прежнему будут выполняться. Фактически, теория относительности требует большего, в том смысле, что она предусматривает, что эти (и все другие физические) законы должны иметь одинаковую форму во всех системах координат. Это вводит тензоры в относительность, которыми представлены все физические величины. ${\displaystyle p}$ ${\displaystyle (x,y,z,t)}$

Говорят, что геодезические являются времениподобными, нулевыми или пространственноподобными, если касательный вектор к одной точке геодезической имеет такую ​​природу. Пути частиц и световых лучей в пространстве-времени представлены времениподобными и нулевыми (светоподобными) геодезическими соответственно. ^[64]

Привилегированный характер пространства-времени 3+1

Свойства ( n + m ) -мерного пространства-времени ^[65]

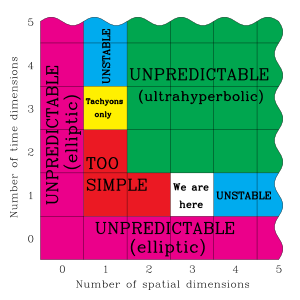
Существует два вида измерений: пространственные (двунаправленные) и временные (однонаправленные). ^[66] Пусть число пространственных измерений будет N , а число временных измерений будет T. То, что N = 3 и T = 1 , оставляя в стороне компактифицированные измерения, вызванные теорией струн и необнаружимые до сих пор, можно объяснить, обратившись к физическим последствиям того, что N отличается от 3, а T отличается от 1. Аргумент часто носит антропный характер и, возможно, является первым в своем роде, хотя и до того, как полная концепция вошла в моду.

Неявное представление о том, что размерность вселенной является особой, впервые приписывается Готфриду Вильгельму Лейбницу , который в « Рассуждении о метафизике» предположил, что мир — это «тот, который одновременно является самым простым в гипотезах и самым богатым в явлениях». ^[67] Иммануил Кант утверждал, что трехмерное пространство является следствием закона обратных квадратов всемирного тяготения . Хотя аргумент Канта имеет историческое значение, Джон Д. Барроу сказал, что он «переворачивает суть дела на передний план: именно трехмерность пространства объясняет, почему мы видим законы силы обратных квадратов в Природе, а не наоборот» (Барроу 2002:204). ^{[примечание 13]}

В 1920 году Пауль Эренфест показал, что если есть только одно временное измерение и более трех пространственных измерений, орбита планеты вокруг своего Солнца не может оставаться стабильной. То же самое верно и для орбиты звезды вокруг центра своей галактики . ^[68] Эренфест также показал, что если есть четное число пространственных измерений, то разные части волнового импульса будут перемещаться с разной скоростью. Если есть пространственные измерения, где k — положительное целое число, то волновые импульсы искажаются. В 1922 году Герман Вейль заявил, что теория электромагнетизма Максвелла может быть выражена в терминах действия только для четырехмерного многообразия. ^[69] Наконец, Тангерлини показал в 1963 году, что когда есть более трех пространственных измерений, электронные орбитали вокруг ядер не могут быть стабильными; электроны либо упадут в ядро , либо рассеются. ^[70] ${\displaystyle 5+2k}$

Макс Тегмарк расширяет предыдущий аргумент следующим антропным образом. ^[71] Если T отличается от 1, поведение физических систем не может быть надежно предсказано на основе знания соответствующих дифференциальных уравнений в частных производных . В такой вселенной не могла бы возникнуть разумная жизнь, способная манипулировать технологиями. Более того, если T > 1 , Тегмарк утверждает, что протоны и электроны были бы нестабильны и могли бы распадаться на частицы, имеющие большую массу, чем они сами. (Это не проблема, если частицы имеют достаточно низкую температуру.) ^[71] Наконец, если N < 3 , гравитация любого рода становится проблематичной, и вселенная, вероятно, была бы слишком простой, чтобы содержать наблюдателей. Например, когда N < 3 , нервы не могут пересекаться, не пересекаясь. ^[71] Следовательно, антропные и другие аргументы исключают все случаи, кроме N = 3 и T = 1 , которые описывают мир вокруг нас.

С другой стороны, в виду создания черных дыр из идеального одноатомного газа под действием его собственной гравитации, Вэй-Сян Фэн показал, что (3 + 1) -мерное пространство-время является пограничной размерностью. Более того, это уникальная размерность , которая может позволить себе «стабильную» газовую сферу с «положительной» космологической постоянной . Однако самогравитирующий газ не может быть стабильно связан, если массовая сфера больше, чем ~10 ²¹ солнечных масс, из-за малой положительности наблюдаемой космологической постоянной. ^[72]

В 2019 году Джеймс Скаргилл утверждал, что сложная жизнь может быть возможна с двумя пространственными измерениями. По мнению Скаргилла, чисто скалярная теория гравитации может позволить локальную гравитационную силу, а двумерные сети могут быть достаточными для сложных нейронных сетей. ^{[73] [74]}

Смотрите также

• Базовое введение в математику искривленного пространства-времени
• Сложное пространство-время
• Мысленные эксперименты Эйнштейна
• Четырехмерность
• География
• Глобальная пространственно-временная структура
• Список пространств-времен
• Метрическое пространство
• Философия пространства и времени
• Подарок
• География времени

Примечания

1. светоносный от латинского lumen , свет, + ferens , несущий; эфир от греческого αἰθήρ ( aithēr ), чистый воздух, ясное небо
2. Заявляя, что одновременность — это вопрос соглашения, Пуанкаре имел в виду, что для того, чтобы вообще говорить о времени, нужно иметь синхронизированные часы, а синхронизация часов должна быть установлена ​​определенной операционной процедурой (соглашением). Эта позиция представляла собой фундаментальный философский разрыв с Ньютоном, который представлял себе абсолютное, истинное время, которое не зависело от работы неточных часов его времени. Эта позиция также представляла собой прямую атаку на влиятельного философа Анри Бергсона , который утверждал, что время, одновременность и длительность являются вопросами интуитивного понимания. ^[19]
3. Операционная процедура, принятая Пуанкаре, была по сути идентична тому, что известно как синхронизация Эйнштейна , хотя ее вариант уже был широко используемой процедурой телеграфистов в середине 19 века. По сути, для синхронизации двух часов один из них посылает световой сигнал от одного к другому и подстраивается под время, которое требуется для прибытия вспышки. ^[19]
4. Отличительной чертой карьеры Эйнштейна, по сути, было использование им визуализированных мысленных экспериментов (Gedanken–Experimente) в качестве фундаментального инструмента для понимания физических проблем. Для специальной теории относительности он использовал движущиеся поезда и вспышки молний для своих самых проницательных прозрений. Для искривленного пространства-времени он рассматривал художника, падающего с крыши, ускоряющиеся лифты, слепых жуков, ползающих по искривленным поверхностям и тому подобное. В своих великих Сольвеевских дебатах с Бором о природе реальности (1927 и 1930) он придумал несколько воображаемых приспособлений, предназначенных для того, чтобы показать, по крайней мере в концепции, способы, с помощью которых можно обойти принцип неопределенности Гейзенберга . Наконец, в глубоком вкладе в литературу по квантовой механике Эйнштейн рассмотрел две частицы, которые кратковременно взаимодействуют, а затем разлетаются так, что их состояния коррелируют, предвосхищая явление, известное как квантовая запутанность . ^[24]
5. В оригинальной версии этой лекции Минковский продолжал использовать такие устаревшие термины, как эфир, но посмертная публикация этой лекции в 1915 году в Annals of Physics ( Annalen der Physik ) была отредактирована Зоммерфельдом, чтобы удалить этот термин. Зоммерфельд также отредактировал опубликованную форму этой лекции, чтобы пересмотреть суждение Минковского об Эйнштейне, превратив его из простого прояснителя принципа относительности в его главного толкователя. ^[25]
6. (В дальнейшем группа G _∞ является группой Галилея, а группа G _{c —} группой Лоренца.) «В связи с этим ясно, что группа G _c в пределе при c = ∞ , т. е. как группа G _∞ , в точности становится полной группой, принадлежащей ньютоновской механике. При таком положении дел, и поскольку G _c математически более понятна, чем G _∞ , математик может, посредством свободной игры воображения, прийти к мысли, что естественные явления на самом деле обладают инвариантностью, не для группы G _∞ , а скорее для группы G _c , где c определенно конечно и лишь чрезвычайно велико, используя обычные единицы измерения». ^[27]
7. Например, группа Лоренца является подгруппой конформной группы в четырех измерениях . ^{[28] : 41–42} Группа Лоренца изоморфна группе Лагерра , преобразующей плоскости в плоскости, ^{[28] : 39–42} она изоморфна группе Мёбиуса плоскости, ^{[29] : 22} и изоморфна группе изометрий в гиперболическом пространстве , которая часто выражается в терминах модели гиперболоида . ^{[30] : 3.2.3}
8. В декартовой плоскости обычное вращение оставляет окружность неизменной. В пространстве-времени гиперболическое вращение сохраняет гиперболическую метрику .
9. Даже без (де)ускорения, т. е. при использовании одной инерциальной системы отсчета O для постоянного высокоскоростного внешнего путешествия и другой инерциальной системы отсчета I для постоянного высокоскоростного внутреннего путешествия — сумма прошедшего времени в этих системах (O и I) короче, чем прошедшее время в неподвижной инерциальной системе отсчета S. Таким образом, ускорение и замедление не являются причиной более короткого прошедшего времени во время внешнего и внутреннего путешествия. Вместо этого использование двух разных постоянных высокоскоростных инерциальных систем отсчета для внешнего и внутреннего путешествия на самом деле является причиной более короткого общего прошедшего времени. Конечно, если один и тот же близнец должен путешествовать наружу и внутрь на участке пути и безопасно переключаться с внешнего на внутренний участок пути, ускорение и замедление необходимы. Если бы движущийся близнец мог ехать в высокоскоростной внешней инерциальной системе отсчета и мгновенно переключаться на высокоскоростную внутреннюю инерциальную систему отсчета, пример все равно работал бы. Дело в том, что настоящая причина должна быть четко указана. Асимметрия возникает из-за сравнения суммы прошедшего времени в двух различных инерциальных системах отсчета (O и I) с прошедшим временем в одной инерциальной системе отсчета S.
10. Легкость анализа релятивистского сценария часто зависит от системы отсчета, в которой выбирается анализ. На этом связанном изображении мы представляем альтернативные взгляды на сценарий поперечного доплеровского сдвига, в котором источник и приемник находятся на максимальном расстоянии друг от друга. (a) Если мы проанализируем сценарий в системе отсчета приемника, мы обнаружим, что анализ сложнее, чем должен быть. Видимое положение небесного объекта смещено относительно его истинного положения (или геометрического положения) из-за движения объекта в течение времени, необходимого его свету, чтобы достичь наблюдателя. Источник будет растянут во времени относительно приемника, но красное смещение, подразумеваемое этим замедлением времени, будет компенсировано синим смещением из-за продольной составляющей относительного движения между приемником и видимым положением источника. (b) Намного проще, если вместо этого мы проанализируем сценарий из системы отсчета источника. Наблюдатель, находящийся в источнике, знает из условия задачи, что приемник находится в ближайшей к нему точке. Это означает, что у приемника нет продольной составляющей движения, чтобы усложнить анализ. Поскольку часы приемника растянуты во времени относительно источника, свет, принимаемый приемником, смещен в синюю сторону на коэффициент гамма .
11. Не все эксперименты характеризуют эффект в терминах красного смещения. Например, эксперимент Кюндига измеряет поперечное голубое смещение с использованием источника Мёссбауэра в центре ротора центрифуги и поглотителя на ободе.
12. Сам Ньютон остро осознавал неотъемлемые трудности этих предположений, но с практической точки зрения принятие этих предположений было единственным способом, с помощью которого он мог добиться прогресса. В 1692 году он написал своему другу Ричарду Бентли: «То, что Гравитация должна быть врожденной, неотъемлемой и существенной для Материи, так что одно тело может действовать на другое на расстоянии через Вакуум, без посредничества чего-либо еще, посредством чего их Действие и Сила могут передаваться от одного к другому, является для меня таким большим Абсурдом, что я верю, что ни один Человек, обладающий компетентной Способностью Мыслить в Философских Вопросах, никогда не сможет впасть в него».
13. Это происходит потому, что закон тяготения (или любой другой закон обратных квадратов ) следует из концепции потока и пропорционального отношения плотности потока и напряженности поля. Если N = 3 , то трехмерные твердые объекты имеют площади поверхности, пропорциональные квадрату их размера в любом выбранном пространственном измерении. В частности, сфера радиуса r имеет площадь поверхности 4 πr ² . В более общем случае, в пространстве N измерений сила гравитационного притяжения между двумя телами, разделенными расстоянием r, будет обратно пропорциональна r ^{N −1} .

Дополнительные подробности

Ссылки

1. Рынасевич, Роберт (12 августа 2004 г.). «Взгляды Ньютона на пространство, время и движение». Стэнфордская энциклопедия философии . Исследовательская лаборатория метафизики, Стэнфордский университет. Архивировано из оригинала 16 июля 2012 г. . Получено 24 марта 2017 г. .
2. Дэвис, Филип Дж. (2006). Математика и здравый смысл: случай творческого напряжения . Уэллсли, Массачусетс: AK Peters. стр. 86. ISBN 978-1-4398-6432-6.
3. Шутц, Бернард (2004). Гравитация с нуля: Вводное руководство по гравитации и общей теории относительности (переиздание). Кембридж: Cambridge University Press . ISBN 0-521-45506-5. Архивировано из оригинала 17 января 2023 . Получено 24 мая 2017 .
4. Фок, В. (1966). Теория пространства, времени и гравитации (2-е изд.). Нью-Йорк: Pergamon Press Ltd. стр. 33. ISBN 0-08-010061-9. Получено 14 октября 2023 г. .
5. Лоуден, ДФ (1982). Введение в тензорное исчисление, теорию относительности и космологию (3-е изд.). Минеола, Нью-Йорк: Dover Publications. стр. 7. ISBN 978-0-486-42540-5.
6. Кольер, Питер (2017). Самое непостижимое: заметки к очень деликатному введению в математику относительности (3-е изд.). Непостижимые книги. ISBN 978-0-9573894-6-5.
7. Роуленд, Тодд. "Manifold". Wolfram Mathworld . Wolfram Research. Архивировано из оригинала 13 марта 2017 г. Получено 24 марта 2017 г.
8. French, AP (1968). Специальная теория относительности . Бока-Ратон, Флорида : CRC Press . стр. 35–60. ISBN 0-7487-6422-4.
9. Тейлор, Эдвин Ф.; Уилер, Джон Арчибальд (1992). Физика пространства-времени: Введение в специальную теорию относительности (2-е изд.). Сан-Франциско, Калифорния: Freeman. ISBN 0-7167-0336-X. Получено 14 апреля 2017 г. .
10. Шерр, Рэйчел Э .; Шаффер, Питер С.; Вокос, Стаматис (июль 2001 г.). «Понимание студентами времени в специальной теории относительности: одновременность и системы отсчета» (PDF) . Американский журнал физики . 69 (S1). Колледж-Парк, Мэриленд: Американская ассоциация учителей физики : S24–S35. arXiv : physics/0207109 . Bibcode : 2001AmJPh..69S..24S. doi : 10.1119/1.1371254. S2CID  8146369. Архивировано (PDF) из оригинала 28 сентября 2018 г. Получено 11 апреля 2017 г.
11. Хьюз, Стефан (2013). Catchers of the Light: Catching Space: Origins, Lunar, Solar, Solar System and Deep Space. Пафос, Кипр: ArtDeCiel Publishing. С. 202–233. ISBN 978-1-4675-7992-6. Архивировано из оригинала 17 января 2023 . Получено 7 апреля 2017 .
12. Уильямс, Мэтт (28 января 2022 г.). «Что такое теория относительности Эйнштейна?». Universe Today . Архивировано из оригинала 3 августа 2022 г. Получено 13 августа 2022 г.
13. Stachel, John (2005). «Френелевский (увлекающий) коэффициент как вызов оптике движущихся тел 19-го века». (PDF) . В Kox, AJ; Eisenstaedt, Jean (ред.). Вселенная общей теории относительности . Бостон, Массачусетс: Birkhäuser. стр. 1–13. ISBN 0-8176-4380-X. Архивировано из оригинала (PDF) 15 апреля 2017 года.
14. "Джордж Фрэнсис Фицджеральд". Библиотека Линды Холл . Архивировано из оригинала 17 января 2023 года . Получено 13 августа 2022 года .
15. "Нобелевская премия по физике 1902 года". NobelPrize.org . Архивировано из оригинала 23 июня 2017 года . Получено 13 августа 2022 года .
16. Pais, Abraham (1982). «Subtle is the Lord–»: Наука и жизнь Альберта Эйнштейна (11-е изд.). Оксфорд: Oxford University Press. ISBN 0-19-853907-X.
17. Darrigol, O. (2005), «Генезис теории относительности» (PDF) , Séminaire Poincaré , 1 : 1–22, Bibcode : 2006eins.book....1D, doi : 10.1007/3-7643-7436-5_1, ISBN 978-3-7643-7435-8, заархивировано (PDF) из оригинала 28 февраля 2008 г. , извлечено 17 июля 2017 г.
18. Миллер, Артур И. (1998). Специальная теория относительности Альберта Эйнштейна . Нью-Йорк: Springer-Verlag. ISBN 0-387-94870-8.
19. Галисон, Питер (2003). Часы Эйнштейна, Карты Пуанкаре: Империи времени. Нью-Йорк: WW Norton & Company, Inc. стр. 13–47. ISBN 0-393-02001-0.
20. Пуанкаре, Анри (1906). «О динамике электрона (Sur la dynamice de l'électron)». Rendiconti del Circolo Matematico di Palermo . 21 : 129–176. Бибкод : 1906RCMP...21..129P. дои : 10.1007/bf03013466. hdl : 2027/uiug.30112063899089 . S2CID  120211823. Архивировано из оригинала 11 июля 2017 года . Проверено 15 июля 2017 г.
21. Захар, Эли (1989) [1983], «Независимое открытие Пуанкаре принципа относительности», Революция Эйнштейна: Исследование эвристики , Чикаго, Иллинойс: Open Court Publishing Company, ISBN 0-8126-9067-2
22. Walter, Scott A. (2007). «Breaking in the 4-vectors: the four-dimensional movement in gravitation, 1905–1910». В Renn, Jürgen; Schemmel, Matthias (eds.). The Genesis of General Relativity, Volume 3. Berlin, Germany: Springer. pp. 193–252. Архивировано из оригинала 28 мая 2024 г. Получено 15 июля 2017 г.
23. Эйнштейн, Альберт (1905). «К электродинамике движущихся тел (Zur Elektrodynamik bewegter Körper)». Аннален дер Физик . 322 (10): 891–921. Бибкод : 1905АнП...322..891Е. дои : 10.1002/andp.19053221004 . Архивировано из оригинала 6 ноября 2018 года . Проверено 7 апреля 2018 г.
24. Айзексон, Уолтер (2007). Эйнштейн: его жизнь и вселенная . Simon & Schuster. стр. 26–27, 122–127, 145–146, 345–349, 448–460. ISBN 978-0-7432-6473-0.
25. Weinstein, Galina (2012). "Пространственно-временной формализм специальной теории относительности Макса Борна, Альберта Эйнштейна и Германа Минковского". arXiv : 1210.6929 [physics.hist-ph].
26. Галисон, Питер Луис (1979). «Пространство–время Минковского: от визуального мышления к абсолютному миру». Исторические исследования в области физических наук . 10 : 85–121. doi :10.2307/27757388. JSTOR  27757388.
27. Минковский, Герман (1909). «Raum und Zeit» («Пространство и время»). Jahresbericht der Deutschen Mathematiker-Vereinigung . Б. Г. Тойбнер: 1–14. Архивировано из оригинала 28 июля 2017 года . Проверено 17 июля 2017 г.
28. Картан, Э.; Фано, Г. (1955) [1915]. «Теория непрерывных групп и геометрии». Энциклопедия чистых и прикладных математических наук . 3 (1): 39–43. Архивировано из оригинала 23 марта 2018 года . Проверено 6 апреля 2018 г.(В 1915 году были опубликованы только страницы 1–21, вся статья, включая страницы 39–43, касающиеся групп Лагерра и Лоренца, была посмертно опубликована в 1955 году в собрании статей Картана и переиздана в Encyclopédie в 1991 году.)
29. Kastrup, HA (2008). «О достижениях конформных преобразований и связанных с ними симметриях в геометрии и теоретической физике». Annalen der Physik . 520 (9–10): 631–690. arXiv : 0808.2730 . Bibcode : 2008AnP...520..631K. doi : 10.1002/andp.200810324. S2CID  12020510.
30. Ratcliffe, JG (1994). "Гиперболическая геометрия". Foundations of Hyperbolic Manifolds . Нью-Йорк. С. 56–104. ISBN 0-387-94348-X.{{cite book}}: CS1 maint: location missing publisher (link)
31. Когут, Джон Б. (2001). Введение в теорию относительности . Массачусетс: Harcourt/Academic Press. ISBN 0-12-417561-9.
32. Рэй д'Инверно; Джеймс Викерс (2022). Введение в теорию относительности Эйнштейна: более глубокое понимание (иллюстрированное издание). Oxford University Press. стр. 26–28. ISBN 978-0-19-886202-4.Выдержка из страницы 27
33. Ландау, Л. Д. и Лифшиц, Э. М. (2013). Классическая теория полей (т. 2).
34. Кэрролл, Шон (2022). Величайшие идеи во Вселенной . Нью-Йорк: Penguin Random House LLC. С. 155–156. ISBN 9780593186589.
35. Curiel, Erik; Bokulich, Peter. «Lightcones and Causal Structure». Стэнфордская энциклопедия философии . Исследовательская лаборатория метафизики, Стэнфордский университет. Архивировано из оригинала 17 мая 2019 года . Получено 26 марта 2017 года .
36. Savitt, Steven. «Бытие и становление в современной физике. 3. Специальная теория относительности». Стэнфордская энциклопедия философии . Исследовательская лаборатория метафизики, Стэнфордский университет. Архивировано из оригинала 11 марта 2017 г. Получено 26 марта 2017 г.
37. Шутц, Бернард Ф. (1985). Первый курс общей теории относительности . Кембридж, Великобритания: Cambridge University Press. стр. 26. ISBN 0-521-27703-5.
38. Вайс, Майкл. "Парадокс близнецов". FAQ по физике и теории относительности . Архивировано из оригинала 27 апреля 2017 г. Получено 10 апреля 2017 г.
39. Молд, Ричард А. (1994). Основные положения теории относительности (1-е изд.). Springer. стр. 42. ISBN 978-0-387-95210-9. Получено 22 апреля 2017 г. .
40. Лернер, Лоуренс С. (1997). Физика для ученых и инженеров, том 2 (1-е изд.). Jones & Bartlett Pub. стр. 1047. ISBN 978-0-7637-0460-5. Получено 22 апреля 2017 г. .
41. Баис, Сандер (2007). Очень специальная теория относительности: Иллюстрированное руководство . Кембридж, Массачусетс: Издательство Гарвардского университета. ISBN 978-0-674-02611-7.
42. Форшоу, Джеффри; Смит, Гэвин (2014). Динамика и теория относительности. John Wiley & Sons. стр. 118. ISBN 978-1-118-93329-9. Получено 24 апреля 2017 г. .
43. Морин, Дэвид (2017). Специальная теория относительности для энтузиастов-новичков . CreateSpace Independent Publishing Platform. ISBN 978-1-5423-2351-2.
44. Ландау, Л. Д.; Лифшиц, Э. М. (2006). Классическая теория полей, курс теоретической физики, том 2 (4-е изд.). Амстердам: Elsevier. С. 1–24. ISBN 978-0-7506-2768-9.
45. Morin, David (2008). Введение в классическую механику: с проблемами и решениями. Cambridge University Press. ISBN 978-0-521-87622-3.
46. Rose, HH (21 апреля 2008 г.). «Оптика высокопроизводительных электронных микроскопов». Science and Technology of Advanced Materials . 9 (1): 014107. Bibcode : 2008STAdM...9a4107R. doi : 10.1088/0031-8949/9/1/014107. PMC 5099802. PMID  27877933 . 
47. Гриффитс, Дэвид Дж. (2013). Революции в физике двадцатого века. Кембридж: Cambridge University Press. стр. 60. ISBN 978-1-107-60217-5. Получено 24 мая 2017 г.
48. Байерс, Нина (1998). «Открытие Э. Нётер глубокой связи между симметриями и законами сохранения». arXiv : physics/9807044 .
49. Idema, Timon (17 апреля 2019 г.). «Механика и теория относительности. Глава 4.3: Системы отсчета». LibreTexts Physics . Программа доступных образовательных решений Калифорнийского государственного университета . Получено 6 июля 2024 г. .
50. Nave, R. "Энергетика распада заряженного пиона". Гиперфизика . Кафедра физики и астрономии, Университет штата Джорджия. Архивировано из оригинала 21 мая 2017 года . Получено 27 мая 2017 года .
51. Тейлор, Эдвин Ф.; Уилер, Джон Арчибальд (1992). Физика пространства-времени: Введение в специальную теорию относительности (2-е изд.). Сан-Франциско, Калифорния: Freeman. ISBN 0-7167-0336-X. Получено 14 апреля 2017 г. .
52. Лоренц, HA; Эйнштейн, A.; Минковский, H.; Вейль, H. (1952). Принцип относительности: Сборник оригинальных мемуаров по специальной и общей теории относительности . Dover Publications. ISBN 0-486-60081-5.
53. Mook, Delo E.; Vargish, Thomas (1987). Inside Relativity. Принстон, Нью-Джерси: Princeton University Press. ISBN 0-691-08472-6.
54. Мурзи, Мауро. «Жюль Анри Пуанкаре (1854–1912)». Интернет-энциклопедия философии (ISSN 2161-0002). Архивировано из оригинала 23 декабря 2020 года . Получено 9 апреля 2018 года .
55. Дезер, С. (1970). «Самовзаимодействие и калибровочная инвариантность». Общая теория относительности и гравитация . 1 (18): 9–8. arXiv : gr-qc/0411023 . Bibcode :1970GReGr...1....9D. doi :10.1007/BF00759198. S2CID  14295121.
56. Грищук, Л. П.; Петров, А. Н.; Попова, АД (1984). «Точная теория гравитационного поля (Эйнштейна) в произвольном фоновом пространстве–времени». Сообщения по математической физике . 94 (3): 379–396. Bibcode :1984CMaPh..94..379G. doi :10.1007/BF01224832. S2CID  120021772. Архивировано из оригинала 25 февраля 2021 г. Получено 9 апреля 2018 г.
57. Розен, Н. (1940). «Общая теория относительности и плоское пространство I». Physical Review . 57 (2): 147–150. Bibcode : 1940PhRv...57..147R. doi : 10.1103/PhysRev.57.147.
58. Вайнберг, С. (1964). «Вывод калибровочной инвариантности и принципа эквивалентности из лоренц-инвариантности S-матрицы». Physics Letters . 9 (4): 357–359. Bibcode : 1964PhL.....9..357W. doi : 10.1016/0031-9163(64)90396-8.
59. Thorne, Kip (1995). Черные дыры и искривления времени: возмутительное наследие Эйнштейна . WW Norton & Company. ISBN 978-0-393-31276-8.
60. Бонди, Х.; Ван дер Бург, MGJ; Мецнер, А. (1962). «Гравитационные волны в общей теории относительности: VII. Волны от осесимметричных изолированных систем». Труды Лондонского королевского общества A . A269 (1336): 21–52. Bibcode :1962RSPSA.269...21B. doi :10.1098/rspa.1962.0161. S2CID  120125096.
61. Сакс, Райнер К. (1962). «Асимптотические симметрии в теории гравитации». Physical Review . 128 (6): 2851–2864. Bibcode : 1962PhRv..128.2851S. doi : 10.1103/PhysRev.128.2851.
62. Strominger, Andrew (2017). "Lectures on the Infrared Structure of Gravity and Gauge Theory". arXiv : 1703.05448 [hep-th]. ...отредактированная стенограмма курса, прочитанного автором в Гарварде в весеннем семестре 2016 года. Он содержит педагогический обзор последних разработок, связывающих предметы мягких теорем, эффекта памяти и асимптотических симметрий в четырехмерной КЭД, неабелевой калибровочной теории и гравитации с приложениями к черным дырам. Будет опубликовано Princeton University Press, 158 страниц.
63. математика.tcd.ie
64. Бэр, Кристиан; Фреденхаген, Клаус (2009). «Лоренцевы многообразия» (PDF) . Квантовая теория поля в искривленном пространстве-времени: концепции и математические основы . Дордрехт: Спрингер. стр. 39–58. ISBN 978-3-642-02779-6. Архивировано из оригинала (PDF) 15 апреля 2017 г. . Получено 14 апреля 2017 г. .
65. Тегмарк, Макс (1 апреля 1997 г.). «О размерности пространства-времени». Классическая и квантовая гравитация . 14 (4): L69–L75. arXiv : gr-qc/9702052 . Bibcode : 1997CQGra..14L..69T. doi : 10.1088/0264-9381/14/4/002. ISSN  0264-9381. S2CID  250904081.
66. Skow, Bradford (2007). «Что делает время отличным от пространства?» (PDF) . Noûs . 41 (2): 227–252. CiteSeerX 10.1.1.404.7853 . doi :10.1111/j.1468-0068.2007.00645.x. Архивировано из оригинала (PDF) 24 августа 2016 года . Получено 13 апреля 2018 года . 
67. Лейбниц, Готфрид (1880). «Рассуждение о метафизике». Die philosophischen schriften von Gottfried Wilhelm Leibniz . Том. 4. Вайдман. стр. 427–463 . Проверено 13 апреля 2018 г.
68. Эренфест, Пол (1920). «Welche Rolle spielt die Drei Dimensionität des Raumes in den Grundgesetzen der Physik?» [Как фундаментальные законы физики подтверждают, что пространство имеет три измерения?]. Аннален дер Физик . 61 (5): 440–446. Бибкод : 1920АнП...366..440Е. дои : 10.1002/andp.19203660503.. См. также Эренфест, П. (1917) «Каким образом в фундаментальных законах физики проявляется тот факт, что пространство имеет три измерения?» Труды Амстердамской академии 20:200.
69. Вейль, Х. (1922). Пространство, время и материя . Переиздание Дувра: 284.
70. Tangherlini, FR (1963). "Поле Шварцшильда в n измерениях и проблема размерности пространства". Nuovo Cimento . 27 (3): 636–651. Bibcode :1963NCim...27..636T. doi :10.1007/BF02784569. S2CID  119683293.
71. Тегмарк, Макс (апрель 1997 г.). "О размерности пространства-времени" (PDF) . Классическая и квантовая гравитация . 14 (4): L69–L75. arXiv : gr-qc/9702052 . Bibcode :1997CQGra..14L..69T. doi :10.1088/0264-9381/14/4/002. S2CID  15694111 . Получено 16 декабря 2006 г. .
72. Feng, WX (3 августа 2022 г.). «Гравотермальный фазовый переход, черные дыры и размерность пространства». Physical Review D. 106 ( 4): L041501. arXiv : 2207.14317 . Bibcode : 2022PhRvD.106d1501F. doi : 10.1103/PhysRevD.106.L041501. S2CID  251196731.
73. Скаргилл, JHC (26 февраля 2020 г.). «Существование жизни в 2 + 1 измерениях». Physical Review Research . 2 (1): 013217. arXiv : 1906.05336 . Bibcode : 2020PhRvR...2a3217S. doi : 10.1103/PhysRevResearch.2.013217. S2CID  211734117.
74. "Жизнь может существовать в двумерной вселенной (согласно физике, во всяком случае)". technologyreview.com . Получено 16 июня 2021 г. .

Дальнейшее чтение

• Барроу, Джон Д .; Типлер, Фрэнк Дж. (1986). Антропный космологический принцип (1-е изд.). Oxford University Press . ISBN 978-0-19-282147-8. LCCN  87028148.
• Джордж Ф. Эллис и Рут М. Уильямс (1992) Плоское и искривленное пространство-время . Oxford University Press. ISBN 0-19-851164-7 
• Лоренц, HA , Эйнштейн, Альберт , Минковский, Герман и Вейль, Герман (1952) Принцип относительности: Сборник оригинальных мемуаров . Дувр.
• Лукас, Джон Рэндольф (1973) Трактат о времени и пространстве . Лондон: Метуэн.
• Пенроуз, Роджер (2004). Дорога к реальности . Оксфорд: Oxford University Press. ISBN 0-679-45443-8.Главы 17–18.
• Тейлор, Э. Ф.; Уилер, Джон А. (1992). Физика пространства-времени, второе издание. Архив Интернета: WH Freeman. ISBN 0-7167-2327-1.
• Аркани-Хамед, Нима (1 декабря 2017 г.). Гибель пространства-времени: почему оно должно распасться на более фундаментальные структуры (речь). 2384-е заседание Общества. Вашингтон, округ Колумбия . Получено 16 июля 2022 г.

Внешние ссылки

• Медиа, связанные с Spacetime на Wikimedia Commons
• Альберт Эйнштейн о пространстве-времени 13-е издание Encyclopaedia Britannica Historical: Статья Альберта Эйнштейна 1926 года
• Энциклопедия пространства-времени и гравитации Scholarpedia Статьи экспертов
• Стэнфордская энциклопедия философии : «Пространство и время: инерциальные системы отсчета» Роберта ДиСалле.