Раздельно-комплексное число

Вещественные числа с дополнительным квадратным корнем +1 присоединены

В алгебре расщепленное комплексное число (или гиперболическое число , также перплексное число , двойное число ) основано на гиперболической единице j, удовлетворяющей условию расщепленное комплексное число имеет две действительные компоненты x и y и записывается как Сопряженное число z равно Поскольку произведение числа z на его сопряженное число является изотропной квадратичной формой . ${\displaystyle j^{2}=1.}$ ${\displaystyle z=x+yj.}$ ${\displaystyle z^{*}=x-yj.}$ ${\displaystyle j^{2}=1,}$ ${\displaystyle N(z):=zz^{*}=x^{2}-y^{2},}$

Набор D всех расщепленных комплексных чисел для ⁠ ⁠ образует алгебру над полем действительных чисел . Два расщепленных комплексных числа w и z имеют произведение wz , которое удовлетворяет Это произведение N над произведением алгебр делает ( D , +, ×, *) композиционной алгеброй . ${\displaystyle z=x+yj}$ ${\displaystyle x,y\in \mathbb {R} }$ ${\displaystyle N(wz)=N(w)N(z).}$

Подобная алгебра, основанная на ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$ и покомпонентных операциях сложения и умножения, ⁠ ⁠ ${\displaystyle (\mathbb {R} ^{2},+,\times ,xy),}$ где xy — квадратичная форма на ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2},}$ также образует квадратичное пространство . Кольцевой изоморфизм

$${\displaystyle {\begin{aligned}D&\to \mathbb {R} ^{2}\\x+yj&\mapsto (x-y,x+y)\end{aligned}}}$$

связывает пропорциональные квадратичные формы, но отображение не является изометрией , поскольку мультипликативное тождество (1, 1) ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$ находится на расстоянии ⁠ ${\displaystyle {\sqrt {2}}}$⁠ от 0, который нормализован в D .

У расщепленных комплексных чисел есть много других названий; см. § Синонимы ниже. См. статью Переменная двигателя для функций расщепленного комплексного числа.

Определение

Расщепленное комплексное число — это упорядоченная пара действительных чисел, записанная в виде

$${\displaystyle z=x+jy}$$

где x и y — действительные числа , а гиперболическая единица ^[1] j удовлетворяет условию

$${\displaystyle j^{2}=+1}$$

В области комплексных чисел мнимая единица i удовлетворяет Смена знака отличает расщепленно-комплексные числа от обычных комплексных. Гиперболическая единица j не является действительным числом, а является независимой величиной. ${\displaystyle i^{2}=-1.}$

Совокупность всех таких z называется плоскостью расщепленного комплекса . Сложение и умножение чисел расщепленного комплекса определяются как

$${\displaystyle {\begin{aligned}(x+jy)+(u+jv)&=(x+u)+j(y+v)\\(x+jy)(u+jv)&=(xu+yv)+j(xv+yu).\end{aligned}}}$$

Это умножение коммутативно , ассоциативно и распространяется относительно сложения.

Сопряженная, модульная и билинейная форма

Так же, как и для комплексных чисел, можно определить понятие расщепленно-комплексного сопряжения . Если

$${\displaystyle z=x+jy~,}$$

тогда сопряжение z определяется как

$${\displaystyle z^{*}=x-jy~.}$$

Сопряженное число — это инволюция , которая удовлетворяет свойствам, аналогичным свойствам комплексного сопряженного числа . А именно,

$${\displaystyle {\begin{aligned}(z+w)^{*}&=z^{*}+w^{*}\\(zw)^{*}&=z^{*}w^{*}\\\left(z^{*}\right)^{*}&=z.\end{aligned}}}$$

Квадрат модуля расщепленного комплексного числа задается изотропной квадратичной формой ${\displaystyle z=x+jy}$

$${\displaystyle \lVert z\rVert ^{2}=zz^{*}=z^{*}z=x^{2}-y^{2}~.}$$

Он обладает свойством композиционной алгебры :

$${\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert ~.}$$

Однако эта квадратичная форма не является положительно определенной , а имеет сигнатуру (1, −1) , поэтому модуль не является нормой .

Соответствующая билинейная форма задается выражением

$${\displaystyle \langle z,w\rangle =\operatorname {\mathrm {Re} } \left(zw^{*}\right)=\operatorname {\mathrm {Re} } \left(z^{*}w\right)=xu-yv~,}$$

где и Здесь действительная часть определяется как . Другое выражение для квадрата модуля тогда ${\displaystyle z=x+jy}$ ${\displaystyle w=u+jv.}$ ${\displaystyle \operatorname {\mathrm {Re} } (z)={\tfrac {1}{2}}(z+z^{*})=x}$

$${\displaystyle \lVert z\rVert ^{2}=\langle z,z\rangle ~.}$$

Поскольку это не положительно-определенная, эта билинейная форма не является внутренним произведением ; тем не менее, билинейная форма часто упоминается как неопределенное внутреннее произведение . Подобное злоупотребление языком относится к модулю как к норме.

Сплит-комплексное число обратимо тогда и только тогда, когда его модуль ненулевой ( ), ${\displaystyle \lVert z\rVert \neq 0}$ таким образом, числа вида x ± jx не имеют обратного. Мультипликативный обратный элемент обратимого элемента задается как

$${\displaystyle z^{-1}={\frac {z^{*}}{{\lVert z\rVert }^{2}}}~.}$$

Раздельно-комплексные числа, которые необратимы, называются нулевыми векторами . Все они имеют вид ( a ± ja ) для некоторого действительного числа a .

Диагональная основа

Имеются два нетривиальных идемпотентных элемента, заданных формулами и Напомним, что идемпотент означает, что и Оба этих элемента равны нулю: ${\displaystyle e={\tfrac {1}{2}}(1-j)}$ ${\displaystyle e^{*}={\tfrac {1}{2}}(1+j).}$ ${\displaystyle ee=e}$ ${\displaystyle e^{*}e^{*}=e^{*}.}$

$${\displaystyle \lVert e\rVert =\lVert e^{*}\rVert =e^{*}e=0~.}$$

Часто удобно использовать e и e ^∗ в качестве альтернативного базиса для плоскости расщепленного комплекса. Этот базис называется диагональным базисом или нулевым базисом . Число расщепленного комплекса z можно записать в нулевом базисе как

$${\displaystyle z=x+jy=(x-y)e+(x+y)e^{*}~.}$$

Если обозначить число для действительных чисел a и b как ( a , b ) , то комплексное умножение расщепления задается как ${\displaystyle z=ae+be^{*}}$

$${\displaystyle \left(a_{1},b_{1}\right)\left(a_{2},b_{2}\right)=\left(a_{1}a_{2},b_{1}b_{2}\right)~.}$$

Комплексно-сопряженное число в диагональном базисе задается как , а квадрат модуля — как $${\displaystyle (a,b)^{*}=(b,a)}$$

$${\displaystyle \lVert (a,b)\rVert ^{2}=ab.}$$

Изоморфизм

Эта коммутативная диаграмма связывает действие гиперболического версора на D с отображением сжатия σ, примененным к ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$

На основе {e, e*} становится ясно, что расщепленно-комплексные числа кольцево изоморфны прямой сумме ⁠ ⁠ ${\displaystyle \mathbb {R} \oplus \mathbb {R} }$ со сложением и умножением, определенными попарно.

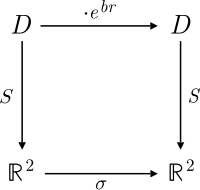
Диагональный базис для плоскости расщепленных комплексных чисел можно вызвать, используя упорядоченную пару ( x , y ) для и сделав отображение ${\displaystyle z=x+jy}$

$${\displaystyle (u,v)=(x,y){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=(x,y)S~.}$$

Теперь квадратичная форма имеет вид : Кроме того, ${\displaystyle uv=(x+y)(x-y)=x^{2}-y^{2}~.}$

$${\displaystyle (\cosh a,\sinh a){\begin{pmatrix}1&1\\1&-1\end{pmatrix}}=\left(e^{a},e^{-a}\right)}$$

таким образом , две параметризованные гиперболы приводятся в соответствие с S.

Действие гиперболического версора тогда соответствует при этом линейном преобразовании отображению сжатия ${\displaystyle e^{bj}\!}$

$${\displaystyle \sigma :(u,v)\mapsto \left(ru,{\frac {v}{r}}\right),\quad r=e^{b}~.}$$

Хотя расщепленная комплексная плоскость и прямая сумма двух действительных прямых лежат в одном и том же классе изоморфизма в категории колец , они различаются по расположению в декартовой плоскости . Изоморфизм, как плоское отображение, состоит из поворота против часовой стрелки на 45° и растяжения на √ 2 . В частности, растяжение иногда вызывало путаницу в связи с площадями гиперболического сектора . Действительно, гиперболический угол соответствует площади сектора в плоскости ⁠ ⁠ ${\displaystyle \mathbb {R} \oplus \mathbb {R} }$ с его «единичной окружностью», заданной выражением Сжатая единичная гипербола расщепленной комплексной плоскости имеет только половину площади в размахе соответствующего гиперболического сектора. Такая путаница может сохраняться, когда геометрия расщепленной комплексной плоскости не отличается от геометрии ⁠ ⁠ . ${\displaystyle \{(a,b)\in \mathbb {R} \oplus \mathbb {R} :ab=1\}.}$ ${\displaystyle \{\cosh a+j\sinh a:a\in \mathbb {R} \}}$ ${\displaystyle \mathbb {R} \oplus \mathbb {R} }$

Геометрия

  Единичная гипербола: ‖ z ‖ = 1

  Сопряженная гипербола: ‖ z ‖ = −1

  Асимптоты: ‖ z ‖ = 0

Двумерное действительное векторное пространство со скалярным произведением Минковского называется (1 + 1) -мерным пространством Минковского и часто обозначается ⁠ ⁠ ${\displaystyle \mathbb {R} ^{1,1}.}$ Так же, как большую часть геометрии евклидовой плоскости ⁠ ⁠ ${\displaystyle \mathbb {R} ^{2}}$ можно описать с помощью комплексных чисел, геометрию плоскости Минковского ⁠ ⁠ ${\displaystyle \mathbb {R} ^{1,1}}$ можно описать с помощью расщепленных комплексных чисел.

Набор точек

$${\displaystyle \left\{z:\lVert z\rVert ^{2}=a^{2}\right\}}$$

является гиперболой для любого ненулевого a в ⁠ ⁠ ${\displaystyle \mathbb {R} .}$ Гипербола состоит из правой и левой ветви, проходящей через ( a , 0) и (− a , 0) . Случай a = 1 называется единичной гиперболой . Сопряженная гипербола задается формулой

$${\displaystyle \left\{z:\lVert z\rVert ^{2}=-a^{2}\right\}}$$

с верхней и нижней ветвью, проходящей через (0, a ) и (0, − a ) . Гипербола и сопряженная гипербола разделены двумя диагональными асимптотами , которые образуют множество нулевых элементов:

$${\displaystyle \left\{z:\lVert z\rVert =0\right\}.}$$

Эти две линии (иногда называемые нулевым конусом ) перпендикулярны и имеют наклоны ±1. ${\displaystyle \mathbb {R} ^{2}}$

Говорят, что расщепленные комплексные числа z и w являются гиперболически-ортогональными , если ⟨ z , w ⟩ = 0 . Хотя это условие аналогично обычной ортогональности, особенно известной в обычной арифметике комплексных чисел, это условие более тонкое. Оно формирует основу для концепции одновременной гиперплоскости в пространстве-времени.

Аналог формулы Эйлера для расщепленно-комплексных чисел:

$${\displaystyle \exp(j\theta )=\cosh(\theta )+j\sinh(\theta ).}$$

Эту формулу можно вывести из разложения в степенной ряд, используя тот факт, что cosh имеет только четные степени, тогда как sinh имеет нечетные степени. ^[2] Для всех действительных значений гиперболического угла θ расщепленное комплексное число λ = exp( jθ ) имеет норму 1 и лежит на правой ветви единичной гиперболы. Такие числа, как λ, называются гиперболическими версорами .

Поскольку λ имеет модуль 1, умножение любого расщепленного комплексного числа z на λ сохраняет модуль z и представляет собой гиперболическое вращение (также называемое усилением Лоренца или отображением сжатия ). Умножение на λ сохраняет геометрическую структуру, переводя гиперболы в себя, а нулевой конус в себя.

Множество всех преобразований плоскости расщепленного комплекса, которые сохраняют модуль (или, что эквивалентно, скалярное произведение), образует группу, называемую обобщенной ортогональной группой O(1, 1) . Эта группа состоит из гиперболических вращений, которые образуют подгруппу, обозначенную SO ⁺ (1, 1) , в сочетании с четырьмя дискретными отражениями, заданными как

$${\displaystyle z\mapsto \pm z}$$и ${\displaystyle z\mapsto \pm z^{*}.}$

Экспоненциальная карта

$${\displaystyle \exp \colon (\mathbb {R} ,+)\to \mathrm {SO} ^{+}(1,1)}$$

перевод θ во вращение посредством exp( jθ ) является групповым изоморфизмом , поскольку применяется обычная экспоненциальная формула:

$${\displaystyle e^{j(\theta +\phi )}=e^{j\theta }e^{j\phi }.}$$

Если расщепляемое комплексное число z не лежит ни на одной из диагоналей, то z имеет полярное разложение .

Алгебраические свойства

В терминах абстрактной алгебры расщепленные комплексные числа можно описать как частное кольца многочленов ⁠ ⁠ по ${\displaystyle \mathbb {R} [x]}$ идеалу , порожденному многочленом ${\displaystyle x^{2}-1,}$

$${\displaystyle \mathbb {R} [x]/(x^{2}-1).}$$

Образ x в частном — это «мнимая» единица j . При таком описании становится ясно, что расщепленные комплексные числа образуют коммутативную алгебру над действительными числами. Алгебра не является полем , поскольку нулевые элементы необратимы. Все ненулевые нулевые элементы являются делителями нуля .

Поскольку сложение и умножение являются непрерывными операциями относительно обычной топологии плоскости, то расщепленные комплексные числа образуют топологическое кольцо .

Алгебра расщепленно-комплексных чисел образует композиционную алгебру, поскольку

$${\displaystyle \lVert zw\rVert =\lVert z\rVert \lVert w\rVert ~}$$

для любых чисел z и w .

Из определения видно, что кольцо расщепленно-комплексных чисел изоморфно _{групповому} кольцу ⁠ ⁠ ${\displaystyle \mathbb {R} [C_{2}]}$ циклической группы C2 над действительными числами ⁠ ⁠ ${\displaystyle \mathbb {R} .}$

Матричные представления

Можно легко представить расщепленные комплексные числа матрицами . Расщепленное комплексное число может быть представлено матрицей ${\displaystyle z=x+jy}$ ${\displaystyle z\mapsto {\begin{pmatrix}x&y\\y&x\end{pmatrix}}.}$

Сложение и умножение расщепленных комплексных чисел затем задаются сложением и умножением матриц. Квадрат модуля z задается определителем соответствующей матрицы.

На самом деле существует много представлений плоскости расщепленного комплекса в четырехмерном кольце действительных матриц 2x2. Действительные кратные единичной матрицы образуют действительную линию в кольце матриц M(2,R). Любая гиперболическая единица m обеспечивает базисный элемент, с помощью которого можно расширить действительную линию до плоскости расщепленного комплекса. Матрицы

$${\displaystyle m={\begin{pmatrix}a&c\\b&-a\end{pmatrix}}}$$

квадрат которой к единичной матрице удовлетворяет Например, когда a = 0, то ( b,c ) является точкой на стандартной гиперболе. В более общем случае, существует гиперповерхность в M(2,R) гиперболических единиц, любая из которых служит базисом для представления расщепленно-комплексных чисел как подкольца M (2,R). ^{[3] [ нужен лучший источник ]} ${\displaystyle a^{2}+bc=1.}$

Число можно представить матрицей   ${\displaystyle z=x+jy}$ ${\displaystyle x\ I+y\ m.}$

История

Использование расщепленных комплексных чисел восходит к 1848 году, когда Джеймс Кокл представил свои тессарины . ^[4] Уильям Кингдон Клиффорд использовал расщепленные комплексные числа для представления сумм спинов. Клиффорд ввел использование расщепленных комплексных чисел в качестве коэффициентов в кватернионной алгебре, которая теперь называется расщепленными бикватернионами . Он назвал ее элементы «моторами», термин, параллельный «роторному» действию обычного комплексного числа, взятого из группы окружности . Расширяя аналогию, функции моторной переменной контрастируют с функциями обычной комплексной переменной .

С конца двадцатого века умножение расщепленного комплекса обычно рассматривалось как лоренцевское усиление плоскости пространства-времени . ^{[5] [6] [7] [8] [9] [10]} В этой модели число z = x + y j представляет собой событие в пространственно-временной плоскости, где x измеряется в секундах, а y в световых секундах . Будущее соответствует квадранту событий { z  : | y | < x } , который имеет полярное разложение расщепленного комплекса . Модель гласит, что z может быть достигнуто из начала координат путем ввода системы отсчета с быстротой a и ожидания ρ наносекунд. Уравнение расщепленного комплекса ${\displaystyle z=\rho e^{aj}\!}$

$${\displaystyle e^{aj}\ e^{bj}=e^{(a+b)j}}$$

Выражение произведений на единичной гиперболе иллюстрирует аддитивность быстрот для коллинеарных скоростей. Одновременность событий зависит от быстроты a ;

$${\displaystyle \{z=\sigma je^{aj}:\sigma \in \mathbb {R} \}}$$

представляет собой линию событий, одновременных с началом координат в системе отсчета с быстротой a .

Два события z и w являются гиперболически-ортогональными , когда канонические события exp( aj ) и j exp( aj ) являются гиперболически ортогональными и лежат на осях системы отсчета, в которой события, одновременные с началом координат, пропорциональны j exp( aj ) . ${\displaystyle z^{*}w+zw^{*}=0.}$

В 1933 году Макс Цорн использовал расщепленные октонионы и отметил свойство композиционной алгебры . Он понял, что конструкция Кэли–Диксона , используемая для генерации алгебр с делением, может быть модифицирована (с множителем гамма, γ ) для построения других композиционных алгебр, включая расщепленные октонионы. Его нововведение было увековечено Адрианом Альбертом , Ричардом Д. Шефером и другими. ^[11] Фактор гамма, с R в качестве базового поля, строит расщепленные комплексные числа как композиционную алгебру. Рецензируя Albert для Mathematical Reviews , NH McCoy написал, что было «введение некоторых новых алгебр порядка 2 ^e над F, обобщающих алгебры Кэли–Диксона». ^[12] Взятие F = R и e = 1 соответствует алгебре этой статьи.

В 1935 году Ж. К. Виньо и А. Дураньона-и-Ведиа разработали комплексную геометрическую алгебру и теорию функций в четырех статьях в Contribución a las Ciencias Físicas y Matemáticas , Национальный университет Ла-Платы , Республика Аргентина (на испанском языке). Эти разъяснительные и педагогические эссе представили тему, получившую широкое признание. ^[13]

В 1941 году Э. Ф. Аллен использовал геометрическую арифметику расщепленного комплекса для построения гиперболы с девятью точками треугольника, вписанного в  zz ^∗ = 1. ^[14 ]

В 1956 году Мечислав Вармус опубликовал «Исчисление приближений» в Bulletin de l'Académie polonaise des sciences (см. ссылку в разделе «Ссылки»). Он разработал две алгебраические системы, каждую из которых он назвал «приближенными числами», вторая из которых образует действительную алгебру. ^[15] DH Lehmer просмотрел статью в Mathematical Reviews и заметил, что эта вторая система изоморфна «гиперболическим комплексным» числам, предмету этой статьи.

В 1961 году Уормус продолжил свое изложение, ссылаясь на компоненты приближенного числа, такие как середина и радиус обозначенного интервала.

Синонимы

Разные авторы использовали множество названий для расщепленных комплексных чисел. Вот некоторые из них:

• ( настоящие ) тессарины , Джеймс Кокл (1848)
• ( алгебраические ) двигатели , У. К. Клиффорд (1882)
• Гиперболические комплексные числа , JC Vignaux (1935), G. Cree (1949) ^[16]
• двумерные числа , У. Бенчивенга (1946)
• действительные гиперболические числа , Н. Смит (1949) ^[17]
• приблизительные числа , Warmus (1956), для использования в интервальном анализе
• двойные числа , И. М. Яглом (1968), Кантор и Солодовников (1989), Хазевинкель (1990), Руни (2014)
• гиперболические числа , В. Миллер и Р. Бёнинг (1968), ^[18] Г. Собчик (1995)
• анормально-комплексные числа , В. Бенц (1973)
• числа-загадки , П. Фьелстад (1986) и Пудиак и Леклер (2009)
• контркомплекс или гиперболический , Кармоди (1988)
• Числа Лоренца , FR Harvey (1990)
• полукомплексные числа , Ф. Антонуччио (1994)
• паракомплексные числа , Кручану, Фортуни и Гадеа (1996)
• расщепленные комплексные числа , Б. Розенфельд (1997) ^[19]
• числа пространства-времени , Н. Борота (2000)
• Числа исследований , П. Лунесто (2001)
• два комплексных числа , С. Олариу (2002)
• расщепленные бинарионы , К. Маккриммон (2004)

Смотрите также

• пространство Минковского
• Сплит-кватернион
• Гиперкомплексное число

Ссылки

1. Владимир В. Кисиль (2012) Геометрия преобразований Мёбиуса: эллиптические, параболические и гиперболические действия SL(2,R) , страницы 2, 161, Imperial College Press ISBN  978-1-84816-858-9
2. Джеймс Кокл (1848) О новом мнимом в алгебре, Philosophical Magazine 33:438
3. Абстрактная алгебра/2x2 вещественные матрицы в Wikibooks
4. Джеймс Кокл (1849) О новом воображаемом в алгебре 34:37–47, London-Edinburgh-Dublin Philosophical Magazine (3) 33 :435–9, ссылка из Библиотеки наследия биоразнообразия .
5. Франческо Антонуччо (1994) Полукомплексный анализ и математическая физика
6. Ф. Катони, Д. Боккалетти, Р. Канната, В. Катони, Э. Никелатти, П. Зампетти. (2008) Математика пространства-времени Минковского , Birkhäuser Verlag , Базель. Глава 4: Тригонометрия в плоскости Минковского. ISBN 978-3-7643-8613-9 . 
7. Франческо Катони; Дино Боккалетти; Роберто Канната; Винченцо Катони; Паоло Зампетти (2011). «Глава 2: Гиперболические числа». Геометрия пространства-времени Минковского . Springer Science & Business Media. ISBN 978-3-642-17977-8.
8. Фьелстад, Пол (1986), «Расширение специальной теории относительности с помощью перплексных чисел», American Journal of Physics , 54 (5): 416–422, Bibcode : 1986AmJPh..54..416F, doi : 10.1119/1.14605
9. Луис Кауфман (1985) «Преобразования в специальной теории относительности», Международный журнал теоретической физики 24:223–36.
10. Собчик, Г. (1995) Hyperbolic Number Plane, также опубликовано в College Mathematics Journal 26:268–80.
11. Роберт Б. Браун (1967) Об обобщенных алгебрах Кэли-Диксона, Pacific Journal of Mathematics 20(3):415–22, ссылка из Project Euclid .
12. NH McCoy (1942) Обзор книги «Квадратичные формы, допускающие композицию» А.А. Альберта, Mathematical Reviews #0006140
13. Виньо, Дж. (1935) «Sobre el numero complejo hiperbolico y su relacion con la geometria de Borel», Contribucion al Estudio de las Ciencias Fisicas y Matematicas , Национальный университет де ла Плата, Республика Аргентина
14. Аллен, Э. Ф. (1941) «О треугольнике, вписанном в прямоугольную гиперболу», American Mathematical Monthly 48(10): 675–681
15. M. Warmus (1956) «Исчисление приближений» Архивировано 09.03.2012 в Wayback Machine , Bulletin de l'Académie polonaise des sciences , том 4, № 5, стр. 253–257, MR 0081372
16. Кри, Джордж К. (1949). Теория чисел системы гиперболических комплексных чисел (диссертация на степень магистра). Университет Макгилла.
17. Смит, Норман Э. (1949). Введение в теорию гиперболических чисел (диссертация магистра). Университет Макгилла.
18. Миллер, Уильям; Бёнинг, Рошель (1968). «Гауссовы, параболические и гиперболические числа». Учитель математики . 61 (4): 377–382. doi :10.5951/MT.61.4.0377. JSTOR  27957849.
19. Розенфельд, Б. (1997) Геометрия групп Ли , стр. 30, Kluwer Academic Publishers ISBN 0-7923-4390-5 

Дальнейшее чтение

• Бенчивенга, Ульдрико (1946) «Sulla rappresentazione geometry delle algebre doppie dotate di modulo», Atti della Reale Accademia delle Scienze e Belle-Lettere di Napoli , Ser (3) v.2 No7. МР 0021123.
• Вальтер Бенц (1973) Vorlesungen uber Geometrie der Algebren , Springer
• Н. А. Борота, Э. Флорес и Т. Дж. Ослер (2000) «Пространственно-временные числа — легкий путь», Математика и компьютерное образование 34: 159–168.
• Н. А. Борота и Т. Дж. Ослер (2002) «Функции пространственно-временной переменной», Математика и компьютерное образование 36: 231–239.
• К. Кармоди, (1988) «Круговые и гиперболические кватернионы, октонионы и седенионы», Appl. Math. Comput. 28:47–72.
• К. Кармоди, (1997) «Круговые и гиперболические кватернионы, октонионы и седенионы – дальнейшие результаты», Appl. Math. Comput. 84:27–48.
• Уильям Кингдон Клиффорд (1882) Математические труды , редактор А. В. Такера, стр. 392, «Дополнительные заметки о бикватернионах»
• V.Cruceanu, P. Fortuny & PM Gadea (1996) Обзор паракомплексной геометрии, Rocky Mountain Journal of Mathematics 26(1): 83–115, ссылка из Project Euclid .
• Де Бур, Р. (1987) «Также известный как список для озадачивающих чисел», Американский журнал физики 55(4):296.
• Энтони А. Харкин и Джозеф Б. Харкин (2004) Геометрия обобщенных комплексных чисел, Mathematics Magazine 77(2):118–29.
• Ф. Риз Харви. Спиноры и калибровки. Academic Press, Сан-Диего. 1990. ISBN 0-12-329650-1 . Содержит описание нормированных алгебр в неопределенной сигнатуре, включая числа Лоренца. 
• Хейзвинкль, М. (1994) «Двойные и дуальные числа», Энциклопедия математики , Советская/AMS/Kluwer, Дордрект.
• Кевин Маккриммон (2004) Вкус йордановой алгебры , стр. 66, 157, Universitext, Springer ISBN 0-387-95447-3 MR 2014924 
• C. Musès, «Прикладные гиперчисла: вычислительные концепции», Appl. Math. Comput. 3 (1977) 211–226.
• C. Musès, «Гиперчисла II — Дальнейшие концепции и вычислительные приложения», Appl. Math. Comput. 4 (1978) 45–66.
• Олариу, Сильвиу (2002) Комплексные числа в N измерениях , Глава 1: Гиперболические комплексные числа в двух измерениях, страницы 1–16, North-Holland Mathematics Studies #190, Elsevier ISBN 0-444-51123-7 . 
• Пудиак, Роберт Д. и Кевин Дж. Леклер (2009) «Основные теоремы алгебры для перплексий», The College Mathematics Journal 40(5):322–35.
• Исаак Яглом (1968) Комплексные числа в геометрии , перевод Э. Примроуза с русского оригинала 1963 г., Academic Press , стр. 18–20.
• J. Rooney (2014). "Обобщенные комплексные числа в механике". В Marco Ceccarelli и Victor A. Glazunov (ред.). Advances on Theory and Practice of Robots and Manipulators: Proceedings of Romansy 2014 XX CISM-IFToMM Symposium on Theory and Practice of Robots and Manipulators . Mechanisms and Machine Science. Vol. 22. Springer. pp. 55–62. doi :10.1007/978-3-319-07058-2_7. ISBN 978-3-319-07058-2.