Резонанс

Тенденция к колебаниям на определенных частотах

Увеличение амплитуды по мере уменьшения затухания и приближения частоты к резонансной частоте управляемого затухающего простого гармонического осциллятора . ^{[1] [2]}

В физике резонанс относится к широкому классу явлений, которые возникают в результате согласования временных или пространственных периодов колебательных объектов. Для колебательной динамической системы, приводимой в движение изменяющейся во времени внешней силой , резонанс возникает, когда частота внешней силы совпадает с собственной частотой системы. ^[3] Резонанс может возникать в различных системах, таких как механические, электрические или акустические системы, и он желателен в определенных приложениях, таких как музыкальные инструменты или радиоприемники. Резонанс также может быть нежелательным, приводя к чрезмерным вибрациям или даже к структурному разрушению в некоторых случаях.

Все системы, включая молекулярные системы и частицы, имеют тенденцию вибрировать на собственной частоте, зависящей от их структуры; эта частота известна как резонансная частота или резонансная частота . Когда колебательная сила, внешняя вибрация, применяется на резонансной частоте динамической системы, объекта или частицы, внешняя вибрация заставит систему колебаться с более высокой амплитудой (с большей силой), чем когда та же сила применяется на других, нерезонансных частотах. ^[4]

Резонансные частоты системы можно определить, когда реакция на внешнюю вибрацию создает амплитуду, которая является относительно максимальной внутри системы. ^[4] Малые периодические силы, которые находятся вблизи резонансной частоты системы, способны создавать колебания большой амплитуды в системе из-за накопления колебательной энергии .

Резонансные явления происходят со всеми типами колебаний или волн : существует механический резонанс , орбитальный резонанс , акустический резонанс , электромагнитный резонанс, ядерный магнитный резонанс (ЯМР), электронный спиновый резонанс (ЭПР) и резонанс квантовых волновых функций . Резонансные системы могут использоваться для генерации колебаний определенной частоты (например, музыкальные инструменты ) или выделения определенных частот из сложной вибрации, содержащей много частот (например, фильтры).

Термин резонанс (от лат. resonantia — «эхо», от resonare — «звучать») возник в области акустики, в частности, в области симпатического резонанса, наблюдаемого в музыкальных инструментах, например, когда одна струна начинает вибрировать и издавать звук после удара по другой.

Обзор

Резонанс возникает, когда система способна хранить и легко передавать энергию между двумя или более различными режимами хранения (например, кинетическая энергия и потенциальная энергия в случае простого маятника). Однако существуют некоторые потери от цикла к циклу, называемые затуханием . Когда затухание мало, резонансная частота приблизительно равна собственной частоте системы, которая является частотой невынужденных колебаний. Некоторые системы имеют несколько отдельных резонансных частот.

Примеры

Толкание человека на качелях — типичный пример резонанса. Нагруженные качели, маятник , имеют собственную частоту колебаний, свою резонансную частоту, и сопротивляются толчкам с более высокой или более низкой скоростью.

Знакомый пример — качели на детской площадке , которые действуют как маятник . Толкание человека на качелях в такт естественному интервалу качания (его резонансной частоте) заставляет качание подниматься все выше и выше (максимальная амплитуда), в то время как попытки толкать качели в более быстром или медленном темпе приводят к меньшим дугам. ^{[5] : стр. 2–24} Это происходит потому, что энергия, поглощаемая качелями, максимизируется, когда толчки соответствуют естественным колебаниям качелей.

Резонанс широко распространен в природе и используется во многих устройствах. Это механизм, с помощью которого генерируются практически все синусоидальные волны и вибрации. Например, когда твердые объекты, такие как металл , стекло или дерево , подвергаются удару, в объекте возникают кратковременные резонансные вибрации. ^{[5] : стр. 2–24} Свет и другое коротковолновое электромагнитное излучение производятся резонансом в атомном масштабе , например, электроны в атомах. Другие примеры резонанса включают:

• Механизмы измерения времени современных часов, например, балансовое колесо в механических часах и кварцевый кристалл в кварцевых часах
• Приливной резонанс залива Фанди
• Акустические резонансы музыкальных инструментов и голосового тракта человека
• Разбивание хрустального бокала под воздействием музыкального тона определенной высоты (его резонансной частоты)
• Идиофоны трения , например, приведение в колебательное движение стеклянного предмета (стакана, бутылки, вазы) путем трения его обода кончиком пальца.
• Электрический резонанс настроенных контуров в радиоприемниках и телевизорах , позволяющий избирательно принимать радиочастоты
• Создание когерентного света путем оптического резонанса в лазерном резонаторе
• Орбитальный резонанс , как показывают примеры некоторых лун гигантских планет Солнечной системы и резонансных групп, таких как плутино.
• Материальные резонансы в атомном масштабе являются основой нескольких спектроскопических методов, используемых в физике конденсированных сред.
  • Электронный спиновый резонанс
  • эффект Мёссбауэра
  • Ядерный магнитный резонанс

Линейные системы

Резонанс проявляется во многих линейных и нелинейных системах как колебания вокруг точки равновесия. Когда система приводится в действие синусоидальным внешним входом, измеренный выход системы может колебаться в ответ. Отношение амплитуды установившихся колебаний выхода к колебаниям входа называется усилением, и усиление может быть функцией частоты синусоидального внешнего входа. Пики усиления на определенных частотах соответствуют резонансам, где амплитуда измеренных колебаний выхода непропорционально велика.

Поскольку многие линейные и нелинейные системы, которые колеблются, моделируются как гармонические осцилляторы вблизи их равновесия, показано выведение резонансной частоты для управляемого, затухающего гармонического осциллятора. Схема RLC используется для иллюстрации связей между резонансом и передаточной функцией системы, частотной характеристикой, полюсами и нулями. Основываясь на примере схемы RLC, эти связи для линейных систем более высокого порядка с несколькими входами и выходами обобщаются.

Управляемый, затухающий гармонический осциллятор

Рассмотрим затухающую массу на пружине, приводимую в движение синусоидальной, внешней силой. Второй закон Ньютона принимает вид

где m — масса, x — смещение массы от точки равновесия, F ₀ — амплитуда движения, ω — угловая частота движения, k — жесткость пружины, c — коэффициент вязкого затухания. Это можно переписать в виде

где

• ${\textstyle \omega _{0}={\sqrt {k/m}}}$называется незатухающей угловой частотой осциллятора или собственной частотой ,
• ${\displaystyle \zeta ={\frac {c}{2{\sqrt {mk}}}}}$называется коэффициентом затухания .

Во многих источниках ω ₀ также называют резонансной частотой . Однако, как показано ниже, при анализе колебаний смещения x ( t ) резонансная частота близка к ω ₀ , но не совпадает с ней . В общем случае резонансная частота близка к собственной частоте, но не обязательно совпадает с ней. ^[6] Пример схемы RLC в следующем разделе дает примеры различных резонансных частот для одной и той же системы.

Общее решение уравнения ( 2 ) представляет собой сумму переходного решения, зависящего от начальных условий, и стационарного решения, которое не зависит от начальных условий и зависит только от амплитуды возбуждения F ₀ , частоты возбуждения ω , незатухающей угловой частоты ω ₀ и коэффициента затухания ζ . Переходное решение затухает за относительно короткий промежуток времени, поэтому для изучения резонанса достаточно рассмотреть стационарное решение.

Можно записать стационарное решение для x ( t ) как функцию, пропорциональную движущей силе с индуцированным изменением фазы φ ,

где ${\displaystyle \varphi =\arctan \left({\frac {2\omega \omega _{0}\zeta }{\omega ^{2}-\omega _{0}^{2}}}\right)+n\pi .}$

Значение фазы обычно принимается равным значению между −180° и 0, поэтому оно представляет собой фазовую задержку как для положительных, так и для отрицательных значений аргумента arctan.

Установившееся изменение амплитуды с относительной частотой и затуханием возбуждаемого простого гармонического осциллятора ${\displaystyle \omega /\omega _{0}}$ ${\displaystyle \zeta }$

Резонанс возникает, когда при определенных частотах возбуждения установившаяся амплитуда x ( t ) велика по сравнению с ее амплитудой при других частотах возбуждения. Для массы на пружине резонанс физически соответствует колебаниям массы, имеющим большие смещения от положения равновесия пружины при определенных частотах возбуждения. Рассматривая амплитуду x ( t ) как функцию частоты возбуждения ω , амплитуда максимальна при частоте возбуждения $${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.}$$

ω _r — резонансная частота для этой системы. Опять же, резонансная частота не равна незатухающей угловой частоте ω ₀ осциллятора. Они пропорциональны, и если коэффициент затухания стремится к нулю, они одинаковы, но для ненулевого затухания они не являются одинаковой частотой. Как показано на рисунке, резонанс может также возникать на других частотах вблизи резонансной частоты, включая ω ₀ , но максимальный отклик достигается на резонансной частоте.

Кроме того, ω _r является действительным и ненулевым только если , поэтому эта система может резонировать только тогда, когда гармонический осциллятор значительно недодемпфирован. Для систем с очень малым коэффициентом затухания и частотой возбуждения вблизи резонансной частоты установившиеся колебания могут стать очень большими. ${\textstyle \zeta <1/{\sqrt {2}}}$

Маятник

Для других управляемых, затухающих гармонических осцилляторов, уравнения движения которых не выглядят точно так же, как масса на примере пружины, резонансная частота остается, но определения ω ₀ и ζ изменяются в зависимости от физики системы. Для маятника длиной ℓ и малым углом смещения θ уравнение ( 1 ) становится $${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}},}$$ $${\displaystyle m\ell {\frac {\mathrm {d} ^{2}\theta }{\mathrm {d} t^{2}}}=F_{0}\sin(\omega t)-mg\theta -c\ell {\frac {\mathrm {d} \theta }{\mathrm {d} t}}}$$

и поэтому

• ${\displaystyle \omega _{0}={\sqrt {\frac {g}{\ell }}},}$
• ${\displaystyle \zeta ={\frac {c}{2m}}{\sqrt {\frac {\ell }{g}}}.}$

Последовательные цепи RLC

Последовательная цепь RLC

Рассмотрим цепь, состоящую из резистора с сопротивлением R , катушки индуктивности L и конденсатора емкости C , соединенных последовательно с током i ( t ) и управляемых источником напряжения с напряжением v _in ( t ). Падение напряжения в цепи равно

Вместо анализа возможного решения этого уравнения, как в примере с массой на пружине выше, в этом разделе будет проанализирован частотный отклик этой схемы. Принимая преобразование Лапласа уравнения ( 4 ), где I ( s ) и V _in ( s ) являются преобразованиями Лапласа тока и входного напряжения соответственно, а s является комплексным параметром частоты в области Лапласа. Переставляя члены, $${\displaystyle sLI(s)+RI(s)+{\frac {1}{sC}}I(s)=V_{\text{in}}(s),}$$ $${\displaystyle I(s)={\frac {s}{s^{2}L+Rs+{\frac {1}{C}}}}V_{\text{in}}(s).}$$

Напряжение на конденсаторе

Последовательная цепь RLC представляет несколько вариантов измерения выходного напряжения. Предположим, что интересующее нас выходное напряжение — это падение напряжения на конденсаторе. Как показано выше, в области Лапласа это напряжение равно или $${\displaystyle V_{\text{out}}(s)={\frac {1}{sC}}I(s)}$$ $${\displaystyle V_{\text{out}}={\frac {1}{LC(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}})}}V_{\text{in}}(s).}$$

Определим для этой схемы собственную частоту и коэффициент затухания, $${\displaystyle \omega _{0}={\frac {1}{\sqrt {LC}}},}$$ $${\displaystyle \zeta ={\frac {R}{2}}{\sqrt {\frac {C}{L}}}.}$$

Отношение выходного напряжения к входному напряжению становится $${\displaystyle H(s)\triangleq {\frac {V_{\text{out}}(s)}{V_{\text{in}}(s)}}={\frac {\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}}$$

H ( s ) — передаточная функция между входным напряжением и выходным напряжением. Эта передаточная функция имеет два полюса — корни полинома в знаменателе передаточной функции — при

и отсутствие нулей-корней полинома в числителе передаточной функции. Более того, при ζ ≤ 1 величина этих полюсов равна собственной частоте ω ₀ , а при ζ < 1/ ${\displaystyle {\sqrt {2}}}$ , нашем условии резонанса в примере с гармоническим осциллятором, полюса ближе к мнимой оси, чем к действительной.

Оценивая H ( s ) вдоль мнимой оси s = iω , передаточная функция описывает частотную характеристику этой схемы. Эквивалентно, частотную характеристику можно проанализировать, взяв преобразование Фурье уравнения ( 4 ) вместо преобразования Лапласа. Передаточная функция, которая также является комплексной, может быть записана как усиление и фаза, $${\displaystyle H(i\omega )=G(\omega )e^{i\Phi (\omega )}.}$$

График амплитуды Боде для напряжения на элементах последовательной цепи RLC. Собственная частота ω ₀ = 1 рад/с , коэффициент затухания ζ = 0,4 . Напряжение конденсатора достигает пика ниже собственной частоты цепи, напряжение индуктора достигает пика выше собственной частоты, а напряжение резистора достигает пика на собственной частоте с пиковым усилением, равным единице. Усиление напряжения на конденсаторе и индукторе, соединенных последовательно, показывает антирезонанс, при этом усиление стремится к нулю на собственной частоте.

Синусоидальное входное напряжение на частоте ω приводит к выходному напряжению на той же частоте, которая масштабируется G ( ω ) и имеет сдвиг фазы Φ ( ω ). Коэффициент усиления и фазу можно отобразить в зависимости от частоты на графике Боде . Для напряжения конденсатора RLC-цепи коэффициент усиления передаточной функции H ( iω ) равен

Обратите внимание на сходство между усилением здесь и амплитудой в уравнении ( 3 ). Опять же, усиление максимизируется на резонансной частоте $${\displaystyle \omega _{r}=\omega _{0}{\sqrt {1-2\zeta ^{2}}}.}$$

Здесь резонанс физически соответствует наличию относительно большой амплитуды установившихся колебаний напряжения на конденсаторе по сравнению с его амплитудой на других частотах возбуждения.

Напряжение на индукторе

Резонансная частота не всегда должна иметь форму, указанную в примерах выше. Для RLC-цепи предположим, что выходное напряжение, представляющее интерес, — это напряжение на индуктивности. Как показано выше, в области Лапласа напряжение на индуктивности равно $${\displaystyle V_{\text{out}}(s)=sLI(s),}$$ $${\displaystyle V_{\text{out}}(s)={\frac {s^{2}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{\text{in}}(s),}$$ $${\displaystyle V_{\text{out}}(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}V_{\text{in}}(s),}$$

используя те же определения для ω ₀ и ζ , что и в предыдущем примере. Передаточная функция между V _in ( s ) и этим новым V _out ( s ) через индуктор равна $${\displaystyle H(s)={\frac {s^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$$

Эта передаточная функция имеет те же полюса, что и передаточная функция в предыдущем примере, но также имеет два нуля в числителе при s = 0. Оценивая H ( s ) вдоль мнимой оси, ее коэффициент усиления становится $${\displaystyle G(\omega )={\frac {\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$$

По сравнению с усилением в уравнении ( 6 ), использующим напряжение конденсатора в качестве выходного сигнала, это усиление имеет коэффициент ω ² в числителе и, следовательно, будет иметь другую резонансную частоту, которая максимизирует усиление. Эта частота равна $${\displaystyle \omega _{r}={\frac {\omega _{0}}{\sqrt {1-2\zeta ^{2}}}},}$$

Итак, для той же схемы RLC, но с напряжением на индукторе в качестве выходного сигнала, резонансная частота теперь больше собственной частоты, хотя она все еще стремится к собственной частоте, поскольку коэффициент затухания стремится к нулю. То, что одна и та же схема может иметь разные резонансные частоты для разных вариантов выходного сигнала, не является противоречием. Как показано в уравнении ( 4 ), падение напряжения на схеме делится между тремя элементами схемы, и каждый элемент имеет разную динамику. Напряжение конденсатора растет медленно, интегрируя ток с течением времени, и поэтому более чувствительно к более низким частотам, тогда как напряжение индуктора растет, когда ток быстро меняется, и поэтому более чувствительно к более высоким частотам. В то время как схема в целом имеет собственную частоту, на которой она имеет тенденцию колебаться, разная динамика каждого элемента схемы заставляет каждый элемент резонировать на немного другой частоте.

Напряжение на резисторе

Предположим, что выходное напряжение, представляющее интерес, — это напряжение на резисторе. В области Лапласа напряжение на резисторе равно $${\displaystyle V_{\text{out}}(s)=RI(s),}$$ $${\displaystyle V_{\text{out}}(s)={\frac {Rs}{L\left(s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}\right)}}V_{\text{in}}(s),}$$

и используя ту же собственную частоту и коэффициент затухания, что и в примере с конденсатором, передаточная функция имеет вид $${\displaystyle H(s)={\frac {2\zeta \omega _{0}s}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$$

Эта передаточная функция также имеет те же полюса, что и предыдущие примеры цепей RLC, но у нее есть только один ноль в числителе при s = 0. Для этой передаточной функции ее коэффициент усиления равен $${\displaystyle G(\omega )={\frac {2\zeta \omega _{0}\omega }{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$$

Резонансная частота, которая максимизирует этот коэффициент усиления, равна , а коэффициент усиления равен единице на этой частоте, поэтому напряжение на резисторе резонирует на собственной частоте цепи, и на этой частоте амплитуда напряжения на резисторе равна амплитуде входного напряжения. $${\displaystyle \omega _{r}=\omega _{0},}$$

Антирезонанс

Некоторые системы демонстрируют антирезонанс, который можно анализировать так же, как и резонанс. Для антирезонанса амплитуда реакции системы на определенных частотах непропорционально мала , а не непропорционально велика. В примере с RLC-цепью это явление можно наблюдать, анализируя как индуктивность, так и конденсатор вместе.

Предположим, что выходное напряжение, представляющее интерес в цепи RLC, представляет собой напряжение на катушке индуктивности и конденсаторе, соединенных последовательно. Уравнение ( 4 ) показало, что сумма напряжений на трех элементах цепи равняется входному напряжению, поэтому измерение выходного напряжения как суммы напряжений на катушке индуктивности и конденсаторе, объединенных вместе, равно v _in за вычетом падения напряжения на резисторе. Предыдущий пример показал, что на собственной частоте системы амплитуда падения напряжения на резисторе равна амплитуде v _in , и поэтому напряжение на катушке индуктивности и конденсаторе, объединенное вместе, имеет нулевую амплитуду. Мы можем показать это с помощью передаточной функции.

Сумма напряжений индуктора и конденсатора равна $${\displaystyle V_{\text{out}}(s)=(sL+{\frac {1}{sC}})I(s),}$$ $${\displaystyle V_{\text{out}}(s)={\frac {s^{2}+{\frac {1}{LC}}}{s^{2}+{\frac {R}{L}}s+{\frac {1}{LC}}}}V_{\text{in}}(s).}$$

Используя те же собственные частоты и коэффициенты затухания, что и в предыдущих примерах, передаточная функция имеет вид $${\displaystyle H(s)={\frac {s^{2}+\omega _{0}^{2}}{s^{2}+2\zeta \omega _{0}s+\omega _{0}^{2}}}.}$$

Этот перенос имеет те же полюса, что и предыдущие примеры, но имеет нули в

Оценивая передаточную функцию вдоль мнимой оси, ее коэффициент усиления равен $${\displaystyle G(\omega )={\frac {\omega _{0}^{2}-\omega ^{2}}{\sqrt {\left(2\omega \omega _{0}\zeta \right)^{2}+(\omega _{0}^{2}-\omega ^{2})^{2}}}}.}$$

Вместо того, чтобы искать резонанс, т. е. пики усиления, обратите внимание, что усиление стремится к нулю при ω = ω ₀ , что дополняет наш анализ напряжения резистора. Это называется антирезонансом , который имеет противоположный резонансу эффект. Вместо того, чтобы приводить к непропорционально большим выходным сигналам на этой частоте, эта схема с этим выбором выхода вообще не имеет отклика на этой частоте. Отфильтрованная частота точно соответствует нулям передаточной функции, которые были показаны в уравнении ( 7 ) и находились на мнимой оси.

Соотношения между резонансом и частотной характеристикой в ​​примере последовательной цепи RLC

Эти примеры цепей RLC иллюстрируют, как резонанс связан с частотной характеристикой системы. В частности, эти примеры иллюстрируют:

• Как можно найти резонансные частоты, ища пики в коэффициенте усиления передаточной функции между входом и выходом системы, например, на графике амплитуды Боде
• Как резонансная частота для одной системы может быть разной для разных вариантов выхода системы
• Связь между собственной частотой системы, коэффициентом затухания системы и резонансной частотой системы
• Связь между собственной частотой системы и величиной полюсов передаточной функции, указанная в уравнении ( 5 ), а следовательно, и связь между полюсами и резонансной частотой
• Связь между нулями передаточной функции и формой коэффициента усиления как функции частоты, а следовательно, связь между нулями и резонансной частотой, которая максимизирует коэффициент усиления.
• Связь между нулями передаточной функции и антирезонансом

В следующем разделе эти концепции распространяются на резонанс в общей линейной системе.

Обобщение резонанса и антирезонанса для линейных систем

Далее рассмотрим произвольную линейную систему с несколькими входами и выходами. Например, в представлении пространства состояний линейная система третьего порядка , инвариантная во времени, с тремя входами и двумя выходами может быть записана как где u _i ( t ) — входы, x _i (t) — переменные состояния, y _i ( t ) — выходы, а A , B , C и D — матрицы, описывающие динамику между переменными. $${\displaystyle {\begin{bmatrix}{\dot {x}}_{1}\\{\dot {x}}_{2}\\{\dot {x}}_{3}\end{bmatrix}}=A{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+B{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},}$$ $${\displaystyle {\begin{bmatrix}y_{1}(t)\\y_{2}(t)\end{bmatrix}}=C{\begin{bmatrix}x_{1}(t)\\x_{2}(t)\\x_{3}(t)\end{bmatrix}}+D{\begin{bmatrix}u_{1}(t)\\u_{2}(t)\\u_{3}(t)\end{bmatrix}},}$$

Эта система имеет матрицу передаточной функции , элементами которой являются передаточные функции между различными входами и выходами. Например, $${\displaystyle {\begin{bmatrix}Y_{1}(s)\\Y_{2}(s)\end{bmatrix}}={\begin{bmatrix}H_{11}(s)&H_{12}(s)&H_{13}(s)\\H_{21}(s)&H_{22}(s)&H_{23}(s)\end{bmatrix}}{\begin{bmatrix}U_{1}(s)\\U_{2}(s)\\U_{3}(s)\end{bmatrix}}.}$$

Каждый H _ij ( s ) представляет собой скалярную передаточную функцию, связывающую один из входов с одним из выходов. Примеры цепей RLC выше имели одно входное напряжение и показывали четыре возможных выходных напряжения — через конденсатор, через индуктор, через резистор и через конденсатор и индуктор, объединенные последовательно — каждое со своей собственной передаточной функцией. Если бы цепь RLC была настроена на измерение всех четырех выходных напряжений, эта система имела бы матрицу передаточной функции 4×1, связывающую один вход с каждым из четырех выходов.

Оцениваемый вдоль мнимой оси, каждый H _ij ( iω ) может быть записан как усиление и фазовый сдвиг, $${\displaystyle H_{ij}(i\omega )=G_{ij}(\omega )e^{i\Phi _{ij}(\omega )}.}$$

Пики усиления на определенных частотах соответствуют резонансам между входом и выходом этой передаточной функции, при условии, что система стабильна .

Каждую передаточную функцию H _ij ( s ) можно также записать в виде дроби, числитель и знаменатель которой являются полиномами от s . $${\displaystyle H_{ij}(s)={\frac {N_{ij}(s)}{D_{ij}(s)}}.}$$

Комплексные корни числителя называются нулями, а комплексные корни знаменателя называются полюсами. Для устойчивой системы положения этих полюсов и нулей на комплексной плоскости дают некоторое указание на то, может ли система резонировать или антирезонансировать и на каких частотах. В частности, любая устойчивая или минимально устойчивая комплексно сопряженная пара полюсов с мнимыми компонентами может быть записана в терминах собственной частоты и коэффициента затухания, как в уравнении ( 5 ). Собственная частота ω ₀ этого полюса является величиной положения полюса на комплексной плоскости, а коэффициент затухания этого полюса определяет, насколько быстро затухает это колебание. В общем, ^[6] $${\displaystyle s=-\zeta \omega _{0}\pm i\omega _{0}{\sqrt {1-\zeta ^{2}}},}$$

• Комплексно сопряженные пары полюсов вблизи мнимой оси соответствуют пику или резонансу в частотной характеристике вблизи собственной частоты полюса. Если пара полюсов находится на мнимой оси, усиление бесконечно на этой частоте.
• Комплексно-сопряженные пары нулей вблизи мнимой оси соответствуют провалу или антирезонансу в частотной характеристике вблизи частоты нуля, т. е. частоты, равной величине нуля. Если пара нулей находится на мнимой оси, усиление равно нулю на этой частоте.

В примере цепи RLC первое обобщение, связывающее полюса с резонансом, наблюдается в уравнении ( 5 ). Второе обобщение, связывающее нули с антирезонансом, наблюдается в уравнении ( 7 ). В примерах гармонического осциллятора, напряжения конденсатора цепи RLC и напряжения индуктора цепи RLC «полюса вблизи мнимой оси» соответствуют значительно затухающему условию ζ < 1/ . ${\displaystyle {\sqrt {2}}}$

Стоячие волны

Масса на пружине имеет одну собственную частоту , так как имеет одну степень свободы.

Физическая система может иметь столько собственных частот, сколько у нее степеней свободы , и может резонировать вблизи каждой из этих собственных частот. Масса на пружине, которая имеет одну степень свободы, имеет одну собственную частоту. Двойной маятник , который имеет две степени свободы, может иметь две собственные частоты. По мере увеличения числа связанных гармонических осцилляторов время, необходимое для передачи энергии от одного к другому, становится значительным. Системы с очень большим числом степеней свободы можно рассматривать как непрерывные, а не как имеющие дискретные осцилляторы. ^{[ необходима цитата ]}

Энергия передается от одного осциллятора к другому в форме волн. Например, струну гитары или поверхность воды в чаше можно смоделировать как континуум небольших связанных осцилляторов, и волны могут перемещаться по ним. Во многих случаях эти системы имеют потенциал резонировать на определенных частотах, образуя стоячие волны с колебаниями большой амплитуды в фиксированных положениях. Резонанс в форме стоячих волн лежит в основе многих известных явлений, таких как звук, производимый музыкальными инструментами, электромагнитные полости, используемые в лазерах и микроволновых печах, и энергетические уровни атомов. ^{[ необходима цитата ]}

Стоячие волны на струне

Стоячая волна ( черного цвета), образующаяся при встрече и наложении двух волн, движущихся слева и справа.

Когда струна фиксированной длины приводится в движение на определенной частоте, волна распространяется вдоль струны с той же частотой. Волны отражаются от концов струны, и в конечном итоге достигается устойчивое состояние с волнами, распространяющимися в обоих направлениях. Форма волны является суперпозицией волн. ^[7]

На определенных частотах устойчивая форма волны не перемещается вдоль струны. В фиксированных положениях, называемых узлами , струна никогда не смещается . Между узлами струна колеблется, и точно посередине между узлами — в положениях, называемых пучностями — колебания имеют наибольшую амплитуду. ^{[8] [9] [10]}

Стоячие волны в струне – основная мода и первые 5 гармоник .

Для струны длины с закрепленными концами смещение струны перпендикулярно оси в момент времени равно ^[7] ${\displaystyle L}$ ${\displaystyle y(x,t)}$ ${\displaystyle x}$ ${\displaystyle t}$ $${\displaystyle y(x,t)=2y_{\text{max}}\sin(kx)\cos(2\pi ft),}$$

где

• ${\displaystyle y_{\text{max}}}$амплитуда лево- и право-бегущих волн , интерферирующих, образуя стоячую волну,
• ${\displaystyle k}$это волновое число ,
• ${\displaystyle f}$это частота .

Частоты, которые резонируют и образуют стоячие волны, связаны с длиной струны следующим образом ^{[11] [9]} $${\displaystyle f={\frac {nv}{2L}},}$$ $${\displaystyle n=1,2,3,\dots }$$

где - скорость волны, а целое число обозначает различные моды или гармоники . Стоячая волна с n = 1 колеблется на основной частоте и имеет длину волны, которая в два раза больше длины струны. Возможные моды колебаний образуют гармонический ряд . ^[11] ${\displaystyle v}$ ${\displaystyle n}$

Резонанс в сложных сетях

Обобщение на сложные сети связанных гармонических осцилляторов показывает, что такие системы имеют конечное число собственных резонансных частот, связанных с топологической структурой самой сети. В частности, такие частоты возникают в результате, связанном с собственными значениями матрицы Лапласа сети. Пусть будет матрицей смежности, описывающей топологическую структуру сети, и соответствующей матрицей Лапласа , где — диагональная матрица степеней узлов сети. Тогда для сети классических и идентичных гармонических осцилляторов, когда синусоидальная движущая сила приложена к определенному узлу, глобальные резонансные частоты сети определяются как , где — собственные значения Лапласа . ^[12] ${\displaystyle {\bf {A}}}$ ${\displaystyle {\bf {L}}={\bf {K}}-{\bf {A}}}$ ${\displaystyle {\bf {K}}={\rm {diag}}\,\{k_{i}\}}$ ${\displaystyle f(t)=F_{0}\sin \omega t}$ ${\displaystyle \omega _{i}={\sqrt {1+\mu _{i}}}}$ ${\displaystyle \mu _{i}}$ ${\displaystyle {\bf {L}}}$

Типы

Механический

Школьный эксперимент с резонирующей массой

Механический резонанс — это тенденция механической системы поглощать больше энергии, когда частота ее колебаний совпадает с собственной частотой вибрации системы, чем на других частотах. Это может вызвать сильные колебательные движения и даже катастрофические разрушения в неправильно построенных конструкциях, включая мосты, здания, поезда и самолеты. При проектировании объектов инженеры должны гарантировать, что частоты механического резонанса компонентов не совпадают с частотами колебаний двигателей или других колеблющихся частей, явление, известное как резонансная катастрофа .

Избежание резонансных катастроф является основной проблемой в каждом проекте по строительству зданий, башен и мостов . В качестве контрмеры можно установить амортизаторы для поглощения резонансных частот и, таким образом, рассеивания поглощенной энергии. Здание Taipei 101 опирается на 660-тонный маятник (730 коротких тонн) — настроенный инерционный демпфер — для устранения резонанса. Кроме того, конструкция спроектирована так, чтобы резонировать на частоте, которая обычно не возникает. Здания в сейсмических зонах часто строятся с учетом колебательных частот ожидаемого движения грунта . Кроме того, инженеры, проектирующие объекты, имеющие двигатели, должны гарантировать, что механические резонансные частоты компонентов не соответствуют частотам колебаний двигателей или других сильно колеблющихся частей.

Часы отсчитывают время с помощью механического резонанса в балансировочном колесе , маятнике или кварцевом кристалле .

Предполагается, что темп шагов бегунов энергетически выгоден из-за резонанса между упругой энергией, запасенной в нижних конечностях, и массой бегуна. ^[13]

Международная космическая станция

Ракетные двигатели Международной космической станции (МКС) управляются автопилотом . Обычно загруженные параметры для управления системой управления двигателями модуля «Звезда» заставляют ракетные двигатели выводить Международную космическую станцию ​​на более высокую орбиту. Ракетные двигатели установлены на шарнирах , и обычно экипаж не замечает их работу. Однако 14 января 2009 года загруженные параметры заставили автопилот раскачивать ракетные двигатели во все больших и больших колебаниях с частотой 0,5 Гц. Эти колебания были запечатлены на видео и длились 142 секунды. ^[14]

Акустический

Акустический резонанс — это ветвь механического резонанса, которая связана с механическими колебаниями в диапазоне частот человеческого слуха, другими словами, со звуком . Для людей слух обычно ограничен частотами между 20  Гц и 20 000 Гц (20  кГц ), ^[15] Многие объекты и материалы действуют как резонаторы с резонансными частотами в этом диапазоне и при ударе механически вибрируют, толкая окружающий воздух, создавая звуковые волны. Это источник многих ударных звуков, которые мы слышим.

Акустический резонанс является важным фактором для изготовителей инструментов, поскольку большинство акустических инструментов используют резонаторы , такие как струны и корпус скрипки , длина трубки во флейте , а также форма и натяжение мембраны барабана.

Подобно механическому резонансу, акустический резонанс может привести к катастрофическому отказу объекта при резонансе. Классический пример этого — разбивание бокала для вина звуком на точной резонансной частоте бокала, хотя на практике это сложно. ^[16]

Электрические

Анимация, иллюстрирующая электрический резонанс в настроенном контуре , состоящем из конденсатора (C) и катушки индуктивности (L), соединенных вместе. Заряд течет вперед и назад между пластинами конденсатора через катушку индуктивности. Энергия колеблется вперед и назад между электрическим полем конденсатора ( E ) и магнитным полем катушки индуктивности ( B ).

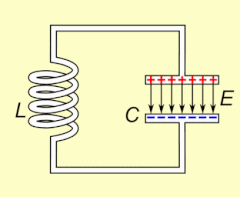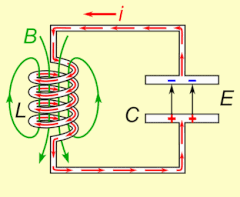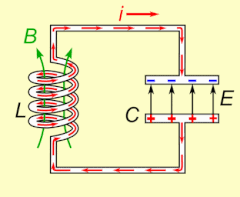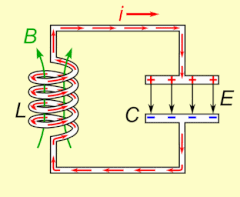
Электрический резонанс происходит в электрической цепи на определенной резонансной частоте , когда импеданс цепи минимален в последовательной цепи или максимален в параллельной цепи (обычно, когда передаточная функция достигает пика по абсолютной величине). Резонанс в цепях используется как для передачи, так и для приема беспроводных коммуникаций, таких как телевидение, сотовые телефоны и радио.

Оптический

Оптическая полость , также называемая оптическим резонатором , представляет собой систему зеркал , которая образует резонатор стоячей волны для световых волн . Оптические полости являются основным компонентом лазеров , окружая среду усиления и обеспечивая обратную связь лазерного света. Они также используются в оптических параметрических генераторах и некоторых интерферометрах . Свет, заключенный в полости, отражается многократно, создавая стоячие волны для определенных резонансных частот. Создаваемые модели стоячих волн называются «модами». Продольные моды отличаются только частотой, в то время как поперечные моды отличаются для разных частот и имеют разные модели интенсивности по всему поперечному сечению пучка. Кольцевые резонаторы и шепчущие галереи являются примерами оптических резонаторов, которые не образуют стоячих волн.

Различные типы резонаторов различаются фокусными расстояниями двух зеркал и расстоянием между ними; плоские зеркала нечасто используются из-за сложности их точного выравнивания. Геометрия (тип резонатора) должна быть выбрана так, чтобы луч оставался стабильным, т. е. размер луча не продолжал расти с каждым отражением. Типы резонаторов также разработаны с учетом других критериев, таких как минимальная перетяжка луча или отсутствие фокусной точки (и, следовательно, интенсивного света в этой точке) внутри полости.

Оптические полости спроектированы так, чтобы иметь очень большой фактор добротности . ^[17] Луч отражается большое количество раз с небольшим затуханием — поэтому ширина частотной линии луча мала по сравнению с частотой лазера.

Дополнительные оптические резонансы — это резонансы направляемых мод и поверхностный плазмонный резонанс , которые приводят к аномальному отражению и высоким затухающим полям при резонансе. В этом случае резонансные моды — это направляемые моды волновода или поверхностные плазмонные моды интерфейса диэлектрик-металл. Эти моды обычно возбуждаются решеткой субволновой длины.

Орбитальный

В небесной механике орбитальный резонанс возникает, когда два вращающихся тела оказывают регулярное, периодическое гравитационное влияние друг на друга, обычно из-за того, что их орбитальные периоды связаны соотношением двух малых целых чисел. Орбитальные резонансы значительно усиливают взаимное гравитационное влияние тел. В большинстве случаев это приводит к нестабильному взаимодействию, при котором тела обмениваются импульсом и смещают орбиты до тех пор, пока резонанс больше не существует. При некоторых обстоятельствах резонансная система может быть стабильной и самокорректирующейся, так что тела остаются в резонансе. Примерами являются резонанс 1:2:4 спутников Юпитера Ганимеда , Европы и Ио и резонанс 2:3 между Плутоном и Нептуном . Нестабильные резонансы с внутренними спутниками Сатурна приводят к появлению зазоров в кольцах Сатурна . Особый случай резонанса 1:1 (между телами с одинаковыми радиусами орбит) заставляет крупные тела Солнечной системы очищать окрестности вокруг своих орбит, выбрасывая почти все остальное вокруг себя; этот эффект используется в текущем определении планеты .

Атомный, корпускулярный и молекулярный

Магнит ЯМР в HWB-NMR, Бирмингем, Великобритания. В его сильном поле 21,2- Тл протонный резонанс находится на частоте 900 МГц.

Ядерный магнитный резонанс (ЯМР) — это название физического резонансного явления, включающего наблюдение определенных квантово-механических магнитных свойств атомного ядра в присутствии приложенного внешнего магнитного поля. Многие научные методы используют явления ЯМР для изучения молекулярной физики , кристаллов и некристаллических материалов с помощью ЯМР-спектроскопии . ЯМР также обычно используется в передовых методах медицинской визуализации, таких как магнитно-резонансная томография (МРТ).

Все ядра, содержащие нечетное число нуклонов, имеют собственный магнитный момент и угловой момент . Ключевой особенностью ЯМР является то, что резонансная частота конкретного вещества прямо пропорциональна силе приложенного магнитного поля. Именно эта особенность используется в методах визуализации; если образец помещен в неоднородное магнитное поле, то резонансные частоты ядер образца зависят от того, в каком месте поля они находятся. Таким образом, частица может быть довольно точно локализована по ее резонансной частоте.

Электронный парамагнитный резонанс , также известный как электронный спиновый резонанс (ЭСР), является спектроскопическим методом, похожим на ЯМР, но использующим неспаренные электроны. Материалы, к которым это может быть применено, гораздо более ограничены, поскольку материал должен иметь неспаренный спин и быть парамагнитным .

Эффект Мёссбауэра — это резонансное и безоткатное испускание и поглощение гамма- фотонов атомами, связанными в твердой форме.

Резонанс в физике элементарных частиц появляется в схожих обстоятельствах с классической физикой на уровне квантовой механики и квантовой теории поля . Резонансы также можно рассматривать как нестабильные частицы, при этом формула в разделе Универсальная резонансная кривая этой статьи применяется, если Γ — скорость распада частицы , а Ω — масса частицы M. В этом случае формула исходит из пропагатора частицы , при этом ее масса заменяется комплексным числом M  +  iΓ . Формула далее связана со скоростью распада частицы оптической теоремой .

Недостатки

Колонна солдат, марширующих ровным шагом по узкому и структурно гибкому мосту, может привести к его опасно большим амплитудным колебаниям . 12 апреля 1831 года подвесной мост Броутон около Солфорда, Англия, рухнул, когда по нему маршировала группа британских солдат. ^[18] С тех пор в британской армии действует постоянный приказ для солдат сбивать шаг при марше по мостам, чтобы избежать резонанса от их обычного марширующего рисунка, влияющего на мост. ^{[19] [20]}

Вибрации двигателя или мотора могут вызывать резонансную вибрацию в его опорных конструкциях, если их собственная частота близка к частоте вибраций двигателя. Типичным примером является дребезжащий звук кузова автобуса, когда двигатель работает на холостом ходу.

Структурный резонанс подвесного моста, вызванный ветрами, может привести к его катастрофическому обрушению. Несколько ранних подвесных мостов в Европе и Соединенных Штатах были разрушены структурным резонансом, вызванным умеренными ветрами. Крушение моста Такома-Нэрроус 7 ноября 1940 года характеризуется в физике как классический пример резонанса. ^[21] Роберт Х. Скэнлан и другие утверждали , что разрушение было вызвано аэроупругим флаттером , сложным взаимодействием между мостом и проходящим через него ветром — примером автоколебаний или своего рода «самоподдерживающейся вибрации», как это называется в нелинейной теории колебаний. ^[22]

Q-фактор

Высокий и низкий Q-фактор

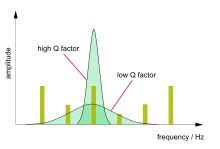
Фактор добротности или добротность — это безразмерный параметр, который описывает, насколько недодемпфирован осциллятор или резонатор, и характеризует полосу пропускания резонатора относительно его центральной частоты. ^{[23] [24]} Высокое значение Q указывает на более низкую скорость потери энергии относительно запасенной энергии, т. е. система слабо демпфирована. Параметр определяется уравнением: . ^[25] $${\displaystyle Q=2\pi {\text{ }}{\frac {\text{ maximum energy stored}}{\text{total energy lost per cycle at resonance}}}}$$

Чем выше Q-фактор, тем больше амплитуда на резонансной частоте и тем меньше полоса пропускания или диапазон частот вокруг резонанса. При электрическом резонансе высокодобротную схему в радиоприемнике сложнее настроить, но она имеет большую избирательность , и поэтому будет лучше отфильтровывать сигналы от других станций. Высокодобротные генераторы более стабильны. ^[25]

Примерами, которые обычно имеют низкий фактор добротности, являются дверные доводчики (Q=0,5). Системы с высоким фактором добротности включают камертоны (Q=1000), атомные часы и лазеры (Q≈10 ¹¹ ). ^[26]

Универсальная резонансная кривая

"Универсальная резонансная кривая", симметричное приближение к нормализованному отклику резонансного контура; значения абсциссы представляют собой отклонение от центральной частоты в единицах центральной частоты, деленной на 2Q; ордината представляет собой относительную амплитуду и фазу в циклах; пунктирные кривые сравнивают диапазон откликов реальных двухполюсных цепей для значения Q , равного 5; для более высоких значений Q наблюдается меньшее отклонение от универсальной кривой. Крестиками отмечены края полосы пропускания 3 дБ (усиление 0,707, сдвиг фазы 45° или 0,125 цикла).

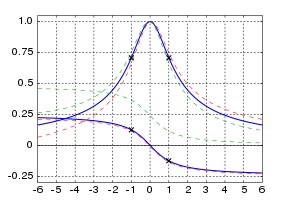
Точная реакция резонанса, особенно для частот, далеких от резонансной частоты, зависит от деталей физической системы и обычно не является строго симметричной относительно резонансной частоты, как показано выше для простого гармонического осциллятора .

Для слабо затухающего линейного осциллятора с резонансной частотой интенсивность колебаний , когда система приводится в движение с частотой возбуждения, обычно аппроксимируется следующей формулой, которая симметрична относительно резонансной частоты: ^[27] ${\displaystyle \omega _{0}}$ ${\displaystyle I}$ ${\displaystyle \omega }$ $${\displaystyle I(\omega )\equiv |\chi |^{2}\propto {\frac {1}{(\omega -\omega _{0})^{2}+\left({\frac {\Gamma }{2}}\right)^{2}}}.}$$

Где восприимчивость связывает амплитуду осциллятора с движущей силой в частотном пространстве: ^[28] ${\displaystyle \chi (\omega )}$ $${\displaystyle x(\omega )=\chi (\omega )F(\omega )}$$

Интенсивность определяется как квадрат амплитуды колебаний. Это функция Лоренца , или распределение Коши , и этот отклик обнаруживается во многих физических ситуациях, связанных с резонансными системами. Γ — это параметр, зависящий от затухания осциллятора, и известен как ширина линии резонанса. Сильно затухающие осцилляторы, как правило, имеют широкую ширину линии и реагируют на более широкий диапазон рабочих частот вокруг резонансной частоты. Ширина линии обратно пропорциональна добротности , которая является мерой остроты резонанса.

В радиотехнике и электронике этот приблизительный симметричный отклик известен как универсальная резонансная кривая , концепция, введенная Фредериком Э. Терманом в 1932 году для упрощения приблизительного анализа радиосхем с диапазоном центральных частот и значений добротности . ^{[29] [30]}

Смотрите также

• Портал электроники
• Физический портал

• Киматика
• Управляемое гармоническое движение
• Сейсмостойкое строительство
• Электрический дипольный спиновый резонанс
• Формант
• Лимбический резонанс
• Нелинейный резонанс
• Нормальный режим
• Положительный отзыв
• резонанс Шумана
• Простое гармоническое движение
• Стохастический резонанс
• Симпатическая струна
• Резонанс (химия)
• резонанс Ферми
• Резонанс (физика элементарных частиц)

Примечания

1. Огата 2005, стр. 617.
2. Гхатак 2005, стр. 6.10.
3. Тейлор, Джон Р. (22 января 2023 г.). Классическая механика . University Science Books (опубликовано 1 марта 2003 г.). стр. 187.
4. Halliday, Resnick & Walker 2005, стр. 324.
5. Hüwel, Lutz (2018). О часах и времени. Морган и Клейпул. ISBN 9781681740966.
6. Хардт 2004.
7. Halliday, Resnick & Walker 2005, стр. 432.
8. Холлидей, Резник и Уокер 2005, стр. 431–432.
9. Serway & Faughn 1992, стр. 472.
10. String Resonance. Digital Sound & Music. 21 мая 2014 г. Идентификатор видео на YouTube: oZ38Y0K8e-Y . Получено 22 августа 2020 г. .
11. Halliday, Resnick & Walker 2005, стр. 434.
12. Бартезаги, Паоло (2023). «Заметки о резонансных и синхронизированных состояниях в сложных сетях». Хаос . 33 (3): 033120. arXiv : 2207.11507 . Bibcode : 2023Chaos..33c3120B. doi : 10.1063/5.0134285. ISSN  1054-1500. PMID  37003810. S2CID  251040250.
13. Снайдер и Фарли 2011.
14. Оберг, Джеймс (4 февраля 2009 г.). «Тряска на космической станции потрясает NASA». NBC News . Архивировано из оригинала 15 августа 2013 г. Получено 1 января 2021 г.
15. Олсон 1967, стр. 248–249.
16. Кафедра физики и астрономии Калифорнийского университета в Лос-Анджелесе. "50. Разбивание стекла со звуком". Руководство по демонстрации лекций . Калифорнийский университет в Лос-Анджелесе . Получено 1 января 2021 г.
17. "Q-фактор, добротность, резонатор, резонатор, генератор, стандарты частоты". Энциклопедия лазерной физики и техники . Получено 1 января 2021 г.
18. Бишоп, RED (1979). Вибрация (Второе издание). Cambridge University Press, Лондон.
19. Смит, Алан (12 апреля 1975 г.). «Мост Броутон рушится!». Manchester Evening News .
20. Браун, Мартин (1993). Дифференциальные уравнения и их приложения: Введение в прикладную математику (4-е изд.). Нью-Йорк: Springer-Verlag. стр. 175. ISBN 0-387-97894-1. Получено 30 мая 2009 г.
21. Сигел, Итан (24 мая 2017 г.). «Наука развенчивает самый большой миф о причинах разрушения мостов». Forbes . Получено 3 января 2021 г. .
22. Биллах и Скэнлан 1991.
23. Харлоу 2004, стр. 2.216.
24. Тули 2006, стр. 77–78.
25. "Частотная характеристика: резонанс, полоса пропускания, добротность" (PDF) . Массачусетский технологический институт . Архивировано (PDF) из оригинала 2022-10-09 . Получено 3 января 2021 .
26. Лаборатория физических измерений (12 мая 2010 г.). «Время и частота от A до Z, от Q до Ra». NIST . Национальный институт стандартов и технологий (NIST) . Получено 1 января 2021 г. .
27. Зигман 1986, стр. 105–108.
28. Аспельмейер, Киппенберг и Марквардт 2014.
29. Терман 1932.
30. Зиберт 1986, стр. 113.

Ссылки

• Aspelmeyer, M ; Kippenberg, Tobias J.; Marquardt, Florian (30 декабря 2014 г.). "Cavity optomechanics" . Reviews of Modern Physics . 86 (4): 1391. arXiv : 1303.0733 . Bibcode :2014RvMP...86.1391A. doi :10.1103/RevModPhys.86.1391. hdl :11858/00-001M-0000-002D-6464-3. S2CID  119252645.
• Billah, K. Yusuf; Scanlan, Robert H (1991). «Резонанс, разрушение моста Tacoma Narrows и учебники по физике для студентов» (PDF) . American Journal of Physics . 59 (2): 118–124. Bibcode :1991AmJPh..59..118B. doi :10.1119/1.16590. Архивировано (PDF) из оригинала 2000-09-19 . Получено 1 января 2021 .
• Гатак, Аджой (2005). Оптика (3-е изд.). Нью-Дели: Тата МакГроу-Хилл. ISBN 978-0-07-058583-6.
• Halliday, David ; Resnick, Robert ; Walker, Jearl (2005). Fundamentals of Physics . Vol. part 2 (7th ed.). John Wiley & Sons Ltd. ISBN 978-0-471-71716-4.
• Хардт, Дэвид (2004). "Понимание полюсов и нулей" (PDF) . 2.14 Анализ и проектирование систем управления с обратной связью . Массачусетский технологический институт . Архивировано (PDF) из оригинала 2022-10-09 . Получено 18 апреля 2020 .
• Harlow, James H., ред. (2004). Electric Power Transformer Engineering. Лондон: CRC Press. ISBN 978-0-8493-1704-0.
• Огата, Кацухико (2005). Системная динамика (4-е изд.). Харлоу: Пирсон. ISBN 978-1-292-02608-4.
• Олсон, Гарри Ф. (1967). Музыка, физика и инженерия . Том 2. Нью-Йорк: Dover Publications. ISBN 978-0-486-21769-7.
• Serway, Raymond A.; Faughn, Jerry S. (1992). College Physics (3-е изд.). Saunders College Publishing. ISBN 0-03-076377-0.
• Siebert, William McC. (1986). Схемы, сигналы и системы. Лондон; Нью-Йорк: MIT Press' McGraw Hill Book Company. ISBN 978-0-262-19229-3.
• Зигман, А.Е. (1986). Лазеры . Университетские научные книги. ISBN 978-0-935702-11-8.
• Снайдер, Кристин Л.; Фарли, Клэр Т. (2011). «Энергетически оптимальная частота шагов при беге: влияние наклона и спада». Журнал экспериментальной биологии . 214 (12): 2089–2095. doi : 10.1242/jeb.053157 . PMID  21613526.
• Терман, Фредерик Эммонс (1932). Радиотехника (1-е изд.). Нью-Йорк: McGraw-Hill Book Company. OCLC  1036819790.
• Тули, Майкл Х. (2006). Электронные схемы: основы и приложения . Оксфорд: Тейлор и Фрэнсис. ISBN 978-0-7506-6923-8.

Внешние ссылки

• Фейнмановские лекции по физике, том I, гл. 23: Резонанс
• Резонанс Архивировано 2017-01-03 в Wayback Machine - глава из онлайн-учебника
• Грин, Брайан , " Резонанс в струнах ". Элегантная Вселенная , NOVA ( PBS )
• Раздел гиперфизики о резонансных концепциях
• Резонанс против резонансного (употребление терминов)
• Резонанс дерева и воздуха в клавесине
• Разбивание стекла со звуком Архивировано 2008-12-02 на Wayback Machine , включая высокоскоростную съемку разбивания стекла