В геометрии нотация Коксетера (также символ Коксетера ) — это система классификации групп симметрии , описывающая углы между фундаментальными отражениями группы Коксетера в скобочной нотации, выражающей структуру диаграммы Коксетера-Дынкина , с модификаторами для указания определенных подгрупп. Нотация названа в честь HSM Coxeter и была более подробно определена Норманом Джонсоном .
Для групп Коксетера , определяемых чистыми отражениями, существует прямое соответствие между скобочной записью и диаграммой Коксетера-Дынкина . Числа в скобочной записи представляют порядки зеркального отражения в ветвях диаграммы Коксетера. Она использует то же упрощение, подавляя 2s между ортогональными зеркалами.
Нотация Коксетера упрощается с помощью экспонент, чтобы представить количество ветвей в строке для линейной диаграммы. Таким образом, группа A n представлена как [3 n −1 ], что подразумевает n узлов, соединенных n−1 ветвями порядка 3. Пример A 2 = [3,3] = [3 2 ] или [3 1,1 ] представляет диаграммы![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]() .
.
Первоначально Коксетер представлял бифуркационные диаграммы с вертикальным расположением чисел, но позже сократил их с помощью записи экспоненты, например, [...,3 p,q ] или [3 p,q,r ], начиная с [3 1,1,1 ] или [3,3 1,1 ] =![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]() как D 4 . Коксетер допускал нули как особые случаи, чтобы соответствовать семейству A n , например A 3 = [3,3,3,3] = [3 4,0,0 ] = [3 4,0 ] = [3 3,1 ] = [3 2,2 ], например
как D 4 . Коксетер допускал нули как особые случаи, чтобы соответствовать семейству A n , например A 3 = [3,3,3,3] = [3 4,0,0 ] = [3 4,0 ] = [3 3,1 ] = [3 2,2 ], например![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]() .
.
Группы Кокстера, образованные циклическими диаграммами, обозначаются круглыми скобками внутри квадратных скобок, например [(p,q,r)] =![]() для группы треугольников (pqr). Если порядки ветвей равны, их можно сгруппировать в виде экспоненты, как длина цикла в скобках, например, [(3,3,3,3)] = [3 [4] ], представляя диаграмму Коксетера
для группы треугольников (pqr). Если порядки ветвей равны, их можно сгруппировать в виде экспоненты, как длина цикла в скобках, например, [(3,3,3,3)] = [3 [4] ], представляя диаграмму Коксетера![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]() .
.![]()
![]()
![]()
![]()
![]() может быть представлено как [3,(3,3,3)] или [3,3 [3] ].
может быть представлено как [3,(3,3,3)] или [3,3 [3] ].
Более сложные диаграммы циклов также могут быть выражены с осторожностью. Паракомпактная группа Коксетера ![]()
![]()
![]()
![]()
![]() может быть представлена нотацией Коксетера [(3,3,(3),3,3)] с вложенными/перекрывающимися скобками, показывающими две смежные петли [(3,3,3)], а также представлена более компактно как [3 [ ]×[ ] ], представляющая ромбическую симметрию диаграммы Коксетера. Паракомпактная полная диаграмма графа
может быть представлена нотацией Коксетера [(3,3,(3),3,3)] с вложенными/перекрывающимися скобками, показывающими две смежные петли [(3,3,3)], а также представлена более компактно как [3 [ ]×[ ] ], представляющая ромбическую симметрию диаграммы Коксетера. Паракомпактная полная диаграмма графа![]() или
или ![]()
![]()
![]() , представлен как [3 [3,3] ] с верхним индексом [3,3] как симметрия его правильной тетраэдрической диаграммы Коксетера.
, представлен как [3 [3,3] ] с верхним индексом [3,3] как симметрия его правильной тетраэдрической диаграммы Коксетера.
Для аффинных и гиперболических групп нижний индекс на единицу меньше числа узлов в каждом случае, поскольку каждая из этих групп была получена путем добавления узла к диаграмме конечной группы.
Диаграмма Коксетера обычно оставляет ветви порядка 2 ненарисованными, но обозначение скобок включает явную 2 для соединения подграфов. Таким образом, диаграмма Коксетера![]()
![]()
![]()
![]()
![]()
![]()
![]() = A 2 × A 2 = 2 A 2 можно представить как [3]×[3] = [3] 2 = [3,2,3]. Иногда явные 2-ветви могут быть включены либо с меткой 2, либо с линией с пробелом:
= A 2 × A 2 = 2 A 2 можно представить как [3]×[3] = [3] 2 = [3,2,3]. Иногда явные 2-ветви могут быть включены либо с меткой 2, либо с линией с пробелом:![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , как идентичное представление, как [3,2,3].
, как идентичное представление, как [3,2,3].
Ранг группы точек Коксетера равен числу узлов, которое также равно размерности. В одномерном пространстве существует одно зеркало, [ ],![]() , тогда как в 2-х измерениях [1],
, тогда как в 2-х измерениях [1],![]()
![]()
![]() или [ ]×[ ] + . 1 — это заполнитель, а не фактический порядок ветвления, а маркер ортогонального неактивного зеркала. Обозначение [ n ,1] представляет группу ранга 3, как [ n ]×[ ] + или
или [ ]×[ ] + . 1 — это заполнитель, а не фактический порядок ветвления, а маркер ортогонального неактивного зеркала. Обозначение [ n ,1] представляет группу ранга 3, как [ n ]×[ ] + или![]()
![]()
![]()
![]()
![]() . Аналогично, [1,1] как [ ]×[ ] + ×[ ] + или
. Аналогично, [1,1] как [ ]×[ ] + ×[ ] + или![]()
![]()
![]()
![]()
![]() порядок 2 и [1,1] + как [ ] + ×[ ] + ×[ ] + или
порядок 2 и [1,1] + как [ ] + ×[ ] + ×[ ] + или![]()
![]()
![]()
![]()
![]() , заказывайте 1!
, заказывайте 1!
Нотация Коксетера представляет вращательную/трансляционную симметрию путем добавления оператора верхнего индекса + за пределами скобок, [X] +, который разрезает порядок группы [X] пополам, таким образом, подгруппу индекса 2. Этот оператор подразумевает, что должно быть применено четное количество операторов, заменяя отражения вращениями (или трансляциями). При применении к группе Коксетера это называется прямой подгруппой , потому что то, что остается, — это только прямые изометрии без отражательной симметрии.
Операторы + также могут применяться внутри скобок, например, [X,Y + ] или [X,(Y,Z) + ], и создают «полупрямые» подгруппы , которые могут включать как отражающие, так и неотражающие генераторы. Полупрямые подгруппы могут применяться только к подгруппам группы Коксетера, которые имеют смежные с ней ветви четного порядка. Элементы в скобках внутри группы Коксетера могут быть снабжены оператором верхнего индекса + , имеющим эффект деления смежных упорядоченных ветвей на половину порядка, поэтому обычно применяется только с четными числами. Например, [4,3 + ] и [4,(3,3) + ] (![]()
![]()
![]()
![]()
![]()
![]()
![]() ).
).
При применении с соседней нечетной ветвью не создается подгруппа индекса 2, а вместо этого создаются перекрывающиеся фундаментальные домены, например, [5,1 + ] = [5/2], которые могут определять дважды обернутые многоугольники, такие как пентаграмма , {5/2}, а [5,3 + ] относится к треугольнику Шварца [5/2,3], плотность 2.
Группы без соседних + элементов можно увидеть в кольцевых узлах диаграммы Коксетера-Дынкина для однородных многогранников и сот, которые связаны с дырочными узлами вокруг + элементов, пустыми кругами с удаленными чередующимися узлами. Так что курносый куб ,![]()
![]()
![]()
![]()
![]() имеет симметрию [4,3] + (
имеет симметрию [4,3] + (![]()
![]()
![]()
![]()
![]() ), и плосконосый тетраэдр ,
), и плосконосый тетраэдр ,![]()
![]()
![]()
![]()
![]() имеет симметрию [4,3 + ] (
имеет симметрию [4,3 + ] (![]()
![]()
![]()
![]()
![]() ), и полукуб , h{4,3} = {3,3} (
), и полукуб , h{4,3} = {3,3} (![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]() ) имеет симметрию [1 + ,4,3] = [3,3] (
) имеет симметрию [1 + ,4,3] = [3,3] (![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]() ).
).
Примечание: Пиритоэдрическая симметрия. ![]()
![]()
![]()
![]()
![]() можно записать как
можно записать как![]()
![]()
![]()
![]()
![]()
![]() , разделив график пробелами для ясности, с генераторами {0,1,2} из группы Коксетера
, разделив график пробелами для ясности, с генераторами {0,1,2} из группы Коксетера![]()
![]()
![]()
![]()
![]() , производя пиритоэдрические генераторы {0,12}, отражение и 3-кратное вращение. А хиральная тетраэдрическая симметрия может быть записана как
, производя пиритоэдрические генераторы {0,12}, отражение и 3-кратное вращение. А хиральная тетраэдрическая симметрия может быть записана как ![]()
![]()
![]()
![]()
![]() или
или ![]()
![]()
![]()
![]()
![]()
![]() , [1 + ,4,3 + ] = [3,3] + , с генераторами {12,0120}.
, [1 + ,4,3 + ] = [3,3] + , с генераторами {12,0120}.
Джонсон расширяет оператор + для работы с заполнителем 1 + узлов, что удаляет зеркала, удваивая размер фундаментального домена и сокращая групповой порядок вдвое. [1] В общем случае эта операция применяется только к отдельным зеркалам, ограниченным ветвями четного порядка. 1 представляет зеркало, поэтому [2p] можно рассматривать как [2p, 1 ], [ 1 ,2p] или [ 1 ,2p, 1 ], как на диаграмме![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]() , с 2 зеркалами, связанными двугранным углом порядка 2p. Эффект удаления зеркала заключается в дублировании соединительных узлов, что можно увидеть на диаграммах Коксетера:
, с 2 зеркалами, связанными двугранным углом порядка 2p. Эффект удаления зеркала заключается в дублировании соединительных узлов, что можно увидеть на диаграммах Коксетера:![]()
![]()
![]()
![]() =
=![]()
![]() , или в скобках: [1 + ,2p, 1 ] = [ 1 ,p, 1 ] = [p].
, или в скобках: [1 + ,2p, 1 ] = [ 1 ,p, 1 ] = [p].
Каждое из этих зеркал можно удалить, так что h[2p] = [1 + ,2p,1] = [1,2p,1 + ] = [p], индекс отражающей подгруппы 2. Это можно показать на диаграмме Кокстера, добавив символ + над узлом:![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]() =
=![]()
![]() .
.
Если удалить оба зеркала, то образуется четвертная подгруппа, при этом порядок ветвления становится точкой инерции половины порядка:
Например, (при p=2): [4,1 + ] = [1 + ,4] = [2] = [ ]×[ ], порядок 4. [1 + ,4,1 + ] = [2] + , порядок 2.
Противоположностью делению пополам является удвоение [2] , которое добавляет зеркало, делит пополам фундаментальную область и удваивает порядок группы.
Операции деления пополам применяются для групп более высокого ранга, например, тетраэдрическая симметрия является половинной группой октаэдрической группы : h[4,3] = [1 + ,4,3] = [3,3], удаляя половину зеркал в 4-ветви. Эффект удаления зеркала заключается в дублировании всех соединительных узлов, что можно увидеть на диаграммах Коксетера:![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]() , h[2p,3] = [1 + ,2p,3] = [(p,3,3)].
, h[2p,3] = [1 + ,2p,3] = [(p,3,3)].
Если узлы индексированы, то полуподгруппы могут быть помечены новыми зеркалами как композиты.![]()
![]()
![]()
![]() , генераторы {0,1} имеют подгруппу
, генераторы {0,1} имеют подгруппу![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]() , генераторы {1,010}, где зеркало 0 удалено и заменено копией зеркала 1, отраженной через зеркало 0. Также дано
, генераторы {1,010}, где зеркало 0 удалено и заменено копией зеркала 1, отраженной через зеркало 0. Также дано![]()
![]()
![]()
![]()
![]() , генераторы {0,1,2}, имеет половину группы
, генераторы {0,1,2}, имеет половину группы![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]() , генераторы {1,2,010}.
, генераторы {1,2,010}.
Удвоение путем добавления зеркала также применяется при обратной операции деления пополам: [[3,3]] = [4,3] или, в более общем смысле, [[(q,q,p)]] = [2p,q].

Джонсон также добавил оператор звездочки или звездочки * для «радикальных» подгрупп, [3], который действует аналогично оператору + , но удаляет вращательную симметрию. Индекс радикальной подгруппы — это порядок удаленного элемента. Например, [4,3*] ≅ [2,2]. Удаленная подгруппа [3] имеет порядок 6, поэтому [2,2] является подгруппой индекса 6 для [4,3].
Радикальные подгруппы представляют собой обратную операцию к расширенной операции симметрии. Например, [4,3*] ≅ [2,2], и в обратном направлении [2,2] может быть расширено как [3[2,2]] ≅ [4,3]. Подгруппы могут быть выражены в виде диаграммы Коксетера:![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]() ≅
≅![]()
![]()
![]() . Удалённый узел (зеркало) приводит к тому, что соседние зеркальные виртуальные зеркала становятся реальными зеркалами.
. Удалённый узел (зеркало) приводит к тому, что соседние зеркальные виртуальные зеркала становятся реальными зеркалами.
Если [4,3] имеет генераторы {0,1,2}, то [4,3 + ], индекс 2, имеет генераторы {0,12}; [1 + ,4,3] ≅ [3,3], индекс 2 имеет генераторы {010,1,2}; в то время как радикальная подгруппа [4,3*] ≅ [2,2], индекс 6, имеет генераторы {01210, 2, (012) 3 }; и, наконец, [1 + ,4,3*], индекс 12 имеет генераторы {0(12) 2 0, (012) 2 01}.

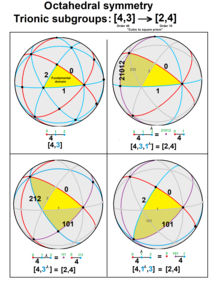




Трионная подгруппа — это подгруппа индекса 3. Джонсон определяет трионную подгруппу с оператором ⅄, индекс 3. Для групп Коксетера ранга 2, [3], трионная подгруппа, [3 ⅄ ] — это [ ], единственное зеркало. А для [3 p ], трионная подгруппа — это [3 p ] ⅄ ≅ [ p ]. Учитывая![]()
![]()
![]()
![]() , с генераторами {0,1}, имеет 3 трионные подгруппы. Их можно дифференцировать, поставив символ ⅄ рядом с удаляемым зеркальным генератором или на ветви для обоих: [3 p ,1 ⅄ ] =
, с генераторами {0,1}, имеет 3 трионные подгруппы. Их можно дифференцировать, поставив символ ⅄ рядом с удаляемым зеркальным генератором или на ветви для обоих: [3 p ,1 ⅄ ] =![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]() ,
, ![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]() , и [3 п ⅄ ] =
, и [3 п ⅄ ] =![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]() с генераторами {0,10101}, {01010,1} или {101,010}.
с генераторами {0,10101}, {01010,1} или {101,010}.
Трионные подгруппы тетраэдрической симметрии: [3,3] ⅄ ≅ [2 + ,4], связывающие симметрию правильного тетраэдра и тетрагонального двуклиноида .
Для групп Коксетера ранга 3, [ p ,3], существует трионная подгруппа [ p ,3 ⅄ ] ≅ [ p /2, p ], или![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() . Например, конечная группа [4,3 ⅄ ] ≅ [2,4], а евклидова группа [6,3 ⅄ ] ≅ [3,6] и гиперболическая группа [8,3 ⅄ ] ≅ [4,8].
. Например, конечная группа [4,3 ⅄ ] ≅ [2,4], а евклидова группа [6,3 ⅄ ] ≅ [3,6] и гиперболическая группа [8,3 ⅄ ] ≅ [4,8].
Нечетная смежная ветвь, p , не понизит порядок группы, но создаст перекрывающиеся фундаментальные домены. Порядок группы останется прежним, в то время как плотность увеличится. Например, икосаэдрическая симметрия [5,3] правильных многогранников икосаэдр становится [5/2,5], симметрией 2 правильных звездчатых многогранников. Она также связывает гиперболические мозаики {p,3} и звездчатые гиперболические мозаики {p/2,p}
Для ранга 4, [ q ,2 p ,3 ⅄ ] = [2 p ,((p,q,q))],![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Например, [3,4,3 ⅄ ] = [4,3,3], или![]()
![]()
![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , генераторы {0,1,2,3} в [3,4,3] с трионной подгруппой [4,3,3] генераторы {0,1,2,32123}. Для гиперболических групп [3,6,3 ⅄ ] = [6,3 [3] ], и [4,4,3 ⅄ ] = [4,4,4].
, генераторы {0,1,2,3} в [3,4,3] с трионной подгруппой [4,3,3] генераторы {0,1,2,32123}. Для гиперболических групп [3,6,3 ⅄ ] = [6,3 [3] ], и [4,4,3 ⅄ ] = [4,4,4].


Джонсон выделил две конкретные трионные подгруппы [4] из [3,3], сначала подгруппу индекса 3 [3,3] ⅄ ≅ [2 + ,4], с [3,3] (![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]() =
=![]()
![]()
![]()
![]() ) генераторы {0,1,2}. Это также можно записать как [(3,3,2 ⅄ )] (
) генераторы {0,1,2}. Это также можно записать как [(3,3,2 ⅄ )] (![]()
![]()
![]()
![]()
![]() ) как напоминание о его генераторах {02,1}. Это уменьшение симметрии является соотношением между правильным тетраэдром и тетрагональным двуклиноидом , представляет собой растяжение тетраэдра перпендикулярно двум противоположным ребрам.
) как напоминание о его генераторах {02,1}. Это уменьшение симметрии является соотношением между правильным тетраэдром и тетрагональным двуклиноидом , представляет собой растяжение тетраэдра перпендикулярно двум противоположным ребрам.
Во-вторых, он определяет связанную подгруппу индекса 6 [3,3] Δ или [(3,3,2 ⅄ )] + (![]()
![]()
![]()
![]()
![]() ), индекс 3 из [3,3] + ≅ [2,2] + , с генераторами {02,1021}, из [3,3] и его генераторами {0,1,2}.
), индекс 3 из [3,3] + ≅ [2,2] + , с генераторами {02,1021}, из [3,3] и его генераторами {0,1,2}.
Эти подгруппы также применяются в более крупных группах Коксетера с подгруппой [3,3] со всеми соседними ветвями четного порядка.

Например, [(3,3) + ,4], [(3,3) ⅄ ,4] и [(3,3) Δ ,4] являются подгруппами [3,3,4], индексы 2, 3 и 6 соответственно. Генераторы [(3,3) ⅄ ,4] ≅ [[4,2,4]] ≅ [8,2 + ,8], порядок 128, являются {02,1,3} из [3,3,4] генераторов {0,1,2,3}. И [(3,3) Δ ,4] ≅ [[4,2 + ,4]], порядок 64, имеет генераторы {02,1021,3}. Также, [3 ⅄ ,4,3 ⅄ ] ≅ [(3,3) ⅄ ,4].
Также связанная группа [3 1,1,1 ] = [3,3,4,1 + ] имеет трионные подгруппы: [3 1,1,1 ] ⅄ = [(3,3) ⅄ ,4,1 + ], порядок 64, и 1=[3 1,1,1 ] Δ = [(3,3) Δ ,4,1 + ] ≅ [[4,2 + ,4]] + , порядок 32.
Центральная инверсия , порядок 2, операционально отличается по размерности. Группа [ ] n = [2 n −1 ] представляет n ортогональных зеркал в n-мерном пространстве или n-плоском подпространстве пространства большей размерности. Зеркала группы [2 n −1 ] пронумерованы . Порядок зеркал не имеет значения в случае инверсии. Матрица центральной инверсии — это , матрица тождественности с отрицательной единицей на диагонали.
Исходя из этого, центральная инверсия имеет генератор как произведение всех ортогональных зеркал. В нотации Коксетера эта группа инверсии выражается добавлением чередования + к каждой ветви 2. Симметрия чередования отмечена на узлах диаграммы Коксетера как открытые узлы.
Диаграмму Коксетера-Дынкина можно разметить с помощью двух явных ветвей, определяющих линейную последовательность зеркал, открытых узлов и общих двойных открытых узлов, чтобы показать цепочку генераторов отражений.
Например, [2 + ,2] и [2,2 + ] являются подгруппами индекса 2 из [2,2],![]()
![]()
![]()
![]()
![]() , и представлены как
, и представлены как![]()
![]()
![]()
![]()
![]() (или
(или![]()
![]()
![]()
![]()
![]()
![]()
![]() ) и
) и![]()
![]()
![]()
![]()
![]() (или
(или![]()
![]()
![]()
![]()
![]()
![]()
![]() ) с генераторами {01,2} и {0,12} соответственно. Их общий индекс подгруппы 4 равен [2 + ,2 + ] и представлен как
) с генераторами {01,2} и {0,12} соответственно. Их общий индекс подгруппы 4 равен [2 + ,2 + ] и представлен как![]()
![]()
![]()
![]()
![]() (или
(или![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ), с двойным открытием
), с двойным открытием![]() отмечая общий узел в двух чередованиях и один генератор роторного отражения {012}.
отмечая общий узел в двух чередованиях и один генератор роторного отражения {012}.
Вращения и вращательные отражения строятся с помощью одного произведения всех отражений призматической группы с одним генератором, [2 p ]×[2 q ]×..., где gcd ( p , q ,...)=1, они изоморфны абстрактной циклической группе Z n порядка n =2 pq .
Четырехмерные двойные вращения, [2 p + ,2 + ,2 q + ] (с gcd ( p , q )=1), которые включают центральную группу, и выражаются Конвеем как ±[C p ×C q ], [5] порядка 2 pq . Из диаграммы Коксетера![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , генераторы {0,1,2,3}, требуется два генератора для [2 p + ,2 + ,2 q + ],
, генераторы {0,1,2,3}, требуется два генератора для [2 p + ,2 + ,2 q + ],![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() как {0123,0132}. Полугруппы, [2 p + ,2 + ,2 q + ] + , или циклический граф, [(2 p + ,2 + ,2 q + ,2 + )],
как {0123,0132}. Полугруппы, [2 p + ,2 + ,2 q + ] + , или циклический граф, [(2 p + ,2 + ,2 q + ,2 + )],![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() Конвей выразил это как [C p ×C q ], порядка pq , с одним генератором, например {0123}.
Конвей выразил это как [C p ×C q ], порядка pq , с одним генератором, например {0123}.
Если есть общий множитель f , двойной поворот можно записать как 1 ⁄ f [2 pf + ,2 + ,2 qf + ] (с gcd ( p , q )=1), генераторы {0123,0132}, порядок 2 pqf . Например, p = q =1, f =2, 1 ⁄ 2 [4 + ,2 + ,4 + ] имеет порядок 4. А 1 ⁄ f [2 pf + ,2 + ,2 qf + ] + , генератор {0123}, имеет порядок pqf . Например, 1 ⁄ 2 [4 + ,2 + ,4 + ] + имеет порядок 2, центральную инверсию .
В общем случае группа n -вращения [2 p 1 + ,2,2 p 2 + ,2,..., p n + ] может потребовать до n генераторов, если gcd( p 1 ,.., p n )>1, как произведение всех зеркал, а затем перестановка последовательных пар. Полугруппа [2 p 1 + ,2,2 p 2 + ,2,..., p n + ] + имеет генераторы в квадрате. n -вращательные отражения аналогичны.

Простые группы с элементами ветвей только нечетного порядка имеют только одну вращательную/трансляционную подгруппу порядка 2, которая также является подгруппой коммутатора , примеры [3,3] + , [3,5] + , [3,3,3] + , [3,3,5] + . Для других групп Кокстера с ветвями четного порядка подгруппа коммутатора имеет индекс 2 c , где c — число несвязных подграфов, когда все ветви четного порядка удалены. [6]
Например, [4,4] имеет три независимых узла на диаграмме Коксетера, если удалить 4 , поэтому ее подгруппа коммутатора имеет индекс 2 3 и может иметь различные представления, все с тремя операторами + : [4 + ,4 + ] + , [1 + ,4,1 + ,4,1 + ], [1 + ,4,4,1 + ] + или [(4 + ,4 + ,2 + )]. Можно использовать общую нотацию с + c в качестве показателя степени группы, например [4,4] +3 .
Группы симметрии диэдра с четными порядками имеют ряд подгрупп. Этот пример показывает два зеркала генератора [4] красным и зеленым цветом и рассматривает все подгруппы с помощью деления пополам, понижения ранга и их прямых подгрупп. Группа [4],![]()
![]()
![]() имеет два генератора зеркал 0 и 1. Каждый генерирует два виртуальных зеркала 101 и 010 путем отражения друг от друга.
имеет два генератора зеркал 0 и 1. Каждый генерирует два виртуальных зеркала 101 и 010 путем отражения друг от друга.
Группа [4,4] имеет 15 малых подгрупп индекса. Эта таблица показывает их все, с желтым фундаментальным доменом для чистых отражательных групп и чередующимися белыми и синими доменами, которые попарно образуют вращательные домены. Голубые, красные и зеленые зеркальные линии соответствуют одинаковым цветным узлам на диаграмме Коксетера. Генераторы подгрупп могут быть выражены как произведения исходных 3 зеркал фундаментального домена, {0,1,2}, соответствующих 3 узлам диаграммы Коксетера,![]()
![]()
![]()
![]()
![]() . Произведение двух пересекающихся линий отражения создает вращение, например {012}, {12} или {02}. Удаление зеркала приводит к появлению двух копий соседних зеркал, напротив удаленного зеркала, например {010} и {212}. Два последовательных вращения сокращают порядок вращения вдвое, например {0101} или {(01) 2 }, {1212} или {(02) 2 }. Произведение всех трех зеркал создает трансрефлексию , например {012} или {120}.
. Произведение двух пересекающихся линий отражения создает вращение, например {012}, {12} или {02}. Удаление зеркала приводит к появлению двух копий соседних зеркал, напротив удаленного зеркала, например {010} и {212}. Два последовательных вращения сокращают порядок вращения вдвое, например {0101} или {(01) 2 }, {1212} или {(02) 2 }. Произведение всех трех зеркал создает трансрефлексию , например {012} или {120}.
Такой же набор из 15 малых подгрупп существует во всех треугольных группах с элементами четного порядка, например, [6,4] в гиперболической плоскости:
Параболическая подгруппа группы Коксетера может быть идентифицирована путем удаления одного или нескольких генераторных зеркал, представленных диаграммой Коксетера. Например, октаэдрическая группа![]()
![]()
![]()
![]()
![]() имеет параболические подгруппы
имеет параболические подгруппы![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]() ,
,![]() ,
,![]() . В скобочной записи [4,3] имеет параболические подгруппы [4],[2],[3] и одно зеркало []. Порядок подгруппы известен, и всегда является целочисленным делителем порядка группы или индексом. Параболические подгруппы также могут быть записаны с узлами x, например
. В скобочной записи [4,3] имеет параболические подгруппы [4],[2],[3] и одно зеркало []. Порядок подгруппы известен, и всегда является целочисленным делителем порядка группы или индексом. Параболические подгруппы также могут быть записаны с узлами x, например![]()
![]()
![]()
![]()
![]() =[4,3] подгруппа путем удаления второго зеркала:
=[4,3] подгруппа путем удаления второго зеркала:![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]() =
=![]()
![]()
![]() = [4,1 × ,3] = [2].
= [4,1 × ,3] = [2].
Подгруппа Петри неприводимой группы Коксетера может быть создана произведением всех генераторов. Это можно увидеть в косом правильном многоугольнике Петри правильного многогранника . Порядок новой группы называется числом Коксетера исходной группы Коксетера. Число Коксетера группы Коксетера равно 2 m / n , где n — ранг, а m — число отражений. Подгруппа Петри может быть записана с верхним индексом π . Например, [3,3] π — подгруппа Петри тетраэдрической группы, циклической группы порядка 4, порожденной роторным отражением . Группа Коксетера ранга 4 будет иметь двойной генератор вращения , например, [4,3,3] π — это порядок 8.
Нотация Коксетера включает в себя обозначение двойных квадратных скобок, [[X]] для выражения автоморфной симметрии в диаграмме Коксетера. Джонсон добавил альтернативное удвоение с помощью угловых скобок <[X]>. Джонсон также добавил префиксный модификатор симметрии [Y[X]], где Y может либо представлять симметрию диаграммы Коксетера [X], либо симметрию фундаментальной области [X].
Например, в 3D эти эквивалентные прямоугольные и ромбические геометрические диаграммы :![]()
![]()
![]()
![]() и
и![]()
![]()
![]()
![]()
![]() , первый удвоен квадратными скобками, [[3 [4] ]] или дважды удвоен как [2[3 [4] ]], с симметрией [2], порядка 4 выше. Чтобы отличить второй, угловые скобки используются для удвоения, <[3 [4] ]> и дважды удвоены как <2[3 [4] ]>, также с другой симметрией [2], порядка 4. Наконец, полная симметрия, где все 4 узла эквивалентны, может быть представлена как [4[3 [4] ]], с симметрией порядка 8, [4] квадрата . Но, рассматривая фундаментальную область тетрагонального двуклиноида, [4] расширенная симметрия квадратного графа может быть обозначена более явно как [(2 + ,4)[3 [4] ]] или [2 + ,4[3 [4] ]].
, первый удвоен квадратными скобками, [[3 [4] ]] или дважды удвоен как [2[3 [4] ]], с симметрией [2], порядка 4 выше. Чтобы отличить второй, угловые скобки используются для удвоения, <[3 [4] ]> и дважды удвоены как <2[3 [4] ]>, также с другой симметрией [2], порядка 4. Наконец, полная симметрия, где все 4 узла эквивалентны, может быть представлена как [4[3 [4] ]], с симметрией порядка 8, [4] квадрата . Но, рассматривая фундаментальную область тетрагонального двуклиноида, [4] расширенная симметрия квадратного графа может быть обозначена более явно как [(2 + ,4)[3 [4] ]] или [2 + ,4[3 [4] ]].
Дальнейшая симметрия существует в циклических и разветвленных диаграммах , , и . имеет симметрию порядка 2 n правильного n -угольника, { n }, и представлена как [ n [3 [ n ] ]]. и представлены как [3[3 1,1,1 ]] = [3,4,3] и [3[3 2,2,2 ]] соответственно, в то время как как [(3,3)[3 1,1,1,1 ]] = [3,3,4,3], с диаграммой, содержащей симметрию порядка 24 правильного тетраэдра , {3,3}. Паракомпактная гиперболическая группа = [3 1,1,1,1,1 ],![]()
![]()
![]()
![]()
![]()
![]() , содержит симметрию 5-клеточного , {3,3,3}, и, таким образом, представлен как [(3,3,3)[3 1,1,1,1,1 ]] = [3,4,3,3,3].
, содержит симметрию 5-клеточного , {3,3,3}, и, таким образом, представлен как [(3,3,3)[3 1,1,1,1,1 ]] = [3,4,3,3,3].
Надстрочный индекс * фактически является обратной операцией, создавая радикальные подгруппы, удаляя связные нечетно-упорядоченные зеркала. [7]
Примеры:
Рассматривая генераторы, двойная симметрия рассматривается как добавление нового оператора, который отображает симметричные позиции в диаграмме Коксетера, делая некоторые исходные генераторы избыточными. Для 3D пространственных групп и 4D точечных групп Коксетер определяет подгруппу индекса два [[X]], [[X] + ], которую он определяет как произведение исходных генераторов [X] на удваивающий генератор. Это похоже на [[X]] + , которая является хиральной подгруппой [[X]]. Так, например, 3D пространственные группы [[4,3,4]] + (I432, 211) и [[4,3,4] + ] (Pm 3 n, 223) являются различными подгруппами [[4,3,4]] (Im 3 m, 229).
В одном измерении двусторонняя группа [ ] представляет собой одну зеркальную симметрию, абстрактную Dih 1 или Z 2 , порядок симметрии 2. Она представлена в виде диаграммы Кокстера–Дынкина с одним узлом,![]() . Группа тождества — это прямая подгруппа [ ] + , Z 1 , порядок симметрии 1. Верхний индекс + просто означает, что альтернативные зеркальные отражения игнорируются, оставляя группу тождества в этом простейшем случае. Коксетер использовал один открытый узел для представления чередования,
. Группа тождества — это прямая подгруппа [ ] + , Z 1 , порядок симметрии 1. Верхний индекс + просто означает, что альтернативные зеркальные отражения игнорируются, оставляя группу тождества в этом простейшем случае. Коксетер использовал один открытый узел для представления чередования,![]() .
.

В двух измерениях прямоугольная группа [2], абстрактная D 2 2 или D 4 , также может быть представлена в виде прямого произведения [ ]×[ ], являющегося произведением двух двусторонних групп, представляет собой два ортогональных зеркала с диаграммой Кокстера,![]()
![]()
![]() , с порядком 4. 2 в [2] получается из линеаризации ортогональных подграфов в диаграмме Кокстера, как
, с порядком 4. 2 в [2] получается из линеаризации ортогональных подграфов в диаграмме Кокстера, как![]()
![]()
![]() с явным порядком ветвления 2. Ромбическая группа , [2] + (
с явным порядком ветвления 2. Ромбическая группа , [2] + (![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]() ), половина прямоугольной группы, симметрия точечной отражательной поверхности , Z 2 , порядок 2.
), половина прямоугольной группы, симметрия точечной отражательной поверхности , Z 2 , порядок 2.
Нотация Коксетера позволяет использовать 1-й заполнитель для групп более низкого ранга, поэтому [1] то же самое, что и [ ], а [1 + ] или [1] + то же самое, что и [ ] + и диаграмма Коксетера![]() .
.
Полная p-угольная группа [p], абстрактная диэдральная группа D 2 p , ( неабелева при p>2), порядка 2 p , порождается двумя зеркалами под углом π / p , представленными диаграммой Коксетера![]()
![]()
![]() . P-угольная подгруппа [p] + , циклическая группа Z p , порядка p , порожденная углом поворота π / p .
. P-угольная подгруппа [p] + , циклическая группа Z p , порядка p , порожденная углом поворота π / p .
В нотации Коксетера двойные скобки используются для представления автоморфного удвоения симметрии путем добавления биссектрисы к фундаментальной области . Например, [[p]] добавляет биссектрису к [p] и изоморфно [2p].
В пределе, переходя к одному измерению, полная апейрогональная группа получается, когда угол стремится к нулю, так что [∞], абстрактно бесконечная диэдральная группа D ∞ , представляет собой два параллельных зеркала и имеет диаграмму Кокстера![]()
![]()
![]() . Апейрогональная группа [∞] + ,
. Апейрогональная группа [∞] + ,![]()
![]()
![]() , абстрактно бесконечная циклическая группа Z ∞ , изоморфная аддитивной группе целых чисел , порождается одним ненулевым переносом.
, абстрактно бесконечная циклическая группа Z ∞ , изоморфная аддитивной группе целых чисел , порождается одним ненулевым переносом.
В гиперболической плоскости существует полная псевдогональная группа [ iπ/λ ] и псевдогональная подгруппа [ iπ/λ ] + ,![]()
![]()
![]() . Эти группы существуют в правильных многоугольниках с бесконечными сторонами, с длиной ребра λ. Все зеркала ортогональны одной прямой.
. Эти группы существуют в правильных многоугольниках с бесконечными сторонами, с длиной ребра λ. Все зеркала ортогональны одной прямой.
Точечные группы в 3-х измерениях можно выразить в скобочной записи, связанной с группами Коксетера ранга 3:
В трех измерениях полная орторомбическая группа или ортопрямоугольная [2,2], абстрактно Z 2 3 , порядок 8, представляет собой три ортогональных зеркала (также представленных на диаграмме Коксетера в виде трех отдельных точек![]()
![]()
![]()
![]()
![]() ). Его также можно представить в виде прямого произведения [ ]×[ ]×[ ], но выражение [2,2] позволяет определять подгруппы:
). Его также можно представить в виде прямого произведения [ ]×[ ]×[ ], но выражение [2,2] позволяет определять подгруппы:
Во-первых, есть «полупрямая» подгруппа, орторомбическая группа , [2,2 + ] (![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]()
![]() ), абстрактно Z 2 × Z 2 , порядка 4. Когда верхний индекс + указан внутри скобок, это означает отражения, полученные только от соседних зеркал (как определено диаграммой Коксетера,
), абстрактно Z 2 × Z 2 , порядка 4. Когда верхний индекс + указан внутри скобок, это означает отражения, полученные только от соседних зеркал (как определено диаграммой Коксетера,![]()
![]()
![]()
![]()
![]() ) чередуются. В общем случае порядки ветвей, соседствующих с узлом + , должны быть четными. В этом случае [2,2 + ] и [2 + ,2] представляют собой две изоморфные подгруппы, которые геометрически различны. Другие подгруппы — это параромбическая группа [2,2] + (
) чередуются. В общем случае порядки ветвей, соседствующих с узлом + , должны быть четными. В этом случае [2,2 + ] и [2 + ,2] представляют собой две изоморфные подгруппы, которые геометрически различны. Другие подгруппы — это параромбическая группа [2,2] + (![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ), также порядок 4, и, наконец, центральная группа [2 + ,2 + ] (
), также порядок 4, и, наконец, центральная группа [2 + ,2 + ] (![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ) порядка 2.
) порядка 2.
Далее следует полная ортогональная p -группа , [2,p] (![]()
![]()
![]()
![]()
![]() ), абстрактно Z 2 ×D 2 p , порядка 4p, представляющего два зеркала под двугранным углом π/ p , и оба ортогональны третьему зеркалу. Это также представлено диаграммой Коксетера как
), абстрактно Z 2 ×D 2 p , порядка 4p, представляющего два зеркала под двугранным углом π/ p , и оба ортогональны третьему зеркалу. Это также представлено диаграммой Коксетера как![]()
![]()
![]()
![]()
![]() .
.
Прямая подгруппа называется пара- p -гональной группой, [2,p] + (![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]()
![]() ), абстрактно D 2 p , порядка 2p, а другая подгруппа — [2,p + ] (
), абстрактно D 2 p , порядка 2p, а другая подгруппа — [2,p + ] (![]()
![]()
![]()
![]()
![]() ) абстрактно Z 2 × Z p , также порядка 2p.
) абстрактно Z 2 × Z p , также порядка 2p.
Полная гиро-p-гональная группа , [2 + ,2 p ] (![]()
![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ), абстрактно D 4 p , порядка 4 p . Гиро- p -гональная группа, [2 + ,2p + ] (
), абстрактно D 4 p , порядка 4 p . Гиро- p -гональная группа, [2 + ,2p + ] (![]()
![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ), абстрактно Z 2 p , порядка 2 p является подгруппой как [2 + ,2 p ], так и [2,2 p + ].
), абстрактно Z 2 p , порядка 2 p является подгруппой как [2 + ,2 p ], так и [2,2 p + ].
Группы полиэдров основаны на симметрии платоновых тел : тетраэдр , октаэдр , куб , икосаэдр и додекаэдр с символами Шлефли {3,3}, {3,4}, {4,3}, {3,5} и {5,3} соответственно. Группы Коксетера для них: [3,3] (![]()
![]()
![]()
![]()
![]() ), [3,4] (
), [3,4] (![]()
![]()
![]()
![]()
![]() ), [3,5] (
), [3,5] (![]()
![]()
![]()
![]()
![]() ) называются полной тетраэдрической симметрией , октаэдрической симметрией и икосаэдрической симметрией с порядками 24, 48 и 120.
) называются полной тетраэдрической симметрией , октаэдрической симметрией и икосаэдрической симметрией с порядками 24, 48 и 120.

Во всех этих симметриях альтернативные отражения могут быть устранены, образуя вращательный тетраэдр [3,3] + (![]()
![]()
![]()
![]()
![]() ), октаэдрический [3,4] + (
), октаэдрический [3,4] + (![]()
![]()
![]()
![]()
![]() ), и икосаэдрический [3,5] + (
), и икосаэдрический [3,5] + (![]()
![]()
![]()
![]()
![]() ) групп порядка 12, 24 и 60. Октаэдрическая группа также имеет уникальную подгруппу индекса 2, называемую группой пиритоэдрической симметрии , [3 + ,4] (
) групп порядка 12, 24 и 60. Октаэдрическая группа также имеет уникальную подгруппу индекса 2, называемую группой пиритоэдрической симметрии , [3 + ,4] (![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]() ), порядка 12, со смесью вращательной и отражательной симметрии. Пиритоэдрическая симметрия также является подгруппой индекса 5 икосаэдрической симметрии:
), порядка 12, со смесью вращательной и отражательной симметрии. Пиритоэдрическая симметрия также является подгруппой индекса 5 икосаэдрической симметрии:![]()
![]()
![]()
![]()
![]() -->
-->![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , с виртуальным зеркалом 1 относительно 0 , {010} и 3-кратным вращением {12}.
, с виртуальным зеркалом 1 относительно 0 , {010} и 3-кратным вращением {12}.
Тетраэдрическая группа, [3,3] (![]()
![]()
![]()
![]()
![]() ), имеет удвоение [[3,3]] (которое может быть представлено цветными узлами
), имеет удвоение [[3,3]] (которое может быть представлено цветными узлами![]()
![]()
![]()
![]()
![]() ), накладывая первое и последнее зеркала друг на друга, и это создает [3,4] (
), накладывая первое и последнее зеркала друг на друга, и это создает [3,4] (![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]() ) группа. Подгруппа [3,4,1 + ] (
) группа. Подгруппа [3,4,1 + ] (![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]() ) то же самое, что [3,3], и [3 + ,4,1 + ] (
) то же самое, что [3,3], и [3 + ,4,1 + ] (![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]() ) то же самое, что и [3,3] + .
) то же самое, что и [3,3] + .
На евклидовой плоскости существуют 3 фундаментальные отражательные группы, образованные 3 зеркалами, представленными диаграммами Кокстера.![]()
![]()
![]()
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() , и
, и![]()
![]()
![]() , и имеют обозначения Коксетера как [4,4], [6,3] и [(3,3,3)]. Скобки последней группы подразумевают цикл диаграммы, а также имеют сокращенное обозначение [3 [3] ].
, и имеют обозначения Коксетера как [4,4], [6,3] и [(3,3,3)]. Скобки последней группы подразумевают цикл диаграммы, а также имеют сокращенное обозначение [3 [3] ].
[[4,4]] как удвоение группы [4,4] создало ту же симметрию, повернутую на π/4 относительно исходного набора зеркал.
Прямые подгруппы вращательной симметрии: [4,4] + , [6,3] + и [(3,3,3)] + . [4 + ,4] и [6,3 + ] являются полупрямыми подгруппами.
В нотации Коксетера ( орбифолдной нотации ) некоторые аффинные подгруппы с низким индексом имеют вид:
Группы четвертого ранга определяют 4-мерные точечные группы :
Группы четвертого ранга также определили трехмерные линейные группы :
Группы ранга четыре определяют 4-мерные дуопризматические группы. В пределе, когда p и q стремятся к бесконечности, они вырождаются в 2 измерения и группы обоев.
Группы четвертого ранга также определили некоторые двумерные группы обоев как предельные случаи четырехмерных групп дуопризм:
Подгруппы [∞,2,∞], (*2222) можно выразить до подгруппы коммутатора индекса 16:

Обозначение Коксетера было расширено до комплексного пространства , C n , где узлы являются унитарными отражениями периода 2 или больше. Узлы помечены индексом, который предполагается равным 2 для обычного действительного отражения, если оно подавлено. Группы комплексных отражений называются группами Шепарда, а не группами Коксетера , и могут использоваться для построения сложных многогранников .
В , группа Шепарда ранга 1![]() , порядка p , представляется как p [ ], [ ] p или ] p [. Он имеет один генератор, представляющий поворот на 2 π / p радиан в комплексной плоскости : .
, порядка p , представляется как p [ ], [ ] p или ] p [. Он имеет один генератор, представляющий поворот на 2 π / p радиан в комплексной плоскости : .
Коксетер записывает комплексную группу ранга 2, p [ q ] r представляет диаграмму Коксетера ![]()
![]()
![]()
![]()
![]() . P и r следует опускать только в том случае, если оба равны 2, что является реальным случаем [ q ]. Порядок группы ранга 2 p [ q ] r равен . [9]
. P и r следует опускать только в том случае, если оба равны 2, что является реальным случаем [ q ]. Порядок группы ранга 2 p [ q ] r равен . [9]
Решения ранга 2, которые генерируют сложные многоугольники: p [4] 2 ( p равно 2,3,4,...), 3 [3] 3 , 3 [6] 2 , 3 [4] 3 , 4 [3 ] 4 , 3 [8] 2 , 4 [6] 2 , 4 [4] 3 , 3 [5] 3 , 5 [3] 5 , 3 [10] 2 , 5 [6] 2 и 5 [4] 3 с диаграммами Коксетера.![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() .
.

Бесконечные группы — это 3 [12] 2 , 4 [8] 2 , 6 [6] 2 , 3 [6] 3 , 6 [4] 3 , 4 [4] 4 , и 6 [3] 6 или![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() ,
,![]()
![]()
![]() .
.
Подгруппы индекса 2 существуют путем удаления действительного отражения: p [2 q ] 2 → p [ q ] p . Также существуют подгруппы индекса r для 4 ветвей: p [4] r → p [ r ] p .
Для бесконечного семейства p [4] 2 для любого p = 2, 3, 4,... существуют две подгруппы: p [4] 2 → [ p ], индекс p , тогда как и p [4] 2 → p [ ]× p [ ], индекс 2.
Группа Коксетера, представленная диаграммой Коксетера ![]()
![]()
![]()
![]()
![]() , дана нотация Коксетера [p,q] для порядков ветвления. Каждый узел в диаграмме Коксетера представляет собой зеркало, по соглашению называемое ρ i (и матрицей R i ). Генераторы этой группы [p,q] являются отражениями: ρ 0 , ρ 1 и ρ 2 . Вращательная подсимметрия задается как произведение отражений: по соглашению σ 0,1 (и матрица S 0,1 ) = ρ 0 ρ 1 представляет собой поворот на угол π/p, а σ 1,2 = ρ 1 ρ 2 представляет собой поворот на угол π/q, а σ 0,2 = ρ 0 ρ 2 представляет собой поворот на угол π/2.
, дана нотация Коксетера [p,q] для порядков ветвления. Каждый узел в диаграмме Коксетера представляет собой зеркало, по соглашению называемое ρ i (и матрицей R i ). Генераторы этой группы [p,q] являются отражениями: ρ 0 , ρ 1 и ρ 2 . Вращательная подсимметрия задается как произведение отражений: по соглашению σ 0,1 (и матрица S 0,1 ) = ρ 0 ρ 1 представляет собой поворот на угол π/p, а σ 1,2 = ρ 1 ρ 2 представляет собой поворот на угол π/q, а σ 0,2 = ρ 0 ρ 2 представляет собой поворот на угол π/2.
[п,д] + ,![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , является подгруппой индекса 2, представленной двумя генераторами вращения, каждый из которых является произведением двух отражений: σ 0,1 , σ 1,2 , и представляющих вращения на углы π/ p и π/ q соответственно.
, является подгруппой индекса 2, представленной двумя генераторами вращения, каждый из которых является произведением двух отражений: σ 0,1 , σ 1,2 , и представляющих вращения на углы π/ p и π/ q соответственно.
С одной четной ветвью, [ p + ,2 q ],![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() или
или![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , является другой подгруппой индекса 2, представленной вращательным генератором σ 0,1 и отражательным ρ 2 .
, является другой подгруппой индекса 2, представленной вращательным генератором σ 0,1 и отражательным ρ 2 .
С четными ветвями, [2 p + ,2 q + ],![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , является подгруппой индекса 4 с двумя генераторами, построенными как произведение всех трех матриц отражения: По соглашению: ψ 0,1,2 и ψ 1,2,0 , которые являются вращательными отражениями , представляющими отражение и вращение или отражение.
, является подгруппой индекса 4 с двумя генераторами, построенными как произведение всех трех матриц отражения: По соглашению: ψ 0,1,2 и ψ 1,2,0 , которые являются вращательными отражениями , представляющими отражение и вращение или отражение.
В случае аффинных групп Кокстера, таких как![]()
![]()
![]()
![]()
![]() , или
, или![]()
![]()
![]() , одно зеркало, обычно последнее, переносится из начала координат. Генератор переноса τ 0,1 (и матрица T 0,1 ) строится как произведение двух (или четного числа) отражений, включая аффинное отражение. Трансрефлексия (отражение плюс перенос) может быть произведением нечетного числа отражений φ 0,1,2 (и матрицы V 0,1,2 ), как подгруппа индекса 4
, одно зеркало, обычно последнее, переносится из начала координат. Генератор переноса τ 0,1 (и матрица T 0,1 ) строится как произведение двух (или четного числа) отражений, включая аффинное отражение. Трансрефлексия (отражение плюс перенос) может быть произведением нечетного числа отражений φ 0,1,2 (и матрицы V 0,1,2 ), как подгруппа индекса 4![]()
![]()
![]()
![]()
![]() : [4 + ,4 + ] =
: [4 + ,4 + ] =![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() .
.
Другой составной генератор, по соглашению как ζ (и матрица Z), представляет собой инверсию , отображающую точку в ее обратную. Для [4,3] и [5,3], ζ = (ρ 0 ρ 1 ρ 2 ) h/2 , где h равно 6 и 10 соответственно, числу Коксетера для каждого семейства. Для 3D группы Коксетера [p,q] (![]()
![]()
![]()
![]()
![]() ), эта подгруппа является поворотным отражением [2 + ,h + ].
), эта подгруппа является поворотным отражением [2 + ,h + ].
Группы Коксетера классифицируются по их рангу, представляющему собой число узлов в их диаграмме Коксетера-Дынкина . Структура групп также приводится с их абстрактными типами групп: В этой статье абстрактные диэдральные группы представлены как Dih n , а циклические группы представлены как Z n , причем Dih 1 = Z 2 .
Например, в 2D группа Коксетера [ p ] (![]()
![]()
![]() ) представлен двумя матрицами отражения R 0 и R 1 , Циклическая симметрия [ p ] + (
) представлен двумя матрицами отражения R 0 и R 1 , Циклическая симметрия [ p ] + (![]()
![]()
![]() ) представлен генератором вращения матрицы S 0,1 .
) представлен генератором вращения матрицы S 0,1 .
Группы Коксетера конечного ранга 3 — это [1, p ], [2, p ], [3,3], [3,4] и [3,5].
Чтобы отразить точку через плоскость (проходящую через начало координат), можно использовать , где — единичная матрица 3×3, а — трехмерный единичный вектор для векторной нормали плоскости. Если норма L2 и равна единице, матрицу преобразования можно выразить как:

Приводимая 3-мерная конечная рефлективная группа является диэдральной симметрией , [ p ,2], порядок 4p ,![]()
![]()
![]()
![]()
![]() . Генераторы отражения — матрицы R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 3 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Тождество. [ p ,2] + (
. Генераторы отражения — матрицы R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 3 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Тождество. [ p ,2] + (![]()
![]()
![]()
![]()
![]() ) генерируется 2 из 3 вращений: S 0,1 , S 1,2 , и S 0,2 . Роторефлексия порядка p генерируется V 0,1,2 , произведением всех 3 отражений.
) генерируется 2 из 3 вращений: S 0,1 , S 1,2 , и S 0,2 . Роторефлексия порядка p генерируется V 0,1,2 , произведением всех 3 отражений.






Простейшая неприводимая 3-мерная конечная рефлективная группа — это тетраэдрическая симметрия , [3,3], порядок 24,![]()
![]()
![]()
![]()
![]() . Генераторы отражения из конструкции D 3 =A 3 представляют собой матрицы R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 3 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Тождество. [3,3] + (
. Генераторы отражения из конструкции D 3 =A 3 представляют собой матрицы R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 3 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Тождество. [3,3] + (![]()
![]()
![]()
![]()
![]() ) генерируется 2 из 3 вращений: S 0,1 , S 1,2 , и S 0,2 . Трионная подгруппа, изоморфная [2 + ,4], порядок 8, генерируется S 0,2 и R 1 . Роторефлексия порядка 4 генерируется V 0,1,2 , произведением всех 3 отражений.
) генерируется 2 из 3 вращений: S 0,1 , S 1,2 , и S 0,2 . Трионная подгруппа, изоморфная [2 + ,4], порядок 8, генерируется S 0,2 и R 1 . Роторефлексия порядка 4 генерируется V 0,1,2 , произведением всех 3 отражений.






Другая неприводимая 3-мерная конечная рефлективная группа — это октаэдрическая симметрия , [4,3], порядок 48,![]()
![]()
![]()
![]()
![]() . Матрицы генераторов отражения: R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 4 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Идентичность. Хиральная октаэдрическая симметрия, [4,3] + , (
. Матрицы генераторов отражения: R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 4 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Идентичность. Хиральная октаэдрическая симметрия, [4,3] + , (![]()
![]()
![]()
![]()
![]() ) генерируется 2 из 3 вращений: S 0,1 , S 1,2 , и S 0,2 . Пиритоэдрическая симметрия [4,3 + ], (
) генерируется 2 из 3 вращений: S 0,1 , S 1,2 , и S 0,2 . Пиритоэдрическая симметрия [4,3 + ], (![]()
![]()
![]()
![]()
![]() ) генерируется отражением R 0 и вращением S 1,2 . Шестикратное роторное отражение генерируется V 0,1,2 , произведением всех трех отражений.
) генерируется отражением R 0 и вращением S 1,2 . Шестикратное роторное отражение генерируется V 0,1,2 , произведением всех трех отражений.






Конечной неприводимой 3-мерной конечной рефлективной группой является икосаэдрическая симметрия , [5,3], порядок 120,![]()
![]()
![]()
![]()
![]() . Матрицы генераторов отражения: R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 5 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Тождество. [5,3] + (
. Матрицы генераторов отражения: R 0 , R 1 , R 2 . R 0 2 =R 1 2 =R 2 2 =(R 0 ×R 1 ) 5 =(R 1 ×R 2 ) 3 =(R 0 ×R 2 ) 2 =Тождество. [5,3] + (![]()
![]()
![]()
![]()
![]() ) генерируется 2 из 3 вращений: S 0,1 , S 1,2 и S 0,2 . 10-кратное роторное отражение генерируется V 0,1,2 , произведением всех 3 отражений.
) генерируется 2 из 3 вращений: S 0,1 , S 1,2 и S 0,2 . 10-кратное роторное отражение генерируется V 0,1,2 , произведением всех 3 отражений.
Существует 4 неприводимые группы Коксетера в 4 измерениях: [3,3,3], [4,3,3], [3 1,1,1 ], [3,4,4], [5,3,3], а также бесконечное семейство дуопризматических групп [ p ,2, q ].
Двупризматическая группа [ p ,2, q ] имеет порядок 4pq .
Дуопризматическая группа может удваиваться до 8 p 2 с двукратным вращением между двумя плоскостями.
Гипертетраэдрическую симметрию [3,3,3], порядок 120, проще всего представить с помощью 4 зеркал в 5 измерениях как подгруппу [4,3,3,3].
Расширенная группа [[3,3,3]], порядок 240, удваивается матрицей вращения T 2-кратного порядка, здесь меняют порядок и знак координат: Имеется 3 генератора {T, R 0 , R 1 }. Поскольку T является самообратным, R 3 =TR 0 T, и R 2 =TR 1 T.
Неприводимая 4-мерная конечная рефлективная группа — это гипероктаэдрическая группа (или гексадекахорическая группа (для 16-клеточной ), B 4 =[4,3,3], порядок 384,![]()
![]()
![]()
![]()
![]()
![]()
![]() . Матрицы генераторов отражения: R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 4 =(R 1 ×R 2 ) 3 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 1 ×R 3 ) 2 =(R 0 ×R 3 ) 2 =Идентичность.
. Матрицы генераторов отражения: R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 4 =(R 1 ×R 2 ) 3 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 1 ×R 3 ) 2 =(R 0 ×R 3 ) 2 =Идентичность.
Хиральная гипероктаэдрическая симметрия, [4,3,3] + , (![]()
![]()
![]()
![]()
![]()
![]()
![]() ) генерируется 3 из 6 вращений: S 0,1 , S 1,2 , S 2,3 , S 0,2 , S 1,3 , и S 0,3 . Гиперпиритоэдрическая симметрия [4,(3,3) + ], (
) генерируется 3 из 6 вращений: S 0,1 , S 1,2 , S 2,3 , S 0,2 , S 1,3 , и S 0,3 . Гиперпиритоэдрическая симметрия [4,(3,3) + ], (![]()
![]()
![]()
![]()
![]()
![]()
![]() ) генерируется отражением R 0 и вращениями S 1,2 и S 2,3 . 8-кратное двойное вращение генерируется W 0,1,2,3 , произведением всех 4 отражений.
) генерируется отражением R 0 и вращениями S 1,2 и S 2,3 . 8-кратное двойное вращение генерируется W 0,1,2,3 , произведением всех 4 отражений.
Половина группы [4,3,3] равна [3,3 1,1 ],![]()
![]()
![]()
![]()
![]()
![]()
![]() , порядок 192. Он разделяет 3 генератора с группой [4,3,3], но имеет две копии соседнего генератора, одна из которых отражена через удаленное зеркало.
, порядок 192. Он разделяет 3 генератора с группой [4,3,3], но имеет две копии соседнего генератора, одна из которых отражена через удаленное зеркало.
Неприводимая 4-мерная конечная рефлективная группа — это икоситетрахорическая группа (для 24-клеточной ), F 4 =[3,4,3], порядок 1152,![]()
![]()
![]()
![]()
![]()
![]()
![]() . Матрицы генераторов отражения: R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 3 = (R 1 × R 2 ) 4 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 1 ×R 3 ) 2 =(R 0 ×R 3 ) 2 =Идентичность.
. Матрицы генераторов отражения: R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 3 = (R 1 × R 2 ) 4 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 1 ×R 3 ) 2 =(R 0 ×R 3 ) 2 =Идентичность.
Хиральная икоситетрахорическая симметрия, [3,4,3] + , (![]()
![]()
![]()
![]()
![]()
![]()
![]() ) генерируется 3 из 6 вращений: S 0,1 , S 1,2 , S 2,3 , S 0,2 , S 1,3 , и S 0,3 . Ионная уменьшенная [3,4,3 + ] группа, (
) генерируется 3 из 6 вращений: S 0,1 , S 1,2 , S 2,3 , S 0,2 , S 1,3 , и S 0,3 . Ионная уменьшенная [3,4,3 + ] группа, (![]()
![]()
![]()
![]()
![]()
![]()
![]() ) генерируется отражением R 0 и вращениями S 1,2 и S 2,3 . 12-кратное двойное вращение генерируется W 0,1,2,3 , произведением всех 4 отражений.
) генерируется отражением R 0 и вращениями S 1,2 и S 2,3 . 12-кратное двойное вращение генерируется W 0,1,2,3 , произведением всех 4 отражений.
Группа [[3,4,3]] расширяет [3,4,3] посредством 2-кратного поворота T, удваивая порядок до 2304.
Гиперикосаэдрическая симметрия, [5,3,3], порядок 14400,![]()
![]()
![]()
![]()
![]()
![]()
![]() . Матрицы генераторов отражения: R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 5 =(R 1 ×R 2 ) 3 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 0 ×R 3 ) 2 =(R 1 ×R 3 ) 2 =Тождество. [5,3,3] + (
. Матрицы генераторов отражения: R 0 , R 1 , R 2 , R 3 . R 0 2 =R 1 2 =R 2 2 =R 3 2 =(R 0 ×R 1 ) 5 =(R 1 ×R 2 ) 3 =(R 2 ×R 3 ) 3 =(R 0 ×R 2 ) 2 =(R 0 ×R 3 ) 2 =(R 1 ×R 3 ) 2 =Тождество. [5,3,3] + (![]()
![]()
![]()
![]()
![]()
![]()
![]() ) генерируется тремя вращениями: S 0,1 = R 0 ×R 1 , S 1,2 = R 1 ×R 2 , S 2,3 = R 2 ×R 3 и т. д.
) генерируется тремя вращениями: S 0,1 = R 0 ×R 1 , S 1,2 = R 1 ×R 2 , S 2,3 = R 2 ×R 3 и т. д.
Группа Коксетера E8 , [3 4,2,1 ],![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , имеет 8 зеркальных узлов, порядок 696729600 (192x10!). E7 и E6, [3 3,2,1 ],
, имеет 8 зеркальных узлов, порядок 696729600 (192x10!). E7 и E6, [3 3,2,1 ],![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() , и [3 2,2,1 ],
, и [3 2,2,1 ],![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() можно построить, игнорируя первое зеркало или первые два зеркала соответственно.
можно построить, игнорируя первое зеркало или первые два зеркала соответственно.
Аффинные матрицы представляются путем добавления дополнительной строки и столбца, причем последняя строка равна нулю, за исключением последней записи 1. Последний столбец представляет собой вектор переноса.
Аффинная группа [∞],![]()
![]()
![]() , может быть задана двумя матрицами отражения, x=0 и x=1.
, может быть задана двумя матрицами отражения, x=0 и x=1.
Аффинная группа [4,4],![]()
![]()
![]()
![]()
![]() , (p4m), можно задать тремя матрицами отражения, отражения относительно оси x (y=0), диагонали (x=y) и аффинного отражения относительно прямой (x=1). [4,4] + (
, (p4m), можно задать тремя матрицами отражения, отражения относительно оси x (y=0), диагонали (x=y) и аффинного отражения относительно прямой (x=1). [4,4] + (![]()
![]()
![]()
![]()
![]() ) (p4) генерируется S 0,1 S 1,2 и S 0,2 . [4 + ,4 + ] (
) (p4) генерируется S 0,1 S 1,2 и S 0,2 . [4 + ,4 + ] (![]()
![]()
![]()
![]()
![]() ) (pgg) генерируется 2-кратным вращением S 0,2 и скользящим отражением (трансрефлексией) V 0,1,2 . [4 + ,4] (
) (pgg) генерируется 2-кратным вращением S 0,2 и скользящим отражением (трансрефлексией) V 0,1,2 . [4 + ,4] (![]()
![]()
![]()
![]()
![]() ) (p4g) генерируется S 0,1 и R 3 . Группа [(4,4,2 + )] (
) (p4g) генерируется S 0,1 и R 3 . Группа [(4,4,2 + )] (![]()
![]()
![]()
![]() ) (смм), генерируется двукратным вращением S 1,3 и отражением R 2 .
) (смм), генерируется двукратным вращением S 1,3 и отражением R 2 .
Аффинная группа [3,6],![]()
![]()
![]()
![]()
![]() , (p6m), можно задать тремя матрицами отражения, отражения относительно оси x (y=0), линии y=(√3/2)x и вертикальной линии x=1.
, (p6m), можно задать тремя матрицами отражения, отражения относительно оси x (y=0), линии y=(√3/2)x и вертикальной линии x=1.
Аффинная группа [3 [3] ] может быть построена как полугруппа![]()
![]()
![]()
![]()
![]() . R 2 заменяется на R' 2 = R 2 ×R 1 ×R 2 , представленное гиперплоскостью: y+(√3/2)x=2. Фундаментальная область представляет собой равносторонний треугольник с длиной ребра 2.
. R 2 заменяется на R' 2 = R 2 ×R 1 ×R 2 , представленное гиперплоскостью: y+(√3/2)x=2. Фундаментальная область представляет собой равносторонний треугольник с длиной ребра 2.
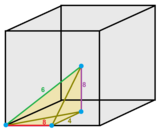
Аффинная группа — это [4,3,4] (![]()
![]()
![]()
![]()
![]()
![]()
![]() ), можно задать четырьмя матрицами отражения. Зеркало R 0 можно поместить на плоскость z=0. Зеркало R 1 можно поместить на плоскость y=z. Зеркало R 2 можно поместить на плоскость x=y. Зеркало R 3 можно поместить на плоскость x=1. [4,3,4] + (
), можно задать четырьмя матрицами отражения. Зеркало R 0 можно поместить на плоскость z=0. Зеркало R 1 можно поместить на плоскость y=z. Зеркало R 2 можно поместить на плоскость x=y. Зеркало R 3 можно поместить на плоскость x=1. [4,3,4] + (![]()
![]()
![]()
![]()
![]()
![]()
![]() ) генерируется S 0,1 , S 1,2 и S 2,3 .
) генерируется S 0,1 , S 1,2 и S 2,3 .
Расширенная группа [[4,3,4]] удваивает порядок группы, добавляя матрицу вращения T 2-кратного размера с фиксированной осью через точки (1,1/2,0) и (1/2,1/2,1/2). Генераторы — {R 0 ,R 1 ,T}. R 2 = T×R 1 ×T и R 3 = T×R 0 ×T.

Группа [4,3 1,1 ] может быть построена из [4,3,4], вычислив [4,3,4,1 + ],![]()
![]()
![]()
![]()
![]()
![]()
![]() , так как R' 3 =R 3 ×R 2 ×R 3 , с новым R' 3 как образом R 2 относительно R 3 .
, так как R' 3 =R 3 ×R 2 ×R 3 , с новым R' 3 как образом R 2 относительно R 3 .
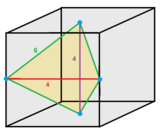
Группа [3 [4] ] может быть построена из [4,3,4], путем удаления первого и последнего зеркал, [1 + ,4,3,4,1 + ],![]()
![]()
![]()
![]()
![]()
![]()
![]() , по R' 1 =R 0 ×R 1 ×R 0 и R' 3 =R 3 ×R 2 ×R 3 .
, по R' 1 =R 0 ×R 1 ×R 0 и R' 3 =R 3 ×R 2 ×R 3 .