нотация Коксетера

Система классификации групп симметрии в геометрии

В геометрии нотация Коксетера (также символ Коксетера ) — это система классификации групп симметрии , описывающая углы между фундаментальными отражениями группы Коксетера в скобочной нотации, выражающей структуру диаграммы Коксетера-Дынкина , с модификаторами для указания определенных подгрупп. Нотация названа в честь HSM Coxeter и была более подробно определена Норманом Джонсоном .

Группы размышлений

Для групп Коксетера , определяемых чистыми отражениями, существует прямое соответствие между скобочной записью и диаграммой Коксетера-Дынкина . Числа в скобочной записи представляют порядки зеркального отражения в ветвях диаграммы Коксетера. Она использует то же упрощение, подавляя 2s между ортогональными зеркалами.

Нотация Коксетера упрощается с помощью экспонент, чтобы представить количество ветвей в строке для линейной диаграммы. Таким образом, группа A _n представлена ​​как [3 ^{n −1} ], что подразумевает n узлов, соединенных n−1 ветвями порядка 3. Пример A ₂ = [3,3] = [3 ² ] или [3 ^1,1 ] представляет диаграммыили.

Первоначально Коксетер представлял бифуркационные диаграммы с вертикальным расположением чисел, но позже сократил их с помощью записи экспоненты, например, [...,3 ^p,q ] или [3 ^p,q,r ], начиная с [3 ^1,1,1 ] или [3,3 ^1,1 ] =или как D ₄ . Коксетер допускал нули как особые случаи, чтобы соответствовать семейству A _n , например A ₃ = [3,3,3,3] = [3 ^4,0,0 ] = [3 ^4,0 ] = [3 ^3,1 ] = [3 ^2,2 ], например==.

Группы Кокстера, образованные циклическими диаграммами, обозначаются круглыми скобками внутри квадратных скобок, например [(p,q,r)] =для группы треугольников (pqr). Если порядки ветвей равны, их можно сгруппировать в виде экспоненты, как длина цикла в скобках, например, [(3,3,3,3)] = [3 ^[4] ], представляя диаграмму Коксетераили.может быть представлено как [3,(3,3,3)] или [3,3 ^[3] ].

Более сложные диаграммы циклов также могут быть выражены с осторожностью. Паракомпактная группа Коксетера может быть представлена ​​нотацией Коксетера [(3,3,(3),3,3)] с вложенными/перекрывающимися скобками, показывающими две смежные петли [(3,3,3)], а также представлена ​​более компактно как [3 ^{[ ]×[ ]} ], представляющая ромбическую симметрию диаграммы Коксетера. Паракомпактная полная диаграмма графаили , представлен как [3 ^[3,3] ] с верхним индексом [3,3] как симметрия его правильной тетраэдрической диаграммы Коксетера.

Для аффинных и гиперболических групп нижний индекс на единицу меньше числа узлов в каждом случае, поскольку каждая из этих групп была получена путем добавления узла к диаграмме конечной группы.

Несвязанные группы

Диаграмма Коксетера обычно оставляет ветви порядка 2 ненарисованными, но обозначение скобок включает явную 2 для соединения подграфов. Таким образом, диаграмма Коксетера= A ₂ × A ₂ = 2 A ₂ можно представить как [3]×[3] = [3] ² = [3,2,3]. Иногда явные 2-ветви могут быть включены либо с меткой 2, либо с линией с пробелом:или, как идентичное представление, как [3,2,3].

Ранг и размерность

Ранг группы точек Коксетера равен числу узлов, которое также равно размерности. В одномерном пространстве существует одно зеркало, [ ],, тогда как в 2-х измерениях [1],или [ ]×[ ] ⁺ . 1 — это заполнитель, а не фактический порядок ветвления, а маркер ортогонального неактивного зеркала. Обозначение [ n ,1] представляет группу ранга 3, как [ n ]×[ ] ⁺ или. Аналогично, [1,1] как [ ]×[ ] ⁺ ×[ ] ⁺ илипорядок 2 и [1,1] ⁺ как [ ] ⁺ ×[ ] ⁺ ×[ ] ⁺ или, заказывайте 1!

Подгруппы

Нотация Коксетера представляет вращательную/трансляционную симметрию путем добавления оператора верхнего индекса ⁺ за пределами скобок, [X] ^+, который разрезает порядок группы [X] пополам, таким образом, подгруппу индекса 2. Этот оператор подразумевает, что должно быть применено четное количество операторов, заменяя отражения вращениями (или трансляциями). При применении к группе Коксетера это называется прямой подгруппой , потому что то, что остается, — это только прямые изометрии без отражательной симметрии.

Операторы ⁺ также могут применяться внутри скобок, например, [X,Y ⁺ ] или [X,(Y,Z) ⁺ ], и создают «полупрямые» подгруппы , которые могут включать как отражающие, так и неотражающие генераторы. Полупрямые подгруппы могут применяться только к подгруппам группы Коксетера, которые имеют смежные с ней ветви четного порядка. Элементы в скобках внутри группы Коксетера могут быть снабжены оператором верхнего индекса ⁺ , имеющим эффект деления смежных упорядоченных ветвей на половину порядка, поэтому обычно применяется только с четными числами. Например, [4,3 ⁺ ] и [4,(3,3) ⁺ ] ().

При применении с соседней нечетной ветвью не создается подгруппа индекса 2, а вместо этого создаются перекрывающиеся фундаментальные домены, например, [5,1 ⁺ ] = [5/2], которые могут определять дважды обернутые многоугольники, такие как пентаграмма , {5/2}, а [5,3 ⁺ ] относится к треугольнику Шварца [5/2,3], плотность 2.

Группы без соседних ⁺ элементов можно увидеть в кольцевых узлах диаграммы Коксетера-Дынкина для однородных многогранников и сот, которые связаны с дырочными узлами вокруг ⁺ элементов, пустыми кругами с удаленными чередующимися узлами. Так что курносый куб ,имеет симметрию [4,3] ⁺ (), и плосконосый тетраэдр ,имеет симметрию [4,3 ⁺ ] (), и полукуб , h{4,3} = {3,3} (или=) имеет симметрию [1 ⁺ ,4,3] = [3,3] (или==).

Примечание: Пиритоэдрическая симметрия. можно записать как, разделив график пробелами для ясности, с генераторами {0,1,2} из группы Коксетера, производя пиритоэдрические генераторы {0,12}, отражение и 3-кратное вращение. А хиральная тетраэдрическая симметрия может быть записана как или , [1 ⁺ ,4,3 ⁺ ] = [3,3] ⁺ , с генераторами {12,0120}.

Разделение подгрупп пополам и расширенных групп

Джонсон расширяет оператор ⁺ для работы с заполнителем 1 ⁺ узлов, что удаляет зеркала, удваивая размер фундаментального домена и сокращая групповой порядок вдвое. ^[1] В общем случае эта операция применяется только к отдельным зеркалам, ограниченным ветвями четного порядка. 1 представляет зеркало, поэтому [2p] можно рассматривать как [2p, 1 ], [ 1 ,2p] или [ 1 ,2p, 1 ], как на диаграммеили, с 2 зеркалами, связанными двугранным углом порядка 2p. Эффект удаления зеркала заключается в дублировании соединительных узлов, что можно увидеть на диаграммах Коксетера:=, или в скобках: [1 ⁺ ,2p, 1 ] = [ 1 ,p, 1 ] = [p].

Каждое из этих зеркал можно удалить, так что h[2p] = [1 ⁺ ,2p,1] = [1,2p,1 ⁺ ] = [p], индекс отражающей подгруппы 2. Это можно показать на диаграмме Кокстера, добавив символ ⁺ над узлом:==.

Если удалить оба зеркала, то образуется четвертная подгруппа, при этом порядок ветвления становится точкой инерции половины порядка:

q[2p] = [1 ⁺ ,2p,1 ⁺ ] = [p] ⁺ , вращательная подгруппа индекса 4.==== .

Например, (при p=2): [4,1 ⁺ ] = [1 ⁺ ,4] = [2] = [ ]×[ ], порядок 4. [1 ⁺ ,4,1 ⁺ ] = [2] ⁺ , порядок 2.

Противоположностью делению пополам является удвоение ^[2] , которое добавляет зеркало, делит пополам фундаментальную область и удваивает порядок группы.

[[п]] = [2п]

Операции деления пополам применяются для групп более высокого ранга, например, тетраэдрическая симметрия является половинной группой октаэдрической группы : h[4,3] = [1 ⁺ ,4,3] = [3,3], удаляя половину зеркал в 4-ветви. Эффект удаления зеркала заключается в дублировании всех соединительных узлов, что можно увидеть на диаграммах Коксетера:=, h[2p,3] = [1 ⁺ ,2p,3] = [(p,3,3)].

Если узлы индексированы, то полуподгруппы могут быть помечены новыми зеркалами как композиты., генераторы {0,1} имеют подгруппу=, генераторы {1,010}, где зеркало 0 удалено и заменено копией зеркала 1, отраженной через зеркало 0. Также дано, генераторы {0,1,2}, имеет половину группы=, генераторы {1,2,010}.

Удвоение путем добавления зеркала также применяется при обратной операции деления пополам: [[3,3]] = [4,3] или, в более общем смысле, [[(q,q,p)]] = [2p,q].

Радикальные подгруппы

Радикальная подгруппа похожа на чередование, но удаляет вращательные генераторы.

Джонсон также добавил оператор звездочки или звездочки * для «радикальных» подгрупп, ^[3], который действует аналогично оператору ⁺ , но удаляет вращательную симметрию. Индекс радикальной подгруппы — это порядок удаленного элемента. Например, [4,3*] ≅ ​​[2,2]. Удаленная подгруппа [3] имеет порядок 6, поэтому [2,2] является подгруппой индекса 6 для [4,3].

Радикальные подгруппы представляют собой обратную операцию к расширенной операции симметрии. Например, [4,3*] ≅ ​​[2,2], и в обратном направлении [2,2] может быть расширено как [3[2,2]] ≅ [4,3]. Подгруппы могут быть выражены в виде диаграммы Коксетера:или≅. Удалённый узел (зеркало) приводит к тому, что соседние зеркальные виртуальные зеркала становятся реальными зеркалами.

Если [4,3] имеет генераторы {0,1,2}, то [4,3 ⁺ ], индекс 2, имеет генераторы {0,12}; [1 ⁺ ,4,3] ≅ [3,3], индекс 2 имеет генераторы {010,1,2}; в то время как радикальная подгруппа [4,3*] ≅ ​​[2,2], индекс 6, имеет генераторы {01210, 2, (012) ³ }; и, наконец, [1 ⁺ ,4,3*], индекс 12 имеет генераторы {0(12) ² 0, (012) ² 01}.

Трионные подгруппы

Пример ранга 2, [6] трионные подгруппы с 3 цветами зеркальных линий

Пример на октаэдрическую симметрию: [4,3 ^⅄ ] = [2,4].

Пример трионной подгруппы на гексагональной симметрии [6,3] отображается на большую симметрию [6,3].

3 место

Пример трионных подгрупп на октагональной симметрии [8,3] отображается на более крупные [4,8] симметрии.

4 место

Трионная подгруппа — это подгруппа индекса 3. Джонсон определяет трионную подгруппу с оператором ⅄, индекс 3. Для групп Коксетера ранга 2, [3], трионная подгруппа, [3 ^⅄ ] — это [ ], единственное зеркало. А для [3 p ], трионная подгруппа — это [3 p ] ^⅄ ≅ [ p ]. Учитывая, с генераторами {0,1}, имеет 3 трионные подгруппы. Их можно дифференцировать, поставив символ ⅄ рядом с удаляемым зеркальным генератором или на ветви для обоих: [3 p ,1 ^⅄ ] ==, =, и [3 п ^⅄ ] ==с генераторами {0,10101}, {01010,1} или {101,010}.

Трионные подгруппы тетраэдрической симметрии: [3,3] ^⅄ ≅ [2 ⁺ ,4], связывающие симметрию правильного тетраэдра и тетрагонального двуклиноида .

Для групп Коксетера ранга 3, [ p ,3], существует трионная подгруппа [ p ,3 ^⅄ ] ≅ [ p /2, p ], или=. Например, конечная группа [4,3 ^⅄ ] ≅ [2,4], а евклидова группа [6,3 ^⅄ ] ≅ [3,6] и гиперболическая группа [8,3 ^⅄ ] ≅ [4,8].

Нечетная смежная ветвь, p , не понизит порядок группы, но создаст перекрывающиеся фундаментальные домены. Порядок группы останется прежним, в то время как плотность увеличится. Например, икосаэдрическая симметрия [5,3] правильных многогранников икосаэдр становится [5/2,5], симметрией 2 правильных звездчатых многогранников. Она также связывает гиперболические мозаики {p,3} и звездчатые гиперболические мозаики {p/2,p}

Для ранга 4, [ q ,2 p ,3 ^⅄ ] = [2 p ,((p,q,q))],=.

Например, [3,4,3 ^⅄ ] = [4,3,3], или=, генераторы {0,1,2,3} в [3,4,3] с трионной подгруппой [4,3,3] генераторы {0,1,2,32123}. Для гиперболических групп [3,6,3 ^⅄ ] = [6,3 ^[3] ], и [4,4,3 ^⅄ ] = [4,4,4].

Трионные подгруппы тетраэдрической симметрии

[3,3] ^⅄ ≅ [2 ⁺ ,4] как один из 3 наборов из 2 ортогональных зеркал в стереографической проекции . Красный, зеленый и синий представляют 3 набора зеркал, а серые линии — удаленные зеркала, оставляющие 2-кратные вращения (фиолетовые ромбы).

Трионные соотношения [3,3]

Джонсон выделил две конкретные трионные подгруппы ^[4] из [3,3], сначала подгруппу индекса 3 [3,3] ^⅄ ≅ [2 ⁺ ,4], с [3,3] (==) генераторы {0,1,2}. Это также можно записать как [(3,3,2 ^⅄ )] () как напоминание о его генераторах {02,1}. Это уменьшение симметрии является соотношением между правильным тетраэдром и тетрагональным двуклиноидом , представляет собой растяжение тетраэдра перпендикулярно двум противоположным ребрам.

Во-вторых, он определяет связанную подгруппу индекса 6 [3,3] ^Δ или [(3,3,2 ^⅄ )] ⁺ (), индекс 3 из [3,3] ⁺ ≅ [2,2] ⁺ , с генераторами {02,1021}, из [3,3] и его генераторами {0,1,2}.

Эти подгруппы также применяются в более крупных группах Коксетера с подгруппой [3,3] со всеми соседними ветвями четного порядка.

Трионные подгрупповые соотношения [3,3,4]

Например, [(3,3) ⁺ ,4], [(3,3) ^⅄ ,4] и [(3,3) ^Δ ,4] являются подгруппами [3,3,4], индексы 2, 3 и 6 соответственно. Генераторы [(3,3) ^⅄ ,4] ≅ [[4,2,4]] ≅ [8,2 ⁺ ,8], порядок 128, являются {02,1,3} из [3,3,4] генераторов {0,1,2,3}. И [(3,3) ^Δ ,4] ≅ [[4,2 ⁺ ,4]], порядок 64, имеет генераторы {02,1021,3}. Также, [3 ^⅄ ,4,3 ^⅄ ] ≅ [(3,3) ^⅄ ,4].

Также связанная группа [3 ^1,1,1 ] = [3,3,4,1 ⁺ ] имеет трионные подгруппы: [3 ^1,1,1 ] ^⅄ = [(3,3) ^⅄ ,4,1 ⁺ ], порядок 64, и 1=[3 ^1,1,1 ] ^Δ = [(3,3) ^Δ ,4,1 ⁺ ] ≅ [[4,2 ⁺ ,4]] ⁺ , порядок 32.

Центральная инверсия

Двумерная центральная инверсия представляет собой поворот на 180 градусов, [2] ⁺

Центральная инверсия , порядок 2, операционально отличается по размерности. Группа [ ] ⁿ = [2 ^{n −1} ] представляет n ортогональных зеркал в n-мерном пространстве или n-плоском подпространстве пространства большей размерности. Зеркала группы [2 ^{n −1} ] пронумерованы ⁠ ⁠ ${\displaystyle 0\dots n-1}$ . Порядок зеркал не имеет значения в случае инверсии. Матрица центральной инверсии — это ⁠ ⁠ ${\displaystyle -I}$ , матрица тождественности с отрицательной единицей на диагонали.

Исходя из этого, центральная инверсия имеет генератор как произведение всех ортогональных зеркал. В нотации Коксетера эта группа инверсии выражается добавлением чередования ⁺ к каждой ветви 2. Симметрия чередования отмечена на узлах диаграммы Коксетера как открытые узлы.

Диаграмму Коксетера-Дынкина можно разметить с помощью двух явных ветвей, определяющих линейную последовательность зеркал, открытых узлов и общих двойных открытых узлов, чтобы показать цепочку генераторов отражений.

Например, [2 ⁺ ,2] и [2,2 ⁺ ] являются подгруппами индекса 2 из [2,2],, и представлены как(или) и(или) с генераторами {01,2} и {0,12} соответственно. Их общий индекс подгруппы 4 равен [2 ⁺ ,2 ⁺ ] и представлен как(или), с двойным открытиемотмечая общий узел в двух чередованиях и один генератор роторного отражения {012}.

Вращения и вращательные отражения

Вращения и вращательные отражения строятся с помощью одного произведения всех отражений призматической группы с одним генератором, [2 p ]×[2 q ]×..., где gcd ( p , q ,...)=1, они изоморфны абстрактной циклической группе Z _n порядка n =2 pq .

Четырехмерные двойные вращения, [2 p ⁺ ,2 ⁺ ,2 q ⁺ ] (с gcd ( p , q )=1), которые включают центральную группу, и выражаются Конвеем как ±[C _p ×C _q ], ^[5] порядка 2 pq . Из диаграммы Коксетера, генераторы {0,1,2,3}, требуется два генератора для [2 p ⁺ ,2 ⁺ ,2 q ⁺ ],как {0123,0132}. Полугруппы, [2 p ⁺ ,2 ⁺ ,2 q ⁺ ] ⁺ , или циклический граф, [(2 p ⁺ ,2 ⁺ ,2 q ⁺ ,2 ⁺ )],Конвей выразил это как [C _p ×C _q ], порядка pq , с одним генератором, например {0123}.

Если есть общий множитель f , двойной поворот можно записать как 1 ⁄ f [2 pf ⁺ ,2 ⁺ ,2 qf ⁺ ] (с gcd ( p , q )=1), генераторы {0123,0132}, порядок 2 pqf . Например, p = q =1, f =2, 1 ⁄ 2 [4 ⁺ ,2 ⁺ ,4 ⁺ ] имеет порядок 4. А 1 ⁄ f [2 pf ⁺ ,2 ⁺ ,2 qf ⁺ ] ⁺ , генератор {0123}, имеет порядок pqf . Например, 1 ⁄ 2 [4 ⁺ ,2 ⁺ ,4 ⁺ ] ⁺ имеет порядок 2, центральную инверсию .

В общем случае группа n -вращения [2 p ₁ ⁺ ,2,2 p ₂ ⁺ ,2,..., p _n ⁺ ] может потребовать до n генераторов, если gcd( p ₁ ,.., p _n )>1, как произведение всех зеркал, а затем перестановка последовательных пар. Полугруппа [2 p ₁ ⁺ ,2,2 p ₂ ⁺ ,2,..., p _n ⁺ ] ⁺ имеет генераторы в квадрате. n -вращательные отражения аналогичны.

Коммутаторные подгруппы

Подгруппы диаграммы Хассе из [4,4], вплоть до ее коммутаторной подгруппы, индекс 8

Простые группы с элементами ветвей только нечетного порядка имеют только одну вращательную/трансляционную подгруппу порядка 2, которая также является подгруппой коммутатора , примеры [3,3] ⁺ , [3,5] ⁺ , [3,3,3] ⁺ , [3,3,5] ⁺ . Для других групп Кокстера с ветвями четного порядка подгруппа коммутатора имеет индекс 2 ^c , где c — число несвязных подграфов, когда все ветви четного порядка удалены. ^[6]

Например, [4,4] имеет три независимых узла на диаграмме Коксетера, если удалить 4 , поэтому ее подгруппа коммутатора имеет индекс 2 ³ и может иметь различные представления, все с тремя операторами ^{+ : [4 +} ,4 ⁺ ] ⁺ , [1 ⁺ ,4,1 ⁺ ,4,1 ⁺ ], [1 ⁺ ,4,4,1 ⁺ ] ⁺ или [(4 ⁺ ,4 ⁺ ,2 ⁺ )]. Можно использовать общую нотацию с + c в качестве показателя степени группы, например [4,4] ⁺³ .

Примеры подгрупп

Примеры подгрупп ранга 2

Группы симметрии диэдра с четными порядками имеют ряд подгрупп. Этот пример показывает два зеркала генератора [4] красным и зеленым цветом и рассматривает все подгруппы с помощью деления пополам, понижения ранга и их прямых подгрупп. Группа [4],имеет два генератора зеркал 0 и 1. Каждый генерирует два виртуальных зеркала 101 и 010 путем отражения друг от друга.

Примеры подгрупп Евклида ранга 3

Группа [4,4] имеет 15 малых подгрупп индекса. Эта таблица показывает их все, с желтым фундаментальным доменом для чистых отражательных групп и чередующимися белыми и синими доменами, которые попарно образуют вращательные домены. Голубые, красные и зеленые зеркальные линии соответствуют одинаковым цветным узлам на диаграмме Коксетера. Генераторы подгрупп могут быть выражены как произведения исходных 3 зеркал фундаментального домена, {0,1,2}, соответствующих 3 узлам диаграммы Коксетера,. Произведение двух пересекающихся линий отражения создает вращение, например {012}, {12} или {02}. Удаление зеркала приводит к появлению двух копий соседних зеркал, напротив удаленного зеркала, например {010} и {212}. Два последовательных вращения сокращают порядок вращения вдвое, например {0101} или {(01) ² }, {1212} или {(02) ² }. Произведение всех трех зеркал создает трансрефлексию , например {012} или {120}.

Примеры гиперболических подгрупп

Такой же набор из 15 малых подгрупп существует во всех треугольных группах с элементами четного порядка, например, [6,4] в гиперболической плоскости:

Параболические подгруппы

Параболическая подгруппа группы Коксетера может быть идентифицирована путем удаления одного или нескольких генераторных зеркал, представленных диаграммой Коксетера. Например, октаэдрическая группаимеет параболические подгруппы,,,,,. В скобочной записи [4,3] имеет параболические подгруппы [4],[2],[3] и одно зеркало []. Порядок подгруппы известен, и всегда является целочисленным делителем порядка группы или индексом. Параболические подгруппы также могут быть записаны с узлами x, например=[4,3] подгруппа путем удаления второго зеркала:или== [4,1 ^× ,3] = [2].

Подгруппа Петри

Подгруппа Петри неприводимой группы Коксетера может быть создана произведением всех генераторов. Это можно увидеть в косом правильном многоугольнике Петри правильного многогранника . Порядок новой группы называется числом Коксетера исходной группы Коксетера. Число Коксетера группы Коксетера равно 2 m / n , где n — ранг, а m — число отражений. Подгруппа Петри может быть записана с верхним индексом π . Например, [3,3] ^π — подгруппа Петри тетраэдрической группы, циклической группы порядка 4, порожденной роторным отражением . Группа Коксетера ранга 4 будет иметь двойной генератор вращения , например, [4,3,3] ^π — это порядок 8.

Расширенная симметрия

Нотация Коксетера включает в себя обозначение двойных квадратных скобок, [[X]] для выражения автоморфной симметрии в диаграмме Коксетера. Джонсон добавил альтернативное удвоение с помощью угловых скобок <[X]>. Джонсон также добавил префиксный модификатор симметрии [Y[X]], где Y может либо представлять симметрию диаграммы Коксетера [X], либо симметрию фундаментальной области [X].

Например, в 3D эти эквивалентные прямоугольные и ромбические геометрические диаграммы : ${\displaystyle {\tilde {A}}_{3}}$и, первый удвоен квадратными скобками, [[3 ^[4] ]] или дважды удвоен как [2[3 ^[4] ]], с симметрией [2], порядка 4 выше. Чтобы отличить второй, угловые скобки используются для удвоения, <[3 ^[4] ]> и дважды удвоены как <2[3 ^[4] ]>, также с другой симметрией [2], порядка 4. Наконец, полная симметрия, где все 4 узла эквивалентны, может быть представлена ​​как [4[3 ^[4] ]], с симметрией порядка 8, [4] квадрата . Но, рассматривая фундаментальную область тетрагонального двуклиноида, [4] расширенная симметрия квадратного графа может быть обозначена более явно как [(2 ⁺ ,4)[3 ^[4] ]] или [2 ⁺ ,4[3 ^[4] ]].

Дальнейшая симметрия существует в циклических и разветвленных диаграммах , , и . имеет симметрию порядка 2 n правильного n -угольника, { n }, и представлена ​​как [ n [3 ^{[ n ]} ]]. и представлены как [3[3 ^1,1,1 ]] = [3,4,3] и [3[3 ^2,2,2 ]] соответственно, в то время как как [(3,3)[3 ^1,1,1,1 ]] = [3,3,4,3], с диаграммой, содержащей симметрию порядка 24 правильного тетраэдра , {3,3}. Паракомпактная гиперболическая группа = [3 ^1,1,1,1,1 ], ${\displaystyle {\tilde {A}}_{n}}$ ${\displaystyle D_{3}}$ ${\displaystyle {\tilde {E}}_{6}}$ ${\displaystyle {\tilde {D}}_{4}}$ ${\displaystyle {\tilde {A}}_{n}}$ ${\displaystyle D_{3}}$ ${\displaystyle {\tilde {E}}_{6}}$ ${\displaystyle {\tilde {D}}_{4}}$ ${\displaystyle {\bar {L}}_{5}}$, содержит симметрию 5-клеточного , {3,3,3}, и, таким образом, представлен как [(3,3,3)[3 ^1,1,1,1,1 ]] = [3,4,3,3,3].

Надстрочный индекс * фактически является обратной операцией, создавая радикальные подгруппы, удаляя связные нечетно-упорядоченные зеркала. ^[7]

Примеры:

Рассматривая генераторы, двойная симметрия рассматривается как добавление нового оператора, который отображает симметричные позиции в диаграмме Коксетера, делая некоторые исходные генераторы избыточными. Для 3D пространственных групп и 4D точечных групп Коксетер определяет подгруппу индекса два [[X]], [[X] ⁺ ], которую он определяет как произведение исходных генераторов [X] на удваивающий генератор. Это похоже на [[X]] ⁺ , которая является хиральной подгруппой [[X]]. Так, например, 3D пространственные группы [[4,3,4]] ⁺ (I432, 211) и [[4,3,4] ⁺ ] (Pm 3 n, 223) являются различными подгруппами [[4,3,4]] (Im 3 m, 229).

Группы первого ранга

В одном измерении двусторонняя группа [ ] представляет собой одну зеркальную симметрию, абстрактную Dih ₁ или Z _{2 ,} порядок симметрии 2. Она представлена ​​в виде диаграммы Кокстера–Дынкина с одним узлом,. Группа тождества — это прямая подгруппа [ ] ⁺ , Z ₁ , порядок симметрии 1. Верхний индекс + просто означает, что альтернативные зеркальные отражения игнорируются, оставляя группу тождества в этом простейшем случае. Коксетер использовал один открытый узел для представления чередования,.

Ранг двух групп

Правильный шестиугольник с отметками на ребрах и вершинах имеет 8 симметрий: [6], [3], [2], [1], [6] ⁺ , [3] ⁺ , [2] ⁺ , [1] ⁺ , причем [3] и [1] существуют в двух формах, в зависимости от того, находятся ли зеркала на ребрах или вершинах.

В двух измерениях прямоугольная группа [2], абстрактная D ₂ ² или D ₄ , также может быть представлена ​​в виде прямого произведения [ ]×[ ], являющегося произведением двух двусторонних групп, представляет собой два ортогональных зеркала с диаграммой Кокстера,, с порядком 4. 2 в [2] получается из линеаризации ортогональных подграфов в диаграмме Кокстера, какс явным порядком ветвления 2. Ромбическая группа , [2] ⁺ (или), половина прямоугольной группы, симметрия точечной отражательной поверхности , Z ₂ , порядок 2.

Нотация Коксетера позволяет использовать 1-й заполнитель для групп более низкого ранга, поэтому [1] то же самое, что и [ ], а [1 ⁺ ] или [1] ⁺ то же самое, что и [ ] ⁺ и диаграмма Коксетера.

Полная p-угольная группа [p], абстрактная диэдральная группа D _{2 p} , ( неабелева при p>2), порядка 2 p , порождается двумя зеркалами под углом π / p , представленными диаграммой Коксетера. P-угольная подгруппа [p] ⁺ , циклическая группа Z _p , порядка p , порожденная углом поворота  π / p .

В нотации Коксетера двойные скобки используются для представления автоморфного удвоения симметрии путем добавления биссектрисы к фундаментальной области . Например, [[p]] добавляет биссектрису к [p] и изоморфно [2p].

В пределе, переходя к одному измерению, полная апейрогональная группа получается, когда угол стремится к нулю, так что [∞], абстрактно бесконечная диэдральная группа D _∞ , представляет собой два параллельных зеркала и имеет диаграмму Кокстера. Апейрогональная группа [∞] ⁺ ,, абстрактно бесконечная циклическая группа Z _∞ , изоморфная аддитивной группе целых чисел , порождается одним ненулевым переносом.

В гиперболической плоскости существует полная псевдогональная группа [ iπ/λ ] и псевдогональная подгруппа [ iπ/λ ] ⁺ ,. Эти группы существуют в правильных многоугольниках с бесконечными сторонами, с длиной ребра λ. Все зеркала ортогональны одной прямой.

Группы третьего ранга

Точечные группы в 3-х измерениях можно выразить в скобочной записи, связанной с группами Коксетера ранга 3:

В трех измерениях полная орторомбическая группа или ортопрямоугольная [2,2], абстрактно Z ₂ ³ , порядок 8, представляет собой три ортогональных зеркала (также представленных на диаграмме Коксетера в виде трех отдельных точек). Его также можно представить в виде прямого произведения [ ]×[ ]×[ ], но выражение [2,2] позволяет определять подгруппы:

Во-первых, есть «полупрямая» подгруппа, орторомбическая группа , [2,2 ⁺ ] (или), абстрактно Z ₂ × Z ₂ , порядка 4. Когда верхний индекс + указан внутри скобок, это означает отражения, полученные только от соседних зеркал (как определено диаграммой Коксетера,) чередуются. В общем случае порядки ветвей, соседствующих с узлом + , должны быть четными. В этом случае [2,2 ⁺ ] и [2 ⁺ ,2] представляют собой две изоморфные подгруппы, которые геометрически различны. Другие подгруппы — это параромбическая группа [2,2] ⁺ (или), также порядок 4, и, наконец, центральная группа [2 ⁺ ,2 ⁺ ] (или) порядка 2.

Далее следует полная ортогональная p -группа , [2,p] (), абстрактно Z ₂ ×D _{2 p} , порядка 4p, представляющего два зеркала под двугранным углом π/ p , и оба ортогональны третьему зеркалу. Это также представлено диаграммой Коксетера как.

Прямая подгруппа называется пара- p -гональной группой, [2,p] ⁺ (или), абстрактно D _{2 p} , порядка 2p, а другая подгруппа — [2,p ⁺ ] () абстрактно Z ₂ × Z _p , также порядка 2p.

Полная гиро-p-гональная группа , [2 ⁺ ,2 p ] (или), абстрактно D _{4 p} , порядка 4 p . Гиро- p -гональная группа, [2 ⁺ ,2p ^​​+ ] (или), абстрактно Z _{2 p} , порядка 2 p является подгруппой как [2 ⁺ ,2 p ], так и [2,2 p ⁺ ].

Группы полиэдров основаны на симметрии платоновых тел : тетраэдр , октаэдр , куб , икосаэдр и додекаэдр с символами Шлефли {3,3}, {3,4}, {4,3}, {3,5} и {5,3} соответственно. Группы Коксетера для них: [3,3] (), [3,4] (), [3,5] () называются полной тетраэдрической симметрией , октаэдрической симметрией и икосаэдрической симметрией с порядками 24, 48 и 120.

Пиритоэдрическая симметрия , [3+,4] является подгруппой индекса 5 икосаэдрической симметрии , [5,3].

Во всех этих симметриях альтернативные отражения могут быть устранены, образуя вращательный тетраэдр [3,3] ⁺ (), октаэдрический [3,4] ⁺ (), и икосаэдрический [3,5] ⁺ () групп порядка 12, 24 и 60. Октаэдрическая группа также имеет уникальную подгруппу индекса 2, называемую группой пиритоэдрической симметрии , [3 ⁺ ,4] (или), порядка 12, со смесью вращательной и отражательной симметрии. Пиритоэдрическая симметрия также является подгруппой индекса 5 икосаэдрической симметрии:-->, с виртуальным зеркалом 1 относительно 0 , {010} и 3-кратным вращением {12}.

Тетраэдрическая группа, [3,3] (), имеет удвоение [[3,3]] (которое может быть представлено цветными узлами), накладывая первое и последнее зеркала друг на друга, и это создает [3,4] (или) группа. Подгруппа [3,4,1 ⁺ ] (или) то же самое, что [3,3], и [3 ⁺ ,4,1 ⁺ ] (или) то же самое, что и [3,3] ⁺ .

Аффинный

На евклидовой плоскости существуют 3 фундаментальные отражательные группы, образованные 3 зеркалами, представленными диаграммами Кокстера.,, и, и имеют обозначения Коксетера как [4,4], [6,3] и [(3,3,3)]. Скобки последней группы подразумевают цикл диаграммы, а также имеют сокращенное обозначение [3 ^[3] ].

[[4,4]] как удвоение группы [4,4] создало ту же симметрию, повернутую на π/4 относительно исходного набора зеркал.

Прямые подгруппы вращательной симметрии: [4,4] ⁺ , [6,3] ⁺ и [(3,3,3)] ⁺ . [4 ⁺ ,4] и [6,3 ⁺ ] являются полупрямыми подгруппами.

В нотации Коксетера ( орбифолдной нотации ) некоторые аффинные подгруппы с низким индексом имеют вид:

Группы четвертого ранга

Точечные группы

Группы четвертого ранга определяют 4-мерные точечные группы :

Подгруппы

Космические группы

Линейные группы

Группы четвертого ранга также определили трехмерные линейные группы :

Дуопризматическая группа

Группы ранга четыре определяют 4-мерные дуопризматические группы. В пределе, когда p и q стремятся к бесконечности, они вырождаются в 2 измерения и группы обоев.

Группы обоев

Группы четвертого ранга также определили некоторые двумерные группы обоев как предельные случаи четырехмерных групп дуопризм:

Подгруппы [∞,2,∞], (*2222) можно выразить до подгруппы коммутатора индекса 16:

Сложные размышления

Диаграмма Хассе со всеми соотношениями подгрупп на группах Шепарда ранга 2.

Обозначение Коксетера было расширено до комплексного пространства , C ⁿ , где узлы являются унитарными отражениями периода 2 или больше. Узлы помечены индексом, который предполагается равным 2 для обычного действительного отражения, если оно подавлено. Группы комплексных отражений называются группами Шепарда, а не группами Коксетера , и могут использоваться для построения сложных многогранников .

В , группа Шепарда ранга 1 ${\displaystyle \mathbb {C} ^{1}}$, порядка p , представляется как _p [ ], [ ] _p или ] _p [. Он имеет один генератор, представляющий поворот на 2 π / p радиан в комплексной плоскости : . ${\displaystyle e^{2\pi i/p}}$

Коксетер записывает комплексную группу ранга 2, _p [ q ] _r представляет диаграмму Коксетера . P и r следует опускать только в том случае, если оба равны 2, что является реальным случаем [ q ]. Порядок группы ранга 2 _p [ q ] _r равен . ^[9] ${\displaystyle g=8/q(1/p+2/q+1/r-1)^{-2}}$

Решения ранга 2, которые генерируют сложные многоугольники: _p [4] ₂ ( p равно 2,3,4,...), ₃ [3] ₃ , ₃ [6] ₂ , ₃ [4] ₃ , ₄ [3 ] ₄ , ₃ [8] ₂ , ₄ [6] ₂ , ₄ [4] ₃ , ₃ [5] ₃ , ₅ [3] ₅ , ₃ [10] ₂ , ₅ [6] ₂ и ₅ [4] ₃ с диаграммами Коксетера.,,,,,,,,,,,,.

Некоторые подгрупповые отношения среди бесконечных групп Шепарда

Бесконечные группы — это ₃ [12] ₂ , ₄ [8] ₂ , ₆ [6] ₂ , ₃ [6] ₃ , ₆ [4] ₃ , ₄ [4] ₄ , и ₆ [3] ₆ или,,,,,,.

Подгруппы индекса 2 существуют путем удаления действительного отражения: _p [2 q ] ₂ → _p [ q ] _p . Также существуют подгруппы индекса r для 4 ветвей: _p [4] _r → _p [ r ] _p .

Для бесконечного семейства _p [4] ₂ для любого p = 2, 3, 4,... существуют две подгруппы: _p [4] ₂ → [ p ], индекс p , тогда как и _p [4] ₂ → _p [ ]× _p [ ], индекс 2.

Вычисление с использованием матриц отражения в качестве генераторов симметрии

Группа Коксетера, представленная диаграммой Коксетера , дана нотация Коксетера [p,q] для порядков ветвления. Каждый узел в диаграмме Коксетера представляет собой зеркало, по соглашению называемое ρ _i (и матрицей R _i ). Генераторы этой группы [p,q] являются отражениями: ρ ₀ , ρ ₁ и ρ ₂ . Вращательная подсимметрия задается как произведение отражений: по соглашению σ _0,1 (и матрица S _0,1 ) = ρ ₀ ρ ₁ представляет собой поворот на угол π/p, а σ _1,2 = ρ ₁ ρ ₂ представляет собой поворот на угол π/q, а σ _0,2 = ρ ₀ ρ ₂ представляет собой поворот на угол π/2.

[п,д] ⁺ ,, является подгруппой индекса 2, представленной двумя генераторами вращения, каждый из которых является произведением двух отражений: σ _0,1 , σ _1,2 , и представляющих вращения на углы π/ p и π/ q соответственно.

С одной четной ветвью, [ p ⁺ ,2 q ],или, является другой подгруппой индекса 2, представленной вращательным генератором σ _0,1 и отражательным ρ ₂ .

С четными ветвями, [2 p ⁺ ,2 q ⁺ ],, является подгруппой индекса 4 с двумя генераторами, построенными как произведение всех трех матриц отражения: По соглашению: ψ _0,1,2 и ψ _1,2,0 , которые являются вращательными отражениями , представляющими отражение и вращение или отражение.

В случае аффинных групп Кокстера, таких как, или, одно зеркало, обычно последнее, переносится из начала координат. Генератор переноса τ _0,1 (и матрица T _0,1 ) строится как произведение двух (или четного числа) отражений, включая аффинное отражение. Трансрефлексия (отражение плюс перенос) может быть произведением нечетного числа отражений φ _0,1,2 (и матрицы V _0,1,2 ), как подгруппа индекса 4: [4 ⁺ ,4 ⁺ ] =.

Другой составной генератор, по соглашению как ζ (и матрица Z), представляет собой инверсию , отображающую точку в ее обратную. Для [4,3] и [5,3], ζ = (ρ ₀ ρ ₁ ρ ₂ ) ^h/2 , где h равно 6 и 10 соответственно, числу Коксетера для каждого семейства. Для 3D группы Коксетера [p,q] (), эта подгруппа является поворотным отражением [2 ⁺ ,h ⁺ ].

Группы Коксетера классифицируются по их рангу, представляющему собой число узлов в их диаграмме Коксетера-Дынкина . Структура групп также приводится с их абстрактными типами групп: В этой статье абстрактные диэдральные группы представлены как Dih _n , а циклические группы представлены как Z _n , причем Dih ₁ = Z ₂ .

2 место

Например, в 2D группа Коксетера [ p ] () представлен двумя матрицами отражения R ₀ и R ₁ , Циклическая симметрия [ p ] ⁺ () представлен генератором вращения матрицы S _0,1 .

3 место

Группы Коксетера конечного ранга 3 — это [1, p ], [2, p ], [3,3], [3,4] и [3,5].

Чтобы отразить точку через плоскость (проходящую через начало координат), можно использовать , где — единичная матрица 3×3, а — трехмерный единичный вектор для векторной нормали плоскости. Если норма L2 и равна единице, матрицу преобразования можно выразить как: ${\displaystyle ax+by+cz=0}$ ${\displaystyle \mathbf {A} =\mathbf {I} -2\mathbf {NN} ^{T}}$ ${\displaystyle \mathbf {I} }$ ${\displaystyle \mathbf {N} }$ ${\displaystyle a,b,}$ ${\displaystyle c}$

${\displaystyle \mathbf {A} =\left[{\begin{smallmatrix}1-2a^{2}&-2ab&-2ac\\-2ab&1-2b^{2}&-2bc\\-2ac&-2bc&1-2c^{2}\end{smallmatrix}}\right]}$

[п,2]

Пример фундаментальных областей, [5,2], как сферические треугольники

Приводимая 3-мерная конечная рефлективная группа является диэдральной симметрией , [ p ,2], порядок 4p ,. Генераторы отражения — матрицы R ₀ , R ₁ , R ₂ . R ₀ ² =R ₁ ² =R ₂ ² =(R ₀ ×R ₁ ) ³ =(R ₁ ×R ₂ ) ³ =(R ₀ ×R ₂ ) ² =Тождество. [ p ,2] ⁺ () генерируется 2 из 3 вращений: S _0,1 , S _1,2 , и S _{0,2 .} Роторефлексия порядка p генерируется V _0,1,2 , произведением всех 3 отражений.

[3,3]

линии отражения для [3,3] =

Простейшая неприводимая 3-мерная конечная рефлективная группа — это тетраэдрическая симметрия , [3,3], порядок 24,. Генераторы отражения из конструкции D ₃ =A _{3 представляют собой матрицы R 0} , R ₁ , R ₂ . R ₀ ² =R ₁ ² =R ₂ ² =(R ₀ ×R ₁ ) ³ =(R ₁ ×R ₂ ) ³ =(R ₀ ×R ₂ ) ² =Тождество. [3,3] ⁺ () генерируется 2 из 3 вращений: S _0,1 , S _1,2 , и S _0,2 . Трионная подгруппа, изоморфная [2 ⁺ ,4], порядок 8, генерируется S _0,2 и R _{1 .} Роторефлексия порядка 4 генерируется V _0,1,2 , произведением всех 3 отражений.

[4,3]

Линии отражения для [4,3] =

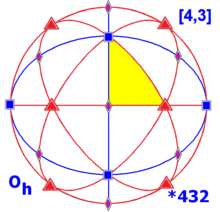
Другая неприводимая 3-мерная конечная рефлективная группа — это октаэдрическая симметрия , [4,3], порядок 48,. Матрицы генераторов отражения: R ₀ , R ₁ , R ₂ . R ₀ ² =R ₁ ² =R ₂ ² =(R ₀ ×R ₁ ) ⁴ =(R ₁ ×R ₂ ) ³ =(R ₀ ×R ₂ ) ² =Идентичность. Хиральная октаэдрическая симметрия, [4,3] ⁺ , () генерируется 2 из 3 вращений: S _0,1 , S _1,2 , и S _0,2 . Пиритоэдрическая симметрия [4,3 ⁺ ], () генерируется отражением R ₀ и вращением S _1,2 . Шестикратное роторное отражение генерируется V _0,1,2 , произведением всех трех отражений.

[5,3]

Линии отражения для [5,3] =

Конечной неприводимой 3-мерной конечной рефлективной группой является икосаэдрическая симметрия , [5,3], порядок 120,. Матрицы генераторов отражения: R ₀ , R ₁ , R ₂ . R ₀ ² =R ₁ ² =R ₂ ² =(R ₀ ×R ₁ ) ⁵ =(R ₁ ×R ₂ ) ³ =(R ₀ ×R ₂ ) ² =Тождество. [5,3] ⁺ () генерируется 2 из 3 вращений: S _0,1 , S _1,2 и S _0,2 . 10-кратное роторное отражение генерируется V _0,1,2 , произведением всех 3 отражений.

4 место

Существует 4 неприводимые группы Коксетера в 4 измерениях: [3,3,3], [4,3,3], [3 ^1,1,1 ], [3,4,4], [5,3,3], а также бесконечное семейство дуопризматических групп [ p ,2, q ].

[п,2,д]

Двупризматическая группа [ p ,2, q ] имеет порядок 4pq .

[[п,2,п]]

Дуопризматическая группа может удваиваться до 8 p ² с двукратным вращением между двумя плоскостями.

[3,3,3]

Гипертетраэдрическую симметрию [3,3,3], порядок 120, проще всего представить с помощью 4 зеркал в 5 измерениях как подгруппу [4,3,3,3].

[[3,3,3]]

Расширенная группа [[3,3,3]], порядок 240, удваивается матрицей вращения T 2-кратного порядка, здесь меняют порядок и знак координат: Имеется 3 генератора {T, R ₀ , R ₁ }. Поскольку T является самообратным, R ₃ =TR ₀ T, и R ₂ =TR ₁ T.

[4,3,3]

Неприводимая 4-мерная конечная рефлективная группа — это гипероктаэдрическая группа (или гексадекахорическая группа (для 16-клеточной ), B ₄ =[4,3,3], порядок 384,. Матрицы генераторов отражения: R ₀ , R ₁ , R ₂ , R ₃ . R ₀ ² =R ₁ ² =R ₂ ² =R ₃ ² =(R ₀ ×R ₁ ) ⁴ =(R ₁ ×R ₂ ) ³ =(R ₂ ×R ₃ ) ³ =(R ₀ ×R ₂ ) ² =(R ₁ ×R ₃ ) ² =(R ₀ ×R ₃ ) ² =Идентичность.

Хиральная гипероктаэдрическая симметрия, [4,3,3] ⁺ , () генерируется 3 из 6 вращений: S _0,1 , S _1,2 , S _2,3 , S _0,2 , S _1,3 , и S _0,3 . Гиперпиритоэдрическая симметрия [4,(3,3) ⁺ ], () генерируется отражением R ₀ и вращениями S _1,2 и S _2,3 . 8-кратное двойное вращение генерируется W _0,1,2,3 , произведением всех 4 отражений.

[3,3^1,1]

Половина группы [4,3,3] равна [3,3 ^1,1 ],, порядок 192. Он разделяет 3 генератора с группой [4,3,3], но имеет две копии соседнего генератора, одна из которых отражена через удаленное зеркало.

[3,4,3]

Неприводимая 4-мерная конечная рефлективная группа — это икоситетрахорическая группа (для 24-клеточной ), F ₄ =[3,4,3], порядок 1152,. Матрицы генераторов отражения: R ₀ , R ₁ , R ₂ , R ₃ . R ₀ ² =R ₁ ² =R ₂ ² =R ₃ ² =(R ₀ ×R ₁ ) ³ = (R ₁ × R ₂ ) ⁴ =(R ₂ ×R ₃ ) ³ =(R ₀ ×R ₂ ) ² =(R ₁ ×R ₃ ) ² =(R ₀ ×R ₃ ) ² =Идентичность.

Хиральная икоситетрахорическая симметрия, [3,4,3] ⁺ , () генерируется 3 из 6 вращений: S _0,1 , S _1,2 , S _2,3 , S _0,2 , S _1,3 , и S _0,3 . Ионная уменьшенная [3,4,3 ⁺ ] группа, () генерируется отражением R ₀ и вращениями S _1,2 и S _2,3 . 12-кратное двойное вращение генерируется W _0,1,2,3 , произведением всех 4 отражений.

[[3,4,3]]

Группа [[3,4,3]] расширяет [3,4,3] посредством 2-кратного поворота T, удваивая порядок до 2304.

[5,3,3]

Гиперикосаэдрическая симметрия, [5,3,3], порядок 14400,. Матрицы генераторов отражения: R ₀ , R ₁ , R ₂ , R ₃ . R ₀ ² =R ₁ ² =R ₂ ² =R ₃ ² =(R ₀ ×R ₁ ) ⁵ =(R ₁ ×R ₂ ) ³ =(R ₂ ×R ₃ ) ³ =(R ₀ ×R ₂ ) ² =(R ₀ ×R ₃ ) ² =(R ₁ ×R ₃ ) ² =Тождество. [5,3,3] ⁺ () генерируется тремя вращениями: S _0,1 = R ₀ ×R ₁ , S _1,2 = R ₁ ×R ₂ , S _2,3 = R ₂ ×R ₃ и т. д.

8 место

[3^4,2,1]

Группа Коксетера E8 , [3 ^4,2,1 ],, имеет 8 зеркальных узлов, порядок 696729600 (192x10!). E7 и E6, [3 ^3,2,1 ],, и [3 ^2,2,1 ],можно построить, игнорируя первое зеркало или первые два зеркала соответственно.

Аффинный ранг 2

Аффинные матрицы представляются путем добавления дополнительной строки и столбца, причем последняя строка равна нулю, за исключением последней записи 1. Последний столбец представляет собой вектор переноса.

[∞]

Аффинная группа [∞],, может быть задана двумя матрицами отражения, x=0 и x=1.

Аффинный ранг 3

[4,4]

Аффинная группа [4,4],, (p4m), можно задать тремя матрицами отражения, отражения относительно оси x (y=0), диагонали (x=y) и аффинного отражения относительно прямой (x=1). [4,4] ⁺ () (p4) генерируется S _0,1 S _1,2 и S _0,2 . [4 ⁺ ,4 ⁺ ] () (pgg) генерируется 2-кратным вращением S _0,2 и скользящим отражением (трансрефлексией) V _0,1,2 . [4 ⁺ ,4] () (p4g) генерируется S _0,1 и R ₃ . Группа [(4,4,2 ⁺ )] () (смм), генерируется двукратным вращением S _1,3 и отражением R ₂ .

[3,6]

Аффинная группа [3,6],, (p6m), можно задать тремя матрицами отражения, отражения относительно оси x (y=0), линии y=(√3/2)x и вертикальной линии x=1.

[3^[3]]

Аффинная группа [3 ^[3] ] может быть построена как полугруппа. R ₂ заменяется на R' ₂ = R ₂ ×R ₁ ×R ₂ , представленное гиперплоскостью: y+(√3/2)x=2. Фундаментальная область представляет собой равносторонний треугольник с длиной ребра 2.

Аффинный ранг 4

[4,3,4]

[4,3,4] фундаментальный домен

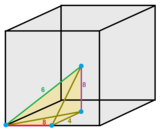
Аффинная группа — это [4,3,4] (), можно задать четырьмя матрицами отражения. Зеркало R ₀ можно поместить на плоскость z=0. Зеркало R ₁ можно поместить на плоскость y=z. Зеркало R ₂ можно поместить на плоскость x=y. Зеркало R ₃ можно поместить на плоскость x=1. [4,3,4] ⁺ () генерируется S _0,1 , S _1,2 и S _2,3 .

[[4,3,4]]

Расширенная группа [[4,3,4]] удваивает порядок группы, добавляя матрицу вращения T 2-кратного размера с фиксированной осью через точки (1,1/2,0) и (1/2,1/2,1/2). Генераторы — {R ₀ ,R ₁ ,T}. R ₂ = T×R ₁ ×T и R ₃ = T×R ₀ ×T.

[4,3^1,1]

[4,3 ^1,1 ] фундаментальная область

Группа [4,3 ^1,1 ] может быть построена из [4,3,4], вычислив [4,3,4,1 ⁺ ],, так как R' ₃ =R ₃ ×R ₂ ×R ₃ , с новым R' ₃ как образом R ₂ относительно R ₃ .

[3^[4]]

[3 ^[4] ] фундаментальная область

Группа [3 ^[4] ] может быть построена из [4,3,4], путем удаления первого и последнего зеркал, [1 ⁺ ,4,3,4,1 ⁺ ],, по R' ₁ =R ₀ ×R ₁ ×R ₀ и R' ₃ =R ₃ ×R ₂ ×R ₃ .

Примечания

1. Джонсон (2018), 11.6 Подгруппы и расширения , стр. 255, деление подгрупп пополам
2. Johnson (2018), стр. 231-236 и стр. 245 Таблица 11.4 Конечные группы изометрий в 3-пространстве
3. Джонсон (2018), 11.6 Подгруппы и расширения , стр. 259, радикальная подгруппа
4. Джонсон (2018), 11.6 Подгруппы и расширения , стр. 258, трионные подгруппы
5. Conway, 2003, стр.46, Таблица 4.2 Хиральные группы II
6. Коксетер и Мозер, 1980, Раздел 9.5 Подгруппа коммутаторов, стр. 124–126
7. Джонсон, Норман В.; Вайс, Азия Ивич (1999). «Кватернионные модулярные группы». Линейная алгебра и ее приложения . 295 (1–3): 159–189. doi : 10.1016/S0024-3795(99)00107-X .
8. Кристаллографические пространственные группы в геометрической алгебре , Д. Хестенс и Дж. Холт, Журнал математической физики. 48, 023514 (2007) (22 страницы) PDF [1]
9. Коксетер, Регулярные комплексные многогранники, 9.7 Отражения двухпорожденных подгрупп. С. 178–179

Ссылки

• HSM Коксетер :
  • Калейдоскопы: избранные труды Х. С. М. Коксетера , под редакцией Ф. Артура Шерка, Питера МакМаллена, Энтони К. Томпсона, Азии Айвик Вайс, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6 [2]  
    • (Документ 22) Коксетер, HSM (1940), «Правильные и полуправильные многогранники I», Math. Z. , 46 : 380–407, doi :10.1007/bf01181449, S2CID  186237114
    • (Документ 23) Коксетер, HSM (1985), «Правильные и полуправильные многогранники II», Math. Z. , 188 (4): 559–591, doi :10.1007/bf01161657, S2CID  120429557
    • (Документ 24) Коксетер, HSM (1988), «Правильные и полуправильные многогранники III», Math. Z. , 200 : 3–45, doi :10.1007/bf01161745, S2CID  186237142
• Coxeter, HSM; Moser, WOJ (1980). Генераторы и отношения для дискретных групп . Нью-Йорк: Springer-Verlag. ISBN 0-387-09212-9.
• Норман Джонсон Однородные многогранники , Рукопись (1991)
  • Н. В. Джонсон: Теория однородных многогранников и сот , доктор философии (1966)
  • Норман В. Джонсон и Азия Айвик Вайс Квадратичные целые числа и группы Коксетера Архивировано 26.03.2023 в Wayback Machine PDF Can. J. Math. Том 51 (6), 1999, стр. 1307–1336
  • NW Johnson: Геометрии и преобразования , (2018) ISBN 978-1-107-10340-5 [3] PDF 
• Конвей, Джон Хортон ; Дельгадо Фридрихс, Олаф; Хьюсон, Дэниел Х.; Терстон, Уильям П. (2001), «О трехмерных пространственных группах», Beiträge zur Algebra und Geometrie , 42 (2): 475–507, ISSN  0138-4821, MR  1865535
• Джон Х. Конвей и Дерек А. Смит, О кватернионах и октонионах , 2003, ISBN 978-1-56881-134-5 
• Симметрии вещей 2008, Джон Х. Конвей, Хайди Бергиель, Хаим Гудман-Штраус, ISBN 978-1-56881-220-5 Гл. 22 35 простых пространственных групп , гл. 25 184 составных пространственных групп , гл. 26 Еще выше , 4D точечные группы