Квантовое состояние

Математическая сущность для описания вероятности каждого возможного измерения в системе.

В квантовой физике квантовое состояние — это математическая сущность, воплощающая знания о квантовой системе. Квантовая механика определяет конструкцию, эволюцию и измерение квантового состояния. Результатом является предсказание для системы, представленной состоянием. Знание квантового состояния и правил эволюции системы во времени исчерпывает все, что можно знать о квантовой системе.

Квантовые состояния могут быть определены по-разному для разных видов систем или проблем. Две широкие категории:

• волновые функции, описывающие квантовые системы с использованием переменных положения или импульса и
• более абстрактные векторные квантовые состояния.

Исторические, образовательные и прикладные задачи обычно содержат волновые функции; современная профессиональная физика использует абстрактные векторные состояния. В обеих категориях квантовые состояния делятся на чистые и смешанные состояния или на когерентные и некогерентные состояния. Категории со специальными свойствами включают стационарные состояния для независимости от времени и квантовые вакуумные состояния в квантовой теории поля .

Из состояний классической механики

Как инструмент для физики, квантовые состояния выросли из состояний в классической механике . Классическое динамическое состояние состоит из набора динамических переменных с четко определенными действительными значениями в каждый момент времени. ^{[1] : 3} Например, состояние пушечного ядра будет состоять из его положения и скорости. Значения состояния развиваются в соответствии с уравнениями движения и, таким образом, остаются строго определенными. Если мы знаем положение пушки и скорость выхода ее снарядов, то мы можем использовать уравнения, содержащие силу тяжести, чтобы точно предсказать траекторию пушечного ядра.

Аналогично, квантовые состояния состоят из наборов динамических переменных, которые развиваются в соответствии с уравнениями движения. Однако значения, полученные из квантовых состояний, являются комплексными числами , квантованными, ограниченными соотношениями неопределенности , ^{[1] : 159} и обеспечивают только распределение вероятностей для результатов для системы. Эти ограничения изменяют природу квантовых динамических переменных. Например, квантовое состояние электрона в двухщелевом эксперименте будет состоять из комплексных значений в области обнаружения и, будучи возведенным в квадрат, предсказывать только распределение вероятностей количества электронов по всему детектору.

Роль в квантовой механике

Процесс описания квантовой системы с помощью квантовой механики начинается с идентификации набора переменных, определяющих квантовое состояние системы. ^{[1] : 204} Набор будет содержать совместимые и несовместимые переменные . Одновременное измерение полного набора совместимых переменных подготавливает систему к уникальному состоянию. Затем состояние детерминировано развивается в соответствии с уравнениями движения . Последующее измерение состояния дает выборку из распределения вероятностей, предсказанного квантово-механическим оператором, соответствующим измерению.

Фундаментально статистическая или вероятностная природа квантовых измерений изменяет роль квантовых состояний в квантовой механике по сравнению с классическими состояниями в классической механике. В классической механике измеряется начальное состояние одного или нескольких тел; состояние развивается в соответствии с уравнениями движения; измерения конечного состояния сравниваются с предсказаниями. В квантовой механике ансамбли одинаково подготовленных квантовых состояний развиваются в соответствии с уравнениями движения, и множество повторных измерений сравниваются с предсказанными распределениями вероятностей. ^{[1] : 204}

Измерения

Измерения, макроскопические операции над квантовыми состояниями, фильтруют состояние. ^{[1] : 196} Каким бы ни было входное квантовое состояние, повторные идентичные измерения дают согласованные значения. По этой причине измерения «подготавливают» квантовые состояния для экспериментов, помещая систему в частично определенное состояние. Последующие измерения могут либо дополнительно подготовить систему — это совместимые измерения — или она может изменить состояние, переопределив его — это называется несовместимыми или дополнительными измерениями. Например, мы можем измерить импульс состояния вдоль оси любое количество раз и получить тот же результат, но если мы измеряем положение после одного измерения импульса, последующие измерения импульса изменяются. Квантовое состояние оказывается неизбежно измененным несовместимыми измерениями. Это известно как принцип неопределенности . ${\displaystyle x}$

Собственные состояния и чистые состояния

Квантовое состояние после измерения находится в собственном состоянии, соответствующем этому измерению и измеренному значению. ^{[1] : 202} Другие аспекты состояния могут быть неизвестны. Повторение измерения не изменит состояние. В некоторых случаях совместимые измерения могут дополнительно уточнить состояние, сделав его собственным состоянием, соответствующим всем этим измерениям. ^[2] Полный набор совместимых измерений создает чистое состояние . Любое состояние, которое не является чистым, называется смешанным состоянием , что более подробно обсуждается ниже. ^{[1] : 204  [3] : 73}

Решения собственных состояний уравнения Шредингера могут быть преобразованы в чистые состояния. Эксперименты редко производят чистые состояния. Поэтому статистические смеси решений должны сравниваться с экспериментами. ^{[1] : 204}

Представления

Одно и то же физическое квантовое состояние может быть выражено математически разными способами, называемыми представлениями . ^[1] Позиционная волновая функция — это одно из представлений, которое часто встречается первым во введениях в квантовую механику. Эквивалентная импульсная волновая функция — это другое представление, основанное на волновой функции. Представления аналогичны системам координат ^{[1] : 244} или подобным математическим устройствам, таким как параметрические уравнения . Выбор представления упростит некоторые аспекты проблемы за счет усложнения других вещей.

В формальной квантовой механике (см. ниже) теория развивается в терминах абстрактного « векторного пространства », избегая какого-либо конкретного представления. Это позволяет многим элегантным концепциям квантовой механики быть выраженными и применяться даже в случаях, когда не существует классического аналога. ^{[1] : 244}

Представления волновой функции

Волновые функции представляют квантовые состояния, особенно когда они являются функциями положения или импульса . Исторически определения квантовых состояний использовали волновые функции до того, как были разработаны более формальные методы. ^{[4] : 268} Волновая функция является комплекснозначной функцией любого полного набора коммутирующих или совместимых степеней свободы . Например, один набор может быть пространственными координатами электрона. Подготовка системы путем измерения полного набора совместимых наблюдаемых дает чистое квантовое состояние . Более распространенная неполная подготовка дает смешанное квантовое состояние . Решения волновой функции уравнений движения Шредингера для операторов, соответствующих измерениям, могут быть легко выражены как чистые состояния; они должны быть объединены со статистическими весами, соответствующими экспериментальной подготовке, чтобы вычислить ожидаемое распределение вероятностей. ^{[1] : 205} ${\displaystyle x,y,z}$

Чистые состояния волновых функций

Плотности вероятности для электрона атома водорода в различных квантовых состояниях.

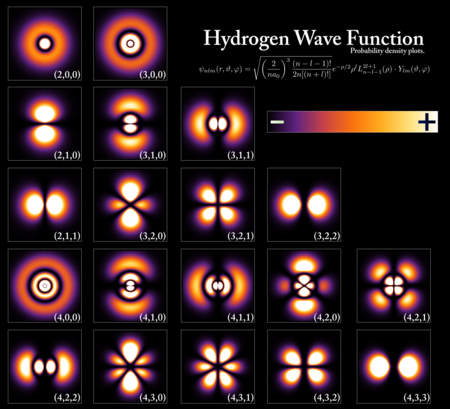
Численные или аналитические решения в квантовой механике могут быть выражены как чистые состояния . Эти состояния решения, называемые собственными состояниями , помечены квантованными значениями, обычно квантовыми числами . Например, при работе с энергетическим спектром электрона в атоме водорода соответствующие чистые состояния идентифицируются главным квантовым числом n , квантовым числом углового момента ℓ , магнитным квантовым числом m и компонентой спина z s _z . Для другого примера, если спин электрона измеряется в любом направлении, например, с помощью эксперимента Штерна-Герлаха , возможны два результата: вверх или вниз. Чистое состояние здесь представлено двумерным комплексным вектором с длиной , равной единице; то есть, с где и являются абсолютными значениями и . ${\displaystyle (\alpha ,\beta )}$ $${\displaystyle |\alpha |^{2}+|\beta |^{2}=1,}$$ ${\displaystyle |\alpha |}$ ${\displaystyle |\beta |}$ ${\displaystyle \alpha }$ ${\displaystyle \beta }$

Постулаты квантовой механики утверждают, что чистые состояния в заданный момент времени t соответствуют векторам в сепарабельном комплексном гильбертовом пространстве , в то время как каждая измеримая физическая величина (такая как энергия или импульс частицы ) связана с математическим оператором, называемым наблюдаемой . Оператор служит линейной функцией , которая действует на состояния системы. Собственные значения оператора соответствуют возможным значениям наблюдаемой. Например, можно наблюдать частицу с импульсом 1 кг⋅м/с тогда и только тогда, когда одно из собственных значений оператора импульса равно 1 кг⋅м/с. Соответствующий собственный вектор (который физики называют собственным состоянием ) с собственным значением 1 кг⋅м/с будет квантовым состоянием с определенным, четко определенным значением импульса 1 кг⋅м/с, без квантовой неопределенности . Если измерить его импульс, то гарантированно получится результат 1 кг⋅м/с.

С другой стороны, система в суперпозиции нескольких различных собственных состояний в общем случае имеет квантовую неопределенность для данной наблюдаемой. Используя обозначение скобок , эта линейная комбинация собственных состояний может быть представлена ​​как: Коэффициент, который соответствует конкретному состоянию в линейной комбинации, является комплексным числом, что допускает эффекты интерференции между состояниями. Коэффициенты зависят от времени. То, как квантовое состояние изменяется во времени, регулируется оператором эволюции во времени . $${\displaystyle |\Psi (t)\rangle =\sum _{n}C_{n}(t)|\Phi _{n}\rangle .}$$

Смешанные состояния волновых функций

Смешанное квантовое состояние соответствует вероятностной смеси чистых состояний; однако различные распределения чистых состояний могут генерировать эквивалентные (т.е. физически неразличимые) смешанные состояния. Смесь квантовых состояний снова является квантовым состоянием.

Смешанное состояние для электронных спинов в формулировке матрицы плотности имеет структуру матрицы , которая является эрмитовой и положительно полуопределенной, и имеет след 1. ^[5] Более сложный случай дается (в скобочной нотации ) синглетным состоянием , которое является примером квантовой запутанности : которая включает в себя суперпозицию совместных спиновых состояний для двух частиц со спином 1 ⁄ 2. Синглетное состояние удовлетворяет свойству, что если спины частиц измеряются вдоль одного и того же направления, то либо спин первой частицы наблюдается вверх, а спин второй частицы наблюдается вниз, либо первая частица наблюдается вниз, а вторая наблюдается вверх, обе возможности возникают с равной вероятностью. ${\displaystyle 2\times 2}$ $${\displaystyle \left|\psi \right\rangle ={\frac {1}{\sqrt {2}}}{\bigl (}\left|\uparrow \downarrow \right\rangle -\left|\downarrow \uparrow \right\rangle {\bigr )},}$$

Чистое квантовое состояние может быть представлено лучом в проективном гильбертовом пространстве над комплексными числами , в то время как смешанные состояния представлены матрицами плотности , которые являются положительными полуопределенными операторами , действующими в гильбертовых пространствах. ^{[6] [3]} Теорема Шредингера–HJW классифицирует множество способов записи заданного смешанного состояния как выпуклой комбинации чистых состояний. ^[7] До того, как конкретное измерение выполняется на квантовой системе, теория дает только распределение вероятностей для результата, и форма, которую принимает это распределение, полностью определяется квантовым состоянием и линейными операторами, описывающими измерение. Распределения вероятностей для различных измерений демонстрируют компромиссы, примером которых является принцип неопределенности : состояние, которое подразумевает узкий разброс возможных результатов для одного эксперимента, обязательно подразумевает широкий разброс возможных результатов для другого.

Статистические смеси состояний являются другим типом линейной комбинации. Статистическая смесь состояний является статистическим ансамблем независимых систем. Статистические смеси представляют степень знания, в то время как неопределенность в квантовой механике является фундаментальной. Математически статистическая смесь не является комбинацией, использующей комплексные коэффициенты, а скорее комбинацией, использующей действительные, положительные вероятности различных состояний . Число представляет вероятность того, что случайно выбранная система находится в состоянии . В отличие от случая линейной комбинации каждая система находится в определенном собственном состоянии. ^{[8] [9]} ${\displaystyle \Phi _{n}}$ ${\displaystyle P_{n}}$ ${\displaystyle \Phi _{n}}$

Ожидаемое значение наблюдаемой величины A — это статистическое среднее измеренных значений наблюдаемой величины. Именно это среднее значение и распределение вероятностей предсказываются физическими теориями. ${\displaystyle {\langle A\rangle }_{\sigma }}$

Не существует состояния, которое одновременно является собственным состоянием для всех наблюдаемых. Например, мы не можем подготовить состояние, в котором и измерение положения Q ( t ) , и измерение импульса P ( t ) (в одно и то же время t ) были бы известны точно; по крайней мере одно из них будет иметь диапазон возможных значений. ^[a] Это содержание соотношения неопределенности Гейзенберга .

Более того, в отличие от классической механики, неизбежно, что выполнение измерения в системе, как правило, изменяет ее состояние . ^{[10] [11] [b]} Точнее: после измерения наблюдаемой величины A система будет находиться в собственном состоянии A ; таким образом, состояние изменилось, если только система уже не находилась в этом собственном состоянии. Это выражает своего рода логическую последовательность: если мы измеряем A дважды в одном и том же ходе эксперимента, причем измерения являются непосредственно последовательными во времени, ^[c] то они дадут те же самые результаты. Однако это имеет некоторые странные последствия, как следует ниже.

Рассмотрим две несовместимые наблюдаемые , A и B , где A соответствует измерению, более раннему по времени, чем B. ^[d] Предположим, что система находится в собственном состоянии B в начале эксперимента. Если мы измеряем только B , все прогоны эксперимента дадут один и тот же результат. Если мы измеряем сначала A , а затем B в одном и том же прогоне эксперимента, система перейдет в собственное состояние A после первого измерения, и мы, как правило, заметим, что результаты B являются статистическими. Таким образом: Квантово-механические измерения влияют друг на друга , и порядок, в котором они выполняются, важен.

Другая особенность квантовых состояний становится важной, если мы рассматриваем физическую систему, состоящую из нескольких подсистем; например, эксперимент с двумя частицами, а не с одной. Квантовая физика допускает определенные состояния, называемые запутанными состояниями , которые показывают определенные статистические корреляции между измерениями двух частиц, которые не могут быть объяснены классической теорией. Подробнее см. запутанность . Эти запутанные состояния приводят к экспериментально проверяемым свойствам ( теорема Белла ), которые позволяют нам различать квантовую теорию и альтернативные классические (неквантовые) модели.

Картина Шредингера против картины Гейзенберга

Можно считать, что наблюдаемые зависят от времени, в то время как состояние σ было зафиксировано один раз в начале эксперимента. Этот подход называется картиной Гейзенберга . (Этот подход был принят в более поздней части обсуждения выше, с изменяющимися во времени наблюдаемыми P ( t ) , Q ( t ) .) Можно, эквивалентно, рассматривать наблюдаемые как фиксированные, в то время как состояние системы зависит от времени; это известно как картина Шредингера . (Этот подход был принят в более ранней части обсуждения выше, с изменяющимся во времени состоянием .) Концептуально (и математически) два подхода эквивалентны; выбор одного из них является вопросом соглашения. ${\textstyle |\Psi (t)\rangle =\sum _{n}C_{n}(t)|\Phi _{n}\rangle }$

Обе точки зрения используются в квантовой теории. В то время как нерелятивистская квантовая механика обычно формулируется в терминах картины Шредингера, картина Гейзенберга часто предпочтительнее в релятивистском контексте, то есть для квантовой теории поля . Сравните с картиной Дирака . ^{[13] : 65}

Формализм в квантовой физике

Чистые состояния как лучи в комплексном гильбертовом пространстве

Квантовая физика чаще всего формулируется в терминах линейной алгебры следующим образом. Любая заданная система отождествляется с некоторым конечномерным или бесконечномерным гильбертовым пространством . Чистые состояния соответствуют векторам с нормой 1. Таким образом, множество всех чистых состояний соответствует единичной сфере в гильбертовом пространстве, поскольку единичная сфера определяется как множество всех векторов с нормой 1.

Умножение чистого состояния на скаляр физически несущественно (пока состояние рассматривается само по себе). Если вектор в комплексном гильбертовом пространстве может быть получен из другого вектора путем умножения на некоторое ненулевое комплексное число, то говорят, что два вектора в соответствуют одному и тому же лучу в проективном гильбертовом пространстве . Обратите внимание, что хотя слово луч используется, собственно говоря, точка в проективном гильбертовом пространстве соответствует прямой, проходящей через начало координат гильбертова пространства, а не полупрямой или лучу в геометрическом смысле . ${\displaystyle H}$ ${\displaystyle H}$ ${\displaystyle \mathbf {P} (H)}$ ${\displaystyle H}$

Обозначение скобок

Расчеты в квантовой механике часто используют линейные операторы , скалярные произведения, дуальные пространства и эрмитово сопряжение . Чтобы сделать такие расчеты плавными и сделать ненужным (в некоторых контекстах) полное понимание базовой линейной алгебры, Поль Дирак изобрел нотацию для описания квантовых состояний, известную как нотация скобок . Хотя подробности этого выходят за рамки данной статьи, вот некоторые следствия этого:

• Выражение, используемое для обозначения вектора состояния (соответствующего чистому квантовому состоянию), имеет вид (где « » можно заменить любыми другими символами, буквами, цифрами или даже словами). Это можно противопоставить обычной математической нотации, где векторы обычно представляют собой строчные латинские буквы, и из контекста ясно, что это действительно векторы. ${\displaystyle |\psi \rangle }$ ${\displaystyle \psi }$
• Дирак определил два вида векторов, бра и кет , дуальные друг другу. ^[e]
• Каждый кет однозначно связан с так называемым бра , обозначаемым , который соответствует тому же физическому квантовому состоянию. Технически, бра является сопряженным кет. Он является элементом дуального пространства и связан с кет теоремой Рисса о представлении . В конечномерном пространстве с выбранным ортонормированным базисом, записанным как вектор-столбец, является вектором-строкой; чтобы получить его, просто возьмите транспонирование и комплексное сопряжение по записям . ${\displaystyle |\psi \rangle }$ ${\displaystyle \langle \psi |}$ ${\displaystyle |\psi \rangle }$ ${\displaystyle \langle \psi |}$ ${\displaystyle |\psi \rangle }$
• Скалярные произведения ^{[f] [g]} (также называемые скобками ) записываются так, чтобы выглядеть как бра и кет рядом друг с другом: . (Фраза «бра-кет» должна напоминать «скобку».) ${\displaystyle \langle \psi _{1}|\psi _{2}\rangle }$

Вращаться

Угловой момент имеет ту же размерность ( M · L ² · T ⁻¹ ), что и постоянная Планка , и в квантовом масштабе ведет себя как дискретная степень свободы квантовой системы. Большинство частиц обладают своего рода внутренним угловым моментом, который вообще не появляется в классической механике и возникает из релятивистского обобщения теории Дирака. Математически он описывается спинорами . В нерелятивистской квантовой механике групповые представления группы Ли SU(2) используются для описания этой дополнительной свободы. Для данной частицы выбор представления (и, следовательно, диапазон возможных значений наблюдаемого спина) задается неотрицательным числом S , которое в единицах приведенной постоянной Планка ħ является либо целым числом (0, 1, 2 ...), либо полуцелым числом (1/2, 3/2, 5/2 ...). Для массивной частицы со спином S ее спиновое квантовое число m всегда принимает одно из 2 S + 1 возможных значений в наборе $${\displaystyle \{-S,-S+1,\ldots ,S-1,S\}}$$

Вследствие этого квантовое состояние частицы со спином описывается векторной волновой функцией со значениями в C2S ⁺¹ . Эквивалентно, она представлена ​​комплекснозначной функцией четырех переменных: одна дискретная квантовая числовая переменная (для спина) добавляется к обычным трем непрерывным переменным (для положения в пространстве ) .

Многочастичные состояния и статистика частиц

Квантовое состояние системы из N частиц, каждая из которых потенциально имеет спин, описывается комплекснозначной функцией с четырьмя переменными на частицу, соответствующими 3 пространственным координатам и спину , например: $${\displaystyle |\psi (\mathbf {r} _{1},\,m_{1};\;\dots ;\;\mathbf {r} _{N},\,m_{N})\rangle .}$$

Здесь спиновые переменные m _ν принимают значения из набора , где — спин ν -й частицы. для частицы, не обладающей спином. $${\displaystyle \{-S_{\nu },\,-S_{\nu }+1,\,\ldots ,\,S_{\nu }-1,\,S_{\nu }\}}$$ ${\displaystyle S_{\nu }}$ ${\displaystyle S_{\nu }=0}$

Обработка идентичных частиц сильно отличается для бозонов (частиц с целым спином) и фермионов (частиц с полуцелым спином). Вышеуказанная функция N -частиц должна быть либо симметризована (в бозонном случае), либо антисимметризована (в фермионном случае) относительно числа частиц. Если не все N частиц идентичны, но некоторые из них идентичны, то функция должна быть (анти)симметризована отдельно по переменным, соответствующим каждой группе идентичных переменных, в соответствии с ее статистикой (бозонной или фермионной).

Электроны — это фермионы с S = 1/2 , фотоны (кванты света) — это бозоны с S = 1 (хотя в вакууме они безмассовы и не могут быть описаны механикой Шредингера).

Когда симметризация или антисимметризация не нужны, N -частичные пространства состояний могут быть получены просто с помощью тензорных произведений одночастичных пространств, к которым мы вернемся позже.

Базисные состояния одночастичных систем

Как и в случае любого гильбертова пространства , если для гильбертова пространства системы выбран базис , то любой кет может быть расширен как линейная комбинация этих базисных элементов. Символически, если заданы базисные кеты , любой кет может быть записан, где c _i — комплексные числа . В физических терминах это описывается, говоря, что было выражено как квантовая суперпозиция состояний . Если базисные кеты выбраны ортонормальными (как это часто бывает), то . ${\displaystyle |{k_{i}}\rangle }$ ${\displaystyle |\psi \rangle }$ $${\displaystyle |\psi \rangle =\sum _{i}c_{i}|{k_{i}}\rangle }$$ ${\displaystyle |\psi \rangle }$ ${\displaystyle |{k_{i}}\rangle }$ ${\displaystyle c_{i}=\langle {k_{i}}|\psi \rangle }$

Стоит отметить одно свойство: нормализованные состояния характеризуются и для ортонормированного базиса это переводится как ${\displaystyle |\psi \rangle }$ $${\displaystyle \langle \psi |\psi \rangle =1,}$$ $${\displaystyle \sum _{i}\left|c_{i}\right|^{2}=1.}$$

Расширения такого рода играют важную роль в измерении в квантовой механике. В частности, если являются собственными состояниями (с собственными значениями k _i ) наблюдаемой, и эта наблюдаемая измеряется в нормализованном состоянии , то вероятность того, что результат измерения равен k _{i ,} равна | c _i | ² . (Условие нормализации выше требует, чтобы общая сумма вероятностей была равна единице.) ${\displaystyle |{k_{i}}\rangle }$ ${\displaystyle |\psi \rangle }$

Особенно важным примером является базис положения , который является базисом, состоящим из собственных состояний с собственными значениями наблюдаемой, которая соответствует измерению положения. ^[h] Если эти собственные состояния невырождены (например, если система представляет собой одну бесспиновую частицу), то любой кет связан с комплекснозначной функцией трехмерного пространства ^[j] Эта функция называется волновой функцией, соответствующей . Аналогично дискретному случаю выше, плотность вероятности нахождения частицы в положении равна , а нормализованные состояния имеют В терминах непрерывного набора базиса положения состояние равно: ${\displaystyle |\mathbf {r} \rangle }$ ${\displaystyle \mathbf {r} }$ ${\displaystyle |\psi \rangle }$ $${\displaystyle \psi (\mathbf {r} )\equiv \langle \mathbf {r} |\psi \rangle .}$$ ${\displaystyle |\psi \rangle }$ ${\displaystyle \mathbf {r} }$ ${\displaystyle |\psi (\mathbf {r} )|^{2}}$ $${\displaystyle \int d^{3}\mathbf {r} \,|\psi (\mathbf {r} )|^{2}=1.}$$ ${\displaystyle |\mathbf {r} \rangle }$ ${\displaystyle |\psi \rangle }$ $${\displaystyle |\psi \rangle =\int d^{3}\mathbf {r} \,\psi (\mathbf {r} )|\mathbf {r} \rangle .}$$

Чистые состояния против связанных состояний

Хотя чистые состояния тесно связаны, они не совпадают со связанными состояниями, принадлежащими чистому точечному спектру наблюдаемой без квантовой неопределенности. Говорят, что частица находится в связанном состоянии , если она остается локализованной в ограниченной области пространства для всех времен. Чистое состояние называется связанным состоянием тогда и только тогда, когда для каждого существует компактное множество такое, что для всех . ^[15] Интеграл представляет вероятность того, что частица будет обнаружена в ограниченной области в любой момент времени . Если вероятность остается произвольно близкой к , то говорят, что частица остается в . ${\displaystyle |\phi \rangle }$ ${\displaystyle \varepsilon >0}$ ${\displaystyle K\subset \mathbb {R} ^{3}}$ $${\displaystyle \int _{K}|\phi (\mathbf {r} ,t)|^{2}\,\mathrm {d} ^{3}\mathbf {r} \geq 1-\varepsilon }$$ ${\displaystyle t\in \mathbb {R} }$ ${\displaystyle K}$ ${\displaystyle t}$ ${\displaystyle 1}$ ${\displaystyle K}$

Суперпозиция чистых состояний

Как упоминалось выше, квантовые состояния могут быть суперпозицией . Если и являются двумя кетами, соответствующими квантовым состояниям, кет также является квантовым состоянием той же системы. Оба и могут быть комплексными числами; их относительная амплитуда и относительная фаза будут влиять на результирующее квантовое состояние. ${\displaystyle |\alpha \rangle }$ ${\displaystyle |\beta \rangle }$ $${\displaystyle c_{\alpha }|\alpha \rangle +c_{\beta }|\beta \rangle }$$ ${\displaystyle c_{\alpha }}$ ${\displaystyle c_{\beta }}$

Записывая суперпозицию состояния с использованием и определяя норму состояния как: и извлекая общие множители, получаем: Общий фазовый множитель впереди не имеет физического эффекта. ^{[16] : 108} Только относительная фаза влияет на физическую природу суперпозиции. $${\displaystyle c_{\alpha }=A_{\alpha }e^{i\theta _{\alpha }}\ \ c_{\beta }=A_{\beta }e^{i\theta _{\beta }}}$$ $${\displaystyle |c_{\alpha }|^{2}+|c_{\beta }|^{2}=A_{\alpha }^{2}+A_{\beta }^{2}=1}$$ $${\displaystyle e^{i\theta _{\alpha }}\left(A_{\alpha }|\alpha \rangle +{\sqrt {1-A_{\alpha }^{2}}}e^{i\theta _{\beta }-i\theta _{\alpha }}|\beta \rangle \right)}$$

Одним из примеров суперпозиции является эксперимент с двумя щелями , в котором суперпозиция приводит к квантовой интерференции . Квантовое состояние эксперимента с двумя щелями представляет собой суперпозицию двух квантовых состояний с одной щелью, одно из которых соответствует левой щели, а другое — правой щели. В плоскости детектора относительная фаза этих двух состояний с одной щелью зависит от разницы расстояний от двух щелей. В зависимости от этой относительной фазы интерференция является конструктивной в некоторых местах и ​​деструктивной в других, создавая интерференционную картину. Мы можем сказать, что суперпозиции состояний находятся в когерентной суперпозиции , по аналогии с когерентностью в других волновых явлениях.

Другим примером важности относительной фазы в квантовой суперпозиции являются осцилляции Раби , где относительная фаза двух состояний изменяется во времени из-за уравнения Шредингера . Результирующая суперпозиция в конечном итоге колеблется вперед и назад между двумя различными состояниями.

Смешанные состояния

Чистое квантовое состояние — это состояние, которое можно описать одним кет-вектором, как описано выше. Смешанное квантовое состояние — это статистический ансамбль чистых состояний (см. квантовую статистическую механику ). ^{[3] : 73}

Смешанные состояния возникают в квантовой механике в двух различных ситуациях: во-первых, когда подготовка системы не полностью известна, и, таким образом, приходится иметь дело со статистическим ансамблем возможных приготовлений; и, во-вторых, когда требуется описать физическую систему, которая запутана с другой, поскольку ее состояние не может быть описано чистым состоянием. В первом случае теоретически может быть другой человек, который знает полную историю системы, и, следовательно, описывает ту же систему как чистое состояние; в этом случае матрица плотности просто используется для представления ограниченного знания квантового состояния. Однако во втором случае существование квантовой запутанности теоретически препятствует существованию полного знания о подсистеме, и невозможно для любого человека описать подсистему запутанной пары как чистое состояние.

Смешанные состояния неизбежно возникают из чистых состояний, когда для составной квантовой системы с запутанным состоянием часть недоступна наблюдателю. ^{[3] : 121–122} Состояние части тогда выражается как частичный след по . ${\displaystyle H_{1}\otimes H_{2}}$ ${\displaystyle H_{2}}$ ${\displaystyle H_{1}}$ ${\displaystyle H_{2}}$

Смешанное состояние не может быть описано одним кет-вектором. ^{[17] : 691–692} Вместо этого оно описывается связанной с ним матрицей плотности (или оператором плотности ), обычно обозначаемым ρ . Матрицы плотности могут описывать как смешанные , так и чистые состояния, рассматривая их на одинаковой основе. Более того, смешанное квантовое состояние в заданной квантовой системе, описываемой гильбертовым пространством, всегда может быть представлено как частичный след чистого квантового состояния (называемого очищением ) в большей двудольной системе для достаточно большого гильбертова пространства . ${\displaystyle H}$ ${\displaystyle H\otimes K}$ ${\displaystyle K}$

Матрица плотности, описывающая смешанное состояние, определяется как оператор вида , где p _s — доля ансамбля в каждом чистом состоянии. Матрицу плотности можно рассматривать как способ использования одночастичного формализма для описания поведения многих подобных частиц путем задания распределения вероятностей (или ансамбля) состояний, в которых эти частицы могут находиться. $${\displaystyle \rho =\sum _{s}p_{s}|\psi _{s}\rangle \langle \psi _{s}|}$$ ${\displaystyle |\psi _{s}\rangle .}$

Простым критерием проверки того, описывает ли матрица плотности чистое или смешанное состояние, является то, что след ρ2 равен 1, если состояние чистое, и меньше 1, если состояние смешанное. ^{[k] [18]} Другим эквивалентным критерием является то, что энтропия ^фон Неймана равна 0 для чистого состояния и строго положительна для смешанного состояния.

Правила измерения в квантовой механике особенно просто сформулировать в терминах матриц плотности. Например, среднее по ансамблю ( ожидаемое значение ) измерения, соответствующего наблюдаемой A, задается выражением , где и являются собственными значениями и собственными значениями соответственно для оператора A , а « tr » обозначает след. ^{[3] : 73} Важно отметить, что происходит два типа усреднения, одно (по ) является обычным ожидаемым значением наблюдаемой, когда квант находится в состоянии , а другое (по ) является статистическим (называемым некогерентным ) средним с вероятностями p _s того, что квант находится в этих состояниях. $${\displaystyle \langle A\rangle =\sum _{s}p_{s}\langle \psi _{s}|A|\psi _{s}\rangle =\sum _{s}\sum _{i}p_{s}a_{i}|\langle \alpha _{i}|\psi _{s}\rangle |^{2}=\operatorname {tr} (\rho A)}$$ ${\displaystyle |\alpha _{i}\rangle }$ ${\displaystyle a_{i}}$ ${\displaystyle i}$ ${\displaystyle |\psi _{s}\rangle }$ ${\displaystyle s}$

По словам Юджина Вигнера , ^[19] концепция смеси была выдвинута Львом Ландау . ^{[20] [14] : 38–41}

Математические обобщения

Состояния можно формулировать в терминах наблюдаемых, а не как векторы в векторном пространстве. Это положительные нормализованные линейные функционалы на C*-алгебре или иногда на других классах алгебр наблюдаемых. Подробнее см. Состояние на C*-алгебре и конструкция Гельфанда–Наймарка–Сигала .

Смотрите также

• Атомный электронный переход
• сфера Блоха
• Состояние Гринбергера-Хорна-Цайлингера
• Основное состояние
• Введение в квантовую механику
• Теорема о запрете клонирования
• Ортонормированный базис
• Теорема PBR
• Квантовый гармонический осциллятор
• Квантовый логический вентиль
• Стационарное состояние
• Коллапс волновой функции
• W состояние

Примечания

1. Во избежание недоразумений: здесь мы имеем в виду, что Q ( t ) и P ( t ) измеряются в одном и том же состоянии, но не в одном и том же ходе эксперимента.
2. Дирак (1958), ^[12] стр. 4: «Если система мала, мы не можем наблюдать ее, не вызывая серьезных возмущений».
3. т.е. разделены нулевой задержкой. Можно представить это как остановку времени, затем выполнение двух измерений одно за другим, затем возобновление времени. Таким образом, измерения произошли в одно и то же время, но все еще можно сказать, какое из них было первым.
4. Для конкретности предположим, что в приведенном выше примере A = Q ( t ₁ ) и B = P ( t ₂ ) , причем t ₂ > t ₁ > 0 .
5. Дирак (1958), ^[12] стр. 20: «Векторы бра, как они здесь представлены, представляют собой совершенно иной вид векторов, чем кеты, и до сих пор между ними нет никакой связи, за исключением существования скалярного произведения бра и кеты».
6. Дирак (1958), ^[12] стр. 19: «Скалярное произведение ⟨ B | A ⟩ теперь появляется как полное скобочное выражение».
7. Готтфрид (2013), ^[13] стр. 31: «определить скалярные произведения как находящиеся между бра и кетами».
8. Обратите внимание, что состояние является суперпозицией различных базисных состояний , поэтому и являются элементами одного и того же гильбертова пространства. Частица в состоянии находится точно в позиции , в то время как частица в состоянии может находиться в разных позициях с соответствующими вероятностями. ${\displaystyle |\psi \rangle }$ ${\displaystyle |\mathbf {r} \rangle }$ ${\displaystyle |\psi \rangle }$ ${\displaystyle |\mathbf {r} \rangle }$ ${\displaystyle |\mathbf {r} \rangle }$ ${\displaystyle \mathbf {r} =(x,y,z)}$ ${\displaystyle |\psi \rangle }$
9. Ландау (1965), ^[14] стр. 17: " ∫ Ψ _{f ′} Ψ _f * dq = δ ( f ′ − f ) " (левая часть соответствует ⟨ f | f ′⟩ ), " ∫ δ ( f ′ − f ) df′ = 1 ".
10. В непрерывном случае базисные кеты не являются единичными кетами (в отличие от состояния ): они нормализованы согласно ^[i], т.е. ( дельта-функция Дирака ), что означает, что ${\displaystyle |\mathbf {r} \rangle }$ ${\displaystyle |\psi \rangle }$ ${\textstyle \int d^{3}\mathbf {r} '\,\langle \mathbf {r} |\mathbf {r} '\rangle =1,}$ ${\displaystyle \langle \mathbf {r} |\mathbf {r} '\rangle =\delta (\mathbf {r} '-\mathbf {r} )}$ ${\displaystyle \langle \mathbf {r} |\mathbf {r} \rangle =\infty .}$
11. Обратите внимание, что этот критерий работает, когда матрица плотности нормализована так, что след ρ равен 1, как это имеет место для стандартного определения, данного в этом разделе. Иногда матрица плотности будет нормализована по-другому, в этом случае критерий будет ${\displaystyle \operatorname {Tr} (\rho ^{2})=(\operatorname {Tr} \rho )^{2}}$

Ссылки

1. Мессия, Альберт (1966). Квантовая механика . Северная Голландия, John Wiley & Sons. ISBN 0486409244.
2. Коэн-Таннуджи, Клод; Диу, Бернар; Лалоэ, Франк (1977). Квантовая механика . Уайли. стр. 231–235.
3. Перес, Эшер (1995). Квантовая теория: концепции и методы . Kluwer Academic Publishers. ISBN 0-7923-2549-4.
4. Уиттекер, сэр Эдмунд (1989-01-01). История теорий эфира и электричества . Том 2. Courier Dover Publications. стр. 87. ISBN 0-486-26126-3.
5. Риффель, Элеанор Г.; Полак, Вольфганг Х. (2011-03-04). Квантовые вычисления: Нежное введение . MIT Press. ISBN 978-0-262-01506-6.
6. Холево, Александр С. (2001). Статистическая структура квантовой теории . Конспект лекций по физике. Springer. стр. 15. ISBN 3-540-42082-7. OCLC  318268606.
7. Киркпатрик, КА (февраль 2006 г.). «Теорема Шредингера-HJW». Foundations of Physics Letters . 19 (1): 95–102. arXiv : quant-ph/0305068 . Bibcode : 2006FoPhL..19...95K. doi : 10.1007/s10702-006-1852-1. ISSN  0894-9875. S2CID  15995449.
8. "Статистическая смесь состояний". Архивировано из оригинала 23 сентября 2019 г. Получено 9 ноября 2021 г.
9. "The Density Matrix". Архивировано из оригинала 15 января 2012 г. Получено 24 января 2012 г.
10. Гейзенберг, В. (1927). Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik, Z. Phys. 43 : 172–198. Перевод как «Фактическое содержание квантовой теоретической кинематики и механики». Также переведено как «Физическое содержание квантовой кинематики и механики» на стр. 62–84 редакторами Джоном Уилером и Войцехом Зуреком, в Квантовая теория и измерения (1983), Princeton University Press, Princeton NJ.
11. Бор, Н. (1927/1928). Квантовый постулат и недавнее развитие атомной теории, Nature Supplement 14 апреля 1928 г., 121: 580–590.
12. Дирак, П. А. М. (1958). Принципы квантовой механики , 4-е издание, Oxford University Press, Оксфорд, Великобритания.
13. Готфрид, Курт ; Ян, Тунг-Моу (2003). Квантовая механика: Основы (2-е, иллюстрированное издание). Springer. ISBN 9780387955766.
14. Лев Ландау ; Евгений Лифшиц (1965). Квантовая механика — нерелятивистская теория (PDF) . Курс теоретической физики. Т. 3 (2-е изд.). Лондон: Pergamon Press.
15. Бланшар, Филипп; Брюнинг, Эрвин (2015). Математические методы в физике . Биркхойзер. п. 431. ИСБН 978-3-319-14044-5.
16. Сасскинд, Леонард; Фридман, Арт; Сасскинд, Леонард (2014). Квантовая механика: теоретический минимум; [что нужно знать, чтобы начать заниматься физикой] . Теоретический минимум / Леонард Сасскинд и Джордж Грабовский. Нью-Йорк, Нью-Йорк: Basic Books. ISBN 978-0-465-06290-4.
17. Цвибах, Бартон (2022). Освоение квантовой механики: основы, теория и приложения . Кембридж, Массачусетс: MIT Press . ISBN 978-0-262-04613-8.
18. Блюм, Теория матрицы плотности и ее применение, стр. 39.
19. Юджин Вигнер (1962). «Замечания по вопросу о разуме и теле» (PDF) . В IJ Good (ред.). The Scientist Speculates . Лондон: Heinemann. С. 284–302.^{[ постоянная мертвая ссылка ]} Сноска 13 на стр. 180
20. Лев Ландау (1927). «Das Dämpfungsproblem in der Wellenmechanik (Проблема затухания в волновой механике)». Zeitschrift für Physik . 45 (5–6): 430–441. Бибкод : 1927ZPhy...45..430L. дои : 10.1007/bf01343064. S2CID  125732617.Английский перевод перепечатан в: D. Ter Haar, ed. (1965). Сборник статей Л. Д. Ландау . Оксфорд: Pergamon Press.стр.8–18

Дальнейшее чтение

Концепция квантовых состояний, в частности содержание раздела «Формализм в квантовой физике» выше, рассматривается в большинстве стандартных учебников по квантовой механике.

Для обсуждения концептуальных аспектов и сравнения с классическими состояниями см.:

• Ишем, Крис Дж. (1995). Лекции по квантовой теории: математические и структурные основы . Imperial College Press . ISBN 978-1-86094-001-9.

Более подробное освещение математических аспектов см.:

• Браттели, Ола ; Робинсон, Дерек В. (1987). Операторные алгебры и квантовая статистическая механика 1. Springer. ISBN 978-3-540-17093-8. 2-е издание.В частности, см. раздел 2.3.

Обсуждение очищения смешанных квантовых состояний см. в Главе 2 конспекта лекций Джона Прескилла по курсу физики 219 в Калтехе.

Для обсуждения геометрических аспектов см.:

• Бенгтссон И.; Жичковский К. (2006). Геометрия квантовых состояний . Кембридж: Издательство Кембриджского университета., второе, переработанное издание (2017)