
В математике теория Галуа , первоначально введенная Эваристом Галуа , обеспечивает связь между теорией поля и теорией групп . Эта связь, фундаментальная теорема теории Галуа , позволяет свести некоторые проблемы теории поля к теории групп, что делает их более простыми и легкими для понимания.
Галуа ввел предмет изучения корней многочленов . Это позволило ему охарактеризовать полиномиальные уравнения , разрешимые в радикалах, в терминах свойств группы перестановок их корней — уравнение разрешимо в радикалах, если его корни можно выразить формулой, включающей только целые числа , корни n- й степени и четыре основные арифметические операции . Это широко обобщает теорему Абеля–Руффини , которая утверждает, что общий многочлен степени не ниже пятой не может быть решен в радикалах.
Теория Галуа использовалась для решения классических задач, включая демонстрацию того, что две задачи древности не могут быть решены в том виде, в котором они были сформулированы ( удвоение куба и трисекция угла ), а также для характеристики правильных многоугольников , которые можно построить (эта характеристика была ранее дана Гауссом , но без доказательства того, что список возможных многоугольников является полным; все известные доказательства того, что эта характеристика является полной, требуют теории Галуа).
Работа Галуа была опубликована Жозефом Лиувиллем через четырнадцать лет после его смерти. Теории потребовалось больше времени, чтобы стать популярной среди математиков и быть хорошо понятой.
Теория Галуа была обобщена до связей Галуа и теории Галуа Гротендика .
Зарождение и развитие теории Галуа было обусловлено следующим вопросом, который был одним из главных открытых математических вопросов вплоть до начала XIX века:
Существует ли формула для вычисления корней полиномиального уравнения пятой (или более высокой) степени через коэффициенты полинома, использующая только обычные алгебраические операции (сложение, вычитание, умножение, деление) и применение радикалов (квадратных корней, кубических корней и т. д.)?
Теорема Абеля–Руффини дает контрпример, доказывающий, что существуют полиномиальные уравнения, для которых такая формула не может существовать. Теория Галуа дает гораздо более полный ответ на этот вопрос, объясняя, почему возможно решить некоторые уравнения, включая все уравнения степени четыре или ниже, указанным выше способом, и почему это невозможно для большинства уравнений степени пять или выше. Более того, она дает способ определения того, может ли быть решено конкретное уравнение, который является как концептуально ясным, так и легко выражаемым в виде алгоритма .
Теория Галуа также дает ясное понимание вопросов, касающихся проблем в построении циркуля и линейки . Она дает элегантную характеристику соотношений длин, которые могут быть построены этим методом. Используя это, становится относительно легко ответить на такие классические проблемы геометрии, как
Теория Галуа возникла в ходе изучения симметричных функций – коэффициенты монического многочлена являются ( с точностью до знака) элементарными симметричными многочленами от корней. Например, ( x – a )( x – b ) = x 2 – ( a + b ) x + ab , где 1, a + b и ab – элементарные многочлены степени 0, 1 и 2 от двух переменных.
Это было впервые формализовано французским математиком XVI века Франсуа Виэтом в формулах Виэта для случая положительных действительных корней. По мнению британского математика XVIII века Чарльза Хаттона [2], выражение коэффициентов многочлена через корни (не только для положительных корней) было впервые понято французским математиком XVII века Альбером Жираром ; Хаттон пишет:
...[Жирар] был первым, кто понял общую доктрину образования коэффициентов степеней из суммы корней и их произведений. Он был первым, кто открыл правила суммирования степеней корней любого уравнения.
В этом ключе дискриминант является симметричной функцией от корней, которая отражает свойства корней — он равен нулю тогда и только тогда, когда многочлен имеет кратный корень, а для квадратичных и кубических многочленов он положителен тогда и только тогда, когда все корни действительны и различны, и отрицателен тогда и только тогда, когда есть пара различных комплексно-сопряженных корней. Подробности см. в разделе Дискриминант: Природа корней .
Кубическое уравнение впервые было частично решено итальянским математиком XV–XVI веков Сципионе дель Ферро , который, однако, не опубликовал свои результаты; однако этот метод решал только один тип кубического уравнения. Это решение было затем независимо переоткрыто в 1535 году Никколо Фонтана Тартальей , который поделился им с Джероламо Кардано , попросив его не публиковать его. Затем Кардано распространил это на множество других случаев, используя похожие аргументы; см. более подробную информацию в Метод Кардано . После открытия работы дель Ферро он почувствовал, что метод Тартальи больше не является секретом, и поэтому он опубликовал свое решение в своем труде Ars Magna 1545 года . [3] Его ученик Лодовико Феррари решил многочлен четвертой степени; его решение также было включено в Ars Magna. Однако в этой книге Кардано не предоставил «общую формулу» для решения кубического уравнения, поскольку в его распоряжении не было ни комплексных чисел , ни алгебраической нотации, чтобы описать общее кубическое уравнение. Благодаря преимуществам современной нотации и комплексных чисел формулы в этой книге работают в общем случае, но Кардано этого не знал. Именно Рафаэль Бомбелли сумел понять, как работать с комплексными числами, чтобы решать все формы кубических уравнений.
Дальнейшим шагом стала работа 1770 года Réflexions sur la résolution algébrique des équations французско-итальянского математика Жозефа Луи Лагранжа в его методе резольвент Лагранжа , где он проанализировал решение Кардано и Феррари для кубик и квартик, рассматривая их в терминах перестановок корней, что дало вспомогательный многочлен более низкой степени, обеспечив единое понимание решений и заложив основу для теории групп и теории Галуа. Однако, что важно, он не рассматривал композицию перестановок. Метод Лагранжа не распространялся на уравнения пятой степени или выше, потому что резольвента имела более высокую степень.
Квинтика была почти доказана как не имеющая общих решений радикалами Паоло Руффини в 1799 году, чьей ключевой идеей было использование групп перестановок , а не просто одной перестановки. Его решение содержало пробел, который Коши считал незначительным, хотя он не был исправлен до работы норвежского математика Нильса Хенрика Абеля , который опубликовал доказательство в 1824 году, тем самым установив теорему Абеля–Руффини .
В то время как Руффини и Абель установили, что общая квинтика не может быть решена, некоторые частные квинтики могут быть решены, такие как x 5 - 1 = 0 , и точный критерий, по которому заданная квинтика или более высокий многочлен могут быть определены как разрешимые или нет, был дан Эваристом Галуа , который показал, что разрешимость многочлена или нет эквивалентна тому, имеет ли группа перестановок его корней — в современных терминах, его группа Галуа — определенную структуру — в современных терминах, является ли она разрешимой группой . Эта группа всегда была разрешима для многочленов степени четыре или ниже, но не всегда так для многочленов степени пять и выше, что объясняет, почему не существует общего решения в более высоких степенях.

В 1830 году Галуа (в возрасте 18 лет) представил в Парижскую академию наук мемуар о своей теории разрешимости в радикалах; статья Галуа была в конечном итоге отклонена в 1831 году как слишком схематичная и за то, что в ней было дано условие в терминах корней уравнения вместо его коэффициентов. Затем Галуа умер на дуэли в 1832 году, а его статья « Mémoire sur les conditions de résolubilité des équations par radicaux » оставалась неопубликованной до 1846 года, когда ее опубликовал Жозеф Лиувилль, сопровождаемый некоторыми его собственными объяснениями. [4] До этой публикации Лиувилль объявил о результате Галуа Академии в речи, которую он произнес 4 июля 1843 года. [5] По словам Аллана Кларка, характеристика Галуа «драматически заменяет работу Абеля и Руффини». [6]
Теория Галуа была печально известна своей сложностью для понимания современниками, особенно на том уровне, на котором они могли бы ее расширить. Например, в своем комментарии 1846 года Лиувилль полностью упустил из виду групповую теоретико-ядро метода Галуа. [7] Жозеф Альфред Серре , который присутствовал на некоторых лекциях Лиувилля, включил теорию Галуа в свой учебник 1866 года (третье издание) Cours d'algèbre supérieure . Ученик Серре, Камиль Жордан , имел еще лучшее понимание, отраженное в его книге 1870 года Traité des substitutions et des équations algébriques . За пределами Франции теория Галуа оставалась более неясной в течение более длительного периода. В Британии Кэли не смог понять ее глубины, а популярные британские учебники по алгебре даже не упоминали теорию Галуа до самого конца века. В Германии труды Кронекера были больше сосредоточены на результате Абеля. Дедекинд мало писал о теории Галуа, но читал лекции по ней в Геттингене в 1858 году, показав очень хорошее понимание. [8] Книги Эугена Нетто 1880-х годов, основанные на «Трактате » Жордана , сделали теорию Галуа доступной для более широкой немецкой и американской аудитории, как и учебник алгебры Генриха Мартина Вебера 1895 года. [9]
Учитывая многочлен, может оказаться, что некоторые из корней связаны различными алгебраическими уравнениями . Например, может оказаться, что для двух корней, скажем, A и B , A 2 + 5 B 3 = 7 . Центральная идея теории Галуа заключается в рассмотрении перестановок (или перестановок) корней таким образом, чтобы любое алгебраическое уравнение, удовлетворяемое корнями, по-прежнему удовлетворялось после перестановки корней. Первоначально теория была разработана для алгебраических уравнений, коэффициенты которых являются рациональными числами . Она естественным образом распространяется на уравнения с коэффициентами в любом поле , но это не будет рассматриваться в простых примерах ниже.
Эти перестановки вместе образуют группу перестановок , также называемую группой Галуа многочлена, которая явно описана в следующих примерах.
Рассмотрим квадратное уравнение
Используя квадратную формулу , мы находим, что два корня равны
Примеры алгебраических уравнений, которым удовлетворяют A и B, включают:
и
Если мы поменяем местами A и B в любом из последних двух уравнений, мы получим еще одно истинное утверждение. Например, уравнение A + B = 4 становится B + A = 4 . Более общеизвестно, что это справедливо для любого возможного алгебраического отношения между A и B, такого, что все коэффициенты рациональны ; то есть в любом таком отношении замена A и B дает еще одно истинное отношение. Это следует из теории симметричных многочленов , которая в этом случае может быть заменена манипуляциями формулами, включающими биномиальную теорему .
Можно возразить, что A и B связаны алгебраическим уравнением A − B − 2 √ 3 = 0 , которое не остается верным при обмене A и B. Однако это соотношение здесь не рассматривается, поскольку оно имеет коэффициент −2 √ 3, который не является рациональным .
Мы приходим к выводу, что группа Галуа многочлена x 2 − 4 x + 1 состоит из двух перестановок: тождественной перестановки, которая оставляет A и B нетронутыми, и транспозиционной перестановки, которая меняет местами A и B. Поскольку все группы с двумя элементами изоморфны , эта группа Галуа изоморфна мультипликативной группе {1, −1} .
Аналогичное обсуждение применимо к любому квадратному многочлену ax 2 + bx + c , где a , b и c — рациональные числа.
Рассмотрим многочлен
Завершив квадрат необычным способом, его можно также записать как
Применяя квадратную формулу к каждому множителю, можно увидеть, что четыре корня равны
Среди 24 возможных перестановок этих четырех корней четыре особенно просты, те, которые состоят в изменении знака 0, 1 или 2 квадратных корней. Они образуют группу, изоморфную четверной группе Клейна .
Теория Галуа подразумевает, что, поскольку многочлен неприводим, группа Галуа имеет по крайней мере четыре элемента. Для доказательства того, что группа Галуа состоит из этих четырех перестановок, достаточно показать, что каждый элемент группы Галуа определяется образом A , что можно показать следующим образом.
Члены группы Галуа должны сохранять любое алгебраическое уравнение с рациональными коэффициентами, содержащее A , B , C и D.
Среди этих уравнений мы имеем:
Отсюда следует, что если φ — перестановка, принадлежащая группе Галуа, то мы должны иметь:
Это означает, что перестановка хорошо определяется образом A и что группа Галуа имеет 4 элемента, а именно:
Это означает, что группа Галуа изоморфна четверной группе Клейна .
В современном подходе начинают с расширения поля L / K (читается « L над K ») и исследуют группу автоморфизмов L , которые фиксируют K. Дополнительные пояснения и примеры см. в статье о группах Галуа .
Связь между двумя подходами следующая. Коэффициенты рассматриваемого многочлена должны выбираться из базового поля K. Верхнее поле L должно быть полем, полученным присоединением корней рассматриваемого многочлена к базовому полю K. Любая перестановка корней, которая соблюдает алгебраические уравнения, как описано выше, приводит к автоморфизму L / K , и наоборот.
В первом примере выше мы изучали расширение Q ( √ 3 )/ Q , где Q — поле рациональных чисел , а Q ( √ 3 ) — поле, полученное из Q присоединением √ 3 . Во втором примере мы изучали расширение Q ( A , B , C , D )/ Q .
Современный подход имеет ряд преимуществ по сравнению с подходом, основанным на группах перестановок.
Понятие разрешимой группы в теории групп позволяет определить, разрешим ли многочлен в радикалах, в зависимости от того, обладает ли его группа Галуа свойством разрешимости. По сути, каждое расширение поля L / K соответствует фактор-группе в композиционном ряду группы Галуа. Если фактор-группа в композиционном ряду является циклической порядка n , и если в соответствующем расширении поля L / K поле K уже содержит примитивный корень n-й степени из единицы , то это радикальное расширение, и элементы L тогда могут быть выражены с помощью корня n-й степени некоторого элемента K .
Если все фактор-группы в ее композиционном ряду циклические, то группа Галуа называется разрешимой , и все элементы соответствующего поля могут быть найдены путем многократного извлечения корней, произведений и сумм элементов из базового поля (обычно Q ).
Одним из величайших триумфов теории Галуа было доказательство того, что для любого n > 4 существуют многочлены степени n , которые не разрешимы в радикалах (это было доказано независимо, с использованием похожего метода, Нильсом Хенриком Абелем за несколько лет до этого, и является теоремой Абеля–Руффини ), и систематический способ проверки того, разрешим ли конкретный многочлен в радикалах. Теорема Абеля–Руффини вытекает из того факта, что для n > 4 симметрическая группа S n содержит простую , нециклическую, нормальную подгруппу , а именно знакопеременную группу A n .
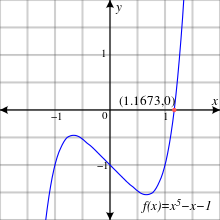
Ван дер Варден [10] приводит полином f ( x ) = x 5 − x − 1 .
По теореме о рациональных корнях это число не имеет рациональных нулей.
Также у него нет линейных множителей по модулю 2 или 3.
Группа Галуа функции f ( x ) по модулю 2 является циклической порядка 6, поскольку f ( x ) по модулю 2 раскладывается на многочлены порядков 2 и 3, ( x 2 + x + 1)( x 3 + x 2 + 1) .
f ( x ) по модулю 3 не имеет линейного или квадратичного множителя, и, следовательно, является неприводимой. Таким образом, ее группа Галуа по модулю 3 содержит элемент порядка 5.
Известно [11] , что группа Галуа по простому модулю изоморфна подгруппе группы Галуа над рациональными числами. Группа перестановок на 5 объектах с элементами порядков 6 и 5 должна быть симметрической группой S 5 , которая, следовательно, является группой Галуа функции f ( x ) .
Это один из простейших примеров неразрешимого многочлена пятой степени. По словам Сержа Ланга , Эмиль Артин был в восторге от этого примера. [12]
Обратная задача Галуа состоит в нахождении расширения поля с заданной группой Галуа.
Пока не указано основное поле , проблема не очень сложна, и все конечные группы встречаются как группы Галуа. Чтобы показать это, можно действовать следующим образом. Выберем поле K и конечную группу G. Теорема Кэли гласит, что G является (с точностью до изоморфизма) подгруппой симметрической группы S на элементах G. Выберем неопределенные { x α } , по одному для каждого элемента α из G , и присоединим их к K , чтобы получить поле F = K ({ x α }) . Внутри F содержится поле L симметрических рациональных функций от { x α } . Группа Галуа F / L есть S , согласно основному результату Эмиля Артина. G действует на F ограничением действия S. Если фиксированное поле этого действия есть M , то, согласно фундаментальной теореме теории Галуа , группа Галуа F / M есть G.
С другой стороны, открыта проблема, является ли каждая конечная группа группой Галуа расширения поля Q рациональных чисел. Игорь Шафаревич доказал, что каждая разрешимая конечная группа является группой Галуа некоторого расширения Q. Различные люди решали обратную задачу Галуа для выбранных неабелевых простых групп . Существование решений было показано для всех, кроме, возможно, одной ( группа Матье M 23 ) из 26 спорадических простых групп. Существует даже многочлен с целыми коэффициентами, группа Галуа которого является группой Монстра .
В форме, упомянутой выше, включая, в частности, фундаментальную теорему теории Галуа , теория рассматривает только расширения Галуа, которые, в частности, являются сепарабельными. Общие расширения полей могут быть разделены на сепарабельное, за которым следует чисто несепарабельное расширение поля . Для чисто несепарабельного расширения F / K существует теория Галуа, в которой группа Галуа заменяется векторным пространством выводов , , т. е. K - линейными эндоморфизмами F, удовлетворяющими правилу Лейбница. В этом соответствии назначается промежуточное поле E. Наоборот, подпространство, удовлетворяющее соответствующим дополнительным условиям, отображается в . При предположении Якобсон (1944) показал, что это устанавливает взаимно-однозначное соответствие. Условие, наложенное Якобсоном, было снято Браннером и Уолдроном (2020), путем указания соответствия с использованием понятий производной алгебраической геометрии .