Перелом

Раскол материалов или конструкций под нагрузкой

Пластическое разрушение металлического образца, деформированного в осевом направлении

Разрушение — это появление трещины или полное разделение объекта или материала на две или более частей под действием напряжения . Разрушение твердого тела обычно происходит из-за развития определенных поверхностей разрыва смещения внутри твердого тела. Если смещение развивается перпендикулярно поверхности, оно называется нормальной трещиной растяжения или просто трещиной ; если смещение развивается тангенциально, оно называется трещиной сдвига , полосой скольжения или дислокацией . ^[1]

Хрупкие изломы происходят без какой-либо видимой деформации перед разрушением. Вязкие изломы происходят после видимой деформации. Прочность на излом, или предел прочности на разрыв, — это напряжение, когда образец разрушается или ломается. Детальное понимание того, как происходит и развивается излом в материалах, является предметом механики разрушения .

Сила

Типичная для алюминия кривая зависимости напряжения от деформации

1. Предел прочности на растяжение
2. Предел текучести
3. Пропорциональное предельное напряжение
4. Перелом
5. Смещение деформации (обычно 0,2%)

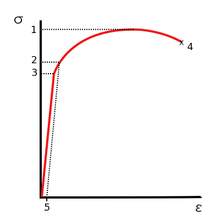
Прочность на излом, также известная как прочность на разрыв, — это напряжение, при котором образец разрушается через трещину. ^[2] Обычно это определяется для данного образца с помощью испытания на растяжение , которое вычерчивает кривую зависимости деформации от напряжения (см. изображение). Конечная зафиксированная точка — это прочность на излом.

Пластичные материалы имеют предел прочности на разрыв ниже предельной прочности на разрыв (UTS), тогда как у хрупких материалов предел прочности на разрыв эквивалентен UTS. ^[2] Если пластичный материал достигает предельной прочности на разрыв в ситуации с контролируемой нагрузкой, ^{[Примечание 1]} он продолжит деформироваться без приложения дополнительной нагрузки, пока не разорвется. Однако, если нагрузка контролируется смещением, ^{[Примечание 2]} деформация материала может снять нагрузку, предотвращая разрыв.

Статистика разрушения случайных материалов имеет очень интригующее поведение и была замечена архитекторами и инженерами довольно рано. Действительно, исследования разрушения или поломки могут быть старейшими физическими научными исследованиями, которые все еще остаются интригующими и очень живыми. Леонардо да Винчи , более 500 лет назад, заметил, что прочность на разрыв номинально идентичных образцов железной проволоки уменьшается с увеличением длины проволоки (см., например, ^[3] для недавнего обсуждения). Аналогичные наблюдения были сделаны Галилео Галилеем более 400 лет назад. Это проявление экстремальной статистики разрушения (больший объем образца может иметь большие дефекты из-за кумулятивных колебаний, где разрушения зарождаются и вызывают более низкую прочность образца). ^[4]

Типы

Существует два типа разрушений: хрупкие и вязкие, без или с пластической деформацией перед разрушением.

Хрупкий

Хрупкое разрушение стекла

Излом алюминиевого шатуна велосипеда, где светлые области показывают хрупкий излом, а темные области — усталостный излом

При хрупком разрушении не происходит никакой видимой пластической деформации перед разрушением. Хрупкое разрушение обычно включает в себя небольшое поглощение энергии и происходит на высоких скоростях — до 2133,6 м/с (7000 фут/с) в стали. ^[5] В большинстве случаев хрупкое разрушение будет продолжаться даже после прекращения нагрузки. ^[6]

В хрупких кристаллических материалах разрушение может происходить путем раскалывания в результате растягивающего напряжения, действующего перпендикулярно кристаллографическим плоскостям с низкой связью (плоскости раскалывания). В аморфных твердых телах , напротив, отсутствие кристаллической структуры приводит к раковистому излому , при этом трещины распространяются перпендикулярно приложенному напряжению.

Прочность материала на разрыв (или напряжение зарождения микротрещин) была впервые теоретически оценена Аланом Арнольдом Гриффитом в 1921 году:

${\displaystyle \sigma _{\mathrm {theoretical} }={\sqrt {\frac {E\gamma }{r_{o}}}}}$

где: -

Поверхность хрупкого скола, полученная с помощью сканирующего электронного микроскопа

${\displaystyle E}$- модуль Юнга материала,

${\displaystyle \gamma }$- поверхностная энергия , а

${\displaystyle r_{o}}$— длина микротрещины (или равновесное расстояние между атомными центрами в кристаллическом теле).

С другой стороны, трещина приводит к концентрации напряжений, моделируемой уравнением Инглиса ^[7]

${\displaystyle \sigma _{\mathrm {elliptical\ crack} }=\sigma _{\mathrm {applied} }\left(1+2{\sqrt {\frac {a}{\rho }}}\right)=2\sigma _{\mathrm {applied} }{\sqrt {\frac {a}{\rho }}}}$(Для острых трещин)

где:

${\displaystyle \sigma _{\mathrm {applied} }}$это нагрузочное напряжение,

${\displaystyle a}$составляет половину длины трещины, и

${\displaystyle \rho }$радиус кривизны на вершине трещины.

Объединяя эти два уравнения, получаем

${\displaystyle \sigma _{\mathrm {fracture} }={\sqrt {\frac {E\gamma \rho }{4ar_{o}}}}.}$

Острые трещины (мелкие ) и крупные дефекты (крупные ) снижают прочность материала на разрыв. ${\displaystyle \rho }$ ${\displaystyle a}$

Недавно ученые открыли сверхзвуковой разрыв — явление распространения трещины в материале со скоростью, превышающей скорость звука. ^[8] Это явление недавно было также подтверждено экспериментом по разрушению резиноподобных материалов.

Основная последовательность типичного хрупкого разрушения такова: введение дефекта либо до, либо после ввода материала в эксплуатацию, медленное и стабильное распространение трещины при повторяющейся нагрузке и внезапное быстрое разрушение, когда трещина достигает критической длины трещины на основе условий, определенных механикой разрушения. ^[6] Хрупкого разрушения можно избежать, контролируя три основных фактора: вязкость разрушения материала (K _c ), номинальный уровень напряжения (σ) и размер введенного дефекта (a). ^[5] Остаточные напряжения, температура, скорость нагрузки и концентрации напряжений также способствуют хрупкому разрушению, влияя на три основных фактора. ^[5]

При определенных условиях пластичные материалы могут проявлять хрупкое поведение. Быстрая нагрузка, низкая температура и условия ограничения трехосного напряжения могут привести к разрушению пластичных материалов без предварительной деформации. ^[5]

Ковкий

Схематическое изображение стадий вязкого разрушения (при чистом растяжении)

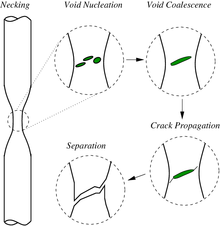
При вязком разрушении происходит обширная пластическая деформация ( образование шейки ) перед разрушением. Термины «разрыв» и «вязкий разрыв» описывают окончательное разрушение пластичных материалов, нагруженных растяжением. Обширная пластичность заставляет трещину распространяться медленно из-за поглощения большого количества энергии перед разрушением. ^{[9] [10]}

Поверхность вязкого разрушения алюминия 6061-T6

Поскольку пластичный разрыв подразумевает высокую степень пластической деформации, поведение разрушения распространяющейся трещины, смоделированное выше, принципиально меняется. Часть энергии от концентраций напряжений на вершинах трещины рассеивается пластической деформацией впереди трещины по мере ее распространения.

Основными этапами вязкого разрушения являются образование микропустот ^{[11] ,} коалесценция микропустот (также известная как образование трещин), распространение трещин и разрушение, часто приводящее к образованию поверхности разрушения в форме чаши и конуса. Микропустоты зарождаются на различных внутренних разрывах, таких как осадки, вторичные фазы, включения и границы зерен в материале. ^[11] По мере увеличения локального напряжения микропустоты растут, объединяются и в конечном итоге образуют непрерывную поверхность разрушения. ^[11] Пластичное разрушение обычно является транскристаллитным , а деформация из-за скольжения дислокаций может вызвать характерную для чаши и конуса кромку сдвига. ^[12]

Слияние микропустот приводит к появлению ямочек на поверхности излома. Форма ямочек сильно зависит от типа нагрузки. Разрушение под действием локальной одноосной растягивающей нагрузки обычно приводит к образованию равноосных ямочек. Разрушения, вызванные сдвигом, приведут к образованию удлиненных или параболических ямочек, которые направлены в противоположных направлениях на соответствующих поверхностях излома. Наконец, разрыв при растяжении приводит к образованию удлиненных ямочек, которые направлены в одном направлении на соответствующих поверхностях излома. ^[11]

Характеристики

Способ, которым трещина распространяется по материалу, дает представление о режиме разрушения. При вязком разрушении трещина движется медленно и сопровождается большим количеством пластической деформации вокруг вершины трещины. Пластичная трещина обычно не распространяется, если не приложено повышенное напряжение, и обычно прекращает распространение при снятии нагрузки. ^[6] В пластичном материале трещина может прогрессировать до участка материала, где напряжения немного ниже, и останавливаться из-за притупляющего эффекта пластических деформаций на вершине трещины. С другой стороны, при хрупком разрушении трещины распространяются очень быстро с небольшой или нулевой пластической деформацией. Трещины, которые распространяются в хрупком материале, будут продолжать расти после возникновения.

Распространение трещин также классифицируется по характеристикам трещины на микроскопическом уровне. Трещина, которая проходит через зерна внутри материала, подвергается транскристаллитному разрушению. Трещина, которая распространяется вдоль границ зерен, называется межкристаллитным разрушением. Обычно связи между зернами материала сильнее при комнатной температуре, чем сам материал, поэтому транскристаллитное разрушение более вероятно. Когда температура повышается достаточно, чтобы ослабить связи зерен, межкристаллитное разрушение становится более распространенным режимом разрушения. ^[6]

Тестирование

Разрушение материалов изучается и количественно определяется несколькими способами. Разрушение в значительной степени определяется вязкостью разрушения ( ), поэтому для ее определения часто проводятся испытания на разрушение. Двумя наиболее широко используемыми методами определения вязкости разрушения являются испытание на трехточечный изгиб и испытание на компактное растяжение . ${\textstyle \mathrm {K} _{\mathrm {c} }}$

Проведя испытания на компактное растяжение и трехточечный изгиб, можно определить вязкость разрушения с помощью следующего уравнения:

${\displaystyle \mathrm {K_{c}} =\sigma _{\mathrm {F} }{\sqrt {\pi \mathrm {c} }}\mathrm {f\ (c/a)} }$

Где:

${\displaystyle \mathrm {f\ (c/a)} }$это эмпирически выведенное уравнение для описания геометрии тестового образца

${\displaystyle \sigma _{\mathrm {F} }}$- это напряжение разрушения, и

${\displaystyle \mathrm {c} }$длина трещины.

Для точного достижения необходимо точно измерить значение . Это делается путем взятия образца для испытаний с его изготовленным надрезом длиной и заострения этого надреза для лучшей имитации вершины трещины, обнаруженной в реальных материалах. ^[13] Циклическое предварительное напряжение образца может затем вызвать усталостную трещину , которая расширяет трещину от изготовленного надреза длиной до . Это значение используется в приведенных выше уравнениях для определения . ^[14] ${\textstyle \mathrm {K} _{\mathrm {c} }}$ ${\textstyle \mathrm {c} }$ ${\textstyle \mathrm {c\prime } }$ ${\textstyle \mathrm {c\prime } }$ ${\textstyle \mathrm {c} }$ ${\textstyle \mathrm {c} }$ ${\textstyle \mathrm {K} _{\mathrm {c} }}$

После этого испытания образец можно переориентировать таким образом, чтобы дальнейшее нагружение нагрузкой (F) расширяло эту трещину, и, таким образом, можно получить кривую зависимости нагрузки от прогиба образца. С помощью этой кривой можно получить наклон линейной части, которая является обратной величиной податливости материала. Затем это используется для вывода f(c/a), как определено выше в уравнении. Зная все эти переменные, можно затем рассчитать. ${\textstyle \mathrm {K} _{\mathrm {c} }}$

Керамика и неорганические стекла

Керамика и неорганические стекла имеют поведение при разрушении, которое отличается от поведения металлических материалов. Керамика имеет высокую прочность и хорошо работает при высоких температурах из-за того, что прочность материала не зависит от температуры. Керамика имеет низкую вязкость, определяемую испытанием под растягивающей нагрузкой; часто керамика имеет значения , которые составляют ~5% от значений, обнаруженных у металлов. ^[14] Однако, как продемонстрировали Фабер и Эванс , вязкость разрушения можно предсказать и улучшить с помощью прогиба трещины вокруг частиц второй фазы. ^[15] Керамика обычно нагружается сжатием в повседневном использовании, поэтому прочность на сжатие часто называют прочностью; эта прочность часто может превышать прочность большинства металлов. Однако керамика хрупкая, и поэтому большая часть работы вращается вокруг предотвращения хрупкого разрушения. Из-за того, как керамика производится и обрабатывается, в материале часто имеются уже существующие дефекты, которые вносят высокую степень изменчивости в хрупкое разрушение по режиму I. ^[14] Таким образом, при проектировании керамики необходимо учитывать вероятностную природу. Распределение Вейбулла прогнозирует вероятность выживания части образцов определенного объема, выдерживающих сигму растягивающего напряжения, и часто используется для более точной оценки успешности керамики в предотвращении разрушения. ${\textstyle \mathrm {K} _{\mathrm {c} }}$

Волоконные пучки

Для моделирования разрушения пучка волокон в 1926 году Томас Пирс представил модель пучка волокон в качестве модели для понимания прочности композитных материалов. ^[16] Пучок состоит из большого количества параллельных пружин Гука одинаковой длины, каждая из которых имеет одинаковые упругие константы. Однако они имеют разные разрушающие напряжения. Все эти пружины подвешены к жесткой горизонтальной платформе. Груз прикреплен к горизонтальной платформе, соединенной с нижними концами пружин. Когда эта нижняя платформа абсолютно жесткая, нагрузка в любой момент времени распределяется поровну (независимо от того, сколько волокон или пружин сломалось и где) между всеми выжившими волокнами. Этот режим распределения нагрузки называется режимом равного распределения нагрузки. Можно также предположить, что нижняя платформа имеет конечную жесткость, так что локальная деформация платформы происходит везде, где пружины выходят из строя, и выжившие соседние волокна должны разделить большую часть той, которая передается от выжившего волокна. Крайним случаем является модель локального распределения нагрузки, где нагрузка от вышедшей из строя пружины или волокна распределяется (обычно поровну) между уцелевшими ближайшими соседними волокнами. ^[4]

Катастрофы

Разрушения, вызванные хрупким разрушением, не ограничиваются какой-либо конкретной категорией инженерных конструкций. ^[5] Хотя хрупкое разрушение встречается реже, чем другие типы разрушений, его воздействие на жизнь и имущество может быть более серьезным. ^[5] Следующие известные исторические разрушения были отнесены к хрупкому разрушению:

• Сосуды под давлением: Великое наводнение с патокой в ​​1919 году ^[5], авария резервуара с патокой в ​​Нью-Джерси в 1973 году ^[6]
• Мосты: обрушение пролёта моста Кинг-стрит в 1962 г., обрушение Силвер-Бридж в 1967 г., ^[5] частичное разрушение моста Хоан в 2000 г.
• Корабли: «Титаник» в 1912 году ^{[6] ,} корабли «Либерти» во время Второй мировой войны ^[5], пароход «Скенектади» в 1943 году ^[6]

Вычислительная механика разрушения

Практически каждая область техники подверглась значительному влиянию компьютеров, и механика разрушения не является исключением. Поскольку существует так мало реальных проблем с аналитическими решениями в замкнутой форме, численное моделирование стало важнейшим инструментом в анализе разрушения. Существуют буквально сотни конфигураций, для которых были опубликованы решения интенсивности напряжения, большинство из которых были получены с помощью численных моделей. Расчеты интеграла J и смещения вершины трещины (CTOD) являются двумя более популярными упругопластическими исследованиями. Кроме того, эксперты используют передовые вычислительные инструменты для изучения уникальных проблем, таких как распространение пластичных трещин, динамическое разрушение и разрушение на интерфейсах. Экспоненциальный рост приложений вычислительной механики разрушения по сути является результатом быстрого развития компьютерных технологий. ^[17]

Наиболее используемые вычислительные численные методы — это методы конечных элементов и граничных интегральных уравнений. Другие методы включают согласование напряжений и смещений, продвижение трещин элементов, в которых последние два относятся к традиционным методам в вычислительной механике разрушения.

Точная сетка, созданная в прямоугольной области в программном обеспечении Ansys (метод конечных элементов)

Метод конечных элементов

Структуры делятся на дискретные элементы типа 1-D балки, 2-D плоского напряжения или плоской деформации, 3-D кирпичей или тетраэдров. Непрерывность элементов обеспечивается с помощью узлов. ^[17]

Метод граничных интегральных уравнений

В этом методе поверхность делится на две области: область, где смещения заданы S _u , и область с тягами, заданными S _T . При заданных граничных условиях напряжения, деформации и смещения внутри тела могут быть теоретически решены вместе с тягами на S _u и смещениями на S _T . Это очень мощный метод для нахождения неизвестных тяг и смещений. ^[17]

Традиционные методы в вычислительной механике разрушения

Эти методы используются для определения параметров механики разрушения с помощью численного анализа. ^[17] Некоторые из традиционных методов в вычислительной механике разрушения, которые обычно использовались в прошлом, были заменены новыми и более продвинутыми методами. Новые методы считаются более точными и эффективными, то есть они могут обеспечить более точные результаты и делать это быстрее, чем старые методы. Не все традиционные методы были полностью заменены, поскольку они все еще могут быть полезны в определенных сценариях, но они могут не быть самым оптимальным выбором для всех приложений.

Некоторые из традиционных методов вычислительной механики разрушения:

• Согласование напряжений и смещений
• Элементарное продвижение трещины
• Контурная интеграция
• Виртуальное расширение трещины

Смотрите также

• Растрескивание под воздействием окружающей среды
• Перелом под воздействием окружающей среды
• Усталость (материал)
• Судебная инженерия
• Судебно-медицинская материаловедение
• Фрактография
• Трещина (геология)
• Излом (минералогия)
• Тесселяция Гилберта
• Коалесценция микропустот
• Нотч (инженерное дело)
• Сезон растрескивания
• Коррозионное растрескивание под напряжением
• Сумасшествие

Примечания

1. Простая ситуация растяжения с контролируемой нагрузкой будет поддерживать образец сверху и подвешивать груз к нижнему концу. Нагрузка на образец тогда не зависит от его деформации.
2. Простая ситуация растяжения с контролируемым смещением — это прикрепить очень жесткий домкрат к концам образца. Когда домкрат выдвигается, он контролирует смещение образца; нагрузка на образец зависит от деформации.

Ссылки

1. Черепанов, ГП, Механика хрупкого разрушения
2. Дегармо, Э. Пол; Блэк, Дж. Т.; Кохсер, Рональд А. (2003), Материалы и процессы в производстве (9-е изд.), Wiley, стр. 32, ISBN 0-471-65653-4.
3. Лунд, младший; Брин, Дж. П., Гражданский. англ. и окр. Сист. 18 (2000) 243
4. Chakrabarti, Bikas K. (декабрь 2017 г.). «История развития статистической физики трещин, поломок и землетрясений: личный отчет». Reports in Advances of Physical Sciences . 01 (4): 1750013. doi : 10.1142/S242494241750013X . ISSN  2424-9424.Текст скопирован из этого источника, который доступен по лицензии Creative Commons Attribution 4.0 International.
5. Рольф, Джон М. Барсом, Стэнли Т. (1999). Контроль разрушения и усталости в конструкциях: применение механики разрушения (3-е изд.). West Conshohocken, Pa.: ASTM. ISBN 0803120826.{{cite book}}: CS1 maint: multiple names: authors list (link)
6. Кэмпбелл, ФК, ред. (2012). Усталость и перелом: понимание основ . Materials Park, Огайо: ASM International. ISBN 978-1615039760.
7. Инглис, Чарльз Э. (1913). «Напряжения в пластине из-за наличия трещин и острых углов» (PDF) . Труды Института военно-морских архитекторов . 55 : 219–230.
8. Чен Чен; Х.П. Чжан; Й. Немчура; К. Рави-Чандар; М. Мардер (ноябрь 2011 г.). «Масштабирование распространения трещин в резиновых листах». Письма по еврофизике . 96 (3): 36009. Бибкод : 2011EL.....9636009C. дои : 10.1209/0295-5075/96/36009. S2CID  5975098.
9. Перес, Нестор (2016). Механика разрушения (2-е изд.). Springer. ISBN 978-3319249971.
10. Каллистер, Уильям Д. младший (2018). Материаловедение и инженерия: введение (8-е изд.). Wiley. С. 236–237. ISBN 978-1-119-40539-9. OCLC  992798630.
11. Эвальдс, HL (1985). Механика разрушения. RJH Wanhill. Лондон: E. Arnold. ISBN 0-7131-3515-8. OCLC  14377078.
12. Аскеланд, Дональд Р. (январь 2015 г.). Наука и инженерия материалов . Райт, Венделин Дж. (седьмое изд.). Бостон, Массачусетс. С. 236–237. ISBN 978-1-305-07676-1. OCLC  903959750.{{cite book}}: CS1 maint: location missing publisher (link)
13. Улучшенное полуаналитическое решение для напряжения в круглых надрезах, более детальный анализ
14. Кортни, Томас Х. (2000), Механическое поведение материалов (3-е изд.), McGraw Hill, ISBN 1-57766-425-6.
15. Faber, KT; Evans, AG (1 апреля 1983 г.). «Процессы прогиба трещины — I. Теория». Acta Metallurgica . 31 (4): 565–576. doi :10.1016/0001-6160(83)90046-9. ISSN  0001-6160.
16. Пирс, Ф. Т., Дж. Текстильная промышленность. 17 (1926) 355
17. Андерсон, TL (2005). Механика разрушения: основы и приложения (3-е изд.). Бока-Ратон, Флорида. ISBN 978-1-4200-5821-5. OCLC  908077872.{{cite book}}: CS1 maint: location missing publisher (link)

Дальнейшее чтение

• Дитер, GE (1988) Механическая металлургия ISBN 0-07-100406-8 
• A. Garcimartin, A. Guarino, L. Bellon и S. Cilberto (1997) "Статистические свойства предвестников разрушения". Physical Review Letters, 79, 3202 (1997)
• Каллистер-младший, Уильям Д. (2002) Материаловедение и инженерия: Введение. ISBN 0-471-13576-3 
• Питер Рис Льюис, Колин Гэгг, Кен Рейнольдс, CRC Press (2004), Судебная экспертиза материалов: практические примеры .

Внешние ссылки

• Музей отказов компонентов (архив 2016 г.), Открытый университет
• Перелом и реконструкция глиняной чаши
• Вязкий излом