В физике квантовое туннелирование , проникновение барьера или просто туннелирование — квантово-механическое явление, при котором объект, такой как электрон или атом, проходит через потенциальный энергетический барьер , который, согласно классической механике , не должен быть пройден из-за того, что объект не обладает достаточной энергией для прохождения или преодоления барьера.
Туннелирование является следствием волновой природы материи , где квантовая волновая функция описывает состояние частицы или другой физической системы , а волновые уравнения, такие как уравнение Шредингера, описывают их поведение. Вероятность прохождения волнового пакета через барьер экспоненциально уменьшается с высотой барьера, шириной барьера и массой туннелирующей частицы, поэтому туннелирование наиболее заметно в частицах с малой массой, таких как электроны или протоны, туннелирующих через микроскопически узкие барьеры. Туннелирование легко обнаружить с барьерами толщиной около 1–3 нм или меньше для электронов и около 0,1 нм или меньше для более тяжелых частиц, таких как протоны или атомы водорода. [1] Некоторые источники описывают простое проникновение волновой функции в барьер, без прохождения на другую сторону, как эффект туннелирования, например, при туннелировании в стенки конечной потенциальной ямы . [2] [3]
Туннелирование играет важную роль в таких физических явлениях, как ядерный синтез [4] и альфа-радиоактивный распад атомных ядер. Приложения туннелирования включают туннельный диод , [5] квантовые вычисления , флэш-память и сканирующий туннельный микроскоп . Туннелирование ограничивает минимальный размер устройств, используемых в микроэлектронике, поскольку электроны легко туннелируют через изолирующие слои и транзисторы , которые тоньше, чем примерно 1 нм. [6]
Эффект был предсказан в начале 20 века. Его признание как общего физического явления произошло в середине века. [7]
Квантовое туннелирование относится к области квантовой механики . Чтобы понять это явление , частицы, пытающиеся преодолеть потенциальный барьер, можно сравнить с мячом, пытающимся перекатиться через холм. Квантовая механика и классическая механика различаются в своей трактовке этого сценария.
Классическая механика предсказывает, что частицы, не имеющие достаточно энергии для классического преодоления барьера, не могут достичь другой стороны. Таким образом, мяч без достаточной энергии для преодоления холма скатится обратно вниз. В квантовой механике частица может с небольшой вероятностью туннелировать на другую сторону, таким образом пересекая барьер. Причина этого различия заключается в том, что материя рассматривается как имеющая свойства волн и частиц .

Волновая функция физической системы частиц определяет все, что можно знать о системе. [8] Поэтому задачи квантовой механики анализируют волновую функцию системы. Используя математические формулировки, такие как уравнение Шредингера , можно вывести временную эволюцию известной волновой функции. Квадрат абсолютного значения этой волновой функции напрямую связан с распределением вероятностей положений частиц, которое описывает вероятность того, что частицы будут измерены в этих положениях.
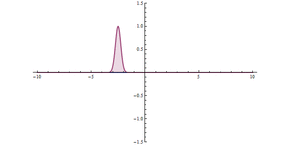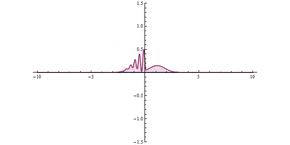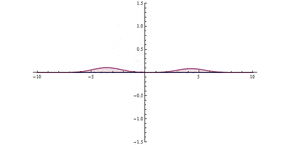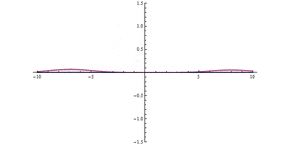
Как показано на анимации, волновой пакет сталкивается с барьером, большая его часть отражается, а часть проходит сквозь барьер. Волновой пакет становится более делокализованным: теперь он находится по обе стороны барьера и имеет меньшую максимальную амплитуду, но равный по интегральному квадрату величины, что означает, что вероятность того, что частица где-то находится, остается равной единице. Чем шире барьер и чем выше энергия барьера, тем ниже вероятность туннелирования.
Некоторые модели туннельного барьера, такие как показанные прямоугольные барьеры , можно проанализировать и решить алгебраически. [9] : 96 Большинство задач не имеют алгебраического решения, поэтому используются численные решения. « Квазиклассические методы » предлагают приближенные решения, которые легче вычислить, такие как приближение ВКБ .
Уравнение Шредингера было опубликовано в 1926 году. Первым человеком, применившим уравнение Шредингера к проблеме, включающей туннелирование между двумя классически разрешенными областями через потенциальный барьер, был Фридрих Хунд в серии статей, опубликованных в 1927 году. Он изучал решения двухъямного потенциала и обсуждал молекулярные спектры . [10] Леонид Мандельштам и Михаил Леонтович независимо друг от друга открыли туннелирование и опубликовали свои результаты в 1928 году. [11]
В 1927 году Лотар Нордхайм , при содействии Ральфа Фаулера , опубликовал статью, в которой обсуждалась термоионная эмиссия и отражение электронов от металлов. Он предположил наличие поверхностного потенциального барьера, который удерживает электроны внутри металла, и показал, что электроны имеют конечную вероятность туннелирования через поверхностный барьер или отражения от него, когда их энергия близка к энергии барьера. Классически электрон либо пропускал, либо отражал со 100% уверенностью, в зависимости от его энергии. В 1928 году Дж. Роберт Оппенгеймер опубликовал две статьи о полевой эмиссии , т. е. эмиссии электронов, вызванной сильными электрическими полями. Нордгейм и Фаулер упростили вывод Оппенгеймера и нашли значения для испускаемых токов и рабочих функций , которые согласуются с экспериментами. [10]
Большим успехом теории туннелирования стало математическое объяснение альфа-распада , которое было разработано в 1928 году Джорджем Гамовым и независимо Рональдом Герни и Эдвардом Кондоном . [12] [13] [14] [15] Последние исследователи одновременно решили уравнение Шредингера для модельного ядерного потенциала и вывели соотношение между периодом полураспада частицы и энергией испускания, которое напрямую зависело от математической вероятности туннелирования. Все три исследователя были знакомы с работами по полевой эмиссии, [10] а Гамов был осведомлен о результатах Мандельштама и Леонтовича. [16]
В ранние дни квантовой теории термин туннельный эффект не использовался, и эффект вместо этого назывался проникновением или просачиванием через барьер. Немецкий термин wellenmechanische Tunneleffekt был использован в 1931 году Вальтером Шоттки. [10] Английский термин туннельный эффект вошел в язык в 1932 году, когда его использовал Яков Френкель в своем учебнике. [10]
В 1957 году Лео Эсаки продемонстрировал туннелирование электронов через барьер шириной в несколько нанометров в полупроводниковой структуре и разработал диод, основанный на туннельном эффекте. [17] В 1960 году, следуя работе Эсаки, Ивар Джайевер экспериментально показал, что туннелирование также имеет место в сверхпроводниках . Спектр туннелирования дал прямое доказательство сверхпроводящей энергетической щели . В 1962 году Брайан Джозефсон предсказал туннелирование сверхпроводящих куперовских пар . Эсаки, Джайевер и Джозефсон разделили Нобелевскую премию по физике 1973 года за свои работы по квантовому туннелированию в твердых телах. [18] [7]
В 1981 году Герд Бинниг и Генрих Рорер разработали новый тип микроскопа, названный сканирующим туннельным микроскопом , который основан на туннелировании и используется для визуализации поверхностей на атомном уровне. Бинниг и Рорер были удостоены Нобелевской премии по физике в 1986 году за свое открытие. [19]
Туннелирование является причиной некоторых важных макроскопических физических явлений.
Туннелирование является источником утечки тока в сверхбольшой интегральной электронике (VLSI) и приводит к существенному потреблению энергии и нагреванию, которые мешают таким устройствам. Это считается нижним пределом того, как могут быть изготовлены элементы микроэлектронных устройств. [20] Туннелирование является фундаментальной техникой, используемой для программирования плавающих затворов флэш-памяти .
Холодная эмиссия электронов имеет отношение к физике полупроводников и сверхпроводников . Она похожа на термоэлектронную эмиссию , когда электроны случайным образом выпрыгивают из поверхности металла, следуя за смещением напряжения, поскольку они статистически оказываются с большей энергией, чем барьер, через случайные столкновения с другими частицами. Когда электрическое поле очень велико, барьер становится достаточно тонким для того, чтобы электроны могли туннелировать из атомного состояния, что приводит к току, который изменяется приблизительно экспоненциально с электрическим полем. [21] Эти материалы важны для флэш-памяти, вакуумных трубок и некоторых электронных микроскопов.
Простой барьер может быть создан путем разделения двух проводников очень тонким изолятором . Это туннельные переходы, изучение которых требует понимания квантового туннелирования. [22] Джозефсоновские переходы используют квантовое туннелирование и сверхпроводимость для создания эффекта Джозефсона . Это имеет применение в точных измерениях напряжений и магнитных полей , [21] а также в многопереходных солнечных элементах .

Диоды — это электрические полупроводниковые приборы , которые пропускают электрический ток в одном направлении больше, чем в другом. Для выполнения своей задачи прибор зависит от обедненного слоя между полупроводниками N-типа и P-типа . Когда они сильно легированы, обедненный слой может быть достаточно тонким для туннелирования. Когда применяется небольшое прямое смещение, ток из-за туннелирования становится значительным. Он имеет максимум в точке, где смещение напряжения таково, что энергетический уровень зон проводимости p и n становится одинаковым. По мере увеличения смещения напряжения две зоны проводимости больше не выстраиваются в линию, и диод действует обычно. [23]
Поскольку туннельный ток быстро падает, можно создать туннельные диоды, которые имеют диапазон напряжений, для которых ток уменьшается с ростом напряжения. Это своеобразное свойство используется в некоторых приложениях, таких как высокоскоростные устройства, где характерная вероятность туннелирования изменяется так же быстро, как и напряжение смещения. [23]
Резонансный туннельный диод использует квантовое туннелирование совершенно иным образом для достижения похожего результата. Этот диод имеет резонансное напряжение, для которого ток благоприятствует определенному напряжению, что достигается путем размещения двух тонких слоев с высокоэнергетической зоной проводимости рядом друг с другом. Это создает квантовую потенциальную яму , которая имеет дискретный самый низкий уровень энергии . Когда этот уровень энергии выше, чем у электронов, туннелирования не происходит, и диод находится в обратном смещении. Как только две энергии напряжения выравниваются, электроны текут как открытый провод. По мере дальнейшего увеличения напряжения туннелирование становится маловероятным, и диод снова действует как обычный диод, прежде чем второй уровень энергии станет заметным. [24]
Европейский исследовательский проект продемонстрировал полевые транзисторы , в которых затвор (канал) управляется посредством квантового туннелирования, а не посредством тепловой инжекции, что снижает напряжение затвора с ≈1 вольта до 0,2 вольта и снижает энергопотребление до 100 раз. Если эти транзисторы можно будет масштабировать до чипов СБИС , они улучшат производительность на единицу мощности интегральных схем . [25] [26]
Хотя модель электропроводности Друде-Лоренца делает превосходные предсказания о природе электронов , проводящих в металлах, ее можно улучшить, используя квантовое туннелирование для объяснения природы столкновений электронов. [21] Когда пакет свободной электронной волны сталкивается с длинным массивом равномерно расположенных барьеров , отраженная часть пакета волны равномерно интерферирует с переданным пакетом между всеми барьерами, так что становится возможной 100% передача. Теория предсказывает, что если положительно заряженные ядра образуют идеально прямоугольный массив, электроны будут туннелировать через металл как свободные электроны, что приведет к чрезвычайно высокой проводимости , и что примеси в металле нарушат ее. [21]
Сканирующий туннельный микроскоп (СТМ), изобретенный Гердом Биннигом и Генрихом Рорером , может позволить получать изображения отдельных атомов на поверхности материала. [21] Он работает, используя связь между квантовым туннелированием и расстоянием. Когда кончик иглы СТМ приближается к поверхности проводимости, которая имеет смещение напряжения, измерение тока электронов, которые туннелируют между иглой и поверхностью, показывает расстояние между иглой и поверхностью. Используя пьезоэлектрические стержни , которые изменяют размер при подаче напряжения, можно регулировать высоту кончика, чтобы поддерживать постоянный туннельный ток. Изменяющиеся во времени напряжения, которые прикладываются к этим стержням, можно регистрировать и использовать для получения изображения поверхности проводника. [21] СТМ имеют точность до 0,001 нм, или около 1% от атомного диаметра. [24]
Квантовое туннелирование является существенным явлением для ядерного синтеза. Температура в звездных ядрах обычно недостаточна для того, чтобы позволить атомным ядрам преодолеть кулоновский барьер и достичь термоядерного синтеза . Квантовое туннелирование увеличивает вероятность проникновения через этот барьер. Хотя эта вероятность все еще мала, чрезвычайно большое количество ядер в ядре звезды достаточно для поддержания устойчивой реакции синтеза. [27]
Радиоактивный распад — это процесс испускания частиц и энергии из нестабильного ядра атома для образования стабильного продукта. Это делается посредством туннелирования частицы из ядра (туннелирование электрона в ядро называется электронным захватом ). Это было первое применение квантового туннелирования. Радиоактивный распад является актуальной проблемой для астробиологии , поскольку это следствие квантового туннелирования создает постоянный источник энергии в течение большого интервала времени для сред за пределами околозвездной обитаемой зоны , где инсоляция была бы невозможна ( подповерхностные океаны ) или неэффективна. [27]
Квантовое туннелирование может быть одним из механизмов гипотетического распада протона . [28] [29]
Химические реакции в межзвездной среде происходят при чрезвычайно низких энергиях. Вероятно, самая фундаментальная ионно-молекулярная реакция включает ионы водорода с молекулами водорода. Скорость квантово-механического туннелирования для той же реакции с использованием изотопа водорода дейтерия , D - + H 2 → H - + HD, была измерена экспериментально в ионной ловушке. Дейтерий был помещен в ионную ловушку и охлажден. Затем ловушка была заполнена водородом. При температурах, используемых в эксперименте, энергетический барьер для реакции не позволил бы реакции успешно пройти с помощью одной только классической динамики. Квантовое туннелирование позволило реакциям происходить в редких столкновениях. Было рассчитано на основе экспериментальных данных, что столкновения происходили одно на сто миллиардов. [30]
В химической кинетике замена легкого изотопа элемента более тяжелым обычно приводит к более медленной скорости реакции. Это обычно объясняется различиями в нулевых колебательных энергиях для химических связей, содержащих более легкие и более тяжелые изотопы, и обычно моделируется с использованием теории переходного состояния . Однако в некоторых случаях наблюдаются большие изотопные эффекты, которые не могут быть учтены полуклассическим подходом, и требуется квантовое туннелирование. RP Bell разработал модифицированный подход к кинетике Аррениуса, который обычно используется для моделирования этого явления. [31]
Включая квантовое туннелирование, можно объяснить астрохимические синтезы различных молекул в межзвездных облаках , такие как синтез молекулярного водорода , воды ( льда ) и важного пребиотического формальдегида . [27] Туннелирование молекулярного водорода наблюдалось в лабораторных условиях. [32]
Квантовое туннелирование является одним из центральных нетривиальных квантовых эффектов в квантовой биологии . [33] Здесь оно важно как электронное туннелирование, так и протонное туннелирование . Электронное туннелирование является ключевым фактором во многих биохимических окислительно-восстановительных реакциях ( фотосинтез , клеточное дыхание ), а также в ферментативном катализе. Протонное туннелирование является ключевым фактором в спонтанной мутации ДНК . [27]
Спонтанная мутация происходит, когда нормальная репликация ДНК происходит после того, как особенно значимый протон туннелировал. [34] Водородная связь соединяет пары оснований ДНК. Двойной потенциал вдоль водородной связи разделяет потенциальный энергетический барьер. Считается, что двойной потенциал асимметричен, причем одна яма глубже другой, так что протон обычно находится в более глубокой яме. Для того чтобы произошла мутация, протон должен туннелировать в более мелкую яму. Движение протона из его обычного положения называется таутомерным переходом . Если репликация ДНК происходит в этом состоянии, правило спаривания оснований для ДНК может быть поставлено под угрозу, что приведет к мутации. [35] Пер-Олов Лоудин был первым, кто разработал эту теорию спонтанной мутации внутри двойной спирали . Другие примеры мутаций, вызванных квантовым туннелированием, в биологии, как полагают, являются причиной старения и рака. [36]

Не зависящее от времени уравнение Шредингера для одной частицы в одном измерении можно записать как или где
Решения уравнения Шредингера принимают различные формы для различных значений x в зависимости от того, является ли M ( x ) положительным или отрицательным. Когда M ( x ) является постоянным и отрицательным, то уравнение Шредингера можно записать в виде
Решения этого уравнения представляют собой бегущие волны с постоянной фазой + k или − k . В качестве альтернативы, если M ( x ) является постоянной и положительной, то уравнение Шредингера можно записать в виде
Решения этого уравнения представляют собой восходящие и нисходящие экспоненты в форме затухающих волн . Когда M ( x ) изменяется в зависимости от положения, возникает та же разница в поведении, в зависимости от того, является ли M(x) отрицательным или положительным. Из этого следует, что знак M ( x ) определяет природу среды, причем отрицательный M ( x ) соответствует среде A, а положительный M ( x ) соответствует среде B. Таким образом, из этого следует, что связь затухающих волн может возникнуть, если область положительного M ( x ) зажата между двумя областями отрицательного M ( x ), тем самым создавая потенциальный барьер.
Математика работы с ситуацией, когда M ( x ) меняется в зависимости от x , сложна, за исключением особых случаев, которые обычно не соответствуют физической реальности. Полное математическое рассмотрение представлено в монографии Фрёмана и Фрёмана 1965 года. Их идеи не были включены в учебники физики, но их поправки имеют небольшой количественный эффект.
Волновая функция выражается как экспонента функции:, где затем разделяется на действительную и мнимую части: где A ( x ) и B ( x ) — действительные функции.
Подставляя второе уравнение в первое и используя тот факт, что действительная часть должна быть равна 0, получаем:
Чтобы решить это уравнение с использованием полуклассического приближения, каждая функция должна быть разложена в степенной ряд по . Из уравнений степенной ряд должен начинаться по крайней мере с порядка , чтобы удовлетворить действительную часть уравнения; для хорошего классического предела предпочтительнее начинать с максимально возможной степени постоянной Планка , что приводит к и со следующими ограничениями на члены самого низкого порядка, и
Здесь можно рассмотреть два крайних случая.
Случай 1
Если амплитуда меняется медленно по сравнению с фазой и что соответствует классическому движению. Разрешение следующего порядка расширения дает
Случай 2
Если фаза меняется медленно по сравнению с амплитудой, и что соответствует туннелированию. Разрешение следующего порядка расширения дает
В обоих случаях из знаменателя видно, что оба эти приближенных решения плохи вблизи классических точек поворота . Вдали от потенциального холма частица ведет себя подобно свободной и колеблющейся волне; под потенциальным холмом частица претерпевает экспоненциальные изменения амплитуды. Рассматривая поведение в этих пределах и классических точках поворота, можно получить глобальное решение.
Для начала выбирается классическая точка поворота и раскладывается в степенной ряд по следующим параметрам :
Сохранение только члена первого порядка обеспечивает линейность:
Используя это приближение, уравнение становится дифференциальным уравнением :
Эту задачу можно решить, используя функции Эйри в качестве решений.
Принимая эти решения для всех классических точек поворота, можно сформировать глобальное решение, связывающее предельные решения. Учитывая два коэффициента по одну сторону классической точки поворота, два коэффициента по другую сторону классической точки поворота можно определить, используя это локальное решение для их соединения.
Следовательно, решения функции Эйри будут асимптотироваться в синус, косинус и показательную функцию в соответствующих пределах. Отношения между и являются и
С найденными коэффициентами можно найти глобальное решение. Таким образом, коэффициент пропускания для частицы, туннелирующей через одиночный потенциальный барьер, равен где находятся две классические точки поворота для потенциального барьера.
Для прямоугольного барьера это выражение упрощается до:
Некоторые физики утверждают, что частицы со спином ноль могут перемещаться быстрее скорости света при туннелировании. [7] Это, по-видимому, нарушает принцип причинности , поскольку тогда существует система отсчета , в которой частица появляется до того, как она покинула ее. В 1998 году Фрэнсис Э. Лоу кратко рассмотрел явление туннелирования с нулевым временем. [37] Совсем недавно экспериментальные данные о времени туннелирования фононов , фотонов и электронов были опубликованы Гюнтером Нимцем . [38] Другой эксперимент, проведенный под руководством AM Steinberg , по-видимому, указывает на то, что частицы могут туннелировать с кажущейся скоростью, превышающей скорость света. [39] [40]
Другие физики, такие как Герберт Уинфул [41] , оспаривали эти утверждения. Уинфул утверждал, что волновой пакет туннелирующей частицы распространяется локально, поэтому частица не может туннелировать через барьер нелокально. Уинфул также утверждал, что эксперименты, которые якобы показывают нелокальное распространение, были неверно истолкованы. В частности, групповая скорость волнового пакета не измеряет его скорость, но связана с количеством времени, в течение которого волновой пакет хранится в барьере. Более того, если квантовое туннелирование моделируется с помощью релятивистского уравнения Дирака , хорошо обоснованные математические теоремы подразумевают, что процесс полностью субсветовой. [42] [43]

Концепция квантового туннелирования может быть расширена до ситуаций, когда существует квантовый транспорт между классически не связанными областями, даже если нет связанного потенциального барьера. Это явление известно как динамическое туннелирование. [44] [45]
Концепция динамического туннелирования особенно подходит для решения проблемы квантового туннелирования в высоких размерностях (d>1). В случае интегрируемой системы , где ограниченные классические траектории ограничены торами в фазовом пространстве , туннелирование можно понимать как квантовый перенос между полуклассическими состояниями, построенными на двух различных, но симметричных торах. [46]
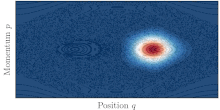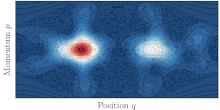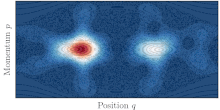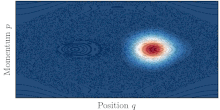
В реальной жизни большинство систем не интегрируемы и демонстрируют различные степени хаоса. Классическая динамика тогда считается смешанной, а фазовое пространство системы обычно состоит из островов регулярных орбит, окруженных большим морем хаотических орбит. Существование хаотического моря, где классически разрешен транспорт, между двумя симметричными торами затем способствует квантовому туннелированию между ними. Это явление называется туннелированием с помощью хаоса. [47] и характеризуется резкими резонансами скорости туннелирования при изменении любого параметра системы.
Когда мал по сравнению с размером регулярных островов, тонкая структура классического фазового пространства играет ключевую роль в туннелировании. В частности, два симметричных тора связаны "через последовательность классически запрещенных переходов через нелинейные резонансы", окружающие два острова. [48]
Несколько явлений ведут себя так же, как квантовое туннелирование. Два примера — это связь затухающих волн [49] (применение волнового уравнения Максвелла к свету ) и применение недисперсионного волнового уравнения из акустики, применяемого к «волнам на струнах» . [ требуется цитата ]
Эти эффекты моделируются аналогично прямоугольному потенциальному барьеру . В этих случаях одна передающая среда , через которую распространяется волна , является одинаковой или почти одинаковой на всем протяжении, и вторая среда, через которую волна распространяется по-другому. Это можно описать как тонкую область среды B между двумя областями среды A. Анализ прямоугольного барьера с помощью уравнения Шредингера можно адаптировать к этим другим эффектам при условии, что волновое уравнение имеет решения в виде бегущей волны в среде A, но действительные экспоненциальные решения в среде B.
В оптике среда A — это вакуум, а среда B — это стекло. В акустике среда A может быть жидкостью или газом, а среда B — твердым телом. В обоих случаях среда A — это область пространства, где полная энергия частицы больше ее потенциальной энергии , а среда B — это потенциальный барьер. Они имеют входящую волну и результирующие волны в обоих направлениях. Может быть больше сред и барьеров, и барьеры не обязательно должны быть дискретными. В этом случае полезны приближения.
Первоначально классическая ассоциация волна-частица была проанализирована как аналог квантового туннелирования [50] , но последующий анализ обнаружил причину динамики жидкости, связанную с вертикальным импульсом, передаваемым частицам вблизи барьера. [51]
Но квантовые частицы способны туннелировать в классически запрещенную область ...
в барьер (стенку) возможно.
Хунд ... был первым, кто использовал квантово-механическое проникновение через барьер ...