Кубическое уравнение

Полиномиальное уравнение 3-й степени

График кубической функции с 3 действительными корнями (где кривая пересекает горизонтальную ось при y = 0 ). Показанный случай имеет две критические точки . Здесь функция равна и, следовательно, три действительных корня равны 2, −1 и −4. ${\displaystyle {\begin{aligned}f(x)&={\frac {1}{4}}\left(x^{3}+3x^{2}-6x-8\right)\\&={\frac {1}{4}}(x-2)(x+1)(x+4)\end{aligned}}}$

В алгебре кубическое уравнение с одной переменной — это уравнение вида , в котором a не равно нулю. $${\displaystyle ax^{3}+bx^{2}+cx+d=0}$$

Решения этого уравнения называются корнями кубической функции, определяемой левой частью уравнения. Если все коэффициенты a , b , c и d кубического уравнения являются действительными числами , то оно имеет по крайней мере один действительный корень (это верно для всех полиномиальных функций нечетной степени ). Все корни кубического уравнения можно найти следующими способами:

• алгебраически : точнее, их можно выразить кубической формулой , включающей четыре коэффициента, четыре основные арифметические операции , квадратные корни и кубические корни . (Это также верно для квадратных (второй степени) и четвертых (четвертой степени) уравнений, но не для уравнений более высоких степеней, согласно теореме Абеля–Руффини .)
• тригонометрически
• Численные приближения корней можно найти с помощью алгоритмов поиска корней, таких как метод Ньютона .

Коэффициенты не обязательно должны быть действительными числами. Многое из того, что рассматривается ниже, справедливо для коэффициентов в любом поле с характеристикой , отличной от 2 и 3. Решения кубического уравнения не обязательно принадлежат к тому же полю, что и коэффициенты. Например, некоторые кубические уравнения с рациональными коэффициентами имеют корни, которые являются иррациональными (и даже недействительными) комплексными числами .

История

Кубические уравнения были известны древним вавилонянам, грекам, китайцам, индийцам и египтянам. ^{[1] [2] [3] Были найдены} вавилонские (20–16 вв. до н. э.) клинописные таблички с таблицами для вычисления кубов и кубических корней. ^{[4] [5]} Вавилоняне могли использовать таблицы для решения кубических уравнений, но нет никаких доказательств, подтверждающих, что они это делали. ^[6] Задача удвоения куба включает в себя простейшее и старейшее изученное кубическое уравнение, и то, для которого древние египтяне не верили, что существует решение. ^[7] В V веке до н. э. Гиппократ свел эту задачу к нахождению двух средних пропорциональных между одной линией и другой, удвоенной ее длины, но не смог решить ее с помощью построения циркуля и линейки , ^[8] задача, которая, как теперь известно, невыполнима. Методы решения кубических уравнений описаны в «Девяти главах математического искусства» — китайском математическом тексте, составленном около II века до н. э. и прокомментированном Лю Хуэем в III веке. ^[2]

В 3 веке нашей эры греческий математик Диофант нашел целочисленные или рациональные решения для некоторых двумерных кубических уравнений ( диофантовы уравнения ). ^{[3] [9]} Считается, что Гиппократ, Менехм и Архимед приблизились к решению задачи удвоения куба с использованием пересекающихся конических сечений , ^[8] хотя историки, такие как Ревиэль Нец, спорят, думали ли греки о кубических уравнениях или просто о задачах, которые могут привести к кубическим уравнениям. Некоторые другие, такие как Т. Л. Хит , который перевел все работы Архимеда, не согласны, выдвигая доказательства того, что Архимед действительно решал кубические уравнения с использованием пересечений двух коник , но также обсуждал условия, при которых корни равны 0, 1 или 2. ^[10]

График кубической функции f ( x ) = 2 x ³  − 3 x ²  − 3 x  + 2 = ( x  + 1) (2 x  − 1) ( x  − 2)

В VII веке астроном-математик династии Тан Ван Сяотун в своем математическом трактате под названием «Цзигу Суаньцзин» систематически установил и численно решил 25 кубических уравнений вида x ³ + px ² + qx = N , 23 из них с p , q ≠ 0 и два из них с q = 0. [ ^11]

В XI веке персидский поэт-математик Омар Хайям (1048–1131) добился значительного прогресса в теории кубических уравнений. В одной из ранних работ он открыл, что кубическое уравнение может иметь более одного решения, и заявил, что его нельзя решить с помощью построений циркулем и линейкой. Он также нашел геометрическое решение. ^{[12] [a]} В своей более поздней работе « Трактат о демонстрации проблем алгебры » он написал полную классификацию кубических уравнений с общими геометрическими решениями, найденными с помощью пересекающихся конических сечений . ^{[13] [14]} Хайям предпринял попытку придумать алгебраическую формулу для извлечения кубических корней. Он писал:

«Мы пытались выразить эти корни алгеброй, но потерпели неудачу. Однако, возможно, что люди, которые придут после нас, добьются успеха». ^[15]

В XII веке индийский математик Бхаскара II попытался решить кубические уравнения, но безуспешно. Однако он привел один пример кубического уравнения: x ³ + 12 x = 6 x ² + 35 . ^[16] В XII веке другой персидский математик, Шараф ад-Дин ат-Туси (1135–1213), написал « Аль-Муадалат» ( Трактат об уравнениях ), в котором рассматривались восемь типов кубических уравнений с положительными решениями и пять типов кубических уравнений , которые могут не иметь положительных решений. Он использовал то, что позже стало известно как метод Хорнера–Руффини, для численного приближения корня кубического уравнения. Он также использовал концепции максимумов и минимумов кривых для решения кубических уравнений, которые могут не иметь положительных решений. ^[17] Он понимал важность дискриминанта кубического уравнения для нахождения алгебраических решений определенных типов кубических уравнений. ^[18]

В своей книге Flos Леонардо де Пизанский, также известный как Фибоначчи (1170–1250), смог близко приблизиться к положительному решению кубического уравнения x ³ + 2 x ² + 10 x = 20. Записав вавилонскими цифрами, он дал результат как 1,22,7,42,33,4,40 (что эквивалентно 1 + 22/60 + 7/60 ²  + 42/60 ³  + 33/60 ⁴  + 4/60 ⁵  + 40/60 ⁶ ), что имеет относительную погрешность около 10 ⁻⁹ . ^[19]

В начале XVI века итальянский математик Сципионе дель Ферро (1465–1526) нашел метод решения класса кубических уравнений, а именно уравнений вида x ³ + mx = n . Фактически, все кубические уравнения можно привести к этой форме, если допустить, что m и n отрицательны, но отрицательные числа в то время ему не были известны. Дель Ферро хранил свое достижение в секрете до самой смерти, пока не рассказал о нем своему ученику Антонио Фиору.

Никколо Фонтана Тарталья

В 1535 году Никколо Тарталья (1500–1557) получил от Зуанне да Кои две задачи на кубические уравнения и объявил, что может их решить. Вскоре ему бросил вызов Фиор, что привело к знаменитому состязанию между ними. Каждый участник должен был внести определенную сумму денег и предложить своему сопернику ряд задач для решения. Тот, кто решит больше задач в течение 30 дней, получит все деньги. Тарталья получил вопросы в виде x ³ + mx = n , для которых он разработал общий метод. Фиор получил вопросы в виде x ³ + mx ² = n , которые оказались для него слишком сложными для решения, и Тарталья выиграл состязание.

Позже Джероламо Кардано (1501–1576) убедил Тарталью раскрыть свой секрет решения кубических уравнений. В 1539 году Тарталья сделал это только при условии, что Кардано никогда его не раскроет, и что если он действительно напишет книгу о кубических уравнениях, то даст Тарталье время для публикации. Несколько лет спустя Кардано узнал о предыдущей работе дель Ферро и опубликовал метод дель Ферро в своей книге Ars Magna в 1545 году, то есть Кардано дал Тарталье шесть лет на публикацию своих результатов (при этом Тарталье присудили премию за независимое решение).

Обещание Кардано Тарталье гласило, что он не опубликует работу Тартальи, и Кардано чувствовал, что он публикует работу дель Ферро, чтобы обойти обещание. Тем не менее, это привело к вызову Кардано от Тартальи, который Кардано отверг. Вызов в конечном итоге был принят учеником Кардано Лодовико Феррари (1522–1565). Феррари превзошел Тарталью в соревновании, и Тарталья потерял и свой престиж, и свой доход. ^[20]

Кардано заметил, что метод Тартальи иногда требовал от него извлечения квадратного корня из отрицательного числа. Он даже включил расчет с этими комплексными числами в Ars Magna , но он не очень его понимал. Рафаэль Бомбелли подробно изучал этот вопрос ^[21] и поэтому часто считается первооткрывателем комплексных чисел.

Франсуа Виет (1540–1603) независимо вывел тригонометрическое решение для кубического уравнения с тремя действительными корнями, а Рене Декарт (1596–1650) расширил работу Виета. ^[22]

Факторизация

Если коэффициенты кубического уравнения являются рациональными числами , можно получить эквивалентное уравнение с целыми коэффициентами, умножив все коэффициенты на общее кратное их знаменателей. Такое уравнение с целыми коэффициентами называется приводимым , если многочлен в левой части является произведением многочленов меньших степеней. По лемме Гаусса , если уравнение приводимо, можно предположить, что множители имеют целые коэффициенты. $${\displaystyle ax^{3}+bx^{2}+cx+d=0,}$$

Найти корни приводимого кубического уравнения проще, чем решить общий случай. Фактически, если уравнение приводимо, один из множителей должен иметь степень один, и, таким образом, иметь вид, где q и p являются взаимно простыми целыми числами . Тест на рациональные корни позволяет найти q и p, рассмотрев конечное число случаев (потому что q должен быть делителем a , а p должен быть делителем d ). $${\displaystyle qx-p}$$

Таким образом, один корень равен , а другие корни являются корнями другого множителя, который можно найти путем деления полинома в столбик . Этот другой множитель равен (Коэффициенты, похоже, не являются целыми числами, но должны быть целыми числами, если p / q является корнем.) ${\displaystyle \textstyle x_{1}={\frac {p}{q}},}$ $${\displaystyle {\frac {a}{q}}x^{2}+{\frac {bq+ap}{q^{2}}}x+{\frac {cq^{2}+bpq+ap^{2}}{q^{3}}}}$$

Тогда остальные корни являются корнями этого квадратного многочлена и могут быть найдены с помощью квадратной формулы .

Пониженный кубический

Кубики вида называются подавленными. Они намного проще общих кубиков, но являются фундаментальными, поскольку изучение любой кубики может быть сведено простой заменой переменной к изучению подавленной кубики. $${\displaystyle t^{3}+pt+q}$$

Пусть будет кубическим уравнением. Замена переменной дает кубическое уравнение (по t ), не имеющее члена по t ² . $${\displaystyle ax^{3}+bx^{2}+cx+d=0}$$ $${\displaystyle x=t-{\frac {b}{3a}}}$$

После деления на единицу получаем подавленное кубическое уравнение с $${\displaystyle t^{3}+pt+q=0,}$$ $${\displaystyle {\begin{aligned}t={}&x+{\frac {b}{3a}}\\p={}&{\frac {3ac-b^{2}}{3a^{2}}}\\q={}&{\frac {2b^{3}-9abc+27a^{2}d}{27a^{3}}}.\end{aligned}}}$$

Корни исходного уравнения связаны с корнями подавленного уравнения соотношениями для . ${\displaystyle x_{1},x_{2},x_{3}}$ ${\displaystyle t_{1},t_{2},t_{3}}$ $${\displaystyle x_{i}=t_{i}-{\frac {b}{3a}},}$$ ${\displaystyle i=1,2,3}$

Дискриминант и природа корней

Характер (действительный или нет, различимый или нет) корней кубического уравнения можно определить без их явного вычисления, используя дискриминант .

Дискриминант

Дискриминант многочлена — это функция его коэффициентов, которая равна нулю тогда и только тогда, когда многочлен имеет кратный корень , или, если он делится на квадрат многочлена, отличного от константы. Другими словами, дискриминант не равен нулю тогда и только тогда, когда многочлен свободен от квадратов .

Если r ₁ , r ₂ , r ₃ являются тремя корнями (не обязательно различными и действительными ) кубического уравнения , то дискриминант равен ${\displaystyle ax^{3}+bx^{2}+cx+d,}$ $${\displaystyle a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}.}$$

Дискриминант подавленной кубической функции равен ${\displaystyle t^{3}+pt+q}$ $${\displaystyle -\left(4\,p^{3}+27\,q^{2}\right).}$$

Дискриминант общей кубической матрицы равен Это произведение и дискриминанта соответствующей пониженной кубической матрицы. Используя формулу, связывающую общую кубическую матрицу и соответствующую пониженную кубическую матрицу, это означает, что дискриминант общей кубической матрицы можно записать как ${\displaystyle ax^{3}+bx^{2}+cx+d}$ $${\displaystyle 18\,abcd-4\,b^{3}d+b^{2}c^{2}-4\,ac^{3}-27\,a^{2}d^{2}.}$$ ${\displaystyle a^{4}}$ $${\displaystyle {\frac {4(b^{2}-3ac)^{3}-(2b^{3}-9abc+27a^{2}d)^{2}}{27a^{2}}}.}$$

Из этого следует, что один из этих двух дискриминантов равен нулю тогда и только тогда, когда другой также равен нулю, и если коэффициенты действительны , два дискриминанта имеют одинаковый знак. Подводя итог, можно сказать, что из любого из этих двух дискриминантов можно вывести одну и ту же информацию.

Для доказательства предыдущих формул можно использовать формулы Виета , чтобы выразить все как многочлены от r ₁ , r ₂ , r ₃ и a . Доказательство тогда приводит к проверке равенства двух многочленов.

Природа корней

Если коэффициенты многочлена являются действительными числами , а его дискриминант не равен нулю, возможны два случая: ${\displaystyle \Delta }$

• Если кубическое уравнение имеет три различных действительных корня ${\displaystyle \Delta >0,}$
• Если кубическое уравнение имеет один действительный корень и два недействительных комплексно-сопряженных корня. ${\displaystyle \Delta <0,}$

Это можно доказать следующим образом. Во-первых, если r — корень многочлена с действительными коэффициентами, то его комплексно-сопряженный корень также является корнем. Таким образом, недействительные корни, если таковые имеются, встречаются как пары комплексно-сопряженных корней. Поскольку кубический многочлен имеет три корня (не обязательно различных) по основной теореме алгебры , по крайней мере один корень должен быть действительным.

Как указано выше, если r ₁ , r ₂ , r ₃ являются тремя корнями кубического уравнения , то дискриминант равен ${\displaystyle ax^{3}+bx^{2}+cx+d}$ $${\displaystyle \Delta =a^{4}(r_{1}-r_{2})^{2}(r_{1}-r_{3})^{2}(r_{2}-r_{3})^{2}}$$

Если три корня действительны и различны, то дискриминант является произведением положительных действительных чисел, то есть ${\displaystyle \Delta >0.}$

Если только один корень, скажем r ₁ , является действительным, то r ₂ и r ₃ являются комплексно сопряженными числами, что подразумевает, что r ₂ – r ₃ является чисто мнимым числом , и, таким образом, что ( r ₂ – r ₃ ) ² является действительным и отрицательным. С другой стороны, r ₁ – r ₂ и r ₁ – r ₃ являются комплексно сопряженными числами, и их произведение является действительным и положительным. ^[23] Таким образом, дискриминант является произведением одного отрицательного числа и нескольких положительных. То есть ${\displaystyle \Delta <0.}$

Множественный корень

Если дискриминант кубического уравнения равен нулю, то кубическое уравнение имеет кратный корень . Если к тому же его коэффициенты действительны, то все его корни действительны.

Дискриминант подавленной кубической функции равен нулю, если Если p также равно нулю, то p = q = 0 , а 0 — тройной корень кубической функции. Если и p ≠ 0 , то кубическая функция имеет простой корень ${\displaystyle t^{3}+pt+q}$ ${\displaystyle 4p^{3}+27q^{2}=0.}$ ${\displaystyle 4p^{3}+27q^{2}=0,}$ $${\displaystyle t_{1}={\frac {3q}{p}}}$$

и двойной корень $${\displaystyle t_{2}=t_{3}=-{\frac {3q}{2p}}.}$$

Другими словами, $${\displaystyle t^{3}+pt+q=\left(t-{\frac {3q}{p}}\right)\left(t+{\frac {3q}{2p}}\right)^{2}.}$$

Этот результат можно доказать, разложив последнее произведение, или получить, решив довольно простую систему уравнений, полученную из формул Виета .

Используя редукцию подавленной кубики, эти результаты можно распространить на общую кубику. Это дает: Если дискриминант кубики равен нулю, то ${\displaystyle ax^{3}+bx^{2}+cx+d}$

• либо, если кубический имеет тройной корень и ${\displaystyle b^{2}=3ac,}$ $${\displaystyle x_{1}=x_{2}=x_{3}=-{\frac {b}{3a}},}$$ $${\displaystyle ax^{3}+bx^{2}+cx+d=a\left(x+{\frac {b}{3a}}\right)^{3}}$$
• или, если кубический имеет двойной корень и простой корень, и таким образом ${\displaystyle b^{2}\neq 3ac,}$ $${\displaystyle x_{2}=x_{3}={\frac {9ad-bc}{2(b^{2}-3ac)}},}$$ $${\displaystyle x_{1}={\frac {4abc-9a^{2}d-b^{3}}{a(b^{2}-3ac)}}.}$$ $${\displaystyle ax^{3}+bx^{2}+cx+d=a(x-x_{1})(x-x_{2})^{2}.}$$

Характеристика 2 и 3

Приведенные выше результаты справедливы, когда коэффициенты относятся к полю характеристики , отличной от 2 или 3, но должны быть изменены для характеристики 2 или 3 из-за задействованных делений на 2 и 3.

Редукция к подавленной кубической функции работает для характеристики 2, но не для характеристики 3. Однако в обоих случаях проще установить и сформулировать результаты для общей кубической функции. Основным инструментом для этого является тот факт, что кратный корень является общим корнем многочлена и его формальной производной . В этих характеристиках, если производная не является константой, она является линейным многочленом в характеристике 3 и является квадратом линейного многочлена в характеристике 2. Следовательно, как для характеристики 2, так и для характеристики 3 производная имеет только один корень. Это позволяет вычислить кратный корень, а третий корень может быть выведен из суммы корней, что обеспечивается формулами Виета .

Отличие от других характеристик состоит в том, что в характеристике 2 формула для двойного корня включает квадратный корень, а в характеристике 3 формула для тройного корня включает кубический корень.

Формула Кардано

Джероламо Кардано приписывают публикацию первой формулы для решения кубических уравнений, приписывая ее Сципионе дель Ферро и Никколо Фонтана Тарталья . Формула применима к подавленным кубическим уравнениям, но, как показано в § Подавленные кубические уравнения, она позволяет решать все кубические уравнения.

Результат Кардано заключается в том, что если — кубическое уравнение, такое, что p и q — действительные числа, причем положительное (это означает, что дискриминант уравнения отрицателен), то уравнение имеет действительный корень , где и — два числа и $${\displaystyle t^{3}+pt+q=0}$$ ${\displaystyle {\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}$ $${\displaystyle {\sqrt[{3}]{u_{1}}}+{\sqrt[{3}]{u_{2}}},}$$ ${\displaystyle u_{1}}$ ${\displaystyle u_{2}}$ ${\displaystyle -{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}$ ${\displaystyle -{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}.}$

Несколько методов получения этого результата см. в разделе «Вывод корней» ниже.

Как показано в § Природа корней, два других корня являются недействительными комплексно-сопряженными числами в этом случае. Позже было показано (Кардано не знал комплексных чисел ), что два других корня получаются путем умножения одного из кубических корней на примитивный кубический корень единицы , а другого кубического корня на другой примитивный кубический корень единицы . То есть, другие корни уравнения — это и ^[24] ${\displaystyle \varepsilon _{1}={\frac {-1+i{\sqrt {3}}}{2}},}$ ${\displaystyle \varepsilon _{2}=\varepsilon _{1}^{2}={\frac {-1-i{\sqrt {3}}}{2}}.}$ ${\displaystyle \varepsilon _{1}{\sqrt[{3}]{u_{1}}}+\varepsilon _{2}{\sqrt[{3}]{u_{2}}}}$ ${\displaystyle \varepsilon _{2}{\sqrt[{3}]{u_{1}}}+\varepsilon _{1}{\sqrt[{3}]{u_{2}}}.}$

Если есть три действительных корня, но теория Галуа позволяет доказать, что если нет рационального корня, корни не могут быть выражены алгебраическим выражением, включающим только действительные числа. Следовательно, уравнение не может быть решено в этом случае со знаниями времен Кардано. Этот случай поэтому был назван casus irreducibilis , что означает неприводимый случай на латыни. ${\displaystyle 4p^{3}+27q^{2}<0,}$

In casus irreducibilis формула Кардано все еще может быть использована, но при использовании кубических корней требуется некоторая осторожность. Первый метод заключается в определении символов и как представляющих главные значения корневой функции (то есть корня, имеющего наибольшую действительную часть). При таком соглашении формула Кардано для трех корней остается действительной, но не является чисто алгебраической, поскольку определение главной части не является чисто алгебраическим, поскольку оно включает неравенства для сравнения действительных частей. Кроме того, использование главного кубического корня может дать неправильный результат, если коэффициенты не являются действительными комплексными числами. Более того, если коэффициенты принадлежат другому полю , главный кубический корень в общем случае не определен. ${\displaystyle {\sqrt {{~}^{~}}}}$ ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$

Второй способ сделать формулу Кардано всегда правильной — это заметить, что произведение двух кубических корней должно быть – p / 3 . Это приводит к тому, что корень уравнения равен В этой формуле символы и обозначают любой квадратный корень и любой кубический корень. Другие корни уравнения получаются либо путем изменения кубического корня, либо, что эквивалентно, путем умножения кубического корня на примитивный кубический корень из единицы, то есть $${\displaystyle C-{\frac {p}{3C}}\quad {\text{with}}\quad C={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$$ ${\displaystyle {\sqrt {{~}^{~}}}}$ ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$ ${\displaystyle \textstyle {\frac {-1\pm {\sqrt {-3}}}{2}}.}$

Эта формула для корней всегда верна, за исключением случая, когда p = q = 0 , при условии, что если p = 0 , квадратный корень выбирается так, что C ≠ 0. Однако формула Кардано бесполезна, если корни являются кубическими корнями Аналогично, формула бесполезна и в случаях, когда кубический корень не нужен, то есть когда кубический многочлен не является неприводимым ; это включает случай ${\displaystyle p=0,}$ ${\displaystyle -q.}$ ${\displaystyle 4p^{3}+27q^{2}=0.}$

Эта формула также верна, когда p и q принадлежат любому полю характеристики , отличной от 2 или 3.

Общая кубическая формула

Кубическая формула для корней общего кубического уравнения (с a ≠ 0 ) может быть выведена из каждого варианта формулы Кардано путем сведения к подавленной кубической. Представленный здесь вариант действителен не только для действительных коэффициентов, но и для коэффициентов a , b , c , d , принадлежащих любому полю характеристики , отличной от 2 или 3. Если коэффициенты являются действительными числами, формула охватывает все комплексные решения, а не только действительные. $${\displaystyle ax^{3}+bx^{2}+cx+d=0}$$

Поскольку формула довольно сложная, имеет смысл разбить ее на более мелкие формулы.

Позволять $${\displaystyle {\begin{aligned}\Delta _{0}&=b^{2}-3ac,\\\Delta _{1}&=2b^{3}-9abc+27a^{2}d.\end{aligned}}}$$

(Оба могут быть выражены как результирующие кубические функции и их производные: ⁠ ${\displaystyle \Delta _{0}}$ ${\displaystyle \Delta _{1}}$ ${\displaystyle \Delta _{1}}$−1/8 а⁠ умножить на результат кубической функции и ее второй производной, иэто ⁠ ${\displaystyle \Delta _{0}}$−1/12 а⁠ умножить на результат первой и второй производных кубического многочлена.)

Тогда пусть символы и интерпретируются как любой квадратный корень и любой кубический корень соответственно (каждое ненулевое комплексное число имеет два квадратных корня и три кубических корня). Знак " ± " перед квадратным корнем может быть либо " + ", либо " – "; выбор почти произволен, и его изменение равносильно выбору другого квадратного корня. Однако, если выбор дает C = 0 (это происходит, если ), то вместо него должен быть выбран другой знак. Если оба выбора дают C = 0 , то есть если дробь ⁠ $${\displaystyle C={\sqrt[{3}]{\frac {\Delta _{1}\pm {\sqrt {\Delta _{1}^{2}-4\Delta _{0}^{3}}}}{2}}},}$$ ${\displaystyle {\sqrt {{~}^{~}}}}$ ${\displaystyle {\sqrt[{3}]{{~}^{~}}}}$ ${\displaystyle \Delta _{0}=0}$ ${\displaystyle \Delta _{0}=\Delta _{1}=0,}$0/0⁠ встречается в следующих формулах; эта дробь должна интерпретироваться как равная нулю (см. конец этого раздела). При этих соглашениях один из корней равен $${\displaystyle x=-{\frac {1}{3a}}\left(b+C+{\frac {\Delta _{0}}{C}}\right){\text{.}}}$$

Остальные два корня можно получить, изменив выбор кубического корня в определении C , или, что эквивалентно, умножив C на примитивный кубический корень из единицы , то есть ⁠–1 ± √ –3/2⁠ . Другими словами, три корня находятся там, где ξ = ⁠ $${\displaystyle x_{k}=-{\frac {1}{3a}}\left(b+\xi ^{k}C+{\frac {\Delta _{0}}{\xi ^{k}C}}\right),\qquad k\in \{0,1,2\}{\text{,}}}$$–1 + √ –3/2⁠ .

Что касается особого случая подавленной кубической, эта формула применима, но бесполезна, когда корни могут быть выражены без кубических корней. В частности, если формула дает, что три корня равны , что означает, что кубический многочлен может быть разложен на множители как Прямое вычисление позволяет проверить, что существование этой факторизации эквивалентно с ${\displaystyle \Delta _{0}=\Delta _{1}=0,}$ ${\displaystyle {\frac {-b}{3a}},}$ ${\displaystyle \textstyle a(x+{\frac {b}{3a}})^{3}.}$ ${\displaystyle \Delta _{0}=\Delta _{1}=0.}$

Тригонометрические и гиперболические решения

Тригонометрическое решение для трех действительных корней

Когда кубическое уравнение с действительными коэффициентами имеет три действительных корня, формулы, выражающие эти корни через радикалы, включают комплексные числа. Теория Галуа позволяет доказать, что когда три корня действительны, и ни один из них не является рациональным ( casus irreducibilis ), нельзя выразить корни через действительные радикалы. Тем не менее, чисто действительные выражения решений могут быть получены с использованием тригонометрических функций , в частности, через косинусы и арккосинусы . ^[25] Точнее, корни подавленной кубической системы равны ^[26] $${\displaystyle t^{3}+pt+q=0}$$ $${\displaystyle t_{k}=2\,{\sqrt {-{\frac {p}{3}}}}\,\cos \left[\,{\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\,\right)-{\frac {2\pi k}{3}}\,\right]\qquad {\text{for }}k=0,1,2.}$$

Эта формула принадлежит Франсуа Виет . ^[22] Она чисто вещественна, когда уравнение имеет три вещественных корня (то есть ). В противном случае она по-прежнему верна, но включает в себя комплексные косинусы и арккосинусы, когда есть только один вещественный корень, и она бессмысленна (деление на ноль), когда p = 0 . ${\displaystyle 4p^{3}+27q^{2}<0}$

Эту формулу можно легко преобразовать в формулу для корней общего кубического уравнения, используя обратную подстановку, описанную в § Пониженная кубическая функция.

Формулу можно доказать следующим образом: Исходя из уравнения t ³ + pt + q = 0 , положим t = u cos  θ . Идея состоит в том, чтобы выбрать u так, чтобы уравнение совпало с тождеством Для этого выберем и разделим уравнение на Это дает Объединяя с указанным выше тождеством, получаем и корни, таким образом,   $${\displaystyle 4\cos ^{3}\theta -3\cos \theta -\cos(3\theta )=0.}$$ ${\displaystyle u=2\,{\sqrt {-{\frac {p}{3}}}}\,,}$ ${\displaystyle {\frac {u^{3}}{4}}.}$ $${\displaystyle 4\cos ^{3}\theta -3\cos \theta -{\frac {3q}{2p}}\,{\sqrt {\frac {-3}{p}}}=0.}$$ $${\displaystyle \cos(3\theta )={\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\,,}$$ $${\displaystyle t_{k}=2\,{\sqrt {-{\frac {p}{3}}}}\,\cos \left[{\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-{\frac {2\pi k}{3}}\right]\qquad {\text{for }}k=0,1,2.}$$

Гиперболическое решение для одного действительного корня

Когда имеется только один действительный корень (и p ≠ 0 ), этот корень можно аналогичным образом представить с помощью гиперболических функций , как ^{[27] [28]} Если p ≠ 0 и неравенства справа не выполняются (случай трех действительных корней), формулы остаются верными, но включают в себя комплексные величины. $${\displaystyle {\begin{aligned}t_{0}&=-2{\frac {|q|}{q}}{\sqrt {-{\frac {p}{3}}}}\cosh \left[{\frac {1}{3}}\operatorname {arcosh} \left({\frac {-3|q|}{2p}}{\sqrt {\frac {-3}{p}}}\right)\right]\qquad {\text{if }}~4p^{3}+27q^{2}>0~{\text{ and }}~p<0,\\t_{0}&=-2{\sqrt {\frac {p}{3}}}\sinh \left[{\frac {1}{3}}\operatorname {arsinh} \left({\frac {3q}{2p}}{\sqrt {\frac {3}{p}}}\right)\right]\qquad {\text{if }}~p>0.\end{aligned}}}$$

Когда p = ±3 , указанные выше значения t ₀ иногда называются кубическим корнем Чебышева. ^[29] Точнее, значения, включающие косинусы и гиперболические косинусы, определяют, когда p = −3 , ту же аналитическую функцию, обозначаемую C _1/3 ( q ) , которая является правильным кубическим корнем Чебышева. Значение, включающее гиперболические синусы, аналогично обозначается S _1/3 ( q ) , когда p = 3 .

Геометрические решения

Решение Омара Хайяма

Геометрическое решение кубического уравнения Омара Хайяма для случая m = 2 , n = 16 , дающее корень 2. Пересечение вертикальной линии на оси x в центре окружности является случайностью проиллюстрированного примера.

Для решения кубического уравнения x ³ + m ² x = n , где n > 0 , Омар Хайям построил параболу y = x ² / m , окружность, диаметр которой — отрезок [0, n / m ² ] на положительной оси x , и вертикальная линия, проходящая через точку пересечения окружности и параболы над осью x . Решение дается длиной горизонтального отрезка от начала координат до пересечения вертикальной линии и оси x (см. рисунок).

Простое современное доказательство выглядит следующим образом. Умножение уравнения на x / m ² и перегруппировка членов дает Левая часть — это значение y ² на параболе. Уравнение окружности имеет вид y ² + x ( x − ⁠ $${\displaystyle {\frac {x^{4}}{m^{2}}}=x\left({\frac {n}{m^{2}}}-x\right).}$$н/м ²⁠ ) ​​= 0 , правая часть — значение y ² на окружности.

Решение с трисектором угла

Кубическое уравнение с действительными коэффициентами можно решить геометрически с помощью циркуля, линейки и трисекториса угла тогда и только тогда, когда оно имеет три действительных корня. ^{[30] : Теор. 1}

Кубическое уравнение может быть решено построением с помощью циркуля и линейки (без трисектора) тогда и только тогда, когда оно имеет рациональный корень. Это означает, что старые задачи трисекции угла и удвоения куба , поставленные древнегреческими математиками , не могут быть решены построением с помощью циркуля и линейки.

Геометрическая интерпретация корней

Три действительных корня

Для кубического уравнения ( 1 ) с тремя действительными корнями корни являются проекцией на ось x вершин A , B и C равностороннего треугольника . Центр треугольника имеет ту же координату x , что и точка перегиба .

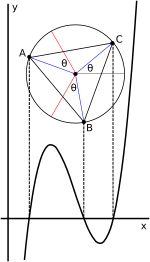
Тригонометрическое выражение Виета для корней в случае трех действительных корней допускает геометрическую интерпретацию в терминах окружности. ^{[ 22] [31]} Когда кубическая функция записана в подавленной форме ( 2 ) , t3 + pt + q = 0 , как показано выше, решение можно выразить как

$${\displaystyle t_{k}=2{\sqrt {-{\frac {p}{3}}}}\cos \left({\frac {1}{3}}\arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)-k{\frac {2\pi }{3}}\right)\quad {\text{for}}\quad k=0,1,2\,.}$$

Вот угол в единичной окружности; принимая ⁠ ${\displaystyle \arccos \left({\frac {3q}{2p}}{\sqrt {\frac {-3}{p}}}\right)}$1/3⁠ этого угла соответствует извлечению кубического корня из комплексного числа; прибавление − k ⁠2π​/3⁠ для k = 1, 2 находит другие кубические корни; и умножение косинусов этих полученных углов накорректирует масштаб. ${\displaystyle 2{\sqrt {-{\frac {p}{3}}}}}$

Для недепрессивного случая ( 1 ) (показанного на прилагаемом графике) депрессивный случай, как указано ранее, получается путем определения t таким образом, что x = t − ⁠б/3 а⁠ поэтому t = x + ⁠б/3 а⁠ . Графически это соответствует простому сдвигу графика по горизонтали при изменении между переменными t и x , без изменения угловых соотношений. Этот сдвиг перемещает точку перегиба и центр окружности на ось y . Следовательно, корни уравнения относительно t в сумме равны нулю.

Один действительный корень

В декартовой плоскости

Наклон линии RA в два раза больше, чем у RH. Обозначим комплексные корни кубического уравнения как g ± hi , g = OM (здесь отрицательно) и h = √ tan ORH = √ наклон линии RH = BE = DA .

Когда график кубической функции строится в декартовой плоскости , если есть только один действительный корень, это абсцисса ( x -координата) горизонтального отрезка кривой (точка R на рисунке). Далее, ^{[32] [33] [34]} если комплексно-сопряженные корни записаны как g ± hi , то действительная часть g является абсциссой точки касания H касательной к кубической функции, которая проходит через x -отрезок R кубической функции (то есть знаковая длина OM, отрицательная на рисунке). Мнимые части ±h являются квадратными корнями тангенса угла между этой касательной и горизонтальной осью. ^{[ необходимо разъяснение ]}

В комплексной плоскости

С одним действительным и двумя комплексными корнями три корня можно представить как точки на комплексной плоскости, как и два корня производной кубического уравнения. Между всеми этими корнями существует интересная геометрическая связь.

Точки на комплексной плоскости, представляющие три корня, служат вершинами равнобедренного треугольника. (Треугольник является равнобедренным, потому что один корень находится на горизонтальной (действительной) оси, а два других корня, будучи комплексно сопряженными, появляются симметрично выше и ниже действительной оси.) Теорема Мардена гласит, что точки, представляющие корни производной кубического уравнения, являются фокусами вискоса Штейнера треугольника — единственного эллипса, который касается треугольника в серединах его сторон. Если угол при вершине на действительной оси меньше ⁠π/3⁠ тогда большая ось эллипса лежит на действительной оси, как и его фокусы, а значит, и корни производной. Если этот угол больше ⁠π/3⁠ , большая ось вертикальна, а ее фокусы, корни производной, являются комплексно сопряженными. И если этот угол ⁠π/3⁠ , треугольник равносторонний, вписанный в треугольник эллипс Штейнера — это просто вписанная окружность треугольника, его фокусы совпадают друг с другом во вписанном центре, который лежит на действительной оси, и, следовательно, производная имеет два действительных корня.

Группа Галуа

Для кубического неприводимого многочлена над полем K характеристики, отличной от 2 и 3, группа Галуа над K — это группа автоморфизмов поля , которые фиксируют K наименьшего расширения K ( поле расщепления ). Поскольку эти автоморфизмы должны переставлять корни многочленов, эта группа является либо группой S ₃ всех шести перестановок трех корней, либо группой A ₃ трех круговых перестановок.

Дискриминант Δ кубической функции является квадратом , где a — старший коэффициент кубической функции, а r ₁ , r ₂ и r ₃ — три корня кубической функции. Как изменение знака при перестановке двух корней, фиксируется группой Галуа только в том случае, если группа Галуа — это A ₃ . Другими словами, группа Галуа — это A ₃ тогда и только тогда, когда дискриминант является квадратом элемента K . $${\displaystyle {\sqrt {\Delta }}=a^{2}(r_{1}-r_{2})(r_{1}-r_{3})(r_{2}-r_{3}),}$$ ${\displaystyle {\sqrt {\Delta }}}$ ${\displaystyle {\sqrt {\Delta }}}$

Поскольку большинство целых чисел не являются квадратами, при работе над полем Q рациональных чисел группа Галуа большинства неприводимых кубических многочленов представляет собой группу S ₃ с шестью элементами. Примером группы Галуа A ₃ с тремя элементами является p ( x ) = x ³ − 3 x − 1 , дискриминант которой равен 81 = 9 ² .

Вывод корней

В этом разделе перегруппированы несколько методов вывода формулы Кардано.

Метод Кардано

Этот метод был разработан Сципионом дель Ферро и Тартальей , но назван в честь Джероламо Кардано , который впервые опубликовал его в своей книге Ars Magna (1545).

Этот метод применим к подавленной кубической матрице t ³ + pt + q = 0. Идея состоит в том, чтобы ввести две переменные u и такие, что и подставить это в подавленную кубическую матрицу, получив ${\displaystyle v}$ ${\displaystyle u+v=t}$ $${\displaystyle u^{3}+v^{3}+(3uv+p)(u+v)+q=0.}$$

В этот момент Кардано наложил условие Это устраняет третий член в предыдущем равенстве, что приводит к системе уравнений ${\displaystyle 3uv+p=0.}$ $${\displaystyle {\begin{aligned}u^{3}+v^{3}&=-q\\uv&=-{\frac {p}{3}}.\end{aligned}}}$$

Зная сумму и произведение u ³ и можно сделать вывод, что они являются двумя решениями квадратного уравнения , так что дискриминант этого уравнения равен , и если предположить, что он положителен, действительные решения этого уравнения равны (после деления на 4 под квадратным корнем): Итак (без потери общности при выборе u или ): Так как сумма кубических корней этих решений является корнем уравнения. То есть является корнем уравнения; это формула Кардано. ${\displaystyle v^{3},}$ $${\displaystyle {\begin{aligned}0&=(x-u^{3})(x-v^{3})\\&=x^{2}-(u^{3}+v^{3})x+u^{3}v^{3}\\&=x^{2}-(u^{3}+v^{3})x+(uv)^{3}\end{aligned}}}$$ $${\displaystyle x^{2}+qx-{\frac {p^{3}}{27}}=0.}$$ ${\displaystyle \Delta =q^{2}+{\frac {4p^{3}}{27}}}$ $${\displaystyle -{\frac {q}{2}}\pm {\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}.}$$ ${\displaystyle v}$ $${\displaystyle u={\sqrt[{3}]{-{\frac {q}{2}}+{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$$ $${\displaystyle v={\sqrt[{3}]{-{\frac {q}{2}}-{\sqrt {{\frac {q^{2}}{4}}+{\frac {p^{3}}{27}}}}}}.}$$ ${\displaystyle u+v=t,}$ $${\displaystyle t={\sqrt[{3}]{-{q \over 2}+{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}+{\sqrt[{3}]{-{q \over 2}-{\sqrt {{q^{2} \over 4}+{p^{3} \over 27}}}}}}$$

Это хорошо работает, когда , но, если квадратный корень, появляющийся в формуле, не является действительным. Поскольку комплексное число имеет три кубических корня, использование формулы Кардано без оглядки даст девять корней, в то время как кубическое уравнение не может иметь больше трех корней. Это было впервые разъяснено Рафаэлем Бомбелли в его книге L'Algebra (1572). Решение состоит в том, чтобы использовать тот факт , что это означает, что нужно вычислить только один кубический корень, и приводит ко второй формуле, приведенной в § Формула Кардано. ${\displaystyle 4p^{3}+27q^{2}>0,}$ ${\displaystyle 4p^{3}+27q^{2}<0,}$ ${\displaystyle uv=-{\frac {p}{3}},}$ ${\displaystyle v={\frac {-p}{3u}}.}$

Другие корни уравнения можно получить, заменив кубический корень или, что эквивалентно, умножив кубический корень на каждый из двух примитивных кубических корней из единицы , которые равны ${\displaystyle {\frac {-1\pm {\sqrt {-3}}}{2}}.}$

Замена Виеты

Подстановка Виета — это метод, введенный Франсуа Виетом (Виета — его латинское имя) в тексте, опубликованном посмертно в 1615 году, который напрямую дает вторую формулу метода Кардано и позволяет избежать проблемы вычисления двух различных кубических корней. ^[35]

Начиная с подавленной кубической функции t ³ + pt + q = 0 , подстановка Виета имеет вид t = w – ⁠п/3 нед.⁠ . ^[б]

Подстановка t = w – ⁠п/3 нед.⁠ преобразует угнетенную кубическую форму в $${\displaystyle w^{3}+q-{\frac {p^{3}}{27w^{3}}}=0.}$$

Умножая на w ³ , получаем квадратное уравнение относительно w ³ : $${\displaystyle (w^{3})^{2}+q(w^{3})-{\frac {p^{3}}{27}}=0.}$$

Пусть будет любым ненулевым корнем этого квадратного уравнения. Если w 1 _, w 2 _и w 3 _{являются} тремя кубическими корнями W , то корни исходного подавленного кубического уравнения равны w ₁ − ⁠ $${\displaystyle W=-{\frac {q}{2}}\pm {\sqrt {{\frac {p^{3}}{27}}+{\frac {q^{2}}{4}}}}}$$п/3 в ₁⁠ , ж ₂ − ⁠п/3 в ₂⁠ , и w ₃ − ⁠п/3 в ₃⁠ . Другой корень квадратного уравнения —Это означает, что изменение знака квадратного корня меняет местами w _i и − ⁠ ${\displaystyle \textstyle -{\frac {p^{3}}{27W}}.}$п/3 в _я⁠ для i = 1, 2, 3 , и, следовательно, не изменяет корни. Этот метод не работает только тогда, когда оба корня квадратного уравнения равны нулю, то есть когда p = q = 0 , в этом случае единственный корень подавленного кубического уравнения равен 0 .

Метод Лагранжа

В своей статье Réflexions sur la résolution algébrique des équations («Мысли об алгебраическом решении уравнений») ^[36] Жозеф Луи Лагранж представил новый метод решения уравнений низкой степени унифицированным способом, надеясь, что он сможет обобщить его для более высоких степеней. Этот метод хорошо работает для кубических и четвертых уравнений , но Лагранжу не удалось применить его к уравнению пятой степени , поскольку для этого требуется решение разрешающего полинома степени не ниже шестой. ^{[37] [38] [39]} Помимо того, что ранее никому это не удавалось, это было первым указанием на несуществование алгебраической формулы для степеней 5 и выше; как было позже доказано теоремой Абеля–Руффини . Тем не менее, современные методы решения разрешимых пятых уравнений в основном основаны на методе Лагранжа. ^[39]

В случае кубических уравнений метод Лагранжа дает то же решение, что и метод Кардано. Метод Лагранжа можно применить непосредственно к общему кубическому уравнению ax ³ + bx ² + cx + d = 0 , но вычисление проще с подавленным кубическим уравнением t ³ + pt + q = 0 .

Основная идея Лагранжа состояла в том, чтобы работать с дискретным преобразованием Фурье корней вместо самих корней. Точнее, пусть ξ будет примитивным третьим корнем из единицы , то есть числом, таким, что ξ ³ = 1 и ξ ² + ξ + 1 = 0 (при работе в пространстве комплексных чисел , имеем , но эта комплексная интерпретация здесь не используется). Обозначая x ₀ , x ₁ и x ₂ три корня кубического уравнения, которое нужно решить, пусть будет дискретным преобразованием Фурье корней. Если s ₀ , s ₁ и s ₂ известны, корни можно восстановить из них с помощью обратного преобразования Фурье, состоящего в обращении этого линейного преобразования; то есть, ${\displaystyle \textstyle \xi ={\frac {-1\pm i{\sqrt {3}}}{2}}=e^{2i\pi /3},}$ $${\displaystyle {\begin{aligned}s_{0}&=x_{0}+x_{1}+x_{2},\\s_{1}&=x_{0}+\xi x_{1}+\xi ^{2}x_{2},\\s_{2}&=x_{0}+\xi ^{2}x_{1}+\xi x_{2},\end{aligned}}}$$ $${\displaystyle {\begin{aligned}x_{0}&={\tfrac {1}{3}}(s_{0}+s_{1}+s_{2}),\\x_{1}&={\tfrac {1}{3}}(s_{0}+\xi ^{2}s_{1}+\xi s_{2}),\\x_{2}&={\tfrac {1}{3}}(s_{0}+\xi s_{1}+\xi ^{2}s_{2}).\end{aligned}}}$$

По формулам Виета известно , что s ₀ равно нулю в случае подавленной кубики, и − ⁠б/а⁠ для общего кубического уравнения. Итак,нужно вычислить только s ₁ и s ₂ . Они не являются симметричными функциями корней (замена x ₁ и x ₂ также меняет местами s ₁ и s ₂ ), но некоторые простые симметричные функции s ₁ и s ₂ также симметричны относительно корней кубического уравнения, которое нужно решить. Таким образом, эти симметричные функции можно выразить через (известные) коэффициенты исходного кубического уравнения, и это позволяет в конечном итоге выразить s i _как корни многочлена с известными коэффициентами. Это хорошо работает для любой степени, но в степенях выше четырех результирующий многочлен, имеющий s _i в качестве корней, имеет степень выше, чем у исходного многочлена, и поэтому бесполезен для решения. Это причина, по которой метод Лагранжа не работает в степенях пять и выше.

В случае кубического уравнения и являются такими симметричными многочленами (см. ниже). Отсюда следует, что и являются двумя корнями квадратного уравнения Таким образом, решение уравнения может быть завершено точно так же, как и методом Кардано, с и вместо u и ${\displaystyle P=s_{1}s_{2},}$ ${\displaystyle S=s_{1}^{3}+s_{2}^{3}}$ ${\displaystyle s_{1}^{3}}$ ${\displaystyle s_{2}^{3}}$ ${\displaystyle z^{2}-Sz+P^{3}=0.}$ ${\displaystyle s_{1}}$ ${\displaystyle s_{2}}$ ${\displaystyle v.}$

В случае пониженной кубики имеем и , тогда как в методе Кардано мы устанавливаем и Таким образом, с точностью до замены u на мы имеем и Другими словами, в этом случае метод Кардано и метод Лагранжа вычисляют абсолютно одно и то же, с точностью до трехкратного увеличения вспомогательных переменных, главное отличие состоит в том, что метод Лагранжа объясняет, почему эти вспомогательные переменные появляются в задаче. ${\displaystyle x_{0}={\tfrac {1}{3}}(s_{1}+s_{2})}$ ${\displaystyle s_{1}s_{2}=-3p,}$ ${\displaystyle x_{0}=u+v}$ ${\displaystyle uv=-{\tfrac {1}{3}}p.}$ ${\displaystyle v,}$ ${\displaystyle s_{1}=3u}$ ${\displaystyle s_{2}=3v.}$

ВычислениеСиП

Прямое вычисление с использованием соотношений ξ ³ = 1 и ξ ² + ξ + 1 = 0 дает Это показывает, что P и S являются симметричными функциями корней. Используя тождества Ньютона , их легко выразить через элементарные симметричные функции корней, давая с e ₁ = 0 , e ₂ = p и e ₃ = − q в случае подавленной кубики, и e ₁ = − ⁠ $${\displaystyle {\begin{aligned}P&=s_{1}s_{2}=x_{0}^{2}+x_{1}^{2}+x_{2}^{2}-(x_{0}x_{1}+x_{1}x_{2}+x_{2}x_{0}),\\S&=s_{1}^{3}+s_{2}^{3}=2(x_{0}^{3}+x_{1}^{3}+x_{2}^{3})-3(x_{0}^{2}x_{1}+x_{1}^{2}x_{2}+x_{2}^{2}x_{0}+x_{0}x_{1}^{2}+x_{1}x_{2}^{2}+x_{2}x_{0}^{2})+12x_{0}x_{1}x_{2}.\end{aligned}}}$$ $${\displaystyle {\begin{aligned}P&=e_{1}^{2}-3e_{2},\\S&=2e_{1}^{3}-9e_{1}e_{2}+27e_{3},\end{aligned}}}$$б/а⁠ , е ₂ = ⁠с/а⁠ и е ₃ = − ⁠г/а⁠ , в общем случае.

Приложения

Кубические уравнения возникают и в других различных контекстах.

В математике

• Трисекция угла и удвоение куба — две древние задачи геометрии , которые, как было доказано, не могут быть решены с помощью линейки и циркуля , поскольку они эквивалентны решению кубического уравнения.
• Теорема Мардена утверждает, что фокусы виэллипс Штейнера любого треугольника можно найти с помощью кубической функции, корни которой являются координатами в комплексной плоскости трех вершин треугольника. Корни первой производной этой кубической функции являются комплексными координатами этих фокусов.
• Площадь правильного семиугольника может быть выражена через кубические корни. Кроме того, отношения длинной диагонали к стороне, стороны к короткой диагонали и отрицательное значение короткой диагонали к длинной диагонали удовлетворяют определенному кубическому уравнению. Кроме того, отношение радиуса вписанной окружности к радиусу описанной окружности семиугольного треугольника является одним из решений кубического уравнения. Значения тригонометрических функций углов, связанных с удовлетворяют кубическим уравнениям. ${\displaystyle 2\pi /7}$
• Если задан косинус (или другая тригонометрическая функция) произвольного угла, то косинус одной трети этого угла является одним из корней кубического уравнения.
• Решение общего уравнения четвертой степени опирается на решение его кубической резольвенты .
• Собственные значения матрицы 3×3 являются корнями кубического многочлена, который является характеристическим многочленом матрицы.
• Характеристическое уравнение постоянного коэффициента третьего порядка или линейное дифференциальное уравнение Коши–Эйлера (равномерные переменные коэффициенты) или разностное уравнение является кубическим уравнением.
• Точки пересечения кубической кривой Безье и прямой линии можно вычислить с помощью прямого кубического уравнения, представляющего кривую Безье.
• Критические точки функции четвертого порядка находятся путем решения кубического уравнения (производная приравнивается к нулю).
• Точки перегиба функции пятой степени являются решением кубического уравнения (вторая производная равна нулю).

В других науках

• В аналитической химии уравнение Шарло , которое можно использовать для определения pH буферных растворов , можно решить с помощью кубического уравнения.
• В термодинамике уравнения состояния (которые связывают давление, объем и температуру вещества), например, уравнение состояния Ван-дер-Ваальса , являются кубическими по объему.
• Кинематические уравнения , включающие линейные скорости ускорения, являются кубическими.
• Скорость сейсмических волн Рэлея является решением кубического уравнения волн Рэлея .
• Установившаяся скорость транспортного средства, движущегося по склону с учетом трения воздуха при заданной входной мощности, решается с помощью кубического уравнения пониженной степени.
• Третий закон движения планет Кеплера является кубическим по большой полуоси.

Примечания

1. В О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Омар Хайям», Архив истории математики Мактьютора , Университет Сент-Эндрюсможно прочитать Эта проблема в свою очередь привела Хайяма к решению кубического уравнения x ³ + 200 x = 20 x ² + 2000 и он нашел положительный корень этого кубического уравнения, рассматривая пересечение прямоугольной гиперболы и окружности. Приближенное численное решение было затем найдено путем интерполяции в тригонометрических таблицах . Геометрическое построение идеально подходило для Омара Хайяма, как это происходит при решении задачи геометрического построения. В конце своей статьи он говорит только, что для этой геометрической задачи, если приближений достаточно, то более простое решение может быть получено путем обращения к тригонометрическим таблицам . Текстуально: Если ищущий удовлетворен оценкой, ему следует заглянуть в таблицу хорд Альмагеста или в таблицу синусов и обратных синусов обсерватории Мотмеда. Затем следует краткое описание этого альтернативного метода (семь строк).
2. Точнее, Виета ввел новую переменную w и наложил условие w ( t + w ) = ⁠п/3⁠ . Это эквивалентно замене t = ⁠п/3 нед.⁠ – w , и отличается от подстановки, которая используется здесь, только сменой знака w . Эта смена знака позволяет получить непосредственно формулы § формулы Кардано.

Ссылки

1. Хёйруп, Йенс (1992), «Вавилонский текст для подвала BM 85200 + НДС 6599. Ретрансляция и анализ», Amphora: юбилейный сборник для Ганса Вуссинга по случаю его 65-летия , Birkhäuser , стр. 315–358, doi :10.1007/978-3-0348-8599-7_16, ISBN 978-3-0348-8599-7
2. Crossley, John; W.-C. Lun, Anthony (1999). Девять глав о математическом искусстве: Companion and Commentary. Oxford University Press. стр. 176. ISBN 978-0-19-853936-0.
3. Ван дер Варден, Геометрия и алгебра древних цивилизаций, глава 4, Цюрих, 1983, ISBN 0-387-12159-5 
4. Кук, Роджер (8 ноября 2012 г.). История математики. John Wiley & Sons. стр. 63. ISBN 978-1-118-46029-0.
5. Немет-Неджат, Карен Ри (1998). Повседневная жизнь в Древней Месопотамии . Greenwood Publishing Group. стр. 306. ISBN 978-0-313-29497-6.
6. Кук, Роджер (2008). Классическая алгебра: ее природа, происхождение и применение. John Wiley & Sons. стр. 64. ISBN 978-0-470-27797-3.
7. Гильбо (1930, стр. 8) утверждает, что «египтяне считали решение невозможным, но греки приблизились к решению».
8. Гильбо (1930, стр. 8–9)
9. Хит, Томас Л. (30 апреля 2009 г.). Диофант Александрийский: исследование по истории греческой алгебры. Мартино Паб. стр. 87–91. ISBN 978-1578987542.
10. Архимед (8 октября 2007 г.). Труды Архимеда . Перевод Т. Л. Хита. Черновая печать. ISBN 978-1603860512.
11. Миками, Ёсио (1974) [1913], «Глава 8 Ван Сяотун и кубические уравнения», Развитие математики в Китае и Японии (2-е изд.), Нью-Йорк: Chelsea Publishing Co., стр. 53–56, ISBN 978-0-8284-0149-4
12. Статья Омара Хайяма, Scripta Math. 26 (1963), страницы 323–337.
13. Дж. Дж. О'Коннор и Э. Ф. Робертсон (1999), Омар Хайям, архив истории математики Мактьютора , утверждают: «Сам Хайям, по-видимому, был первым, кто задумал общую теорию кубических уравнений».
14. Гильбо (1930, стр. 9) утверждает: «Омар Аль Хай из Хорассана, около 1079 г. н. э., сделал больше всего для того, чтобы поднять решение алгебраических уравнений до уровня метода пересечения коник».
15. Берггрен, JL (18 января 2017 г.). Эпизоды математики средневекового ислама. Спрингер. ISBN 978-1-4939-3780-6.
16. Датта, Бибхутибхушан ; Сингх, Авадхеш Нараян (2004), «Уравнение высшей степени», История индуистской математики: Справочник , том. 2, Дели, Индия: Бхараттья Кала Пракашан, с. 76, ISBN 81-86050-86-8
17. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Шараф ад-Дин аль-Музаффар аль-Туси», Архив истории математики MacTutor , Университет Сент-Эндрюс
18. Берггрен, Дж. Л. (1990), «Инновации и традиции в Муадалате Шарафа ад-Дина ат-Туси», Журнал Американского восточного общества , 110 (2): 304–309, doi : 10.2307/604533, JSTOR  604533
19. О'Коннор, Джон Дж.; Робертсон, Эдмунд Ф. , «Фибоначчи», Архив истории математики Мактьютора , Университет Сент-Эндрюс
20. Кац, Виктор (2004). История математики. Бостон: Addison Wesley. стр. 220. ISBN 9780321016188.
21. Ла Наве, Федерика; Мазур, Барри (2002), «Читая Бомбелли», The Mathematical Intelligencer , 24 (1): 12–21, doi :10.1007/BF03025306, S2CID  189888034
22. Nickalls, RWD (июль 2006 г.). «Виет, Декарт и кубическое уравнение» (PDF) . Mathematical Gazette . 90 (518): 203–208. doi :10.1017/S0025557200179598. S2CID  124980170.
23. Пратт, Орсон (1866). Новый и простой метод решения кубических и биквадратных уравнений: охватывающий несколько новых формул, значительно упрощающих этот раздел математической науки. Лонгманс, Грин, Ридер и Дайер. стр. 13. ISBN 9781974130924. ...если два корня мнимые, то произведение положительно...
24. "Решение для подавленного кубического уравнения". Математическое решение . Получено 2022-11-23 .
25. Zucker, IJ (июль 2008 г.). «Кубическое уравнение — новый взгляд на неприводимый случай». Mathematical Gazette . 92 : 264–268. doi :10.1017/S0025557200183135. S2CID  125986006.
26. Шелби, Сэмюэл, ред. (1975). Стандартные математические таблицы CRC. CRC Press. ISBN 0-87819-622-6.
27. Это формулы (80) и (83) Вайсштейна, Эрика В. «Кубическая формула». Из MathWorld—A Wolfram Web Resource. https://mathworld.wolfram.com/CubicFormula.html, переписанные для получения связной записи.
28. Холмс, GC, «Использование гиперболических косинусов при решении кубических полиномов», Mathematical Gazette 86. Ноябрь 2002 г., 473–477.
29. Абрамовиц, Милтон; Стиган, Ирен А., ред. Справочник по математическим функциям с формулами, графиками и математическими таблицами , Довер (1965), гл. 22, стр. 773
30. Gleason, Andrew Mattei (март 1988). «Трисекция угла, семиугольник и трискайдекагон» (PDF) . The American Mathematical Monthly . 95 (3): 185–194. doi :10.2307/2323624. JSTOR  2323624. Архивировано из оригинала (PDF) 2015-12-19.
31. Nickalls, RWD (ноябрь 1993 г.), «Новый подход к решению кубического уравнения: раскрыто решение Кардано» (PDF) , The Mathematical Gazette , 77 (480): 354–359, doi :10.2307/3619777, ISSN  0025-5572, JSTOR  3619777, S2CID  172730765См. особенно рис. 2.
32. Энрикес, Гарсия (июнь–июль 1935 г.), «Графическая интерпретация комплексных корней кубических уравнений», American Mathematical Monthly , 42 (6): 383–384, doi :10.2307/2301359, JSTOR  2301359
33. Барр, К. Ф. (1918), «Обсуждения: относительно графика кубического уравнения, имеющего комплексные корни», American Mathematical Monthly , 25 (6): 268–269, doi : 10.2307/2972885, JSTOR  2972885
34. Ирвин, Фрэнк; Райт, Х. Н. (1917), «Некоторые свойства полиномиальных кривых». Annals of Mathematics , 19 (2): 152–158, doi :10.2307/1967772, JSTOR  1967772
35. ван дер Варден, Бартель Леенерт (1985), «От Вьета до Декарта», История алгебры: от аль-Хваризми до Эмми Нётер , Springer-Verlag , ISBN 3-540-13610-X
36. Лагранж, Жозеф-Луи (1869) [1771], «Réflexions sur la resolution algébrique des équations», в Серре, Жозеф-Альфред (ред.), Œuvres de Lagrange , vol. III, Готье-Виллар, стр. 205–421.
37. Прасолов, Виктор; Соловьев, Юрий (1997), Эллиптические функции и эллиптические интегралы, AMS Bookstore, ISBN 978-0-8218-0587-9, §6.2, стр. 134
38. Клайн, Моррис (1990), Математическая мысль от древности до современности, Oxford University Press US, ISBN 978-0-19-506136-9, Алгебра в восемнадцатом веке: Теория уравнений
39. Даниэль Лазард, «Решение квинтик в радикалах», в Олаве Арнфинне Лаудале, Рагни Пиене , Наследие Нильса Хенрика Абеля , стр. 207–225, Берлин, 2004. ISBN 3-540-43826-2 

• Гильбо, Люси (1930), «История решения кубического уравнения», Mathematics News Letter , 5 (4): 8–12, doi :10.2307/3027812, JSTOR  3027812

Дальнейшее чтение

• Энглин, В. С.; Ламбек, Иоахим (1995), «Математика в эпоху Возрождения», Наследие Фалеса , Springers, стр. 125–131, ISBN 978-0-387-94544-6Гл. 24.
• Денс, Т. (ноябрь 1997 г.), «Кубики, хаос и метод Ньютона», Mathematical Gazette , 81 (492), Mathematical Association : 403–408, doi : 10.2307/3619617, ISSN  0025-5572, JSTOR  3619617, S2CID  125196796
• Даннетт, Р. (ноябрь 1994 г.), «Ньютон–Рафсон и кубическое», Mathematical Gazette , 78 (483), Mathematical Association : 347–348, doi : 10.2307/3620218, ISSN  0025-5572, JSTOR  3620218, S2CID  125643035
• Якобсон, Натан (2009), Основы алгебры , т. 1 (2-е изд.), Довер, ISBN 978-0-486-47189-1
• Митчелл, Д. В. (ноябрь 2007 г.), «Решение кубических уравнений путем решения треугольников», Mathematical Gazette , 91 , Mathematical Association : 514–516, doi : 10.1017/S0025557200182178, ISSN  0025-5572, S2CID  124710259
• Митчелл, Д.У. (ноябрь 2009 г.), "Степени φ как корни кубических", Mathematical Gazette , 93 , Mathematical Association , doi :10.1017/S0025557200185237, ISSN  0025-5572, S2CID  126286653
• Press, WH; Teukolsky, SA; Vetterling, WT; Flannery, BP (2007), «Раздел 5.6 Квадратные и кубические уравнения», Numerical Recipes: The Art of Scientific Computing (3-е изд.), Нью-Йорк: Cambridge University Press, ISBN 978-0-521-88068-8
• Рехтшаффен, Эдгар (июль 2008 г.), «Действительные корни кубических уравнений: явная формула для квазирешений», Mathematical Gazette , 92 , Mathematical Association : 268–276, doi : 10.1017/S0025557200183147, ISSN  0025-5572, S2CID  125870578
• Цукер, И. Дж. (июль 2008 г.), «Кубическое уравнение – новый взгляд на неприводимый случай», Mathematical Gazette , 92 , Mathematical Association : 264–268, doi : 10.1017/S0025557200183135, ISSN  0025-5572, S2CID  125986006

Внешние ссылки

• «Формула Кардано», Энциклопедия математики , EMS Press , 2001 [1994]
• История квадратных, кубических и четвертых уравнений в архиве MacTutor .
• 500 лет НЕ преподавания КУБИЧЕСКОЙ ФОРМУЛЫ. С чем, по их мнению, вы не справитесь? – Видео Mathologer на YouTube об истории кубических уравнений и решении Кардано, а также о решении Феррари для уравнений четвертой степени