Факторный анализ

Факторный анализ — это статистический метод, используемый для описания изменчивости среди наблюдаемых, коррелированных переменных в терминах потенциально меньшего числа ненаблюдаемых переменных, называемых факторами . Например, возможно, что вариации в шести наблюдаемых переменных в основном отражают вариации в двух ненаблюдаемых (базовых) переменных. Факторный анализ ищет такие совместные вариации в ответ на ненаблюдаемые скрытые переменные . Наблюдаемые переменные моделируются как линейные комбинации потенциальных факторов плюс термины « ошибка », поэтому факторный анализ можно рассматривать как особый случай моделей с ошибками в переменных . ^[1]

Проще говоря, факторная нагрузка переменной количественно определяет степень, в которой переменная связана с данным фактором. ^[2]

Распространенное обоснование методов факторного анализа заключается в том, что полученная информация о взаимозависимостях между наблюдаемыми переменными может быть использована позже для сокращения набора переменных в наборе данных. Факторный анализ обычно используется в психометрии , психологии личности , биологии, маркетинге , управлении продуктами , исследовании операций , финансах и машинном обучении . Он может помочь в работе с наборами данных, где имеется большое количество наблюдаемых переменных, которые, как считается, отражают меньшее количество базовых/скрытых переменных. Это один из наиболее часто используемых методов взаимозависимости, который применяется, когда соответствующий набор переменных показывает систематическую взаимозависимость, и цель состоит в том, чтобы найти скрытые факторы, которые создают общность.

Статистическая модель

Определение

Модель пытается объяснить набор наблюдений в каждом из индивидуумов с набором общих факторов ( ), где факторов на единицу меньше, чем наблюдений на единицу ( ). Каждый индивидуум имеет свои собственные общие факторы, и они связаны с наблюдениями через матрицу факторной нагрузки ( ), для одного наблюдения, согласно $p$ $n$ $k$ $f_{i,j}$ $k<p$ $k$ $L\in \mathbb {R} ^{p\times k}$

x_{i,m}-\mu _{i}=l_{i,1}f_{1,m}+\dots +l_{i,k}f_{k,m}+\varepsilon _{i,m}

где

$x_{i,m}$ - это значение го наблюдения го индивидуума, $i$ $m$
$\mu _{i}$ - среднее значение для th-го наблюдения, $i$
$l_{i,j}$ - нагрузка для y-го наблюдения y-го фактора, $i$ $j$
$f_{j,m}$ - значение го фактора го индивидуума, и $j$ $m$
$\varepsilon _{i,m}$ - это -й ненаблюдаемый стохастический член ошибки с нулевым средним и конечной дисперсией. $(i,m)$

В матричной записи

X-\mathrm {M} =LF+\varepsilon

где матрица наблюдений , матрица нагрузок , матрица факторов , матрица ошибок и матрица средних значений , причем й элемент — это просто . $X\in \mathbb {R} ^{p\times n}$ $L\in \mathbb {R} ^{p\times k}$ $F\in \mathbb {R} ^{k\times n}$ $\varepsilon \in \mathbb {R} ^{p\times n}$ $\mathrm {M} \in \mathbb {R} ^{p\times n}$ $(i,m)$ $\mathrm {M} _{i,m}=\mu _{i}$

Также мы сделаем следующие предположения : $F$

$F$ и независимы. $\varepsilon$
$\mathrm {E} (F)=0$ ; где ожидание $\mathrm {E}$
$\mathrm {Cov} (F)=I$ где — ковариационная матрица , позволяющая убедиться в том, что факторы некоррелированы, а — матрица идентичности . $\mathrm {Cov}$ $I$

Предположим . Тогда $\mathrm {Cov} (X-\mathrm {M} )=\Sigma$

\Sigma =\mathrm {Cov} (X-\mathrm {M} )=\mathrm {Cov} (LF+\varepsilon ),\,

и поэтому из условий 1 и 2, наложенных выше, и , давая $F$ $E[LF]=LE[F]=0$ $Cov(LF+\epsilon )=Cov(LF)+Cov(\epsilon )$

\Sigma =L\mathrm {Cov} (F)L^{T}+\mathrm {Cov} (\varepsilon ),\,

или, установив , $\Psi :=\mathrm {Cov} (\varepsilon )$

\Sigma =LL^{T}+\Psi .\,

Для любой ортогональной матрицы , если мы положим и , критерии того, что являются факторами и факторными нагрузками, по-прежнему сохраняются. Следовательно, набор факторов и факторных нагрузок является уникальным только с точностью до ортогонального преобразования . $Q$ $L^{\prime }=\ LQ$ $F^{\prime }=Q^{T}F$

Пример

Предположим, что у психолога есть гипотеза о том, что существует два вида интеллекта , «вербальный интеллект» и «математический интеллект», ни один из которых не наблюдается напрямую. ^{[примечание 1]} Доказательства гипотезы ищутся в экзаменационных баллах по каждой из 10 различных академических областей 1000 студентов. Если каждый студент выбирается случайным образом из большой популяции , то 10 баллов каждого студента являются случайными величинами. Гипотеза психолога может гласить, что для каждой из 10 академических областей средний балл по группе всех студентов, которые разделяют некоторую общую пару значений для вербального и математического «интеллекта», равен некоторой константе , умноженной на их уровень вербального интеллекта, плюс еще одной константе, умноженной на их уровень математического интеллекта, т. е. это линейная комбинация этих двух «факторов». Числа для конкретного предмета, на которые умножаются два вида интеллекта для получения ожидаемого балла, постулируются гипотезой как одинаковые для всех пар уровней интеллекта и называются «факторной нагрузкой» для этого предмета. ^{[ необходимо уточнение ]} Например, гипотеза может предполагать, что прогнозируемая средняя способность ученика в области астрономии составляет

{10 × вербальный интеллект ученика} + {6 × математический интеллект ученика}.

Числа 10 и 6 — это факторные нагрузки, связанные с астрономией. Другие академические предметы могут иметь другие факторные нагрузки.

Два студента, предположительно имеющие одинаковые степени вербального и математического интеллекта, могут иметь разные измеренные способности в астрономии, поскольку индивидуальные способности отличаются от средних способностей (предсказанные выше) и из-за самой ошибки измерения. Такие различия составляют то, что в совокупности называется «ошибкой» — статистический термин, который означает величину, на которую индивидуум, как измерено, отличается от того, что является средним или предсказанным его или ее уровнями интеллекта (см. ошибки и остатки в статистике ).

Наблюдаемые данные, которые пойдут в факторный анализ, будут представлять собой 10 баллов каждого из 1000 студентов, всего 10 000 чисел. Факторные нагрузки и уровни двух видов интеллекта каждого студента должны быть выведены из данных.

Математическая модель того же примера

Далее матрицы будут обозначены индексированными переменными. Индексы «субъекта» будут обозначены буквами , и , со значениями от до , которые равны в приведенном выше примере. Индексы «фактора» будут обозначены буквами , и , со значениями от до , которые равны в приведенном выше примере. Индексы «экземпляра» или «выборки» будут обозначены буквами , и , со значениями от до . В приведенном выше примере, если выборка студентов участвовала в экзаменах, балл студента th за экзамен th определяется как . Цель факторного анализа — охарактеризовать корреляции между переменными , для которых являются конкретным экземпляром или набором наблюдений. Для того чтобы переменные были на равных условиях, они нормализуются в стандартные баллы : $a$ $b$ $c$ $1$ $p$ $10$ $p$ $q$ $r$ $1$ $k$ $2$ $i$ $j$ $k$ $1$ $N$ $N=1000$ $p=10$ $i$ $a$ $x_{ai}$ $x_{a}$ $x_{ai}$ $z$

z_{ai}={\frac {x_{ai}-{\hat {\mu }}_{a}}{{\hat {\sigma }}_{a}}}

где выборочное среднее равно:

{\hat {\mu }}_{a}={\tfrac {1}{N}}\sum _{i}x_{ai}

а дисперсия выборки определяется по формуле:

{\hat {\sigma }}_{a}^{2}={\tfrac {1}{N-1}}\sum _{i}(x_{ai}-{\hat {\mu }}_{a})^{2}

Модель факторного анализа для данной выборки выглядит следующим образом:

{\begin{matrix}z_{1,i}&=&\ell _{1,1}F_{1,i}&+&\ell _{1,2}F_{2,i}&+&\varepsilon _{1,i}\\\vdots &&\vdots &&\vdots &&\vdots \\z_{10,i}&=&\ell _{10,1}F_{1,i}&+&\ell _{10,2}F_{2,i}&+&\varepsilon _{10,i}\end{matrix}}

или, более кратко:

z_{ai}=\sum _{p}\ell _{ap}F_{pi}+\varepsilon _{ai}

где

$F_{1i}$ является "вербальным интеллектом" ученика, $i$
$F_{2i}$ это «математический интеллект» ученика, $i$
$\ell _{ap}$ являются факторными нагрузками для -го субъекта, для . $a$ $p=1,2$

В матричной записи имеем

Z=LF+\varepsilon

Обратите внимание, что удвоение шкалы, по которой измеряется «вербальный интеллект» — первый компонент в каждом столбце, и одновременное уменьшение вдвое факторных нагрузок для вербального интеллекта не приводит к изменению модели. Таким образом, общность не теряется, если предположить, что стандартное отклонение факторов для вербального интеллекта равно . То же самое касается и математического интеллекта. Более того, по аналогичным причинам общность не теряется, если предположить, что два фактора не коррелируют друг с другом. Другими словами: $F$ $1$

\sum _{i}F_{pi}F_{qi}=\delta _{pq}

где — дельта Кронекера ( когда и когда ). Предполагается, что ошибки не зависят от факторов: $\delta _{pq}$ $0$ $p\neq q$ $1$ $p=q$

\sum _{i}F_{pi}\varepsilon _{ai}=0

Поскольку любое вращение решения также является решением, это затрудняет интерпретацию факторов. См. недостатки ниже. В этом конкретном примере, если мы заранее не знаем, что два типа интеллекта не коррелируют, то мы не можем интерпретировать два фактора как два разных типа интеллекта. Даже если они не коррелируют, мы не можем сказать, какой фактор соответствует вербальному интеллекту, а какой — математическому интеллекту без внешнего аргумента.

Значения нагрузок , средних и дисперсий «ошибок» должны быть оценены с учетом наблюдаемых данных и (предположение об уровнях факторов фиксировано для данного ). «Основная теорема» может быть выведена из приведенных выше условий: $L$ $\mu$ $\varepsilon$ $X$ $F$ $F$

\sum _{i}z_{ai}z_{bi}=\sum _{j}\ell _{aj}\ell _{bj}+\sum _{i}\varepsilon _{ai}\varepsilon _{bi}

Член слева — это -член корреляционной матрицы ( матрицы, полученной как произведение матрицы стандартизированных наблюдений с ее транспонированием) наблюдаемых данных, и его диагональные элементы будут s. Второй член справа будет диагональной матрицей с членами, меньшими единицы. Первый член справа — это «редуцированная корреляционная матрица», и она будет равна корреляционной матрице, за исключением ее диагональных значений, которые будут меньше единицы. Эти диагональные элементы редуцированной корреляционной матрицы называются «общностями» (которые представляют собой долю дисперсии в наблюдаемой переменной, которая учитывается факторами): $(a,b)$ $p\times p$ $p\times N$ $p$ $1$

h_{a}^{2}=1-\psi _{a}=\sum _{j}\ell _{aj}\ell _{aj}

Данные выборки не будут точно подчиняться фундаментальному уравнению, приведенному выше, из-за ошибок выборки, неадекватности модели и т. д. Целью любого анализа вышеуказанной модели является нахождение факторов и нагрузок , которые дают «наилучшее соответствие» данным. В факторном анализе наилучшее соответствие определяется как минимум среднеквадратической ошибки в недиагональных остатках корреляционной матрицы: ^[3] $z_{ai}$ $F_{pi}$ $\ell _{ap}$

\varepsilon ^{2}=\sum _{a\neq b}\left[\sum _{i}z_{ai}z_{bi}-\sum _{j}\ell _{aj}\ell _{bj}\right]^{2}

Это эквивалентно минимизации недиагональных компонентов ковариации ошибок, которые в уравнениях модели имеют ожидаемые значения, равные нулю. Это следует противопоставить анализу главных компонент, который стремится минимизировать среднеквадратичную ошибку всех остатков. ^[3] До появления высокоскоростных компьютеров значительные усилия были направлены на поиск приближенных решений проблемы, в частности, на оценку общностей другими способами, что затем значительно упрощало проблему, давая известную сокращенную корреляционную матрицу. Затем это использовалось для оценки факторов и нагрузок. С появлением высокоскоростных компьютеров задачу минимизации можно решать итеративно с достаточной скоростью, и общности вычисляются в процессе, а не требуются заранее. Алгоритм MinRes особенно подходит для этой проблемы, но вряд ли является единственным итеративным средством поиска решения.

Если допускается корреляция факторов решения (например, при вращении «облимина»), то соответствующая математическая модель использует косые координаты , а не ортогональные.

Геометрическая интерпретация

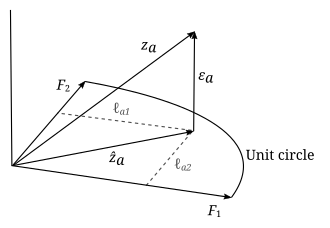
Параметрам и переменным факторного анализа можно дать геометрическую интерпретацию. Данные ( ), факторы ( ) и ошибки ( ) можно рассматривать как векторы в -мерном евклидовом пространстве (пространстве выборки), представленные как , и соответственно. Поскольку данные стандартизированы, векторы данных имеют единичную длину ( ). Векторы факторов определяют -мерное линейное подпространство (т.е. гиперплоскость) в этом пространстве, на которое векторы данных проецируются ортогонально. Это следует из уравнения модели $z_{ai}$ $F_{pi}$ $\varepsilon _{ai}$ $N$ $\mathbf {z} _{a}$ $\mathbf {F} _{p}$ ${\boldsymbol {\varepsilon }}_{a}$ $||\mathbf {z} _{a}||=1$ $k$

\mathbf {z} _{a}=\sum _{p}\ell _{ap}\mathbf {F} _{p}+{\boldsymbol {\varepsilon }}_{a}

и независимость факторов и ошибок: . В приведенном выше примере гиперплоскость — это просто 2-мерная плоскость, определяемая двумя векторами факторов. Проекция векторов данных на гиперплоскость задается как $\mathbf {F} _{p}\cdot {\boldsymbol {\varepsilon }}_{a}=0$

{\hat {\mathbf {z} }}_{a}=\sum _{p}\ell _{ap}\mathbf {F} _{p}

и ошибки являются векторами из этой спроецированной точки в точку данных и перпендикулярны гиперплоскости. Цель факторного анализа — найти гиперплоскость, которая в некотором смысле «лучше всего подходит» к данным, поэтому неважно, как выбираются векторы факторов, которые определяют эту гиперплоскость, пока они независимы и лежат в гиперплоскости. Мы можем указать их как ортогональные и нормальные ( ) без потери общности. После того, как будет найден подходящий набор факторов, их также можно произвольно вращать внутри гиперплоскости, так что любое вращение векторов факторов будет определять ту же гиперплоскость, а также будет решением. В результате в приведенном выше примере, в котором подходящая гиперплоскость является двумерной, если мы заранее не знаем, что два типа интеллекта не коррелируют, то мы не можем интерпретировать два фактора как два разных типа интеллекта. Даже если они не коррелируют, мы не можем сказать, какой фактор соответствует вербальному интеллекту, а какой — математическому интеллекту, или являются ли факторы линейными комбинациями обоих, без внешнего аргумента. $\mathbf {F} _{p}\cdot \mathbf {F} _{q}=\delta _{pq}$

Векторы данных имеют единичную длину. Элементы корреляционной матрицы для данных задаются как . Корреляционную матрицу можно геометрически интерпретировать как косинус угла между двумя векторами данных и . Диагональные элементы будут, очевидно, s, а недиагональные элементы будут иметь абсолютные значения, меньшие или равные единице. «Редуцированная корреляционная матрица» определяется как $\mathbf {z} _{a}$ $r_{ab}=\mathbf {z} _{a}\cdot \mathbf {z} _{b}$ $\mathbf {z} _{a}$ $\mathbf {z} _{b}$ $1$

{\hat {r}}_{ab}={\hat {\mathbf {z} }}_{a}\cdot {\hat {\mathbf {z} }}_{b}

Цель факторного анализа — выбрать подгоночную гиперплоскость так, чтобы редуцированная корреляционная матрица воспроизводила корреляционную матрицу как можно ближе, за исключением диагональных элементов корреляционной матрицы, которые, как известно, имеют единичное значение. Другими словами, цель — воспроизвести как можно точнее взаимные корреляции в данных. В частности, для подгоночной гиперплоскости средняя квадратическая ошибка в недиагональных компонентах

\varepsilon ^{2}=\sum _{a\neq b}\left(r_{ab}-{\hat {r}}_{ab}\right)^{2}

минимизировать, и это достигается путем минимизации его относительно набора векторов ортонормальных факторов. Видно, что

r_{ab}-{\hat {r}}_{ab}={\boldsymbol {\varepsilon }}_{a}\cdot {\boldsymbol {\varepsilon }}_{b}

Термин справа — это просто ковариация ошибок. В модели ковариация ошибок заявлена как диагональная матрица, и поэтому указанная выше задача минимизации фактически даст «наилучшее соответствие» модели: она даст выборочную оценку ковариации ошибок, которая имеет ее недиагональные компоненты, минимизированные в смысле среднего квадрата. Можно видеть, что поскольку являются ортогональными проекциями векторов данных, их длина будет меньше или равна длине проецируемого вектора данных, которая равна единице. Квадрат этих длин — это просто диагональные элементы приведенной корреляционной матрицы. Эти диагональные элементы приведенной корреляционной матрицы известны как «общности»: ${\hat {z}}_{a}$

{h_{a}}^{2}=||{\hat {\mathbf {z} }}_{a}||^{2}=\sum _{p}{\ell _{ap}}^{2}

Большие значения общностей будут указывать на то, что подходящая гиперплоскость достаточно точно воспроизводит корреляционную матрицу. Средние значения факторов также должны быть ограничены нулем, из чего следует, что средние значения ошибок также будут равны нулю.

Практическая реализация

Виды факторного анализа

Исследовательский факторный анализ

Исследовательский факторный анализ (EFA) используется для выявления сложных взаимосвязей между элементами и групповыми элементами, которые являются частью единых концепций. ^[4] Исследователь не делает никаких априорных предположений о связях между факторами. ^[4]

Факторный анализ подтверждения

Конфирматорный факторный анализ (CFA) — это более сложный подход, который проверяет гипотезу о том, что элементы связаны с определенными факторами. ^[4] CFA использует моделирование структурных уравнений для проверки модели измерения, в которой нагрузка на факторы позволяет оценить взаимосвязи между наблюдаемыми переменными и ненаблюдаемыми переменными. ^[4] Подходы моделирования структурных уравнений могут учитывать погрешность измерения и являются менее ограничительными, чем оценка методом наименьших квадратов . ^[4] Гипотетические модели проверяются на основе фактических данных, и анализ демонстрирует нагрузки наблюдаемых переменных на скрытые переменные (факторы), а также корреляцию между скрытыми переменными. ^[4]

Типы извлечения факторов

Анализ главных компонент (PCA) — широко используемый метод извлечения факторов, который является первой фазой EFA. ^[4] Веса факторов вычисляются для извлечения максимально возможной дисперсии, при этом последовательная факторизация продолжается до тех пор, пока не останется никакой значимой дисперсии. ^[4] Затем факторная модель должна быть повернута для анализа. ^[4]

Канонический факторный анализ, также называемый каноническим факторингом Рао, — это другой метод вычисления той же модели, что и PCA, который использует метод главной оси. Канонический факторный анализ ищет факторы, которые имеют наивысшую каноническую корреляцию с наблюдаемыми переменными. Канонический факторный анализ не подвержен произвольному масштабированию данных.

Общий факторный анализ, также называемый анализом главных факторов (PFA) или факторизацией по главной оси (PAF), ищет наименьшее количество факторов, которые могут объяснить общую дисперсию (корреляцию) набора переменных.

Факторизация изображений основана на матрице корреляции прогнозируемых переменных, а не фактических переменных, где каждая переменная прогнозируется на основе других с использованием множественной регрессии .

Альфа-факторинг основан на максимизации надежности факторов, предполагая, что переменные выбираются случайным образом из вселенной переменных. Все другие методы предполагают, что случаи выбираются выборочно, а переменные фиксированы.

Модель факторной регрессии представляет собой комбинаторную модель факторной модели и регрессионной модели; или, альтернативно, ее можно рассматривать как гибридную факторную модель ^[5] , факторы которой частично известны.

Терминология

Факторные нагрузки: Общность — это квадрат стандартизированной внешней нагрузки элемента. Аналогично r-квадрату Пирсона , квадрат факторной нагрузки — это процент дисперсии в этой индикаторной переменной, объясняемый фактором. Чтобы получить процент дисперсии во всех переменных, объясняемых каждым фактором, сложите сумму квадратов факторных нагрузок для этого фактора (столбца) и разделите на количество переменных. (Количество переменных равно сумме их дисперсий, поскольку дисперсия стандартизированной переменной равна 1.) Это то же самое, что и деление собственного значения фактора на количество переменных.
При интерпретации, согласно одному из правил подтверждающего факторного анализа, факторные нагрузки должны быть .7 или выше, чтобы подтвердить, что независимые переменные, определенные априори, представлены определенным фактором, на том основании, что уровень .7 соответствует примерно половине дисперсии в индикаторе, объясняемой фактором. Однако стандарт .7 является высоким, и реальные данные могут не соответствовать этому критерию, поэтому некоторые исследователи, особенно в исследовательских целях, будут использовать более низкий уровень, такой как .4 для центрального фактора и .25 для других факторов. В любом случае факторные нагрузки должны интерпретироваться в свете теории, а не произвольных уровней отсечения.
При косоугольном вращении можно исследовать как матрицу шаблонов, так и матрицу структур. Матрица структур — это просто матрица факторной нагрузки, как при ортогональном вращении, представляющая дисперсию в измеряемой переменной, объясненную фактором на основе как уникальных, так и общих вкладов. Матрица шаблонов, напротив, содержит коэффициенты , которые просто представляют уникальные вклады. Чем больше факторов, тем ниже коэффициенты шаблонов, как правило, поскольку будет больше общих вкладов в объясняемую дисперсию. Для косоугольного вращения исследователь смотрит как на коэффициенты структуры, так и на коэффициенты шаблонов при присвоении метки фактору. Принципы косоугольного вращения могут быть выведены как из перекрестной энтропии, так и из ее двойной энтропии. ^[6]
Общность: Сумма квадратов факторных нагрузок для всех факторов для данной переменной (строки) представляет собой дисперсию этой переменной, учтенную всеми факторами. Общность измеряет процент дисперсии данной переменной, объясняемой всеми факторами совместно, и может интерпретироваться как надежность индикатора в контексте постулируемых факторов.
Ложные решения: Если общность превышает 1,0, то это ложное решение, которое может быть следствием слишком малой выборки или выбора извлечь слишком много или слишком мало факторов.
Уникальность переменной: Изменчивость переменной за вычетом ее общности.
Собственные значения/характеристические корни: Собственные значения измеряют количество вариаций в общей выборке, учтенных каждым фактором. Отношение собственных значений — это отношение объясняющей важности факторов по отношению к переменным. Если фактор имеет низкое собственное значение, то он мало способствует объяснению дисперсий в переменных и может игнорироваться как менее важный, чем факторы с более высокими собственными значениями.
Извлечение сумм квадратов нагрузок: Начальные собственные значения и собственные значения после извлечения (перечисленные SPSS как «Суммы извлечения квадратов нагрузок») одинаковы для извлечения PCA, но для других методов извлечения собственные значения после извлечения будут ниже, чем их начальные аналоги. SPSS также печатает «Суммы вращения квадратов нагрузок», и даже для PCA эти собственные значения будут отличаться от начальных и извлеченных собственных значений, хотя их общая сумма будет одинаковой.
Факторные баллы
Оценки компонентов (в PCA): Объясняется с точки зрения PCA, а не с точки зрения факторного анализа.
Баллы каждого случая (строка) по каждому фактору (столбец). Чтобы вычислить факторный балл для данного случая для данного фактора, берут стандартизированный балл случая по каждой переменной, умножают на соответствующие нагрузки переменной для данного фактора и суммируют эти произведения. Вычисление факторных баллов позволяет искать выбросы факторов. Кроме того, факторные баллы могут использоваться в качестве переменных в последующем моделировании.

Критерии определения количества факторов

Исследователи хотят избежать таких субъективных или произвольных критериев сохранения факторов, как «это имело смысл для меня». Для решения этой проблемы был разработан ряд объективных методов, позволяющих пользователям определять соответствующий диапазон решений для исследования. ^[7] Однако эти различные методы часто не соглашаются друг с другом относительно количества факторов, которые следует сохранить. Например, параллельный анализ может предложить 5 факторов, в то время как MAP Велицера предлагает 6, поэтому исследователь может запросить как 5-, так и 6-факторные решения и обсудить каждое с точки зрения их связи с внешними данными и теорией.

Современные критерии

Параллельный анализ Хорна (PA): ^[8] Метод моделирования на основе Монте-Карло, который сравнивает наблюдаемые собственные значения с полученными из некоррелированных нормальных переменных. Фактор или компонент сохраняется, если соответствующее собственное значение больше 95-го процентиля распределения собственных значений, полученных из случайных данных. PA является одним из наиболее часто рекомендуемых правил для определения количества сохраняемых компонентов, ^[7]^[9], но многие программы не включают эту опцию (заметным исключением является R ). ^[10] Однако Форман предоставил как теоретические, так и эмпирические доказательства того, что его применение может быть нецелесообразным во многих случаях, поскольку его производительность значительно зависит от размера выборки , дискриминации элементов и типа коэффициента корреляции . ^[11]

Тест MAP Велицера (1976) ^[12] , описанный Кортни (2013) ^[13], «включает в себя полный анализ главных компонентов с последующим изучением ряда матриц частных корреляций» (стр. 397 (хотя эта цитата не встречается в Велицере (1976), а указанный номер страницы находится за пределами страниц цитаты). Квадратичная корреляция для шага «0» (см. рисунок 4) представляет собой среднеквадратичную внедиагональную корреляцию для непарциализированной корреляционной матрицы. На шаге 1 первый главный компонент и связанные с ним элементы исключаются. После этого вычисляется среднеквадратическая внедиагональная корреляция для последующей корреляционной матрицы для шага 1. На шаге 2 первые два главных компонента исключаются, и снова вычисляется результирующая среднеквадратическая внедиагональная корреляция. Вычисления выполняются для k минус один шаг (k представляет собой общее количество переменных в матрице). После этого все средние Квадратичные корреляции для каждого шага выстраиваются в линию, и номер шага в анализе, который привел к наименьшей средней квадратичной частной корреляции, определяет количество компонентов или факторов для сохранения. ^[12] При этом методе компоненты сохраняются до тех пор, пока дисперсия в матрице корреляции представляет собой систематическую дисперсию, в отличие от остаточной или погрешной дисперсии. Хотя методологически методология близка к анализу главных компонентов, было показано, что метод MAP достаточно хорошо справляется с определением количества факторов для сохранения в многофакторных имитационных исследованиях. ^[7]^[14]^[15]^[16] Эта процедура доступна через пользовательский интерфейс SPSS, ^[13] а также через пакет psych для языка программирования R. [ ^17]^[18]

Старые методы

Критерий Кайзера: Правило Кайзера заключается в отбрасывании всех компонентов с собственными значениями ниже 1,0 – это собственное значение, равное информации, учтенной средним одним элементом. ^[19] Критерий Кайзера используется по умолчанию в SPSS и большинстве статистических программ, но не рекомендуется при использовании в качестве единственного критерия отсечения для оценки числа факторов, поскольку он имеет тенденцию к чрезмерному извлечению факторов. ^[20] Была создана вариация этого метода, где исследователь вычисляет доверительные интервалы для каждого собственного значения и оставляет только факторы, у которых весь доверительный интервал больше 1,0. ^[14]^[21]

График осыпи : ^[22] Тест осыпи Кэттелла отображает компоненты как ось X, а соответствующие собственные значения как ось Y. При движении вправо, к более поздним компонентам, собственные значения падают. Когда падение прекращается и кривая делает изгиб в сторону менее крутого спада, тест осыпи Кэттелла говорит о том, что нужно отбросить все дальнейшие компоненты после того, который начинается с изгиба. Это правило иногда критикуют за то, что оно поддается контролируемому исследователем «подтасовке». То есть, поскольку выбор «локтя» может быть субъективным, поскольку кривая имеет несколько изгибов или является плавной кривой, исследователь может поддаться искушению установить пороговое значение на уровне числа факторов, требуемых его исследовательской программой. ^{[ необходима ссылка ]}

Критерии объяснения дисперсии: Некоторые исследователи просто используют правило сохранения достаточного количества факторов для учета 90% (иногда 80%) дисперсии. Если цель исследователя подчеркивает экономность (объяснение дисперсии с помощью как можно меньшего количества факторов), критерий может быть всего 50%.

Байесовские методы

Помещая априорное распределение по числу скрытых факторов и затем применяя теорему Байеса, байесовские модели могут возвращать распределение вероятностей по числу скрытых факторов. Это было смоделировано с использованием индийского процесса «буфета» ^[23], но может быть смоделировано более просто, помещая любое дискретное априорное распределение (например, отрицательное биномиальное распределение ) по числу компонентов.

Методы вращения

Выход PCA максимизирует дисперсию, учтенную первым фактором, затем вторым фактором и т. д. Недостатком этой процедуры является то, что большинство элементов загружаются на ранние факторы, в то время как очень немногие элементы загружаются на более поздние переменные. Это затрудняет интерпретацию факторов путем чтения списка вопросов и нагрузок, поскольку каждый вопрос сильно коррелирует с первыми несколькими компонентами, в то время как очень немногие вопросы сильно коррелируют с последними несколькими компонентами.

Вращение служит для того, чтобы сделать вывод более простым для интерпретации. Выбирая другую основу для тех же главных компонентов – то есть выбирая другие факторы для выражения той же корреляционной структуры – можно создавать переменные, которые легче интерпретировать.

Вращения могут быть ортогональными или косыми; косые вращения позволяют факторам коррелировать. ^[24] Эта повышенная гибкость означает, что возможно больше вращений, некоторые из которых могут быть лучше для достижения указанной цели. Однако это также может затруднить интерпретацию факторов, поскольку некоторая информация «учитывается дважды» и включается несколько раз в различные компоненты; некоторые факторы могут даже казаться почти дубликатами друг друга.

Ортогональные методы

Существуют два широких класса ортогональных вращений: те, которые ищут разреженные строки (где каждая строка является случаем, т.е. субъектом), и те, которые ищут разреженные столбцы (где каждый столбец является переменной).

Простые факторы: эти вращения пытаются объяснить все факторы, используя только несколько важных переменных. Этот эффект может быть достигнут с помощью Varimax (наиболее распространенное вращение).
Простые переменные: эти вращения пытаются объяснить все переменные, используя только несколько важных факторов. Этот эффект может быть достигнут с помощью Quartimax или невращающихся компонентов PCA.
Оба: эти ротации пытаются найти компромисс между обеими вышеуказанными целями, но в процессе могут достичь соответствия, которое плохо подходит для обеих задач; как таковые, они непопулярны по сравнению с вышеуказанными методами. Equamax — один из таких ротаций.

Проблемы с вращением факторов

Может быть сложно интерпретировать факторную структуру, когда каждая переменная нагружает несколько факторов. Небольшие изменения в данных иногда могут нарушить баланс в критерии ротации факторов, так что получается совершенно иная ротация факторов. Это может затруднить сравнение результатов разных экспериментов. Эта проблема проиллюстрирована сравнением разных исследований мировых культурных различий. Каждое исследование использовало разные меры культурных переменных и давало по-разному повернутый результат факторного анализа. Авторы каждого исследования считали, что они открыли что-то новое, и придумали новые названия для найденных ими факторов. Более позднее сравнение исследований показало, что результаты были довольно похожими, когда сравнивались не повернутые результаты. Распространенная практика ротации факторов скрыла сходство между результатами разных исследований. ^[25]

Факторный анализ высшего порядка

Анализ факторов высшего порядка — это статистический метод, состоящий из повторяющихся шагов факторного анализа — косого вращения — факторного анализа повернутого фактора. Его достоинство заключается в том, что он позволяет исследователю увидеть иерархическую структуру изучаемых явлений. Для интерпретации результатов можно либо умножить матрицу первичного факторного паттерна на матрицы факторных паттернов высшего порядка (Gorsuch, 1983) и, возможно, применить вращение Varimax к результату (Thompson, 1990), либо использовать решение Шмида-Леймана (SLS, Schmid & Leiman, 1957, также известное как преобразование Шмида-Леймана), которое приписывает вариацию первичных факторов факторам второго порядка.

Исследовательский факторный анализ (EFA) в сравнении с анализом главных компонентов (PCA)

Факторный анализ связан с анализом главных компонент (PCA), но эти два метода не идентичны. ^[26] В этой области существуют значительные разногласия по поводу различий между этими двумя методами. PCA можно рассматривать как более базовую версию разведочного факторного анализа (EFA), который был разработан в ранние дни до появления высокоскоростных компьютеров. Как PCA, так и факторный анализ направлены на уменьшение размерности набора данных, но подходы, используемые для этого, различаются для двух методов. Факторный анализ явно разработан с целью выявления определенных ненаблюдаемых факторов из наблюдаемых переменных, тогда как PCA напрямую не решает эту задачу; в лучшем случае PCA обеспечивает приближение к требуемым факторам. ^[27] С точки зрения разведочного анализа собственные значения PCA представляют собой завышенные компонентные нагрузки, т. е. загрязненные дисперсией ошибок. ^[28]^[29]^[30]^[31]^[32]^[33]

Хотя EFA и PCA рассматриваются как синонимичные методы в некоторых областях статистики, это подвергалось критике. ^[34]^[35] Факторный анализ «имеет дело с предположением о наличии базовой причинной структуры : [он] предполагает, что ковариация в наблюдаемых переменных обусловлена наличием одной или нескольких скрытых переменных (факторов), которые оказывают причинное влияние на эти наблюдаемые переменные». ^[36] Напротив, PCA не предполагает и не зависит от такой базовой причинной связи. Исследователи утверждают, что различия между двумя методами могут означать, что существуют объективные преимущества для предпочтения одного другому на основе аналитической цели. Если факторная модель сформулирована неправильно или предположения не выполняются, то факторный анализ даст ошибочные результаты. Факторный анализ успешно использовался там, где адекватное понимание системы позволяет хорошо формулировать начальные модели. PCA использует математическое преобразование исходных данных без каких-либо предположений о форме ковариационной матрицы. Целью PCA является определение линейных комбинаций исходных переменных и выбор нескольких из них, которые можно использовать для суммирования набора данных без потери большого количества информации. ^[37]

Аргументы, противопоставляющие PCA и EFA

Фабригар и др. (1999) ^[34] рассматривают ряд причин, по которым можно предположить, что PCA не эквивалентен факторному анализу:

Иногда предполагается, что PCA вычислительно быстрее и требует меньше ресурсов, чем факторный анализ. Фабригар и др. предполагают, что легкодоступные компьютерные ресурсы сделали эту практическую проблему неактуальной.
PCA и факторный анализ могут давать схожие результаты. Этот момент также рассматривают Фабригар и др.; в некоторых случаях, когда общности низкие (например, 0,4), эти два метода дают расходящиеся результаты. Фактически, Фабригар и др. утверждают, что в случаях, когда данные соответствуют предположениям модели общего фактора, результаты PCA являются неточными.
Существуют определенные случаи, когда факторный анализ приводит к «случаям Хейвуда». Они охватывают ситуации, в которых 100% или более дисперсии в измеряемой переменной оцениваются как учтенные моделью. Фабригар и др. предполагают, что эти случаи на самом деле информативны для исследователя, указывая на неправильно указанную модель или нарушение модели общего фактора. Отсутствие случаев Хейвуда в подходе PCA может означать, что такие проблемы остаются незамеченными.
Исследователи получают дополнительную информацию из подхода PCA, например, оценку индивидуума по определенному компоненту; такая информация не получается из факторного анализа. Однако, как утверждают Фабригар и др., типичная цель факторного анализа — т. е. определение факторов, учитывающих структуру корреляций между измеряемыми переменными — не требует знания оценок факторов, и, таким образом, это преимущество сводится на нет. Также возможно вычислить оценки факторов из факторного анализа.

Дисперсия против ковариации

Факторный анализ учитывает случайную ошибку , которая присуща измерению, тогда как PCA этого не делает. Этот момент проиллюстрирован Брауном (2009), ^[38], который указал, что в отношении корреляционных матриц, задействованных в расчетах:

«В PCA 1,00 ставятся на диагональ, что означает, что необходимо учитывать всю дисперсию в матрице (включая дисперсию, уникальную для каждой переменной, дисперсию, общую для переменных, и дисперсию ошибок). Таким образом, по определению, это будет включать всю дисперсию в переменных. Напротив, в EFA общности ставятся на диагональ, что означает, что необходимо учитывать только дисперсию, общую для других переменных (исключая дисперсию, уникальную для каждой переменной, и дисперсию ошибок). Таким образом, по определению, это будет включать только дисперсию, общую для переменных».
— Браун (2009), Анализ главных компонентов и исследовательский факторный анализ — Определения, различия и выбор

По этой причине Браун (2009) рекомендует использовать факторный анализ, когда существуют теоретические идеи о взаимосвязях между переменными, тогда как PCA следует использовать, если целью исследователя является изучение закономерностей в данных.

Различия в процедуре и результатах

Различия между PCA и факторным анализом (FA) дополнительно проиллюстрированы Зуром (2009): ^[35]

PCA позволяет получить главные компоненты, которые учитывают максимальную величину дисперсии наблюдаемых переменных; FA учитывает общую дисперсию в данных.
PCA вставляет единицы на диагонали корреляционной матрицы; FA корректирует диагонали корреляционной матрицы с помощью уникальных факторов.
PCA минимизирует сумму квадратов перпендикулярных расстояний до оси компонента; FA оценивает факторы, которые влияют на отклики наблюдаемых переменных.
Оценки компонентов в PCA представляют собой линейную комбинацию наблюдаемых переменных, взвешенных по собственным векторам ; наблюдаемые переменные в FA представляют собой линейные комбинации базовых и уникальных факторов.
В PCA полученные компоненты не поддаются интерпретации, т.е. они не представляют собой базовые «конструкции»; в FA базовые конструкции могут быть помечены и легко интерпретированы при наличии точной спецификации модели.

В психометрии

История

Чарльз Спирмен был первым психологом, обсудившим общий факторный анализ ^[39] и сделал это в своей статье 1904 года. ^[40] В ней было предоставлено мало подробностей о его методах и рассматривались однофакторные модели. ^[41] Он обнаружил, что баллы школьников по широкому кругу, казалось бы, не связанных между собой предметов, положительно коррелировали, что привело его к постулату о том, что в основе когнитивных способностей человека лежит и формирует их одна общая умственная способность, или g .

Первоначальное развитие общего факторного анализа с несколькими факторами было дано Луисом Терстоуном в двух статьях в начале 1930-х годов, ^[42]^[43] обобщенных в его книге 1935 года «Вектор разума» . ^[44] Терстоун ввел несколько важных концепций факторного анализа, включая общность, уникальность и вращение. ^[45] Он выступал за «простую структуру» и разработал методы вращения, которые можно было использовать как способ достижения такой структуры. ^[39]

В методологии Q Уильям Стивенсон , ученик Спирмена, различал анализ фактора R , ориентированный на изучение межиндивидуальных различий, и анализ фактора Q , ориентированный на субъективные внутрииндивидуальные различия. ^[46]^[47]

Рэймонд Кеттелл был ярым сторонником факторного анализа и психометрии и использовал многофакторную теорию Терстоуна для объяснения интеллекта. Кеттелл также разработал тест каменистой осыпи и коэффициенты подобия.

Применение в психологии

Факторный анализ используется для выявления «факторов», которые объясняют различные результаты в различных тестах. Например, исследование интеллекта показало, что люди, которые получают высокие баллы в тесте на вербальные способности, также хорошо справляются с другими тестами, требующими вербальных способностей. Исследователи объяснили это, используя факторный анализ для выделения одного фактора, часто называемого вербальным интеллектом, который представляет собой степень, в которой человек способен решать задачи, связанные с вербальными навыками. ^{[ необходима цитата ]}

Факторный анализ в психологии чаще всего ассоциируется с исследованиями интеллекта. Однако он также использовался для поиска факторов в широком диапазоне областей, таких как личность, установки, убеждения и т. д. Он связан с психометрией , поскольку может оценить валидность инструмента, обнаружив, действительно ли инструмент измеряет постулированные факторы. ^{[ необходима цитата ]}

Преимущества

Сокращение количества переменных путем объединения двух или более переменных в один фактор. Например, производительность в беге, метании мяча, отбивании, прыжках и поднятии тяжестей можно объединить в один фактор, такой как общие спортивные способности. Обычно в матрице элементов по людям факторы выбираются путем группировки связанных элементов. В методе анализа Q-фактора матрица транспонируется, и факторы создаются путем группировки связанных людей. Например, либералы, либертарианцы, консерваторы и социалисты могут образовывать отдельные группы.
Определение групп взаимосвязанных переменных, чтобы увидеть, как они связаны друг с другом. Например, Кэрролл использовал факторный анализ для построения своей теории трех слоев . Он обнаружил, что фактор, называемый «широкое зрительное восприятие», относится к тому, насколько хорошо человек справляется со зрительными задачами. Он также обнаружил фактор «широкого слухового восприятия», относящийся к способности выполнять слуховые задачи. Кроме того, он обнаружил глобальный фактор, называемый «g» или общий интеллект, который относится как к «широкому зрительному восприятию», так и к «широкому слуховому восприятию». Это означает, что человек с высоким «g» скорее всего будет иметь как высокую способность «зрительного восприятия», так и высокую способность «слухового восприятия», и что «g» поэтому объясняет значительную часть того, почему человек хорош или плох в обеих этих областях.

Недостатки

"...каждая ориентация математически одинаково приемлема. Но оказалось, что различные факторные теории различаются как в плане ориентации факторных осей для данного решения, так и в плане чего-либо еще, так что подгонка модели не оказалась полезной для различения теорий". (Sternberg, 1977 ^[48] ). Это означает, что все вращения представляют собой различные базовые процессы, но все вращения являются одинаково допустимыми результатами стандартной оптимизации факторного анализа. Поэтому невозможно выбрать правильное вращение, используя только факторный анализ.
Факторный анализ может быть хорош лишь настолько, насколько позволяют данные. В психологии, где исследователям часто приходится полагаться на менее валидные и надежные меры, такие как самоотчеты, это может быть проблематично.
Интерпретация факторного анализа основана на использовании «эвристики», которая представляет собой решение, которое «удобно, даже если не абсолютно верно». ^[49] Для одних и тех же данных, факторизованных одинаковым образом, можно сделать более одной интерпретации, и факторный анализ не может определить причинно-следственную связь.

В кросс-культурном исследовании

Факторный анализ — часто используемый метод в кросс-культурном исследовании. Он служит для извлечения культурных измерений . Наиболее известные модели культурных измерений разработаны Гертом Хофстедом , Рональдом Инглхартом , Кристианом Вельцелем , Шаломом Шварцем и Майклом Минковым. Популярная визуализация — культурная карта мира Инглхарта и Вельцеля . ^[25]

В политологии

В исследовании, проведенном в начале 1965 года, политические системы по всему миру были изучены с помощью факторного анализа для построения соответствующих теоретических моделей и исследований, сравнения политических систем и создания типологических категорий. ^[50] Для этих целей в данном исследовании были определены семь основных политических измерений, которые связаны с широким спектром политического поведения: эти измерения - Доступ, Дифференциация, Консенсус, Секционализм, Легитимация, Интерес и Теория и исследования лидерства.

Другие политологи изучают измерение внутренней политической эффективности, используя четыре новых вопроса, добавленных в Национальное исследование выборов 1988 года. Здесь факторный анализ используется для того, чтобы обнаружить, что эти пункты измеряют единое понятие, отличное от внешней эффективности и политического доверия, и что эти четыре вопроса обеспечивали наилучшую меру внутренней политической эффективности на тот момент времени. ^[51]

В маркетинге

Основные шаги:

Определите основные характеристики, которые потребители используют для оценки продуктов в этой категории.
Используйте количественные методы маркетинговых исследований (например, опросы ) для сбора данных от выборки потенциальных клиентов относительно их оценок всех атрибутов продукта.
Введите данные в статистическую программу и запустите процедуру факторного анализа. Компьютер выдаст набор базовых атрибутов (или факторов).
Используйте эти факторы для построения карт восприятия и других инструментов позиционирования продукта .

Сбор информации

Этап сбора данных обычно выполняется специалистами по маркетинговым исследованиям. Вопросы опроса просят респондента оценить образец продукта или описания концепций продукта по ряду атрибутов. Выбирается от пяти до двадцати атрибутов. Они могут включать такие вещи, как: простота использования, вес, точность, долговечность, красочность, цена или размер. Выбранные атрибуты будут различаться в зависимости от изучаемого продукта. Один и тот же вопрос задается обо всех продуктах в исследовании. Данные по нескольким продуктам кодируются и вводятся в статистическую программу, такую как R , SPSS , SAS , Stata , STATISTICA , JMP и SYSTAT.

Анализ

Анализ выделит базовые факторы, объясняющие данные, с помощью матрицы ассоциаций. ^[52] Факторный анализ — это метод взаимозависимости. Рассматривается полный набор взаимозависимых отношений. Спецификация зависимых переменных, независимых переменных или причинности отсутствует. Факторный анализ предполагает, что все данные рейтинга по различным атрибутам могут быть сведены к нескольким важным измерениям. Это сокращение возможно, поскольку некоторые атрибуты могут быть связаны друг с другом. Рейтинг, присвоенный любому атрибуту, частично является результатом влияния других атрибутов. Статистический алгоритм разбивает рейтинг (называемый исходной оценкой) на его различные компоненты и реконструирует частичные оценки в базовые факторные оценки. Степень корреляции между исходной исходной оценкой и окончательной факторной оценкой называется факторной нагрузкой .

Преимущества

Можно использовать как объективные, так и субъективные атрибуты при условии, что субъективные атрибуты можно преобразовать в баллы.
Факторный анализ позволяет выявить скрытые измерения или конструкции, которые прямой анализ выявить не может.
Это просто и недорого.

Недостатки

Полезность зависит от способности исследователей собрать достаточный набор атрибутов продукта. Если важные атрибуты исключены или проигнорированы, ценность процедуры снижается.
Если наборы наблюдаемых переменных очень похожи друг на друга и отличаются от других элементов, факторный анализ назначит им один фактор. Это может скрыть факторы, которые представляют более интересные отношения. ^{[ необходимо уточнение ]}
Для наименования факторов может потребоваться знание теории, поскольку, казалось бы, непохожие атрибуты могут сильно коррелировать по неизвестным причинам.

В области физических и биологических наук

Факторный анализ также широко используется в физических науках, таких как геохимия , гидрохимия , ^[53] астрофизика и космология , а также в биологических науках, таких как экология , молекулярная биология , нейронаука и биохимия .

В управлении качеством грунтовых вод важно связать пространственное распределение различных химических параметров с различными возможными источниками, которые имеют различные химические сигнатуры. Например, сульфидная шахта, вероятно, будет связана с высокими уровнями кислотности, растворенными сульфатами и переходными металлами. Эти сигнатуры могут быть идентифицированы как факторы с помощью факторного анализа R-режима, а местоположение возможных источников может быть предложено путем контурирования баллов факторов. ^[54]

В геохимии различные факторы могут соответствовать различным минеральным ассоциациям и, следовательно, минерализации. ^[55]

В микроматричном анализе

Факторный анализ может быть использован для обобщения данных микрочипов ДНК олигонуклеотидов высокой плотности на уровне зонда для Affymetrix GeneChips. В этом случае скрытая переменная соответствует концентрации РНК в образце. ^[56]

Выполнение

Факторный анализ был реализован в нескольких программах статистического анализа с 1980-х годов:

БМДП
JMP (статистическое программное обеспечение)
Mplus (статистическое программное обеспечение)]
Python : модуль scikit-learn ^[57]
R (с базовой функцией factanal или функцией fa в пакете psych ). Вращения реализованы в пакете R GPArotation .
SAS (с использованием PROC FACTOR или PROC CALIS)
СПСС ^[58]
Стата

Автономный

Фактор [1] — бесплатное программное обеспечение для факторного анализа, разработанное Университетом Ровира и Вирджили

Смотрите также

Примечания

^ В этом примере «вербальный интеллект» и «математический интеллект» являются скрытыми переменными. Тот факт, что они не наблюдаются напрямую, делает их скрытыми.

Ссылки

^ Jöreskog, Karl G. (1983). «Факторный анализ как модель ошибок в переменных». Принципы современных психологических измерений . Hillsdale: Erlbaum. стр. 185–196. ISBN 0-89859-277-1.
^ Бандалос, Дебора Л. (2017). Теория измерений и ее применение в социальных науках . Guilford Press.
^ abc Harman, Harry H. (1976). Современный факторный анализ . Издательство Чикагского университета. С. 175, 176. ISBN 978-0-226-31652-9.
^ abcdefghi Polit DF Beck CT (2012). Исследования в области сестринского дела: создание и оценка доказательств для сестринской практики, 9-е изд . Филадельфия, США: Wolters Klower Health, Lippincott Williams & Wilkins.
^ Meng, J. (2011). «Раскройте кооперативные регуляции генов с помощью микроРНК и факторов транскрипции в глиобластоме с использованием модели неотрицательного гибридного фактора». Международная конференция по акустике, речи и обработке сигналов . Архивировано из оригинала 2011-11-23.
^ Liou, C.-Y.; Musicus, BR (2008). «Кросс-энтропийная аппроксимация структурированных гауссовых ковариационных матриц» (PDF) . IEEE Transactions on Signal Processing . 56 (7): 3362–3367. Bibcode :2008ITSP...56.3362L. doi :10.1109/TSP.2008.917878. S2CID 15255630.
^ abc Цвик, Уильям Р.; Велисер, Уэйн Ф. (1986). «Сравнение пяти правил определения количества сохраняемых компонентов». Psychological Bulletin . 99 (3): 432–442. doi :10.1037/0033-2909.99.3.432.
^ Хорн, Джон Л. (июнь 1965 г.). «Обоснование и проверка числа факторов в факторном анализе». Психометрика . 30 (2): 179–185. doi :10.1007/BF02289447. PMID 14306381. S2CID 19663974.
^ Добрибан, Эдгар (2017-10-02). «Методы перестановки для факторного анализа и PCA». arXiv : 1710.00479v2 [math.ST].
^ * Ледесма, РД; Валеро-Мора, П. (2007). «Определение количества факторов для сохранения в EFA: простая в использовании компьютерная программа для проведения параллельного анализа». Practical Assessment Research & Evaluation . 12 (2): 1–11.
^ Тран, США и Форман, А.К. (2009). Производительность параллельного анализа при извлечении одномерности в присутствии двоичных данных. Образовательные и психологические измерения, 69, 50-61.
^ ab Velicer, WF (1976). «Определение числа компонентов из матрицы частных корреляций». Psychometrika . 41 (3): 321–327. doi :10.1007/bf02293557. S2CID 122907389.
^ ab Courtney, MGR (2013). Определение количества факторов для сохранения в EFA: использование SPSS R-Menu v2.0 для более разумных оценок. Практическая оценка, исследования и оценка, 18(8). Доступно онлайн: http://pareonline.net/getvn.asp?v=18&n=8 Архивировано 2015-03-17 на Wayback Machine
^ ab Warne, RT; Larsen, R. (2014). «Оценка предлагаемой модификации правила Гуттмана для определения количества факторов в исследовательском факторном анализе». Психологическое тестирование и моделирование оценки . 56 : 104–123.
^ Ruscio, John; Roche, B. (2012). «Определение количества факторов, которые следует сохранить в исследовательском факторном анализе, используя сравнительные данные известной факторной структуры». Психологическая оценка . 24 (2): 282–292. doi :10.1037/a0025697. PMID 21966933.
^ Гарридо, Л. Э., Абад, Ф. Дж., Понсода, В. (2012). Новый взгляд на параллельный анализ Хорна с порядковыми переменными. Психологические методы. Расширенная онлайн-публикация. doi : 10.1037/a0030005
^ Ревелль, Уильям (2007). «Определение числа факторов: пример NEO-PI-R» (PDF) . {{cite journal}}: Цитировать журнал требует |journal=( помощь )
^ Ревелль, Уильям (8 января 2020 г.). «psych: процедуры психологических, психометрических и личностных исследований».
^ Кайзер, Генри Ф. (апрель 1960 г.). «Применение электронных компьютеров в факторном анализе». Образовательные и психологические измерения . 20 (1): 141–151. doi :10.1177/001316446002000116. S2CID 146138712.
^ Бандалос, DL; Бём-Кауфман, MR (2008). «Четыре распространенных заблуждения в исследовательском факторном анализе». В Lance, Charles E.; Vandenberg, Robert J. (ред.). Статистические и методологические мифы и городские легенды: доктрина, правда и вымысел в организационных и социальных науках . Taylor & Francis. стр. 61–87. ISBN 978-0-8058-6237-9.
^ Ларсен, Р.; Уорн, Р. Т. (2010). «Оценка доверительных интервалов для собственных значений в исследовательском факторном анализе». Методы исследования поведения . 42 (3): 871–876. doi : 10.3758/BRM.42.3.871 . PMID 20805609.
^ Кеттелл, Рэймонд (1966). «Тест осыпи для числа факторов». Многомерные поведенческие исследования . 1 (2): 245–76. doi :10.1207/s15327906mbr0102_10. PMID 26828106.
^ Алпайдин (2020). Введение в машинное обучение (5-е изд.). С. 528–9.
^ "Методы ротации факторов". Stack Exchange . Получено 7 ноября 2022 г. .
^ ab Fog, A (2022). «Двумерные модели культурных различий: статистический и теоретический анализ» (PDF) . Кросс-культурные исследования . 57 (2–3): 115–165. doi :10.1177/10693971221135703. S2CID 253153619.
^ Бартоломью, DJ; Стил, F.; Гэлбрейт, J.; Мустаки, I. (2008). Анализ многомерных данных по социальным наукам . Статистика в серии социальных и поведенческих наук (2-е изд.). Тейлор и Фрэнсис. ISBN 978-1584889601.
^ Jolliffe IT Principal Component Analysis , Серия: Springer Series in Statistics, 2-е изд., Springer, NY, 2002, XXIX, 487 стр. 28 иллюстраций. ISBN 978-0-387-95442-4
^ Кеттелл, Р. Б. (1952). Факторный анализ . Нью-Йорк: Harper.
^ Фрухтер, Б. (1954). Введение в факторный анализ . Ван Ностранд.
^ Кеттелл, Р. Б. (1978). Использование факторного анализа в поведенческих и биологических науках . Нью-Йорк: Пленум.
^ Чайлд, Д. (2006). Основы факторного анализа, 3-е издание . Bloomsbury Academic Press.
^ Горсач, Р. Л. (1983). Факторный анализ, 2-е издание . Хиллсдейл, Нью-Джерси: Erlbaum.
^ Макдональд, РП (1985). Факторный анализ и родственные методы . Хиллсдейл, Нью-Джерси: Erlbaum.
^ ab Fabrigar; et al. (1999). "Оценка использования исследовательского факторного анализа в психологических исследованиях" (PDF) . Психологические методы.
^ ab Suhr, Diane (2009). "Анализ главных компонент против исследовательского факторного анализа" (PDF) . Труды SUGI 30 . Получено 5 апреля 2012 г. .
^ SAS Statistics. "Анализ главных компонент" (PDF) . Учебник поддержки SAS .
^ Меглен, RR (1991). «Исследование больших баз данных: хемометрический подход с использованием анализа главных компонент». Журнал хемометрии . 5 (3): 163–179. doi :10.1002/cem.1180050305. S2CID 120886184.
^ Браун, Дж. Д. (январь 2009 г.). «Анализ главных компонентов и исследовательский факторный анализ – Определения, различия и выбор» (PDF) . Shiken: JALT Testing & Evaluation SIG Newsletter . Получено 16 апреля 2012 г.
^ ab Mulaik, Stanley A (2010). Основы факторного анализа. Второе издание . Бока-Ратон, Флорида: CRC Press. стр. 6. ISBN 978-1-4200-9961-4.
^ Спирмен, Чарльз (1904). «Общий интеллект, объективно определенный и измеренный». Американский журнал психологии . 15 (2): 201–293. doi :10.2307/1412107. JSTOR 1412107.
^ Бартоломью, DJ (1995). «Спирмен и происхождение и развитие факторного анализа». Британский журнал математической и статистической психологии . 48 (2): 211–220. doi :10.1111/j.2044-8317.1995.tb01060.x.
^ Терстоун, Луис (1931). «Многофакторный анализ». Psychological Review . 38 (5): 406–427. doi :10.1037/h0069792.
^ Терстоун, Луис (1934). «Векторы разума». Психологический обзор . 41 : 1–32. doi :10.1037/h0075959.
^ Терстоун, Л. Л. (1935). Векторы разума. Многофакторный анализ для выделения первичных черт . Чикаго, Иллинойс: Издательство Чикагского университета.
^ Бок, Роберт (2007). «Переосмысление Терстоуна». В Cudeck, Роберт; MacCallum, Роберт C. (ред.). Факторный анализ в 100. Mahwah, Нью-Джерси: Lawrence Erlbaum Associates. стр. 37. ISBN 978-0-8058-6212-6.
^ Маккеун, Брюс (21.06.2013). Методология Q. SAGE Publications. ISBN 9781452242194. OCLC 841672556.
^ Стивенсон, У. (август 1935 г.). «Техника факторного анализа». Nature . 136 (3434): 297. Bibcode :1935Natur.136..297S. doi : 10.1038/136297b0 . ISSN 0028-0836. S2CID 26952603.
^ Стернберг, Р. Дж. (1977). Метафоры разума: концепции природы интеллекта . Нью-Йорк: Cambridge University Press. С. 85–111.^{[ требуется проверка ]}
^ "Factor Analysis". Архивировано из оригинала 18 августа 2004 г. Получено 22 июля 2004 г.
^ Грегг, Филлип М.; Бэнкс, Артур С. (1965). «Измерения политических систем: факторный анализ кросс-политического исследования». American Political Science Review . 59 (3): 602–614. doi :10.2307/1953171. JSTOR 1953171. S2CID 145459216.
^ Ниеми, Ричард Г.; Крейг, Стивен К.; Маттей, Франко (декабрь 1991 г.). «Измерение внутренней политической эффективности в исследовании национальных выборов 1988 г.». American Political Science Review . 85 (4): 1407–1413. doi :10.2307/1963953. ISSN 0003-0554. JSTOR 1963953. S2CID 146641381.
^ Риттер, Н. (2012). Сравнение методов без распределения и без распределения в факторном анализе. Доклад, представленный на конференции Юго-западной ассоциации образовательных исследований (SERA) 2012, Новый Орлеан, Луизиана (ED529153).
^ Суббарао, К.; Суббарао, Невада; Чанду, С.Н. (декабрь 1996 г.). «Характеристика загрязнения подземных вод с помощью факторного анализа». Экологическая геология . 28 (4): 175–180. Бибкод : 1996EnGeo..28..175S. дои : 10.1007/s002540050091. S2CID 129655232.
^ Лав, Д.; Холлбауэр, Д.К.; Амос, А.; Хранова, Р.К. (2004). «Факторный анализ как инструмент управления качеством грунтовых вод: два примера из Южной Африки». Физика и химия Земли . 29 (15–18): 1135–43. Bibcode : 2004PCE....29.1135L. doi : 10.1016/j.pce.2004.09.027.
^ Barton, ES; Hallbauer, DK (1996). "Состав микроэлементов и изотопов U—Pb в типах пирита в протерозойском Черном рифе, последовательность Трансвааль, Южная Африка: последствия для генезиса и возраста". Chemical Geology . 133 (1–4): 173–199. Bibcode :1996ChGeo.133..173B. doi :10.1016/S0009-2541(96)00075-7.
^ Хохрейтер, Зепп; Клеверт, Джорк-Арне; Обермайер, Клаус (2006). «Новый метод суммирования данных уровня зонда affymetrix». Биоинформатика . 22 (8): 943–9. doi : 10.1093/биоинформатика/btl033 . ПМИД 16473874.
^ "sklearn.decomposition.FactorAnalysis — документация scikit-learn 0.23.2". scikit-learn.org .
^ MacCallum, Robert (июнь 1983 г.). «Сравнение программ факторного анализа в SPSS, BMDP и SAS». Psychometrika . 48 (2): 223–231. doi :10.1007/BF02294017. S2CID 120770421.

Дальнейшее чтение

Чайлд, Деннис (2006), Основы факторного анализа (3-е изд.), Continuum International , ISBN 978-0-8264-8000-2.
Fabrigar, LR; Wegener, DT; MacCallum, RC; Strahan, EJ (сентябрь 1999 г.). «Оценка использования исследовательского факторного анализа в психологических исследованиях». Psychological Methods . 4 (3): 272–299. doi :10.1037/1082-989X.4.3.272.
BT Gray (1997) Анализ факторов высшего порядка (Доклад конференции)
Дженнрих, Роберт И., «Вращение к простым нагрузкам с использованием функции потери компонентов: косой случай», Психометрика , т. 71, № 1, стр. 173–191, март 2006 г.
Katz, Jeffrey Owen и Rohlf, F. James. Первичная функциональная плоскость продукта: косой поворот к простой структуре. Multivariate Behavioral Research , апрель 1975 г., том 10, стр. 219–232.
Кац, Джеффри Оуэн и Рольф, Ф. Джеймс. Functionplane: новый подход к простому структурному вращению. Psychometrika , март 1974 г., т. 39, № 1, стр. 37–51.
Katz, Jeffrey Owen, и Rohlf, F. James. Анализ кластеров с использованием функциональных точек. Systematic Zoology , сентябрь 1973 г., том 22, № 3, стр. 295–301.
Мулайк, С.А. (2010), Основы факторного анализа , Chapman & Hall.
Преподаватель, К. Дж.; Маккаллум, Р. К. (2003). «Ремонт электрической факторной анализирующей машины Тома Свифта» (PDF) . Понимание статистики . 2 (1): 13–43. doi :10.1207/S15328031US0201_02. hdl : 1808/1492 .
Дж. Шмид и Дж. М. Лейман (1957). Разработка иерархических факторных решений. Психометрика , 22(1), 53–61.
Томпсон, Б. (2004), Исследовательский и подтверждающий факторный анализ: понимание концепций и приложений , Вашингтон, округ Колумбия: Американская психологическая ассоциация , ISBN 978-1591470939.

Ханс-Георг Вольф, Катя Прейзинг (2005)Исследование структуры элементов и факторов более высокого порядка с помощью решения Шмидта-Леймана: синтаксические коды для методов исследования поведения SPSS и SAS, инструменты и компьютеры , 37 (1), 48-58

Внешние ссылки

На Викискладе есть медиафайлы по теме Факторный анализ .

Руководство для начинающих по факторному анализу
Исследовательский факторный анализ. Рукопись книги Такера, Л. и Маккаллума Р. (1993). Получено 8 июня 2006 г. из: [2] Архивировано 23 мая 2013 г. на Wayback Machine
Гарсон, Г. Дэвид, "Факторный анализ" из Statnotes: Topics in Multivariate Analysis . Получено 13 апреля 2009 г. из StatNotes: Topics in Multivariate Analysis, от Г. Дэвида Гарсона из Университета штата Северная Каролина, Программа государственного управления
Факторный анализ на 100 — материалы конференции
FARMS — Факторный анализ для надежного суммирования микрочипов, пакет R