Функция действительной переменной

Математическая функция

В математическом анализе и приложениях в геометрии , прикладной математике , технике и естественных науках функция действительной переменной — это функция , областью определения которой являются действительные числа или ее подмножество , содержащее интервал положительной длины. Большинство рассматриваемых и изучаемых вещественных функций дифференцируемы в некотором интервале. Наиболее широко рассматриваемыми такими функциями являются вещественные функции , которые являются вещественнозначными функциями действительной переменной, то есть функциями действительной переменной, кодоменой которой является множество действительных чисел. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

Тем не менее, кодоменой функции действительной переменной может быть любое множество. Однако часто предполагается, что оно имеет структуру векторного пространства над реальными объектами. То есть кодоменом может быть евклидово пространство , координатный вектор , набор матриц действительных чисел заданного размера или -алгебра , такая как комплексные числа или кватернионы . Структурное векторное пространство кодомена индуцирует структуру -векторного пространства функций. Если кодомен имеет структуру -алгебры, то же самое верно и для функций. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$

Образом функции действительной переменной является кривая в кодобласти. В этом контексте функция, определяющая кривую, называется параметрическим уравнением кривой.

Когда кодоменой функции действительной переменной является конечномерное векторное пространство , функцию можно рассматривать как последовательность действительных функций. Это часто используется в приложениях.

Реальная функция

График действительной функции

Действительная функция — это функция из подмножества где обозначает , как обычно, множество действительных чисел . То есть областью определения вещественной функции является подмножество , а ее кодомен. Обычно предполагается, что область определения содержит интервал положительной длины. ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} ,}$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} }$ ${\displaystyle \mathbb {R} .}$

Основные примеры

Для многих часто используемых действительных функций областью определения является весь набор действительных чисел, а функция непрерывна и дифференцируема в каждой точке области. Говорят, что эти функции всюду определены, непрерывны и дифференцируемы. Это случай:

• Все полиномиальные функции , включая постоянные и линейные функции.
• Функции синуса и косинуса
• Экспоненциальная функция

Некоторые функции определены везде, но не непрерывны в некоторых точках. Например

• Ступенчатая функция Хевисайда определена всюду, но не непрерывна в нуле.

Некоторые функции всюду определены и непрерывны, но не всюду дифференцируемы. Например

• Абсолютная величина определена, непрерывна всюду и дифференцируема всюду, кроме нуля.
• Кубический корень определен, непрерывен всюду и дифференцируем всюду, кроме нуля.

Многие общие функции определены не везде, но непрерывны и дифференцируемы всюду, где они определены. Например:

• Рациональная функция представляет собой частное двух полиномиальных функций и не определена в нулях знаменателя.
• Функция тангенса не определена для случаев, когда k — любое целое число. ${\displaystyle {\frac {\pi }{2}}+k\pi ,}$
• Функция логарифма определяется только для положительных значений переменной.

Некоторые функции непрерывны во всей области определения и не дифференцируемы в некоторых точках. Это случай:

• Квадратный корень определяется только для неотрицательных значений переменной и не дифференцируем в точке 0 (дифференцируем для всех положительных значений переменной).

Общее определение

Функция действительной переменной с действительным знаком — это функция , которая принимает в качестве входных данных действительное число , обычно представляемое переменной x , для создания другого действительного числа, значения функции, обычно обозначаемого f ( x ). Для простоты в этой статье вещественная функция действительной переменной будет называться просто функцией . Чтобы избежать какой-либо двусмысленности, другие типы функций, которые могут возникнуть, будут явно указаны.

Некоторые функции определены для всех действительных значений переменных (говорят, что они определены всюду), но некоторые другие функции определяются только в том случае, если значение переменной берется из подмножества X из ℝ, области определения функции, которая всегда предполагается, что он содержит интервал положительной длины. Другими словами, вещественная функция действительной переменной — это функция

${\displaystyle f:X\to \mathbb {R} }$

такой, что его область определения X является подмножеством ℝ, содержащим интервал положительной длины.

Простым примером функции с одной переменной может быть:

${\displaystyle f:X\to \mathbb {R} }$

${\displaystyle X=\{x\in \mathbb {R} \,:\,x\geq 0\}}$

${\displaystyle f(x)={\sqrt {x}}}$

что является квадратным корнем из x .

Изображение

Образ функции — это набор всех значений f , когда переменная x работает во всей области определения f . Для непрерывной (см. определение ниже) действительной функции со связной областью изображения изображение представляет собой либо интервал, либо одно значение. В последнем случае функция является постоянной функцией . ${\displaystyle f(x)}$

Прообраз данного действительного числа y — это множество решений уравнения y = f ( x ) .

Домен

Область определения функции нескольких действительных переменных представляет собой подмножество ℝ, которое иногда определяется явно. Фактически, если ограничить область определения X функции f подмножеством Y ⊂ X , формально получится другая функция — ограничение f на Y , которая обозначается f _{| Ю.}​ На практике часто не вредно отождествлять f и f _{| Y} и опустить индекс _{| Ю.}​

И наоборот, иногда можно естественным образом расширить область определения данной функции, например, путем непрерывности или аналитического продолжения . Это означает, что нецелесообразно явно определять область определения функции действительной переменной.

Алгебраическая структура

Арифметические операции могут применяться к функциям следующим образом:

• Для каждого вещественного числа r везде определена постоянная функция . ${\displaystyle (x)\mapsto r}$
• Для каждого действительного числа r и каждой функции f функция имеет ту же область определения, что и f (или определена везде, если r = 0). ${\displaystyle rf:(x)\mapsto rf(x)}$
• Если f и g — две функции соответствующих областей X и Y такие, что X ∩ Y содержит открытое подмножество ℝ, то и — это функции, которые имеют область определения, содержащую X ∩ Y . ${\displaystyle f+g:(x)\mapsto f(x)+g(x)}$ ${\displaystyle f\,g:(x)\mapsto f(x)\,g(x)}$

Отсюда следует, что функции от n переменных, определенные всюду, и функции от n переменных, определенные в некоторой окрестности данной точки, образуют коммутативные алгебры над вещественными числами (ℝ-алгебры).

Аналогичным образом можно определить, какая функция является функцией, только если набор точек ( x ) в области определения f таких, что f ( x ) ≠ 0 , содержит открытое подмножество ℝ. Это ограничение означает, что две вышеупомянутые алгебры не являются полями . ${\displaystyle 1/f:(x)\mapsto 1/f(x),}$

Непрерывность и предел

Предел действительной функции действительной переменной.

До второй половины XIX века математики рассматривали только непрерывные функции . Тогда понятие непрерывности было разработано для функций одной или нескольких действительных переменных задолго до формального определения топологического пространства и непрерывного отображения между топологическими пространствами. Поскольку непрерывные функции действительной переменной широко распространены в математике, стоит определить это понятие без ссылки на общее понятие непрерывных отображений между топологическими пространствами.

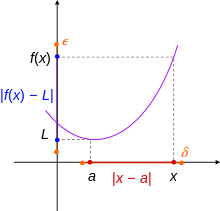
Для определения непрерывности полезно рассмотреть функцию расстояния ℝ, которая является всюду определенной функцией двух действительных переменных: ${\displaystyle d(x,y)=|x-y|}$

Функция f является непрерывной в точке , которая находится внутри ее области определения, если для каждого положительного действительного числа ε существует такое положительное действительное число φ , что для всех таких, что Другими словами, φ можно выбрать достаточно малым, чтобы иметь изображение f интервала радиуса φ с центром в, содержащегося в интервале длины 2 ε с центром в. Функция непрерывна, если она непрерывна в каждой точке своей области определения. ${\displaystyle a}$ ${\displaystyle |f(x)-f(a)|<\varepsilon }$ ${\displaystyle x}$ ${\displaystyle d(x,a)<\varphi .}$ ${\displaystyle a}$ ${\displaystyle f(a).}$

Предел вещественной функции действительной переменной таков . ^[1] Пусть a — точка топологического замыкания области X функции f . Функция f имеет предел L , когда x стремится к a , обозначаемый

${\displaystyle L=\lim _{x\to a}f(x),}$

если выполнено следующее условие: для каждого положительного действительного числа ε > 0 существует положительное действительное число δ > 0 такое, что

${\displaystyle |f(x)-L|<\varepsilon }$

для всех x в области определения таких, что

${\displaystyle d(x,a)<\delta .}$

Если предел существует, он уникален. Если a находится внутри области, предел существует тогда и только тогда, когда функция непрерывна в точке a . В этом случае мы имеем

${\displaystyle f(a)=\lim _{x\to a}f(x).}$

Когда a находится на границе области определения f и если f имеет предел в точке a , последняя формула позволяет «расширить непрерывностью» область определения f до a .

Исчисление

Можно собрать несколько функций, каждая из которых имеет действительную переменную, скажем

${\displaystyle y_{1}=f_{1}(x)\,,\quad y_{2}=f_{2}(x)\,,\ldots ,y_{n}=f_{n}(x)}$

в вектор, параметризованный x :

${\displaystyle \mathbf {y} =(y_{1},y_{2},\ldots ,y_{n})=[f_{1}(x),f_{2}(x),\ldots ,f_{n}(x)]}$

Производная вектора y — это векторные производные от f _i ( x ) для i = 1, 2, ..., n :

${\displaystyle {\frac {d\mathbf {y} }{dx}}=\left({\frac {dy_{1}}{dx}},{\frac {dy_{2}}{dx}},\ldots ,{\frac {dy_{n}}{dx}}\right)}$

Можно также выполнить линейные интегралы вдоль пространственной кривой, параметризованной x , с вектором положения r = r ( x ), путем интегрирования по переменной x :

${\displaystyle \int _{a}^{b}\mathbf {y} (x)\cdot d\mathbf {r} =\int _{a}^{b}\mathbf {y} (x)\cdot {\frac {d\mathbf {r} (x)}{dx}}dx}$

где · — скалярное произведение , а x = a и x = b — начало и конец кривой.

Теоремы

С помощью определений интегрирования и производных можно сформулировать ключевые теоремы, включая фундаментальную теорему исчисления , интегрирование по частям и теорему Тейлора . Оценку смеси интегралов и производных можно выполнить, используя теорему дифференцирования под знаком интеграла .

Неявные функции

Действительнозначная неявная функция действительной переменной не записывается в виде « y = f ( x )». Вместо этого отображение происходит из пространства ℝ ² в нулевой элемент в ℝ (просто обычный ноль 0):

${\displaystyle \phi :\mathbb {R} ^{2}\to \{0\}}$

и

${\displaystyle \phi (x,y)=0}$

представляет собой уравнение с переменными. Неявные функции — это более общий способ представления функций, поскольку если:

${\displaystyle y=f(x)}$

тогда мы всегда можем определить:

${\displaystyle \phi (x,y)=y-f(x)=0}$

но обратное не всегда возможно, т. е. не все неявные функции имеют вид этого уравнения.

Одномерные пространственные кривые в ℝ n

Пространственная кривая в 3d. Вектор положения r параметризуется скаляром t . При r = a красная линия — касательная к кривой, а синяя плоскость — нормаль к кривой.

Формулировка

Даны функции r ₁ = r ₁ ( t ) , r ₂ = r ₂ ( t ) , ..., r _n = r _n ( t ) всех общей переменной t , так что:

${\displaystyle {\begin{aligned}r_{1}:\mathbb {R} \rightarrow \mathbb {R} &\quad r_{2}:\mathbb {R} \rightarrow \mathbb {R} &\cdots &\quad r_{n}:\mathbb {R} \rightarrow \mathbb {R} \\r_{1}=r_{1}(t)&\quad r_{2}=r_{2}(t)&\cdots &\quad r_{n}=r_{n}(t)\\\end{aligned}}}$

или вместе взятые:

${\displaystyle \mathbf {r} :\mathbb {R} \rightarrow \mathbb {R} ^{n}\,,\quad \mathbf {r} =\mathbf {r} (t)}$

тогда параметризованный n -кортеж,

${\displaystyle \mathbf {r} (t)=[r_{1}(t),r_{2}(t),\ldots ,r_{n}(t)]}$

описывает одномерную пространственную кривую .

Касательная линия к кривой

В точке r ( t = c ) = a = ( a ₁ , a ₂ , ..., an ) для некоторой постоянной t = c уравнения одномерной касательной к кривой в этой точке _{задаются} в терминах обычных производных r ₁ ( t ), r ₂ ( t ), ..., r _n ( t ) и r по t :

${\displaystyle {\frac {r_{1}(t)-a_{1}}{dr_{1}(t)/dt}}={\frac {r_{2}(t)-a_{2}}{dr_{2}(t)/dt}}=\cdots ={\frac {r_{n}(t)-a_{n}}{dr_{n}(t)/dt}}}$

Нормальная плоскость к кривой

Уравнение n -мерной гиперплоскости, нормальной к касательной в точке r = a , имеет вид:

${\displaystyle (p_{1}-a_{1}){\frac {dr_{1}(t)}{dt}}+(p_{2}-a_{2}){\frac {dr_{2}(t)}{dt}}+\cdots +(p_{n}-a_{n}){\frac {dr_{n}(t)}{dt}}=0}$

или в терминах скалярного произведения :

${\displaystyle (\mathbf {p} -\mathbf {a} )\cdot {\frac {d\mathbf {r} (t)}{dt}}=0}$

где p = ( p ₁ , p ₂ , ..., p _n ) — точки на плоскости , а не на пространственной кривой.

Связь с кинематикой

Кинематические величины классической частицы: масса m , положение r , скорость v , ускорение a .

Физическая и геометрическая интерпретация d r ( t )/ dt — это « скорость » точечной частицы , движущейся по пути r ( t ), трактуя r как координаты вектора пространственного положения, параметризованные временем t , и является вектором касательная к пространственной кривой для всех t в мгновенном направлении движения. В момент t = c пространственная кривая имеет касательный вектор d r ( t )/ dt | _{t = c} , а гиперплоскость, нормальная к пространственной кривой в точке t = c , также нормальна к касательной в точке t = c . Любой вектор в этой плоскости ( p − a ) должен быть нормален к d r ( t )/ dt | _{т знак равно с} .

Аналогично, d ² r ( t )/ dt ² — это « ускорение » частицы и вектор, нормаль к кривой, направленный вдоль радиуса кривизны .

Матричные функции

Матрица также может быть функцией одной переменной . Например, матрица вращения в 2d:

${\displaystyle R(\theta )={\begin{bmatrix}\cos \theta &-\sin \theta \\\sin \theta &\cos \theta \\\end{bmatrix}}}$

– матричная функция угла поворота относительно начала координат. Аналогично в специальной теории относительности матрица преобразования Лоренца для чистого повышения (без вращений):

${\displaystyle \Lambda (\beta )={\begin{bmatrix}{\frac {1}{\sqrt {1-\beta ^{2}}}}&-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&0&0\\-{\frac {\beta }{\sqrt {1-\beta ^{2}}}}&{\frac {1}{\sqrt {1-\beta ^{2}}}}&0&0\\0&0&1&0\\0&0&0&1\\\end{bmatrix}}}$

является функцией параметра повышения β = v / c , в котором v — относительная скорость между системами отсчета (непрерывная переменная), а c — скорость света , константа.

Банахово и гильбертово пространство и квантовая механика.

Обобщая предыдущий раздел, можно сказать, что выходные данные функции действительной переменной также могут находиться в банаховом или гильбертовом пространстве . В этих пространствах определены деление, умножение и пределы, поэтому такие понятия, как производная и интеграл, по-прежнему применяются. Особенно часто это происходит в квантовой механике, где берут производную от кета или оператора . Это происходит, например, в общем нестационарном уравнении Шредингера :

${\displaystyle i\hbar {\frac {\partial }{\partial t}}\Psi ={\hat {H}}\Psi }$

где берется производная волновой функции, которая может быть элементом нескольких различных гильбертовых пространств.

Комплексная функция действительной переменной

Комплексная функция действительной переменной может быть определена путем ослабления при определении действительнозначных функций ограничения кодомена действительными числами и разрешения комплексных значений.

Если f ( x ) такая комплексная функция, ее можно разложить как

ж ( Икс ) знак равно г ( Икс ) + яч ( Икс ) ,

где g и h — вещественные функции. Другими словами, изучение комплекснозначных функций легко сводится к изучению пар вещественнозначных функций.

Мощность множеств функций действительной переменной

Мощность набора действительных функций действительной переменной , равна , что строго больше мощности континуума ( т . е. набора всех действительных чисел). Этот факт легко проверяется кардинальной арифметикой: ${\displaystyle \mathbb {R} ^{\mathbb {R} }=\{f:\mathbb {R} \to \mathbb {R} \}}$ ${\displaystyle \beth _{2}=2^{\mathfrak {c}}}$

$${\displaystyle \mathrm {card} (\mathbb {R} ^{\mathbb {R} })=\mathrm {card} (\mathbb {R} )^{\mathrm {card} (\mathbb {R} )}={\mathfrak {c}}^{\mathfrak {c}}=(2^{\aleph _{0}})^{\mathfrak {c}}=2^{\aleph _{0}\cdot {\mathfrak {c}}}=2^{\mathfrak {c}}.}$$

Кроме того, если набор такой, что , то мощность набора также , так как ${\displaystyle X}$ ${\displaystyle 2\leq \mathrm {card} (X)\leq {\mathfrak {c}}}$ ${\displaystyle X^{\mathbb {R} }=\{f:\mathbb {R} \to X\}}$ ${\displaystyle 2^{\mathfrak {c}}}$

$${\displaystyle 2^{\mathfrak {c}}=\mathrm {card} (2^{\mathbb {R} })\leq \mathrm {card} (X^{\mathbb {R} })\leq \mathrm {card} (\mathbb {R} ^{\mathbb {R} })=2^{\mathfrak {c}}.}$$

Однако множество непрерывных функций имеет строго меньшую мощность — мощность континуума . Это следует из того, что непрерывная функция полностью определяется своим значением на плотном подмножестве своей области определения. ^[2] Таким образом, мощность множества непрерывных вещественных функций от вещественных чисел не превышает мощности множества вещественных функций рациональной переменной. По кардинальной арифметике: ${\displaystyle C^{0}(\mathbb {R} )=\{f:\mathbb {R} \to \mathbb {R} :f\ \mathrm {continuous} \}}$ ${\displaystyle {\mathfrak {c}}}$

$${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))\leq \mathrm {card} (\mathbb {R} ^{\mathbb {Q} })=(2^{\aleph _{0}})^{\aleph _{0}}=2^{\aleph _{0}\cdot \aleph _{0}}=2^{\aleph _{0}}={\mathfrak {c}}.}$$

С другой стороны, поскольку существует явная биекция между и набор постоянных функций , который образует подмножество , также должен выполняться. Следовательно, . ${\displaystyle \mathbb {R} }$ ${\displaystyle \{f:\mathbb {R} \to \mathbb {R} :f(x)\equiv x_{0}\}}$ ${\displaystyle C^{0}(\mathbb {R} )}$ ${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))\geq {\mathfrak {c}}}$ ${\displaystyle \mathrm {card} (C^{0}(\mathbb {R} ))={\mathfrak {c}}}$

Смотрите также

• Реальный анализ
• Функция нескольких действительных переменных
• Комплексный анализ
• Функция нескольких комплексных переменных

Рекомендации

1. Р. Курант. Дифференциальное и интегральное исчисление . Том. 2. Библиотека классической литературы Wiley. стр. 46–47. ISBN 0-471-60840-8.
2. Рудин, В. (1976). Принципы математического анализа . Нью-Йорк: МакГроу-Хилл. стр. 98–99. ISBN 0-07-054235X.

• Ф. Эйрес, Э. Мендельсон (2009). Исчисление . Серия набросков Шаума (5-е изд.). МакГроу Хилл. ISBN 978-0-07-150861-2.
• Р. Вреде, М. Р. Шпигель (2010). Продвинутое исчисление . Серия набросков Шаума (3-е изд.). МакГроу Хилл. ISBN 978-0-07-162366-7.
• Н. Бурбаки (2004). Функции действительной переменной: элементарная теория. Спрингер. ISBN 354-065-340-6.

Внешние ссылки

• Многомерное исчисление
• Л. А. Талман (2007) Дифференцируемость функций многих переменных