Релятивистская квантовая химия

Теории квантовой химии, объясненные с помощью релятивистской механики

Релятивистская квантовая химия объединяет релятивистскую механику с квантовой химией для расчета свойств и структуры элементов , особенно для более тяжелых элементов периодической таблицы . Ярким примером является объяснение цвета золота : из-за релятивистских эффектов оно не серебристое, как большинство других металлов. ^[1]

Термин релятивистские эффекты был разработан в свете истории квантовой механики. Первоначально квантовая механика была разработана без учета теории относительности . ^[2] Релятивистские эффекты — это те расхождения между значениями, рассчитанными с помощью моделей, которые учитывают относительность, и тех, которые ее не учитывают. ^[3] Релятивистские эффекты важны для более тяжелых элементов с высокими атомными номерами , таких как лантаноиды и актиниды . ^[4]

Релятивистские эффекты в химии можно рассматривать как возмущения или небольшие поправки к нерелятивистской теории химии, которая разработана из решений уравнения Шредингера . Эти поправки влияют на электроны по-разному в зависимости от скорости электронов по сравнению со скоростью света . Релятивистские эффекты более заметны в тяжелых элементах, потому что только в этих элементах электроны достигают достаточных скоростей для того, чтобы элементы имели свойства, отличающиеся от того, что предсказывает нерелятивистская химия. ^[5]

История

Начиная с 1935 года, Берта Свирлз описала релятивистскую трактовку многоэлектронной системы ^[6] , несмотря на утверждение Поля Дирака 1929 года о том, что единственные несовершенства, оставшиеся в квантовой механике, «приводят к трудностям только тогда, когда речь идет о высокоскоростных частицах, и поэтому не имеют значения при рассмотрении атомной и молекулярной структуры и обычных химических реакций, в которых она, действительно, обычно достаточно точна, если пренебречь относительной вариацией массы и скорости и предположить только кулоновские силы между различными электронами и атомными ядрами». ^[7]

Химики-теоретики в целом соглашались с мнением Дирака до 1970-х годов, когда релятивистские эффекты были обнаружены в тяжелых элементах. ^[8] Уравнение Шредингера было разработано без учета теории относительности в статье Шредингера 1926 года. ^[9] Релятивистские поправки были внесены в уравнение Шредингера (см. уравнение Клейна–Гордона ) для описания тонкой структуры атомных спектров, но это развитие и другие не сразу просочились в химическое сообщество. Поскольку атомные спектральные линии в основном находились в области физики, а не в области химии, большинство химиков были незнакомы с релятивистской квантовой механикой, и их внимание было сосредоточено на более легких элементах, типичных для фокуса органической химии того времени. ^[10]

Мнение Дирака о роли релятивистской квантовой механики для химических систем неверно по двум причинам. Во-первых, электроны в атомных орбиталях s и p движутся со значительной долей скорости света. Во-вторых, релятивистские эффекты приводят к косвенным последствиям, которые особенно очевидны для атомных орбиталей d и f . ^[8]

Качественное лечение

Релятивистский фактор Лоренца (γ) как функция скорости. Для малой скорости (ордината) равна , но при стремится к бесконечности. ${\displaystyle E_{\text{rel}}}$ ${\displaystyle E_{0}=mc^{2},}$ ${\displaystyle v_{\text{e}}\to c}$ ${\displaystyle E_{\text{rel}}}$

Одним из наиболее важных и известных результатов теории относительности является то, что релятивистская масса электрона увеличивается с ростом

$${\displaystyle m_{\text{rel}}={\frac {m_{\text{e}}}{\sqrt {1-(v_{\text{e}}/c)^{2}}}},}$$

где - масса покоя электрона , скорость электрона и скорость света соответственно. Рисунок справа иллюстрирует этот релятивистский эффект как функцию скорости. ${\displaystyle m_{e},v_{e},c}$

Это имеет непосредственное отношение к радиусу Бора ( ), который определяется выражением ${\displaystyle a_{0}}$

$${\displaystyle a_{0}={\frac {\hbar }{m_{\text{e}}c\alpha }},}$$

где — приведенная постоянная Планка , а α — постоянная тонкой структуры (релятивистская поправка для модели Бора ). ${\displaystyle \hbar }$

Бор подсчитал, что 1s-орбитальный электрон атома водорода, вращающийся по орбите с радиусом Бора 0,0529 нм, движется со скоростью, близкой к 1/137 скорости света. ^[11] Можно распространить это на более крупный элемент с атомным номером Z , используя выражение для 1s-электрона, где v — его радиальная скорость , т. е. его мгновенная скорость по касательной к радиусу атома. Для золота с Z  = 79 v  ≈ 0,58 c , поэтому 1s-электрон будет двигаться со скоростью, составляющей 58% от скорости света. Подставляя это вместо v / c в уравнение для релятивистской массы, находим, что m _rel  = 1,22 m _e , и, в свою очередь, подставляя это для радиуса Бора выше, находим, что радиус сокращается на 22%. ${\displaystyle v\approx {\frac {Zc}{137}}}$

Если подставить «релятивистскую массу» в уравнение для радиуса Бора, то можно записать $${\displaystyle a_{\text{rel}}={\frac {\hbar {\sqrt {1-(v_{\text{e}}/c)^{2}}}}{m_{\text{e}}c\alpha }}.}$$

Соотношение релятивистского и нерелятивистского радиусов Бора как функция скорости электрона

Из этого следует, что $${\displaystyle {\frac {a_{\text{rel}}}{a_{0}}}={\sqrt {1-(v_{\text{e}}/c)^{2}}}.}$$

Справа приведенное выше отношение релятивистского и нерелятивистского радиусов Бора было построено как функция скорости электрона. Обратите внимание, как релятивистская модель показывает, что радиус уменьшается с ростом скорости.

Когда трактовка Бора распространяется на водородные атомы , радиус Бора становится где - главное квантовое число , а Z - целое число для атомного номера . В модели Бора угловой момент задается как . Подставляя в уравнение выше и решая для , получаем $${\displaystyle r={\frac {n^{2}}{Z}}a_{0}={\frac {n^{2}\hbar ^{2}4\pi \varepsilon _{0}}{m_{\text{e}}Ze^{2}}},}$$ ${\displaystyle n}$ ${\displaystyle mv_{\text{e}}r=n\hbar }$ ${\displaystyle v_{\text{e}}}$ $${\displaystyle {\begin{aligned}r&={\frac {n^{2}a_{0}}{Z}}={\frac {n\hbar }{mv_{\text{e}}}},\\v_{\text{e}}&={\frac {Z}{n^{2}a_{0}}}{\frac {n\hbar }{m}},\\{\frac {v_{\text{e}}}{c}}&={\frac {Z\alpha }{n}}={\frac {Ze^{2}}{4\pi \varepsilon _{0}\hbar cn}}.\end{aligned}}}$$

С этого момента атомные единицы могут быть использованы для упрощения выражения до $${\displaystyle v_{\text{e}}={\frac {Z}{n}}.}$$

Подставляя это в выражение для соотношения Бора, упомянутое выше, получаем $${\displaystyle {\frac {a_{\text{rel}}}{a_{0}}}={\sqrt {1-\left({\frac {Z}{nc}}\right)^{2}}}.}$$

На этом этапе можно увидеть, что низкое значение и высокое значение приводят к . Это соответствует интуиции: электроны с более низкими главными квантовыми числами будут иметь более высокую плотность вероятности оказаться ближе к ядру. Ядро с большим зарядом заставит электрон иметь большую скорость. Более высокая скорость электрона означает увеличенную релятивистскую массу электрона, и в результате электроны будут находиться около ядра большую часть времени и тем самым сокращать радиус для малых главных квантовых чисел. ^[12] ${\displaystyle n}$ ${\displaystyle Z}$ ${\displaystyle {\frac {a_{\text{rel}}}{a_{0}}}<1}$

Отклонения периодической таблицы

Меркурий

Ртуть (Hg) является жидкостью вплоть до  температуры плавления примерно −39 °C . Силы связи для связей Hg–Hg слабее, чем для их непосредственных соседей, таких как кадмий (т.пл. 321 °C) и золото (т.пл. 1064 °C). Сокращение лантаноидов лишь частично объясняет эту аномалию. ^{[11] Поскольку} орбиталь 6s ² сокращается из-за релятивистских эффектов и, следовательно, может вносить лишь слабый вклад в любую химическую связь, связь Hg–Hg должна быть в основном результатом сил Ван-дер-Ваальса . ^{[11] [13] [14]}

Газообразная ртуть в основном одноатомна, Hg(г). Hg ₂ (г) образуется редко и имеет низкую энергию диссоциации, как и ожидалось из-за отсутствия прочных связей. ^[15]

Au ₂ (г) и Hg(г) аналогичны H ₂ (г) и He(г) в отношении того, что имеют одинаковую природу различия. Релятивистское сокращение орбитали 6s ² приводит к тому, что газообразную ртуть иногда называют псевдоблагородным газом . ^[11]

Цвет золота и цезия

Спектральные кривые отражения для алюминиевых (Al), серебряных (Ag) и золотых (Au) металлических зеркал

Окраска щелочного металла: рубидий (серебристый) и цезий (золотистый).

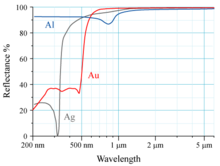
Отражательная способность алюминия (Al), серебра (Ag) и золота (Au) показана на графике справа. Человеческий глаз воспринимает электромагнитное излучение с длиной волны около 600 нм как желтое. Золото поглощает синий свет больше, чем другие видимые длины волн света; поэтому отраженный свет, достигающий глаза, не имеет синего цвета по сравнению с падающим светом. Поскольку желтый цвет является дополнительным к синему, это делает кусок золота под белым светом желтым для человеческого глаза.

Электронный переход с 5d-орбитали на 6s-орбиталь ответственен за это поглощение. Аналогичный переход происходит в серебре, но релятивистские эффекты меньше, чем в золоте. В то время как 4d-орбиталь серебра испытывает некоторое релятивистское расширение и 5s-орбитальное сжатие, расстояние 4d–5s в серебре намного больше, чем расстояние 5d–6s в золоте. Релятивистские эффекты увеличивают расстояние 5d-орбитали от ядра атома и уменьшают расстояние 6s-орбитали. Из-за уменьшенного расстояния 6s-орбитали электронный переход в основном поглощает в фиолетово-синей области видимого спектра, в отличие от УФ-области. ^[16]

Цезий , самый тяжелый из щелочных металлов , который можно собрать в количествах, достаточных для просмотра, имеет золотистый оттенок, тогда как другие щелочные металлы серебристо-белые. Однако релятивистские эффекты не очень значительны при Z = 55 для цезия (недалеко от Z = 47 для серебра). Золотистый цвет цезия возникает из-за уменьшения частоты света, необходимого для возбуждения электронов щелочных металлов по мере понижения группы. Для лития через рубидий эта частота находится в ультрафиолетовом диапазоне, но для цезия она достигает сине-фиолетового конца видимого спектра; другими словами, плазмонная частота щелочных металлов становится ниже от лития к цезию. Таким образом, цезий пропускает и частично поглощает фиолетовый свет преимущественно, в то время как другие цвета (имеющие более низкую частоту) отражаются; поэтому он кажется желтоватым. ^[17]

Свинцово-кислотный аккумулятор

Без теории относительности свинец ( Z = 82) должен вести себя так же, как олово ( Z = 50), поэтому оловянно-кислотные батареи должны работать так же хорошо, как свинцово-кислотные батареи, обычно используемые в автомобилях. Однако расчеты показывают, что около 10 В из 12 В, производимых 6-элементной свинцово-кислотной батареей, возникают исключительно из-за релятивистских эффектов, что объясняет, почему оловянно-кислотные батареи не работают. ^[18]

Эффект инертной пары

В комплексах Tl(I) ( таллий ), Pb(II) ( свинец ) и Bi(III) ( висмут ) существует пара электронов 6s ^2. Эффект инертной пары заключается в тенденции этой пары электронов противостоять окислению из-за релятивистского сжатия орбитали 6s. ^[8]

Другие эффекты

Дополнительные явления, обычно вызываемые релятивистскими эффектами, следующие:

• Влияние релятивистских эффектов на металлофильные взаимодействия неопределенно. Хотя Рунеберг и др. (1999) вычислили эффект притяжения, ^[19] Ван и др. (2021) вместо этого вычислили эффект отталкивания. ^[20]
• Стабильность анионов золота и платины в таких соединениях, как аурид цезия . ^[21]
• Немного сниженная реактивность франция по сравнению с цезием. ^{[22] [23]}
• Около 10% сжатия лантаноидов объясняется релятивистской массой высокоскоростных электронов и меньшим радиусом Бора, который в результате этого возникает. ^[24]

Смотрите также

• Энергия ионизации
• Электроотрицательность
• Сродство к электрону
• Квантовая механика
• Релятивистская квантовая механика

Ссылки

1. Пекка Пююккё (январь 2012 г.). «Релятивистские эффекты в химии: более распространены, чем вы думали». Annual Review of Physical Chemistry . 63 (1): 45–64. Bibcode : 2012ARPC...63...45P. doi : 10.1146/annurev-physchem-032511-143755. PMID  22404585.
2. Клеппнер, Дэниел (1999). "Краткая история атомной физики в двадцатом веке" (PDF) . Обзоры современной физики . 71 (2): S78–S84. Bibcode :1999RvMPS..71...78K. doi :10.1103/RevModPhys.71.S78. Архивировано из оригинала (PDF) 2016-03-03 . Получено 2012-07-17 .
3. Калдор, У.; Уилсон, Стивен (2003). Теоретическая химия и физика тяжелых и сверхтяжелых элементов. Дордрехт, Нидерланды: Kluwer Academic Publishers. стр. 4. ISBN 978-1-4020-1371-3.
4. Калдор, У.; Уилсон, Стивен (2003). Теоретическая химия и физика тяжелых и сверхтяжелых элементов. Дордрехт, Нидерланды: Kluwer Academic Publishers. стр. 2. ISBN 978-1-4020-1371-3.
5. Гупта, В. П. (22 октября 2015 г.). Принципы и применение квантовой химии. Elsevier Science. ISBN 978-0-12-803478-1. Получено 2024-01-07 .
6. Swirles, B. (1935). "Релятивистское самосогласованное поле". Труды Королевского общества A: Математические, физические и инженерные науки . 152 (877): 625–649. Bibcode :1935RSPSA.152..625S. doi : 10.1098/rspa.1935.0211 .
7. Дирак, П. А. М. (1929). «Квантовая механика многоэлектронных систем». Труды Королевского общества A: математические, физические и инженерные науки . 123 (792): 714–733. Bibcode : 1929RSPSA.123..714D. doi : 10.1098/rspa.1929.0094 . JSTOR  95222.
8. Pyykkö, Pekka (1988). «Релятивистские эффекты в структурной химии». Chemical Reviews . 88 (3): 563–594. doi :10.1021/cr00085a006.
9. Эрвин Шрёдингер (1926). «Über das Verhältnis der Heisenberg-Born-Jordanschen Quantenmechanik zu der meinem» (PDF) . Аннален дер Физик (на немецком языке). 384 (8). Лейпциг: 734–756. Бибкод : 1926АнП...384..734С. дои : 10.1002/andp.19263840804. Архивировано из оригинала (PDF) 17 декабря 2008 г.
10. Калдор, У.; Уилсон, Стивен, ред. (2003). Теоретическая химия и физика тяжелых и сверхтяжелых элементов. Дордрехт, Нидерланды: Kluwer Academic Publishers. стр. 17. ISBN 978-1-4020-1371-3.
11. Norrby, Lars J. (1991). «Почему ртуть жидкая? Или почему релятивистские эффекты не попадают в учебники по химии?». Журнал химического образования . 68 (2): 110. Bibcode : 1991JChEd..68..110N. doi : 10.1021/ed068p110.
12. Питцер, Кеннет С. (1979). «Релятивистские эффекты в химических свойствах» (PDF) . Accounts of Chemical Research . 12 (8): 271–276. doi :10.1021/ar50140a001. S2CID  95601322.
13. Кальво, Флоран; Паль, Эльке; Червь, Майкл; Швердтфегер, Питер (2013). «Доказательства низкотемпературного плавления ртути благодаря теории относительности». Angewandte Chemie, международное издание . 52 (29): 7583–7585. дои : 10.1002/anie.201302742. ISSN  1521-3773. ПМИД  23780699.
14. Howes2013-06-21T00:00:00+01:00, Лора. "Относительность, лежащая в основе текучести ртути". Chemistry World . Получено 2022-01-21 .{{cite web}}: CS1 maint: numeric names: authors list (link)
15. Zehnacker, A (1 июня 1987 г.). «Экспериментальное исследование холодного димера ртути». Журнал химической физики . 86 (11): 6565–6566. Bibcode : 1987JChPh..86.6565Z. doi : 10.1063/1.452401.
16. Pyykkö, Pekka; Desclaux, Jean Paul (1979). «Относительность и периодическая система элементов». Accounts of Chemical Research . 12 (8): 276. doi :10.1021/ar50140a002.
17. Addison, CC (1984). Химия жидких щелочных металлов . Wiley. стр. 7. ISBN 9780471905080.
18. Ахуджа, Раджив; Бломквист, Андерс; Ларссон, Питер; Пюиккё, Пекка; Залески-Эйгерд, Патрик (2011). «Относительность и свинцово-кислотная батарея». Physical Review Letters . 106 (1): 018301. arXiv : 1008.4872 . Bibcode : 2011PhRvL.106a8301A. doi : 10.1103/PhysRevLett.106.018301. PMID  21231773. S2CID  39265906.
19. Рунеберг, Нино; Шютц, Мартин; Вернер, Ганс-Йоахим (1999). «Аурофильное притяжение, интерпретируемое методами локальной корреляции». J. Chem. Phys. 110 (15): 7210–7215. Bibcode : 1999JChPh.110.7210R. doi : 10.1063/1.478665.
20. Wan, Qingyun; Yang, Jun; To, Wai-Pong; Che, Chi-Ming (2021-01-05). "Сильное отталкивание металла-металла Паули приводит к отталкивающей металлофильности в металлоорганических комплексах с закрытой оболочкой d 8 и d 10". Труды Национальной академии наук . 118 (1): e2019265118. Bibcode : 2021PNAS..11819265W. doi : 10.1073/pnas.2019265118 . ISSN  0027-8424. PMC 7817198. PMID 33372160  . 
21. Янсен, Мартин (декабрь 2005 г.). «Влияние релятивистского движения электронов на химию золота и платины». Solid State Sciences . 7 (12): 1464–1474. Bibcode :2005SSSci...7.1464J. doi : 10.1016/j.solidstatesciences.2005.06.015 .
22. "IYPT 2019 Elements 087: Francium: Not the most reactable group 1 element". Исследования повседневных химических соединений . 6 ноября 2019 г.
23. Андреев, СВ; Летохов, ВС; Мишин, ВИ (21 сентября 1987 г.). "Лазерная резонансная фотоионизационная спектроскопия ридберговских уровней в Fr". Physical Review Letters . 59 (12): 1274–1276. Bibcode :1987PhRvL..59.1274A. doi :10.1103/PhysRevLett.59.1274. PMID  10035190.
24. Pyykko, Pekka (1 мая 1988 г.). «Релятивистские эффекты в структурной химии». Chemical Reviews . 88 (3): 563–594. doi :10.1021/cr00085a006.

Дальнейшее чтение

• PA Christiansen; WC Ermler; KS Pitzer. Релятивистские эффекты в химических системах. Annual Review of Physical Chemistry 1985 , 36 , 407–432. doi :10.1146/annurev.pc.36.100185.002203