Суперсимметричная теория стохастической динамики

Теория стохастических уравнений в частных производных

Суперсимметричная теория стохастической динамики или стохастики ( СТД ) — это точная теория стохастических (частных) дифференциальных уравнений (СДУ), класс математических моделей с самой широкой применимостью, охватывающий, в частности, все непрерывные во времени динамические системы с шумом и без него. Основная польза теории с физической точки зрения — строгое теоретическое объяснение повсеместного спонтанного дальнодействующего динамического поведения, которое проявляется в различных дисциплинах через такие явления, как 1/f , мерцание и тресковые шумы, а также степенная статистика или закон Ципфа для мгновенных процессов, таких как землетрясения и нейролавины. С математической точки зрения СТД интересна тем, что она связывает две основные части математической физики — теорию динамических систем и топологические теории поля . Помимо этих и смежных дисциплин, таких как алгебраическая топология и суперсимметричные теории поля , STS также связана с традиционной теорией стохастических дифференциальных уравнений и теорией псевдоэрмитовых операторов.

Теория началась с применения процедуры фиксации калибровки BRST к уравнениям Ланжевена ^{[1] [2]} , которая позднее была адаптирована к классической механике ^{[3] [4] [5] [6]} и ее стохастическому обобщению ^[7] , уравнениям Ланжевена более высокого порядка ^[8] , а в последнее время и к уравнениям произвольной формы ^[9] , что позволило связать формализм BRST с концепцией операторов переноса и распознать спонтанное нарушение суперсимметрии BRST как стохастическое обобщение динамического хаоса .

Основная идея теории заключается в изучении, вместо траекторий, временной эволюции дифференциальных форм , определяемой SDE . Эта эволюция имеет внутреннюю BRST или топологическую суперсимметрию, представляющую сохранение топологии и/или концепции близости в фазовом пространстве посредством непрерывной динамики времени. Теория определяет модель как хаотическую , в обобщенном, стохастическом смысле, если ее основное состояние не является суперсимметричным, т. е. если суперсимметрия нарушается спонтанно. Соответственно, возникающее дальнодействующее поведение, которое всегда сопровождает динамический хаос и его производные, такие как турбулентность и самоорганизованная критичность, можно понимать как следствие теоремы Голдстоуна .

История и связь с другими теориями

Первая связь между суперсимметрией и стохастической динамикой была установлена ​​в двух статьях 1979 и 1982 годов Джорджио Паризи и Николя Сурласа, ^{[1] [2],} которые продемонстрировали, что применение процедуры фиксации калибровки BRST к СДУ Ланжевена, т. е. к СДУ с линейными фазовыми пространствами, векторными полями градиентного потока и аддитивными шумами, приводит к N=2 суперсимметричным моделям. Первоначальной целью их работы была размерная редукция , т. е. специфическое устранение расходимостей в диаграммах Фейнмана, предложенное несколькими годами ранее Амноном Ахарони , Йозефом Имри и Шан-кеном Ма . ^[10] С тех пор была установлена ​​связь между так возникшей суперсимметрией уравнений Ланжевена и несколькими физическими концепциями ^{[11] [12] [13] [14] [8], включая} теоремы о флуктуационной диссипации , ^[14] равенство Яржинского , ^[15] принцип микроскопической обратимости Онзагера , ^[16] решения уравнений Фоккера–Планка, ^[17] самоорганизация , ^[18] и т. д.

Аналогичный подход был использован для установления того , что классическая механика ^{[3] [4]} ее стохастическое обобщение ^[7] и СДУ Ланжевена более высокого порядка ^[8] также имеют суперсимметричные представления. Реальные динамические системы, однако, никогда не являются чисто ланжевеновскими или классическими механическими. Кроме того, физически осмысленные СДУ Ланжевена никогда не нарушают суперсимметрию спонтанно. Поэтому для цели идентификации спонтанного нарушения суперсимметрии как динамического хаоса необходимо обобщение подхода Паризи–Сурласа на СДУ общего вида. Это обобщение могло произойти только после строгой формулировки теории псевдоэрмитовых операторов ^[19], поскольку оператор стохастической эволюции является псевдоэрмитовым в общем случае. Такое обобщение ^[9] показало, что все СДУ обладают N=1 BRST или топологической суперсимметрией (TS), и это открытие завершает историю связи между суперсимметрией и СДУ.

Параллельно с подходом BRST-процедуры к SDE математики, работающие в области теории динамических систем, ввели и изучили концепцию обобщенного оператора переноса, определенного для случайных динамических систем. ^{[20] [21]} Эта концепция лежит в основе важнейшего объекта STS, оператора стохастической эволюции, и придает ему прочный математический смысл.

STS имеет тесную связь с алгебраической топологией, а ее топологический сектор принадлежит к классу моделей, известных как топологическая или когомологическая теория поля типа Виттена . ^{[22] [23] [24] [25] [26] [27]} Как суперсимметричная теория, подход BRST-процедуры к SDE можно рассматривать как одну из реализаций концепции отображения Николаи. ^{[28] [29]}

Подход Паризи-Сурла к SDE Ланжевена

В контексте суперсимметричного подхода к стохастической динамике термин СДУ Ланжевена обозначает СДУ с евклидовым фазовым пространством, векторным полем градиентного потока и аддитивным гауссовым белым шумом , ${\displaystyle X=\mathbb {R} ^{n}}$

$${\displaystyle {\dot {x}}(t)=-\partial U(x(t))+(2\Theta )^{1/2}\xi (t),}$$где , — шумовая переменная, — интенсивность шума, а , что в координатах и ​​, — векторное поле градиентного потока, причем — функция Ланжевена, часто интерпретируемая как энергия чисто диссипативной стохастической динамической системы. ${\displaystyle x\in X}$ ${\displaystyle \xi \in \mathbb {R} ^{n}}$ ${\displaystyle \Theta }$ ${\displaystyle \partial U(x)}$ ${\displaystyle (\partial U(x))^{i}\equiv \delta ^{ij}\partial _{j}U(x)}$ ${\displaystyle \partial _{i}U(x)\equiv \partial U(x)/\partial x^{i}}$ ${\displaystyle U(x)}$

Метод Паризи–Сурласа — это способ построения представления интеграла по траектории для СДУ Ланжевена. Его можно рассматривать как процедуру фиксации калибровки BRST , которая использует СДУ Ланжевена в качестве условия калибровки. А именно, рассматривается следующий функциональный интеграл,

$${\displaystyle {\mathcal {W}}=\left\langle \int \dots \int J\left(\prod \nolimits _{\tau }\delta ({\dot {x}}(\tau )-{\mathcal {F}}(x(\tau )))\right)Dx\right\rangle _{\text{noise}},}$$

где обозначает правую часть уравнения Ланжевена, — операция стохастического усреднения, где — нормализованное распределение конфигураций шума, ${\displaystyle {\mathcal {F}}}$ ${\displaystyle \textstyle \langle \cdot \rangle _{\text{noise}}\equiv \int \dots \int \cdot P(\xi )D\xi }$ ${\displaystyle P(\xi )\propto e^{-\int _{t'}^{t}d\tau \xi ^{2}(\tau )/2}}$

${\displaystyle \textstyle J=\operatorname {Det} {\frac {\delta ({\dot {x}}(\tau )-{\mathcal {F}}(x(\tau )))}{\delta x(\tau ')}}}$

— якобиан соответствующей функциональной производной, а интегрирование по траекториям ведется по всем замкнутым траекториям, , где и — начальный и конечный моменты временной эволюции. ${\displaystyle x(t)=x(t')}$ ${\displaystyle t'}$ ${\displaystyle t>t'}$

Уменьшение размеров

Конструкция Паризи–Сурласа, изначально направленная на «размерную редукцию», была предложена в 1976 году Амноном Ахарони , Йозефом Имри и Шан-кеном Ма ^[10], которые доказали, что для всех порядков в разложении возмущений критические показатели в d -мерной (4 < d < 6) системе с короткодействующим обменом и случайным замороженным полем такие же, как и в ( d –2)-мерной чистой системе. ^[30] Их аргументы показали, что «диаграммы Фейнмана, которые дают ведущее сингулярное поведение для случайного случая, тождественно равны, за исключением комбинаторных факторов, соответствующим диаграммам Фейнмана для чистого случая в двух измерениях меньше». ^[30]

... Паризи и Сурлас ... заметили, что наиболее инфракрасно-расходящиеся диаграммы - это те, у которых максимальное количество случайных источников вставок, и, если пренебречь другими диаграммами, то остается диаграммное расширение для классической теории поля в присутствии случайных источников. Паризи и Сурлас
затем указали, что лежащее в основе явление для связи между случайными системами и чистыми системами в двух измерениях меньше заключается в том, что классическая теория поля в присутствии случайных источников пертурбативно эквивалентна соответствующей квантовой теории поля в двух измерениях меньше. Паризи и Сурлас объяснили эту размерную редукцию скрытой суперсимметрией. ^[30]

Топологическая интерпретация

Топологические аспекты конструкции Паризи–Сурласа можно кратко изложить следующим образом. ^{[22] [31]} Дельта-функционал, т. е. совокупность бесконечного числа дельта-функций, гарантирует, что только решения СДУ Ланжевена вносят вклад в . В контексте процедуры BRST эти решения можно рассматривать как копии Грибова . Каждое решение вносит либо положительную, либо отрицательную единицу: причем является индексом так называемого отображения Николаи, , которое в данном случае является отображением из пространства замкнутых путей в в пространство конфигураций шума, отображением, которое обеспечивает конфигурацию шума, при которой заданный замкнутый путь является решением СДУ Ланжевена. можно рассматривать как реализацию теоремы Пуанкаре–Хопфа на бесконечномерном пространстве близких путей с СДУ Ланжевена, играющим роль векторного поля, и с решениями СДУ Ланжевена, играющими роль критических точек с индексом . не зависит от конфигурации шума, поскольку имеет топологический характер. То же самое справедливо и для ее стохастического среднего, которое является не функцией распределения модели, а ее индексом Виттена . ${\displaystyle {\mathcal {W}}}$ ${\textstyle {\mathcal {W}}=\textstyle \left\langle I_{N}(\xi )\right\rangle _{\text{noise}}}$ ${\textstyle I_{N}(\xi )=\sum _{\text{solutions}}\operatorname {sign} J}$ ${\textstyle \xi =({\dot {x}}+\partial U)/(2\Theta )^{1/2}}$ ${\textstyle X}$ ${\textstyle I_{N}(\xi )}$ ${\displaystyle \operatorname {sign} J}$ ${\textstyle I_{N}(\xi )}$ ${\displaystyle {\mathcal {W}}}$

Представление интеграла по траектории

С помощью стандартной теоретико-полевой техники, включающей введение дополнительного поля, называемого множителем Лагранжа, и пары фермионных полей, называемых духами Фаддеева–Попова , индексу Виттена можно придать следующий вид: ${\displaystyle B}$ ${\displaystyle \chi ,{\bar {\chi }}}$

$${\displaystyle {\mathcal {W}}=\int \dots \int _{p.b.c.}e^{(Q,\Psi )}D\Phi ,}$$

где обозначает совокупность всех полей, pbc обозначает периодические граничные условия, так называемый калибровочный фермион, , с и , и BRST-симметрию, определенную через ее действие на произвольный функционал как . В формализме BRST Q-точные части, такие как , служат инструментами фиксации калибровки. Следовательно, выражение интеграла по траектории для можно интерпретировать как модель, действие которой не содержит ничего, кроме члена фиксации калибровки. Это определяющая черта топологических теорий поля типа Виттена , и в этом конкретном случае подхода процедуры BRST к SDE BRST-симметрия может быть также признана топологической суперсимметрией. ^[22] ${\displaystyle \Phi }$ ${\displaystyle \textstyle \Psi =\int _{t'}^{t}d\tau (\imath _{\dot {x}}-{\bar {d}})(\tau )}$ ${\displaystyle \textstyle \imath _{\dot {x}}=i{\bar {\chi }}_{j}{\dot {x}}^{j}}$ ${\textstyle \textstyle {\bar {d}}=-i{\bar {\chi }}_{j}\delta ^{jk}(\partial _{k}U+\Theta iB_{k})}$ ${\displaystyle A(\Phi )}$ ${\displaystyle (Q,A(\Phi ))=\textstyle \int _{t'}^{t}d\tau (\chi ^{i}(\tau )\delta /\delta x^{i}(\tau )+B_{i}(\tau )\delta /\delta {\bar {\chi }}_{i}(\tau ))A(\Phi )}$ ${\displaystyle (Q,\Psi )}$ ${\displaystyle {\mathcal {W}}}$

Обычный способ объяснить процедуру BRST — сказать, что симметрия BRST генерирует фермионную версию калибровочных преобразований, тогда как ее общее влияние на интеграл по траектории заключается в ограничении интегрирования только конфигурациями, которые удовлетворяют заданному условию калибровки. Эта интерпретация применима также к подходу Паризи–Сурласа, где деформации траектории и Ланжевеновское SDE играют роль калибровочных преобразований и условия калибровки соответственно.

Представительство оператора

Физические фермионы в физике высоких энергий и моделях конденсированного состояния имеют антипериодические граничные условия по времени. Нетрадиционные периодические граничные условия для фермионов в выражении интеграла по траекториям для индекса Виттена являются источником топологического характера этого объекта. Эти граничные условия проявляются в операторном представлении индекса Виттена как оператора чередования знаков, где — оператор числа духов/фермионов и конечновременного оператора стохастической эволюции (SEO), , где — бесконечно малый SEO с производной Ли вдоль индексного векторного поля, — лапласианом, — внешней производной , которая является оператором, представляющим топологическую суперсимметрию (TS), и , где и — бозонные и фермионные импульсы, и с квадратными скобками, обозначающими биградуированный коммутатор, т. е. он является антикоммутатором, если оба оператора являются фермионными (содержат нечетное общее число ' и '), и коммутатором в противном случае. Внешняя производная и являются суперзарядами . Они нильпотентны , например, , и коммутативны с SEO. Другими словами, СДУ Ланжевена обладают N=2 суперсимметрией. Тот факт, что является суперзарядом, случаен. Для СДУ произвольной формы это неверно. $${\displaystyle {\mathcal {W}}=\operatorname {Tr} (-1)^{\hat {n}}{\hat {\mathcal {M}}}_{tt'},}$$ ${\textstyle {\hat {n}}}$ ${\textstyle {\hat {\mathcal {M}}}_{tt'}=e^{-(t-t'){\hat {H}}}}$ $${\displaystyle {\hat {H}}={\hat {L}}_{-\partial U}-\Theta {\hat {\triangle }}=[{\hat {d}},{\hat {\bar {d}}}],}$$ ${\displaystyle \textstyle {\hat {L}}}$ ${\textstyle {\hat {\triangle }}}$ ${\displaystyle \textstyle {\hat {d}}=\chi ^{i}\partial /\partial x^{i}}$ ${\displaystyle \textstyle {\hat {\bar {d}}}=-(i{\hat {\bar {\chi }}}_{i})\delta ^{ij}(\partial _{j}U+\Theta (i{\hat {B}}_{j}))}$ ${\displaystyle i{\hat {B}}_{j}=\partial /\partial x^{j}}$ ${\displaystyle i{\hat {\bar {\chi }}}_{j}=\partial /\partial \chi ^{j}}$ ${\displaystyle \chi }$ ${\displaystyle {\hat {\bar {\chi }}}}$ ${\displaystyle \textstyle {\hat {\bar {d}}}}$ ${\displaystyle {\hat {d}}^{2}=0}$ ${\displaystyle \textstyle {\hat {\bar {d}}}}$

Гильбертово пространство

Волновые функции являются функциями не только бозонных переменных, , но также чисел Грассмана или фермионов, , из касательного пространства . Волновые функции можно рассматривать как дифференциальные формы на с фермионами, играющими роль дифференциалов . ^[26] Концепция бесконечно малых SEO обобщает оператор Фоккера–Планка , который по сути является SEO, действующим на высших дифференциальных формах, имеющих смысл полных распределений вероятностей . Дифференциальные формы меньшей степени можно интерпретировать, по крайней мере локально на , как условные распределения вероятностей . ^[32] Рассмотрение пространств дифференциальных форм всех степеней как волновых функций модели является математической необходимостью. Без него индекс Виттена, представляющий наиболее фундаментальный объект модели — функцию статистической суммы шума — не существовал бы, а динамическая функция статистической суммы не представляла бы число неподвижных точек SDE (см. ниже). Наиболее общее понимание волновых функций – это объекты, не зависящие от координат, которые содержат информацию не только о траекториях, но и об эволюции дифференциалов и/или показателей Ляпунова . ^[33] ${\displaystyle x\in X}$ ${\displaystyle \chi \in TX}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle \chi \equiv dx\wedge }$ ${\displaystyle X}$

Связь с нелинейной сигма-моделью и алгебраической топологией

В работе ^[26] была введена модель, которую можно рассматривать как одномерный прототип топологических нелинейных сигма-моделей (TNSM), ^[23] подкласса топологических теорий поля типа Виттена . Одномерная TNSM определена для римановых фазовых пространств , тогда как для евклидовых фазовых пространств она сводится к модели Паризи–Сурласа. Ее ключевым отличием от STS является оператор диффузии, который является лапласианом Ходжа для одномерной TNSM и для STS. Это различие неважно в контексте связи между STS и алгебраической топологией, связи, установленной теорией одномерной TNSM (см., например, работы ^{[26] [22]} ). ${\displaystyle \textstyle {\hat {L}}_{e_{a}}{\hat {L}}_{e_{a}}}$

Модель определяется следующим оператором эволюции , где , будучи метрикой, — лапласиан Ходжа , а дифференциальные формы из внешней алгебры фазового пространства , рассматриваются как волновые функции. Существует преобразование подобия , , которое приводит оператор эволюции к явно эрмитовой форме с . В евклидовом случае — гамильтониан N=2 суперсимметричной квантовой механики . Можно ввести два эрмитовских оператора, и , такие, что . Это показывает, что спектр и/или является действительным и неотрицательным. Это также верно для SEOs СДУ Ланжевена. Однако для СДУ произвольной формы это уже не так, поскольку собственные значения SEO могут быть отрицательными и даже комплексными, что фактически позволяет спонтанно нарушать TS. ${\textstyle {\hat {H}}={\hat {L}}_{-\partial U}+\Theta [{\hat {d}},{\hat {d}}^{\dagger }]}$ ${\textstyle (\partial U)^{i}=g^{ij}\partial _{j}U}$ ${\textstyle g}$ ${\textstyle [{\hat {d}},{\hat {d}}^{\dagger }]}$ ${\textstyle \Omega (X)}$ ${\displaystyle {\hat {H}}\to {\hat {H}}_{U}=e^{U/2\Theta }{\hat {H}}e^{-U/2\Theta }}$ ${\displaystyle {\hat {H}}_{U}=\Theta [{\hat {d}}_{U},{\hat {d}}_{U}^{\dagger }]}$ ${\displaystyle {\hat {d}}_{U}=e^{U/2\Theta }{\hat {d}}e^{-U/2\Theta }=\chi ^{i}(\partial /\partial x^{i}-\partial _{i}U/2\Theta )}$ ${\displaystyle {\hat {H}}_{U}}$ ${\displaystyle {\hat {q}}_{1}=({\hat {d}}_{U}+{\hat {d}}_{U}^{\dagger })/2^{1/2}}$ ${\displaystyle {\hat {q}}_{2}=i({\hat {d}}_{U}-{\hat {d}}_{U}^{\dagger })/2^{1/2}}$ ${\displaystyle {\hat {H}}_{U}=\Theta {\hat {q}}_{1}^{2}=\Theta {\hat {q}}_{2}^{2}}$ ${\displaystyle {\hat {H}}_{U}}$ ${\displaystyle {\hat {H}}}$

Следующие свойства оператора эволюции 1D TNSM сохраняются даже для SEO SDE произвольной формы. Оператор эволюции коммутирует с оператором степени дифференциальных форм. В результате , где и — пространство дифференциальных форм степени . Кроме того, из-за наличия TS, , где — суперсимметричные собственные состояния, , нетривиальные в когомологиях де Рама, тогда как остальные являются парами несуперсимметричных собственных состояний вида и . Все суперсимметричные собственные состояния имеют ровно нулевое собственное значение и, за исключением случайных ситуаций, все несуперсимметричные состояния имеют ненулевые собственные значения. Несуперсимметричные пары собственных состояний не вносят вклад в индекс Виттена, который равен разнице чисел суперсимметричных состояний четных и нечетных степеней. Для компактных , каждый класс когомологий де Рама обеспечивает одно суперсимметричное собственное состояние, а индекс Виттена равен эйлеровой характеристике фазового пространства. ${\displaystyle \textstyle {\hat {H}}={\hat {H}}^{(\dim X)}\oplus \dots \oplus {\hat {H}}^{(0)}}$ ${\displaystyle \textstyle {\hat {H}}^{(k)}={\hat {H}}|_{\Omega ^{(k)}}}$ ${\displaystyle \Omega ^{(n)}(X)}$ ${\displaystyle n}$ ${\textstyle \Omega (X)={\mathcal {H}}\oplus {\mathcal {N}}\oplus ({\hat {d}}{\mathcal {N}})}$ ${\textstyle {\mathcal {H}}}$ ${\textstyle \theta 's}$ ${\textstyle |\vartheta \rangle }$ ${\textstyle {\hat {d}}|\vartheta \rangle }$ ${\textstyle {\mathcal {W}}=\#\{{\text{even }}\theta 's\}-\#\{{\text{odd }}\theta 's\}.}$ ${\displaystyle X}$

Процедура BRST для SDE произвольной формы

Метод Паризи–Сурласа BRST-процедурного подхода к уравнениям Ланжевена также был адаптирован к классической механике, ^[3] стохастическому обобщению классической механики, ^[7] уравнениям Ланжевена более высокого порядка, ^[8] и, совсем недавно, к уравнениям Ланжевена произвольной формы. ^[9] Хотя существуют стандартные методы, которые позволяют рассматривать модели с цветными шумами, более многомерные «базовые пространства», описываемые частичными уравнениями СДУ и т. д., ключевые элементы STS можно обсудить с использованием следующего базового класса уравнений СДУ, где — точка в фазовом пространстве, для простоты предполагаемая как замкнутое топологическое многообразие , — достаточно гладкое векторное поле , называемое векторным полем потока, из касательного пространства , и — набор достаточно гладких векторных полей, которые определяют, как система связана с шумом, который называется аддитивным / мультипликативным в зависимости от того, являются ли ' независимыми / зависящими от положения на . $${\displaystyle {\dot {x}}(t)=F(x(t))+(2\Theta )^{1/2}e_{a}(x(t))\xi ^{a}(t),}$$ ${\textstyle x\in X}$ ${\displaystyle F(x)\in TX_{x}}$ ${\displaystyle X}$ ${\displaystyle e_{a}\in TX,a=1,\ldots ,\dim X}$ ${\displaystyle e_{a}}$ ${\displaystyle X}$

Неоднозначность представления интеграла по траекториям и дилемма Ито–Стратоновича

Процедура фиксации калибровки BRST проходит по тем же направлениям, что и в случае SDE Ланжевена. Топологическая интерпретация процедуры BRST точно такая же, а представление интеграла по траекториям индекса Виттена определяется калибровочным фермионом, , заданным тем же выражением, но с обобщенной версией . Однако есть одна важная тонкость, которая появляется на пути к операторному представлению модели. В отличие от SDE Ланжевена, классической механики и других SDE с аддитивными шумами, представление интеграла по траекториям конечного времени SEO является неоднозначным объектом. Эта неоднозначность возникает из-за некоммутативности операторов импульсов и положения, например, . В результате в представлении интеграла по траекториям имеется целое однопараметрическое семейство возможных интерпретаций в операторном представлении, , где обозначает произвольную волновую функцию. Соответственно, существует целое -семейство бесконечно малых SEO, где , являющееся внутренним умножением на индексное векторное поле, и «смещенное» потоковое векторное поле, являющееся . Примечательно, что в отличие от Ланжевеновских SDE, не является суперзарядом , и STS не может быть идентифицирована как N=2 суперсимметричная теория в общем случае. ${\displaystyle \textstyle \Psi }$ ${\textstyle \textstyle {\bar {d}}=\imath _{F}-\Theta \imath _{e_{a}}(Q,\imath _{e_{a}})}$ ${\displaystyle {\hat {B}}{\hat {x}}\neq {\hat {x}}{\hat {B}}}$ ${\displaystyle B(\tau )x(\tau )}$ ${\displaystyle (\alpha {\hat {B}}{\hat {x}}+(1-\alpha ){\hat {x}}{\hat {B}})|\psi (\tau )\rangle }$ ${\displaystyle |\psi (\tau )\rangle }$ ${\displaystyle \alpha }$ $${\displaystyle {\hat {H}}_{\alpha }={\hat {L}}_{F}-\Theta {\hat {L}}_{e_{a}}{\hat {L}}_{e_{a}}=[{\hat {d}},{\hat {\bar {d}}}_{\alpha }],}$$ ${\displaystyle \textstyle {\hat {\bar {d}}}_{\alpha }={\hat {\imath }}_{F_{\alpha }}-\Theta {\hat {\imath }}_{e_{a}}{\hat {L}}_{e_{a}}}$ ${\displaystyle {\hat {\imath }}_{F_{\alpha }}}$ ${\displaystyle \textstyle F_{\alpha }=F-\Theta (2\alpha -1)(e_{a}\cdot \partial )e_{a}}$ ${\displaystyle {\hat {\bar {d}}}_{\alpha }}$

Представление стохастической динамики в виде интеграла по траектории эквивалентно традиционному пониманию SDE как непрерывного временного предела стохастических разностных уравнений , где различные выборы параметров называются «интерпретациями» SDE. Выбор , для которого и который известен в квантовой теории как правило симметризации Вейля , известен как интерпретация Стратоновича , тогда как как интерпретация Ито . В то время как в квантовой теории симметризация Вейля предпочтительна, поскольку она гарантирует эрмитовость гамильтонианов, в STS предпочтителен подход Стратоновича–Вейля, поскольку он соответствует наиболее естественному математическому смыслу конечновременного SEO, обсуждаемого ниже, — стохастически усредненного отката, индуцированного диффеоморфизмами, определенными SDE. ${\displaystyle \alpha }$ ${\displaystyle \alpha =1/2}$ ${\displaystyle \textstyle F_{1/2}=F}$ ${\displaystyle \alpha =1}$

Собственная система оператора стохастической эволюции

Три возможных типа спектров SEO на 3D-сфере. Каждая линия троек графиков представляет . для трех типов спектров. Черные точки в начале координат для первой и последней линий представляют суперсимметричные собственные состояния из нулевой и третьей когомологий 3-й сферы. Для типов b и c (самые быстрорастущие) основные (собственные) состояния не являются суперсимметричными, поскольку имеют ненулевые собственные значения. TS нарушается спонтанно. Вертикальные линии со стрелками визуализируют оператор суперсимметрии. ${\displaystyle spec{\hat {H}}^{(n)},}$ ${\displaystyle n=0,...3}$

По сравнению с SEO СДУ Ланжевена, SEO общего вида СДУ является псевдоэрмитовым. ^[19] В результате собственные значения несуперсимметричных собственных состояний не ограничены действительными положительными числами, тогда как собственные значения суперсимметричных собственных состояний по-прежнему равны нулю. Так же, как для СДУ Ланжевена и нелинейной сигма-модели, структура собственной системы СДУ восстанавливает топологический характер индекса Виттена: вклады несуперсимметричных пар собственных состояний исчезают, и только суперсимметричные состояния вносят вклад в эйлерову характеристику (замкнутого) . Среди других свойств спектров СДУ является то, что и никогда не нарушают TS, т. е . . В результате на рисунке справа представлены три основных типа спектров СДУ. Два типа, которые имеют отрицательные (действительные части) собственные значения, соответствуют спонтанно нарушенному TS. Все типы спектров SEO реализуемы, как можно установить, например, из точного соотношения между теорией кинематического динамо и STS. ^[34] ${\displaystyle X}$ ${\displaystyle \textstyle {\hat {H}}^{(\operatorname {dim} X)}}$ ${\displaystyle \textstyle {\hat {H}}^{(0)}}$ ${\displaystyle \textstyle Re(\operatorname {spec} {\hat {H}}^{(\operatorname {dim} X)})\geq 0}$

STS без процедуры BRST

Математический смысл оператора стохастической эволюции

Конечновременное SEO может быть получено другим, более математическим способом, основанным на идее непосредственного изучения действий, вызванных SDE, на дифференциальных формах, без прохождения процедуры фиксации калибровки BRST. Полученное таким образом конечновременное SEO известно в теории динамических систем как обобщенный оператор переноса ^{[20] [21]} , и оно также использовалось в классической теории SDE (см., например, ^{[35] [36]} ). Вкладом в эту конструкцию от STS ^[9] является изложение суперсимметричной структуры, лежащей в ее основе, и установление ее связи с процедурой BRST для SDE.

А именно, для любой конфигурации шума, , и начального условия, , SDE определяет единственное решение/траекторию, . Даже для конфигураций шума, которые не дифференцируемы по времени, , решение дифференцируемо по начальному условию, . ^[37] Другими словами, SDE определяет семейство зависящих от конфигурации шума диффеоморфизмов фазового пространства в себя, . Этот объект можно понимать как совокупность и/или определение всех зависящих от конфигурации шума траекторий, . Диффеоморфизмы вызывают действия или откаты , . В отличие, скажем, от траекторий в , откаты являются линейными объектами даже для нелинейных . Линейные объекты могут быть усреднены, и усреднение по конфигурациям шума, , приводит к конечному по времени SEO, которое является уникальным и соответствует интерпретации Стратоновича–Вейля подхода BRST-процедуры к SDE, . ${\displaystyle \xi }$ ${\displaystyle x(t')=x'\in X}$ ${\displaystyle x(t)\in X}$ ${\displaystyle t}$ ${\displaystyle x'}$ ${\displaystyle M_{tt'}:X\to X}$ ${\displaystyle x(t)=M_{tt'}(x')}$ ${\displaystyle \textstyle M_{t't}^{*}:\Omega (X)\to \Omega (X)}$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle M_{t't}^{*}}$ ${\displaystyle \xi }$ ${\displaystyle {\hat {\mathcal {M}}}_{tt'}=\langle M_{t't}^{*}\rangle _{\text{noise}}=e^{-(t-t'){\hat {H}}_{1/2}}}$

В рамках этого определения конечновременной SEO индекс Виттена можно распознать как точный след обобщенного оператора переноса. ^{[20] [21]} Он также связывает индекс Виттена с индексом Лефшеца , , топологической константой, которая равна эйлеровой характеристике (замкнутого) фазового пространства. А именно, . ${\textstyle \textstyle I_{L}=\operatorname {Tr} (-1)^{\hat {n}}M_{t't}^{*}=\sum _{x\in \operatorname {fix} M_{tt'}}\operatorname {sign} \operatorname {det} (\delta _{j}^{i}-\partial M_{tt'}^{i}(x)/\partial x^{j})}$ ${\textstyle \textstyle {\mathcal {W}}=\operatorname {Tr} (-1)^{\hat {n}}\langle M_{t't}^{*}\rangle _{\text{noise}}=\langle \operatorname {Tr} (-1)^{\hat {n}}M_{t't}^{*}\rangle _{\text{noise}}=I_{L}}$

Значение суперсимметрии и эффекта бабочки

Суперсимметрия N=2 СДУ Ланжевена была связана с принципом микроскопической обратимости Онзагера ^[16] и равенством Яржинского . ^[15] В классической механике была предложена связь между соответствующей суперсимметрией N=2 и эргодичностью . ^[6] В СДУ общего вида, где физические аргументы могут быть неприменимы, доступно объяснение TS на более низком уровне. Это объяснение основано на понимании конечновременного SEO как стохастически усредненного обратного образа диффеоморфизмов, определенных СДУ (см. подраздел выше). На этой картине вопрос о том, почему любое СДУ имеет TS, совпадает с вопросом о том, почему внешняя производная коммутирует с обратным образом любого диффеоморфизма. Ответ на этот вопрос — дифференцируемость соответствующего отображения. Другими словами, наличие TS является алгебраической версией утверждения о том, что поток с непрерывным временем сохраняет непрерывность . Две изначально близкие точки останутся близкими в ходе эволюции, что является еще одним способом сказать, что это диффеоморфизм. ${\displaystyle X}$ ${\displaystyle M_{tt'}}$

В детерминированных хаотических моделях изначально близкие точки могут разойтись в пределе бесконечно долгой временной эволюции. Это знаменитый эффект бабочки , который эквивалентен утверждению, что теряет дифференцируемость в этом пределе. В алгебраическом представлении динамики эволюция в бесконечно долгом временном пределе описывается основным состоянием СЭО, а эффект бабочки эквивалентен спонтанному разрушению TS, т. е. ситуации, когда основное состояние не является суперсимметричным. Примечательно, что в отличие от традиционного понимания детерминированной хаотической динамики, спонтанный разрыв TS работает и для стохастических случаев. Это важнейшее обобщение, поскольку детерминированная динамика, по сути, является математической идеализацией. Реальные динамические системы не могут быть изолированы от своего окружения и, таким образом, всегда испытывают стохастическое влияние. ${\displaystyle M_{tt'}}$

Спонтанное нарушение суперсимметрии и динамический хаос

Процедура фиксации калибровки BRST, применяемая к SDE, приводит непосредственно к индексу Виттена. Индекс Виттена имеет топологический характер и не реагирует ни на какие возмущения. В частности, все корреляторы отклика, вычисленные с использованием индекса Виттена, обращаются в нуль. Этот факт имеет физическую интерпретацию в STS: физический смысл индекса Виттена — это статсумма шума ^[32] , и поскольку нет обратного воздействия от динамической системы к шуму, индекс Виттена не имеет информации о деталях SDE. Напротив, информация о деталях модели содержится в другом следоподобном объекте теории, динамической статсумме, где apbc обозначает антипериодические граничные условия для фермионных полей и периодические граничные условия для бозонных полей. Стандартным образом динамическая статсумма может быть повышена до производящего функционала путем связывания модели с внешними зондирующими полями. $${\displaystyle {\mathcal {Z}}_{tt'}=\int \dots \int _{a.p.b.c.}e^{(Q,\Psi )}D\Phi =\operatorname {Tr} {\hat {\mathcal {M}}}_{tt'},}$$

Для широкого класса моделей динамическая статсумма обеспечивает нижнюю границу для стохастически усредненного числа неподвижных точек диффеоморфизмов, определенных SDE, Здесь индекс пробегает «физические состояния», т. е. собственные состояния, которые растут быстрее всего со скоростью экспоненциального роста, заданной как, , а параметр можно рассматривать как стохастическую версию динамической энтропии, такой как топологическая энтропия . Положительная энтропия является одним из ключевых признаков детерминированного хаоса. Следовательно, ситуация с положительным должна быть идентифицирована как хаотическая в обобщенном, стохастическом смысле, поскольку она подразумевает положительную энтропию: . В то же время, положительный подразумевает, что TS нарушается спонтанно, то есть основное состояние не является суперсимметричным, поскольку его собственное значение не равно нулю. Другими словами, положительная динамическая энтропия является причиной для определения спонтанного нарушения TS как стохастического обобщения концепции динамического хаоса. Примечательно, что SDE Ланжевена никогда не бывают хаотичными, поскольку спектр их SEO действительно неотрицателен. $${\displaystyle \left.{\mathcal {Z}}_{tt'}\right|_{t-t'\to \infty }=\sum \nolimits _{p}e^{-(t-t'){\mathsf {E}}_{p}}\leq \langle \#\{{\text{fixed points of }}M_{t't}\}\rangle _{\text{noise}}\propto e^{(t-t')S}.}$$ ${\displaystyle p}$ ${\textstyle \Gamma _{g}=-\min _{\alpha }\operatorname {Re} {\mathsf {E}}_{\alpha }\geq 0}$ ${\displaystyle S}$ ${\displaystyle \Gamma _{g}}$ ${\displaystyle 0<\Gamma _{g}\leq S}$ ${\displaystyle \Gamma _{g}}$

Полный список причин, по которым спонтанное нарушение ТС следует рассматривать как стохастическое обобщение концепции динамического хаоса, выглядит следующим образом. ^[38]

• Положительная динамическая энтропия.
• Согласно теореме Голдстоуна , спонтанное нарушение TS должно формировать дальнодействующее динамическое поведение, одним из проявлений которого является эффект бабочки , обсуждавшийся выше в контексте значения TS.
• Из свойств собственной системы SEO следует, что TS может быть спонтанно нарушена только в случае . Этот вывод можно рассматривать как стохастическое обобщение теоремы Пуанкаре–Бендиксона для детерминированного хаоса. ${\displaystyle \dim X\geq 3}$
• В детерминированном случае интегрируемые модели в смысле динамических систем имеют хорошо определенные глобальные устойчивые и неустойчивые многообразия . Бра/кеты глобальных основных состояний таких моделей являются дуальными Пуанкаре глобальных устойчивых/неустойчивых многообразий. Эти основные состояния являются суперсимметричными, так что TS не нарушается спонтанно. Напротив, когда модель неинтегрируема или хаотична, ее глобальные (не)устойчивые многообразия не являются хорошо определенными топологическими многообразиями, а скорее имеют фрактальную, самовозвращающуюся структуру, которую можно описать с помощью концепции ветвящихся многообразий. ^[39] Волновые функции, которые могут представлять такие многообразия, не могут быть суперсимметричными. Следовательно, нарушение TS неразрывно связано с концепцией неинтегрируемости в смысле динамических систем, что на самом деле является еще одним широко принятым определением детерминированного хаоса. ${\displaystyle F}$

Все вышеперечисленные особенности нарушения TS работают как для детерминированных, так и для стохастических моделей. Это контрастирует с традиционным детерминированным хаосом , чьи основанные на траекториях свойства, такие как топологическое смешивание , в принципе не могут быть обобщены на стохастический случай, поскольку, как и в квантовой динамике, все траектории возможны при наличии шума и, скажем, свойство топологического смешивания тривиально выполняется всеми моделями с ненулевой интенсивностью шума.

STS как топологическая теория поля

Квадрат acbd представляет собой инстантон, т. е. семейство траекторий детерминированного потока (пунктирные стрелочные кривые), ведущих из одной критической точки (b) в другую (a). Брак/кет ( / ) локально суперсимметричных основных состояний (вакуумов), соответствующих этим критическим точкам, являются дуальными по Пуанкаре локальным нестабильным/устойчивым многообразиям. Операторы являются дуальными по Пуанкаре вертикальным/горизонтальным линиям. Значением инстантонного матричного элемента является число пересечения (разница в числах положительных (черных) и отрицательных (белых) пересечений). Он инвариантен относительно временной эволюции, обусловленной потоком, . ${\displaystyle \langle a|}$ ${\displaystyle |b\rangle }$ ${\displaystyle {\hat {O}}_{1,2}}$ ${\displaystyle {\hat {O}}_{1}(0)\to {\hat {O}}_{1}(t)}$

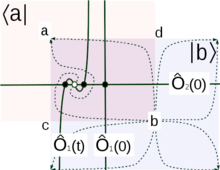
Топологический сектор STS может быть признан членом топологических теорий поля типа Виттена . ^{[22] [23] [25] [ 26] [27]} Другими словами, некоторые объекты в STS имеют топологический характер, и индекс Виттена является наиболее известным примером. Существуют и другие классы топологических объектов. Один класс объектов связан с инстантонами , т. е. переходной динамикой. Смятие бумаги, сворачивание белка и многие другие нелинейные динамические процессы в ответ на гашение, т. е. на внешние (внезапные) изменения параметров, могут быть признаны инстантонной динамикой. С математической точки зрения инстантоны являются семействами решений детерминированных уравнений движения, , которые ведут, скажем, от менее устойчивой неподвижной точки к более устойчивой неподвижной точке. Некоторые матричные элементы, вычисленные на инстантонах, имеют топологическую природу. Пример таких матричных элементов можно определить для пары критических точек и , причем более устойчивы, чем , Здесь и являются бра и кет соответствующих пертурбативных суперсимметричных основных состояний или вакуумов, которые являются дуальными по Пуанкаре локальными устойчивыми и неустойчивыми многообразиями соответствующей критической точки; обозначает хронологическое упорядочение; 's являются наблюдаемыми, которые являются дуальными по Пуанкаре некоторыми замкнутыми подмногообразиями в ; являются наблюдаемыми в представлении Гейзенберга, причем является несущественным моментом отсчета времени. Критические точки имеют разные индексы устойчивости, так что состояния и топологически неэквивалентны, поскольку они представляют неустойчивые многообразия различной размерности. Вышеуказанные матричные элементы не зависят от , поскольку они фактически представляют число пересечений -многообразий на инстантоне, как показано на рисунке. ${\displaystyle {\dot {x}}=F}$ ${\displaystyle F}$ ${\displaystyle a}$ ${\displaystyle b}$ ${\displaystyle a}$ ${\displaystyle b}$ $${\displaystyle \left.\int \dots \int _{x(\pm \infty )=a,b}\left(\prod \nolimits _{i}O_{i}(t_{i})\right)e^{({\mathcal {Q}},\Psi )}D\Phi \right|_{\Theta \to 0}=\langle a|{\mathcal {T}}\left(\prod \nolimits _{i}{\hat {O}}_{i}(t_{i})\right)|b\rangle .}$$ ${\displaystyle \langle a|}$ ${\displaystyle |b\rangle }$ ${\displaystyle {\mathcal {T}}}$ ${\displaystyle O}$ ${\displaystyle X}$ ${\displaystyle {\hat {O}}(t)={\hat {\mathcal {M}}}_{t_{0},t}{\hat {O}}{\hat {\mathcal {M}}}_{t,t_{0}}}$ ${\displaystyle t_{0}}$ ${\displaystyle |a\rangle }$ ${\displaystyle |b\rangle }$ ${\displaystyle t_{i}'s}$ ${\displaystyle O}$

Вышеуказанные инстантонные матричные элементы точны только в детерминированном пределе. В общем стохастическом случае можно рассматривать глобальные суперсимметричные состояния 's из классов когомологий Де Рама и наблюдаемые , которые являются двойственными по Пуанкаре замкнутыми многообразиями, нетривиальными в гомологиях . Следующие матричные элементы являются топологическими инвариантами, представляющими структуру кольца когомологий Де Рама . ${\displaystyle \theta }$ ${\displaystyle X}$ ${\displaystyle \gamma }$ ${\displaystyle X}$ ${\displaystyle \textstyle \langle \theta _{\alpha }|{\mathcal {T}}\left(\prod \nolimits _{i}{\hat {\gamma }}_{i}(t_{i})\right)|\theta _{\beta }\rangle ,}$ ${\displaystyle X}$

Приложения

Суперсимметричная теория стохастической динамики может быть интересна по-разному. Например, STS предлагает многообещающую реализацию концепции суперсимметрии . В общем, в контексте суперсимметрии есть две основные проблемы. Первая — установление связей между этой математической сущностью и реальным миром. В STS суперсимметрия является наиболее распространенной симметрией в природе, поскольку она относится ко всем динамическим системам с непрерывным временем. Вторая — спонтанное нарушение суперсимметрии . Эта проблема особенно важна для физики частиц, поскольку суперсимметрия элементарных частиц , если она существует в чрезвычайно малых масштабах, должна спонтанно нарушаться в больших масштабах. Эта проблема нетривиальна, поскольку суперсимметрию трудно нарушить спонтанно, что является причиной введения мягкого или явного нарушения суперсимметрии . ^[40] В STS спонтанное нарушение суперсимметрии действительно является нетривиальным динамическим явлением, которое было по-разному известно в разных дисциплинах как хаос , турбулентность , самоорганизованная критичность и т. д.

Ниже приведены несколько более конкретных применений STS.

Классификация стохастической динамики

Стохастические динамические системы можно классифицировать в зависимости от того, нарушается ли TS спонтанно или нет (упорядоченные/симметричные), и является ли векторное поле потока интегрируемым или неинтегрируемым (иногда хаотичным). Симметричная фаза может быть идентифицирована как тепловое равновесие (T). Упорядоченная неинтегрируемая фаза может быть названа хаосом (C), поскольку она содержит обычный детерминированный хаос. Упорядоченная интегрируемая фаза может быть названа хаосом, вызванным шумом (N), поскольку нарушение TS включает в себя антиинстантоны, которые исчезают в детерминированном пределе. N - фаза также известна в литературе как самоорганизованная критичность.

STS обеспечивает классификацию стохастических моделей в зависимости от того, нарушено ли TS и интегрируемости поля вектора потока. Его можно представить в виде части общей фазовой диаграммы на границе хаоса (см. рисунок справа). Фазовая диаграмма обладает следующими свойствами:

• Для физических моделей TS со временем восстанавливается с увеличением интенсивности шума.
• Симметричную фазу можно назвать тепловым равновесием или Т-фазой, поскольку основное состояние является суперсимметричным состоянием стационарного распределения полной вероятности.
• В детерминированном пределе упорядоченная фаза эквивалентна детерминированной хаотической динамике с неинтегрируемым потоком.
• Упорядоченную неинтегрируемую фазу можно назвать хаосом или С-фазой, поскольку к ней относится обычный детерминированный хаос.
• Упорядоченную интегрируемую фазу можно назвать хаосом, вызванным шумом, или N-фазой, поскольку она исчезает в детерминированном пределе. TS нарушается конденсацией (анти-)инстантонов (см. ниже).
• При более сильных шумах резкая граница NC должна размываться, переходя в кроссовер, поскольку (анти)инстантоны теряют свою индивидуальность, и стороннему наблюдателю становится трудно отличить один процесс туннелирования от другого.

Демистификация самоорганизованной критичности

Многие внезапные (или мгновенные) процессы в природе, такие как, например, треск , демонстрируют статистику без масштаба, часто называемую законом Ципфа . В качестве объяснения этого своеобразного спонтанного динамического поведения было предложено полагать, что некоторые стохастические динамические системы имеют тенденцию к самонастройке на критическую точку , феноменологический подход, известный как самоорганизованная критичность (SOC). ^[41] STS предлагает альтернативную точку зрения на это явление. ^[42] В STS SOC - это не что иное, как динамика в N-фазе. В частности, определяющей чертой N-фазы является своеобразный механизм нарушения TS. В отличие от C-фазы, где TS нарушается неинтегрируемостью потока, в N -фазе TS спонтанно нарушается из-за конденсации конфигураций инстантонов и вызванных шумом антиинстантонов, т. е. обращенных во времени инстантонов. Эти процессы можно грубо интерпретировать как вызванные шумом туннельные события между, например, различными аттракторами. Качественно динамика в N -фазе представляется внешнему наблюдателю как последовательность внезапных скачков или «лавин», которые должны демонстрировать безмасштабное поведение/статистику в результате теоремы Голдстоуна . Эта картина динамики в N-фазе является именно тем динамическим поведением, которое концепция SOC была разработана для объяснения. В отличие от первоначального понимания SOC, ^[43] ее интерпретация STS имеет мало общего с традиционной теорией критических явлений , где безмасштабное поведение связано с нестабильными неподвижными точками потока ренормгруппы .

Кинематическая теория динамо

Магнитогидродинамическое явление кинематического динамо также может быть идентифицировано как спонтанный срыв TS. ^[34] Этот результат следует из эквивалентности между оператором эволюции магнитного поля и SEO соответствующего SDE, описывающего поток фоновой материи. Возникшее таким образом соответствие STS-кинематическое динамо доказывает, в частности, что возможны оба типа спектров срыва TS с действительными и комплексными собственными значениями основного состояния, поскольку известны кинематические динамо с обоими типами наиболее быстрорастущих собственных мод. ^[44]

Динамика переходных процессов

Хорошо известно, что различные типы переходной динамики, такие как гасящие, демонстрируют спонтанное поведение на больших расстояниях. В случае гасящих фазовых переходов это поведение часто приписывается близости критичности. Известно, что гасящие, которые не демонстрируют фазового перехода, также демонстрируют характеристики на больших расстояниях, наиболее известными примерами являются эффект Баркгаузена и различные реализации концепции потрескивающего шума . Интуитивно привлекательно, что теоретические объяснения поведения без масштаба в гасящих должны быть одинаковыми для всех гасящих, независимо от того, производит ли он фазовый переход; STS предлагает такое объяснение. А именно, переходная динамика по сути является составным инстантоном, и TS по сути нарушается внутри инстантонов. Несмотря на то, что нарушение TS внутри инстантонов происходит не совсем из-за явления спонтанного нарушения симметрии глобальным основным состоянием, это эффективное нарушение TS также должно приводить к поведению без масштаба. Это понимание подтверждается тем фактом, что конденсированные инстантоны приводят к появлению логарифмов в корреляционных функциях. ^[45] Эта картина переходной динамики объясняет вычислительную эффективность цифровых мемкомпьютерных машин. ^[46]

Смотрите также

• Стохастическое квантование

Ссылки

1. Parisi, G.; Sourlas, N. (1979). «Случайные магнитные поля, суперсимметрия и отрицательные размерности». Physical Review Letters . 43 (11): 744–745. Bibcode : 1979PhRvL..43..744P. doi : 10.1103/PhysRevLett.43.744.
2. Parisi, G. (1982). "Суперсимметричные теории поля и стохастические дифференциальные уравнения". Nuclear Physics B. 206 ( 2): 321–332. Bibcode :1982NuPhB.206..321P. doi :10.1016/0550-3213(82)90538-7.
3. Gozzi, E.; Reuter, M. (1990). «Классическая механика как топологическая теория поля». Physics Letters B. 240 ( 1–2): 137–144. Bibcode :1990PhLB..240..137G. doi :10.1016/0370-2693(90)90422-3.
4. Niemi, AJ (1995). "Нижняя граница для числа периодических классических траекторий". Physics Letters B. 355 ( 3–4): 501–506. Bibcode :1995PhLB..355..501N. doi :10.1016/0370-2693(95)00780-o.
5. Niemi, AJ; Pasanen, P. (1996-10-03). "Топологическая σ-модель, гамильтонова динамика и число Лефшеца в пространстве петель". Physics Letters B . 386 (1): 123–130. arXiv : hep-th/9508067 . Bibcode :1996PhLB..386..123N. doi :10.1016/0370-2693(96)00941-0. S2CID  119102809.
6. Gozzi, E.; Reuter, M. (1989-12-28). «Алгебраическая характеристика эргодичности». Physics Letters B. 233 ( 3): 383–392. Bibcode :1989PhLB..233..383G. doi :10.1016/0370-2693(89)91327-0.
7. Tailleur, J.; Tănase-Nicola, S.; Kurchan, J. (2006-02-01). "Уравнение Крамерса и суперсимметрия". Журнал статистической физики . 122 (4): 557–595. arXiv : cond-mat/0503545 . Bibcode :2006JSP...122..557T. doi :10.1007/s10955-005-8059-x. ISSN  0022-4715. S2CID  119716999.
8. Кляйнерт, Х.; Шабанов, С.В. (1997-10-27). "Суперсимметрия в стохастических процессах с производными по времени более высокого порядка". Physics Letters A . 235 (2): 105–112. arXiv : quant-ph/9705042 . Bibcode :1997PhLA..235..105K. doi :10.1016/s0375-9601(97)00660-9. S2CID  119459346.
9. Овчинников, IV (2016-03-28). "Введение в суперсимметричную теорию стохастики". Энтропия . 18 (4): 108. arXiv : 1511.03393 . Bibcode : 2016Entrp..18..108O. doi : 10.3390/e18040108 . S2CID  2388285.
10. Aharony, A.; Imry, Y.; Ma, SK (1976). «Понижение размерности при фазовых переходах со случайными полями». Physical Review Letters . 37 (20): 1364–1367. Bibcode : 1976PhRvL..37.1364A. doi : 10.1103/PhysRevLett.37.1364.
11. Cecotti, S; Girardello, L (1983-01-01). «Стохастические и парастохастические аспекты суперсимметричных функциональных мер: новый непертурбативный подход к суперсимметрии». Annals of Physics . 145 (1): 81–99. Bibcode : 1983AnPhy.145...81C. doi : 10.1016/0003-4916(83)90172-0 .
12. Zinn-Justin, J. (1986-09-29). «Перенормировка и стохастическое квантование». Nuclear Physics B. 275 ( 1): 135–159. Bibcode :1986NuPhB.275..135Z. doi :10.1016/0550-3213(86)90592-4.
13. Dijkgraaf, R.; Orlando, D.; Reffert, S. (2010-01-11). «Связь теорий поля посредством стохастического квантования». Nuclear Physics B. 824 ( 3): 365–386. arXiv : 0903.0732 . Bibcode : 2010NuPhB.824..365D. doi : 10.1016/j.nuclphysb.2009.07.018. S2CID  2033425.
14. Kurchan, J. (1992-07-01). "Суперсимметрия в динамике спинового стекла". Journal de Physique I. 2 ( 7): 1333–1352. Bibcode :1992JPhy1...2.1333K. doi :10.1051/jp1:1992214. ISSN  1155-4304. S2CID  124073976.
15. Маллик, К.; Моше, М.; Орланд, Х. (2007-11-13). "Суперсимметрия и неравновесные рабочие соотношения". arXiv : 0711.2059 [cond-mat.stat-mech].
16. Gozzi, E. (1984). «Принцип микроскопической обратимости Онзагера и суперсимметрия». Physical Review D. 30 ( 6): 1218–1227. Bibcode :1984PhRvD..30.1218G. doi :10.1103/physrevd.30.1218.
17. Бернстайн, М. (1984). «Суперсимметрия и бистабильное уравнение Фоккера-Планка». Physical Review Letters . 52 (22): 1933–1935. Bibcode : 1984PhRvL..52.1933B. doi : 10.1103/physrevlett.52.1933.
18. Олемской, А. И; Хоменко, А. В; Олемской, Д. А (2004-02-01). "Полевая теория самоорганизации". Physica A: Статистическая механика и ее приложения . 332 : 185–206. Bibcode :2004PhyA..332..185O. doi :10.1016/j.physa.2003.10.035.
19. Mostafazadeh, A. (2002-07-19). «Псевдоэрмитовость против PT-симметрии III: Эквивалентность псевдоэрмитовости и наличие антилинейных симметрий». Журнал математической физики . 43 (8): 3944–3951. arXiv : math-ph/0203005 . Bibcode :2002JMP....43.3944M. doi :10.1063/1.1489072. ISSN  0022-2488. S2CID  7096321.
20. Reulle, D. (2002). "Динамические дзета-функции и операторы переноса" (PDF) . Notices of the AMS . 49 (8): 887.
21. Рюэль, Д. (1 декабря 1990 г.). «Расширение теории определителей Фредгольма». Публикации Mathématiques de l'Institut des Hautes Études Scientifiques . 72 (1): 175–193. дои : 10.1007/bf02699133. ISSN  0073-8301. S2CID  121869096.
22. Бирмингем, Д.; Блау, М.; Раковски, М.; Томпсон, Г. (1991). «Топологическая теория поля». Physics Reports . 209 (4–5): 129–340. Bibcode : 1991PhR...209..129B. doi : 10.1016/0370-1573(91)90117-5.
23. Witten, E. (1988-09-01). "Топологические сигма-модели". Communications in Mathematical Physics . 118 (3): 411–449. Bibcode : 1988CMaPh.118..411W. doi : 10.1007/BF01466725. ISSN  0010-3616. S2CID  34042140.
24. Baulieu, L.; Singer, IM (1988). «Топологическая сигма-модель». Communications in Mathematical Physics . 125 (2): 227–237. doi :10.1007/BF01217907. S2CID  120150962.
25. Witten, E. (1988-09-01). "Топологическая квантовая теория поля". Communications in Mathematical Physics . 117 (3): 353–386. Bibcode :1988CMaPh.117..353W. doi :10.1007/BF01223371. ISSN  0010-3616. S2CID  43230714.
26. Witten, E. (1982). «Суперсимметрия и теория Морса». Журнал дифференциальной геометрии . 17 (4): 661–692. doi : 10.4310/jdg/1214437492 . ISSN  0022-040X.
27. Labastida, JMF (1989-12-01). "Интерпретация топологических квантовых теорий поля с помощью теории Морзе". Communications in Mathematical Physics . 123 (4): 641–658. Bibcode :1989CMaPh.123..641L. CiteSeerX 10.1.1.509.3123 . doi :10.1007/BF01218589. ISSN  0010-3616. S2CID  53555484. 
28. Nicolai, H. (1980-12-22). "Суперсимметрия и меры функциональной интеграции". Nuclear Physics B. 176 ( 2): 419–428. Bibcode :1980NuPhB.176..419N. doi :10.1016/0550-3213(80)90460-5. hdl : 11858/00-001M-0000-0013-5E89-E .
29. Николаи, Х. (1980-01-28). "О новой характеристике скалярных суперсимметричных теорий" (PDF) . Physics Letters B. 89 ( 3): 341–346. Bibcode : 1980PhLB...89..341N. doi : 10.1016/0370-2693(80)90138-0.
30. Клейн, А .; Ландау, Л. Дж.; Перес, Дж. Ф. (1984). «Суперсимметрия и размерная редукция Паризи-Сурласа: строгое доказательство». Communications in Mathematical Physics . 94 (4): 459–482. Bibcode : 1984CMaPh..94..459K. doi : 10.1007/BF01403882. S2CID  120640917.
31. Baulieu, L.; Grossman, B. (1988). «Топологическая интерпретация стохастического квантования». Physics Letters B. 212 ( 3): 351–356. Bibcode :1988PhLB..212..351B. doi :10.1016/0370-2693(88)91328-7.
32. Овчинников, IV (2013-01-15). "Топологическая теория поля динамических систем. II". Хаос: междисциплинарный журнал нелинейной науки . 23 (1): 013108. arXiv : 1212.1989 . Bibcode :2013Chaos..23a3108O. doi :10.1063/1.4775755. ISSN  1054-1500. PMID  23556945. S2CID  34229910.
33. Грэм, Р. (1988). «Показатели Ляпунова и суперсимметрия стохастических динамических систем». EPL . 5 (2): 101–106. Bibcode :1988EL......5..101G. doi :10.1209/0295-5075/5/2/002. ISSN  0295-5075. S2CID  250788554.
34. Овчинников, IV; Энслин, TA (2016). «Кинематическое динамо, нарушение суперсимметрии и хаос». Physical Review D. 93 ( 8): 085023. arXiv : 1512.01651 . Bibcode : 2016PhRvD..93h5023O. doi : 10.1103/PhysRevD.93.085023. S2CID  59367815.
35. Анкона, А.; Элворти, К.Д.; Эмери, М.; Кунита, Х. (2013). Стохастическая дифференциальная геометрия в Сен-Флуре . Springer. ISBN 9783642341700. OCLC  811000422.
36. Кунита, Х. (1997). Стохастические потоки и стохастические дифференциальные уравнения . Cambridge University Press. ISBN 978-0521599252. OCLC  36864963.
37. Славик, А. (2013). «Обобщенные дифференциальные уравнения: Дифференцируемость решений относительно начальных условий и параметров». Журнал математического анализа и приложений . 402 (1): 261–274. doi : 10.1016/j.jmaa.2013.01.027 .
38. Овчинников, IV; Ди Вентра, M. (2019). «Хаос как явление нарушения симметрии». Modern Physics Letters B . 33 (24): 1950287–1950474. arXiv : 1702.06561 . Bibcode :2019MPLB...3350287O. doi :10.1142/S0217984919502877. S2CID  203039897.
39. Гилмор, Р.; Лефранк, М. (2011). Топология хаоса: Алиса в стране растяжения и сжатия . Wiley-VCH. ISBN 9783527410675. OCLC  967841676.
40. Chung, DJH; Everett, LL; Kane, GL; King, SF; Lykken, J.; Wang, Lian-Tao (2005-02-01). "Мягкий лагранжиан, нарушающий суперсимметрию: теория и приложения". Physics Reports . 407 (1–3): 1–203. arXiv : hep-ph/0312378 . Bibcode :2005PhR...407....1C. doi :10.1016/j.physrep.2004.08.032. S2CID  119344585.
41. Уоткинс, Н.У.; Прюсснер, Г.; Чепмен, С.К.; Кросби, Н.Б.; Дженсен, Х.Дж. (01.01.2016). «25 лет самоорганизованной критичности: концепции и противоречия». Space Science Reviews . 198 (1–4): 3–44. arXiv : 1504.04991 . Bibcode : 2016SSRv..198....3W. doi : 10.1007/s11214-015-0155-x. ISSN  0038-6308. S2CID  34782655.
42. Овчинников, IV (2016-06-01). "Суперсимметричная теория стохастики: демистификация самоорганизованной критичности". В Skiadas CH и Skiadas C. (ред.). Справочник по применению теории хаоса . Chapman and Hall/CRC. стр. 271–305. doi :10.1201/b20232. ISBN 9781466590441.
43. Бак, П.; Тан, К.; Визенфельд, К. (1987). «Самоорганизованная критичность: объяснение шума 1/f». Physical Review Letters . 59 (4): 381–384. Bibcode :1987PhRvL..59..381B. doi :10.1103/PhysRevLett.59.381. PMID  10035754. S2CID  7674321.
44. Bouya, I.; Dormy, E. (2013-03-01). «Возвращаясь к динамо потока ABC». Physics of Fluids . 25 (3): 037103–037103–10. arXiv : 1206.5186 . Bibcode : 2013PhFl...25c7103B. doi : 10.1063/1.4795546. ISSN  1070-6631. S2CID  118722952.
45. Френкель, Е.; Лосев, А.; Некрасов, Н. (2007). «Заметки об инстантонах в топологической теории поля и за ее пределами». Nuclear Physics B: Proceedings Supplements . 171 : 215–230. arXiv : hep-th/0702137 . Bibcode :2007NuPhS.171..215F. doi :10.1016/j.nuclphysbps.2007.06.013. S2CID  14914819.
46. Ди Вентра, М.; Траверса, Ф. Л.; Овчинников, И. В. (2017). «Топологическая теория поля и вычисления с инстантонами». Annalen der Physik . 2017 (12): 1700123. arXiv : 1609.03230 . Bibcode : 2017AnP...52900123D. doi : 10.1002/andp.201700123. ISSN  1521-3889. S2CID  9437990.