stringtranslate.com

Мезоамериканский календарь длинного счета

Восточная сторона стелы C, Киригуа с мифической датой сотворения мира 13 бактунов , 0 катунов, 0 тунов, 0 виналов, 0 кинов, 4 ахау 8 кумуку — 11 августа 3114 г. до н. э. по пролептическому григорианскому календарю .

Мезоамериканский календарь длинного счета — это неповторяющийся календарь с основанием 20 и основанием 18, который использовался доколумбовыми мезоамериканскими культурами, в первую очередь майя . По этой причине его часто называют календарем длинного счета майя . Используя модифицированную двадцатеричную систему исчисления, календарь длинного счета определяет день, подсчитывая количество дней, прошедших с мифической даты сотворения мира , которая соответствует 11 августа 3114 г. до н. э. в пролептическом григорианском календаре . [a] Календарь длинного счета широко использовался на памятниках.

Фон

Два наиболее широко используемых календаря в доколумбовой Мезоамерике были 260-дневный Tzolkʼin и 365-дневный Haabʼ . Эквивалентные ацтекские календари известны на языке науатль как Tonalpohualli и Xiuhpohualli соответственно.

Комбинация дат Хааб и Цолкин определяет день в комбинации, который не повторяется в течение 18 980 дней (52 цикла Хааб по 365 дней равны 73 циклам Цолкин по 260 дней, приблизительно 52 года), период, известный как Календарный Круг . Для определения дней в периодах, превышающих этот, жители Мезоамерики использовали календарь Длинного Счета.

Длинные периоды счета

Деталь, показывающая колонки глифов из части стелы La Mojarra Stela 1 II в. н. э . Левая колонка дает дату по Длинному счету 8.5.16.9.7, или 156 г. н. э. Другие видимые колонки — это глифы из эпиольмекского письма .

Календарь Длинного счета определяет дату, отсчитывая количество дней от начальной даты, которая обычно рассчитывается как 11 августа 3114 г. до н. э. в пролептическом григорианском календаре или 6 сентября в юлианском календаре (или −3113 в астрономической нумерации лет). Было много споров о точной корреляции между западными календарями и календарями Длинного счета. Дата 11 августа основана на корреляции с GMT.

Завершение 13 bʼakʼtuns (11 августа 3114 г. до н. э.) знаменует сотворение мира людей согласно майя. В этот день Поднятый-вверх-Небо-Владыка приказал, чтобы три камня были установлены связанными с ним богами в Лежащем-вниз-Небе, Первом-Трех-Каменном-Месте. Поскольку небо все еще лежало на изначальном море, оно было черным. Установка трех камней центрировала космос, что позволило небу подняться, открыв солнце . [1]

Вместо использования схемы с основанием 10 дни Длинного счета подсчитывались по модифицированной схеме с основанием 20. В чистой схеме с основанием 20 0.0.0.1.5 равно 25, а 0.0.0.2.0 равно 40. Однако Длинный счет не является чистой 20-ричной системой, поскольку вторая цифра справа (и только эта цифра) сбрасывается до нуля, когда достигает 18. [ необходима цитата ] Таким образом, 0.0.1.0.0 не представляет 400 дней, а только 360 дней, а 0.0.0.17.19 представляет 359 дней.

Название bʼakʼtun было придумано современными учеными. Нумерованный длинный счет уже не использовался к тому времени, когда испанцы прибыли на полуостров Юкатан , хотя ненумерованные kʼatuns и tuns все еще использовались. Вместо этого майя использовали сокращенный короткий счет .

Мезоамериканские цифры

Цифры майя

Даты Длинного счета записываются мезоамериканскими цифрами, как показано в этой таблице. Точка представляет 1, а черта равна 5. Глиф ракушки использовался для представления концепции нуля. Календарь Длинного счета требовал использования нуля в качестве заполнителя и представляет собой одно из самых ранних применений концепции нуля в истории .

На памятниках майя синтаксис Длинного счета более сложен. Последовательность дат указана один раз, в начале надписи, и открывается так называемым ISIG (Introductory Series Initial Glyph), который читается как tzik-a(h) habʼ [покровитель месяца Haabʼ] («почитаем был счет года с покровителем [месяца]»). [2] Далее следуют 5 цифр Длинного счета, за которыми следует Календарный круг (tzolkʼin и Haabʼ) и дополнительная серия . Дополнительная серия является необязательной и содержит лунные данные, например, возраст Луны в день и рассчитанную продолжительность текущей лунации. [b] Затем текст продолжается с указанием того, что происходило в эту дату.

Ниже представлен рисунок полной надписи майя, выполненной методом длинного счета.

Самые ранние длинные подсчеты

Самая ранняя из обнаруженных современных надписей Длинного счета находится на стеле 2 в Чьяпа-де-Корсо , Чьяпас , Мексика, и датируется 36 годом до н. э., хотя стела 2 из Такалик-Абах , Гватемала, может быть более ранней. [3] [2] Сильно потрепанная надпись Длинного счета на стеле 2 из Такалик-Абах показывает 7  бактунов , за которыми следуют к'атунов с предположительным коэффициентом 6, но это может быть также 11 или 16, что дает диапазон возможных дат между 236 и 19 годами до н. э. [c] [ необходима цитата ]

Хотя стела Такалик Абадж 2 остается спорной, эта таблица включает ее, а также шесть других артефактов с восемью старейшими надписями Длинного счета по мнению профессора Дартмута Винсента Х. Мальмстрёма (два артефакта содержат две даты, и Мальмстрём не включает стелу Такалик Абадж 2). [4] [5] Интерпретации надписей на некоторых артефактах различаются. [4] [6] [7]

Из шести памятников три находятся на западной окраине родины майя, а три — на несколько сотен километров западнее, что наводит некоторых исследователей на мысль, что календарь Длинного счета существовал еще до майя. [11] Стела 1 из Ла-Мохарры, статуэтка из Тустлы, Стела C из Трес-Сапотес и Стела 2 из Чьяпы — все они написаны в эпиольмекском , а не майяском стиле. [12] Стела 2 из Эль-Бауля, с другой стороны, была создана в стиле Исапы .

Первый несомненно майянский артефакт — Стела 29 из Тикаля , датируемая по Длинному счету 292 годом н. э. (8.12.14.8.15), более чем на 300 лет позже Стелы 2 из Чьяпа-де-Корсо. [13]

Совсем недавно, с открытием в Гватемале текста на каменном блоке Сан-Бартоло (место майя) ( ок. 300 г. до н. э.), [14] утверждалось, что этот текст отмечает предстоящее празднование окончания периода времени. Этот период времени, как можно было предположить, должен был закончиться где-то между 7.3.0.0.0 (295 г. до н. э.) и 7.5.0.0.0 (256 г. до н. э.). [15] Помимо того, что это самый ранний из обнаруженных на сегодняшний день иероглифических текстов майя, это, возможно, самое раннее на сегодняшний день свидетельство нотации длинного счета в Мезоамерике.

Соотношения между западными календарями и Длинным счетом

Обратная сторона стелы C из Трес-Сапотес , археологического памятника ольмеков.
Это вторая старейшая дата Длинного счета, обнаруженная на сегодняшний день. Цифры 7.16.6.16.18 переводятся как 1 сентября 32 г. до н. э. (по григорианскому календарю). Глифы, окружающие дату, считаются одним из немногих сохранившихся примеров эпиольмекского письма .

Календари майя и западные календари коррелируются с помощью юлианского номера дня (JDN) начальной даты текущего творения — 13.0.0.0.0, 4 Ajaw , 8 Kumkʼu. [d] Это называется «константой корреляции». Общепринятая константа корреляции — это модифицированная константа Томпсона 2, « Гудман –Мартинес – Томпсон » или корреляция GMT в 584 283 дня. Используя корреляцию GMT, текущее творение началось 6 сентября, −3113 ( юлианское астрономическое) — 11 августа 3114 г. до н. э. в пролептическом григорианском календаре . Изучение корреляции календарей майя и западных календарей называется вопросом корреляции. [16] [17] [18] [19] [20] Корреляция GMT также называется корреляцией 11.16 .

В своей книге «Разрушение кода майя » Майкл Д. Коу пишет: «Несмотря на океаны чернил, которые были пролиты по этому вопросу, сейчас нет ни малейшего шанса, что эти трое ученых (объединяемых с GMT, когда говорят о корреляции) были не правы...» [21] Доказательства корреляции с GMT являются историческими, астрономическими и археологическими:

Исторические : Круглые даты календаря с соответствующей юлианской датой записаны в Relación de las cosas de Yucatán Диего де Ланды ( написано около 1566 г.), Chronicle of Oxkutzcab и книгах Chilam Balam . Де Ланда записывает дату, которая является окончанием Tun в Short Count . Oxkutzcab содержит 12 окончаний Tun. Брикер и Брикер обнаруживают, что только корреляция GMT согласуется с этими датами. [22] Книга Chilam Balam из Чумайеля [23] содержит единственную колониальную ссылку на классические даты длинного счета. Дата юлианского календаря 11.16.0.0.0 (2 ноября 1539 г.) подтверждает корреляцию GMT. [24]

В « Анналах какчикелей» содержится множество дат Цолькин, соотнесенных с европейскими датами. Они подтверждают корреляцию по Гринвичу. [25] Уикс, Сакс и Прагер переписали три гадательных календаря из горной Гватемалы. Они обнаружили, что календарь 1772 года подтверждает корреляцию по Гринвичу. [26] Падение столицы империи ацтеков, Теночтитлана , произошло 13 августа 1521 года. [27] Ряд различных летописцев писали, что дата события по Цолькин ( Тональпоуалли ) была 1 Змеи. [28]

Ученые после завоевания, такие как Саагун и Дуран, записали даты Тональпоуалли с календарной датой. Многие коренные общины в мексиканских штатах Веракрус, Оахака и Чьяпас [29] и в Гватемале, в основном те, которые говорят на языках майя Ишиль, Мам, Покомчи и Киче, придерживаются Цолькин и во многих случаях Хааб. [30] Все они согласуются с корреляцией по Гринвичу. Мунро Эдмонсен изучил 60 месоамериканских календарей, 20 из которых имеют известные корреляции с европейскими календарями, и обнаружил замечательную согласованность между ними, и что только корреляция по Гринвичу соответствует историческим, этнографическим и астрономическим свидетельствам. [31]

Астрономический : Любая правильная корреляция должна соответствовать астрономическому содержанию классических надписей. Корреляция GMT отлично справляется с сопоставлением лунных данных в дополнительных сериях . [32] Например: Надпись в Храме Солнца в Паленке сообщает, что на Длинный счет 9.16.4.10.8 было завершено 26 дней в 30-дневной лунации. [33] Этот Длинный счет также является датой записи для таблицы затмений Дрезденского кодекса . [34] [e]

Используя третий метод, систему Паленке, [36] новолуние было бы первым вечером, когда можно было бы посмотреть на запад после захода Солнца и увидеть тонкий полумесяц. Учитывая нашу современную способность точно знать, куда смотреть, когда полумесяц Луны благоприятно расположен, с отличного места, в редких случаях, используя бинокль или телескоп, наблюдатели могут увидеть и сфотографировать полумесяц Луны менее чем через день после соединения. Как правило, большинство наблюдателей не могут увидеть новую Луну невооруженным глазом до первого вечера, когда лунные фазовые сутки составляют по крайней мере 1,5. [37] [38] [39] [40] [41] [42] Если предположить, что новолуние является первым днем, когда лунные фазовые сутки составляют по крайней мере 1,5 в шесть вечера в часовом поясе UTC−6 (часовой пояс области майя), корреляция GMT будет точно соответствовать многим лунным надписям. В этом примере день фазы Луны был 27,7 (26 дней, считая от нуля) в 6 вечера после соединения в 1:25 утра 10 октября 755 года и новолуния, когда день фазы Луны был 1,7 в 6 вечера 11 октября 755 года (по юлианскому календарю). Это хорошо работает для многих, но не для всех лунных надписей.

Современные астрономы называют соединение Солнца и Луны (время, когда Солнце и Луна имеют одинаковую эклиптическую долготу) новолунием. Но мезоамериканская астрономия была наблюдательной , а не теоретической. Жители Мезоамерики не знали о коперниканской природе солнечной системы — у них не было теоретического понимания орбитальной природы небесных тел. Некоторые авторы анализируют лунные надписи, основываясь на этом современном понимании движений Луны, но нет никаких доказательств того, что мезоамериканцы разделяли его.

Первый метод, по-видимому, использовался для других надписей, таких как стела Киргуа E (9.17.0.0.0). Согласно третьему методу, эта стела должна показывать возраст Луны в 26 дней, но на самом деле она регистрирует новолуние. [43] Используя корреляцию GMT в шесть утра в часовом поясе UTC−6, это было бы за 2,25 дня до соединения, поэтому она могла бы регистрировать первый день, когда нельзя было увидеть убывающую Луну.

Фулс [44] проанализировал эти надписи и нашел убедительные доказательства в пользу системы Паленке и корреляции с GMT; однако он предостерег: «Анализ лунного ряда показывает, что для расчета возраста и положения Луны в шестимесячном цикле использовались по крайней мере два разных метода и формулы...», что дает сезоны затмений, когда Луна находится вблизи своего восходящего или нисходящего узла, и затмение, вероятно, произойдет. Даты, преобразованные с использованием корреляции с GMT, хорошо согласуются с таблицами затмений Дрезденского кодекса. [45] Дрезденский кодекс содержит таблицу Венеры , в которой записаны гелиакические восходы Венеры. Используя корреляцию с GMT, они хорошо согласуются с современными астрономическими расчетами. [46]

Археологические : Различные предметы, которые могут быть связаны с определенными датами Длинного счета, были датированы изотопами . В 1959 году Пенсильванский университет провел датирование по углероду образцов десяти деревянных перемычек из Тикаля . [47] Они были вырезаны с датой, эквивалентной 741 году нашей эры, с использованием корреляции по Гринвичу. Средняя дата по углероду составила 746±34 года. Недавно один из них, Перемычка 3 из Храма I, был снова проанализирован с использованием более точных методов и, как было обнаружено, близко соответствует корреляции по Гринвичу. [48] В 2012 году с использованием современного радиоуглеродного датирования AMS была датирована одна балка из Тикаля, что также убедительно подтверждает GMT. [49]

Если предлагаемая корреляция должна согласовываться только с одной из этих линий доказательств, то может быть множество других возможностей. Астрономы предложили много корреляций, например: Лаунсбери , [50] Фулс и др. , [51] Бём и Бём [52] [53] и Сток. [54]

Сегодня, 9 ноября 2024 года ( UTC ), в длинном счёте это 13.0.12.1.1 (с использованием корреляции GMT).

2012 и длинный счет

Согласно « Пополь Вух» , книге, в которой собраны подробности рассказов о сотворении мира, известных майя колониальной эпохи, человечество живет в четвертом мире. [55] « Пополь Вух» описывает первые три творения, которые боги не смогли создать, и создание успешного четвертого мира, куда были помещены люди. В Длинном счете майя предыдущее творение закончилось в конце 13-го бактуна.

Предыдущее творение закончилось по Длинному счету 12.19.19.17.19. Другое 12.19.19.17.19 произошло 20 декабря 2012 года (по григорианскому календарю), за которым последовало начало 14-го бактуна, 13.0.0.0.0, 21 декабря 2012 года. [f] В фрагментарном корпусе майя есть только две ссылки на 13-й бактун текущего творения: Памятник Тортугеро 6, часть надписи правителя и недавно обнаруженная иероглифическая лестница Ла Корона 2, блок V. [57]

Иногда надписи майя ссылаются на будущие предсказанные события или памятные даты, которые произойдут в даты, которые лежат за пределами 2012 года (то есть за пределами завершения 13-го  бактуна текущей эры). Большинство из них имеют форму «дистанционных дат», где указана некоторая дата Длинного счета вместе с Дистанционным числом, которое должно быть добавлено к дате Длинного счета, чтобы получить эту будущую дату.

Например, на западной панели Храма Надписей в Паленке часть текста проецируется в будущее к 80-й годовщине Календарного Круга (CR) со дня восшествия на престол знаменитого правителя Паленке К'инича Джанааба ' Пакаля (восшествие на престол Пакаля произошло в Календарный Круг 5 Ламата 1 Мола, по Длинному Счету 9.9.2.4.8, что эквивалентно 27 июля 615 г. н. э. в пролептическом григорианском календаре ). [g] Это делается путем начала с даты рождения Пакаля 9.8.9.13.0 8 Аджава 13 Попа (24 марта 603 г. н. э. по григорианскому календарю ) и добавления к ней Расстояния 10.11.10.5.8. [58]

Этот расчет достигает 80-го календарного раунда с момента его вступления на престол, дня, который также имеет дату CR 5 Ламата 1 Моля , но который лежит более чем на 4000 лет в будущем от времени Пакаля — дня 21 октября 4772 года. Надпись отмечает [ необходима цитата ] , что этот день выпадет через восемь дней после завершения 1-го пиктуна (с момента создания или нулевой даты системы Длинного счета), где пиктун является следующим по величине порядком после бактуна в Длинном счете. Если бы дата завершения этого пиктуна — 13 октября 4772 года — была записана в нотации Длинного счета, ее можно было бы представить как 1.0.0.0.0.0. Дата 80-й годовщины CR, восемь дней спустя, была бы 1.0.0.0.0.8 5 Ламата 1 Моля. [58] [59]

Несмотря на шумиху, вызванную датой 2012 года, Сьюзан Милбрат, куратор латиноамериканского искусства и археологии в Музее естественной истории Флориды , заявила, что «У нас нет никаких записей или знаний о том, что [майя] думали, что мир придет к концу» в 2012 году. [60] USA Today пишет : «Для древних майя это был огромный праздник, чтобы дойти до конца целого цикла», - говорит Сандра Нобл, исполнительный директор Фонда содействия развитию мезоамериканских исследований в Кристал-Ривер, Флорида . По ее словам, представление 21 декабря 2012 года как события конца света или момента космического сдвига - это «полная выдумка и шанс для многих людей нажиться » » . [60] « Будет еще один цикл», - говорит Э. Уиллис Эндрюс В., директор Института среднеамериканских исследований (MARI) при Университете Тулейна . «Мы знаем, что майя считали, что до этого был еще один, и это означает, что они были согласны с идеей о существовании еще одного после этого». [61]

Конвертация между Длинным счетом и западными календарями

Вычисление даты по западному календарю с помощью длинного счета

Важно знать разницу между юлианским и григорианским календарями при расчете даты западного календаря из даты длинного счета. [h]

Используя в качестве примера дату Длинного счета 9.10.11.17.0 (дата Длинного счета, упомянутая на табличке дворца в Паленке), сначала вычислите количество дней, прошедших с нулевой даты (11 августа 3114 г. до н. э.; корреляция со временем по Гринвичу в пролептическом григорианском календаре , 6 сентября −3113 г. по юлианскому астрономическому календарю).

Затем добавьте корреляцию с GMT к общему количеству дней.

1 372 300 + 584 283 = 1 956 583

Это число — юлианский день .

Чтобы преобразовать юлианский день в дату пролептического григорианского календаря : [62]

Из этого числа вычтите ближайшее меньшее число юлианского дня (в таблице ниже), в данном случае 1 940 206, что соответствует 600 году н.э.

1 956 583 – 1 940 206 = 16 377

Затем разделите это число на 365 дней (неопределенный год).

16,377 / 365 = 44.86849

Остаток составляет 44,86849 года, что составляет 44 года и 317 дней. Полная дата года — 644 г. н. э. Теперь вычислите номер месяца и дня, принимая во внимание високосные дни за 44 года. В григорианском календаре каждый четвертый год является високосным, за исключением столетий, не делящихся нацело на 400 (например, 100, 200, 300). Когда год делится на 400 (например, 400, 800 и т. д.), не добавляйте дополнительный день. Вычисленный год — 644 г. н. э. Количество високосных дней, учитывая, что год 600 не является високосным, равно 10. Вычитание этого из 317 оставшихся дней дает 307; Другими словами, 307-й день 644 года н. э., то есть 3 ноября. Подводя итог: дата Длинного счета 9.10.11.17.0 соответствует 3 ноября 644 года н. э. в пролептическом григорианском календаре .

Чтобы преобразовать юлианский день в юлианскую/григорианскую астрономическую дату ( пролептический юлианский календарь до 46 г. до н.э.):

Используйте астрономический алгоритм, такой как метод Миуса [63], чтобы преобразовать юлианский день в юлианскую/григорианскую дату с астрономической датировкой отрицательных лет: [i]

В этом примере:

ввод: юлианский день J J = J + 0,5 // 1 956 583,5 Z = целая часть J  // 1 956 583 F = дробная часть J  // 0,5if  Z < 2,299,161 then  // Julian?  A = Z else  alpha = floor(( Z - 1,867,216.25) / 36,524.25) // 15  A = Z + 1 + alpha - floor( alpha / 4.0) // 2,436,129  // Операция floor округляет десятичное число до ближайшего меньшего целого числа.  // Например, floor(1.5) = 1 и floor(−1.5) = -2 end ifB = A + 1524 // 1,958,107 C = пол(( B - 122.1) / 365.25) // 5,360 D = пол(365.25 × C ) // 1,957,740 E = пол(( B - D ) / 30.6001) // 11 день = B - D - пол(30.6001 × E ) + F  // 31.5если  E < 14 , то  месяц = ​​E - 1 // 10 , иначе  месяц = ​​E - 13, конец, еслиесли  месяц > 2 , то  год = C - 4716 // 644 , иначе  год = C - 4715, конец, есливозврат ( год , месяц , день )

В этом примере юлианская дата — полдень 31 октября 644 года. Метод Миуса недействителен для отрицательных чисел года (астрономических), поэтому следует использовать другой метод, например метод Питера Баума [64] .

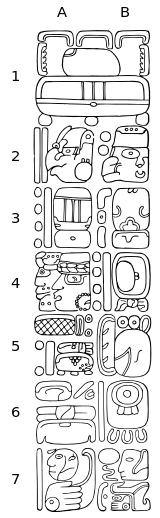
Вычисление полной даты длинного счета

Надпись серии «Инициал» в Чичен-Ице . Эта дата (глифы A2, B2, ..., A5) — 10.2.9.1.9 9 Мулук 7 Сак, что соответствует 28 июля 878 года (GMT по григорианскому календарю).

Полная дата Длинного счета включает не только пять цифр Длинного счета, но также двухсимвольные даты Цолькин и двухсимвольные даты Хааб. Таким образом, пятизначный Длинный счет может быть подтвержден четырьмя другими символами («календарная круглая дата»).

Возьмем в качестве примера дату Календарного Круга 9.12.2.0.16 (Длинный Счет) 5 Кибин (Цолькин) 14 Йашкин (Хааб). Можно проверить правильность этой даты с помощью следующего расчета.

Возможно, проще выяснить, сколько дней прошло с 4 Аджава 8 Кумку и показать, как образовалась дата 5 Киба 14 Йашк'ина.

Расчет части даты Цолькин

Дата Цолкин отсчитывается вперед от 4 Аджава. Чтобы вычислить числовую часть даты Цолкин, добавьте 4 к общему количеству дней, указанному в дате, а затем разделите общее количество дней на 13.

(4 + 1,383,136) / 13 = 106,395 (и 5/13)

Это означает, что было завершено 106 395 полных 13-дневных циклов, а числовая часть даты Цолькин равна 5.

Чтобы вычислить день, разделите общее количество дней в длинном счете на 20, поскольку существует двадцать названий дней.

1,383,136 / 20 = 69,156 (и 16/20)

Это означает, что 16 названий дней должны быть отсчитаны от Аджава. Это дает Кибу. Следовательно, дата Цолькина — 5 Кибу.

Расчет части даты Хааб

Дата Хааб 8 Кумку — девятый день восемнадцатого месяца. До начала следующего года осталось 17 дней.

Вычтите 17 дней из общей суммы, чтобы узнать, сколько полных лет Хааба содержится в ней.

1,383,136 − 17 = 1,383,119
на 365
1,383,119 / 365 = 3,789 и (134/365)

Таким образом, прошло 3789 полных Хаабов, а остаток 134 — это 135-й день в новом Хаабе, поскольку остаток 0 указывал бы на первый день.

Найдите, в каком месяце находится этот день. Разделив остаток 134 на 20, получим шесть полных месяцев и остаток 14, что указывает на 15-й день. Таким образом, дата в Хаабе лежит в седьмом месяце, который является Йашкин. Пятнадцатый день Йашкин — 14, таким образом, дата Хаабе — 14 Йашкин.

Таким образом, дата длинного счета 9.12.2.0.16 5 Киба 14 Йашкина подтверждается.

Пиктуны и высшие чины

Есть также четыре редко используемых периода более высокого порядка над bʼakʼtun: piktun , kalabtun , kʼinchiltun и alautun . Все эти слова являются изобретениями майянистов. Каждый из них состоит из 20 меньших единиц. [65] [66] [j] [67]

Во многих надписях дата текущего создания указана как большое количество 13, предшествующих 13.0.0.0.0 4 Ахау 8 Кумку. Например, позднеклассический памятник из Кобы , Стела 1. Дата создания выражена как 13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.13.0.0.0.0, где единицы измерения — это 13 в девятнадцати знаках больше, чем bʼakʼtun. [68] [69] [70] [71] Некоторые авторы считают, что 13 были символом завершения и не представляли собой фактическое число. [72]

Большинство надписей, в которых они используются, имеют форму дат расстояний и Долгих исчислений — они указывают базовую дату, число расстояния, которое прибавляется или вычитается, и полученный Долгий счет.

Первый пример ниже взят из Schele (1987). Второй взят из Stuart (2005 стр. 60, 77) [73]

Храм Креста в Паленке, табличка, Шеле (1987 стр.)
12.19.13.4.0 8 Аджав 18 Цек в предыдущую эпоху
6.14.0 Число расстояния, связанное с «датой эры»
13.0.0.0.0 4 Аджав 8 Кумку

Храм в Паленке XIX, Южная панель G2-H6 Стюарт (2005 стр. 60, 77)
12.10.1.13.2 9 Ик' 5 Мол (местопребывание ГИ в предыдущую эпоху)
2.8.3.8.0
1.18.5.3.2 9 Ик' 15 Ке (возрождение ГИ, эта дата также в Храме Креста)

На табличке с надписями имеется следующая надпись: [72]
9.8.9.13.0 8 Аджав 13 Поп
10.11.10.5.8
1.0.0.0.0.8

Дрезденский кодекс содержит другой метод записи чисел расстояний. Это Кольцевые числа. Конкретные даты в Дрезденском кодексе часто даются расчетами, включающими Кольцевые числа. Фёрстеман [74] идентифицировал их, но Уилсон (1924) : 24–25  позже разъяснил, как они работают. Кольцевые числа представляют собой интервалы дней между датой Эры Базы 4 Ajaw 8 Kumkʼu и более ранней датой Кольцевой базы, где заполнитель для числа дней в интервале обведен изображением перевязанной красной ленты. К этой более ранней дате Кольцевой базы добавляется еще один подсчет дней вперед, который Томпсон [75] называет Длинным кругом, что приводит к конечной дате в Длинном счете, которая дается как дата записи для использования в определенной таблице в кодексе. [76]

Номер кольца (12) 12.12.17.3.1 13 Имикс 9 Во (7.2.14.19 до (13) 13.0.0.0.0)
номер расстояния (0) 10.13.13.3.2
Длинный счет 10.6.10.6.3 13 Акбал 1 Канкин

Номер кольца (часть DN, предшествующая дате эры) 7.2.14.19
Добавьте номер кольца к дате номера кольца, чтобы получить 13.0.0.0.0

Томпсон [77] содержит таблицу типичных длинных расчетов по Саттервейту. [73]

«Числа змеи» в Дрезденском кодексе на стр. 61–69 представляют собой таблицу дат, использующую базовую дату 1.18.1.8.0.16 в предыдущей эре (5 482 096 дней). [78] [79] [80]

Смотрите также

Примечания

  1. ^ Корреляция между Длинным счетом и западными календарями рассчитывается в соответствии с той, которая используется большинством исследователей майя, известной как (модифицированная) корреляция GMT или корреляция Гудмана-Мартинеса-Томпсона. Альтернативная корреляция, которая иногда используется, откладывает начальную дату на два дня позже. 11 августа 3114 г. до н. э. — дата в пролептическом григорианском календаре , которая приходится на 6 сентября −3113 г. по юлианскому астрономическому календарю .
  2. ^ В этой последовательности примечателен глиф с девятью вариантами форм, обозначенный ранними эпиграфистами как G. Он был связан с циклом Властелинов Ночи, известным из источников колониальной эпохи в Центральной Мексике, но предлагались и альтернативные объяснения. См. Томпсона.
  3. ^ Для ясности: существуют надписи Длинного счета, которые относятся к датам ранее I в. до н. э., но они были вырезаны гораздо позже, в ретроспективной манере.
  4. ^ Все сохранившиеся надписи майя, представляющие эту базовую дату, писали ее с помощью «13» бактунов, а не «0». Но при использовании «13.0.0.0.0» в качестве базовой даты в расчетах, «13» бактунов имеет числовое значение 0, как если бы оно было написано как « 0 .0.0.0.0». Это легко спутать, когда «13» бактунов имеет фактическое значение 13 в текущем бактуне, как в дате майя на сегодня: 13.0.12.1.1 (=17:24, суббота, 9 ноября 2024 г. ( UTC )).
  5. ^ По словам Томпсона [35] «Точка, от которой отсчитывается возраст Луны, точно не известна. Возможными причинами являются исчезновение старой Луны, соединение или появление новой Луны... Бейер (1973a) считал, что расчет производился с момента исчезновения старой Луны. Последний метод подсчета (исчезновение старой Луны) все еще распространен в некоторых деревнях цельталей, чолей и цоцилей в Чьяпасе...»
  6. ↑ Различные источники относят это событие к другим датам, в частности к 23 декабря. [56]
  7. ^ Григорианский, с использованием корреляции GMT JDN=584283.
  8. ^ В 46 г. до н. э. Юлий Цезарь принял соглашение о трех годах из двенадцати месяцев примерно по 30 дней каждый, чтобы получить год из 365 дней и високосный год из 366 дней. Это сделало продолжительность гражданского года 365,25 дней, что близко к продолжительности солнечного года в 365,2422 дня. Это юлианский календарь . К 1582 году наблюдалось заметное расхождение между зимним солнцестоянием и Рождеством и весенним равноденствием и Пасхой . Папа Григорий XIII с помощью итальянского астронома Алоизия Лилиуса ( Луиджи Лилио ) реформировал эту систему, отменив дни с 5 по 14 октября 1582 года. Это сблизило гражданский и тропический годы. Он также пропустил три дня каждые четыре столетия, постановив, что столетия являются високосными только в том случае, если они делятся нацело на 400. Так, например, 1700, 1800 и 1900 годы не являются високосными, а 1600 и 2000 — високосными. Это григорианский календарь . Астрономические вычисления вернут нулевой год, а годы до него — отрицательные числа. Это астрономическое датирование. Годы до 46 г. до н. э. рассчитываются как пролептические юлианские даты . В историческом датировании нет нулевого года. В историческом датировании за 1 годом до н. э. следует 1 год н. э. Например, год -3113 (астрономическое датирование) совпадает с 3114 годом до н. э. (историческое датирование). Во многих книгах о майя и во многих компьютерных программах для преобразования календаря майя используется пролептический григорианский календарь . В этом календаре все даты до начала григорианского календаря пересмотрены так, как если бы григорианский календарь использовался до его принятия в октябре 1582 года. Хотя эта система популярна среди майянистов , она редко используется кем-либо еще, поэтому, например, даты, преобразованные с использованием этой системы, бесполезны для изучения астрономии майя .
  9. ^ Астрономические алгоритмы вычисляют день как десятичное число, равное дню и дроби дня. Юлианская дата начинается в полдень. Астрономическое датирование имеет год 0. В историческом датировании за 1 годом до н. э. следует 1 годом н. э. Астрономические годы до 0 записываются со знаком минус. Например, год 3114 до н. э. — это год −3113 астрономический.
  10. ^ "... у нас есть четкие доказательства того, что текущий цикл Бактуна не заканчивается на 13, как это было в прошлый раз, а продолжается до 20. Другими словами, за 13.0.0.0.0 последуют 14.0.0.0.0, 15.0.0.0.0 и так далее до 19.0.0.0.0. Текст из Паленке, Мексика, ясно показывает это, когда в нем записано завершение 1 Пиктуна, следующей единицы после Бактуна, в 4772 году н. э.

Ссылки

  1. ^ Фрейдель, Шеле и Паркер (1993, стр. 59–75).
  2. ↑ Бут, стр. 2.
  3. ^ Грэм (1992, стр. 331, см. рис. 5 для линейного рисунка памятника)
  4. ^ ab Malmström, Vincent Herschel (1997). "Глава 6". Циклы Солнца, Тайны Луны . University of Texas Press . ISBN 978-0-292-75197-2. Архивировано из оригинала 24 августа 2011 . Получено 22 августа 2010 .Примечание: григорианские даты Мальмстрёма на три-четыре дня позже, чем это можно было бы получить с помощью корреляции 584283 (таблица Википедии была исправлена).
  5. ^ "Vincent H. Mahlstrom". Кафедра географии, преподавательский состав и сотрудники . Дартмутский колледж . Получено 17 февраля 2014 г.
  6. ^ abcdef Маркус, Джойс (1976). «Истоки мезоамериканской письменности» (PDF) . Annual Review of Anthropology . 5 . Annual Reviews Inc. : 49–54. doi :10.1146/annurev.an.05.100176.000343.
  7. ^ abcde Riese, Berthold (1988). "Эпиграфия юго-восточной зоны в отношении к другим частям царства майя". В Boone, Elizabeth Hill; Willey, Gordon Randolph (ред.). Юго-восточная классическая зона майя: доклады симпозиума в Дамбартон-Оксе, 6 и 7 октября 1984 г. Вашингтон, округ Колумбия: Дамбартон-Окс, попечители Гарвардского университета. стр. 68. ISBN 978-0-88402-170-4.
  8. ^ Mora-Marín, David F. (2005). «Kaminaljuyu stela 10: Script classification and languages ​​affiliation». Ancient Mesoamerica . 16 (1). Cambridge University Press : 63–87. doi :10.1017/S0956536105050029. ISSN  0956-5361. S2CID  162510333. Параллельный сдвиг *oo Ͼ *uu Ͼ *u в языке ч'олан косвенно подтверждается использованием логограммы T548 TUN/HABʼ с начальным знаком серии на стеле 2 Такалик Абадж (236–19 гг. до н. э.; Justeson and Mathews 1983; MoraMarín 2001:253).
  9. ^ abcd Стюарт, Дэвид (2004). "Глава 11: Начало династии Копан: Обзор иероглифических и исторических свидетельств". В Белл, Эллен Э.; Кануто, Марчелло А.; Шарер, Роберт Дж. (ред.). Понимание раннего классического Копана . Филадельфия, Пенсильвания: Музей археологии Пенсильванского университета . стр. 219. ISBN 978-1-931707-51-0.
  10. ^ abc Очоа, Лоренцо; Ли, Томас А., ред. (1983). Антропология и история лос-миксов и майас (на испанском языке). Мексика: Национальный автономный университет Мексики , Институт филологических исследований, Центр исследований майя. стр. 191, 194. ISBN. 978-968-5804-97-4.
  11. ^ Диль (2004, стр. 186).
  12. ^ «Очерк предшествующей документации эпиольмекских текстов», Раздел 5 в Peréz de Lara & Justeson (2005).
  13. ^ Коу и Кунц (2002), стр. 87
  14. ^ Сатурно и др. 2006
  15. ^ Хирон-Абрего 2012
  16. ^ Томпсон, Дж. Эрик. "Хронология майя: вопрос корреляции" (PDF) . mesoweb.com . Получено 6 сентября 2015 г. .
  17. ^ Томпсон, Дж. Э. С. Иероглифическое письмо майя. Забытые книги. стр. 73. ISBN 978-1-60506-860-2.
  18. ^ "Разъяснения: дебаты о корреляции". alignment2012.com . Получено 6 сентября 2015 г. .
  19. ^ "Календарь майя: проблема корреляции". hermetic.ch . Получено 6 сентября 2015 г. .
  20. ^ "FAMSI – FAQ о 2012: Конец света? – FAQ – Что такое эта константа корреляции?". famsi.org . Получено 6 сентября 2015 г.
  21. ↑ Взлом кода майя , 1992, стр. 114.
  22. ^ Брикер, Харви М.; Брикер, Виктория Рейфлер (1 августа 2011 г.). Астрономия в кодексах майя . Мемуары Американского философского общества. Американское философское общество. стр. 85. ISBN 978-0871692658Если считать, что 12 окончаний «тун» в «Хронике Ошкуцкаба» относятся к 12 последовательным годам, и если даты календаря (за исключением даты, содержащей месяц Кех) верны при переводе в общепринятый календарь, то корреляция «11.16» является единственно возможной.
  23. ↑ Книга Чилам Балам Чумайеля Ральфа Л. Ройса, Вашингтон, округ Колумбия; Институт Карнеги, 1933, стр. 79, 83
  24. ^ Эдмонсон, Манро С. (декабрь 1976 г.). «Реформа календаря майя 11.16.0.0.0». Current Anthropology . 17 (4): 713–17. doi :10.1086/201806. JSTOR  2741269. S2CID  145181714.
  25. ^ Ресинос 1953, стр. 33 Ресинос приводит 2 Тихакс (Эцнаб) — 10 сентября 1541 г. ( по юлианскому календарю ). Дата, которая ознаменовала разрушение города Гватемала, основанного у подножия вулкана Агуа. «После периода сильных дождей произошло землетрясение, а затем наводнение (лахар ) , которое разрушило старый город Гватемала».
  26. ^ Weeks, John M.; Sachse, Frauke; Prager, Christian M. (15 мая 2013 г.). Maya Daykeeping: Three Calendars from Highland Guatemala (Mesoamerican Worlds) . University Press of Colorado. стр. 176–84. ISBN 978-1607322467.В Приложении 2, Заметки о корреляции календарей майя и григорианского календаря , авторы приводят примеры 9 декабря 1722 г. = 8 кей 20 укаб сидж (8 маник 0 йаш) и 9 декабря 1723 г. = 9 э 20 укаб сидж (9 эб 0 йаш). «Используя константу корреляции Томпсона A = 584 283, все значения из календарного раунда соответствуют информации в календаре киче 1722 г.».
  27. ^ (Диас 1904: 2:129)
  28. ^ (Саагун 1975: 12:122)
  29. ↑ Майлз, Сусанна В., «Анализ современных среднеамериканских календарей: исследование сохранения». В книге «Аккультурация в Америке » . Под редакцией Сола Такса, стр. 273. Чикаго: Издательство Чикагского университета, 1952.
  30. ↑ Барбара Тедлок, Время и горные майя, пересмотренное издание (1992, стр. 1)
  31. ^ Эдмонсон, Манро С. (1988). Книга года Среднеамериканские календарные системы . Солт-Лейк-Сити: Издательство Университета Юты. ISBN 0-87480-288-1.
  32. ^ «Лунные глифы в календарях майя – Лунная серия – Дополнительные и лунные глифы». astras-stargate.com . Получено 6 сентября 2015 г. .
  33. ^ Fuls (2007) Ancient Mesoamerica , 18, 273–282 Cambridge University Press. по Robertson 1991: Vol. 4: p. 95.
  34. ^ Финли, Майкл Джон. "Таблица затмений Дрезденского кодекса" . Получено 1 января 2018 г.
  35. ^ Томпсон, Дж. Эрик С. (1950). Иероглифическое письмо майя, введение. стр. 236
  36. ^ Авени 2001
  37. ^ «Наблюдение за полумесяцем», Sky & Telescope , июль 1994 г., 14
  38. ↑ «В поисках самой молодой Луны», Sky & Telescope , декабрь 1996 г., 104–105.
  39. ^ «Молодые Луны и Исламский Календарь», Sky & Telescope , Декабрь 1996, 106
  40. ↑ «В поисках тонких полумесяцев», Sky & Telescope , февраль 2004 г., 102–106
  41. ^ «Охота за молодой Луной в 2005 году», Sky and Telescope , февраль 2005 г., стр. 75–76.
  42. ^ «Какой самый тонкий полумесяц вы можете увидеть?». Sky and Telescope. 13 декабря 2017 г.
  43. ^ Stray, G. (2007). Майя и другие древние календари. Walker. стр. 40. ISBN 978-0-8027-1634-7.
  44. ^ Андреас Фулс (2007). Древняя Мезоамерика, 18, 273–282 Cambridge University Press.
  45. ↑ Брикер и Брикер, стр. 249–366.
  46. ↑ Брикер и Брикер, стр. 163–248.
  47. ^ Ральф, Элизабет К. (1965). «Обзор радиоуглеродных дат из Тикаля и проблема корреляции календаря майя». American Antiquity . 30 (4): 421–427. doi :10.2307/277941. JSTOR  277941. S2CID  163676704.
  48. ^ Кеннетт, Дуглас Дж.; Хайдас, Ирка; Каллетон, Брендан Дж.; Белмечери, Соумайя; Мартин, Саймон; Нефф, Гектор; и др. (11 апреля 2013 г.). «Сопоставление древних календарей майя и современных европейских календарей с высокоточным датированием AMS 14C». Scientific Reports . 3 : 1597. Bibcode :2013NatSR...3E1597K. doi :10.1038/srep01597. PMC 3623374 . PMID  23579869. 
  49. ^ [1]Кеннетт, Дуглас Дж. и др., «Соотнесение древних календарей майя и современных европейских календарей с высокоточным датированием AMS 14C», Научные отчеты 3.1, 2013 г.
  50. ^ Вывод корреляции майяского и юлианского календарей из хронологии Венеры Дрезденского кодекса, в книге «Небо в майянской литературе» (1992)
  51. ^ Фулс, Андреас. «Вопрос корреляции». archaeoastronomie.de . Получено 6 сентября 2015 г. .
  52. ^ Владимир Бём; Богумил Бём. «Свидания Майя». герметик.гл . Проверено 6 сентября 2015 г.
  53. ^ "Датирование майя, астрономия майя, корреляция MD/JD". volny.cz . Получено 6 сентября 2015 г. .
  54. ^ Сток, Антон. «Датировка таблицы затмений Дрезденского кодекса и проблема корреляции». baktun.de . Получено 6 сентября 2015 г.
  55. ^ Шеле и Фрейдель (1990), стр. 429–30.
  56. ^ Шеле и Фридель (1992).
  57. ^ «Заметки о новом тексте из Ла-Короны». decipherment.wordpress.com . Расшифровка майя. 30 июня 2012 г. Получено 6 сентября 2015 г.
  58. ^ аб Шеле (1992, стр. 93–95)
  59. ^ Шеле и Фрейдель (1990, стр. 430 , № 39)
  60. ^ ab MacDonald, G. Jeffrey (27 марта 2007 г.). «Предсказывает ли календарь майя апокалипсис 2012 года?». USA Today . Gannett Company .
  61. ^ Ривет, Райан (25 июня 2008 г.). «Небо не падает». Новая волна . Тулейнский университет . Архивировано из оригинала 18 апреля 2011 г.
  62. ^ Кеттунен, Харри; Хельмке, Кристоф (2014). «Введение в иероглифы майя» (PDF) . Словацкий археологический и исторический институт. Wayeb . Братислава: Университет Коменского.
  63. ^ Меус, Жан (2009) [1991]. «Глава 7: Джулиан Дэй». Астрономические алгоритмы (второе изд.). Уиллман-Белл. п. 63. ИСБН 978-0-943396-61-3. с исправлениями по состоянию на 10 августа 2009 г.
  64. ^ Баум, Питер. "Метод преобразования дат". Архивировано из оригинала 10 сентября 2014 г.
  65. ↑ Томпсон 1960, стр. 314, 316, 148–49 Приложение IV: «Я всегда предполагал, что бактуны были сгруппированы не по 13, а по 20, поскольку доказательства, подтверждающие двадцатеричное количество бактунов в Дрездене, Паленке и Копане, слишком убедительны, чтобы их можно было отвергнуть».
  66. ^ Грофе, Майкл Джон (2007). Серия «Змея»: прецессия в Дрезденском кодексе майя . стр. 55. Иногда майя также записывали интервалы времени, даже большие, чем 13 Бактунов, например, один Пиктун, состоящий из 20 Бактунов. Это имеет отношение к текущему обсуждению Серии «Змея».
  67. ^ Мартин. «Время, королевская власть и вселенная майя». penn.museum .
  68. ↑ Рис. 444 в Wagner 2006, стр. 283.
  69. ^ Шеле и Фрейдель 1992, стр. 430
  70. ^ Д. Фрейдель; Л. Шеле; Дж. Паркер (1993). Космос майя: три тысячи лет на пути шамана . Т. 62, рис. 2:1.
  71. ^ "Коллекция рисунков Schele". research.famsi.org . Получено 6 сентября 2015 г. .
  72. ^ ab Anderson, Lloyd B. (2008). "20 или 13 бактунов в пиктуне?" (PDF) . traditionalhighcultures.org . Архивировано из оригинала (PDF) 14 мая 2015 г. . Получено 6 сентября 2015 г. .
  73. ^ ab Thompson, J. Eric S. "Distances across Era Date" (PDF) . traditionalhighcultures.org . Архивировано из оригинала (PDF) 17 ноября 2009 г. . Получено 13 января 2013 г. .таблица от Томпсона
  74. ^ Фёрстеман, Эрнст. Комментарий к рукописи майя в Королевской публичной библиотеке Дрездена . Т. IV. № 2. Музей американской археологии и археологии и этнографии Пибоди, Гарвардский университет. С. 222–264.
  75. ↑ Томпсон 1972, стр. 20–21.
  76. ^ Грофе, Майкл Джон (2007). Серия «Змея»: прецессия в Дрезденском кодексе майя . стр. 55.
  77. ↑ Томпсон 1972, стр. 20–22.
  78. ^ Бейер, Герман (1933). «Поправки к «Змеиным числам» Дрезденского кодекса майя». Антропос (Св. Габриэль Мёдлинг в Вене) . 28 : 1–7.
  79. ↑ Длинное положение дат числа змеи . Том I. Мексика: Труды 27-го Международного конгресса Америки, Мексика, 1939. 1943. С. 401–05.
  80. ^ Грофе, Майкл Джон (2007). Серия «Змея»: прецессия в Дрезденском кодексе майя . стр. 63.

Библиография

Внешние ссылки