Принцип самосогласованности Новикова , также известный как гипотеза самосогласованности Новикова и закон сохранения истории Ларри Нивена , — принцип, разработанный российским физиком Игорем Дмитриевичем Новиковым в середине 1980-х годов. Новиков намеревался решить проблему парадоксов в путешествиях во времени , что теоретически разрешено в некоторых решениях общей теории относительности , содержащих то, что известно как замкнутые времениподобные кривые . Принцип утверждает, что если существует событие, которое может вызвать парадокс или любое «изменение» прошлого, то вероятность этого события равна нулю. Таким образом, было бы невозможно создать временные парадоксы .
Физикам давно известно, что некоторые решения общей теории относительности содержат замкнутые времениподобные кривые — например, метрику Гёделя . Новиков обсуждал возможность замкнутых времениподобных кривых (ЗВК) в книгах, которые он написал в 1975 и 1983 годах, [1] высказывая мнение, что будут разрешены только самосогласованные путешествия назад во времени. [2] В статье 1990 года Новикова и нескольких других, « Проблема Коши в пространстве-времени с замкнутыми времениподобными кривыми», [3] авторы утверждают:
Единственный тип нарушения причинности, который авторы сочли бы неприемлемым, — это тот, который воплощен в научно-фантастической концепции возвращения назад во времени и убийства себя в молодом возрасте («изменение прошлого»). Несколько лет назад один из нас (Новиков) кратко рассмотрел возможность существования ЗВК и утверждал, что они не могут повлечь за собой этот тип нарушения причинности: события в ЗВК уже гарантированно являются самосогласованными, утверждал Новиков; они влияют друг на друга по замкнутой кривой саморегулирующимся, циклическим, самосогласованным образом. Другие авторы недавно пришли к той же точке зрения.
Мы воплотим эту точку зрения в принципе самосогласованности, который утверждает, что единственные решения законов физики, которые могут иметь место локально в реальной Вселенной, — это те, которые являются глобально самосогласованными. Этот принцип позволяет построить локальное решение уравнений физики только в том случае, если это локальное решение может быть расширено до части (не обязательно уникального) глобального решения, которое хорошо определено во всех несингулярных областях пространства-времени.
Среди соавторов этой статьи 1990 года были Кип Торн , Майк Моррис и Ульви Юртсевер, которые в 1988 году возобновили интерес к теме путешествий во времени в общей теории относительности своей статьей «Червоточины, машины времени и слабое энергетическое условие» [4] , в которой было показано, что новое решение общей теории относительности, известное как проходимая червоточина , может привести к замкнутым времениподобным кривым, и в отличие от предыдущих решений, содержащих ЗВК, оно не требует нереалистичных условий для Вселенной в целом. После обсуждений с ведущим автором статьи 1990 года Джоном Фридманом они убедили себя, что путешествия во времени не обязательно должны приводить к неразрешимым парадоксам, независимо от объекта, отправленного через червоточину. [5] : 509

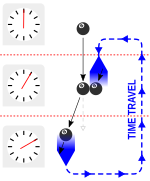
В ответ физик Джозеф Полчински написал им письмо, в котором утверждал, что можно избежать проблемы свободы воли, применив потенциально парадоксальный мысленный эксперимент с бильярдным шаром, отправленным назад во времени через червоточину. В сценарии Полчински бильярдный шар выстреливается в червоточину под углом таким образом, что если он продолжит свой путь, то выйдет в прошлом под правильным углом, чтобы столкнуться со своим более ранним «я», сбив его с пути и не дав ему войти в червоточину в первую очередь. Торн назвал этот сценарий « парадоксом Полчински » в 1994 году. [6] : 510–511
Рассмотрев сценарий, Фернандо Эчеверрия и Гуннар Клинкхаммер, два студента Калтеха (где преподавал Торн), пришли к решению проблемы, которое излагает те же элементы, что и решение, которое Фейнман и Уилер [7] назвали решением «скользящего удара», чтобы избежать несоответствий, возникающих из-за циклов причинности. В пересмотренном сценарии мяч из будущего появляется под другим углом, чем тот, который генерирует парадокс, и наносит своему младшему «я» скользящий удар вместо того, чтобы полностью отбросить его от червоточины. Этот удар изменяет его траекторию как раз на нужную величину, то есть он будет перемещаться назад во времени под углом, необходимым для нанесения своему младшему «я» необходимого скользящего удара. Эчеверрия и Клинкхаммер фактически обнаружили, что существует более одного самосогласованного решения с немного разными углами для скользящего удара в каждой ситуации. Более поздний анализ Торна и Роберта Форварда показал, что для определенных начальных траекторий бильярдного шара на самом деле может существовать бесконечное число самосогласованных решений. [6] : 511–513
Эчеверрия, Клинкхаммер и Торн опубликовали статью, в которой обсуждались эти результаты, в 1991 году; [8] кроме того, они сообщили, что пытались найти какие-либо начальные условия для бильярдного шара, для которых не было бы самосогласованных расширений, но не смогли этого сделать. Таким образом, вполне вероятно, что существуют самосогласованные расширения для каждой возможной начальной траектории, хотя это и не было доказано. [9] : 184 Это применимо только к начальным условиям за пределами области пространства-времени, нарушающей хронологию, [9] : 187 которая ограничена горизонтом Коши . [10] Это может означать, что принцип самосогласованности Новикова на самом деле не накладывает никаких ограничений на системы за пределами области пространства-времени, где возможны путешествия во времени, а только внутри нее.
Даже если самосогласованные расширения могут быть найдены для произвольных начальных условий за пределами горизонта Коши, открытие того, что может быть несколько различных самосогласованных расширений для одного и того же начального условия — действительно, Эчеверриа и др. нашли бесконечное количество согласованных расширений для каждой проанализированной ими начальной траектории [9] : 184 — можно рассматривать как проблематичное, поскольку классически, похоже, нет способа решить, какое расширение выберут законы физики. Чтобы обойти эту трудность, Торн и Клинкхаммер проанализировали сценарий бильярдного шара с помощью квантовой механики, [6] : 514–515 выполнив квантово-механическую сумму по историям ( интеграл по траектории ), используя только согласованные расширения, и обнаружили, что это привело к четко определенной вероятности для каждого согласованного расширения. Авторы «Проблемы Коши в пространстве-времени с замкнутыми времениподобными кривыми» пишут:
Самый простой способ навязать принцип самосогласованности в квантовой механике (в классическом пространстве-времени) — это формулировка суммы по историям, в которую включаются все те, и только те, истории, которые являются самосогласованными. Оказывается, что, по крайней мере формально (по модулю таких вопросов, как сходимость суммы), для каждого выбора начальной, нерелятивистской волновой функции бильярдного шара до горизонта Коши , такая сумма по историям дает уникальные, самосогласованные вероятности для результатов всех наборов последующих измерений. ... Мы подозреваем, в более общем плане, что для любой квантовой системы в классическом пространстве-времени-кротовой норе со стабильным горизонтом Коши сумма по всем самосогласованным историям даст уникальные, самосогласованные вероятности для результатов всех наборов измерений, которые можно было бы выбрать.
Принцип согласованности Новикова предполагает определенные условия относительно того, какой тип путешествия во времени возможен. В частности, он предполагает, что либо существует только одна временная линия , либо что любые альтернативные временные линии (например, постулируемые многомировой интерпретацией квантовой механики ) недоступны.
Учитывая эти предположения, ограничение, что путешествие во времени не должно приводить к противоречивым результатам, можно рассматривать просто как тавтологию , самоочевидную истину, которая не может быть ложной. Однако принцип самосогласованности Новикова призван выйти за рамки простого утверждения о том, что история должна быть последовательной, делая дополнительное нетривиальное предположение о том, что вселенная подчиняется тем же локальным законам физики в ситуациях, связанных с путешествием во времени, что и в областях пространства-времени, в которых отсутствуют замкнутые времениподобные кривые. Это проясняется в вышеупомянутой «Проблеме Коши в пространстве-времени с замкнутыми времениподобными кривыми» [3] , где авторы пишут:
То, что принцип самосогласованности не является полностью тавтологическим, становится ясно, если рассмотреть следующую альтернативу: законы физики могут допускать ЗВК; и когда ЗВК происходят, они могут вызывать новые виды локальной физики, с которыми мы ранее не сталкивались. ... Принцип самосогласованности призван исключить такое поведение. Он настаивает на том, что локальная физика управляется теми же типами физических законов, с которыми мы имеем дело при отсутствии ЗВК: законами, которые влекут за собой самосогласованную однозначность для полей. По сути, принцип самосогласованности является принципом отсутствия новой физики. Если кто-то с самого начала склонен игнорировать или недооценивать возможность новой физики, то он будет считать самосогласованность тривиальным принципом.
Предположения принципа самосогласованности могут быть распространены на гипотетические сценарии, включающие разумных путешественников во времени, а также неразумные объекты, такие как бильярдные шары. Авторы «Проблемы Коши в пространстве-времени с замкнутыми времениподобными кривыми » прокомментировали этот вопрос в заключении статьи, написав:
Если ЗВК разрешены, и если вышеизложенное видение приспособления теоретической физики к ним окажется более или менее правильным, то что это будет означать относительно философского понятия свободы воли для людей и других разумных существ? Это, безусловно, будет означать, что разумные существа не могут изменить прошлое. Такое изменение несовместимо с принципом самосогласованности. Следовательно, любое существо, которое прошло через червоточину и попыталось изменить прошлое, было бы лишено возможности внести изменения физическим законом; т. е. «свободная воля» существа была бы ограничена. Хотя это ограничение имеет более глобальный характер, чем ограничения на свободу воли, которые следуют из стандартных локальных законов физики, для нас не очевидно, что это ограничение более строгое, чем те, которые налагаются стандартным физическим законом. [3]
Аналогично физик и астроном Дж. Крейг Уиллер приходит к выводу, что:
Согласно гипотезе о согласованности, любые сложные межличностные взаимодействия должны работать самосогласованно, чтобы не было парадокса. Это решение. Это означает, если понимать буквально, что если машины времени существуют, не может быть никакой свободной воли. Вы не можете заставить себя убить себя в молодости, если вы путешествуете назад во времени. Вы можете сосуществовать, ходить в пиво, праздновать вместе свой день рождения, но каким-то образом обстоятельства будут диктовать, что вы не можете вести себя таким образом, который приводит к парадоксу во времени. Новиков поддерживает эту точку зрения другим аргументом: физика уже ограничивает вашу свободу воли каждый день. Вы можете заставить себя летать или проходить сквозь бетонную стену, но гравитация и физика конденсированного состояния диктуют, что вы не можете. Почему, спрашивает Новиков, ограничение согласованности, налагаемое на путешественника во времени, отличается? [11]
Логика временной петли, придуманная робототехником и футуристом Гансом Моравецом [12], представляет собой гипотетическую систему вычислений, которая использует принцип самосогласованности Новикова для вычисления ответов гораздо быстрее, чем это возможно при стандартной модели вычислительной сложности с использованием машин Тьюринга . В этой системе компьютер отправляет результат вычисления назад во времени и полагается на принцип самосогласованности, чтобы заставить отправленный результат быть правильным, при условии, что машина может надежно получать информацию из будущего и при условии, что алгоритм и базовый механизм формально правильны . Неправильный результат или отсутствие результата все еще могут быть получены, если механизм или алгоритм путешествия во времени не гарантируют точности.
Простым примером является алгоритм итерационного метода . Моравек утверждает:
Создайте вычислительный блок, который принимает входные данные, представляющие собой приблизительное решение некоторой задачи, и выдает выходные данные, которые являются улучшенным приближением. Обычно вы применяете такие вычисления повторно конечное число раз, а затем довольствуетесь лучшим, но все еще приблизительным результатом. При соответствующей отрицательной задержке возможно и другое: [...] результат каждой итерации функции возвращается во времени, чтобы служить «первым» приближением. Как только машина активируется, так называемая «фиксированная точка» F, входные данные, которые выдают идентичные выходные данные, обычно сигнализирующие об идеальном ответе, появляются (по необычайному совпадению!) немедленно и устойчиво. [...] Если итерация не сходится, то есть если F не имеет фиксированной точки, выходы и входы компьютера отключатся или зависнут в маловероятном промежуточном состоянии.
Физик Дэвид Дойч в 1991 году показал, что эта модель вычислений может решать задачи NP за полиномиальное время , [13] а Скотт Ааронсон позже расширил этот результат, чтобы показать, что модель также может быть использована для решения задач PSPACE за полиномиальное время. [14] [15] Дойч показывает, что квантовые вычисления с отрицательной задержкой — путешествие во времени назад — производят только самосогласованные решения, а область нарушения хронологии накладывает ограничения, которые не очевидны с помощью классических рассуждений. [13] Исследователи опубликовали в 2014 году моделирование, в котором, как они утверждают, подтвердили модель Дойча с фотонами. [16] Однако в статье Толксдорфа и Верча было показано, что условие самосогласованности Дойча может быть выполнено с произвольной точностью в любой квантовой системе, описанной в соответствии с релятивистской квантовой теорией поля, даже в пространстве-времени, которое не допускает замкнутых времениподобных кривых, что ставит под сомнение, действительно ли модель Дойча характерна для квантовых процессов, имитирующих замкнутые времениподобные кривые в смысле общей теории относительности . [17] В более поздней статье [18] те же авторы показывают, что условие неподвижной точки ЗВК Дойча также может быть выполнено в любой системе, подчиняющейся законам классической статистической механики , даже если оно не построено квантовыми системами. Авторы приходят к выводу, что, следовательно, условие Дойча не является специфичным для квантовой физики и не зависит от квантовой природы физической системы, чтобы оно могло быть выполнено. В результате Толксдорф и Верч утверждают, что условие Дойча недостаточно конкретно, чтобы допускать утверждения о сценариях путешествий во времени или их гипотетической реализации квантовой физикой.
Альтернативное предложение было позже представлено Сетом Ллойдом [19] [20] , основанным на пост-селекции и интегралах по траектории. В частности, интеграл по траектории выполняется по однозначным полям, что приводит к самосогласованным историям.
Парадокс Полчинского.