Скалярный потенциал

Когда разность потенциальных энергий зависит только от смещения

В математической физике скалярный потенциал описывает ситуацию, когда разность потенциальных энергий объекта в двух различных положениях зависит только от положений, а не от пути, пройденного объектом при перемещении из одного положения в другое. Это скалярное поле в трехмерном пространстве : беснаправленная величина ( скаляр ), которая зависит только от своего местоположения. Знакомый пример — потенциальная энергия, обусловленная гравитацией .

Вектор поля (справа) и соответствующий скалярный потенциал (слева).

Скалярный потенциал является фундаментальным понятием в векторном анализе и физике (прилагательное скалярный часто опускается, если нет опасности путаницы с векторным потенциалом ). Скалярный потенциал является примером скалярного поля . При наличии векторного поля F скалярный потенциал P определяется следующим образом: ^[1] где ∇ P — градиент P , а вторая часть уравнения — это минус градиент для функции декартовых координат x, y, z . ^[a] В некоторых случаях математики могут использовать положительный знак перед градиентом для определения потенциала. ^[2] Из-за этого определения P в терминах градиента направление F в любой точке является направлением самого крутого убывания P в этой точке, его величина — это скорость этого убывания на единицу длины. $${\displaystyle \mathbf {F} =-\nabla P=-\left({\frac {\partial P}{\partial x}},{\frac {\partial P}{\partial y}},{\frac {\partial P}{\partial z}}\right),}$$

Для того чтобы F можно было описать только с помощью скалярного потенциала, любое из следующих эквивалентных утверждений должно быть верным:

1. ${\displaystyle -\int _{a}^{b}\mathbf {F} \cdot d\mathbf {l} =P(\mathbf {b} )-P(\mathbf {a} ),}$где интегрирование ведется по жордановой дуге, проходящей из точки a в точку b, а P ( b ) — это P, вычисленное в точке b .
2. ${\displaystyle \oint \mathbf {F} \cdot d\mathbf {l} =0,}$где интеграл берется по любому простому замкнутому пути, также известному как жорданова кривая .
3. ${\displaystyle {\nabla }\times {\mathbf {F} }=0.}$

Первое из этих условий представляет собой фундаментальную теорему о градиенте и справедливо для любого векторного поля, которое является градиентом дифференцируемого однозначного скалярного поля P. Второе условие является требованием к F , чтобы оно могло быть выражено как градиент скалярной функции. Третье условие повторно выражает второе условие в терминах ротора F , используя фундаментальную теорему о роторе . Вектор поля F, удовлетворяющий этим условиям, называется безвихревым (консервативным).

Гравитационная потенциальная яма увеличивающейся массы, где F = –∇ P

Скалярные потенциалы играют важную роль во многих областях физики и техники. Гравитационный потенциал — это скалярный потенциал, связанный с гравитацией на единицу массы, т. е. ускорением, вызванным полем, как функцией положения. Гравитационный потенциал — это гравитационная потенциальная энергия на единицу массы. В электростатике электрический потенциал — это скалярный потенциал, связанный с электрическим полем , т. е. с электростатической силой на единицу заряда . В этом случае электрический потенциал — это электростатическая потенциальная энергия на единицу заряда. В гидродинамике безвихревые пластинчатые поля имеют скалярный потенциал только в особом случае, когда это поле Лапласа . Некоторые аспекты ядерной силы можно описать потенциалом Юкавы . Потенциал играет важную роль в лагранжевых и гамильтоновых формулировках классической механики . Кроме того, скалярный потенциал является фундаментальной величиной в квантовой механике .

Не каждое векторное поле имеет скалярный потенциал. Те, которые имеют, называются консервативными , что соответствует понятию консервативной силы в физике. Примерами неконсервативных сил являются силы трения, магнитные силы и в механике жидкости соленоидальное поле скорости поля. Однако по теореме Гельмгольца о разложении все векторные поля могут быть описаны в терминах скалярного потенциала и соответствующего векторного потенциала . В электродинамике электромагнитные скалярный и векторный потенциалы известны вместе как электромагнитный четырехпотенциал .

Условия интегрируемости

Если F — консервативное векторное поле (также называемое безвихревым , безроторным или потенциальным ) , и его компоненты имеют непрерывные частные производные , потенциал F относительно опорной точки r ₀ определяется в терминах линейного интеграла : где C — параметризованный путь от r ₀ до r , $${\displaystyle V(\mathbf {r} )=-\int _{C}\mathbf {F} (\mathbf {r} )\cdot \,d\mathbf {r} =-\int _{a}^{b}\mathbf {F} (\mathbf {r} (t))\cdot \mathbf {r} '(t)\,dt,}$$ $${\displaystyle \mathbf {r} (t),a\leq t\leq b,\mathbf {r} (a)=\mathbf {r_{0}} ,\mathbf {r} (b)=\mathbf {r} .}$$

Тот факт, что линейный интеграл зависит от пути C только через его конечные точки r ₀ и r , по сути, является свойством независимости пути консервативного векторного поля. Основная теорема линейных интегралов подразумевает, что если V определено таким образом, то F = –∇ V , так что V является скалярным потенциалом консервативного векторного поля F . Скалярный потенциал определяется не только векторным полем: действительно, градиент функции не изменяется, если к нему добавляется константа. Если V определено в терминах линейного интеграла, неоднозначность V отражает свободу в выборе опорной точки r ₀ .

Высота как потенциальная энергия гравитации

однородное гравитационное поле вблизи поверхности Земли

График двумерного среза гравитационного потенциала внутри и вокруг однородного сферического тела. Точки перегиба сечения находятся на поверхности тела.

Примером является (почти) однородное гравитационное поле вблизи поверхности Земли. Оно имеет потенциальную энергию , где U — гравитационная потенциальная энергия, а h — высота над поверхностью. Это означает, что гравитационная потенциальная энергия на контурной карте пропорциональна высоте. На контурной карте двумерный отрицательный градиент высоты — это двумерное векторное поле, векторы которого всегда перпендикулярны контурам, а также перпендикулярны направлению силы тяжести. Но на холмистой местности, представленной контурной картой, трехмерный отрицательный градиент U всегда указывает прямо вниз в направлении силы тяжести; F . Однако мяч, катящийся с холма, не может двигаться прямо вниз из-за нормальной силы поверхности холма, которая отменяет компонент силы тяжести, перпендикулярный поверхности холма. Компонент силы тяжести, который остается для перемещения мяча, параллелен поверхности: где θ — угол наклона, а компонент F _{S ,} перпендикулярный силе тяжести, равен Эта сила F _P , параллельная земле, максимальна, когда θ составляет 45 градусов. $${\displaystyle U=mgh}$$ $${\displaystyle \mathbf {F} _{\mathrm {S} }=-mg\ \sin \theta }$$ $${\displaystyle \mathbf {F} _{\mathrm {P} }=-mg\ \sin \theta \ \cos \theta =-{1 \over 2}mg\sin 2\theta .}$$

Пусть Δ h будет равномерным интервалом высоты между контурами на контурной карте, и пусть Δ x будет расстоянием между двумя контурами. Тогда так что Однако на контурной карте градиент обратно пропорционален Δ x , что не похоже на силу F _P : высота на контурной карте не является в точности двумерным потенциальным полем. Величины сил различны, но направления сил одинаковы как на контурной карте, так и на холмистой области поверхности Земли, представленной контурной картой. $${\displaystyle \theta =\tan ^{-1}{\frac {\Delta h}{\Delta x}}}$$ $${\displaystyle F_{P}=-mg{\Delta x\,\Delta h \over \Delta x^{2}+\Delta h^{2}}.}$$

Давление как потенциал подъема

В механике жидкости жидкость в равновесии, но в присутствии однородного гравитационного поля пронизана однородной выталкивающей силой, которая нейтрализует силу тяготения: так жидкость сохраняет свое равновесие. Эта выталкивающая сила является отрицательным градиентом давления : $${\displaystyle \mathbf {f_{B}} =-\nabla p.}$$

Поскольку выталкивающая сила направлена ​​вверх, в направлении, противоположном силе тяжести, то давление в жидкости увеличивается вниз. Давление в статическом водоеме увеличивается пропорционально глубине под поверхностью воды. Поверхности постоянного давления — это плоскости, параллельные поверхности, которую можно охарактеризовать как плоскость нулевого давления.

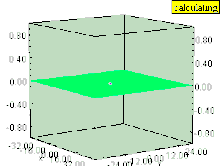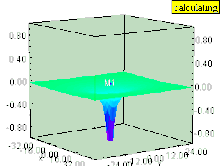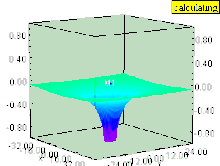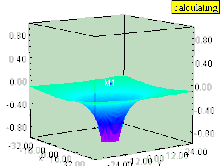
Если в жидкости есть вертикальный вихрь (ось вращения которого перпендикулярна поверхности), то вихрь вызывает понижение в поле давления. Поверхность жидкости внутри вихря тянется вниз, как и любые поверхности равного давления, которые все еще остаются параллельными поверхности жидкости. Эффект сильнее всего внутри вихря и быстро уменьшается с расстоянием от оси вихря.

Выталкивающая сила, действующая со стороны жидкости на твердый объект, погруженный и окруженный этой жидкостью, может быть получена путем интегрирования отрицательного градиента давления вдоль поверхности объекта: $${\displaystyle F_{B}=-\oint _{S}\nabla p\cdot \,d\mathbf {S} .}$$

Скалярный потенциал в евклидовом пространстве

В трехмерном евклидовом пространстве ⁠ ⁠ ${\displaystyle \mathbb {R} ^{3}}$ скалярный потенциал безвихревого векторного поля E задается выражением , где dV ( r' ) — бесконечно малый элемент объема относительно r ' . Тогда Это справедливо при условии, что E непрерывно и асимптотически стремится к нулю к бесконечности, затухая быстрее, чем 1/ r , и если дивергенция E также стремится к нулю к бесконечности, затухая быстрее, чем 1/ r ² . $${\displaystyle \Phi (\mathbf {r} )={\frac {1}{4\pi }}\int _{\mathbb {R} ^{3}}{\frac {\operatorname {div} \mathbf {E} (\mathbf {r} ')}{\left\|\mathbf {r} -\mathbf {r} '\right\|}}\,dV(\mathbf {r} ')}$$ $${\displaystyle \mathbf {E} =-\mathbf {\nabla } \Phi =-{\frac {1}{4\pi }}\mathbf {\nabla } \int _{\mathbb {R} ^{3}}{\frac {\operatorname {div} \mathbf {E} (\mathbf {r} ')}{\left\|\mathbf {r} -\mathbf {r} '\right\|}}\,dV(\mathbf {r} ')}$$

Записывая по-другому, пусть будет ньютоновским потенциалом . Это фундаментальное решение уравнения Лапласа , означающее, что лапласиан Γ равен отрицательной дельта-функции Дирака : Тогда скалярный потенциал является дивергенцией свертки E с Γ : $${\displaystyle \Gamma (\mathbf {r} )={\frac {1}{4\pi }}{\frac {1}{\|\mathbf {r} \|}}}$$ $${\displaystyle \nabla ^{2}\Gamma (\mathbf {r} )+\delta (\mathbf {r} )=0.}$$ $${\displaystyle \Phi =\operatorname {div} (\mathbf {E} *\Gamma ).}$$

Действительно, свертка безвихревого векторного поля с вращательно-инвариантным потенциалом также безвихревая. Для безвихревого векторного поля G можно показать, что Следовательно, как и требовалось. $${\displaystyle \nabla ^{2}\mathbf {G} =\mathbf {\nabla } (\mathbf {\nabla } \cdot {}\mathbf {G} ).}$$ $${\displaystyle \nabla \operatorname {div} (\mathbf {E} *\Gamma )=\nabla ^{2}(\mathbf {E} *\Gamma )=\mathbf {E} *\nabla ^{2}\Gamma =-\mathbf {E} *\delta =-\mathbf {E} }$$

В более общем случае формула справедлива в n -мерном евклидовом пространстве ( n > 2 ) с ньютоновским потенциалом, заданным тогда как , где ω _n - объем единичного n -шара. Доказательство идентично. В качестве альтернативы, интегрирование по частям (или, более строго, свойства свертки ) дает $${\displaystyle \Phi =\operatorname {div} (\mathbf {E} *\Gamma )}$$ $${\displaystyle \Gamma (\mathbf {r} )={\frac {1}{n(n-2)\omega _{n}\|\mathbf {r} \|^{n-2}}}}$$ $${\displaystyle \Phi (\mathbf {r} )=-{\frac {1}{n\omega _{n}}}\int _{\mathbb {R} ^{n}}{\frac {\mathbf {E} (\mathbf {r} ')\cdot (\mathbf {r} -\mathbf {r} ')}{\|\mathbf {r} -\mathbf {r} '\|^{n}}}\,dV(\mathbf {r} ').}$$

Смотрите также

• Теорема о градиенте
• Основная теорема векторного анализа
• Эквипотенциальные (изопотенциальные) линии и поверхности

Примечания

1. Вторая часть этого уравнения верна только для декартовых координат, другие системы координат, такие как цилиндрические или сферические координаты, будут иметь более сложные представления, выведенные из фундаментальной теоремы о градиенте .

Ссылки

1. Голдстейн, Герберт. Классическая механика (2-е изд.). С. 3–4. ISBN 978-0-201-02918-5.
2. См. [1] для примера, где потенциал определен без отрицательного знака. Другие ссылки, такие как Louis Leithold, The Calculus with Analytic Geometry (5-е изд.), стр. 1199избегайте использования термина «потенциал» при нахождении функции по ее градиенту.

Внешние ссылки

• Медиа, связанные с Scalar potential на Wikimedia Commons