Собственные значения и собственные векторы

Concepts from linear algebra

В линейной алгебре собственный вектор ( / ˈ aɪ ɡ ən -/ EYE -gən- ) или характеристический вектор — это вектор , направление которого не изменяется при заданном линейном преобразовании . Точнее, собственный вектор , линейного преобразования , масштабируется постоянным множителем , , когда к нему применяется линейное преобразование: . Часто важно знать эти векторы в линейной алгебре. Соответствующее собственное значение , характеристическое значение или характеристический корень — это множитель . ${\displaystyle \mathbf {v} }$ ${\displaystyle T}$ ${\displaystyle \lambda }$ ${\displaystyle T\mathbf {v} =\lambda \mathbf {v} }$ ${\displaystyle \lambda }$

Геометрически векторы — это многомерные величины с величиной и направлением, часто изображаемые в виде стрелок. Линейное преобразование вращает , растягивает или сдвигает векторы, на которые оно действует. Его собственные векторы — это те векторы, которые только растягиваются, без вращения или сдвига. Соответствующее собственное значение — это коэффициент, на который собственный вектор растягивается или сжимается. Если собственное значение отрицательно, направление собственного вектора меняется на противоположное. ^[1]

Собственные векторы и собственные значения линейного преобразования служат для его характеристики, и поэтому они играют важную роль во всех областях, где применяется линейная алгебра, от геологии до квантовой механики . В частности, часто бывает так, что система представлена ​​линейным преобразованием, выходные данные которого подаются в качестве входных данных для того же преобразования ( обратная связь ). В таком приложении наибольшее собственное значение имеет особое значение, поскольку оно управляет долгосрочным поведением системы после многих применений линейного преобразования, а связанный с ним собственный вектор является устойчивым состоянием системы.

Определение

Рассмотрим матрицу A и ненулевой вектор длины Если умножение A на (обозначается как ) просто масштабируется на коэффициент λ , где λ — скаляр , то называется собственным вектором A , а λ — соответствующим собственным значением. Это соотношение можно выразить как: . ^[2] ${\displaystyle n{\times }n}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle n.}$ ${\displaystyle \mathbf {v} }$ ${\displaystyle A\mathbf {v} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle \mathbf {v} }$ ${\displaystyle A\mathbf {v} =\lambda \mathbf {v} }$

Существует прямое соответствие между квадратными матрицами n -на- n и линейными преобразованиями из n -мерного векторного пространства в себя, при условии любого базиса векторного пространства. Следовательно, в конечномерном векторном пространстве эквивалентно определять собственные значения и собственные векторы, используя либо язык матриц , либо язык линейных преобразований. ^{[3] [4]}

В следующем разделе представлена ​​более общая точка зрения, которая охватывает также бесконечномерные векторные пространства .

Обзор

Собственные значения и собственные векторы играют важную роль в анализе линейных преобразований. Префикс eigen- заимствован из немецкого слова eigen ( родственного английскому слову own ) для «собственный», «характеристический», «собственный». ^{[5] [6]} Первоначально используемые для изучения главных осей вращательного движения твердых тел , собственные значения и собственные векторы имеют широкий спектр приложений, например, в анализе устойчивости , анализе вибрации , атомных орбиталях , распознавании лиц и диагонализации матриц .

По сути, собственный вектор v линейного преобразования T — это ненулевой вектор, который при применении к нему T не меняет направления. Применение T к собственному вектору только масштабирует собственный вектор на скалярное значение λ , называемое собственным значением. Это условие можно записать в виде уравнения, называемого уравнением собственного значения или собственным уравнением . В общем случае λ может быть любым скаляром . Например, λ может быть отрицательным, и в этом случае собственный вектор меняет направление как часть масштабирования, или он может быть нулевым или комплексным . $${\displaystyle T(\mathbf {v} )=\lambda \mathbf {v} ,}$$

В этом отображении сдвига красная стрелка меняет направление, а синяя стрелка — нет. Синяя стрелка — собственный вектор этого отображения сдвига, поскольку она не меняет направления, а поскольку ее длина неизменна, ее собственное значение равно 1.

Действительная и симметричная матрица 2×2, представляющая растяжение и сдвиг плоскости. Собственные векторы матрицы (красные линии) — это два специальных направления, так что каждая точка на них будет просто скользить по ним.

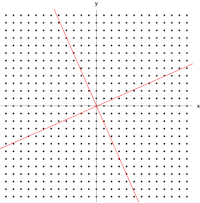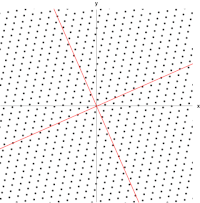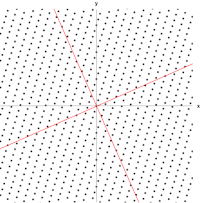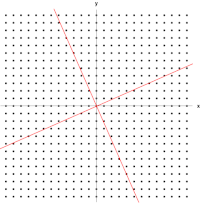
Пример здесь, основанный на Моне Лизе , дает простую иллюстрацию. Каждая точка на картине может быть представлена ​​как вектор, указывающий из центра картины в эту точку. Линейное преобразование в этом примере называется сдвиговым отображением . Точки в верхней половине перемещаются вправо, а точки в нижней половине перемещаются влево, пропорционально тому, насколько далеко они находятся от горизонтальной оси, проходящей через середину картины. Векторы, указывающие на каждую точку на исходном изображении, поэтому наклоняются вправо или влево и становятся длиннее или короче в результате преобразования. Точки вдоль горизонтальной оси вообще не перемещаются при применении этого преобразования. Следовательно, любой вектор, который указывает прямо вправо или влево без вертикальной составляющей, является собственным вектором этого преобразования, потому что отображение не меняет его направления. Более того, все эти собственные векторы имеют собственное значение, равное единице, потому что отображение также не меняет их длину.

Линейные преобразования могут принимать множество различных форм, отображая векторы в различных векторных пространствах, поэтому собственные векторы также могут принимать множество форм. Например, линейное преобразование может быть дифференциальным оператором , например , в этом случае собственные векторы являются функциями, называемыми собственными функциями , которые масштабируются этим дифференциальным оператором, например Альтернативно, линейное преобразование может принимать форму матрицы n на n , в этом случае собственные векторы являются матрицами n на 1. Если линейное преобразование выражено в виде матрицы n на n A , то уравнение собственных значений для линейного преобразования выше можно переписать как умножение матриц , где собственный вектор v является матрицей n на 1. Для матрицы собственные значения и собственные векторы могут быть использованы для разложения матрицы — например, путем ее диагонализации . ${\displaystyle {\tfrac {d}{dx}}}$ $${\displaystyle {\frac {d}{dx}}e^{\lambda x}=\lambda e^{\lambda x}.}$$ $${\displaystyle A\mathbf {v} =\lambda \mathbf {v} ,}$$

Собственные значения и собственные векторы порождают множество тесно связанных математических понятий, и при их наименовании обычно используется префикс «собственный» :

• Набор всех собственных векторов линейного преобразования, каждый из которых связан с соответствующим собственным значением, называется собственной системой этого преобразования. ^{[7] [8]}
• Множество всех собственных векторов T , соответствующих одному и тому же собственному значению, вместе с нулевым вектором называется собственным пространством или характеристическим пространством T , связанным с этим собственным значением. ^[9]
• Если набор собственных векторов T образует базис области определения T , то этот базис называется собственным базисом .

История

Собственные значения часто вводятся в контексте линейной алгебры или теории матриц . Однако исторически они возникли при изучении квадратичных форм и дифференциальных уравнений .

В XVIII веке Леонард Эйлер изучал вращательное движение твердого тела и открыл важность главных осей . ^[a] Жозеф-Луи Лагранж понял, что главные оси являются собственными векторами матрицы инерции. ^[10]

В начале 19 века Огюстен-Луи Коши увидел, как их работа может быть использована для классификации квадратных поверхностей , и обобщил ее на произвольные измерения. ^[11] Коши также ввел термин racine caractéristique (характеристический корень) для того, что теперь называется собственным значением ; его термин сохранился в характеристическом уравнении . ^[b]

Позже Жозеф Фурье использовал работу Лагранжа и Пьера-Симона Лапласа для решения уравнения теплопроводности методом разделения переменных в своей знаменитой книге 1822 года «Аналитическая теория тепла» . ^[12] Шарль-Франсуа Штурм развил идеи Фурье дальше и привлек к ним внимание Коши, который объединил их со своими собственными идеями и пришел к тому факту, что действительные симметричные матрицы имеют действительные собственные значения. ^[11] Это было распространено Шарлем Эрмитом в 1855 году на то, что сейчас называется эрмитовыми матрицами . ^[13]

Примерно в то же время Франческо Бриоски доказал, что собственные значения ортогональных матриц лежат на единичной окружности , ^[11] а Альфред Клебш нашел соответствующий результат для кососимметричных матриц . ^[13] Наконец, Карл Вейерштрасс прояснил важный аспект в теории устойчивости, начатой ​​Лапласом, поняв, что дефектные матрицы могут вызывать нестабильность. ^[11]

В то же время Жозеф Лиувилль изучал проблемы собственных значений, подобные проблемам Штурма; дисциплина, которая выросла из их работы, теперь называется теорией Штурма–Лиувилля . ^[14] Шварц изучал первое собственное значение уравнения Лапласа в общих областях к концу 19-го века, в то время как Пуанкаре изучал уравнение Пуассона несколько лет спустя. ^[15]

В начале 20-го века Давид Гильберт изучал собственные значения интегральных операторов , рассматривая операторы как бесконечные матрицы. ^[16] Он был первым, кто использовал немецкое слово eigen , что означает «собственный», ^[6] для обозначения собственных значений и собственных векторов в 1904 году, ^[c] хотя он, возможно, следовал связанному использованию Германа фон Гельмгольца . Некоторое время стандартным термином в английском языке было «собственное значение», но более характерный термин «собственное значение» является стандартным сегодня. ^[17]

Первый численный алгоритм для вычисления собственных значений и собственных векторов появился в 1929 году, когда Рихард фон Мизес опубликовал степенной метод . Один из самых популярных методов сегодня, алгоритм QR , был предложен независимо Джоном ГФ Фрэнсисом ^[18] и Верой Кублановской ^[19] в 1961 году. ^{[20] [21]}

Собственные значения и собственные векторы матриц

Собственные значения и собственные векторы часто представляются студентам в контексте курсов линейной алгебры, посвященных матрицам. ^{[22] [23]} Кроме того, линейные преобразования в конечномерном векторном пространстве могут быть представлены с помощью матриц, ^{[3] [4],} что особенно распространено в числовых и вычислительных приложениях. ^[24]

Матрица A действует , растягивая вектор x , не меняя его направления, поэтому x является собственным вектором A.

Рассмотрим n -мерные векторы, сформированные как список из n скаляров, например, трехмерные векторы $${\displaystyle \mathbf {x} ={\begin{bmatrix}1\\-3\\4\end{bmatrix}}\quad {\mbox{and}}\quad \mathbf {y} ={\begin{bmatrix}-20\\60\\-80\end{bmatrix}}.}$$

Говорят, что эти векторы являются скалярными кратными друг другу, параллельными или коллинеарными , если существует скаляр λ такой, что $${\displaystyle \mathbf {x} =\lambda \mathbf {y} .}$$

В этом случае, . ${\displaystyle \lambda =-{\frac {1}{20}}}$

Теперь рассмотрим линейное преобразование n -мерных векторов, определяемое матрицей A размером n на n , или где для каждой строки $${\displaystyle A\mathbf {v} =\mathbf {w} ,}$$ $${\displaystyle {\begin{bmatrix}A_{11}&A_{12}&\cdots &A_{1n}\\A_{21}&A_{22}&\cdots &A_{2n}\\\vdots &\vdots &\ddots &\vdots \\A_{n1}&A_{n2}&\cdots &A_{nn}\\\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\\\vdots \\v_{n}\end{bmatrix}}={\begin{bmatrix}w_{1}\\w_{2}\\\vdots \\w_{n}\end{bmatrix}}}$$ $${\displaystyle w_{i}=A_{i1}v_{1}+A_{i2}v_{2}+\cdots +A_{in}v_{n}=\sum _{j=1}^{n}A_{ij}v_{j}.}$$

Если окажется, что v и w являются скалярными множителями, то есть если

тогда v — собственный вектор линейного преобразования A , а масштабный коэффициент λ — собственное значение, соответствующее этому собственному вектору. Уравнение ( 1 ) — это уравнение собственных значений для матрицы A.

Уравнение ( 1 ) можно эквивалентно записать как

где I — единичная матрица размером n на n , а 0 — нулевой вектор.

Собственные значения и характеристический полином

Уравнение ( 2 ) имеет ненулевое решение v тогда и только тогда, когда определитель матрицы ( A − λI ) равен нулю. Поэтому собственные значения A являются значениями λ , которые удовлетворяют уравнению

Используя формулу Лейбница для определителей , левая часть уравнения ( 3 ) является полиномиальной функцией переменной λ , а степень этого полинома равна n , порядку матрицы A. Ее коэффициенты зависят от элементов матрицы A , за исключением того, что ее член степени n всегда равен (−1) ⁿ λ ⁿ . Этот полином называется характеристическим полиномом матрицы A. Уравнение ( 3 ) называется характеристическим уравнением или секулярным уравнением матрицы A.

Основная теорема алгебры подразумевает, что характеристический многочлен матрицы A размером n на n , будучи многочленом степени n , может быть разложен на множители n линейных членов:

где каждое λ _i может быть действительным, но в общем случае является комплексным числом. Числа λ ₁ , λ ₂ , ..., λ _n , которые могут не все иметь различные значения, являются корнями многочлена и являются собственными значениями A .

В качестве краткого примера, который более подробно описан в разделе примеров далее, рассмотрим матрицу $${\displaystyle A={\begin{bmatrix}2&1\\1&2\end{bmatrix}}.}$$

Взяв определитель ( A − λI ) , характеристический многочлен A равен $${\displaystyle \det(A-\lambda I)={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}=3-4\lambda +\lambda ^{2}.}$$

Приравнивая характеристический многочлен к нулю, он имеет корни при λ=1 и λ=3 , которые являются двумя собственными значениями A. Собственные векторы, соответствующие каждому собственному значению, можно найти, решив для компонентов v в уравнении . В этом примере собственные векторы — это любые ненулевые скалярные кратные ${\displaystyle \left(A-\lambda I\right)\mathbf {v} =\mathbf {0} }$ $${\displaystyle \mathbf {v} _{\lambda =1}={\begin{bmatrix}1\\-1\end{bmatrix}},\quad \mathbf {v} _{\lambda =3}={\begin{bmatrix}1\\1\end{bmatrix}}.}$$

Если все элементы матрицы A являются действительными числами, то коэффициенты характеристического многочлена также будут действительными числами, но собственные значения могут по-прежнему иметь ненулевые мнимые части. Элементы соответствующих собственных векторов, следовательно, также могут иметь ненулевые мнимые части. Аналогично, собственные значения могут быть иррациональными числами, даже если все элементы матрицы A являются рациональными числами или даже если они все целые числа. Однако, если все элементы матрицы A являются алгебраическими числами , которые включают рациональные числа, собственные значения также должны быть алгебраическими числами.

Недействительные корни действительного многочлена с действительными коэффициентами можно сгруппировать в пары комплексно сопряженных чисел , а именно, с двумя членами каждой пары, имеющими мнимые части, которые отличаются только знаком, и одинаковую действительную часть. Если степень нечетная, то по теореме о промежуточном значении по крайней мере один из корней является действительным. Следовательно, любая действительная матрица с нечетным порядком имеет по крайней мере одно действительное собственное значение, тогда как действительная матрица с четным порядком может не иметь никаких действительных собственных значений. Собственные векторы, связанные с этими комплексными собственными значениями, также являются комплексными и также появляются в комплексно сопряженных парах.

Спектр матрицы

Спектр матрицы — это список собственных значений, повторяющихся в соответствии с кратностью; в альтернативной записи — множество собственных значений с их кратностями.

Важной величиной, связанной со спектром, является максимальное абсолютное значение любого собственного значения. Это известно как спектральный радиус матрицы.

Алгебраическая кратность

Пусть λ _{i —} собственное значение матрицы A размером n на n . Алгебраическая кратность μ _A ( λ _i ) собственного значения — это его кратность как корня характеристического многочлена, то есть наибольшее целое число k, такое, что ( λ − λ _i ) ^k делит этот многочлен нацело . ^{[9] [25] [26]}

Предположим, что матрица A имеет размерность n и d ≤ n различных собственных значений. В то время как уравнение ( 4 ) разлагает характеристический многочлен матрицы A на произведение n линейных членов с некоторыми потенциально повторяющимися членами, характеристический многочлен также может быть записан как произведение d членов, каждый из которых соответствует отдельному собственному значению и возведен в степень алгебраической кратности, $${\displaystyle \det(A-\lambda I)=(\lambda _{1}-\lambda )^{\mu _{A}(\lambda _{1})}(\lambda _{2}-\lambda )^{\mu _{A}(\lambda _{2})}\cdots (\lambda _{d}-\lambda )^{\mu _{A}(\lambda _{d})}.}$$

Если d = n, то правая часть является произведением n линейных членов, и это то же самое, что и уравнение ( 4 ). Размер алгебраической кратности каждого собственного значения связан с размерностью n как $${\displaystyle {\begin{aligned}1&\leq \mu _{A}(\lambda _{i})\leq n,\\\mu _{A}&=\sum _{i=1}^{d}\mu _{A}\left(\lambda _{i}\right)=n.\end{aligned}}}$$

Если μ _A ( λ _i ) = 1, то λ _i называется простым собственным значением . ^[26] Если μ _A ( λ _i ) равно геометрической кратности λ _i , γ _A ( λ _i ), определенной в следующем разделе, то λ _i называется полупростым собственным значением .

Собственные пространства, геометрическая кратность и собственный базис для матриц

Дано конкретное собственное значение λ матрицы A размером n на n , определим множество E как все векторы v, которые удовлетворяют уравнению ( 2 ), $${\displaystyle E=\left\{\mathbf {v} :\left(A-\lambda I\right)\mathbf {v} =\mathbf {0} \right\}.}$$

С одной стороны, это множество является в точности ядром или нулевым пространством матрицы ( A − λI ). С другой стороны, по определению любой ненулевой вектор, удовлетворяющий этому условию, является собственным вектором A, связанным с λ . Таким образом, множество E является объединением нулевого вектора с множеством всех собственных векторов A , связанных с λ , и E равно нулевому пространству ( A − λI ). E называется собственным пространством или характеристическим пространством A, связанным с λ . ^{[27] [9]} В общем случае λ является комплексным числом, а собственные векторы являются комплексными матрицами размера n на 1. Свойство нулевого пространства состоит в том, что оно является линейным подпространством , поэтому E является линейным подпространством . ${\displaystyle \mathbb {C} ^{n}}$

Поскольку собственное пространство E является линейным подпространством, оно замкнуто относительно сложения. То есть, если два вектора u и v принадлежат множеству E , записанному как u , v ∈ E , то ( u + v ) ∈ E или, что эквивалентно, A ( u + v ) = λ ( u + v ) . Это можно проверить, используя дистрибутивное свойство умножения матриц. Аналогично, поскольку E является линейным подпространством, оно замкнуто относительно скалярного умножения. То есть, если v ∈ E и α является комплексным числом, ( α v ) ∈ E или, что эквивалентно, A ( α v ) = λ ( α v ) . Это можно проверить, заметив, что умножение комплексных матриц на комплексные числа коммутативно . Пока u + v и α v не равны нулю, они также являются собственными векторами A , связанными с λ .

Размерность собственного пространства E, связанного с λ , или, что эквивалентно, максимальное число линейно независимых собственных векторов, связанных с λ , называется геометрической кратностью собственного значения . Поскольку E также является нулевым пространством ( A − λI ), геометрическая кратность λ является размерностью нулевого пространства ( A − λI ), также называемой нулевым значением ( A − λI ), которая относится к размерности и рангу ( A − λI ) как ${\displaystyle \gamma _{A}(\lambda )}$ $${\displaystyle \gamma _{A}(\lambda )=n-\operatorname {rank} (A-\lambda I).}$$

Из-за определения собственных значений и собственных векторов геометрическая кратность собственного значения должна быть не менее единицы, то есть каждое собственное значение имеет не менее одного связанного с ним собственного вектора. Более того, геометрическая кратность собственного значения не может превышать его алгебраическую кратность. Кроме того, напомним, что алгебраическая кратность собственного значения не может превышать n . $${\displaystyle 1\leq \gamma _{A}(\lambda )\leq \mu _{A}(\lambda )\leq n}$$

Чтобы доказать неравенство , рассмотрим, как определение геометрической кратности подразумевает существование ортонормированных собственных векторов , таких что . Поэтому мы можем найти (унитарную) матрицу, первые столбцы которой являются этими собственными векторами, а остальные столбцы могут быть любым ортонормированным набором векторов, ортогональных этим собственным векторам . Тогда имеет полный ранг и, следовательно, обратим. Оценивая , мы получаем матрицу, верхний левый блок которой является диагональной матрицей . Это можно увидеть, оценив то, что левая часть делает с базисными векторами первого столбца. Реорганизуя и добавляя с обеих сторон, мы получаем , поскольку коммутирует с . Другими словами, аналогично , и . Но из определения мы знаем, что содержит множитель , что означает, что алгебраическая кратность должна удовлетворять . ${\displaystyle \gamma _{A}(\lambda )\leq \mu _{A}(\lambda )}$ ${\displaystyle \gamma _{A}(\lambda )}$ ${\displaystyle {\boldsymbol {v}}_{1},\,\ldots ,\,{\boldsymbol {v}}_{\gamma _{A}(\lambda )}}$ ${\displaystyle A{\boldsymbol {v}}_{k}=\lambda {\boldsymbol {v}}_{k}}$ ${\displaystyle V}$ ${\displaystyle \gamma _{A}(\lambda )}$ ${\displaystyle n-\gamma _{A}(\lambda )}$ ${\displaystyle A}$ ${\displaystyle V}$ ${\displaystyle D:=V^{T}AV}$ ${\displaystyle \lambda I_{\gamma _{A}(\lambda )}}$ ${\displaystyle -\xi V}$ ${\displaystyle (A-\xi I)V=V(D-\xi I)}$ ${\displaystyle I}$ ${\displaystyle V}$ ${\displaystyle A-\xi I}$ ${\displaystyle D-\xi I}$ ${\displaystyle \det(A-\xi I)=\det(D-\xi I)}$ ${\displaystyle D}$ ${\displaystyle \det(D-\xi I)}$ ${\displaystyle (\xi -\lambda )^{\gamma _{A}(\lambda )}}$ ${\displaystyle \lambda }$ ${\displaystyle \mu _{A}(\lambda )\geq \gamma _{A}(\lambda )}$

Предположим, что имеет различные собственные значения , где геометрическая кратность равна . Общая геометрическая кратность , является размерностью суммы всех собственных пространств собственных значений , или, что эквивалентно, максимальным числом линейно независимых собственных векторов . Если , то ${\displaystyle A}$ ${\displaystyle d\leq n}$ ${\displaystyle \lambda _{1},\ldots ,\lambda _{d}}$ ${\displaystyle \lambda _{i}}$ ${\displaystyle \gamma _{A}(\lambda _{i})}$ ${\displaystyle A}$ $${\displaystyle {\begin{aligned}\gamma _{A}&=\sum _{i=1}^{d}\gamma _{A}(\lambda _{i}),\\d&\leq \gamma _{A}\leq n,\end{aligned}}}$$ ${\displaystyle A}$ ${\displaystyle A}$ ${\displaystyle \gamma _{A}=n}$

• Прямая сумма собственных подпространств всех собственных значений представляет собой все векторное пространство . ${\displaystyle A}$ ${\displaystyle \mathbb {C} ^{n}}$
• Базис может быть образован из линейно независимых собственных векторов ; такой базис называется собственным базисом ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle n}$ ${\displaystyle A}$
• Любой вектор в можно записать в виде линейной комбинации собственных векторов . ${\displaystyle \mathbb {C} ^{n}}$ ${\displaystyle A}$

Дополнительные свойства собственных значений

Пусть будет произвольной матрицей комплексных чисел с собственными значениями . Каждое собственное значение появляется в этом списке раз, где — алгебраическая кратность собственного значения. Ниже приведены свойства этой матрицы и ее собственных значений: ${\displaystyle A}$ ${\displaystyle n\times n}$ ${\displaystyle \lambda _{1},\ldots ,\lambda _{n}}$ ${\displaystyle \mu _{A}(\lambda _{i})}$ ${\displaystyle \mu _{A}(\lambda _{i})}$

• След , определяемый как сумма его диагональных элементов, также является суммой всех собственных значений, ^{[28] [29] [30} ] ${\displaystyle A}$

  ${\displaystyle \operatorname {tr} (A)=\sum _{i=1}^{n}a_{ii}=\sum _{i=1}^{n}\lambda _{i}=\lambda _{1}+\lambda _{2}+\cdots +\lambda _{n}.}$

• Определитель представляет собой произведение всех его собственных значений, ^{[28] [31] [32]} ${\displaystyle A}$

  ${\displaystyle \det(A)=\prod _{i=1}^{n}\lambda _{i}=\lambda _{1}\lambda _{2}\cdots \lambda _{n}.}$

• Собственные значения -й степени , т.е. собственные значения , для любого положительного целого числа , равны . ${\displaystyle k}$ ${\displaystyle A}$ ${\displaystyle A^{k}}$ ${\displaystyle k}$ ${\displaystyle \lambda _{1}^{k},\ldots ,\lambda _{n}^{k}}$
• Матрица обратима тогда и только тогда , когда каждое собственное значение не равно нулю. ${\displaystyle A}$
• Если обратим, то собственные значения являются и геометрическая кратность каждого собственного значения совпадает. Более того, поскольку характеристический многочлен обратного является обратным многочленом исходного, собственные значения имеют одинаковую алгебраическую кратность. ${\displaystyle A}$ ${\displaystyle A^{-1}}$ ${\textstyle {\frac {1}{\lambda _{1}}},\ldots ,{\frac {1}{\lambda _{n}}}}$
• Если равно своему сопряженному транспонированному , или, что эквивалентно, если является эрмитовым , то каждое собственное значение является действительным. То же самое верно для любой симметричной действительной матрицы. ${\displaystyle A}$ ${\displaystyle A^{*}}$ ${\displaystyle A}$
• Если является не только эрмитовым, но и положительно-определенным , положительно-полуопределенным, отрицательно-определенным или отрицательно-полуопределенным, то каждое собственное значение является положительным, неотрицательным, отрицательным или неположительным соответственно. ${\displaystyle A}$
• Если унитарно , то каждое собственное значение имеет абсолютное значение . ${\displaystyle A}$ ${\displaystyle |\lambda _{i}|=1}$
• Если — матрица и — ее собственные значения, то собственные значения матрицы (где — единичная матрица) равны . Более того, если , то собственные значения равны . В более общем случае для полинома собственные значения матрицы равны . ${\displaystyle A}$ ${\displaystyle n\times n}$ ${\displaystyle \{\lambda _{1},\ldots ,\lambda _{k}\}}$ ${\displaystyle I+A}$ ${\displaystyle I}$ ${\displaystyle \{\lambda _{1}+1,\ldots ,\lambda _{k}+1\}}$ ${\displaystyle \alpha \in \mathbb {C} }$ ${\displaystyle \alpha I+A}$ ${\displaystyle \{\lambda _{1}+\alpha ,\ldots ,\lambda _{k}+\alpha \}}$ ${\displaystyle P}$ ${\displaystyle P(A)}$ ${\displaystyle \{P(\lambda _{1}),\ldots ,P(\lambda _{k})\}}$

Левые и правые собственные векторы

Многие дисциплины традиционно представляют векторы как матрицы с одним столбцом, а не как матрицы с одной строкой. По этой причине слово «собственный вектор» в контексте матриц почти всегда относится к правому собственному вектору , а именно вектору- столбцу , который умножает справа матрицу в определяющем уравнении, уравнении ( 1 ), ${\displaystyle n\times n}$ ${\displaystyle A}$ $${\displaystyle A\mathbf {v} =\lambda \mathbf {v} .}$$

Проблема собственных значений и собственных векторов может быть также определена для векторов- строк , которые оставили матрицу умножения . В этой формулировке определяющее уравнение имеет вид ${\displaystyle A}$ $${\displaystyle \mathbf {u} A=\kappa \mathbf {u} ,}$$

где — скаляр, а — матрица. Любой вектор-строка, удовлетворяющий этому уравнению, называется левым собственным вектором и — его связанным собственным значением. Транспонируем это уравнение, ${\displaystyle \kappa }$ ${\displaystyle u}$ ${\displaystyle 1\times n}$ ${\displaystyle u}$ ${\displaystyle A}$ ${\displaystyle \kappa }$ $${\displaystyle A^{\textsf {T}}\mathbf {u} ^{\textsf {T}}=\kappa \mathbf {u} ^{\textsf {T}}.}$$

Сравнивая это уравнение с уравнением ( 1 ), сразу следует, что левый собственный вектор равен транспонированному правому собственному вектору с тем же собственным значением. Более того, поскольку характеристический многочлен равен характеристическому многочлену , левые и правые собственные векторы связаны с теми же собственными значениями. ${\displaystyle A}$ ${\displaystyle A^{\textsf {T}}}$ ${\displaystyle A^{\textsf {T}}}$ ${\displaystyle A}$ ${\displaystyle A}$

Диагонализация и собственное разложение

Предположим, что собственные векторы матрицы A образуют базис, или, что эквивалентно, A имеет n линейно независимых собственных векторов v ₁ , v ₂ , ..., v _n с соответствующими собственными значениями λ ₁ , λ ₂ , ..., λ _n . Собственные значения не обязательно должны быть различными. Определим квадратную матрицу Q , столбцы которой являются n линейно независимыми собственными векторами матрицы A ,

${\displaystyle Q={\begin{bmatrix}\mathbf {v} _{1}&\mathbf {v} _{2}&\cdots &\mathbf {v} _{n}\end{bmatrix}}.}$

Поскольку каждый столбец Q является собственным вектором A , правое умножение A на Q масштабирует каждый столбец Q на соответствующее ему собственное значение,

${\displaystyle AQ={\begin{bmatrix}\lambda _{1}\mathbf {v} _{1}&\lambda _{2}\mathbf {v} _{2}&\cdots &\lambda _{n}\mathbf {v} _{n}\end{bmatrix}}.}$

Имея это в виду, определим диагональную матрицу Λ, где каждый диагональный элемент Λ _ii является собственным значением, связанным с i -м столбцом матрицы Q. Тогда

${\displaystyle AQ=Q\Lambda .}$

Поскольку столбцы Q линейно независимы, Q обратим. Умножая обе части уравнения справа на Q ⁻¹ ,

${\displaystyle A=Q\Lambda Q^{-1},}$

или вместо этого умножив обе стороны на Q ⁻¹ ,

${\displaystyle Q^{-1}AQ=\Lambda .}$

Следовательно, A можно разложить на матрицу, составленную из ее собственных векторов, диагональную матрицу с собственными значениями вдоль диагонали и матрицу, обратную матрице собственных векторов. Это называется собственным разложением и является преобразованием подобия . Такая матрица A называется подобной диагональной матрице Λ или диагонализируемой . Матрица Q является матрицей изменения базиса преобразования подобия. По сути, матрицы A и Λ представляют одно и то же линейное преобразование, выраженное в двух разных базисах. Собственные векторы используются в качестве базиса при представлении линейного преобразования как Λ.

Наоборот, предположим, что матрица A диагонализируема. Пусть P — невырожденная квадратная матрица, такая что P ⁻¹ AP — некоторая диагональная матрица D . Умножая обе на P слева , получаем AP = PD . Таким образом, каждый столбец P должен быть собственным вектором A , собственное значение которого является соответствующим диагональным элементом D . Поскольку столбцы P должны быть линейно независимыми для того, чтобы P была обратимой, существует n линейно независимых собственных векторов A . Из этого следует, что собственные векторы A образуют базис тогда и только тогда, когда A диагонализируема.

Матрица, которая не диагонализируется, называется дефектной . Для дефектных матриц понятие собственных векторов обобщается до обобщенных собственных векторов , а диагональная матрица собственных значений обобщается до жордановой нормальной формы . Над алгебраически замкнутым полем любая матрица A имеет жорданову нормальную форму и, следовательно, допускает базис обобщенных собственных векторов и разложение в обобщенные собственные пространства .

Вариационная характеристика

В эрмитовом случае собственным значениям можно дать вариационную характеристику. Наибольшее собственное значение является максимальным значением квадратичной формы . Значение , которое реализует этот максимум, является собственным вектором. ${\displaystyle H}$ ${\displaystyle \mathbf {x} ^{\textsf {T}}H\mathbf {x} /\mathbf {x} ^{\textsf {T}}\mathbf {x} }$ ${\displaystyle \mathbf {x} }$

Примеры матриц

Пример двумерной матрицы

Матрица преобразования A = сохраняет направление фиолетовых векторов, параллельных v _{λ =1} = [1 −1] ^T , и синих векторов, параллельных v _{λ =3} = [1 1] ^T . Красные векторы не параллельны ни одному из собственных векторов, поэтому их направления изменяются в результате преобразования. Длины фиолетовых векторов не изменяются после преобразования (из-за их собственного значения 1), в то время как синие векторы в три раза длиннее исходных (из-за их собственного значения 3). См. также: Расширенная версия, показывающая все четыре квадранта . ${\displaystyle \left[{\begin{smallmatrix}2&1\\1&2\end{smallmatrix}}\right]}$

Рассмотрим матрицу $${\displaystyle A={\begin{bmatrix}2&1\\1&2\end{bmatrix}}.}$$

Рисунок справа показывает влияние этого преобразования на координаты точек на плоскости. Собственные векторы v этого преобразования удовлетворяют уравнению ( 1 ), а значения λ , для которых определитель матрицы ( A  −  λI ) равен нулю, являются собственными значениями.

Используя определитель, находим характеристический многочлен A , $${\displaystyle {\begin{aligned}\det(A-\lambda I)&=\left|{\begin{bmatrix}2&1\\1&2\end{bmatrix}}-\lambda {\begin{bmatrix}1&0\\0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &1\\1&2-\lambda \end{vmatrix}}\\[6pt]&=3-4\lambda +\lambda ^{2}\\[6pt]&=(\lambda -3)(\lambda -1).\end{aligned}}}$$

Приравняв характеристический многочлен к нулю, получим корни при λ =1 и λ =3 , которые являются двумя собственными значениями A.

При λ =1 уравнение ( 2 ) принимает вид: $${\displaystyle (A-I)\mathbf {v} _{\lambda =1}={\begin{bmatrix}1&1\\1&1\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}}$$ $${\displaystyle 1v_{1}+1v_{2}=0}$$

Любой ненулевой вектор с v ₁ = − v ₂ решает это уравнение. Следовательно, является собственным вектором A, соответствующим λ = 1, как и любой скалярный кратный этого вектора. $${\displaystyle \mathbf {v} _{\lambda =1}={\begin{bmatrix}v_{1}\\-v_{1}\end{bmatrix}}={\begin{bmatrix}1\\-1\end{bmatrix}}}$$

При λ =3 уравнение ( 2 ) принимает вид $${\displaystyle {\begin{aligned}(A-3I)\mathbf {v} _{\lambda =3}&={\begin{bmatrix}-1&1\\1&-1\end{bmatrix}}{\begin{bmatrix}v_{1}\\v_{2}\end{bmatrix}}={\begin{bmatrix}0\\0\end{bmatrix}}\\-1v_{1}+1v_{2}&=0;\\1v_{1}-1v_{2}&=0\end{aligned}}}$$

Любой ненулевой вектор с v ₁ = v ₂ решает это уравнение. Следовательно, $${\displaystyle \mathbf {v} _{\lambda =3}={\begin{bmatrix}v_{1}\\v_{1}\end{bmatrix}}={\begin{bmatrix}1\\1\end{bmatrix}}}$$

является собственным вектором A, соответствующим λ = 3, как и любое скалярное кратное этого вектора.

Таким образом, векторы v _{λ =1} и v _{λ =3} являются собственными векторами матрицы A , связанными с собственными значениями λ =1 и λ =3 соответственно.

Пример трехмерной матрицы

Рассмотрим матрицу $${\displaystyle A={\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}.}$$

Характеристический многочлен A равен $${\displaystyle {\begin{aligned}\det(A-\lambda I)&=\left|{\begin{bmatrix}2&0&0\\0&3&4\\0&4&9\end{bmatrix}}-\lambda {\begin{bmatrix}1&0&0\\0&1&0\\0&0&1\end{bmatrix}}\right|={\begin{vmatrix}2-\lambda &0&0\\0&3-\lambda &4\\0&4&9-\lambda \end{vmatrix}},\\[6pt]&=(2-\lambda ){\bigl [}(3-\lambda )(9-\lambda )-16{\bigr ]}=-\lambda ^{3}+14\lambda ^{2}-35\lambda +22.\end{aligned}}}$$

Корни характеристического многочлена — 2, 1 и 11, которые являются единственными тремя собственными значениями A. Эти собственные значения соответствуют собственным векторам , , и , или любым их ненулевым кратным. ${\displaystyle {\begin{bmatrix}1&0&0\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle {\begin{bmatrix}0&-2&1\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle {\begin{bmatrix}0&1&2\end{bmatrix}}^{\textsf {T}}}$

Пример трехмерной матрицы с комплексными собственными значениями

Рассмотрим матрицу циклической перестановки $${\displaystyle A={\begin{bmatrix}0&1&0\\0&0&1\\1&0&0\end{bmatrix}}.}$$

Эта матрица сдвигает координаты вектора на одну позицию вверх и перемещает первую координату вниз. Ее характеристический полином равен 1 −  λ ³ , корни которого равны , где — мнимая единица с . $${\displaystyle {\begin{aligned}\lambda _{1}&=1\\\lambda _{2}&=-{\frac {1}{2}}+i{\frac {\sqrt {3}}{2}}\\\lambda _{3}&=\lambda _{2}^{*}=-{\frac {1}{2}}-i{\frac {\sqrt {3}}{2}}\end{aligned}}}$$ ${\displaystyle i}$ ${\displaystyle i^{2}=-1}$

Для действительного собственного значения λ ₁ = 1 любой вектор с тремя равными ненулевыми элементами является собственным вектором. Например, $${\displaystyle A{\begin{bmatrix}5\\5\\5\end{bmatrix}}={\begin{bmatrix}5\\5\\5\end{bmatrix}}=1\cdot {\begin{bmatrix}5\\5\\5\end{bmatrix}}.}$$

Для комплексно-сопряженной пары мнимых собственных значений, $${\displaystyle \lambda _{2}\lambda _{3}=1,\quad \lambda _{2}^{2}=\lambda _{3},\quad \lambda _{3}^{2}=\lambda _{2}.}$$

Тогда и $${\displaystyle A{\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}}={\begin{bmatrix}\lambda _{2}\\\lambda _{3}\\1\end{bmatrix}}=\lambda _{2}\cdot {\begin{bmatrix}1\\\lambda _{2}\\\lambda _{3}\end{bmatrix}},}$$ $${\displaystyle A{\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}={\begin{bmatrix}\lambda _{3}\\\lambda _{2}\\1\end{bmatrix}}=\lambda _{3}\cdot {\begin{bmatrix}1\\\lambda _{3}\\\lambda _{2}\end{bmatrix}}.}$$

Следовательно, два других собственных вектора A являются комплексными и имеют собственные значения λ ₂ и λ ₃ соответственно. Два комплексных собственных вектора также появляются в комплексно-сопряженной паре, ${\displaystyle \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}1&\lambda _{2}&\lambda _{3}\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}1&\lambda _{3}&\lambda _{2}\end{bmatrix}}^{\textsf {T}}}$ $${\displaystyle \mathbf {v} _{\lambda _{2}}=\mathbf {v} _{\lambda _{3}}^{*}.}$$

Пример диагональной матрицы

Матрицы с элементами только по главной диагонали называются диагональными матрицами . Собственные значения диагональной матрицы — это сами диагональные элементы. Рассмотрим матрицу $${\displaystyle A={\begin{bmatrix}1&0&0\\0&2&0\\0&0&3\end{bmatrix}}.}$$

Характеристический многочлен A равен $${\displaystyle \det(A-\lambda I)=(1-\lambda )(2-\lambda )(3-\lambda ),}$$

который имеет корни λ ₁ = 1 , λ ₂ = 2 и λ ₃ = 3. Эти корни являются диагональными элементами , а также собственными значениями  A.

Каждый диагональный элемент соответствует собственному вектору, единственный ненулевой компонент которого находится в той же строке, что и этот диагональный элемент. В примере собственные значения соответствуют собственным векторам, $${\displaystyle \mathbf {v} _{\lambda _{1}}={\begin{bmatrix}1\\0\\0\end{bmatrix}},\quad \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}0\\1\\0\end{bmatrix}},\quad \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}0\\0\\1\end{bmatrix}},}$$

соответственно, а также скалярные кратные этих векторов.

Пример треугольной матрицы

Матрица, элементы которой выше главной диагонали все равны нулю, называется нижней треугольной матрицей , а матрица, элементы которой ниже главной диагонали все равны нулю, называется верхней треугольной матрицей . Как и в случае с диагональными матрицами, собственные значения треугольных матриц являются элементами главной диагонали.

Рассмотрим нижнюю треугольную матрицу, $${\displaystyle A={\begin{bmatrix}1&0&0\\1&2&0\\2&3&3\end{bmatrix}}.}$$

Характеристический многочлен A равен $${\displaystyle \det(A-\lambda I)=(1-\lambda )(2-\lambda )(3-\lambda ),}$$

который имеет корни λ ₁ = 1 , λ ₂ = 2 и λ ₃ = 3. Эти корни являются диагональными элементами , а также собственными значениями  A.

Эти собственные значения соответствуют собственным векторам, $${\displaystyle \mathbf {v} _{\lambda _{1}}={\begin{bmatrix}1\\-1\\{\frac {1}{2}}\end{bmatrix}},\quad \mathbf {v} _{\lambda _{2}}={\begin{bmatrix}0\\1\\-3\end{bmatrix}},\quad \mathbf {v} _{\lambda _{3}}={\begin{bmatrix}0\\0\\1\end{bmatrix}},}$$

соответственно, а также скалярные кратные этих векторов.

Пример матрицы с повторяющимися собственными значениями

Как и в предыдущем примере, нижняя треугольная матрица имеет характеристический многочлен, являющийся произведением ее диагональных элементов, $${\displaystyle A={\begin{bmatrix}2&0&0&0\\1&2&0&0\\0&1&3&0\\0&0&1&3\end{bmatrix}},}$$ $${\displaystyle \det(A-\lambda I)={\begin{vmatrix}2-\lambda &0&0&0\\1&2-\lambda &0&0\\0&1&3-\lambda &0\\0&0&1&3-\lambda \end{vmatrix}}=(2-\lambda )^{2}(3-\lambda )^{2}.}$$

Корни этого многочлена, а значит и собственные значения, равны 2 и 3. Алгебраическая кратность каждого собственного значения равна 2; другими словами, они оба являются двойными корнями. Сумма алгебраических кратностей всех различных собственных значений равна μ _A = 4 = n , порядок характеристического многочлена и размерность A .

С другой стороны, геометрическая кратность собственного значения 2 равна только 1, поскольку его собственное пространство охватывается всего одним вектором и, следовательно, является одномерным. Аналогично, геометрическая кратность собственного значения 3 равна 1, поскольку его собственное пространство охватывается всего одним вектором . Общая геометрическая кратность γ _A равна 2, что является наименьшим возможным значением для матрицы с двумя различными собственными значениями. Геометрические кратности определяются в следующем разделе. ${\displaystyle {\begin{bmatrix}0&1&-1&1\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle {\begin{bmatrix}0&0&0&1\end{bmatrix}}^{\textsf {T}}}$

Тождество собственного вектора и собственного значения

Для эрмитовой матрицы квадрат нормы j -го компонента нормализованного собственного вектора можно вычислить, используя только собственные значения матрицы и собственные значения соответствующей младшей матрицы , где — подматрица, образованная путем удаления j -й строки и столбца из исходной матрицы. ^{[33] [34] [35]} Это тождество также распространяется на диагонализуемые матрицы и многократно переоткрывалось в литературе. ^{[34] [36]} $${\displaystyle |v_{i,j}|^{2}={\frac {\prod _{k}{(\lambda _{i}-\lambda _{k}(M_{j}))}}{\prod _{k\neq i}{(\lambda _{i}-\lambda _{k})}}},}$$ ${\textstyle M_{j}}$

Собственные значения и собственные функции дифференциальных операторов

Определения собственных значений и собственных векторов линейного преобразования T остаются в силе, даже если базовое векторное пространство является бесконечномерным гильбертовым или банаховым пространством . Широко используемый класс линейных преобразований, действующих на бесконечномерных пространствах, — это дифференциальные операторы на функциональных пространствах . Пусть D — линейный дифференциальный оператор на пространстве C ^∞ бесконечно дифференцируемых действительных функций действительного аргумента t . Уравнение собственных значений для D — это дифференциальное уравнение $${\displaystyle Df(t)=\lambda f(t)}$$

Функции, удовлетворяющие этому уравнению, являются собственными векторами D и обычно называются собственными функциями .

Пример оператора производной

Рассмотрим производный оператор с уравнением на собственные значения ${\displaystyle {\tfrac {d}{dt}}}$ $${\displaystyle {\frac {d}{dt}}f(t)=\lambda f(t).}$$

Это дифференциальное уравнение можно решить, умножив обе части на dt / f ( t ) и проинтегрировав . Его решение, экспоненциальная функция, является собственной функцией оператора производной. В этом случае собственная функция сама является функцией своего соответствующего собственного значения. В частности, при λ = 0 собственная функция f ( t ) является константой. $${\displaystyle f(t)=f(0)e^{\lambda t},}$$

В основной статье о собственных функциях приведены и другие примеры.

Общее определение

Понятие собственных значений и собственных векторов естественным образом распространяется на произвольные линейные преобразования в произвольных векторных пространствах. Пусть V — любое векторное пространство над некоторым полем K скаляров , а T — линейное преобразование, отображающее V в V , $${\displaystyle T:V\to V.}$$

Мы говорим, что ненулевой вектор v ∈ V является собственным вектором T тогда и только тогда, когда существует скаляр λ ∈ K такой, что

Это уравнение называется уравнением собственных значений для T , а скаляр λ является собственным значением T, соответствующим собственному вектору v . T ( v ) является результатом применения преобразования T к вектору v , тогда как λ v является произведением скаляра λ на v . ^{[37] [38]}

Собственные пространства, геометрическая кратность и собственный базис

При заданном собственном значении λ рассмотрим множество $${\displaystyle E=\left\{\mathbf {v} :T(\mathbf {v} )=\lambda \mathbf {v} \right\},}$$

который является объединением нулевого вектора с множеством всех собственных векторов, связанных с  λ . E называется собственным пространством или характеристическим пространством T, связанным с  λ . ^[39]

По определению линейного преобразования, $${\displaystyle {\begin{aligned}T(\mathbf {x} +\mathbf {y} )&=T(\mathbf {x} )+T(\mathbf {y} ),\\T(\alpha \mathbf {x} )&=\alpha T(\mathbf {x} ),\end{aligned}}}$$

для x ,  y  ∈ V и α  ∈ K. Следовательно, если u и v являются собственными векторами T , связанными с собственным значением λ , а именно u ,  v  ∈ E , то $${\displaystyle {\begin{aligned}T(\mathbf {u} +\mathbf {v} )&=\lambda (\mathbf {u} +\mathbf {v} ),\\T(\alpha \mathbf {v} )&=\lambda (\alpha \mathbf {v} ).\end{aligned}}}$$

Итак, и u + v, и α v являются либо нулями, либо собственными векторами T , связанными с λ , а именно u + v , α v ∈ E , и E замкнуто относительно сложения и скалярного умножения. Собственное пространство E, связанное с λ, является, таким образом, линейным подпространством V. ^[40] Если это подпространство имеет размерность 1, его иногда называют собственной линией . ^[41]

Геометрическая кратность γ _T ( λ ) собственного значения λ — это размерность собственного пространства, связанного с λ , т. е. максимальное число линейно независимых собственных векторов, связанных с этим собственным значением. ^{[9] [26] [42]} По определению собственных значений и собственных векторов, γ _T ( λ ) ≥ 1, поскольку каждое собственное значение имеет по крайней мере один собственный вектор.

Собственные пространства T всегда образуют прямую сумму . Как следствие, собственные векторы различных собственных значений всегда линейно независимы. Следовательно, сумма размерностей собственных пространств не может превышать размерность n векторного пространства, на котором действует T , и не может быть более n различных собственных значений. ^[d]

Любое подпространство, охватываемое собственными векторами T, является инвариантным подпространством T , и ограничение T на такое подпространство диагонализуемо. Более того, если все векторное пространство V может быть охватываемо собственными векторами T , или, что эквивалентно, если прямая сумма собственных пространств, связанных со всеми собственными значениями T, является всем векторным пространством V , то базис V , называемый собственным базисом, может быть образован из линейно независимых собственных векторов T. Когда T допускает собственный базис, T диагонализуемо.

Спектральная теория

Если λ является собственным значением T , то оператор ( T − λI ) не является взаимно-однозначным , и, следовательно, его обратный оператор ( T − λI ) ⁻¹ не существует. Обратное верно для конечномерных векторных пространств, но не для бесконечномерных векторных пространств. В общем случае оператор ( T − λI ) может не иметь обратного оператора, даже если λ не является собственным значением.

По этой причине в функциональном анализе собственные значения могут быть обобщены на спектр линейного оператора T как множество всех скаляров λ, для которых оператор ( T − λI ) не имеет ограниченного обратного. Спектр оператора всегда содержит все его собственные значения, но не ограничивается ими.

Ассоциативные алгебры и теория представлений

Можно обобщить алгебраический объект, действующий на векторное пространство, заменив один оператор, действующий на векторное пространство, представлением алгебры – ассоциативной алгеброй, действующей на модуль . Изучение таких действий является областью теории представлений .

Представление теории веса является аналогом собственных значений, в то время как весовые векторы и весовые пространства являются аналогами собственных векторов и собственных пространств соответственно.

Собственный пучок Гекке является тензорным кратным самого себя и рассматривается в соответствии Ленглендса .

Динамические уравнения

Простейшие разностные уравнения имеют вид

${\displaystyle x_{t}=a_{1}x_{t-1}+a_{2}x_{t-2}+\cdots +a_{k}x_{t-k}.}$

Решение этого уравнения относительно x относительно t находится с помощью его характеристического уравнения

${\displaystyle \lambda ^{k}-a_{1}\lambda ^{k-1}-a_{2}\lambda ^{k-2}-\cdots -a_{k-1}\lambda -a_{k}=0,}$

которые можно найти, сложив в матричную форму набор уравнений, состоящий из вышеприведенного дифференциального уравнения и k  – 1 уравнений, дающих k -мерную систему первого порядка в сложенном векторе переменных в терминах его однократно запаздывающего значения, и взяв характеристическое уравнение матрицы этой системы. Это уравнение дает k характеристических корней для использования в уравнении решения ${\displaystyle x_{t-1}=x_{t-1},\ \dots ,\ x_{t-k+1}=x_{t-k+1},}$ ${\displaystyle {\begin{bmatrix}x_{t}&\cdots &x_{t-k+1}\end{bmatrix}}}$ ${\displaystyle \lambda _{1},\,\ldots ,\,\lambda _{k},}$

${\displaystyle x_{t}=c_{1}\lambda _{1}^{t}+\cdots +c_{k}\lambda _{k}^{t}.}$

Аналогичная процедура используется для решения дифференциального уравнения вида

${\displaystyle {\frac {d^{k}x}{dt^{k}}}+a_{k-1}{\frac {d^{k-1}x}{dt^{k-1}}}+\cdots +a_{1}{\frac {dx}{dt}}+a_{0}x=0.}$

Расчет

Вычисление собственных значений и собственных векторов — это тема, где теория, представленная в учебниках элементарной линейной алгебры, часто очень далека от практики.

Классический метод

Классический метод заключается в том, чтобы сначала найти собственные значения, а затем вычислить собственные векторы для каждого собственного значения. Он в нескольких отношениях плохо подходит для неточной арифметики, такой как числа с плавающей точкой .

Собственные значения

Собственные значения матрицы можно определить, найдя корни характеристического полинома. Это легко для матриц, но сложность быстро возрастает с размером матрицы. ${\displaystyle A}$ ${\displaystyle 2\times 2}$

Теоретически коэффициенты характеристического многочлена могут быть вычислены точно, поскольку они являются суммами произведений элементов матрицы; и существуют алгоритмы, которые могут найти все корни многочлена произвольной степени с любой требуемой точностью . ^[43] Однако этот подход нежизнеспособен на практике, поскольку коэффициенты будут загрязнены неизбежными ошибками округления , а корни многочлена могут быть чрезвычайно чувствительной функцией коэффициентов (как показано на примере многочлена Уилкинсона ). ^[43] Даже для матриц, элементы которых являются целыми числами, вычисление становится нетривиальным, поскольку суммы очень длинные; постоянный член является определителем , который для матрицы является суммой различных произведений. ^[e] ${\displaystyle n\times n}$ ${\displaystyle n!}$

Явные алгебраические формулы для корней многочлена существуют только если степень равна 4 или меньше. Согласно теореме Абеля–Руффини не существует общей, явной и точной алгебраической формулы для корней многочлена степени 5 или больше. (Общность имеет значение, поскольку любой многочлен степени является характеристическим многочленом некоторой сопутствующей матрицы порядка .) Поэтому для матриц порядка 5 или больше собственные значения и собственные векторы не могут быть получены явной алгебраической формулой и поэтому должны вычисляться приближенными численными методами . Даже точная формула для корней многочлена степени 3 численно непрактична. ${\displaystyle n}$ ${\displaystyle n}$ ${\displaystyle n}$

Собственные векторы

Как только (точное) значение собственного значения известно, соответствующие собственные векторы могут быть найдены путем нахождения ненулевых решений уравнения собственных значений, которое становится системой линейных уравнений с известными коэффициентами. Например, как только известно, что 6 является собственным значением матрицы $${\displaystyle A={\begin{bmatrix}4&1\\6&3\end{bmatrix}}}$$

мы можем найти его собственные векторы, решив уравнение , то есть ${\displaystyle Av=6v}$ $${\displaystyle {\begin{bmatrix}4&1\\6&3\end{bmatrix}}{\begin{bmatrix}x\\y\end{bmatrix}}=6\cdot {\begin{bmatrix}x\\y\end{bmatrix}}}$$

Это матричное уравнение эквивалентно двум линейным уравнениям , то есть $${\displaystyle \left\{{\begin{aligned}4x+y&=6x\\6x+3y&=6y\end{aligned}}\right.}$$          ${\displaystyle \left\{{\begin{aligned}-2x+y&=0\\6x-3y&=0\end{aligned}}\right.}$

Оба уравнения сводятся к одному линейному уравнению . Следовательно, любой вектор вида , для любого ненулевого действительного числа , является собственным вектором с собственным значением . ${\displaystyle y=2x}$ ${\displaystyle {\begin{bmatrix}a&2a\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle a}$ ${\displaystyle A}$ ${\displaystyle \lambda =6}$

Матрица выше имеет еще одно собственное значение . Аналогичное вычисление показывает, что соответствующие собственные векторы являются ненулевыми решениями , то есть любым вектором вида , для любого ненулевого действительного числа . ${\displaystyle A}$ ${\displaystyle \lambda =1}$ ${\displaystyle 3x+y=0}$ ${\displaystyle {\begin{bmatrix}b&-3b\end{bmatrix}}^{\textsf {T}}}$ ${\displaystyle b}$

Простые итерационные методы

Обратный подход, сначала поиск собственных векторов, а затем определение каждого собственного значения из его собственного вектора, оказывается гораздо более податливым для компьютеров. Самый простой алгоритм здесь состоит в выборе произвольного начального вектора и последующем многократном умножении его на матрицу (опционально нормализуя вектор, чтобы сохранить его элементы разумного размера); это заставляет вектор сходиться к собственному вектору. Вариация заключается в том, чтобы вместо этого умножить вектор на ; это заставляет его сходиться к собственному вектору собственного значения, ближайшего к . ${\displaystyle (A-\mu I)^{-1}}$ ${\displaystyle \mu \in \mathbb {C} }$

Если является (хорошим приближением) собственным вектором , то соответствующее собственное значение можно вычислить как ${\displaystyle \mathbf {v} }$ ${\displaystyle A}$

${\displaystyle \lambda ={\frac {\mathbf {v} ^{*}A\mathbf {v} }{\mathbf {v} ^{*}\mathbf {v} }}}$

где обозначает сопряженное транспонирование . ${\displaystyle \mathbf {v} ^{*}}$ ${\displaystyle \mathbf {v} }$

Современные методы

Эффективные и точные методы вычисления собственных значений и собственных векторов произвольных матриц не были известны до тех пор, пока в 1961 году не был разработан алгоритм QR . ^[43] Объединение преобразования Хаусхолдера с LU-разложением приводит к алгоритму с лучшей сходимостью, чем у алгоритма QR. ^{[ требуется ссылка ]} Для больших эрмитовых разреженных матриц алгоритм Ланцоша является одним из примеров эффективного итеративного метода вычисления собственных значений и собственных векторов, среди нескольких других возможностей. ^[43]

Большинство численных методов, вычисляющих собственные значения матрицы, также определяют набор соответствующих собственных векторов как побочный продукт вычисления, хотя иногда разработчики решают отбросить информацию о собственных векторах, как только она больше не нужна.

Приложения

Геометрические преобразования

Собственные векторы и собственные значения могут быть полезны для понимания линейных преобразований геометрических фигур. В следующей таблице представлены некоторые примеры преобразований на плоскости вместе с их матрицами 2×2, собственными значениями и собственными векторами.

Характеристическое уравнение для поворота — это квадратное уравнение с дискриминантом , которое является отрицательным числом, когда θ не является целым кратным 180°. Поэтому, за исключением этих особых случаев, два собственных значения являются комплексными числами, ; и все собственные векторы имеют недействительные элементы. Действительно, за исключением этих особых случаев, поворот изменяет направление каждого ненулевого вектора в плоскости. ${\displaystyle D=-4(\sin \theta )^{2}}$ ${\displaystyle \cos \theta \pm i\sin \theta }$

A linear transformation that takes a square to a rectangle of the same area (a squeeze mapping) has reciprocal eigenvalues.

Principal component analysis

PCA of the multivariate Gaussian distribution centered at ${\displaystyle (1,3)}$ with a standard deviation of 3 in roughly the ${\displaystyle (0.878,0.478)}$ direction and of 1 in the orthogonal direction. The vectors shown are unit eigenvectors of the (symmetric, positive-semidefinite) covariance matrix scaled by the square root of the corresponding eigenvalue. Just as in the one-dimensional case, the square root is taken because the standard deviation is more readily visualized than the variance.

The eigendecomposition of a symmetric positive semidefinite (PSD) matrix yields an orthogonal basis of eigenvectors, each of which has a nonnegative eigenvalue. The orthogonal decomposition of a PSD matrix is used in multivariate analysis, where the sample covariance matrices are PSD. This orthogonal decomposition is called principal component analysis (PCA) in statistics. PCA studies linear relations among variables. PCA is performed on the covariance matrix or the correlation matrix (in which each variable is scaled to have its sample variance equal to one). For the covariance or correlation matrix, the eigenvectors correspond to principal components and the eigenvalues to the variance explained by the principal components. Principal component analysis of the correlation matrix provides an orthogonal basis for the space of the observed data: In this basis, the largest eigenvalues correspond to the principal components that are associated with most of the covariability among a number of observed data.

Principal component analysis is used as a means of dimensionality reduction in the study of large data sets, such as those encountered in bioinformatics. In Q methodology, the eigenvalues of the correlation matrix determine the Q-methodologist's judgment of practical significance (which differs from the statistical significance of hypothesis testing; cf. criteria for determining the number of factors). More generally, principal component analysis can be used as a method of factor analysis in structural equation modeling.

Graphs

In spectral graph theory, an eigenvalue of a graph is defined as an eigenvalue of the graph's adjacency matrix ${\displaystyle A}$, or (increasingly) of the graph's Laplacian matrix due to its discrete Laplace operator, which is either ${\displaystyle D-A}$ (sometimes called the combinatorial Laplacian) or ${\displaystyle I-D^{-1/2}AD^{-1/2}}$ (sometimes called the normalized Laplacian), where ${\displaystyle D}$ is a diagonal matrix with ${\displaystyle D_{ii}}$ equal to the degree of vertex ${\displaystyle v_{i}}$, and in ${\displaystyle D^{-1/2}}$, the ${\displaystyle i}$th diagonal entry is ${\textstyle 1/{\sqrt {\deg(v_{i})}}}$. The ${\displaystyle k}$th principal eigenvector of a graph is defined as either the eigenvector corresponding to the ${\displaystyle k}$th largest or ${\displaystyle k}$th smallest eigenvalue of the Laplacian. The first principal eigenvector of the graph is also referred to merely as the principal eigenvector.

The principal eigenvector is used to measure the centrality of its vertices. An example is Google's PageRank algorithm. The principal eigenvector of a modified adjacency matrix of the World Wide Web graph gives the page ranks as its components. This vector corresponds to the stationary distribution of the Markov chain represented by the row-normalized adjacency matrix; however, the adjacency matrix must first be modified to ensure a stationary distribution exists. The second smallest eigenvector can be used to partition the graph into clusters, via spectral clustering. Other methods are also available for clustering.

Markov chains

A Markov chain is represented by a matrix whose entries are the transition probabilities between states of a system. In particular the entries are non-negative, and every row of the matrix sums to one, being the sum of probabilities of transitions from one state to some other state of the system. The Perron–Frobenius theorem gives sufficient conditions for a Markov chain to have a unique dominant eigenvalue, which governs the convergence of the system to a steady state.

Vibration analysis

Mode shape of a tuning fork at eigenfrequency 440.09 Hz

Eigenvalue problems occur naturally in the vibration analysis of mechanical structures with many degrees of freedom. The eigenvalues are the natural frequencies (or eigenfrequencies) of vibration, and the eigenvectors are the shapes of these vibrational modes. In particular, undamped vibration is governed by $${\displaystyle m{\ddot {x}}+kx=0}$$or $${\displaystyle m{\ddot {x}}=-kx}$$

That is, acceleration is proportional to position (i.e., we expect ${\displaystyle x}$ to be sinusoidal in time).

In ${\displaystyle n}$ dimensions, ${\displaystyle m}$ becomes a mass matrix and ${\displaystyle k}$ a stiffness matrix. Admissible solutions are then a linear combination of solutions to the generalized eigenvalue problem $${\displaystyle kx=\omega ^{2}mx}$$where ${\displaystyle \omega ^{2}}$ is the eigenvalue and ${\displaystyle \omega }$ is the (imaginary) angular frequency. The principal vibration modes are different from the principal compliance modes, which are the eigenvectors of ${\displaystyle k}$ alone. Furthermore, damped vibration, governed by $${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=0}$$leads to a so-called quadratic eigenvalue problem, $${\displaystyle \left(\omega ^{2}m+\omega c+k\right)x=0.}$$

This can be reduced to a generalized eigenvalue problem by algebraic manipulation at the cost of solving a larger system.

The orthogonality properties of the eigenvectors allows decoupling of the differential equations so that the system can be represented as linear summation of the eigenvectors. The eigenvalue problem of complex structures is often solved using finite element analysis, but neatly generalize the solution to scalar-valued vibration problems.

Tensor of moment of inertia

In mechanics, the eigenvectors of the moment of inertia tensor define the principal axes of a rigid body. The tensor of moment of inertia is a key quantity required to determine the rotation of a rigid body around its center of mass.

Stress tensor

In solid mechanics, the stress tensor is symmetric and so can be decomposed into a diagonal tensor with the eigenvalues on the diagonal and eigenvectors as a basis. Because it is diagonal, in this orientation, the stress tensor has no shear components; the components it does have are the principal components.

Schrödinger equation

The wavefunctions associated with the bound states of an electron in a hydrogen atom can be seen as the eigenvectors of the hydrogen atom Hamiltonian as well as of the angular momentum operator. They are associated with eigenvalues interpreted as their energies (increasing downward: ${\displaystyle n=1,\,2,\,3,\,\ldots }$) and angular momentum (increasing across: s, p, d, ...). The illustration shows the square of the absolute value of the wavefunctions. Brighter areas correspond to higher probability density for a position measurement. The center of each figure is the atomic nucleus, a proton.

An example of an eigenvalue equation where the transformation ${\displaystyle T}$ is represented in terms of a differential operator is the time-independent Schrödinger equation in quantum mechanics:

${\displaystyle H\psi _{E}=E\psi _{E}\,}$

where ${\displaystyle H}$, the Hamiltonian, is a second-order differential operator and ${\displaystyle \psi _{E}}$, the wavefunction, is one of its eigenfunctions corresponding to the eigenvalue ${\displaystyle E}$, interpreted as its energy.

However, in the case where one is interested only in the bound state solutions of the Schrödinger equation, one looks for ${\displaystyle \psi _{E}}$ within the space of square integrable functions. Since this space is a Hilbert space with a well-defined scalar product, one can introduce a basis set in which ${\displaystyle \psi _{E}}$ and ${\displaystyle H}$ can be represented as a one-dimensional array (i.e., a vector) and a matrix respectively. This allows one to represent the Schrödinger equation in a matrix form.

The bra–ket notation is often used in this context. A vector, which represents a state of the system, in the Hilbert space of square integrable functions is represented by ${\displaystyle |\Psi _{E}\rangle }$. In this notation, the Schrödinger equation is:

${\displaystyle H|\Psi _{E}\rangle =E|\Psi _{E}\rangle }$

where ${\displaystyle |\Psi _{E}\rangle }$ is an eigenstate of ${\displaystyle H}$ and ${\displaystyle E}$ represents the eigenvalue. ${\displaystyle H}$ is an observable self-adjoint operator, the infinite-dimensional analog of Hermitian matrices. As in the matrix case, in the equation above ${\displaystyle H|\Psi _{E}\rangle }$ is understood to be the vector obtained by application of the transformation ${\displaystyle H}$ to ${\displaystyle |\Psi _{E}\rangle }$.

Wave transport

Light, acoustic waves, and microwaves are randomly scattered numerous times when traversing a static disordered system. Even though multiple scattering repeatedly randomizes the waves, ultimately coherent wave transport through the system is a deterministic process which can be described by a field transmission matrix ${\displaystyle \mathbf {t} }$.^[44][45] The eigenvectors of the transmission operator ${\displaystyle \mathbf {t} ^{\dagger }\mathbf {t} }$ form a set of disorder-specific input wavefronts which enable waves to couple into the disordered system's eigenchannels: the independent pathways waves can travel through the system. The eigenvalues, ${\displaystyle \tau }$, of ${\displaystyle \mathbf {t} ^{\dagger }\mathbf {t} }$ correspond to the intensity transmittance associated with each eigenchannel. One of the remarkable properties of the transmission operator of diffusive systems is their bimodal eigenvalue distribution with ${\displaystyle \tau _{\max }=1}$ and ${\displaystyle \tau _{\min }=0}$.^[45] Furthermore, one of the striking properties of open eigenchannels, beyond the perfect transmittance, is the statistically robust spatial profile of the eigenchannels.^[46]

Molecular orbitals

In quantum mechanics, and in particular in atomic and molecular physics, within the Hartree–Fock theory, the atomic and molecular orbitals can be defined by the eigenvectors of the Fock operator. The corresponding eigenvalues are interpreted as ionization potentials via Koopmans' theorem. In this case, the term eigenvector is used in a somewhat more general meaning, since the Fock operator is explicitly dependent on the orbitals and their eigenvalues. Thus, if one wants to underline this aspect, one speaks of nonlinear eigenvalue problems. Such equations are usually solved by an iteration procedure, called in this case self-consistent field method. In quantum chemistry, one often represents the Hartree–Fock equation in a non-orthogonal basis set. This particular representation is a generalized eigenvalue problem called Roothaan equations.

Geology and glaciology

In geology, especially in the study of glacial till, eigenvectors and eigenvalues are used as a method by which a mass of information of a clast fabric's constituents' orientation and dip can be summarized in a 3-D space by six numbers. In the field, a geologist may collect such data for hundreds or thousands of clasts in a soil sample, which can only be compared graphically such as in a Tri-Plot (Sneed and Folk) diagram,^[47][48] or as a Stereonet on a Wulff Net.^[49]

The output for the orientation tensor is in the three orthogonal (perpendicular) axes of space. The three eigenvectors are ordered ${\displaystyle \mathbf {v} _{1},\mathbf {v} _{2},\mathbf {v} _{3}}$ by their eigenvalues ${\displaystyle E_{1}\geq E_{2}\geq E_{3}}$;^[50] ${\displaystyle \mathbf {v} _{1}}$ then is the primary orientation/dip of clast, ${\displaystyle \mathbf {v} _{2}}$ is the secondary and ${\displaystyle \mathbf {v} _{3}}$ is the tertiary, in terms of strength. The clast orientation is defined as the direction of the eigenvector, on a compass rose of 360°. Dip is measured as the eigenvalue, the modulus of the tensor: this is valued from 0° (no dip) to 90° (vertical). The relative values of ${\displaystyle E_{1}}$, ${\displaystyle E_{2}}$, and ${\displaystyle E_{3}}$ are dictated by the nature of the sediment's fabric. If ${\displaystyle E_{1}=E_{2}=E_{3}}$, the fabric is said to be isotropic. If ${\displaystyle E_{1}=E_{2}>E_{3}}$, the fabric is said to be planar. If ${\displaystyle E_{1}>E_{2}>E_{3}}$, the fabric is said to be linear.^[51]

Basic reproduction number

The basic reproduction number ( ${\displaystyle R_{0}}$) is a fundamental number in the study of how infectious diseases spread. If one infectious person is put into a population of completely susceptible people, then ${\displaystyle R_{0}}$ is the average number of people that one typical infectious person will infect. The generation time of an infection is the time, ${\displaystyle t_{G}}$, from one person becoming infected to the next person becoming infected. In a heterogeneous population, the next generation matrix defines how many people in the population will become infected after time ${\displaystyle t_{G}}$ has passed. The value ${\displaystyle R_{0}}$ is then the largest eigenvalue of the next generation matrix.^[52][53]

Eigenfaces

Eigenfaces as examples of eigenvectors

In image processing, processed images of faces can be seen as vectors whose components are the brightnesses of each pixel.^[54] The dimension of this vector space is the number of pixels. The eigenvectors of the covariance matrix associated with a large set of normalized pictures of faces are called eigenfaces; this is an example of principal component analysis. They are very useful for expressing any face image as a linear combination of some of them. In the facial recognition branch of biometrics, eigenfaces provide a means of applying data compression to faces for identification purposes. Research related to eigen vision systems determining hand gestures has also been made.

Similar to this concept, eigenvoices represent the general direction of variability in human pronunciations of a particular utterance, such as a word in a language. Based on a linear combination of such eigenvoices, a new voice pronunciation of the word can be constructed. These concepts have been found useful in automatic speech recognition systems for speaker adaptation.

See also

• Antieigenvalue theory
• Eigenoperator
• Eigenplane
• Eigenmoments
• Eigenvalue algorithm
• Quantum states
• Jordan normal form
• List of numerical-analysis software
• Nonlinear eigenproblem
• Normal eigenvalue
• Quadratic eigenvalue problem
• Singular value
• Spectrum of a matrix

Notes

1. Note:
   • In 1751, Leonhard Euler proved that any body has a principal axis of rotation: Leonhard Euler (presented: October 1751; published: 1760) "Du mouvement d'un corps solide quelconque lorsqu'il tourne autour d'un axe mobile" (On the movement of any solid body while it rotates around a moving axis), Histoire de l'Académie royale des sciences et des belles lettres de Berlin, pp. 176–227. On p. 212, Euler proves that any body contains a principal axis of rotation: "Théorem. 44. De quelque figure que soit le corps, on y peut toujours assigner un tel axe, qui passe par son centre de gravité, autour duquel le corps peut tourner librement & d'un mouvement uniforme." (Theorem. 44. Whatever be the shape of the body, one can always assign to it such an axis, which passes through its center of gravity, around which it can rotate freely and with a uniform motion.)
   • In 1755, Johann Andreas Segner proved that any body has three principal axes of rotation: Johann Andreas Segner, Specimen theoriae turbinum [Essay on the theory of tops (i.e., rotating bodies)] ( Halle ("Halae"), (Germany): Gebauer, 1755). (https://books.google.com/books?id=29 p. xxviiii [29]), Segner derives a third-degree equation in t, which proves that a body has three principal axes of rotation. He then states (on the same page): "Non autem repugnat tres esse eiusmodi positiones plani HM, quia in aequatione cubica radices tres esse possunt, et tres tangentis t valores." (However, it is not inconsistent [that there] be three such positions of the plane HM, because in cubic equations, [there] can be three roots, and three values of the tangent t.)
   • The relevant passage of Segner's work was discussed briefly by Arthur Cayley. See: A. Cayley (1862) "Report on the progress of the solution of certain special problems of dynamics," Report of the Thirty-second meeting of the British Association for the Advancement of Science; held at Cambridge in October 1862, 32: 184–252; see especially pp. 225–226.
2. Kline 1972, pp. 807–808 Augustin Cauchy (1839) "Mémoire sur l'intégration des équations linéaires" (Memoir on the integration of linear equations), Comptes rendus, 8: 827–830, 845–865, 889–907, 931–937. From p. 827: "On sait d'ailleurs qu'en suivant la méthode de Lagrange, on obtient pour valeur générale de la variable prinicipale une fonction dans laquelle entrent avec la variable principale les racines d'une certaine équation que j'appellerai l'équation caractéristique, le degré de cette équation étant précisément l'order de l'équation différentielle qu'il s'agit d'intégrer." (One knows, moreover, that by following Lagrange's method, one obtains for the general value of the principal variable a function in which there appear, together with the principal variable, the roots of a certain equation that I will call the "characteristic equation", the degree of this equation being precisely the order of the differential equation that must be integrated.)
3. See:
   • David Hilbert (1904) "Grundzüge einer allgemeinen Theorie der linearen Integralgleichungen. (Erste Mitteilung)" (Fundamentals of a general theory of linear integral equations. (First report)), Nachrichten von der Gesellschaft der Wissenschaften zu Göttingen, Mathematisch-Physikalische Klasse (News of the Philosophical Society at Göttingen, mathematical-physical section), pp. 49–91. From p. 51: "Insbesondere in dieser ersten Mitteilung gelange ich zu Formeln, die die Entwickelung einer willkürlichen Funktion nach gewissen ausgezeichneten Funktionen, die ich 'Eigenfunktionen' nenne, liefern: ..." (In particular, in this first report I arrive at formulas that provide the [series] development of an arbitrary function in terms of some distinctive functions, which I call eigenfunctions: ... ) Later on the same page: "Dieser Erfolg ist wesentlich durch den Umstand bedingt, daß ich nicht, wie es bisher geschah, in erster Linie auf den Beweis für die Existenz der Eigenwerte ausgehe, ... " (This success is mainly attributable to the fact that I do not, as it has happened until now, first of all aim at a proof of the existence of eigenvalues, ... )
   • For the origin and evolution of the terms eigenvalue, characteristic value, etc., see: Earliest Known Uses of Some of the Words of Mathematics (E)
4. For a proof of this lemma, see Roman 2008, Theorem 8.2 on p. 186; Shilov 1977, p. 109; Hefferon 2001, p. 364; Beezer 2006, Theorem EDELI on p. 469; and Lemma for linear independence of eigenvectors
5. By doing Gaussian elimination over formal power series truncated to ${\displaystyle n}$ terms it is possible to get away with ${\displaystyle O(n^{4})}$ operations, but that does not take combinatorial explosion into account.

Citations

1. Burden & Faires 1993, p. 401.
2. Gilbert Strang. "6: Eigenvalues and Eigenvectors". Introduction to Linear Algebra (PDF) (5 ed.). Wellesley-Cambridge Press.
3. Herstein 1964, pp. 228, 229.
4. Nering 1970, p. 38.
5. Betteridge 1965.
6. "Eigenvector and Eigenvalue". www.mathsisfun.com. Retrieved 19 August 2020.
7. Press et al. 2007, p. 536.
8. Wolfram.com: Eigenvector.
9. Nering 1970, p. 107.
10. Hawkins 1975, §2.
11. Hawkins 1975, §3.
12. Kline 1972, p. 673.
13. Kline 1972, pp. 807–808.
14. Kline 1972, pp. 715–716.
15. Kline 1972, pp. 706–707.
16. Kline 1972, p. 1063, p..
17. Aldrich 2006.
18. Francis 1961, pp. 265–271.
19. Kublanovskaya 1962.
20. Golub & Van Loan 1996, §7.3.
21. Meyer 2000, §7.3.
22. Cornell University Department of Mathematics (2016) Lower-Level Courses for Freshmen and Sophomores. Accessed on 2016-03-27.
23. University of Michigan Mathematics (2016) Math Course Catalogue Archived 2015-11-01 at the Wayback Machine. Accessed on 2016-03-27.
24. Press et al. 2007, p. 38.
25. Fraleigh 1976, p. 358.
26. Golub & Van Loan 1996, p. 316.
27. Anton 1987, pp. 305, 307.
28. Beauregard & Fraleigh 1973, p. 307.
29. Herstein 1964, p. 272.
30. Nering 1970, pp. 115–116.
31. Herstein 1964, p. 290.
32. Nering 1970, p. 116.
33. Wolchover 2019.
34. Denton et al. 2022.
35. Van Mieghem 2014.
36. Van Mieghem 2024.
37. Korn & Korn 2000, Section 14.3.5a.
38. Friedberg, Insel & Spence 1989, p. 217.
39. Roman 2008, p. 186 §8
40. Nering 1970, p. 107; Shilov 1977, p. 109 Lemma for the eigenspace
41. Lipschutz & Lipson 2002, p. 111.
42. Roman 2008, p. 189 §8.
43. Trefethen & Bau 1997.
44. Vellekoop & Mosk 2007, pp. 2309–2311.
45. Rotter & Gigan 2017, p. 15005.
46. Bender et al. 2020, p. 165901.
47. Graham & Midgley 2000, pp. 1473–1477.
48. Sneed & Folk 1958, pp. 114–150.
49. Knox-Robinson & Gardoll 1998, p. 243.
50. Busche, Christian; Schiller, Beate. "Endogene Geologie - Ruhr-Universität Bochum". www.ruhr-uni-bochum.de.
51. Benn & Evans 2004, pp. 103–107.
52. Diekmann, Heesterbeek & Metz 1990, pp. 365–382.
53. Heesterbeek & Diekmann 2000.
54. Xirouhakis, Votsis & Delopoulus 2004.

Sources

• Aldrich, John (2006), "Eigenvalue, eigenfunction, eigenvector, and related terms", in Miller, Jeff (ed.), Earliest Known Uses of Some of the Words of Mathematics
• Anton, Howard (1987), Elementary Linear Algebra (5th ed.), New York: Wiley, ISBN 0-471-84819-0
• Beauregard, Raymond A.; Fraleigh, John B. (1973), A First Course In Linear Algebra: with Optional Introduction to Groups, Rings, and Fields, Boston: Houghton Mifflin Co., ISBN 0-395-14017-X
• Beezer, Robert A. (2006), A first course in linear algebra, Free online book under GNU licence, University of Puget Sound
• Bender, Nicholas; Yamilov, Alexey; Yilmaz, Hasan; Cao, Hui (14 October 2020). "Fluctuations and Correlations of Transmission Eigenchannels in Diffusive Media". Physical Review Letters. 125 (16): 165901. arXiv:2004.12167. Bibcode:2020PhRvL.125p5901B. doi:10.1103/physrevlett.125.165901. ISSN 0031-9007. PMID 33124845. S2CID 216553547.
• Benn, D.; Evans, D. (2004), A Practical Guide to the study of Glacial Sediments, London: Arnold, pp. 103–107
• Betteridge, Harold T. (1965), The New Cassell's German Dictionary, New York: Funk & Wagnall, LCCN 58-7924
• Burden, Richard L.; Faires, J. Douglas (1993), Numerical Analysis (5th ed.), Boston: Prindle, Weber and Schmidt, ISBN 0-534-93219-3
• Denton, Peter B.; Parke, Stephen J.; Tao, Terence; Zhang, Xining (January 2022). "Eigenvectors from Eigenvalues: A Survey of a Basic Identity in Linear Algebra" (PDF). Bulletin of the American Mathematical Society. 59 (1): 31–58. arXiv:1908.03795. doi:10.1090/bull/1722. S2CID 213918682. Archived (PDF) from the original on 19 January 2022.
• Diekmann, O; Heesterbeek, JA; Metz, JA (1990), "On the definition and the computation of the basic reproduction ratio R0 in models for infectious diseases in heterogeneous populations", Journal of Mathematical Biology, 28 (4): 365–382, doi:10.1007/BF00178324, hdl:1874/8051, PMID 2117040, S2CID 22275430
• Fraleigh, John B. (1976), A First Course In Abstract Algebra (2nd ed.), Reading: Addison-Wesley, ISBN 0-201-01984-1
• Francis, J. G. F. (1961), "The QR Transformation, I (part 1)", The Computer Journal, 4 (3): 265–271, doi:10.1093/comjnl/4.3.265
• Francis, J. G. F. (1962), "The QR Transformation, II (part 2)", The Computer Journal, 4 (4): 332–345, doi:10.1093/comjnl/4.4.332
• Friedberg, Stephen H.; Insel, Arnold J.; Spence, Lawrence E. (1989), Linear algebra (2nd ed.), Englewood Cliffs, NJ: Prentice Hall, ISBN 0-13-537102-3
• Golub, Gene H.; Van Loan, Charles F. (1996), Matrix computations (3rd ed.), Baltimore, MD: Johns Hopkins University Press, ISBN 978-0-8018-5414-9
• Graham, D.; Midgley, N. (2000), "Graphical representation of particle shape using triangular diagrams: an Excel spreadsheet method", Earth Surface Processes and Landforms, 25 (13): 1473–1477, Bibcode:2000ESPL...25.1473G, doi:10.1002/1096-9837(200012)25:13<1473::AID-ESP158>3.0.CO;2-C, S2CID 128825838
• Hawkins, T. (1975), "Cauchy and the spectral theory of matrices", Historia Mathematica, 2: 1–29, doi:10.1016/0315-0860(75)90032-4
• Heesterbeek, J. A. P.; Diekmann, Odo (2000), Mathematical epidemiology of infectious diseases, Wiley series in mathematical and computational biology, West Sussex, England: John Wiley & Sons^{[permanent dead link]}
• Hefferon, Jim (2001), Linear Algebra, Colchester, VT: Online book, St Michael's College
• Herstein, I. N. (1964), Topics In Algebra, Waltham: Blaisdell Publishing Company, ISBN 978-1114541016
• Kline, Morris (1972), Mathematical thought from ancient to modern times, Oxford University Press, ISBN 0-19-501496-0
• Knox-Robinson, C.; Gardoll, Stephen J. (1998), "GIS-stereoplot: an interactive stereonet plotting module for ArcView 3.0 geographic information system", Computers & Geosciences, 24 (3): 243, Bibcode:1998CG.....24..243K, doi:10.1016/S0098-3004(97)00122-2
• Korn, Granino A.; Korn, Theresa M. (2000), "Mathematical Handbook for Scientists and Engineers: Definitions, Theorems, and Formulas for Reference and Review", New York: McGraw-Hill (2nd Revised ed.), Bibcode:1968mhse.book.....K, ISBN 0-486-41147-8
• Kublanovskaya, Vera N. (1962), "On some algorithms for the solution of the complete eigenvalue problem", USSR Computational Mathematics and Mathematical Physics, 1 (3): 637–657, doi:10.1016/0041-5553(63)90168-X
• Lipschutz, Seymour; Lipson, Marc (12 August 2002). Schaum's Easy Outline of Linear Algebra. McGraw Hill Professional. p. 111. ISBN 978-007139880-0.
• Meyer, Carl D. (2000), Matrix analysis and applied linear algebra, Philadelphia: Society for Industrial and Applied Mathematics (SIAM), ISBN 978-0-89871-454-8
• Nering, Evar D. (1970), Linear Algebra and Matrix Theory (2nd ed.), New York: Wiley, LCCN 76091646
• Press, William H.; Teukolsky, Saul A.; Vetterling, William T.; Flannery, Brian P. (2007), Numerical Recipes: The Art of Scientific Computing (3rd ed.), Cambridge University Press, ISBN 978-0521880688
• Roman, Steven (2008), Advanced linear algebra (3rd ed.), New York: Springer Science + Business Media, ISBN 978-0-387-72828-5
• Rotter, Stefan; Gigan, Sylvain (2 March 2017). "Light fields in complex media: Mesoscopic scattering meets wave control". Reviews of Modern Physics. 89 (1): 015005. arXiv:1702.05395. Bibcode:2017RvMP...89a5005R. doi:10.1103/RevModPhys.89.015005. S2CID 119330480.
• Shilov, Georgi E. (1977), Linear algebra, Translated and edited by Richard A. Silverman, New York: Dover Publications, ISBN 0-486-63518-X
• Sneed, E. D.; Folk, R. L. (1958), "Pebbles in the lower Colorado River, Texas, a study of particle morphogenesis", Journal of Geology, 66 (2): 114–150, Bibcode:1958JG.....66..114S, doi:10.1086/626490, S2CID 129658242
• Trefethen, Lloyd N.; Bau, David (1997), Numerical Linear Algebra, SIAM
• Van Mieghem, Piet (18 January 2014). "Graph eigenvectors, fundamental weights and centrality metrics for nodes in networks". arXiv:1401.4580 [math.SP].
• Vellekoop, I. M.; Mosk, A. P. (15 August 2007). "Focusing coherent light through opaque strongly scattering media". Optics Letters. 32 (16): 2309–2311. Bibcode:2007OptL...32.2309V. doi:10.1364/OL.32.002309. ISSN 1539-4794. PMID 17700768. S2CID 45359403.
• Weisstein, Eric W. "Eigenvector". mathworld.wolfram.com. Retrieved 4 August 2019.
• Weisstein, Eric W. (n.d.). "Eigenvalue". mathworld.wolfram.com. Retrieved 19 August 2020.
• Wolchover, Natalie (13 November 2019). "Neutrinos Lead to Unexpected Discovery in Basic Math". Quanta Magazine. Retrieved 27 November 2019.
• Xirouhakis, A.; Votsis, G.; Delopoulus, A. (2004), Estimation of 3D motion and structure of human faces (PDF), National Technical University of Athens
• Van Mieghem, P. (2024). "Eigenvector components of symmetric, graph-related matrices". Linear Algebra and Its Applications. 692: 91–134. doi:10.1016/j.laa.2024.03.035.

Further reading

• Golub, Gene F.; van der Vorst, Henk A. (2000), "Eigenvalue Computation in the 20th Century" (PDF), Journal of Computational and Applied Mathematics, 123 (1–2): 35–65, Bibcode:2000JCoAM.123...35G, doi:10.1016/S0377-0427(00)00413-1, hdl:1874/2663
• Hill, Roger (2009). "λ – Eigenvalues". Sixty Symbols. Brady Haran for the University of Nottingham.
• Kuttler, Kenneth (2017), An introduction to linear algebra (PDF), Brigham Young University
• Strang, Gilbert (1993), Introduction to linear algebra, Wellesley, MA: Wellesley-Cambridge Press, ISBN 0-9614088-5-5
• Strang, Gilbert (2006), Linear algebra and its applications, Belmont, CA: Thomson, Brooks/Cole, ISBN 0-03-010567-6

External links

• What are Eigen Values? – non-technical introduction from PhysLink.com's "Ask the Experts"
• Eigen Values and Eigen Vectors Numerical Examples – Tutorial and Interactive Program from Revoledu.
• Introduction to Eigen Vectors and Eigen Values – lecture from Khan Academy
• Eigenvectors and eigenvalues | Essence of linear algebra, chapter 10 – A visual explanation with 3Blue1Brown
• Matrix Eigenvectors Calculator from Symbolab (Click on the bottom right button of the 2×12 grid to select a matrix size. Select an ${\displaystyle n\times n}$ size (for a square matrix), then fill out the entries numerically and click on the Go button. It can accept complex numbers as well.)

Wikiversity uses introductory physics to introduce Eigenvalues and eigenvectors

Theory

• Computation of Eigenvalues
• Numerical solution of eigenvalue problems Edited by Zhaojun Bai, James Demmel, Jack Dongarra, Axel Ruhe, and Henk van der Vorst