stringtranslate.com

Теорема Понселе–Штайнера

Провести параллель (h) к диаметру g через любую заданную точку P. Выбрать вспомогательную точку C в любом месте прямой, проходящей через B и P вне BP. (Штайнер)

В разделе математики , известном как евклидова геометрия , теорема Понселе–Штайнера является одним из нескольких результатов, касающихся построений с помощью циркуля и линейки, имеющих дополнительные ограничения, налагаемые на традиционные правила. Этот результат, связанный с эквивалентностью ржавого циркуля и построениями Штейнера , утверждает, что все, что может быть построено с помощью линейки и циркуля вместе, может быть построено с помощью одной линейки, при условии, что заданы один круг и его центр :

Любое евклидово построение, поскольку заданными и требуемыми элементами являются точки (или линии), если оно может быть завершено как циркулем, так и линейкой вместе, может быть завершено одной линейкой при условии, что на плоскости существует не менее одной окружности с ее центром.

Хотя циркуль может значительно облегчить построение, подразумевается, что после того, как нарисован первый круг, циркуль не имеет функционального назначения. Все построения остаются возможными, хотя естественно подразумевается, что круги и их дуги не могут быть нарисованы без циркуля. Все точки, которые однозначно определяют построение, которые можно определить с помощью циркуля, в равной степени определяются и без него, хотя и с большими трудностями.

Это означает только то, что циркуль может использоваться в эстетических целях, а не в целях строительства. Другими словами, циркуль может использоваться после того, как все ключевые точки определены, для того, чтобы "заполнить" дуги исключительно в визуальных или художественных целях, если это желательно, а не как необходимый шаг к строительству. Ничего существенного для целей геометрического строительства не теряется, если пренебречь построением дуг окружности.

История

" Геометрические построения, выполненные с помощью прямой линии и фиксированного круга, как предмет преподавания в высших учебных заведениях и для практического использования; Якоб Штейнером, доктором философии, королевским прусским профессором и выдающимся преподавателем математики в коммерческой школе в Берлине. С двумя медными табличками. Берлин, с Фердинандом Думмлером . 1833 г. "

В десятом веке персидский математик Абу аль-Вафа Бузджани (940−998) рассматривал геометрические построения с использованием линейки и циркуля с фиксированным отверстием, так называемого ржавого циркуля . Построения этого типа, по-видимому, имели некоторое практическое значение, поскольку их использовали художники Леонардо да Винчи и Альбрехт Дюрер в Европе в конце пятнадцатого века. Новая точка зрения развилась в середине шестнадцатого века, когда размер отверстия считался фиксированным, но произвольным, и вопрос о том, сколько построений Евклида можно было получить, был первостепенным. [1]

Математик эпохи Возрождения Лодовико Феррари , ученик Джероламо Кардано, в «математическом соревновании» с Никколо Фонтана Тарталья смог показать, что «все Евклида» (то есть построения с помощью линейки и циркуля в первых шести книгах « Начал» Евклида ) можно выполнить с помощью линейки и ржавого циркуля. В течение десяти лет Кардано, Тарталья и ученик Тартальи Бенедетти получили дополнительные наборы решений . [2] В течение следующего столетия эти решения были в целом забыты, пока в 1673 году Георг Мор не опубликовал (анонимно и на голландском языке) Euclidis Curiosi , содержащий его собственные решения. Мор только слышал о существовании более ранних результатов, и это побудило его работать над проблемой. [3]

Демонстрация того, что «все построения Евклида» можно выполнить с помощью линейки и ржавого циркуля, не то же самое, что доказательство того, что все построения с помощью линейки и циркуля можно выполнить с помощью линейки и просто ржавого циркуля. Такое доказательство потребовало бы формализации того, что можно построить с помощью линейки и циркуля. Эта основа была предоставлена ​​Жаном Виктором Понселе в 1822 году, будучи мотивированным работой Мора над теоремой Мора-Маскерони . Он также предположил и предложил возможное доказательство того, что линейка и ржавый циркуль будут эквивалентны линейке и циркулю, и, более того, ржавый циркуль нужно использовать только один раз. Результат этой теоремы, что линейка и одиночный круг с заданным центром эквивалентны линейке и циркулю, был доказан Якобом Штайнером в 1833 году. [4] [1]

Значительный вклад в эту область позднее внесли Франческо Севери , Лазар Карно , Карл фон Штаудт , Джузеппе Пеано и другие.

Связанные концепции и конструкции

Различные другие понятия, инструменты, терминология и т. д. часто ассоциируются (иногда вольно) с теоремой Понселе-Штайнера. Некоторые из них перечислены здесь.

Конструкции Штейнера

Термин «построение Штейнера» обычно относится к любой геометрической конструкции, которая использует только линейный инструмент, и иногда просто называется построением только с помощью линейки . Как ограниченная парадигма построения , не делается никаких оговорок о том, какие геометрические объекты уже существуют на плоскости или об их относительном размещении; любые такие условия постулируются заранее. Кроме того, не делается никаких выводов о том, что возможно или невозможно построить. Построения, выполненные в соответствии с теоремой Понселе-Штейнера — полагаясь исключительно на использование линейки без помощи циркуля — являются, таким образом, особым подмножеством построений Штейнера .

В то время как конструкции Штейнера изучают линейку, теорема Понселе-Штейнера предполагает существование окружности с центром и утверждает, что одна окружность эквивалентна циркулю. В широком смысле конструкции Штейнера могут включать любое количество окружностей, включая ни одной, уже нарисованных на плоскости, с центрами или без них. Они также могут включать всевозможные уникальные формы и кривые, уже существующие на плоскости, при условии, что линейка является единственным физическим инструментом в распоряжении геометра.

Следовательно, все построения, придерживающиеся теоремы Понселе-Штайнера, являются построениями Штейнера, хотя не все построения Штейнера соблюдают строгое условие, что существует только одна окружность с центром на плоскости. Теорема Понселе-Штайнера не требует фактического циркуля — предполагается, что окружность уже существует на плоскости — поэтому все построения, демонстрирующие теорему Понселе-Штайнера, являются построениями Штейнера.

Ржавый компас

Ржавый компас описывает компас, шарнир которого настолько заржавел, что расплавился, так что его ножки — игла и карандаш — не могут регулировать ширину. По сути, это компас, расстояние которого фиксировано, и который рисует круги предопределенного и постоянного, но произвольного радиуса. Круги можно рисовать с центром в любой произвольной точке, но радиус неизменен.

Как ограниченная парадигма строительства, конструкции ржавого циркуля допускают использование линейки и циркуля фиксированной ширины. Эквивалентность ржавого циркуля:

Все пункты, необходимые для однозначного описания любой конструкции с использованием циркуля и линейки, могут быть получены с помощью линейки и циркуля фиксированной ширины.

Естественно, что циркуль произвольного радиуса можно использовать в эстетических целях; для строительства можно использовать только дугу одного конкретного циркуля фиксированной ширины.

В некотором смысле ржавый циркуль является обобщением и упрощением теоремы Понселе-Штайнера. Хотя он и не более мощный, он, безусловно, более удобный. Теорема Понселе-Штайнера требует, чтобы на плоскости была размещена одна окружность с произвольным радиусом и центром. Поскольку это единственная нарисованная окружность, не имеет значения, была ли она нарисована ржавым циркулем или нет. Однако преимущество общих конструкций с ржавым циркулем заключается в том, что циркуль можно использовать многократно для перерисовки окружностей с центром в любой желаемой точке, хотя и с тем же радиусом, что упрощает многие построения. Естественно, если все построения возможны с одной окружностью, произвольно размещенной на плоскости, то то же самое можно, безусловно, сказать о линейке и ржавом циркуле, с помощью которых можно произвольно разместить по крайней мере одну окружность.

Известно, что линейки и ржавого циркуля достаточно для построения всего, что возможно с помощью линейки и стандартного циркуля — с подразумеваемым пониманием того, что дуги окружности произвольного радиуса не могут быть нарисованы, и их нужно рисовать только в эстетических целях, а не в конструктивных. Исторически это было доказано, когда была доказана теорема Понселе-Штайнера, которая является более сильным результатом. Таким образом, ржавый циркуль не слабее теоремы Понселе-Штайнера. Ржавый циркуль также не сильнее.

Теорема Понселе-Штайнера сводит эквивалентность ржавого компаса Феррари, заявленную в то время, к одноразовому компасу:

Все пункты, необходимые для однозначного описания любой конструкции с использованием циркуля и линейки, могут быть получены с помощью одной лишь линейки после того, как будет нанесен первый круг.

Теорема Понселе-Штайнера берет сценарий ржавого компаса и полностью ломает компас после первого использования. Однако с одноразовым компасом геометр может разместить первый круг произвольно. Теорема Понселе-Штайнера предполагает, что геометр не имеет никакого контроля над размещением.

Проективная геометрия и ее связь с теоремой Понселе-Штайнера

Проективная геометрия — это изучение геометрических свойств, которые инвариантны относительно проективных преобразований . Хотя это отдельная тема сама по себе, многие концепции проективной геометрии применяются здесь к конструкциям Штейнера. Жан-Виктор Понселе внес большой вклад в эту тему, когда он постулировал теорему этой статьи, которую Якоб Штейнер позже доказал. Многие из связанных концепций, разработанных в проективной геометрии, включают, но не ограничиваются: совпадение , «точки на бесконечности», перспектива и перспективность , проективность , отношения и перекрестные отношения , сопряженные элементы, устойчивые или неподвижные точки инволюций, инварианты, двойственность , однородность и гомография, линейные преобразования, проективные гармоники , пучки (линий или окружностей) и другие. Тщательное рассмотрение конструкций Штейнера и их доказательств требует знаний в проективной геометрии, хотя предмет проективной геометрии не ограничивается построениями только с помощью линейки.

Карандаши линий или кругов

Термин «карандаш» относится к набору геометрических объектов, которые все имеют общее свойство, которое однозначно идентифицируется ровно двумя его элементами, и является термином, обычно используемым только в геометрических контекстах. В случае с пучком линий , свойством обычно является прохождение через одну и ту же точку или совпадение. В случае с пучком окружностей , общая коаксиальная система (имеющая одну и ту же радикальную ось) является обычной интерпретацией. Действительно, пучок точек обычно относится к набору всех точек на данной линии. Хотя это обычные значения, любое свойство, которое выбирает геометр, является действительным при условии, что для установления базового набора требуется два элемента — не больше и не меньше. По сути, карандаш — это целый набор (потенциально бесконечных) геометрических объектов, которые полностью определяются любыми двумя и каждыми двумя различными членами из его набора. Таким образом, любые два подобных объекта определяют весь набор, к которому принадлежат или не принадлежат другие подобные объекты. Аналогично, набор геометрических объектов, определяемый ровно тремя его элементами, называется пучком . Карандаши являются общей темой во многих публикациях по геометрии на протяжении всей истории, хотя этот термин сегодня используется реже. Карандаши были обобщены и на более высокие измерения (например, пучок плоскостей ). В этой статье карандаши явно не упоминаются, хотя некоторые конструкции, встречающиеся в ней, и в проективной геометрии в более широком смысле, на самом деле неявно используют понятие карандаша, часто с помощью другой терминологии или явным обращением к базовому свойству. Термин здесь определен из-за его общего использования во многих цитируемых ссылках, поддерживающих содержание этой статьи.

Теорема Штейнера / Ошибка Гильберта

Не путать с теоремой Штейнера о параллельных осях , поризмом Штейнера или теоремой Штейнера–Лемуса .

Если необходимо задать только одну окружность и никакой другой специальной информации, теорема Штейнера подразумевает, что центр окружности должен быть указан вместе с дугой окружности. Это делается путем доказательства невозможности построения центра окружности только с помощью линейки, используя только одну окружность на плоскости, без ее центра. Используется аргумент с использованием проективных преобразований и конических сечений Штейнера .

Если на плоскости имеется только одна окружность, ее центр невозможно построить с помощью одной лишь линейки.

Также приписываемое Дэвиду Гильберту и известное как Ошибка Гильберта , наивное резюме доказательства выглядит следующим образом. При использовании инструмента линейки возможны только линейные проективные преобразования, а линейные проективные преобразования являются обратимыми операциями. Прямые проецируются на прямые при любом линейном проективном преобразовании, в то время как конические сечения проецируются на конические сечения при линейном проективном преобразовании, но последние перекошены таким образом, что эксцентриситеты , фокусы и центры окружностей не сохраняются. При различных последовательностях отображений центр не отображается однозначно и обратимо . Это было бы не так, если бы прямые можно было использовать для определения центра окружности. Поскольку линейные преобразования являются обратимыми операциями и, таким образом, давали бы уникальные результаты, тот факт, что уникальные результаты невозможны, подразумевает невозможность построений центральной точки. Уникальность построенного центра зависела бы от дополнительной информации, не предоставляемой одной окружностью, что сделало бы построение обратимым.

Таким образом, невозможно построить все, что можно построить с помощью линейки и циркуля, с помощью одной линейки. Следовательно, требования теоремы Понселе-Штайнера не могут быть ослаблены относительно центра окружности. Если центр единственной данной окружности не указан, то ее нельзя получить с помощью одной линейки. Многие построения невозможны с помощью одной линейки. Необходимо что-то еще, и достаточно окружности с указанным центром.

Альтернативные каркасы для одиночного круга с центром

В качестве альтернативы центр может быть опущен с достаточной дополнительной информацией. Это не ослабление теоремы Понселе-Штайнера, а просто альтернативная структура. И это не противоречие теореме Штайнера, которая предполагает только одну окружность. Включение этой достаточной альтернативной информации, которая в большинстве случаев включает по крайней мере две окружности, устраняет неоднозначность отображений при проективных преобразованиях, тем самым позволяя различным конструкциям Штайнера восстанавливать центр окружности.

Большинство этих альтернатив требуют по крайней мере двух окружностей без центров, а также некоторой другой уникальной информации. Некоторые альтернативы включают две концентрические или две пересекающиеся окружности, или три окружности, или другие вариации, в которых предоставленные окружности лишены своих центров. В каждой из них выполняется некоторый дополнительный уникальный, но достаточный критерий, такой как концентричность, точки пересечения, третья окружность и т. д. соответственно. Существуют и другие конфигурации (см. более подробный список в следующем разделе), такие как некоторые конфигурации с одним кругом, где предоставляется достаточная альтернативная информация. В любом из этих случаев центр круга может быть построен, тем самым сводя проблему к гипотезе теоремы Понселе-Штайнера (с дополнительным удобством наличия дополнительных окружностей на плоскости, все центры которых теперь могут быть построены).

Конструктивный план доказательства

Чтобы доказать теорему, необходимо доказать возможность каждой из основных конструкций циркуля и линейки с использованием одной только линейки (при условии, что окружность и ее центр существуют на плоскости), поскольку они являются основами или элементарными шагами для всех других конструкций. То есть, все конструкции можно записать в виде серии шагов, включающих эти пять основных конструкций:

Проиллюстрированы основные конструкции с 1 по 5 слева направо. Верхний ряд — заданная информация, нижний ряд — желаемая конструкция; красный цвет указывает на более новую информацию.
  1. Создание линии через две существующие точки
  2. Создание окружности через одну точку с центром в другой точке
  3. Создание точки, которая является пересечением двух существующих непараллельных линий.
  4. Создание одной или двух точек на пересечении линии и окружности (если они пересекаются)
  5. Создание одной или двух точек на пересечении двух окружностей (если они пересекаются).

Если эти основы могут быть достигнуты с помощью только линейки и произвольной окружности (с центром), вписанной в плоскость, то утверждение, являющееся теоремой этой статьи, будет доказано.

#1 – Линия, проходящая через две точки

Это можно сделать с помощью одной только линейки. Ни циркуль, ни круг не требуются.

#2 – Окружность, проходящая через одну точку с определенным центром

Понятно, что дугу окружности нельзя нарисовать без циркуля. Окружность считается заданной любыми двумя точками, одна из которых определяет центр, а другая находится на окружности на радиусе. Любая такая пара определяет уникальную окружность, хотя обратное неверно : для любой заданной окружности не существует уникальной пары, определяющей ее. В соответствии с целью теоремы, которую мы стремимся доказать, фактическая окружность не обязательно должна быть нарисована, но по эстетическим причинам. Эта теорема утверждает, что окружность, определенная таким образом, достаточна; это утверждение будет рассмотрено далее в статье.

#3 – Пересечение двух линий

Эту конструкцию можно также выполнить напрямую с помощью линейки.

#4, #5 – Пересечения, включающие окружность

Таким образом, для доказательства теоремы достаточно доказать возможность построения только построений № 4 и № 5 с использованием лишь линейки и заданной окружности с центром.

Примечания и предостережения относительно конструктивного доказательства

Далее следуют некоторые примечания и комментарии относительно теоремы, доказательств и связанных с ней тем рассмотрения.

Относительно круга

Круговая номенклатура

В приведенных ниже конструкциях окружность, определяемая центральной точкой P и точкой на ее окружности Q , через которую проходит дуга окружности, обозначается P(Q) . Поскольку большинство окружностей не нарисованы циркулем, центр и точки окружности названы явно. Дуга, если она нарисована, также может быть названа, например, окружность c . Согласно теореме, когда нарисована окружность циркулем, она просто упоминается как заданная окружность или предоставленная окружность .

Круг общности

Предоставленная окружность всегда должна предполагаться произвольно размещенной на плоскости с произвольным радиусом. Многие примеры конструктивности с линейкой, которые можно найти в различных источниках в сети и офлайн, предполагают, что окружность не размещена в общем положении . Вместо этого, например, конструктивность многоугольника может постулировать, что окружность является описывающей . Такие предположения упрощают конструкцию, но не доказывают общности утверждения о конструктивности. Для целей этой теоремы мы можем предположить, что окружность действительно является полностью общей.

Использование дуги предоставленного круга(ов)

Точки пересечения между любой прямой и заданной окружностью могут быть найдены непосредственно, как и точки пересечения между дугами двух окружностей, если они указаны. Теорема Понселе-Штайнера не запрещает нормальное обращение с уже нарисованными на плоскости окружностями; применяются обычные правила построения. Теорема запрещает только построение новых дуг окружностей с помощью циркуля.

Относительно применения

Удобство использования

Конструктивное доказательство не просто служит доказательством теоремы, но также демонстрирует практическое применение самых основных конструкций, так что утверждение о конструктивности с помощью линейки может быть использовано на практике в самом общем случае. Поскольку все геометрические конструкции могут быть выражены как последовательность пяти основных конструктивных шагов, а нижеприведенные конструкции демонстрируют и обосновывают каждую из них, необходимо, чтобы доказать теорему, следовательно, все возможные конструкции могут быть реализованы соответствующим образом.

Общность и простота

Некоторые конкретные цели построения — например, построение квадрата — потенциально могут иметь относительно простые решения построения, которые не будут продемонстрированы в статье, несмотря на ее простоту. Исключение таких построений уменьшает объем статьи. Цель этих решений заключается в том, что такие построения могут быть не повсеместными или недостаточно полезными, особенно для целей доказательства теоремы. Хотя теорема и конструкции, найденные здесь, могут быть использованы для построения любой фигуры, не делается никаких заявлений о существовании более простых (использующих только линейку) альтернатив для какой-либо конкретной конструкции.

Произвольное размещение точек

Построения Штейнера и те построения, которые здесь доказывают теорему Понселе-Штейнера, требуют произвольного размещения точек в пространстве. Эти построения опираются на концепцию неподвижных точек (и неподвижных линий), где результирующее построение не зависит от произвольности, использованной во время построения. Они известны как инварианты преобразования . В некоторых парадигмах построения — например, в геометрическом определении конструктивного числа — произвольное размещение точек может быть запрещено. Традиционная геометрия не имеет такого ограничения на размещение точек; с таким ограничением против размещения произвольных точек одиночный круг действительно слабее циркуля. Однако это можно примирить. Построения Штейнера могут быть использованы в качестве основы для множества конструктивных чисел, если вводить в множество только те точки, которые являются неподвижными/инвариантными, игнорируя произвольно размещенные точки, требуемые во время построения.

Относительно доказательства и подхода

Сомнения по поводу конструкций №1 или №3: определение линий и их пересечение

Любые сомнения относительно конструкций № 1 или № 3 в равной степени относятся к традиционной парадигме построения, которая включает циркуль, и, таким образом, не являются проблемами, уникальными для теоремы Понселе-Штайнера. Их обоснования — если таковые будут даны — не будут рассматриваться в этой статье.

Сомнения по поводу конструкции №2: определение и построение окружностей

Конструкция №2 не должна вызывать беспокойства. Хотя бесспорно, что уникальная окружность определяется точкой центра и точкой на ее окружности, уместным вопросом является то, является ли это достаточной информацией для целей построения только с помощью линейки или требуется нарисованная дуга. Согласно фундаментальным конструкциям, дуга окружности используется только в традиционных парадигмах построения для целей пересечений окружность-окружность и окружность-линия, в них дуга окружности используется непосредственно для определения точек пересечения. Таким образом, если конструкции №4 и №5 выполнимы без дуги окружности, с которой происходит пересечение, то это докажет необязательность рисования дуги. Следовательно, это будет означать, что конструкция №2 фактически удовлетворяется простой маркировкой двух точек, определяющих уникальную окружность. Это утверждение будет рассмотрено позже в этой статье.

Выбор конструкции среди вариантов

В общих конструкциях часто есть несколько вариаций, которые дадут тот же результат. Выбор, сделанный в таком варианте, может быть сделан без потери общности . Однако, когда конструкция используется для доказательства того, что что-то может быть сделано, нет необходимости описывать все эти различные варианты, и для ясности изложения ниже будет приведен только один вариант. Это служит как доказательством возможности, так и демонстрацией методологии. Варианты, выбранные ниже, сделаны так из-за их повсеместности и обобщаемости в применении, а не из-за их простоты или удобства при каком-либо конкретном наборе особых условий.

Альтернативные доказательства

Существуют альтернативные доказательства теоремы Понселе-Штайнера, происходящие из алгебраического подхода к геометрии . Опираясь на уравнения и числовые значения в реальном координатном пространстве , посредством изоморфизма с евклидовой плоскостью, это довольно современная интерпретация, которая требует, чтобы понятия длины , расстояния и координатных положений были импортированы в плоскость. Алгебраическое доказательство иллюстрирует зависимость теоремы от аксиомы Архимеда , которая не может быть сформулирована в логике первого порядка . Это выходит далеко за рамки традиционной геометрии. В этой статье используется более традиционный подход и теорема доказывается с использованием чисто геометрических конструктивных методов, что также демонстрирует практическое применение.

Конструктивное доказательство

Далее следует доказательство теоремы и полезные конструкции, использующие только линейку.

Некоторые предварительные построения

Для доказательства приведенных выше конструкций #4 и #5, которые включены ниже, ниже также объясняются несколько необходимых промежуточных конструкций, поскольку они часто используются и на них ссылаются. Это также конструкции, использующие только линейку. Все конструкции ниже опираются на базовые конструкции #1,#2,#3 и любые другие конструкции, перечисленные до них.

Параллельно прямой, имеющей коллинеарный отрезок, разделенный пополам

Это построение не требует использования данной окружности. Естественно, любая линия, проходящая через центр данной окружности, неявно имеет разделенный пополам сегмент: диаметр делится пополам центром. Анимированный GIF-файл , встроенный во введении к этой статье, демонстрирует это построение — опирающееся на разделенный пополам диаметр; дуга окружности никогда не используется — которое здесь повторяется без окружности и с перечисленными шагами.

Построение параллельной прямой, проходящей через произвольную точку, заданной произвольной прямой, имеющей вложенный в нее отрезок, деленный пополам.

Дана произвольная прямая n (черного цвета), на которой находятся две точки A и B , имеющие среднюю точку M между ними, и произвольная точка P на плоскости (предполагается, что она не лежит на прямой n ), через которую необходимо провести параллельную прямой n :

  1. Постройте линию AP (красного цвета).
  2. Постройте линию BP (оранжевого цвета).
  3. Определим произвольную точку R на прямой AP .
  4. Постройте линию BR (зеленого цвета).
  5. Постройте линию MR (светло-голубого цвета).
  6. Прямые MR и BP пересекаются в точке X.
  7. Постройте линию AX (фиолетового цвета).
  8. Прямые BR и AX пересекаются в точке Q.
  9. Постройте линию PQ (темно-синего цвета) — искомую параллель.

В некоторой литературе отрезок разделенной пополам линии иногда рассматривается как одномерная «окружность», существующая на линии. В качестве альтернативы, в некоторой литературе отрезок разделенной пополам линии рассматривается как двумерная окружность в трехмерном пространстве с линией, проходящей через диаметр, но не параллельной плоскости, таким образом пересекая плоскость построения в двух точках на окружности, а середина просто является предписанным центром окружности.

Эта конструкция является частным случаем проективной гармонически сопряженной конструкции, которая в данной статье не демонстрируется.

Создание отрезка, разделенного пополам на линии

Если прямая проходит через центр окружности, то отрезок, определяемый диаметром, проходящим через окружность, делится пополам центром окружности. В общем случае, однако, любая другая прямая на плоскости может иметь построенный на ней отрезок, разделенный пополам. Это построение требует использования данной окружности.

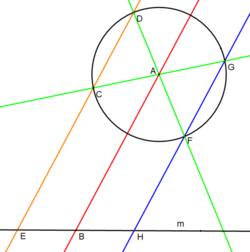
Построение произвольного отрезка прямой, разделенного пополам на заданной прямой.

Имея линию m (черного цвета) и окружность с центром в точке A , мы хотим создать на линии точки E , B и H так, чтобы B была средней точкой:

  1. Нарисуйте произвольную линию (красного цвета), проходящую через центр заданной окружности A и желаемую середину B (выбранную произвольно) на линии m .
    • Обратите внимание, что красная линия AB проходит через центр окружности и выделяет диаметр, разделенный центром окружности пополам. Любая параллель может быть проведена из этой линии согласно предыдущему построению.
  2. Выберем произвольную точку C на данной окружности
    • Для удобства точка не должна лежать на перпендикуляре к линии АВ, проходящей через центр окружности.
  3. Постройте прямую (оранжевого цвета), проходящую через точку C и параллельную красной линии AB .
    • Если точка C находится на перпендикуляре AB, проходящем через центр окружности, то параллель будет касательной к окружности. Построение возможно и другими способами, не перечисленными в этой статье, но выбирать такую ​​точку также необязательно.
    • Эта параллель пересекает данную окружность в точке D.
    • Эта параллель также пересекает черную линию m в точке E , определяя один конец отрезка.
  4. Создайте две линии (зеленого цвета), AC и AD , каждая из которых проходит через центр данной окружности.
    • Эти зеленые линии пересекают заданную окружность в точках G и F соответственно.
  5. Линия FG (синего цвета) пересекает линию m в точке H , определяя другую конечную точку отрезка линии.
    • Теперь существует сегмент EH, совпадающий с линией m и имеющий среднюю точку B.

Поскольку точка C выбрана произвольно, нет необходимости в том, чтобы она неудобно находилась на перпендикуляре линии AB, проходящей через центр окружности. Однако если это так, линия CD — это просто касательная линия к окружности, проходящая через точку C , которая совпадает с точкой D. Такое построение возможно, хотя оно и не приводится в этой статье. Точки F и G могут быть построены, как и прежде, и также будут равны друг другу. И снова, линия GF — это просто касательная линия к окружности в этой точке. Таким образом, точки E , H и их середина B могут быть найдены, как и прежде, с небольшим изменением, добавляющим подпостроение.

Построение параллели любой прямой

Это построение требует использования данной окружности. Для того чтобы обобщить построение параллельных линий на все возможные линии, а не только те, которые имеют коллинеарный отрезок, разделенный пополам, необходимо иметь дополнительную информацию. В соответствии с теоремой Понселе-Штайнера, окружность (с центром) является объектом выбора для этого построения.

Чтобы построить параллельную прямую любой заданной прямой, проходящей через любую точку плоскости, мы тривиально объединяем два построения:

  1. Любая линия, от которой требуется провести параллель, должна иметь построенный на ней сегмент, разделенный пополам, если таковой еще не существует.
  2. Затем параллель строится в соответствии с предыдущим параллельным построением, включающим коллинеарный отрезок, разделенный пополам.

В альтернативных конструкциях, которые не продемонстрированы в этой статье, параллель может быть построена из любой пары прямых, которые уже параллельны друг другу; таким образом, третья параллель может быть получена из любых двух, без использования окружности. Кроме того, параллель любой прямой может быть построена всякий раз, когда в плоскости существует любой параллелограмм , также без использования данной окружности.

Построение перпендикулярной линии

Построение перпендикулярной линии.

Эта конструкция требует использования заданной окружности и использует теорему Фалеса .

Из данной прямой m и данной точки A на плоскости требуется построить перпендикуляр к этой прямой через точку. При условии, что дана окружность O(r) .

  1. Если желаемая прямая, из которой требуется провести перпендикуляр, m , не проходит через данную окружность, как показано на рисунке, или также проходит через центр данной окружности, то можно произвольно построить новую параллельную прямую (красного цвета) так, чтобы она проходила через данную окружность, но не через ее центр, и перпендикуляр следует провести из этой прямой.
  2. Эта красная линия, которая проходит через данную окружность , но не через ее центр, пересечет данную окружность в двух точках, B и C.
  3. Проведите линию BO (оранжевого цвета) через центр круга.
    • Эта прямая пересекает данную окружность в точке D.
    • Угол ∠ BOD равен 180°.
  4. Нарисуйте линию DC (светло-зеленого цвета).
    • Эта линия перпендикулярна красным (и, следовательно, черным) линиям BC и m .
    • По теореме Фалеса угол ∠BCD равен 90° .
  5. Постройте параллельную прямой DC через точку A, используя предыдущие построения.
    • Перпендикуляр исходной черной линии m теперь существует в плоскости, линии DC .
    • Через любую точку плоскости можно провести параллель любой прямой.

Если линия, из которой нужно провести перпендикуляр, проходит через центр окружности, альтернативным подходом будет построение касательных к окружности в точках пересечения линий с использованием построений Штейнера. В данной статье это не демонстрируется.

Другим вариантом в случае, если прямая проходит через центр окружности, было бы построение параллельной ей через окружность в произвольной точке. Равнобедренная трапеция (или потенциально равнобедренный треугольник) образована точками пересечения с окружностью обеих прямых. Две непараллельные стороны которой можно продолжить до точки пересечения между ними, и провести оттуда линию через центр окружности. Эта линия перпендикулярна, а диаметр делится центром пополам.

С помощью альтернативного построения, не продемонстрированного в этой статье, перпендикуляр любой линии может быть построен без окружности, при условии, что на плоскости существует любой квадрат .

Построение середины любого отрезка (деление отрезка пополам)

Построение середины произвольного отрезка по неколлинеарной параллельной прямой.

Дан отрезок AB , который нужно разделить пополам. При желании можно указать параллельную прямую m на плоскости.

  1. Если прямая m , параллельная отрезку AB , не существует на плоскости, то ее необходимо построить согласно более ранним построениям с использованием заданной окружности на плоскости (не изображена).
    • Для этого построения не требуется заданная окружность на плоскости, если параллель уже существует.
    • Параллель можно расположить на плоскости произвольно, главное, чтобы она не была коллинеарна отрезку прямой.
  2. Произвольно выберем точку C на плоскости, не лежащую на одной прямой или отрезке прямой.
    • В качестве альтернативы можно построить точку C как пересечение прямых AD и BE , при условии, что точки D и E уже существуют на параллельной прямой m .
  3. Начертите линию AC (красного цвета), пересекающую линию m в точке D.
  4. Начертите линию BC (оранжевого цвета), пересекающую линию m в точке E.
  5. Нарисуйте две линии, AE и BD (каждая светло-зеленого цвета), пересекающиеся в точке X.
  6. Начертите линию CX (синего цвета), пересекающую отрезок AB в точке M.
    • Точка M — искомая середина отрезка AB .
    • Линия CX также делит пополам отрезок DE.

Для дополнительной перспективы, в некотором смысле эта конструкция является вариантом предыдущей конструкции параллели из отрезка, разделенного пополам, и, следовательно, также является частным случаем проективного гармонического сопряжения (не представленного в этой статье). Это тот же набор линий, взятый в целом, но построенный в другом порядке и из другого начального набора условий, достигающий другой конечной цели.

Поскольку любой произвольный сегмент на одной из двух параллельных линий может быть разделен пополам, и любая линия с разделенным пополам сегментом на ней может иметь параллельную конструкцию, два сценария являются геометрически эквивалентными предложениями. Они подразумевают друг друга; простая конструкция может преобразовать один сценарий в другой, не используя никакой дополнительной информации.

Также стоит отметить, что если трапеция ABED является равнобедренной трапецией, то биссектриса CX также является перпендикуляром к ней. Равнобедренная трапеция образуется, когда прямые AB и DE каждая проходят через окружность и пересекаются в этих определяющих точках, и в этом случае перпендикуляр к ней является осевой линией окружности. Если прямая DE сама является осевой линией, то центр окружности найден, если он еще не был известен.

Кроме того, если ABED — параллелограмм, то построение не будет выполнено так, как оно написано. Точка X может быть найдена обычным образом, но точка C не будет существовать. Вместо этого биссектриса может быть построена как параллельная линия AD или BE через точку X. Однако в альтернативном построении любой отрезок линии может быть разделен пополам, если на плоскости существует параллелограмм (не показано в этой статье).

Вращение отрезка прямой

Для определения окружности требуется только центр и одна точка - любая точка - на окружности. В принципе новая точка B' строится так, что окружность A(B) равна окружности A(B') , хотя точка B не равна точке B' . По сути, отрезок AB поворачивается вокруг оси точки A , в AB' , для другого набора определяющих точек для той же окружности.

Конструкция Штейнера вращения отрезка прямой

Один из способов сделать это, удовлетворяющий большинству условий, заключается в следующем:

  1. Нарисуйте отрезок AB (черного цвета).
  2. Постройте параллельную (красного цвета) линию AB через центр, точку O , данной окружности.
    • Параллельная прямая пересекает данную окружность в некоторой точке b .
  3. Выберем произвольно точку b' на данной окружности, не лежащую на одной прямой с прямой Ob .
  4. Нарисуйте линию Обь (оранжевого цвета).
  5. Постройте параллельную Ob' прямую через точку A (выделена пурпурным цветом).
  6. Нарисуйте линию bb' (светло-зеленого цвета), соединяющую точки на окружности.
  7. Постройте параллельную линию bb' через точку B (синего цвета).
  8. Пересечем синюю и розовую параллели из точек B и A соответственно.
    • Это точка B' .
    • Точка B' — искомая точка, вращающая отрезок прямой и определяющая ту же окружность с центром в точке A.

Эта конструкция не сработает, если желаемое вращение диаметрально противоположно окружности (т. е. вращение на полкруга). Одним из решений этого сценария является использование двух отдельных конструкций вращения, ни одна из которых не является вращением на полкруга от предыдущей, а одна действует как промежуточный шаг. Выберите любой угол вращения произвольно, завершите вращение, затем выберите дополнительный угол и выполните вращение во второй раз.

Существует второе, альтернативное решение конструкции вращения, основанное на проекциях и перспективных точках. Хотя оно избегает вышеупомянутого осложнения вращения полукруга, у него есть свои собственные осложнения, которые аналогичным образом решаются с помощью промежуточных конструкций вращения. Конструкция не более универсальна. Она не демонстрируется в этой статье.

Построение радикальной оси между окружностями

Построение радикальной оси между окружностями с помощью одной только линейки.

Эта конструкция требует использования заданного круга (который не изображен) для ранее продемонстрированных упомянутых подконструкций.

Предположим, что две окружности A ( B ) и C ( D ) заданы неявно, определены только точками A , B , C и D на плоскости, с определенными их центрами, но не построенными циркулем. Радикальная ось , линия m (темно-синего цвета), между двумя окружностями может быть построена:

  1. Проведите линию AC (оранжевого цвета) через центры окружностей.
  2. Нарисуйте отрезок BD (красного цвета) между точками на окружности кругов.
  3. Найдите середину M отрезка BD .
  4. Начертите линии AM и CM (обе светло-зеленого цвета), соединяющие середину сегмента с каждым из центров окружности.
  5. Постройте прямую j (фиолетового цвета), проходящую через точку B и перпендикулярную AM .
    • Прямая j является радикальной осью между окружностью M ( B ) и окружностью A ( B ) .
  6. Постройте линию k (темно-зеленого цвета), проходящую через точку D и перпендикулярную CM .
    • Прямая k является радикальной осью между окружностью M ( B ) и окружностью C ( D ) .
  7. Прямые j и k пересекаются в точке X.
    • Если прямые j и k параллельны, то середина отрезка M лежит на прямой AC - центры окружностей A(B) , C(D) и M(B) лежат на одной прямой - и построение не удастся. Требуется альтернативный подход (см. ниже).
    • Точка X является центром силы между окружностями A ( B ) , C ( D ) и M ( B ) и, следовательно, является единственной точкой, которая лежит на радикальной оси между любыми двумя из трех окружностей.
    • Следовательно, по транзитивности точка X существует на радикальной оси между окружностями A ( B ) и C ( D ) .
  8. Постройте прямую m (темно-синего цвета) , перпендикулярную прямой AC и проходящую через точку X.
    • Линия m — искомая радикальная ось.

В случае, если построение радикальной оси не удается из-за отсутствия точки пересечения X между параллельными прямыми j и k , что является результатом совпадения расположения средней точки M на прямой AC , требуется альтернативный подход. Один из таких подходов — вращать отрезок AB вокруг точки оси A (центра окружности A ( B ) ). Достигнув произвольного вращения AB' , определяющего ту же окружность, построение радикальной оси можно начинать заново без проблем.

Пересечение прямой с окружностью (Конструкция №4)

Построение точек пересечения прямой и окружности с помощью одной только линейки.

Эта конструкция требует использования предоставленной окружности, O ( r ) . Любая линия может быть естественным образом пересечена любой окружностью, нарисованной циркулем.

Дана линия m (черного цвета) и окружность P(Q) , которая не построена циркулем. Точки пересечения окружности P(Q) и линии m , которые являются точками A и B , могут быть построены:

  1. Проведите линию PQ (красного цвета) через точки, определяющие окружность.
    • Если точка O лежит на одной прямой с линией PQ, то отрезок PQ необходимо повернуть вокруг центральной точки P окружности, и построение следует начать заново.
  2. Постройте параллельную (оранжевого цвета) линию PQ через центр O предоставленной окружности.
    • Параллельная прямая пересекает указанную окружность в двух точках, одна из которых выбирается произвольно : R.
  3. Проведите линию PO (светло-зеленого цвета) через центры двух окружностей (т.е. ту, которую дает построение циркуля, и ту, которую предстоит пересечь).
  4. Нарисуйте линию QR (светло-голубого цвета), соединяющую две точки на окружностях двух кругов.
  5. Пересечем прямые PO и QR в точке X.
    • Если точка X не существует из-за параллельности прямых PO и QR (что является следствием того , что окружности P(Q) и O(r) имеют одинаковые радиусы), то вернитесь к шагу 2 и выберите альтернативную точку пересечения R.
  6. Выбрав произвольно точку M на прямой m так, чтобы она не лежала на прямой PO , проведем прямую PM (фиолетового цвета).
    • Для простоты построения и только в том случае, если линия PQ не параллельна линии m , линии PM и PQ могут совпадать.
  7. Нарисуйте линию MX (коричневого цвета).
  8. Постройте параллельную (темно-фиолетовую) линию PM через центр O предоставленной окружности.
    • Параллельная прямая пересекает прямую MX в точке N.
  9. Постройте параллельную (желтого цвета ) прямой m через точку N.
    • Параллельная прямая пересекает указанную окружность в точках C и D.
    • Если параллельная прямая не пересекает указанную окружность, то и прямая m не пересекает окружность P(Q) .
  10. Нарисуйте линии CX и DX (обе темно-синего цвета).
    • Обе эти линии пересекают линию m в точках A и B соответственно.
  11. Точки A и B — искомые точки пересечения прямой m и окружности P(Q) .

Пересечение двух окружностей (Конструкция №5)

Пересечение двух окружностей становится тривиальной комбинацией двух более ранних конструкций:

  1. Постройте радикальную ось между двумя окружностями.
  2. Постройте точки пересечения между радикальной осью и любой из двух произвольно выбранных окружностей:
    • Радикальная ось представляет собой прямую, поэтому данное построение возможно согласно предыдущему построению: базовая конструкция №4.
  3. Эти точки и есть искомые точки пересечения окружностей.
    • Две окружности и радикальная ось пересекаются в одних и тех же геометрических местах точек: в двух точках, в одной точке, если они касательные, или ни в одной, если они не пересекаются.
    • Если радикальная ось не пересекает ни одну окружность, то она не пересекает ни одну из них, и обе окружности также не пересекаются.

Окружность, проходящая через одну точку с центром в другой точке (Конструкция №2, пересмотренная)

Вторая базовая конструкция — описание полного круга только с его центром и одной точкой на радиусе, определяющем окружность — никогда не нуждалась в построении дуги с помощью циркуля для того, чтобы круг можно было использовать в конструкциях. А именно, пересечения кругов как с кругами, так и с линиями, которые вместе являются сутью всех конструкций, включающих круг, достижимы без дуги. То есть, любой круг, определенный центральной точкой и точкой на его окружности, может быть пересечен любой линией и любым другим аналогичным образом определенным кругом; ничего не теряется, если опустить дугу. Таким образом, определение круга его центром и любой произвольной точкой на его окружности достаточно для полного описания всего круга и использования его в конструкциях. Таким образом, дуга служит только эстетической цели. Базовая конструкция № 2 удовлетворена.

Заключение

Поскольку было показано, что все пять основных построений можно осуществить с помощью одной лишь линейки, при условии, что на плоскости расположена одна окружность с центром, это доказывает теорему Понселе-Штейнера.

Практическое применение

Теорема Понселе-Штайнера является фундаментальным результатом проективной геометрии, имеющим важные практические приложения для геометров и математиков. Для практикующих геометров понимание этой теоремы имеет решающее значение, поскольку она демонстрирует мощь проективных методов и предоставляет альтернативные методы решения классических задач построения, а также более широкие идеи.

Практические приложения теоремы Понселе-Штайнера выходят за рамки чистой математики. В таких областях, как компьютерная графика и вычислительная геометрия , она предлагает эффективные алгоритмы для геометрических построений без необходимости более прямых и длительных подходов. Это может привести к более рационализированным и надежным реализациям программного обеспечения. Кроме того, теорема имеет значение в архитектурном проектировании и инжиниринге , где она может упростить определенные процессы черчения и моделирования и поддается улучшению методов проектирования и моделирования. Часто координаты могут быть вычислены с использованием последовательности линейных уравнений , а не квадратных корней , связанных с окружностью, что позволяет более быстрые, точные и более численно устойчивые вычисления. Фактически, Поль Дирак применил проективную геометрию в своем вкладе в развитие квантовой механики . [5]

Теорема не только имеет историческое значение, но и, как и проективная геометрия в более широком смысле, предлагает более глубокое понимание природы геометрических построений и взаимосвязей между различными геометрическими инструментами и геометрическими структурами. Она бросает вызов традиционному мышлению о том, что необходимо для геометрических построений, и открывает геометру новые пути решения задач. Освоение идей проективной геометрии повышает способность геометра подходить к проблемам с разных точек зрения, способствуя креативности и универсальности в его работе.

Другие типы ограниченного строительства

Ограниченные конструкции с использованием компаса

Конструкции, использующие только компас

Теорему Понселе–Штайнера можно противопоставить теореме Мора–Маскерони , которая гласит, что любое построение с помощью циркуля и линейки можно выполнить, используя только циркуль. Линейка не требуется, но для эстетических целей; больше ничего на плоскости не нужно.

Ржавый компас

Ограничение ржавого циркуля позволяет использовать циркуль и линейку, при условии, что циркуль создаёт окружности фиксированного радиуса. Хотя конструкции ржавого циркуля исследовались с 10-го века, и было показано, что все Евклида можно построить с ржавым циркулем к 17-му веку, теорема Понселе-Штайнера доказывает, что ржавый циркуль и линейка вместе более чем достаточны для любого и всех евклидовых построений. Действительно, ржавый циркуль становится инструментом, упрощающим построения по сравнению с простой линейкой и одним кругом. С другой стороны, теорема Понселе-Штайнера не только фиксирует ширину ржавого циркуля, но и гарантирует, что циркуль сломается после первого использования.

Жесткий и разрушающийся компас

Теорема эквивалентности компаса доказывает , что жесткий компас (также называемый современным компасом) — тот, который сохраняет свой интервал при подъеме с плоскости — эквивалентен традиционному разрушающемуся компасу (также называемому делителем) — тому, который не сохраняет свой интервал, таким образом «сбрасываясь на ноль» каждый раз, когда его поднимают с плоскости. Возможность переноса расстояний (т. е. построение конгруэнтных окружностей, перенос окружности на плоскости) — операция, ставшая тривиальной благодаря фиксируемой апертуре жесткого компаса — была доказана Евклидом как возможная с разрушающимся компасом. Следовательно, жесткий компас и разрушающийся компас эквивалентны; то, что может быть построено одним, может быть построено другим.

Можно справедливо отметить, что способность переводить окружности с помощью разрушающегося циркуля является, в некотором смысле, более чистым результатом. Это доказывает, что операция может быть достигнута абстрактным образом, сохранена в самой геометрии, а не как свойство физического инструмента, предназначенного для определенной цели и не интегрированного в плоскость.

Фактически, перемещение окружности может быть выполнено с использованием только складного циркуля, без инструмента линейки. Поскольку это верно даже в парадигме построения только с циркулем, эквивалентность не зависит от линейки, дополняющей складной циркуль. В этой парадигме, кроме того, операция перемещения окружности требует не более трех дополнительных окружностей (применений циркуля) по сравнению с жестким циркулем.

Ограниченные конструкции Штейнера

Требование, предъявляемое к теореме Понселе-Штайнера, а именно, что на плоскости должна существовать хотя бы одна окружность с центром, с тех пор было обобщено или усилено, включив в нее альтернативные, но столь же ограничительные условия.

Несомненно, существуют и другие уникальные сценарии, кроме перечисленных здесь. Это не исчерпывающий список возможностей.

Понселе-Штайнера без центра круга

В некоторых конфигурациях — или альтернативных парадигмах — центр окружности может быть полностью опущен, и все равно весь Евклид остается конструируемым. В каждом из следующих сценариев предоставленные окружности лишены своих центров. Подход к этим ситуациям заключается в построении центра окружности из предоставленной информации, оставляя окружность с центром на плоскости. Таким образом, это проблемы, сводимые к той, которая уже была решена теоремой Понселе-Штайнера. Следовательно, они являются геометрически эквивалентными сценариями; окружность с центром может быть использована для построения любого из этих сценариев, и любой из этих сценариев может создать окружность с ее центром.

Эти сценарии не противоречат теореме Штайнера, которая, хотя указание центра является абсолютно необходимым, также предполагает, что на плоскости существует только одна окружность без какой-либо другой ключевой информации.

Сценарии с одним кругом

В одном из самых простых альтернативных сценариев достаточно одной окружности. Необходимо, чтобы на плоскости существовали два различных набора из двух параллельных линий, так что эти два набора из двух линий не были бы все взаимно параллельными, или, что эквивалентно, ни один параллелограмм на плоскости. В качестве альтернативы у нас может быть только три параллельные линии, одна из которых является средней линией, то есть средней линией, равноудаленной от двух других.

Сценарии двух кругов

В двух других таких альтернативах достаточно иметь две концентрические окружности или две различные пересекающиеся окружности, из которых имеются два случая: две точки пересечения и одна точка пересечения (касательные окружности).

Существуют и другие вариации. Достаточно иметь два произвольных круга, при условии, что на центральной линии, проходящей через них, или на радикальной оси между ними задана хотя бы одна точка, или при условии, что на плоскости произвольно существует не менее одного набора из двух параллельных линий.

Три круга

В качестве альтернативы также достаточно иметь три непересекающихся окружности [6], при условии, что они не все принадлежат к одной и той же соосной (или коаксиальной) системе окружностей, то есть каждая пара из трех данных окружностей должна иметь между собой отдельную радикальную ось.

В каждом из этих сценариев существует больше информации, чем просто один или два круга. В сценариях с двумя кругами тот факт, что они концентричны или имеют определяемые точки пересечения, или существование точки либо на центральной линии, либо на радикальной оси, представляет собой дополнительную часть информации, выходящую за рамки простого наличия второго круга. Третий круг предоставляет значительную информацию. К сожалению, в случаях с одним кругом, одной точки или линии явно недостаточно.

Понселе-Штайнера без полной дуги окружности

Дуга окружности Севери

В другой альтернативе весь круг вообще не требуется. В 1904 году Франческо Севери доказал, что любой малой дуги (круга) вместе с центром будет достаточно. [7] Это построение ломает ржавый циркуль в любой точке до завершения первого круга, но после его начала, таким образом рисуя некоторую непрерывную часть дуги круга на плоскости, и все же все построения остаются возможными. Таким образом, условия, предполагающие теорему Понселе-Штейнера, действительно могут быть ослаблены, но только относительно полноты дуги окружности, а не, согласно теореме Штейнера, относительно центра.

Теорема демонстрирует конструкцию Штейнера точек пересечения между прямой и окружностью дуги, независимо от размера или положения дуги, используя только линейку и дугу. Конструкция также не использует центр окружности дуги. Хотя центр требуется для завершения всего Евклида, как доказывают теорема Штейнера и теорема Понселе-Штейнера, центр не нужен для пересечения прямой с окружностью этой дуги. Используя эту конструкцию, дугу и центр окружности дуги, все вышеприведенные конструкции Понселе-Штейнера одинаково достижимы, хотя и с большими трудностями.

Доказательство Севери показывает, что любая дуга окружности полностью характеризует окружность и позволяет найти точки пересечения (линий) с ней. При включении ее центра вся окружность описывается. Следовательно, минимальное требование теоремы Понселе-Штейнера об одной окружности по-прежнему выполняется. Окружность остается полностью определенной и полностью используемой, независимо от отсутствия некоторой части завершенной дуги. Поскольку конструкция Севери пересекает линии с окружностью дуги, а теорема Понселе-Штейнера строит пересечения окружность-окружность с помощью линейки, нет дополнительной необходимости обосновывать пересечения окружность-окружность в рамках этой ограниченной парадигмы.

Дуга, связанная с пропусками центра окружности

Также в каждом из ранее упомянутых сценариев, в которых центры окружностей опущены, полнота дуги окружности не является необходимой, согласно теореме Севери. Однако в случае двух пересекающихся окружностей их точки пересечения должны быть явно указаны всякий раз, когда дуги окружности(окружностей) не существуют там, где есть точки пересечения. То есть, если точки пересечения между двумя окружностями дуг не могут быть найдены напрямую с помощью двух дуг, они должны быть указаны. В противном случае полнота дуги окружности излишня.

Ограничения потока управления

Хотя это относительно новая концепция, вытекающая из вычислительных систем , понятие потока управления и его различные ограничения в контексте геометрии также являются предметом изучения. Поскольку это относится к геометрическим конструкциям, эти ограничения обычно накладываются на геометра. Как и в случае с конструируемыми числами , запреты на произвольное размещение точек являются одним из возможных ограничений потока управления, ранее обсуждавшихся в этой статье. В вышеупомянутой теореме Мора-Маскерони могут быть наложены ограничения на радиус компаса, такие как минимумы и максимумы, заданные набором начальных точек. Другие примеры могут включать ограничения на последовательности и порядок построения, ветвление решений и повторение или повторение шагов.

Расширенные, освобожденные или неусисные конструкции

Вместо того, чтобы еще больше ограничивать правила построения, не менее интересно изучать ослабление ограничений. Иногда их называют расширенными конструкциями , потому что они расширяют то, что можно построить, расширяя допустимый набор инструментов. Эти конструкции также называются конструкциями neusis (от греческого ), потому что они используют инструменты, отличные от циркуля и линейки, или освобожденными конструкциями , потому что они смягчают ограничения традиционной парадигмы.

Так же, как геометры изучали, что остается возможным построить (и как), когда на традиционные правила построения накладываются дополнительные ограничения, такие как только циркуль, только линейка, ржавый циркуль и т. д., они также изучали, какие конструкции становятся возможными, которые уже не были возможны, когда снимаются естественные ограничения, присущие традиционным правилам построения. Задаются такие вопросы, как «что становится конструктивным», «как это можно построить», «какое наименьшее количество традиционных правил должно быть нарушено», «какие простейшие инструменты необходимы», «какие, казалось бы, разные инструменты эквивалентны», «как новая парадигма упрощает традиционные конструкции» и т. д.

Произвольный угол не может быть трисектирован с использованием традиционных правил циркуля и линейки, например, но трисекция становится конструктивной, если допустить дополнительный инструмент эллипса на плоскости, который сам по себе не является конструктивным. Некоторые из традиционных нерешенных задач, таких как трисекция угла, удвоение куба , квадратура круга , нахождение кубических корней и т. д., поскольку было доказано, что их невозможно решить только с помощью циркуля и линейки, были решены с использованием расширенного набора инструментов. В целом, объекты, изученные для расширения области конструктивного, включали:

Каждый из трех вышеприведенных категориальных подходов имеет свои собственные уникальные решения трисекции угла, как и различные инструменты и кривые.

Древние геометры считали конструкции с помощью циркуля и линейки (известные как плоские конструкции ) идеальными и предпочтительными. Во-вторых, они предпочитали сплошные конструкции , которые включали использование конических сечений на плоскости, отличных от окружности. В-третьих, они отдавали предпочтение использованию произвольных гладких кривых на плоскости (таких как архимедова спираль), и меньше всего — использованию неусейса (альтернативных физических ручных инструментов). Сомнительно, что древние геометры — по крайней мере, западного мира — вообще рассматривали складывание бумаги.

Термин невсис (единственное число) или конструкция невсис может также относиться к определенному инструменту или методу, использовавшемуся древними геометрами.

Градуированная линейка уникальна тем, что она определяет метрику , а также норму , и дает начало алгебраической трактовке геометрии , декартову графику , и импортирует стандартную единицу для пропорциональности сегментов. Алгебраический подход к геометрии предлагает четкое доказательство теоремы Понселе-Штайнера. Некоторые алгебраические операции, выполняемые в геометрической плоскости, даже в традиционной геометрии, имеют смысл только в контексте установленной полевой алгебры, например, извлечение квадратных корней .

Приближения

Стоит отметить, что во всех парадигмах построения неявным правилом является то, что все построения должны завершаться конечным числом применений доступных инструментов (обычно циркуля и линейки) и давать точные предполагаемые результаты. Принято считать само собой разумеющимся, что, исходя в основном из философских соображений, таких как платоновский идеализм и операционализм, [8] древнегреческие геометры подчеркивали конечность и точность в своих построениях. Целые дискуссии можно было бы вести, если бы любое из этих условий было смягчено.

Для любой иной неконструируемой фигуры:

Например, трисекция угла может быть выполнена точно с помощью циркуля и линейки, используя бесконечную последовательность биссекций угла. Если построение завершается на некоторой конечной итерации, точная аппроксимация трисекции может быть достигнута с произвольной точностью. Хотя каждая точка, линия или окружность являются допустимой конструкцией, то, что она стремится приблизить, никогда не может быть по-настоящему достигнуто в конечных применениях циркуля и/или линейки.

Существуют, в качестве альтернативы, точно конструктивные неитеративно построенные фигуры, которые являются разумными приближениями для неконструктивных фигур. Например, существует относительно простая неитеративно построенная аппроксимация семиугольника .

Дальнейшие обобщения

Теорема Понселе-Штейнера была обобщена на более высокие измерения , например, трехмерная вариация, где линейка заменена плоскостью , а круг с центром заменен сферой с центром. По сути, это вариация трехмерной геометрии «только с линейкой» . Хотя исследования продолжаются, и некоторые предложения еще предстоит доказать, многие свойства, применимые к двумерному случаю, также применимы к более высоким измерениям, как реализации проективной геометрии. Кроме того, ведутся некоторые исследования по обобщению теоремы Понселе-Штейнера на неевклидовы геометрии.

Смотрите также

Примечания

  1. ^ ab Eves 1963, стр.205
  2. ^ https://www.encyclepedia.com/people/science-and-technology/mathematics-biographys/giovanni-battista-benedetti .
  3. ^ Ретц и Кейн 1989, стр.195
  4. ^ Джейкоб Штайнер (1833). Die geometrischen Konstructionen, ausgeführt mittelst der geraden Linie und eines festen Kreises, als Lehrgegenstand auf höheren Unterrichts-Anstalten und zur praktischen Benutzung (на немецком языке). Берлин: Фердинанд Дюммлер . Проверено 2 апреля 2013 г.
  5. ^ Farmelo, Graham (15 сентября 2005 г.). "Скрытая геометрия Дирака" (PDF) . Эссе. Nature . 437 (7057). Nature Publishing Group: 323. Bibcode : 2005Natur.437..323F. doi : 10.1038/437323a. PMID  16163331. S2CID  34940597.
  6. ^ Математический мир Вольфрама
  7. ^ Ретц и Кейн 1989, стр. 196
  8. ^ Blåsjö, Viktor (2022). «Операционализм: интерпретация философии древнегреческой геометрии». Foundations of Science . 27 (2): 587–708. doi :10.1007/s10699-021-09791-4.

Ссылки

Дальнейшее чтение

Внешние ссылки