Теория балок Эйлера–Бернулли

Метод расчета нагрузок в строительстве

Эту вибрирующую стеклянную балку можно смоделировать как консольную балку с ускорением, переменной линейной плотностью, переменным модулем сопротивления сечения, некоторым видом рассеивания, пружинящей конечной нагрузкой и, возможно, точечной массой на свободном конце.

Теория балок Эйлера–Бернулли (также известная как инженерная теория балок или классическая теория балок ) ^[1] является упрощением линейной теории упругости , которая обеспечивает средства расчета несущих и отклоняющих характеристик балок . Она охватывает случай, соответствующий малым отклонениям балки , которая подвергается только боковым нагрузкам. Игнорируя эффекты деформации сдвига и вращательной инерции, она, таким образом, является частным случаем теории балок Тимошенко–Эренфеста . Она была впервые сформулирована около 1750 года, ^[2], но не применялась в больших масштабах до разработки Эйфелевой башни и колеса обозрения в конце 19 века. После этих успешных демонстраций она быстро стала краеугольным камнем инженерии и средством осуществления Второй промышленной революции .

Были разработаны дополнительные математические модели , такие как теория пластин , но простота теории балок делает ее важным инструментом в науках, особенно в строительной и машиностроительной инженерии .

История

Схема поперечного сечения изогнутой балки, показывающая нейтральную ось.

Преобладающий консенсус заключается в том, что Галилео Галилей предпринял первые попытки разработать теорию балок, но недавние исследования утверждают, что Леонардо да Винчи был первым, кто сделал важные наблюдения. Да Винчи не хватало закона Гука и исчисления, чтобы завершить теорию, тогда как Галилея сдерживало неверное предположение, которое он сделал. ^[3]

Луч Бернулли назван в честь Якоба Бернулли , который сделал важные открытия. Леонард Эйлер и Даниил Бернулли были первыми, кто составил полезную теорию около 1750 года. ^[4]

Уравнение статической балки

Уравнение Эйлера–Бернулли описывает связь между прогибом балки и приложенной нагрузкой: ^[5]

${\displaystyle {\frac {\mathrm {d} ^{2}}{\mathrm {d} x^{2}}}\left(EI{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q\,}$

Кривая описывает прогиб балки в направлении в некотором положении (напомним, что балка моделируется как одномерный объект). — распределенная нагрузка, другими словами, сила на единицу длины (аналогично давлению, являющемуся силой на единицу площади); она может быть функцией , , или других переменных. — модуль упругости и — инерционный момент площади поперечного сечения балки. должен быть рассчитан относительно оси, перпендикулярной приложенной нагрузке. ^{[N 1]} Явно, для балки, ось которой ориентирована вместе с нагрузкой вдоль , поперечное сечение балки находится в плоскости , а соответствующий инерционный момент площади равен ${\displaystyle w(x)}$ ${\displaystyle z}$ ${\displaystyle x}$ ${\displaystyle q}$ ${\displaystyle x}$ ${\displaystyle w}$ ${\displaystyle E}$ ${\displaystyle I}$ ${\displaystyle I}$ ${\displaystyle x}$ ${\displaystyle z}$ ${\displaystyle yz}$

${\displaystyle I=\iint z^{2}\;dy\;dz,}$

где предполагается, что центр тяжести поперечного сечения находится в точке . ${\displaystyle y=z=0}$

Часто произведение (известное как жесткость при изгибе ) является константой, так что ${\displaystyle EI}$

${\displaystyle EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=q(x).\,}$

Это уравнение, описывающее прогиб однородной статической балки, широко используется в инженерной практике. Табличные выражения для прогиба для обычных конфигураций балок можно найти в инженерных справочниках. Для более сложных ситуаций прогиб можно определить, решив уравнение Эйлера–Бернулли с использованием таких методов, как « прямое интегрирование », « метод Маколея », « метод моментной площади » , « метод сопряженной балки », « принцип виртуальной работы », « метод Кастильяно », « метод гибкости », « метод прогиба наклона », « метод распределения момента » или « метод прямой жесткости ». ${\displaystyle w}$

Здесь определены соглашения о знаках, поскольку в литературе можно найти различные соглашения. ^[5] В этой статье используется правая система координат с осью справа, осью, направленной вверх, и осью, направленной внутрь рисунка. Знак изгибающего момента принимается положительным, когда вектор крутящего момента, связанный с изгибающим моментом на правой стороне сечения, находится в положительном направлении, то есть положительное значение создает сжимающее напряжение на нижней поверхности. При таком выборе соглашения о знаках изгибающего момента, чтобы иметь , необходимо, чтобы сила сдвига, действующая на правую сторону сечения, была положительной в направлении, чтобы достичь статического равновесия моментов. Если интенсивность нагрузки принимается положительной в положительном направлении, то необходимо для равновесия сил. ${\displaystyle x}$ ${\displaystyle z}$ ${\displaystyle y}$ ${\displaystyle M}$ ${\displaystyle y}$ ${\displaystyle M}$ ${\displaystyle dM=Qdx}$ ${\displaystyle Q}$ ${\displaystyle z}$ ${\displaystyle q}$ ${\displaystyle z}$ ${\displaystyle dQ=-qdx}$

Последовательные производные прогиба имеют важный физический смысл: - наклон балки, представляющий собой угол поворота против часовой стрелки вокруг оси в пределе малых перемещений; ${\displaystyle w}$ ${\displaystyle dw/dx}$ ${\displaystyle y}$

${\displaystyle M=-EI{\frac {d^{2}w}{dx^{2}}}}$

изгибающий момент в балке; и

${\displaystyle Q=-{\frac {d}{dx}}\left(EI{\frac {d^{2}w}{dx^{2}}}\right)}$

— это поперечная сила в балке.

Изгиб балки Эйлера–Бернулли. Каждое поперечное сечение балки расположено под углом 90 градусов к нейтральной оси.

Напряжения в балке можно рассчитать по приведенным выше выражениям после определения прогиба, вызванного заданной нагрузкой.

Вывод уравнения изгиба

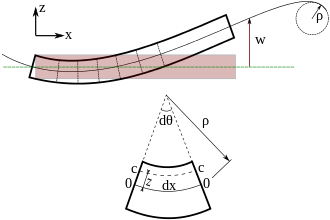
Ввиду основополагающей важности уравнения изгибающего момента в машиностроении, мы приведем его краткий вывод. Перейдем к полярным координатам. Длина нейтральной оси на рисунке равна Длина волокна с радиальным расстоянием ниже нейтральной оси равна Следовательно, деформация этого волокна равна ${\displaystyle \rho d\theta .}$ ${\displaystyle z}$ ${\displaystyle (\rho +z)d\theta .}$

${\displaystyle {\frac {\left(\rho +z-\rho \right)\ d\theta }{\rho \ d\theta }}={\frac {z}{\rho }}.}$

Напряжение этого волокна равно где - модуль упругости в соответствии с законом Гука . Вектор дифференциальной силы, возникающий из-за этого напряжения, определяется как ${\displaystyle E{\dfrac {z}{\rho }}}$ ${\displaystyle E}$ ${\displaystyle d\mathbf {F} ,}$

${\displaystyle d\mathbf {F} =E{\frac {z}{\rho }}dA\mathbf {e_{x}} .}$

Это дифференциальный вектор силы, действующий на правую сторону сечения, показанного на рисунке. Мы знаем, что он находится в направлении , поскольку рисунок ясно показывает, что волокна в нижней половине находятся в напряжении. — дифференциальный элемент площади в месте расположения волокна. Дифференциальный вектор изгибающего момента, связанный с, задается выражением ${\displaystyle \mathbf {e_{x}} }$ ${\displaystyle dA}$ ${\displaystyle d\mathbf {M} }$ ${\displaystyle d\mathbf {F} }$

${\displaystyle d\mathbf {M} =-z\mathbf {e_{z}} \times d\mathbf {F} =-\mathbf {e_{y}} E{\frac {z^{2}}{\rho }}dA.}$

Это выражение справедливо для волокон в нижней половине балки. Выражение для волокон в верхней половине балки будет аналогичным, за исключением того, что вектор плеча момента будет иметь положительное направление, а вектор силы будет иметь направление , так как верхние волокна находятся в состоянии сжатия. Но результирующий вектор изгибающего момента все еще будет иметь направление , так как Поэтому мы интегрируем по всему поперечному сечению балки и получаем для вектора изгибающего момента, приложенного к правому поперечному сечению балки, выражение ${\displaystyle z}$ ${\displaystyle -x}$ ${\displaystyle -y}$ ${\displaystyle \mathbf {e_{z}} \times -\mathbf {e_{x}} =-\mathbf {e_{y}} .}$ ${\displaystyle \mathbf {M} }$

${\displaystyle \mathbf {M} =\int d\mathbf {M} =-\mathbf {e_{y}} {\frac {E}{\rho }}\int {z^{2}}\ dA=-\mathbf {e_{y}} {\frac {EI}{\rho }},}$

где — второй момент площади . Из исчисления мы знаем, что когда мало, как для балки Эйлера–Бернулли, мы можем сделать приближение , где — радиус кривизны . Следовательно, ${\displaystyle I}$ ${\displaystyle {\dfrac {dw}{dx}}}$ ${\displaystyle {\dfrac {1}{\rho }}\simeq {\dfrac {d^{2}w}{dx^{2}}}}$ ${\displaystyle \rho }$

${\displaystyle \mathbf {M} =-\mathbf {e_{y}} EI{d^{2}w \over dx^{2}}.}$

Это векторное уравнение можно разделить в определении единичного вектора изгиба ( ориентирован как ), и в уравнении изгиба: ${\displaystyle M}$ ${\displaystyle \mathbf {e_{y}} }$

${\displaystyle M=-EI{d^{2}w \over dx^{2}}.}$

Уравнение динамической балки

Модель колебания широкополочной балки ( Ɪ-балки ), рассчитанная методом конечных элементов .

Уравнение динамики балки — это уравнение Эйлера–Лагранжа для следующего действия:

${\displaystyle S=\int _{t_{1}}^{t_{2}}\int _{0}^{L}\left[{\frac {1}{2}}\mu \left({\frac {\partial w}{\partial t}}\right)^{2}-{\frac {1}{2}}EI\left({\frac {\partial ^{2}w}{\partial x^{2}}}\right)^{2}+q(x)w(x,t)\right]dxdt.}$

Первый член представляет кинетическую энергию, где - масса на единицу длины, второй член представляет потенциальную энергию, обусловленную внутренними силами (при рассмотрении с отрицательным знаком), а третий член представляет потенциальную энергию, обусловленную внешней нагрузкой . Уравнение Эйлера-Лагранжа используется для определения функции, которая минимизирует функционал . Для динамической балки Эйлера-Бернулли уравнение Эйлера-Лагранжа имеет вид ${\displaystyle \mu }$ ${\displaystyle q(x)}$ ${\displaystyle S}$

${\displaystyle {\cfrac {\partial ^{2}}{\partial x^{2}}}\left(EI{\cfrac {\partial ^{2}w}{\partial x^{2}}}\right)=-\mu {\cfrac {\partial ^{2}w}{\partial t^{2}}}+q(x).}$

Когда балка однородна и не зависит от , уравнение балки упрощается: ${\displaystyle E}$ ${\displaystyle I}$ ${\displaystyle x}$

${\displaystyle EI{\cfrac {\partial ^{4}w}{\partial x^{4}}}=-\mu {\cfrac {\partial ^{2}w}{\partial t^{2}}}+q\,.}$

Свободная вибрация

При отсутствии поперечной нагрузки имеем уравнение свободных колебаний . Это уравнение можно решить, используя разложение Фурье смещения в сумму гармонических колебаний вида ${\displaystyle q}$

${\displaystyle w(x,t)={\text{Re}}[{\hat {w}}(x)~e^{-i\omega t}]}$

где - частота вибрации. Тогда для каждого значения частоты можно решить обыкновенное дифференциальное уравнение ${\displaystyle \omega }$

${\displaystyle EI~{\cfrac {\mathrm {d} ^{4}{\hat {w}}}{\mathrm {d} x^{4}}}-\mu \omega ^{2}{\hat {w}}=0\,.}$

Общее решение приведенного выше уравнения:

${\displaystyle {\hat {w}}=A_{1}\cosh(\beta x)+A_{2}\sinh(\beta x)+A_{3}\cos(\beta x)+A_{4}\sin(\beta x)\quad {\text{with}}\quad \beta :=\left({\frac {\mu \omega ^{2}}{EI}}\right)^{1/4}}$

где константы. Эти константы уникальны для заданного набора граничных условий. Однако решение для смещения не уникально и зависит от частоты. Эти решения обычно записываются как ${\displaystyle A_{1},A_{2},A_{3},A_{4}}$

${\displaystyle {\hat {w}}_{n}=A_{1}\cosh(\beta _{n}x)+A_{2}\sinh(\beta _{n}x)+A_{3}\cos(\beta _{n}x)+A_{4}\sin(\beta _{n}x)\quad {\text{with}}\quad \beta _{n}:=\left({\frac {\mu \omega _{n}^{2}}{EI}}\right)^{1/4}\,.}$

Величины называются собственными частотами балки. Каждое из решений смещения называется модой , а форма кривой смещения называется формой моды . ${\displaystyle \omega _{n}}$

Пример: Консольная балка

Формы мод для первых четырех мод колеблющейся консольной балки.

Граничные условия для консольной балки длиной (фиксированной на ) имеют вид ${\displaystyle L}$ ${\displaystyle x=0}$

${\displaystyle {\begin{aligned}&{\hat {w}}_{n}=0~,~~{\frac {d{\hat {w}}_{n}}{dx}}=0\quad {\text{at}}~~x=0\\&{\frac {d^{2}{\hat {w}}_{n}}{dx^{2}}}=0~,~~{\frac {d^{3}{\hat {w}}_{n}}{dx^{3}}}=0\quad {\text{at}}~~x=L\,.\end{aligned}}}$

Если применить эти условия, то нетривиальные решения будут существовать только в том случае, если Это нелинейное уравнение может быть решено численно. Первые четыре корня — это , , , и . ${\displaystyle \cosh(\beta _{n}L)\,\cos(\beta _{n}L)+1=0\,.}$ ${\displaystyle \beta _{1}L=0.596864\pi }$ ${\displaystyle \beta _{2}L=1.49418\pi }$ ${\displaystyle \beta _{3}L=2.50025\pi }$ ${\displaystyle \beta _{4}L=3.49999\pi }$

Соответствующие собственные частоты вибрации:

${\displaystyle \omega _{1}=\beta _{1}^{2}{\sqrt {\frac {EI}{\mu }}}={\frac {3.5160}{L^{2}}}{\sqrt {\frac {EI}{\mu }}}~,~~\dots }$

Граничные условия также можно использовать для определения форм колебаний из решения для смещения:

${\displaystyle {\hat {w}}_{n}=A_{1}\left[(\cosh \beta _{n}x-\cos \beta _{n}x)+{\frac {\cos \beta _{n}L+\cosh \beta _{n}L}{\sin \beta _{n}L+\sinh \beta _{n}L}}(\sin \beta _{n}x-\sinh \beta _{n}x)\right]}$

Консольная балка возбуждается вблизи резонансной частоты моды 2.

Неизвестная константа (на самом деле константы, поскольку для каждого есть одна ), которая в общем случае является комплексной, определяется начальными условиями при скорости и смещениях балки. Обычно значение используется при построении форм мод. Решения задачи о незатухающей силе имеют неограниченные смещения, когда частота возбуждения совпадает с собственной частотой , т. е. балка может резонировать . Таким образом, собственные частоты балки соответствуют частотам, на которых может возникнуть резонанс . ${\displaystyle n}$ ${\displaystyle A_{1}}$ ${\displaystyle t=0}$ ${\displaystyle A_{1}=1}$ ${\displaystyle \omega _{n}}$

Пример: свободно-свободная (неопорная) балка

Первые четыре моды колеблющейся свободно-свободной балки Эйлера-Бернулли.

Свободно-свободная балка — это балка без каких-либо опор. ^[6] Граничные условия для свободно-свободной балки длиной от до задаются следующим образом: ${\displaystyle L}$ ${\displaystyle x=0}$ ${\displaystyle x=L}$

${\displaystyle {\frac {d^{2}{\hat {w}}_{n}}{dx^{2}}}=0~,~~{\frac {d^{3}{\hat {w}}_{n}}{dx^{3}}}=0\quad {\text{at}}~~x=0\,{\text{and}}\,x=L\,.}$

Если применить эти условия, то нетривиальные решения будут существовать только в том случае, если

${\displaystyle \cosh(\beta _{n}L)\,\cos(\beta _{n}L)-1=0\,.}$

Это нелинейное уравнение можно решить численно. Первые четыре корня — , , , и . ${\displaystyle \beta _{1}L=1.50562\pi }$ ${\displaystyle \beta _{2}L=2.49975\pi }$ ${\displaystyle \beta _{3}L=3.50001\pi }$ ${\displaystyle \beta _{4}L=4.50000\pi }$

Соответствующие собственные частоты колебаний:

${\displaystyle \omega _{1}=\beta _{1}^{2}{\sqrt {\frac {EI}{\mu }}}={\frac {22.3733}{L^{2}}}{\sqrt {\frac {EI}{\mu }}}~,~~\dots }$

Граничные условия также можно использовать для определения форм колебаний из решения для смещения:

${\displaystyle {\hat {w}}_{n}=A_{1}{\Bigl [}(\cos \beta _{n}x+\cosh \beta _{n}x)-{\frac {\cos \beta _{n}L-\cosh \beta _{n}L}{\sin \beta _{n}L-\sinh \beta _{n}L}}(\sin \beta _{n}x+\sinh \beta _{n}x){\Bigr ]}}$

Как и в случае консольной балки, неизвестные константы определяются начальными условиями при скорости и смещениях балки. Кроме того, решения задачи о недемпфированной силе имеют неограниченные смещения, когда частота возбуждения совпадает с собственной частотой . ${\displaystyle t=0}$ ${\displaystyle \omega _{n}}$

Пример: зажато-зажатая балка

Граничные условия двойной защемленной балки ^[7] длины (фиксированной при и ) имеют вид ${\displaystyle L}$ ${\displaystyle x=0}$ ${\displaystyle x=L}$

${\displaystyle {\hat {w}}_{n}=0~,~~{\frac {d{\hat {w}}_{n}}{dx}}=0\quad {\text{at}}~~x=0\,{\text{and}}\,x=L\,.}$

Это подразумевает, что существуют решения для Установка обеспечивает это условие. Перестановка для собственной частоты дает ${\displaystyle \sin(\beta _{n}L)\,\sinh(\beta _{n}L)=0\,.}$ ${\displaystyle \beta _{n}:={\frac {n\pi }{L}}}$

${\displaystyle \omega _{n}={\frac {n^{2}\pi ^{2}}{L^{2}}}{\sqrt {\frac {EI}{\mu }}}}$

Стресс

Помимо прогиба, уравнение балки описывает силы и моменты и, таким образом, может быть использовано для описания напряжений . По этой причине уравнение балки Эйлера–Бернулли широко используется в машиностроении , особенно гражданском и механическом, для определения прочности (а также прогиба) балок при изгибе.

Как изгибающий момент , так и сила сдвига вызывают напряжения в балке. Напряжение, вызванное силой сдвига, максимально вдоль нейтральной оси балки (когда ширина балки, t, постоянна вдоль поперечного сечения балки; в противном случае необходимо оценить интеграл, включающий первый момент и ширину балки для конкретного поперечного сечения), а максимальное растягивающее напряжение находится либо на верхней, либо на нижней поверхности. Таким образом, максимальное главное напряжение в балке может быть не на поверхности и не в центре, а в некоторой общей области. Однако напряжения силы сдвига пренебрежимо малы по сравнению с напряжениями изгибающего момента во всех балках, кроме самых толстых, а также тот факт, что концентрации напряжений обычно возникают на поверхностях, что означает, что максимальное напряжение в балке, скорее всего, будет на поверхности.

Простой или симметричный изгиб

Элемент изогнутой балки: волокна образуют концентрические дуги, верхние волокна сжаты, а нижние растянуты.

Для поперечных сечений балки, симметричных относительно плоскости, перпендикулярной нейтральной плоскости, можно показать, что растягивающее напряжение, испытываемое балкой, может быть выражено как:

${\displaystyle \sigma ={\frac {Mz}{I}}=-zE~{\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}.\,}$

Здесь — расстояние от нейтральной оси до интересующей точки; — изгибающий момент. Обратите внимание, что это уравнение подразумевает, что чистый изгиб (положительного знака) вызовет нулевое напряжение на нейтральной оси, положительное (растягивающее) напряжение на «верху» балки и отрицательное (сжимающее) напряжение на дне балки; а также подразумевает, что максимальное напряжение будет на верхней поверхности, а минимальное — на нижней. Это изгибающее напряжение может быть наложено на аксиально приложенные напряжения, что вызовет смещение нейтральной (нулевой) оси. ${\displaystyle z}$ ${\displaystyle M}$

Максимальные напряжения в поперечном сечении

Величины, используемые при определении момента сопротивления сечения балки.

Максимальное растягивающее напряжение в поперечном сечении находится в месте , а максимальное сжимающее напряжение находится в месте, где высота поперечного сечения составляет . Эти напряжения ${\displaystyle z=c_{1}}$ ${\displaystyle z=-c_{2}}$ ${\displaystyle h=c_{1}+c_{2}}$

${\displaystyle \sigma _{1}={\cfrac {Mc_{1}}{I}}={\cfrac {M}{S_{1}}}~;~~\sigma _{2}=-{\cfrac {Mc_{2}}{I}}=-{\cfrac {M}{S_{2}}}}$

Величины представляют собой модули сечения ^[5] и определяются как ${\displaystyle S_{1},S_{2}}$

${\displaystyle S_{1}={\cfrac {I}{c_{1}}}~;~~S_{2}={\cfrac {I}{c_{2}}}}$

Модуль сечения объединяет всю важную геометрическую информацию о сечении балки в одну величину. Для случая, когда балка дважды симметрична, и у нас есть один модуль сечения . ${\displaystyle c_{1}=c_{2}}$ ${\displaystyle S=I/c}$

Деформация в балке Эйлера–Бернулли

Нам нужно выражение для деформации в терминах прогиба нейтральной поверхности, чтобы связать напряжения в балке Эйлера–Бернулли с прогибом. Чтобы получить это выражение, мы используем предположение, что нормали к нейтральной поверхности остаются нормальными во время деформации и что прогибы малы. Эти предположения подразумевают, что балка изгибается в дугу окружности радиуса (см. Рисунок 1) и что нейтральная поверхность не меняет своей длины во время деформации. ^[5] ${\displaystyle \rho }$

Пусть — длина элемента нейтральной поверхности в недеформированном состоянии. При малых прогибах элемент не меняет своей длины после изгиба, а деформируется в дугу окружности радиуса . Если — угол, опирающийся на эту дугу, то . ${\displaystyle \mathrm {d} x}$ ${\displaystyle \rho }$ ${\displaystyle \mathrm {d} \theta }$ ${\displaystyle \mathrm {d} x=\rho ~\mathrm {d} \theta }$

Рассмотрим теперь другой сегмент элемента на расстоянии выше нейтральной поверхности. Начальная длина этого элемента равна . Однако после изгиба длина элемента становится . Деформация в этом сегменте балки определяется как ${\displaystyle z}$ ${\displaystyle \mathrm {d} x}$ ${\displaystyle \mathrm {d} x'=(\rho -z)~\mathrm {d} \theta =\mathrm {d} x-z~\mathrm {d} \theta }$

${\displaystyle \varepsilon _{x}={\cfrac {\mathrm {d} x'-\mathrm {d} x}{\mathrm {d} x}}=-{\cfrac {z}{\rho }}=-\kappa ~z}$

где - кривизна балки. Это дает нам осевую деформацию балки как функцию расстояния от нейтральной поверхности. Однако нам все еще нужно найти связь между радиусом кривизны и прогибом балки . ${\displaystyle \kappa }$ ${\displaystyle w}$

Соотношение между кривизной и прогибом балки

Пусть P — точка на нейтральной поверхности балки на расстоянии от начала системы координат. Наклон балки приблизительно равен углу, образуемому нейтральной поверхностью с осью для малых углов, встречающихся в теории балок. Следовательно, при таком приближении ${\displaystyle x}$ ${\displaystyle (x,z)}$ ${\displaystyle x}$

${\displaystyle \theta (x)={\cfrac {\mathrm {d} w}{\mathrm {d} x}}}$

Поэтому для бесконечно малого элемента соотношение можно записать как ${\displaystyle \mathrm {d} x}$ ${\displaystyle \mathrm {d} x=\rho ~\mathrm {d} \theta }$

${\displaystyle {\cfrac {1}{\rho }}={\cfrac {\mathrm {d} \theta }{\mathrm {d} x}}={\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}=\kappa }$

Следовательно, деформация в балке может быть выражена как

${\displaystyle \varepsilon _{x}=-z\kappa }$

Соотношения напряжение-деформация

Для однородного изотропного линейно-упругого материала напряжение связано с деформацией соотношением , где - модуль Юнга . Следовательно, напряжение в балке Эйлера-Бернулли определяется выражением ${\displaystyle \sigma =E\varepsilon }$ ${\displaystyle E}$

${\displaystyle \sigma _{x}=-zE{\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}$

Обратите внимание, что приведенное выше соотношение, по сравнению с соотношением между осевым напряжением и изгибающим моментом, приводит к

${\displaystyle M=-EI{\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}}$

Поскольку сила сдвига определяется выражением , мы также имеем ${\displaystyle Q=\mathrm {d} M/\mathrm {d} x}$

${\displaystyle Q=-EI{\cfrac {\mathrm {d} ^{3}w}{\mathrm {d} x^{3}}}}$

Граничные соображения

Уравнение балки содержит производную четвертого порядка в . Для нахождения единственного решения нам нужны четыре граничных условия. Граничные условия обычно моделируют опоры , но они также могут моделировать точечные нагрузки, распределенные нагрузки и моменты. Граничные условия опоры или смещения используются для фиксации значений смещения ( ) и поворотов ( ) на границе. Такие граничные условия также называются граничными условиями Дирихле . Граничные условия нагрузки и момента включают высшие производные и представляют собой поток импульса . Граничные условия потока также называются граничными условиями Неймана . ${\displaystyle x}$ ${\displaystyle w(x,t)}$ ${\displaystyle w}$ ${\displaystyle \mathrm {d} w/\mathrm {d} x}$ ${\displaystyle w}$

В качестве примера рассмотрим консольную балку, которая встроена на одном конце и свободна на другом, как показано на соседнем рисунке. На встроенном конце балки не может быть никакого смещения или поворота балки. Это означает, что на левом конце как прогиб, так и наклон равны нулю. Поскольку на свободном конце балки не приложен внешний изгибающий момент, изгибающий момент в этом месте равен нулю. Кроме того, если к балке не приложена внешняя сила, сила сдвига на свободном конце также равна нулю.

Принимая координату левого конца за , а правого конца за (длину балки), эти утверждения преобразуются в следующий набор граничных условий (предположим, что — константа): ${\displaystyle x}$ ${\displaystyle 0}$ ${\displaystyle L}$ ${\displaystyle EI}$

Консольная балка.

${\displaystyle w|_{x=0}=0\quad ;\quad {\frac {\partial w}{\partial x}}{\bigg |}_{x=0}=0\qquad {\mbox{(fixed end)}}\,}$

${\displaystyle {\frac {\partial ^{2}w}{\partial x^{2}}}{\bigg |}_{x=L}=0\quad ;\quad {\frac {\partial ^{3}w}{\partial x^{3}}}{\bigg |}_{x=L}=0\qquad {\mbox{(free end)}}\,}$

Простая опора (штифт или ролик) эквивалентна точечной силе на балке, которая регулируется таким образом, чтобы зафиксировать положение балки в этой точке. Фиксированная опора или зажим эквивалентны комбинации точечной силы и точечного крутящего момента, которые регулируются таким образом, чтобы зафиксировать как положение, так и наклон балки в этой точке. Точечные силы и крутящие моменты, будь то от опор или напрямую приложенные, разделят балку на набор сегментов, между которыми уравнение балки даст непрерывное решение, учитывая четыре граничных условия, по два на каждом конце сегмента. Предполагая, что произведение EI является константой, и определяя, где F — величина точечной силы, а где M — величина точечного крутящего момента, граничные условия, подходящие для некоторых общих случаев, приведены в таблице ниже. Изменение конкретной производной w через границу по мере увеличения x обозначается с последующей этой производной. Например, где — значение на нижней границе верхнего сегмента, а — значение на верхней границе нижнего сегмента. Когда значения конкретной производной не только непрерывны на границе, но и фиксированы, граничное условие записывается, например, что фактически представляет собой два отдельных уравнения (например, = фиксировано). ${\displaystyle \lambda =F/EI}$ ${\displaystyle \tau =M/EI}$ ${\displaystyle \Delta }$ ${\displaystyle \Delta w''=w''(x+)-w''(x-)}$ ${\displaystyle w''(x+)}$ ${\displaystyle w''}$ ${\displaystyle w''(x-)}$ ${\displaystyle w''}$ ${\displaystyle \Delta w''=0^{*}}$ ${\displaystyle w''(x-)=w''(x+)}$

Обратите внимание, что в первых случаях, когда точечные силы и моменты расположены между двумя сегментами, есть четыре граничных условия, два для нижнего сегмента и два для верхнего. Когда силы и моменты прикладываются к одному концу балки, есть два граничных условия, которые применяются на этом конце. Знак точечных сил и моментов на конце будет положительным для нижнего конца, отрицательным для верхнего конца.

Соображения по загрузке

Приложенные нагрузки могут быть представлены либо через граничные условия, либо через функцию , которая представляет внешнюю распределенную нагрузку. Использование распределенной нагрузки часто благоприятствует простоте. Однако граничные условия часто используются для моделирования нагрузок в зависимости от контекста; эта практика особенно распространена в анализе вибрации. ${\displaystyle q(x,t)}$

По своей природе распределенная нагрузка очень часто представляется кусочно, поскольку на практике нагрузка обычно не является непрерывной функцией. Точечные нагрузки можно моделировать с помощью дельта- функции Дирака . Например, рассмотрим статическую однородную консольную балку длины с направленной вверх точечной нагрузкой, приложенной к свободному концу. Используя граничные условия, это можно моделировать двумя способами. В первом подходе приложенная точечная нагрузка аппроксимируется сдвигающей силой, приложенной к свободному концу. В этом случае определяющее уравнение и граничные условия следующие: ${\displaystyle L}$ ${\displaystyle F}$

${\displaystyle {\begin{aligned}&EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=0\\&w|_{x=0}=0\quad ;\quad {\frac {\mathrm {d} w}{\mathrm {d} x}}{\bigg |}_{x=0}=0\quad ;\quad {\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}{\bigg |}_{x=L}=0\quad ;\quad -EI{\frac {\mathrm {d} ^{3}w}{\mathrm {d} x^{3}}}{\bigg |}_{x=L}=F\,\end{aligned}}}$

Альтернативно мы можем представить точечную нагрузку как распределение с использованием функции Дирака. В этом случае уравнение и граничные условия будут такими:

${\displaystyle {\begin{aligned}&EI{\frac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}=F\delta (x-L)\\&w|_{x=0}=0\quad ;\quad {\frac {\mathrm {d} w}{\mathrm {d} x}}{\bigg |}_{x=0}=0\quad ;\quad {\frac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}{\bigg |}_{x=L}=0\,\end{aligned}}}$

Обратите внимание, что граничное условие силы сдвига (третья производная) удалено, иначе возникло бы противоречие. Это эквивалентные краевые задачи , и обе дают решение

${\displaystyle w={\frac {F}{6EI}}(3Lx^{2}-x^{3})\,~.}$

Приложение нескольких точечных нагрузок в разных местах приведет к кусочной функции. Использование функции Дирака значительно упрощает такие ситуации; в противном случае балку пришлось бы разделить на секции, каждая из которых имела бы четыре граничных условия, решаемых отдельно. Хорошо организованное семейство функций, называемых функциями сингулярности, часто используется в качестве сокращения для функции Дирака, ее производной и ее первообразных . ${\displaystyle w(x)}$

Динамические явления также можно моделировать с помощью статического уравнения балки, выбирая соответствующие формы распределения нагрузки. Например, свободные колебания балки можно учесть с помощью функции нагрузки:

${\displaystyle q(x,t)=\mu {\frac {\partial ^{2}w}{\partial t^{2}}}\,}$

где - линейная плотность массы балки, не обязательно константа. При такой зависящей от времени нагрузке уравнение балки будет частным дифференциальным уравнением : ${\displaystyle \mu }$

${\displaystyle {\frac {\partial ^{2}}{\partial x^{2}}}\left(EI{\frac {\partial ^{2}w}{\partial x^{2}}}\right)=-\mu {\frac {\partial ^{2}w}{\partial t^{2}}}.}$

Другой интересный пример описывает отклонение балки, вращающейся с постоянной угловой частотой : ${\displaystyle \omega }$

${\displaystyle q(x)=\mu \omega ^{2}w(x)\,}$

Это распределение центростремительной силы . Обратите внимание, что в этом случае является функцией смещения (зависимой переменной), а уравнение балки будет автономным обыкновенным дифференциальным уравнением . ${\displaystyle q}$

Примеры

Трехточечный изгиб

Испытание на изгиб в трех точках является классическим экспериментом в механике. Оно представляет собой случай балки, покоящейся на двух роликовых опорах и подвергающейся сосредоточенной нагрузке, приложенной в середине балки. Сдвиг постоянен по абсолютной величине: он составляет половину центральной нагрузки, P / 2. Он меняет знак в середине балки. Изгибающий момент изменяется линейно от одного конца, где он равен 0, и центра, где его абсолютное значение равно PL / 4, где риск разрыва является наиболее важным. Деформация балки описывается полиномом третьей степени по половине балки (другая половина симметрична). Изгибающие моменты ( ), сдвигающие силы ( ) и прогибы ( ) для балки, подверженной центральной точечной нагрузке и асимметричной точечной нагрузке, приведены в таблице ниже. ^[5] ${\displaystyle M}$ ${\displaystyle Q}$ ${\displaystyle w}$

Консольные балки

Другой важный класс задач включает консольные балки. Изгибающие моменты ( ), поперечные силы ( ) и прогибы ( ) для консольной балки, подверженной точечной нагрузке на свободном конце и равномерно распределенной нагрузке, приведены в таблице ниже. ^[5] ${\displaystyle M}$ ${\displaystyle Q}$ ${\displaystyle w}$

Решения для ряда других часто встречающихся конфигураций легко доступны в учебниках по механике материалов и инженерных справочниках.

Статически неопределимые балки

Изгибающие моменты и поперечные силы в балках Эйлера–Бернулли часто можно определить непосредственно с помощью статического баланса сил и моментов . Однако при определенных граничных условиях число реакций может превышать число независимых уравнений равновесия. ^[5] Такие балки называются статически неопределимыми .

Встроенные балки, показанные на рисунке ниже, являются статически неопределимыми. Для определения напряжений и прогибов таких балок наиболее прямым методом является решение уравнения балки Эйлера–Бернулли с соответствующими граничными условиями. Но прямые аналитические решения уравнения балки возможны только для простейших случаев. Поэтому для решения статически неопределимых задач балки часто используются дополнительные методы, такие как линейная суперпозиция.

Метод суперпозиции заключается в сложении решений ряда статически определимых задач, которые выбираются таким образом, чтобы граничные условия для суммы отдельных задач совпадали с граничными условиями исходной задачи.

Другая часто встречающаяся статически неопределимая задача балки — консольная балка со свободным концом, опирающимся на ролик. ^[5] Изгибающие моменты, поперечные силы и прогибы такой балки перечислены ниже:

Расширения

Кинематические предположения, на которых основана теория балок Эйлера–Бернулли, позволяют расширить ее до более продвинутого анализа. Простая суперпозиция допускает трехмерную поперечную нагрузку. Использование альтернативных конститутивных уравнений может допустить вязкоупругую или пластическую деформацию балки. Теория балок Эйлера–Бернулли также может быть расширена до анализа изогнутых балок, потери устойчивости балки , составных балок и геометрически нелинейного прогиба балки.

Теория балок Эйлера–Бернулли не учитывает эффекты поперечной деформации сдвига . В результате она недооценивает прогибы и переоценивает собственные частоты. Для тонких балок (отношение длины балки к толщине порядка 20 и более) эти эффекты не имеют большого значения. Однако для толстых балок эти эффекты могут быть значительными. Для учета этих эффектов были разработаны более продвинутые теории балок, такие как теория балок Тимошенко (разработанная ученым российского происхождения Стивеном Тимошенко ).

Большие прогибы

Луч Эйлера–Бернулли

Первоначальная теория Эйлера–Бернулли справедлива только для бесконечно малых деформаций и малых вращений. Теорию можно напрямую распространить на задачи, включающие умеренно большие вращения, при условии, что деформация остается малой, используя деформации фон Кармана . ^[8]

Гипотезы Эйлера–Бернулли о том, что плоские сечения остаются плоскими и нормальными к оси балки, приводят к смещениям вида

${\displaystyle u_{1}=u_{0}(x)-z{\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}~;~~u_{2}=0~;~~u_{3}=w_{0}(x)}$

Используя определение лагранжевой деформации Грина из теории конечных деформаций , мы можем найти деформации Кармана для балки, которые справедливы для больших поворотов, но малых деформаций, отбрасывая все члены более высокого порядка (которые содержат более двух полей), за исключением Результирующие деформации принимают вид: ${\displaystyle {\frac {\partial {w}}{\partial {x^{i}}}}{\frac {\partial {w}}{\partial {x^{j}}}}.}$

${\displaystyle {\begin{aligned}\varepsilon _{11}&={\cfrac {\mathrm {d} {u_{0}}}{\mathrm {d} {x}}}-z{\cfrac {\mathrm {d} ^{2}{w_{0}}}{\mathrm {d} {x^{2}}}}+{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}-z{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\right)^{2}+\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]\approx {\cfrac {\mathrm {d} {u_{0}}}{\mathrm {d} {x}}}-z{\cfrac {\mathrm {d} ^{2}{w_{0}}}{\mathrm {d} {x^{2}}}}+{\frac {1}{2}}\left({\frac {\mathrm {d} {w_{0}}}{\mathrm {d} {x}}}\right)^{2}\\[0.25em]\varepsilon _{22}&=0\\[0.25em]\varepsilon _{33}&={\frac {1}{2}}\left({\frac {\mathrm {d} {w_{0}}}{\mathrm {d} {x}}}\right)^{2}\\[0.25em]\varepsilon _{23}&=0\\[0.25em]\varepsilon _{31}&=-{\frac {1}{2}}\left[\left({\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}-z{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\right)\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)\right]\approx 0\\[0.25em]\varepsilon _{12}&=0.\end{aligned}}}$

Из принципа виртуальной работы баланс сил и моментов в балках дает нам уравнения равновесия

${\displaystyle {\begin{aligned}{\cfrac {\mathrm {d} N_{xx}}{\mathrm {d} x}}+f(x)&=0\\{\cfrac {\mathrm {d} ^{2}M_{xx}}{\mathrm {d} x^{2}}}+q(x)+{\cfrac {\mathrm {d} }{\mathrm {d} x}}\left(N_{xx}{\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)&=0\end{aligned}}}$

где - осевая нагрузка, - поперечная нагрузка, и ${\displaystyle f(x)}$ ${\displaystyle q(x)}$

${\displaystyle N_{xx}=\int _{A}\sigma _{xx}~\mathrm {d} A~;~~M_{xx}=\int _{A}z\sigma _{xx}~\mathrm {d} A}$

Для замыкания системы уравнений нам нужны определяющие уравнения , связывающие напряжения с деформациями (и, следовательно, напряжения со смещениями). Для больших поворотов и малых деформаций эти соотношения имеют вид

${\displaystyle {\begin{aligned}N_{xx}&=A_{xx}\left[{\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-B_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\\M_{xx}&=B_{xx}\left[{\cfrac {\mathrm {d} u_{0}}{\mathrm {d} x}}+{\frac {1}{2}}\left({\cfrac {\mathrm {d} w_{0}}{\mathrm {d} x}}\right)^{2}\right]-D_{xx}{\cfrac {\mathrm {d} ^{2}w_{0}}{\mathrm {d} x^{2}}}\end{aligned}}}$

где

${\displaystyle A_{xx}=\int _{A}E~\mathrm {d} A~;~~B_{xx}=\int _{A}zE~\mathrm {d} A~;~~D_{xx}=\int _{A}z^{2}E~\mathrm {d} A~.}$

Величина представляет собой жесткость при растяжении , - связанную жесткость при растяжении и изгибе , - жесткость при изгибе . ${\displaystyle A_{xx}}$ ${\displaystyle B_{xx}}$ ${\displaystyle D_{xx}}$

Для ситуации, когда балка имеет однородное поперечное сечение и не имеет осевой нагрузки, основное уравнение для балки Эйлера–Бернулли с большим углом поворота имеет вид

${\displaystyle EI~{\cfrac {\mathrm {d} ^{4}w}{\mathrm {d} x^{4}}}-{\frac {3}{2}}~EA~\left({\cfrac {\mathrm {d} w}{\mathrm {d} x}}\right)^{2}\left({\cfrac {\mathrm {d} ^{2}w}{\mathrm {d} x^{2}}}\right)=q(x)}$

Смотрите также

• Прикладная механика
• Изгиб
• Изгибающий момент
• Выпучивание
• Жесткость на изгиб
• Обобщенная теория балок
• Теория пластин
• Теория сэндвича
• Диаграмма сдвига и момента
• Функция сингулярности
• Деформация (материаловедение)
• теория балки Тимошенко
• Теорема о трех моментах (теорема Клапейрона)
• Испытание на трехточечный изгиб

Ссылки

Примечания

1. Для балки Эйлера–Бернулли, не находящейся под какой-либо осевой нагрузкой, эта ось называется нейтральной осью .

Цитаты

1. Тимошенко, С. (1953). История сопротивления материалов . Нью-Йорк: McGraw-Hill.
2. Трусделл, К. (1960). Рациональная механика гибких или упругих тел 1638–1788 гг . Venditioni Exponunt Орелла Фюссли Туричи.
3. Ballarini, Roberto (18 апреля 2003 г.). "The Da Vinci-Euler-Bernoulli Beam Theory?". Mechanical Engineering Magazine Online . Архивировано из оригинала 23 июня 2006 г. Получено 22 июля 2006 г.
4. Хан, Сон М.; Бенаройя, Хайм; Вэй, Тимоти (22 марта 1999 г.). "Динамика поперечно вибрирующих балок с использованием четырех инженерных теорий" (PDF) . Журнал звука и вибрации . 225 (5). Academic Press: 935. Bibcode :1999JSV...225..935H. doi :10.1006/jsvi.1999.2257. Архивировано из оригинала (PDF) 20 июля 2011 г. . Получено 15 апреля 2007 г. .
5. Гир, Дж. М.; Тимошенко, СП (1997). Механика материалов . PWS.
6. Кареста, Мауро. "Вибрации свободно-свободной балки" (PDF) . Получено 20.03.2019 .
7. Ирвин, Том. "Pinned-Pinned Beam" . Получено 13 октября 2024 г.
8. Редди, Дж. Н. (2007). Нелинейный конечно-элементный анализ . Oxford University Press.

Дальнейшее чтение

• EA Witmer (1991–1992). «Элементарная теория балок Бернулли-Эйлера». MIT Unified Engineering Course Notes . стр. 5–114 по 5–164.

Внешние ссылки

• Напряжение и прогиб балки, таблицы прогиба балки