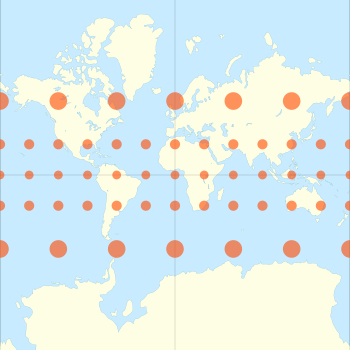
проекция Меркатора

Цилиндрическая конформная проекция карты

Проекция Меркатора на мир между 85° ю.ш. и 85° с.ш. Обратите внимание на сравнение размеров Гренландии и Африки.

Проекция Меркатора с индикатрисой деформации Тиссо .

Карта мира Меркатора 1569 года ( Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendate Accommodata ), показывающая широты от 66 ° южной широты до 80 ° северной широты.

Проекция Меркатора ( / m ər ˈ k eɪ t ər / ) — это конформная цилиндрическая картографическая проекция, впервые представленная фламандским географом и картографом Герардом Меркатором в 1569 году. В XVIII веке она стала стандартной картографической проекцией для навигации из-за ее свойства представлять линии румба как прямые линии. При применении к картам мира проекция Меркатора увеличивает размер земель по мере их удаления от экватора . Поэтому такие массивы суши, как Гренландия и Антарктида, кажутся намного больше, чем они есть на самом деле, по сравнению с массивами суши вблизи экватора. В настоящее время проекция Меркатора широко используется, поскольку, помимо морской навигации, она хорошо подходит для веб-карт в Интернете .

История

Джозеф Нидхэм , историк Китая, предположил, что некоторые звездные карты китайской династии Сун могли быть составлены с использованием проекции Меркатора; ^[1] однако это утверждение было представлено без доказательств, и историк астрономии Казухико Миядзима, используя картометрический анализ, пришел к выводу, что эти карты использовали равнопромежуточную проекцию . ^[2]

В XIII веке самые ранние из сохранившихся карт-портоланов Средиземного моря, которые, как правило, не считаются основанными на какой-либо преднамеренной проекции карты, включали в себя сети роз ветров из перекрещивающихся линий, которые могли использоваться для установки пеленга судна при плавании между точками на карте; область Земли, покрываемая такими картами, была достаточно мала, чтобы курс постоянного пеленга был приблизительно прямым на карте. ^{[3] [4]} Карты обладают поразительной точностью, не встречающейся в картах, составленных современными европейскими или арабскими учеными, и их построение остается загадочным; на основе картометрического анализа, который, по-видимому, противоречит научному консенсусу, было высказано предположение, что они возникли в какой-то неизвестной досредневековой картографической традиции, возможно, свидетельствующей о каком-то древнем понимании проекции Меркатора. ^[5]

Немецкий эрудит Эрхард Эцлауб выгравировал миниатюрные «компасные карты» (примерно 10×8 см) Европы и частей Африки, охватывающие широты 0°–67°, чтобы иметь возможность корректировать свои карманные солнечные часы . Проекция, обнаруженная на этих картах, датируемых 1511 годом, была заявлена ​​Джоном Снайдером в 1987 году как та же самая проекция, что и у Меркатора. ^[6] Однако, учитывая геометрию солнечных часов, эти карты вполне могли быть основаны на похожей центральной цилиндрической проекции , предельном случае гномонической проекции , которая является основой солнечных часов. Снайдер исправил свою оценку на «похожую проекцию» в 1993 году. ^[7]

Португальский математик и космограф Педру Нунес первым описал математический принцип локсодромии или локсодромии, пути с постоянным направлением, измеренным относительно истинного севера, который может использоваться в морской навигации для выбора направления компаса. В 1537 году он предложил построить морской атлас, состоящий из нескольких крупномасштабных листов в равнопрямоугольной проекции, как способ минимизировать искажение направлений. Если бы эти листы были приведены к одному масштабу и собраны, они бы приближались к проекции Меркатора.

Локсодромальные линии на глобусе Меркатора 1541 года

В 1541 году фламандский географ и картограф Герард Меркатор нанес сеть локсодромных линий на земной глобус , который он сделал для Николя Перрено . ^[8]

В 1569 году Меркатор объявил о новой проекции, опубликовав большую карту мира размером 202 на 124 см (80 на 49 дюймов) и напечатав ее на восемнадцати отдельных листах. Меркатор назвал карту Nova et Aucta Orbis Terrae Descriptio ad Usum Navigantium Emendata : «Новое и дополненное описание Земли, исправленное для использования моряками». Это название, наряду с подробным объяснением использования проекции, которое появляется как раздел текста на карте, показывает, что Меркатор точно понимал, чего он достиг, и что он намеревался использовать проекцию для помощи в навигации. Меркатор никогда не объяснял метод построения или то, как он к нему пришел. На протяжении многих лет выдвигались различные гипотезы, но в любом случае дружба Меркатора с Педро Нунесом и его доступ к локсодромическим таблицам, созданным Нунесом, вероятно, помогли его усилиям. ^[9]

Английский математик Эдвард Райт опубликовал первые точные таблицы для построения проекции в 1599 году и, более подробно, в 1610 году, назвав свой трактат «Некоторые ошибки в навигации». Первая математическая формулировка была опубликована около 1645 года математиком по имени Генри Бонд ( ок.  1600–1678 ). Однако математик Томас Харриот разработал, но никогда не публиковал эту математику , начиная с 1589 года. ^[10]

Разработка проекции Меркатора представляла собой крупный прорыв в морской картографии XVI века. Однако она намного опередила свое время, поскольку старые навигационные и геодезические методы не были совместимы с ее использованием в навигации. Две основные проблемы препятствовали ее немедленному применению: невозможность определения долготы на море с достаточной точностью и тот факт, что в навигации использовались магнитные направления вместо географических . Только в середине XVIII века, после изобретения морского хронометра и изучения пространственного распределения магнитного склонения , проекция Меркатора смогла быть полностью принята мореплавателями.

Несмотря на эти ограничения определения местоположения, проекцию Меркатора можно найти на многих картах мира в течение столетий после первой публикации Меркатора. Однако она не стала доминировать на картах мира до 19 века, когда проблема определения местоположения была в значительной степени решена. После того как проекция Меркатора стала обычной для коммерческих и образовательных карт, она подверглась постоянной критике со стороны картографов за ее несбалансированное представление массивов суши и ее неспособность полезно отображать полярные регионы.

Критика ненадлежащего использования проекции Меркатора привела к появлению шквала новых изобретений в конце 19-го и начале 20-го века, часто напрямую рекламируемых как альтернативы проекции Меркатора. Из-за этого давления издатели постепенно сократили использование проекции в течение 20-го века. Однако появление веб-картографирования дало проекции резкое возрождение в форме проекции Веб-Меркатора .

Сегодня Меркатор можно найти на морских картах, иногда на картах мира и в картографических веб-сервисах, но коммерческие атласы в значительной степени отказались от него, а настенные карты мира можно найти во многих альтернативных проекциях. Google Maps , которые полагались на него с 2005 года, по-прежнему используют его для локальных карт, но отказались от проекции с настольных платформ в 2017 году для карт, которые масштабируются в локальных областях. Многие другие картографические онлайн-сервисы по-прежнему используют исключительно Web Mercator.

Характеристики

Сравнение касательных и секущих форм нормальной, косой и поперечной проекций Меркатора со стандартными параллелями красного цвета

Проекцию Меркатора можно визуализировать как результат обертывания цилиндра плотно вокруг сферы, с двумя поверхностями, касающимися друг друга по окружности на полпути между полюсами их общей оси, а затем конформно разворачивать поверхность сферы наружу на цилиндр, что означает, что в каждой точке проекция равномерно масштабирует изображение небольшой части сферической поверхности, не искажая ее иным образом, сохраняя углы между пересекающимися кривыми. После этого этот цилиндр разворачивается на плоскую плоскость, чтобы создать карту. В этой интерпретации масштаб поверхности сохраняется точно вдоль окружности, где цилиндр касается сферы, но нелинейно увеличивается для точек, удаленных от контактной окружности. Однако, равномерно сжимая полученную плоскую карту, в качестве последнего шага, можно выбрать любую пару окружностей, параллельных контактной окружности и равноудаленных от нее, чтобы сохранить их масштаб, называемый стандартными параллелями ; тогда область между выбранными окружностями будет иметь свой масштаб меньше, чем на сфере, достигая минимума на контактной окружности. Иногда это визуализируют как проекцию на цилиндр, который является секущей (разрезает) сферу, хотя эта картина вводит в заблуждение, поскольку стандартные параллели не расположены на том же расстоянии друг от друга на карте, что и кратчайшее расстояние между ними через внутреннюю часть сферы. ^[11]

Первоначальным и наиболее распространенным аспектом проекции Меркатора для карт Земли является нормальный аспект, для которого ось цилиндра является осью вращения Земли , которая проходит через Северный и Южный полюса, а контактная окружность является земным экватором . Как и для всех цилиндрических проекций в нормальном аспекте, круги широты и меридианы долготы являются прямыми и перпендикулярными друг другу на карте, образуя сетку прямоугольников. Хотя круги широты на Земле тем меньше, чем ближе они к полюсам, они растянуты в направлении восток-запад, чтобы иметь одинаковую длину на любой цилиндрической проекции карты. Среди цилиндрических проекций проекция Меркатора является уникальной проекцией, которая уравновешивает это растяжение с востока на запад точно соответствующим растяжением с севера на юг, так что в каждом месте масштаб локально однороден, а углы сохраняются.

Проекция Меркатора в нормальном аспекте отображает траектории постоянного пеленга (называемые локсодромами или локсодромами ) на сфере в прямые линии на карте и, таким образом, идеально подходит для морской навигации : курсы и пеленги измеряются с помощью компаса или транспортира, а соответствующие направления легко переносятся из точки в точку на карте, например, с помощью параллельной линейки .

Поскольку линейный масштаб карты Меркатора в нормальном аспекте увеличивается с широтой, он искажает размер географических объектов вдали от экватора и передает искаженное восприятие общей геометрии планеты. На широтах более 70° северной или южной широты проекция Меркатора практически непригодна, ^{[ по мнению кого? ]} потому что линейный масштаб становится бесконечно большим на полюсах. Поэтому карта Меркатора никогда не может полностью показать полярные области (но см. Использование ниже для применения косой и поперечной проекций Меркатора).

Проекцию Меркатора часто сравнивают и путают с центральной цилиндрической проекцией , которая является результатом проецирования точек со сферы на касательный цилиндр вдоль прямых радиальных линий, как будто из источника света, расположенного в центре Земли. ^[12] Обе имеют экстремальные искажения вдали от экватора и не могут показать полюса. Однако это разные проекции и они имеют разные свойства.

Искажение размеров

Пропорции искаженного и реального размера. Обратите внимание, что карта многократно прерывается по политическим линиям.

Цилиндрические проекции на 360°: равнопрямоугольная, Миллера, Меркатора и истинно цилиндрическая.

Как и во всех проекциях карт , формы или размеры являются искажениями истинного расположения поверхности Земли. Проекция Меркатора преувеличивает области, далекие от экватора ; чем ближе к полюсам Земли, тем больше искажение.

Примеры искажения размера

• Гренландия кажется такого же размера, как Африка , хотя на самом деле площадь Африки в 14 раз больше. ^[13]
  • Реальная площадь Гренландии сопоставима с площадью Демократической Республики Конго .
  • Африка кажется примерно такого же размера, как Южная Америка , хотя на самом деле Африка в полтора раза больше.
• Кажется, что Аляска такого же размера, как Австралия , хотя на самом деле Австралия в 4,5 раза больше.
  • Аляска также занимает на карте такую ​​же площадь, как и Бразилия , тогда как площадь Бразилии почти в 5 раз больше площади Аляски.
• Мадагаскар и Великобритания выглядят примерно одинакового размера, хотя на самом деле Мадагаскар более чем в два раза больше Великобритании.

Критика

Из-за больших искажений площади суши критики, такие как Джордж Келлауэй и Ирвинг Фишер, считают проекцию непригодной для общих карт мира. Предполагается, что она повлияла на взгляды людей на мир: поскольку она показывает страны вблизи экватора слишком маленькими по сравнению с Европой и Северной Америкой, предполагается, что она заставляет людей считать эти страны менее важными. ^[14] Сам Меркатор использовал равновеликую синусоидальную проекцию для отображения относительных площадей. Однако, несмотря на такую ​​критику, проекция Меркатора была, особенно в конце 19-го и начале 20-го веков, возможно, самой распространенной проекцией, используемой на картах мира. ^{[15] [16] [17]}

В 1940-х годах атласы в основном перестали использовать проекцию Меркатора для карт мира или для областей, удаленных от экватора, предпочитая другие цилиндрические проекции или формы равновеликой проекции . Однако проекция Меркатора по-прежнему широко используется для областей вблизи экватора, где искажения минимальны. Она также часто встречается на картах часовых поясов. ^[18]

Арно Петерс вызвал споры, начавшиеся в 1972 году, когда он предложил то, что сейчас обычно называют проекцией Галла–Петерса , чтобы исправить проблемы Меркатора, утверждая, что это его собственная оригинальная работа, не ссылаясь на предыдущие работы картографов, такие как работа Галла от 1855 года. Проекция, которую он продвигал, является конкретной параметризацией цилиндрической равновеликой проекции . В ответ на это в резолюции 1989 года семи североамериканских географических групп было осуждено использование цилиндрических проекций для универсальных карт мира, которые включали как Меркатора, так и Галла–Петерса. ^[19]

Использует

Локсодром (синяя) в сравнении с дугой большого круга (красная) между Лиссабоном, Португалия, и Гаваной, Куба. Вверху: ортографическая проекция. Внизу: проекция Меркатора.

Практически каждая морская карта в печати основана на проекции Меркатора из-за ее уникальных благоприятных свойств для навигации. Она также широко используется службами уличных карт, размещенными в Интернете, из-за ее уникальных благоприятных свойств для локальных карт, вычисляемых по запросу. ^[20] Проекции Меркатора также сыграли важную роль в математической разработке тектоники плит в 1960-х годах. ^[21]

Морская навигация

Проекция Меркатора была разработана для использования в морской навигации из-за ее уникального свойства представлять любой курс постоянного пеленга как прямой сегмент. Такой курс, известный как румб (альтернативно называемый линией румба или локсодромией), предпочтителен в морской навигации, поскольку суда могут плыть в постоянном направлении компаса. Это уменьшает сложные, подверженные ошибкам исправления курса, которые в противном случае были бы необходимы при плавании по другому курсу.

Для небольших расстояний (по сравнению с радиусом Земли) разница между курсом по румбу и курсом по большому кругу незначительна. Даже для больших расстояний простота постоянного пеленга делает его привлекательным. Как заметил Меркатор, на таком курсе корабль не прибудет по кратчайшему пути, но он обязательно прибудет. Плавание по румбу означало, что все, что нужно было сделать морякам, — это держаться постоянного курса, пока они знали, где они были, когда начали, где они намеревались быть, когда закончили, и имели карту в проекции Меркатора, которая правильно показывала эти две координаты. ^[22]

Веб-Меркатор

Многие крупные онлайн-сервисы уличного картографирования ( Bing Maps , Google Maps , Mapbox , MapQuest , OpenStreetMap , Yahoo! Maps и другие) используют вариант проекции Меркатора для своих картографических изображений ^[23], называемый Web Mercator или Google Web Mercator. Несмотря на очевидное изменение масштаба на мировом уровне (мелкие масштабы), проекция хорошо подходит в качестве интерактивной карты мира, которую можно плавно масштабировать до локальных (крупномасштабных) карт, где искажения относительно невелики из-за почти конформности вариантной проекции .

Системы мозаичного отображения основных онлайн-сервисов уличного картографирования отображают большую часть мира при самом низком уровне масштабирования как единое квадратное изображение, исключая полярные регионы путем усечения на широтах φ _max  = ±85,05113°. (См. ниже.) Значения широты за пределами этого диапазона отображаются с использованием другого соотношения, которое не расходится при  φ  = ±90°. ^{[ необходима ссылка ]}

Поперечная проекция Меркатора

Поперечная проекция Меркатора наклоняет ось цилиндра так, что она становится перпендикулярной оси Земли. Стандартная касательная линия затем совпадает с меридианом и его противоположным меридианом, давая постоянный масштабный коэффициент вдоль этих меридианов и делая проекцию полезной для картографирования регионов, которые преимущественно простираются с севера на юг. В своей более сложной эллипсоидальной форме большинство национальных систем координат по всему миру используют поперечную проекцию Меркатора, как и универсальная поперечная система координат Меркатора .

Косая проекция Меркатора

Косая проекция Меркатора с осью (вне кадра справа) на 2,38 м южнее Триумфальной арки в Париже, Франция. ^[24] Логарифмическое расхождение таково, что прямоугольный монумент имеет яйцевидную форму, а двенадцать расходящихся проспектов его кольцевой развязки параллельны.

Косая проекция Меркатора наклоняет ось цилиндра от оси Земли на выбранный угол, так что ее касательные или секущие линии контакта представляют собой окружности, которые также наклонены относительно параллелей широты Земли. ^[25] Практические применения косой проекции, такие как национальные системы координат, используют эллипсоидальные развертки косой проекции Меркатора , чтобы поддерживать низкую вариацию масштаба вдоль поверхностной проекции оси цилиндра.

Математика

Цилиндрические проекции

Хотя поверхность Земли лучше всего моделируется сплющенным эллипсоидом вращения , для мелкомасштабных карт эллипсоид аппроксимируется сферой радиуса a , где a составляет приблизительно 6371 км. Эта сферическая аппроксимация Земли может быть смоделирована меньшей сферой радиуса R , называемой в этом разделе глобусом . Глобус определяет масштаб карты. Различные цилиндрические проекции определяют, как географические детали переносятся с глобуса на цилиндр, касательный к нему на экваторе. Затем цилиндр разворачивается, чтобы получить плоскую карту. ^{[26] [27] [ нужна страница ]} Дробь ⁠Р/а⁠ называется представительной долей (RF) или главным масштабом проекции. Например, карта Меркатора, напечатанная в книге, может иметь экваториальную ширину 13,4 см, что соответствует радиусу шара 2,13 см, и RF приблизительно ⁠1/300М⁠ (M используется как сокращение от 1 000 000 при написании RF), тогда как оригинальная карта Меркатора 1569 года имела ширину 198 см, что соответствует радиусу глобуса 31,5 см, а RF составляло около ⁠1/20М⁠ .

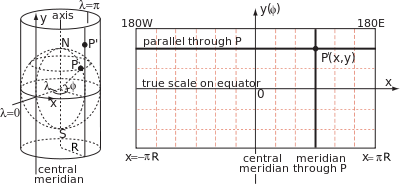
Цилиндрическая проекция карты задается формулами, связывающими географические координаты широты  φ и долготы  λ с декартовыми координатами на карте с началом на экваторе и осью x вдоль экватора. По построению все точки на одном меридиане лежат на одной и той же образующей ^[a] цилиндра при постоянном значении x , но расстояние y вдоль образующей (измеренное от экватора) является произвольной ^[b] функцией широты, y ( φ ). В общем случае эта функция не описывает геометрическую проекцию (как световых лучей на экран) из центра земного шара на цилиндр, что является лишь одним из неограниченного числа способов концептуально спроецировать цилиндрическую карту.

Поскольку цилиндр касается земного шара на экваторе, масштабный коэффициент между земным шаром и цилиндром равен единице на экваторе, но больше нигде. В частности, поскольку радиус параллели или круга широты равен R  cos  φ , соответствующая параллель на карте должна быть растянута в ⁠ раз1/соз φ⁠ = sec φ . Этот масштабный фактор на параллели условно обозначается как k , а соответствующий масштабный фактор на меридиане обозначается как  h . ^[28]

Масштабный фактор

Проекция Меркатора является конформной . Одним из следствий этого является «изотропия масштабных факторов», что означает, что масштабный фактор точки не зависит от направления, так что малые формы сохраняются проекцией. Это означает, что вертикальный масштабный фактор, h , равен горизонтальному масштабному фактору, k . Поскольку k = sec φ , то и h должен быть таким же .

График показывает изменение этого масштабного коэффициента с широтой. Некоторые числовые значения приведены ниже.

на широте 30° масштабный коэффициент равен   k  = сек 30° = 1,15,

на широте 45° масштабный коэффициент равен   k  = сек 45° = 1,41,

на широте 60° масштабный коэффициент равен   k  = sec 60° = 2,

на широте 80° масштабный коэффициент равен   k  = сек 80° = 5,76,

на широте 85° масштабный коэффициент равен   k  = сек 85° = 11,5

Коэффициент масштабирования площади является произведением параллельной и меридиональной шкал hk = sec ² φ . Для Гренландии, принимая 73° за срединную широту, hk = 11,7. Для Австралии, принимая 25° за срединную широту, hk = 1,2. Для Великобритании, принимая 55° за срединную широту, hk = 3,04.

Изменение в зависимости от широты иногда обозначается несколькими линейными шкалами , как показано ниже.

Индикатрисы Тиссо в проекции Меркатора

Классический способ показать искажение, присущее проекции, — использовать индикатрису Тиссо . Николя Тиссо заметил, что масштабные коэффициенты в точке на картографической проекции, заданные числами h и k , определяют эллипс в этой точке. Для цилиндрических проекций оси эллипса выровнены по меридианам и параллелям. ^{[29] [c]} Для проекции Меркатора h  =  k , поэтому эллипсы вырождаются в окружности с радиусом, пропорциональным значению масштабного коэффициента для этой широты. Эти окружности отображаются на спроецированной карте с экстремальными вариациями в размере, что указывает на вариации масштаба Меркатора.

Преобразования проекции Меркатора

Вывод

Как обсуждалось выше, условие изотропии подразумевает, что h = k = sec φ . Рассмотрим точку на земном шаре радиусом R с долготой λ и широтой φ . Если φ увеличивается на бесконечно малую величину, dφ , точка перемещается R dφ вдоль меридиана земного шара радиусом R , поэтому соответствующее изменение y , dy , должно быть hR dφ = R  sec  φ dφ . Поэтому y′ ( φ ) =  R  sec  φ . Аналогично, увеличение λ на dλ перемещает точку R cos φ dλ вдоль параллели земного шара, поэтому dx = kR cos φ dλ = R dλ . То есть, x′ ( λ ) =  R . Интегрируя уравнения

${\displaystyle x'(\lambda )=R,\qquad y'(\varphi )=R\sec \varphi ,}$

при x ( λ ₀ ) = 0 и y (0) = 0, дает x(λ) и y(φ) . Значение λ ₀ является долготой произвольного центрального меридиана, который обычно, но не всегда, совпадает с Гринвичским (т.е. равен нулю). Углы λ и φ выражаются в радианах. Интегралом секущей функции , ^{[30] [31]}

${\displaystyle x=R(\lambda -\lambda _{0}),\qquad y=R\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right].}$

Функция y ( φ ) наносится рядом с φ для случая R  = 1: она стремится к бесконечности на полюсах. Линейные значения оси y обычно не отображаются на печатных картах; вместо этого некоторые карты показывают нелинейную шкалу значений широты справа. Чаще всего карты показывают только сетку выбранных меридианов и параллелей.

Обратные преобразования

${\displaystyle \lambda =\lambda _{0}+{\frac {x}{R}},\qquad \varphi =2\tan ^{-1}\left[\exp \left({\frac {y}{R}}\right)\right]-{\frac {\pi }{2}}\,.}$

Выражение справа от второго уравнения определяет функцию Гудермана ; то есть, φ  = gd( ⁠у/Р⁠ ): поэтому прямое уравнение можно записать как y  =  R ·gd ⁻¹ ( φ ). ^[30]

Альтернативные выражения

Существует множество альтернативных выражений для y ( φ ), все они получены с помощью элементарных преобразований. ^[31]

${\displaystyle {\begin{aligned}y&=&{\frac {R}{2}}\ln \left[{\frac {1+\sin \varphi }{1-\sin \varphi }}\right]&=&{R}\ln \left[{\frac {1+\sin \varphi }{\cos \varphi }}\right]&=R\ln \left(\sec \varphi +\tan \varphi \right)\\[2ex]&=&R\tanh ^{-1}\left(\sin \varphi \right)&=&R\sinh ^{-1}\left(\tan \varphi \right)&=R\operatorname {sgn} (\varphi )\cosh ^{-1}\left(\sec \varphi \right)=R\operatorname {gd} ^{-1}(\varphi ).\end{aligned}}}$

Соответствующие обратные величины:

${\displaystyle \varphi =\sin ^{-1}\left(\tanh {\frac {y}{R}}\right)=\tan ^{-1}\left(\sinh {\frac {y}{R}}\right)=\operatorname {sgn} (y)\sec ^{-1}\left(\cosh {\frac {y}{R}}\right)=\operatorname {gd} {\frac {y}{R}}.}$

Для углов, выраженных в градусах:

${\displaystyle x={\frac {\pi R(\lambda ^{\circ }-\lambda _{0}^{\circ })}{180}},\qquad \quad y=R\ln \left[\tan \left(45+{\frac {\varphi ^{\circ }}{2}}\right)\right].}$

Вышеприведенные формулы записаны в терминах радиуса шара R. Часто бывает удобно работать непосредственно с шириной карты W  = 2 π R. Например, основные уравнения преобразования становятся

${\displaystyle x={\frac {W}{2\pi }}\left(\lambda -\lambda _{0}\right),\qquad \quad y={\frac {W}{2\pi }}\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\right].}$

Усечение и соотношение сторон

Ордината y проекции Меркатора становится бесконечной на полюсах, и карта должна быть усечена на некоторой широте менее девяноста градусов. Это не обязательно должно быть сделано симметрично. Оригинальная карта Меркатора усечена на 80° с. ш. и 66° ю. ш., в результате чего европейские страны были смещены к центру карты. Соотношение сторон его карты ⁠198/120⁠ = 1,65. Использовались даже более экстремальные усечения: финский школьный атлас был усечен примерно на 76° с. ш. и 56° ю. ш., соотношение сторон 1,97.

Большая часть веб-картографирования использует масштабируемую версию проекции Меркатора с соотношением сторон 1. В этом случае максимальная достигаемая широта должна соответствовать y  = ± ⁠Вт/2⁠ , или эквивалентно ⁠у/Р⁠  =  π . Для вычисления соответствующих широт можно использовать любую из формул обратного преобразования:

${\displaystyle \varphi =\tan ^{-1}\left[\sinh \left({\frac {y}{R}}\right)\right]=\tan ^{-1}\left[\sinh \pi \right]=\tan ^{-1}\left[11.5487\right]=85.05113^{\circ }.}$

Геометрия малых элементов

Отношения между y ( φ ) и свойствами проекции, такими как преобразование углов и изменение масштаба, следуют из геометрии соответствующих малых элементов на глобусе и карте. На рисунке ниже показана точка P на широте  φ и долготе  λ на глобусе и близлежащая точка Q на широте φ  +  δφ и долготе λ  +  δλ . Вертикальные линии PK и MQ являются дугами меридианов длиной Rδφ . ^[d] Горизонтальные линии PM и KQ являются дугами параллелей длиной R (cos  φ ) δλ . Соответствующие точки на проекции определяют прямоугольник шириной  δx и высотой  δy .

Для малых элементов угол PKQ приблизительно прямой и поэтому

${\displaystyle \tan \alpha \approx {\frac {R\cos \varphi \,\delta \lambda }{R\,\delta \varphi }},\qquad \qquad \tan \beta ={\frac {\delta x}{\delta y}},}$

Ранее упомянутые коэффициенты масштабирования от шара к цилиндру определяются как

параллельный масштабный коэффициент     ${\displaystyle \quad k(\varphi )\;=\;{\frac {P'M'}{PM}}\;=\;{\frac {\delta x}{R\cos \varphi \,\delta \lambda }},}$

меридиональный масштабный фактор   ${\displaystyle \quad h(\varphi )\;=\;{\frac {P'K'}{PK}}\;=\;{\frac {\delta y}{R\delta \varphi \,}}.}$

Поскольку меридианы отображаются в линии постоянной x , мы должны иметь x = R ( λ − λ ₀ ) и δx  =  Rδλ , ( λ в радианах). Поэтому в пределе бесконечно малых элементов

${\displaystyle \tan \beta ={\frac {R\sec \varphi }{y'(\varphi )}}\tan \alpha \,,\qquad k=\sec \varphi \,,\qquad h={\frac {y'(\varphi )}{R}}.}$

В случае проекции Меркатора y' ( φ ) = R sec φ , так что это дает нам h = k и α = β . Тот факт, что h = k, является изотропией масштабных коэффициентов, обсуждавшихся выше. Тот факт, что α = β отражает другое следствие конформности отображения, а именно тот факт, что курс плавания с постоянным азимутом на земном шаре отображается в ту же постоянную сетку пеленга на карте.

Формулы для расстояния

Преобразование расстояния линейки на карте Меркатора в истинное ( большое окружное ) расстояние на сфере осуществляется прямолинейно вдоль экватора, но больше нигде. Одна из проблем заключается в изменении масштаба в зависимости от широты, а другая заключается в том, что прямые линии на карте ( линии румба ), кроме меридианов или экватора, не соответствуют большим окружностям.

Различие между локсодромией (парусным) и ортодромическим (истинным) расстоянием было ясно понято Меркатором. (См. легенду 12 на карте 1569 года.) Он подчеркивал, что локсодромие является приемлемым приближением для истинного локсодромии для курсов короткой или средней протяженности, особенно на низких широтах. Он даже количественно определяет свое утверждение: «Когда локсодромии, которые должны быть измерены вблизи экватора, не превышают 20 градусов большого круга, или 15 градусов около Испании и Франции, или 8 и даже 10 градусов в северных частях, удобно использовать локсодромии».

Для измерения линейкой короткой линии со средней точкой на широте  φ , где масштабный коэффициент равен k  = sec  φ  =  ⁠1/соз  φ⁠ :

Истинное расстояние = расстояние по локсодромии ≅ расстояние по линейке × cos  φ / RF. (короткие линии)

При радиусе и длине большой окружности, равных 6371 км и 40030 км соответственно, RF составляет ⁠1/300М⁠ , для которого R  = 2,12 см и W  = 13,34 см, подразумевает, что измерение линейки 3 мм. в любом направлении от точки на экваторе соответствует приблизительно 900 км. Соответствующие расстояния для широт 20°, 40°, 60° и 80° составляют 846 км, 689 км, 450 км и 156 км соответственно.

Более длинные расстояния требуют иных подходов.

На экваторе

Масштаб равен единице на экваторе (для несекущей проекции). Поэтому интерпретация измерений линейки на экваторе проста:

Истинное расстояние = расстояние линейки / RF (экватор)

Для приведенной выше модели с RF =  ⁠1/300М⁠ , 1 см соответствует 3000 км.

О других параллелях

На любой другой параллели масштабный коэффициент равен sec φ, так что

Расстояние параллельности = расстояние линейки × cos  φ / RF (параллельно).

Для приведенной выше модели 1 см соответствует 1500 км на широте 60°.

Это не кратчайшее расстояние между выбранными конечными точками на параллели, поскольку параллель не является большим кругом. Разница невелика для коротких расстояний, но увеличивается с увеличением λ , продольного расстояния. Для двух точек, A и B, разделенных 10° долготы на параллели под углом 60°, расстояние вдоль параллели примерно на 0,5 км больше расстояния по большому кругу. (Расстояние AB вдоль параллели равно ( a  cos  φ )  λ . Длина хорды AB равна 2( a  cos  φ ) sin  ⁠λ/2⁠ . Эта хорда стягивает угол в центре, равный 2arcsin(cos  φ  sin  ⁠λ/2⁠ ) ​​и расстояние по большому кругу между A и B равно 2 a  arcsin(cos  φ  sin  ⁠λ/2⁠ ).) В крайнем случае, когда продольное разделение составляет 180°, расстояние вдоль параллели составляет половину окружности этой параллели; т. е. 10 007,5 км. С другой стороны, геодезическая между этими точками представляет собой дугу большого круга, проходящую через полюс и образующую угол 60° в центре: длина этой дуги составляет одну шестую часть окружности большого круга, около 6 672 км. Разница составляет 3 338 км, поэтому расстояние линейки, измеренное по карте, является совершенно обманчивым даже после поправки на широтное изменение масштабного коэффициента.

На меридиане

Меридиан карты — это большой круг на земном шаре, но непрерывное изменение масштаба означает, что измерение линейкой само по себе не может дать истинное расстояние между удаленными точками на меридиане. Однако, если карта отмечена точной и мелкой шкалой широты, с которой широта может быть прочитана напрямую, как в случае с картой мира Меркатора 1569 года (листы 3, 9, 15) и всеми последующими морскими картами, — расстояние по меридиану между двумя широтами φ ₁ и φ ₂ просто

${\displaystyle m_{12}=a|\varphi _{1}-\varphi _{2}|.}$

Если широты конечных точек не могут быть определены с уверенностью, то их можно найти вместо этого путем вычисления расстояния линейки. Называя расстояния линейки конечных точек на карте меридианом, измеренным от экватора y ₁ и y ₂ , истинное расстояние между этими точками на сфере дается с помощью любой из обратных формул Меркатора:

${\displaystyle m_{12}=a\left|\tan ^{-1}\left[\sinh \left({\frac {y_{1}}{R}}\right)\right]-\tan ^{-1}\left[\sinh \left({\frac {y_{2}}{R}}\right)\right]\right|,}$

где R можно рассчитать из ширины W карты по формуле R  =  ⁠Вт/2π​⁠ . Например, на карте с R  = 1 значения y  = 0, 1, 2, 3 соответствуют широтам φ  = 0°, 50°, 75°, 84° и, следовательно, последовательные интервалы в 1 см на карте соответствуют интервалам широты на глобусе 50°, 25°, 9° и расстояниям 5560 км, 2780 км и 1000 км на Земле.

На румбе

Прямая линия на карте Меркатора под углом α к меридианам называется локсодромией . Когда α  =  ⁠π/2⁠ или ⁠3π​/2⁠ румб соответствует одной из параллелей; только одна, экватор, является большим кругом. Когда α  = 0 или π, он соответствует большому кругу меридиана (если продолжить вокруг Земли). Для всех других значений это спираль от полюса до полюса на земном шаре, пересекающая все меридианы под тем же углом, и, таким образом, не является большим кругом. ^[31] В этом разделе обсуждается только последний из этих случаев.

Если α не равно ни 0, ни π, то приведенный выше рисунок бесконечно малых элементов показывает, что длина бесконечно малой локсодромии на сфере между широтами φ ; и φ  +  δφ равна sec α  δφ . Поскольку α постоянна на локсодромии, это выражение можно проинтегрировать, чтобы получить для  конечных  локсодромий на Земле:

${\displaystyle r_{12}=a\sec \alpha \,|\varphi _{1}-\varphi _{2}|=a\,\sec \alpha \;\Delta \varphi .}$

Еще раз, если Δ φ можно прочитать непосредственно из точной шкалы широты на карте, то расстояние по локсодромии между точками карты с широтами φ ₁ и φ ₂ дается выше. Если такой шкалы нет, то расстояния по линейке между конечными точками и экватором, y ₁ и y ₂ , дают результат через обратную формулу:

${\displaystyle r_{12}=a\sec \alpha \left|\tan ^{-1}\sinh \left({\frac {y_{1}}{R}}\right)-\tan ^{-1}\sinh \left({\frac {y_{2}}{R}}\right)\right|.}$

Эти формулы дают локсодромные расстояния на сфере, которые могут значительно отличаться от истинных расстояний, определение которых требует более сложных вычислений. ^[e]

Обобщение на эллипсоид

Когда Земля моделируется сфероидом ( эллипсоидом вращения ), проекция Меркатора должна быть изменена, чтобы она оставалась конформной . Уравнения преобразования и масштабный коэффициент для несекущей версии следующие ^[32] $${\displaystyle {\begin{aligned}x&=R\left(\lambda -\lambda _{0}\right),\\y&=R\ln \left[\tan \left({\frac {\pi }{4}}+{\frac {\varphi }{2}}\right)\left({\frac {1-e\sin \varphi }{1+e\sin \varphi }}\right)^{\frac {e}{2}}\right]=R\left(\sinh ^{-1}\left(\tan \varphi \right)-e\tanh ^{-1}(e\sin \varphi )\right),\\k&=\sec \varphi {\sqrt {1-e^{2}\sin ^{2}\varphi }}.\end{aligned}}}$$

Масштабный коэффициент равен единице на экваторе, как и должно быть, поскольку цилиндр касается эллипсоида на экваторе. Эллипсоидальная коррекция масштабного коэффициента увеличивается с широтой, но она никогда не превышает e ² , коррекция менее 1%. (Значение e ² составляет около 0,006 для всех референц-эллипсоидов.) Это намного меньше неточности масштаба, за исключением очень близких к экватору областей. Только точные проекции Меркатора регионов вблизи экватора потребуют эллипсоидальных коррекций.

Обратное уравнение решается итеративно, поскольку учитывается изометрическая широта .

Смотрите также

• Картография
• Центральная цилиндрическая проекция – более искаженная; иногда ошибочно описывается как метод построения проекции Меркатора.
• Конформная проекция карты
• Равнопрямоугольная проекция – менее искаженная, но не равновеликая
• Проекция Галла–Петерса – равновеликая цилиндрическая проекция
• Иорданская поперечная проекция Меркатора
• Список картографических проекций
• Карта мира Меркатора 1569 года
• Морская карта
• Отсутствие Новой Зеландии на картах — часто считается, что это вызвано проекцией Меркатора.
• Сеть рамблайн
• Индикатриса Тиссо
• Поперечная проекция Меркатора
• Универсальная поперечная система координат Меркатора

Примечания

1. Образующей цилиндра является прямая линия на поверхности, параллельная оси цилиндра.
2. Функция y ( φ ) не является полностью произвольной: она должна быть монотонно возрастающей и антисимметричной ( y (− φ ) = − y ( φ ), так что y (0)=0): она обычно непрерывна с непрерывной первой производной.
3. Более общий пример индикатрисы Тиссо: трипель-проекция Винкеля .
4. R — радиус земного шара.
5. См . расстояние по дуге большого круга , формулы Винсенти или Mathworld.

Ссылки

1. Нидхэм, Джозеф (1959). Наука и цивилизация в Китае . Т. 3. Cambridge University Press. С. 277, 545.
2. Миядзима, Казухико (1998). «Методы проецирования в китайских, корейских и японских звездных картах». Highlights of Astronomy . 11 (2): 712–715. doi : 10.1017/s1539299600018554 .
3. Шаловиц, Аарон Л. (1969). «Карта, которая сделала историю навигации». Журнал Вашингтонской академии наук . 59 (7–9): 180–186. JSTOR  24535986.
4. Николаи, Р. (2015). «Досредневековое происхождение карт-портоланов: новые геодезические свидетельства». Isis . 106 (3): 517–543. doi : 10.1086/683532. hdl : 1874/327279 . PMID  26685516.
5. Николаи, Р. (2015). «Досредневековое происхождение карт-портоланов: новые геодезические свидетельства». Isis . 106 (3): 517–543. doi : 10.1086/683532. hdl : 1874/327279 . PMID  26685516.
6. Снайдер 1987, стр. 38.
7. Снайдер 1993, стр. 48.
8. Крейн, Николас (2002). Меркатор: человек, который нанес на карту планету . Лондон: Weidenfeld & Nicolson. Гл. 9.
9. Лейтао, Энрике; Гаспар, Хоаким Алвес (3 июля 2014 г.). «Глобусы, румбические таблицы и предыстория проекции Меркатора». Имаго Мунди . 66 (2): 180–195. дои : 10.1080/03085694.2014.902580. ISSN  0308-5694.
10. Монмонье 2004, стр. 72.
11. Лапейн, Мильенко (2024). «Проблема в «Базовой картографии»". Международный журнал картографии . 10 (1): 118–131. Bibcode : 2024IJCar..10..118L. doi : 10.1080/23729333.2022.2157106.
    Керковиц, Кристиан (2024). «Секущие цилиндры — зло. Исследование стандартных линий универсальной поперечной проекции Меркатора и универсальной полярной стереографической проекции». ISPRS International Journal of Geo-Information . 13 (2): 56. Bibcode : 2024IJGI...13...56K. doi : 10.3390/ijgi13020056 .
12. Фредерик Рики, В.; Тучинский, Филип М. (май 1980 г.). «Применение географии к математике: история интеграла секущей». Mathematics Magazine . 53 (3): 164. doi :10.2307/2690106. JSTOR  2690106. Получено 18 августа 2022 г.
13. "Эта анимированная карта показывает истинный размер каждой страны". Nature Index . 2019-08-27 . Получено 2023-06-20 .
14. "Проекция Меркатора против проекции Петерса, часть 1". Мэтт Т. Розенберг, about.com.
15. Kellaway, GP (1946). Map Projections стр. 37–38. Лондон: Methuen & Co. LTD. (Согласно этому источнику, утверждалось, что проекция Меркатора использовалась в «империалистических целях»)
16. Абельсон, CE (1954). Common Map Projections s. 4. Севенокс: WH Smith & Sons.
17. Чемберлин, Уэллман (1947). Круглая Земля на плоской бумаге , с. 99. Вашингтон, округ Колумбия: Национальное географическое общество.
18. Монмонье 2004, стр. 124–128.
19. Американский картограф. 1989. 16(3): 222–223.
20. «Почему Меркатор для Интернета? Разве Меркатор не плох?». www.mapthematics.com . Получено 12.11.2024 .^{[ самостоятельно опубликованный источник ]}
21. Кокс, Аллан, ред. (1973). Тектоника плит и геомагнитные инверсии . WH Freeman. стр. 46.
22. Осборн 2013, стр. 39–40.
23. Баттерсби, Сара Э.; Финн, Майкл П.; Юзери, Э. Линн; Ямамото, Кристина Х. (1 июня 2014 г.). «Последствия Web Mercator и его использование в онлайн-картографии». Cartographica: Международный журнал географической информации и геовизуализации . 49 (2): 85–101. doi :10.3138/carto.49.2.2313. ISSN  0317-7173.
24. «Меркатор: Экстремум».
25. «Проекция Меркатора».
26. Снайдер 1987, стр. 37–95.
27. Снайдер 1993.
28. Снайдер. Рабочее руководство, стр. 20.
29. Снайдер 1987, с. 20; Снайдер 1993, стр. 147–149.
30. NIST. См. разделы 4.26#ii и 4.23#viii
31. Osborne 2013, Глава 2
32. Осборн 2013, Главы 5, 6

Библиография

• Малинг, Дерек Хилтон (1992), Системы координат и картографические проекции (второе издание), Pergamon Press, ISBN 0-08-037233-3.
• Монмонье, Марк (2004), Локсодромии и войны карт: Социальная история проекции Меркатора (издание в твердом переплете), Чикаго: Издательство Чикагского университета, ISBN 0-226-53431-6
• Olver, FWJ; Lozier, DW; Boisvert, RF; et al., ред. (2010), Справочник NIST по математическим функциям, Cambridge University Press
• Осборн, Питер (14 ноября 2013 г.), «Проекции Меркатора» , doi : 10.5281/zenodo.35392(Дополнения: файлы Maxima, а также код и рисунки Latex)
• Снайдер, Джон П. (1993), Сплющивание Земли: две тысячи лет картографических проекций , Издательство Чикагского университета, ISBN 0-226-76747-7
• Снайдер, Джон П. (1987), Картографические проекции – рабочее руководство. Профессиональная статья Геологической службы США 1395, Типография правительства США, Вашингтон, округ КолумбияЭту статью можно скачать со страниц USGS. Она дает полную информацию о большинстве проекций, вместе с интересными вводными разделами, но не выводит ни одну из проекций из первых принципов.

Дальнейшее чтение

• Рапп, Ричард Х. (1991), Геометрическая геодезия, часть I , Университет штата Огайо, кафедра геодезических наук и геодезии, hdl :1811/24333

Внешние ссылки

• Ad maiorem Gerardi Mercatoris gloriam - содержит изображения карты мира Меркатора 1569 года в высоком разрешении.
• Таблица примеров и свойств всех распространенных проекций с сайта radicalcartography.net.
• Интерактивный Java-апплет для изучения метрических деформаций проекции Меркатора.
• Проекция Меркатора в Университете Британской Колумбии
• Координаты Google Карт
• Меркатор Экстремальный