Вибрация

Механические колебания около точки равновесия

Вибрация (от латинского vibrō  «трясти») — механическое явление, при котором происходят колебания вокруг точки равновесия . Вибрация может быть детерминированной, если колебания можно точно охарактеризовать (например, периодическое движение маятника ) , или случайной , если колебания можно проанализировать только статистически (например, движение шины на гравийной дороге).

Вибрация может быть желательной: например, движение камертона , трости деревянного духового инструмента или гармошки , мобильного телефона или диффузора громкоговорителя .

Однако во многих случаях вибрация нежелательна, поскольку приводит к потере энергии и созданию нежелательного звука . Например, вибрационные движения двигателей , электродвигателей или любого работающего механического устройства обычно нежелательны. Такие вибрации могут быть вызваны дисбалансом вращающихся частей, неравномерным трением или зацеплением зубьев шестерни . Тщательное проектирование обычно сводит к минимуму нежелательные вибрации.

Исследования звука и вибрации тесно связаны (оба относятся к акустике ). Звук или волны давления генерируются вибрирующими структурами (например, голосовыми связками ); эти волны давления также могут вызывать вибрацию структур (например, барабанной перепонки ). Следовательно, попытки снизить шум часто связаны с проблемами вибрации. ^[1]

Один из возможных режимов вибрации круглого барабана (см. другие режимы).

Подвеска автомобиля . Проектирование системы контроля вибрации осуществляется в рамках акустического , автомобильного или машиностроения .

Вибрации при обработке являются обычным явлением в процессе субтрактивного производства .

Типы

Свободная вибрация или собственная вибрация возникает, когда механическая система приводится в движение с помощью начального воздействия и ей разрешено свободно вибрировать. Примерами этого типа вибрации является то, что ребенка тянут назад на качелях и отпускают, или ударяют по камертону, и он начинает звучать. Механическая система вибрирует на одной или нескольких своих собственных частотах и ​​затухает до состояния неподвижности.

Вынужденная вибрация – это когда к механической системе прикладывается изменяющееся во времени возмущение (нагрузка, смещение, скорость или ускорение). Возмущение может быть периодическим и установившимся входным сигналом, переходным входным сигналом или случайным входным сигналом. Периодический входной сигнал может быть гармоническим или негармоническим возмущением. Примеры этих типов вибрации включают тряску стиральной машины из-за дисбаланса, вибрацию при транспортировке, вызванную двигателем или неровной дорогой, или вибрацию здания во время землетрясения. Для линейных систем частота установившегося вибрационного отклика, возникающего в результате приложения периодического гармонического воздействия, равна частоте приложенной силы или движения, при этом величина отклика зависит от фактической механической системы.

Затухающая вибрация: Когда энергия вибрирующей системы постепенно рассеивается из-за трения и других сопротивлений, вибрации называются затухающими. Вибрации постепенно уменьшаются, изменяются по частоте или интенсивности или прекращаются, и система остается в равновесном положении. Примером этого типа вибрации является подвеска автомобиля , демпфируемая амортизатором .

Изоляция

Виброизоляция — это предотвращение передачи вибрации от одного компонента системы к другим частям той же системы, например, в зданиях или механических системах . ^[2] Вибрация нежелательна во многих областях, в первую очередь в инженерных системах и жилых помещениях, и были разработаны методы предотвращения передачи вибрации на такие системы. Вибрации распространяются посредством механических волн, и некоторые механические связи проводят вибрации более эффективно, чем другие. Пассивная виброизоляция использует материалы и механические связи, которые поглощают и гасят эти механические волны. Активная виброизоляция включает в себя датчики и исполнительные механизмы, которые создают помехи, которые нейтрализуют входящую вибрацию.

Тестирование

Испытание на вибрацию осуществляется путем введения в конструкцию функции воздействия, обычно с помощью вибростенда какого-либо типа. Альтернативно, ИУ (испытуемое устройство) крепится к «столу» шейкера. Испытание на вибрацию проводится для проверки реакции тестируемого устройства (DUT) на определенную вибрационную среду. Измеряемым ответом может быть способность функционировать в условиях вибрации, усталостный ресурс, резонансные частоты или скрип и дребезжащий звук ( NVH ). Испытание на скрип и дребезжание проводится с помощью специального тихого вибростенда , который во время работы издает очень низкий уровень шума.

Для относительно низкочастотного воздействия (обычно менее 100 Гц) используются сервогидравлические (электрогидравлические) вибросита. Для более высоких частот (обычно от 5 Гц до 2000 Гц) используются электродинамические шейкеры. Как правило, одна или несколько «входных» или «контрольных» точек, расположенных на стороне тестируемого устройства вибрационного устройства, поддерживают заданное ускорение. ^[1] Другие «реагирующие» точки могут испытывать более высокие уровни вибрации (резонанс) или более низкий уровень вибрации (антирезонанс или демпфирование), чем контрольная точка(и). Часто желательно добиться антирезонанса, чтобы система не становилась слишком шумной или чтобы уменьшить нагрузку на определенные части из-за режимов вибрации, вызванных определенными частотами вибрации. ^[3]

Наиболее распространенными видами услуг по вибрационным испытаниям, проводимыми лабораториями вибрационных испытаний, являются синусоидальные и случайные. Синусоидальные (по одной частоте) тесты проводятся для изучения структурной реакции тестируемого устройства (DUT). На заре вибрационных испытаний контроллеры вибрационных машин были ограничены только управлением синусоидальным движением, поэтому проводились только синусоидальные испытания. Позже более сложные аналоговые, а затем и цифровые контроллеры смогли обеспечить случайное управление (все частоты одновременно). Обычно считается, что случайный тест (все частоты одновременно) более точно воспроизводит реальную среду, например, воздействие дороги на движущийся автомобиль.

Большинство испытаний на вибрацию проводится одновременно по «одной оси ИУ», хотя большая часть реальной вибрации возникает в различных осях одновременно. MIL-STD-810G, выпущенный в конце 2008 года, метод испытаний 527, требует тестирования нескольких возбудителей. Приспособление для испытаний на вибрацию ^[4] , используемое для крепления ИУ к вибраторному столу, должно быть рассчитано на частотный диапазон спектра испытаний на вибрацию. Трудно спроектировать приспособление для испытаний на вибрацию, которое дублировало бы динамический отклик (механическое сопротивление) ^[5] фактического используемого крепления. По этой причине, чтобы обеспечить повторяемость между испытаниями на вибрацию, вибрационные приспособления проектируются без резонанса ^[5] в пределах диапазона частот испытаний. Как правило, для светильников меньшего размера и более низких частотных диапазонов разработчик может выбрать конструкцию светильника, свободную от резонансов в тестовом диапазоне частот. Это становится более трудным по мере увеличения размера ИУ и увеличения частоты испытаний. В этих случаях стратегии многоточечного управления ^[6] могут смягчить некоторые резонансы, которые могут возникнуть в будущем.

Некоторые методы испытаний на вибрацию ограничивают количество перекрестных помех (перемещение точки срабатывания во взаимно перпендикулярном направлении к испытуемой оси), которые может проявлять приспособление для испытаний на вибрацию. Устройства, специально предназначенные для отслеживания или регистрации вибраций, называются виброскопами .

Анализ

Анализ вибрации (ВА), применяемый в промышленности или в условиях технического обслуживания, направлен на снижение затрат на техническое обслуживание и время простоя оборудования за счет обнаружения неисправностей оборудования. ^{[7] [8]} VA является ключевым компонентом программы мониторинга состояния (CM), и его часто называют профилактическим обслуживанием (PdM). ^[9] Чаще всего VA используется для обнаружения неисправностей вращающегося оборудования (вентиляторов, двигателей, насосов, коробок передач и т. д.), таких как дисбаланс, несоосность, неисправности подшипников качения и резонансные состояния. ^[10]

VA может использовать единицы смещения, скорости и ускорения, отображаемые в виде временного сигнала (TWF), но чаще всего используется спектр, полученный в результате быстрого преобразования Фурье TWF. Спектр вибрации предоставляет важную информацию о частоте, которая позволяет точно определить неисправный компонент.

Основы анализа вибрации можно понять, изучив простую модель «Масса-пружина-демпфер» . Действительно, даже такую ​​сложную конструкцию, как кузов автомобиля, можно смоделировать как «сумму» простых моделей масса-пружина-демпфер. Модель масса-пружина-демпфер является примером простого гармонического осциллятора . Математика, используемая для описания его поведения, идентична другим простым гармоническим генераторам, таким как схема RLC .

Примечание. Эта статья не включает пошаговые математические выводы, а фокусируется на основных уравнениях и концепциях анализа вибрации. Пожалуйста, обратитесь к ссылкам в конце статьи для получения подробных выводов.

Свободная вибрация без демпфирования

Простая модель массовой пружины

Чтобы начать исследование системы «масса-пружина-демпфер», предположим, что демпфирование незначительно и что к массе не прилагается внешняя сила (т. е. свободная вибрация). Сила, приложенная к массе пружиной, пропорциональна степени растяжения пружины «x» (при условии, что пружина уже сжата из-за веса массы). Константа пропорциональности k представляет собой жесткость пружины и измеряется в единицах сила/расстояние (например, фунт-сила/дюйм или Н/м). Знак минус указывает на то, что сила всегда противодействует движению прикрепленной к ней массы:

${\displaystyle F_{s}=-kx.\!}$

Сила, создаваемая массой, пропорциональна ускорению массы, как это определяется вторым законом движения Ньютона :

${\displaystyle \Sigma \ F=ma=m{\ddot {x}}=m{\frac {d^{2}x}{dt^{2}}}.}$

Сумма сил, действующих на массу, тогда порождает обыкновенное дифференциальное уравнение : ${\displaystyle \ m{\ddot {x}}+kx=0.}$

Простое гармоническое движение системы масса-пружина.

Предполагая, что возникновение вибрации начинается с растяжения пружины на расстояние А и ее отпускания, решение приведенного выше уравнения, описывающего движение массы, будет:

${\displaystyle x(t)=A\cos(2\pi f_{n}t).\!}$

_В этом решении говорится, что он будет совершать простые гармонические движения с амплитудой A и частотой fn . Число f _n называется незатухающей собственной частотой . Для простой системы масса-пружина f _n определяется как:

${\displaystyle f_{n}={1 \over {2\pi }}{\sqrt {k \over m}}.\!}$

Примечание: угловая частота ω (ω=2 π f ) в радианах в секунду часто используется в уравнениях, поскольку она упрощает уравнения, но обычно преобразуется в обычную частоту (единицы Гц или, что эквивалентно, циклов в секунду) при указании частота системы. Если известны масса и жесткость системы, приведенная выше формула может определить частоту, с которой система вибрирует после того, как она пришла в движение начальным возмущением. Каждая вибрирующая система имеет одну или несколько собственных частот, нарушая которые она вибрирует. Это простое соотношение можно использовать, чтобы в целом понять, что происходит с более сложной системой, когда мы добавляем массу или жесткость. Например, приведенная выше формула объясняет, почему при полной загрузке легкового или грузового автомобиля подвеска кажется «мягче», чем при незагруженном — масса увеличилась, что снизило собственную частоту системы.

Что заставляет систему вибрировать: с точки зрения сохранения энергии

Колебательное движение можно понять с точки зрения сохранения энергии . В приведенном выше примере пружина растянулась на величину x, и поэтому в пружине сохраняется некоторая потенциальная энергия ( ). После отпускания пружина стремится вернуться в нерастянутое состояние (которое является состоянием с минимальной потенциальной энергией) и при этом ускоряет массу. В тот момент, когда пружина достигла своего нерастянутого состояния, вся потенциальная энергия, которую мы передали, растягивая ее, преобразуется в кинетическую энергию ( ). Затем масса начинает замедляться, потому что теперь она сжимает пружину и в процессе передает кинетическую энергию обратно в ее потенциал. Таким образом, колебание пружины представляет собой переход туда и обратно кинетической энергии в потенциальную. В этой простой модели масса продолжает вечно колебаться с одной и той же величиной, но в реальной системе затухание всегда рассеивает энергию, в конечном итоге приводя пружину в состояние покоя. ${\displaystyle {\tfrac {1}{2}}kx^{2}}$ ${\displaystyle {\tfrac {1}{2}}mv^{2}}$

Свободная вибрация с демпфированием

Модель масса-пружина-демпфер

Когда к модели добавляется «вязкий» демпфер, создается сила, пропорциональная скорости массы. Демпфирование называется вязким, поскольку оно моделирует воздействие жидкости внутри объекта. Константа пропорциональности c называется коэффициентом демпфирования и имеет единицы измерения силы относительно скорости (фунт-сила-с/дюйм или Н⋅с/м).

${\displaystyle F_{\text{d}}=-cv=-c{\dot {x}}=-c{\frac {dx}{dt}}.}$

Суммирование сил, действующих на массу, приводит к следующему обыкновенному дифференциальному уравнению:

${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=0.}$

Решение этого уравнения зависит от величины демпфирования. Если демпфирование достаточно малое, система все равно вибрирует, но со временем вибрировать перестает. Этот случай называется недостаточным демпфированием, что важно при анализе вибрации. Если демпфирование увеличивается до такой степени, что система больше не колеблется, система достигла точки критического демпфирования . Если демпфирование превышает критическое значение, система перегружена . Значение, которого должен достичь коэффициент демпфирования для критического демпфирования в модели «масса-пружина-демпфер», равно:

${\displaystyle c_{\text{c}}=2{\sqrt {\text{km}}}.}$

Для характеристики степени демпфирования в системе используется коэффициент, называемый коэффициентом демпфирования (также известный как коэффициент демпфирования и % критического демпфирования). Этот коэффициент демпфирования представляет собой просто отношение фактического демпфирования к величине демпфирования, необходимой для достижения критического демпфирования. Формула для коэффициента демпфирования ( ) модели масса-пружина-демпфер: ${\displaystyle \zeta }$

${\displaystyle \zeta ={c \over 2{\sqrt {\text{km}}}}.}$

Например, металлические конструкции (например, фюзеляжи самолетов, коленчатые валы двигателей) имеют коэффициенты демпфирования менее 0,05, тогда как автомобильные подвески находятся в пределах 0,2–0,3. Решение системы с недостаточным демпфированием для модели «масса-пружина-демпфер» следующее:

${\displaystyle x(t)=Xe^{-\zeta \omega _{n}t}\cos \left({\sqrt {1-\zeta ^{2}}}\omega _{n}t-\phi \right),\qquad \omega _{n}=2\pi f_{n}.}$

Свободная вибрация с коэффициентом демпфирования 0,1 и 0,3.

Значение X , начальная величина и фазовый сдвиг определяются степенью растяжения пружины. Формулы для этих значений можно найти в ссылках. ${\displaystyle \phi ,}$

Затухающие и незатухающие собственные частоты

Основными моментами, на которые следует обратить внимание в решении, являются экспоненциальный член и косинус. Экспоненциальный член определяет, насколько быстро система «затухает»: чем больше коэффициент демпфирования, тем быстрее она затухает до нуля. Косинусная функция является колеблющейся частью решения, но частота колебаний отличается от незатухающего случая.

Частота в этом случае называется «затухающей собственной частотой» и связана с незатухающей собственной частотой по следующей формуле: ${\displaystyle f_{\text{d}},}$

${\displaystyle f_{\text{d}}=f_{n}{\sqrt {1-\zeta ^{2}}}.}$

Затухающая собственная частота меньше, чем незатухающая собственная частота, но во многих практических случаях коэффициент затухания относительно невелик, и, следовательно, разница незначительна. Поэтому описания затухающего и незатухаемого сигналов часто опускаются при указании собственной частоты (например, при коэффициенте затухания 0,1 затухающая собственная частота всего на 1% меньше, чем незатухающая).

Графики сбоку показывают, как коэффициенты демпфирования 0,1 и 0,3 влияют на то, как система «звенит» с течением времени. На практике часто производится экспериментальное измерение свободной вибрации после удара (например, молотка), а затем определяется собственная частота системы путем измерения скорости колебаний, а также коэффициент демпфирования путем измерения скорости разлагаться. Собственная частота и коэффициент демпфирования важны не только при свободной вибрации, но и характеризуют поведение системы в условиях вынужденной вибрации.

^[11]

Принудительная вибрация с демпфированием

Поведение модели пружинного демпфера меняется с добавлением гармонической силы. Сила этого типа может быть создана, например, вращающимся дисбалансом.

${\displaystyle F=F_{0}\sin(2\pi ft).\!}$

Суммирование сил, действующих на массу, приводит к следующему обыкновенному дифференциальному уравнению:

${\displaystyle m{\ddot {x}}+c{\dot {x}}+kx=F_{0}\sin(2\pi ft).}$

Стационарное решение этой задачи можно записать в виде :

${\displaystyle x(t)=X\sin(2\pi ft+\phi ).\!}$

Результат гласит, что масса будет колебаться с той же частотой f приложенной силы, но со сдвигом фазы. ${\displaystyle \phi .}$

Амплитуда вибрации «X» определяется по следующей формуле.

${\displaystyle X={F_{0} \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}}.}$

Где «r» определяется как отношение частоты гармонической силы к незатухающей собственной частоте модели масса-пружина-демпфер.

${\displaystyle r={\frac {f}{f_{n}}}.}$

Фазовый сдвиг определяется по следующей формуле. ${\displaystyle \phi ,}$

${\displaystyle \phi =\arctan \left({\frac {-2\zeta r}{1-r^{2}}}\right).}$

График этих функций, называемый «частотной характеристикой системы», представляет собой одну из наиболее важных особенностей вынужденной вибрации. В слегка демпфированной системе, когда частота воздействия близка к собственной частоте ( ), амплитуда вибрации может стать чрезвычайно высокой. Это явление называется резонансом (впоследствии собственную частоту системы часто называют резонансной частотой). В системах подшипников ротора любая скорость вращения, вызывающая резонансную частоту, называется критической скоростью . ${\displaystyle r\approx 1}$

Если в механической системе возникает резонанс, это может быть очень вредным и привести к возможному выходу системы из строя. Следовательно, одной из основных целей анализа вибрации является предсказание того, когда может возникнуть этот тип резонанса, а затем определение того, какие шаги следует предпринять, чтобы предотвратить его возникновение. Как показывает график амплитуды, добавление демпфирования может значительно уменьшить величину вибрации. Кроме того, величину можно уменьшить, если собственную частоту можно сместить от частоты воздействия путем изменения жесткости или массы системы. Если систему нельзя изменить, возможно, можно сместить частоту воздействия (например, изменив скорость машины, создающей силу).

Ниже приведены некоторые другие моменты, касающиеся вынужденной вибрации, показанной на графиках частотных характеристик.

• При данном соотношении частот амплитуда вибрации X прямо пропорциональна амплитуде силы (например, если вы удвоите силу, вибрация удвоится). ${\displaystyle F_{0}}$
• При незначительном демпфировании или его отсутствии вибрация находится в фазе с частотой воздействия, когда отношение частот r  < 1, и на 180 градусов сдвинуто по фазе, когда отношение частот r  > 1.
• Когда r  ≪ 1, амплитуда представляет собой просто прогиб пружины под действием статической силы. Этот прогиб называется статическим прогибом. Следовательно, когда r  ≪ 1, влияние демпфера и массы минимально. ${\displaystyle F_{0}.}$ ${\displaystyle \delta _{st}.}$
• Когда r  ≫ 1, амплитуда вибрации фактически меньше статического отклонения. В этой области сила, создаваемая массой ( F  =  ma ), доминирует, поскольку ускорение, воспринимаемое массой, увеличивается с частотой. Поскольку прогиб пружины X в этой области уменьшается, сила, передаваемая пружиной ( F  =  kx ) на основание, уменьшается. Таким образом, система масса-пружина-демпфер изолирует гармоническую силу от монтажного основания, что называется виброизоляцией . Увеличение демпфирования фактически снижает эффект виброизоляции при r  ≫ 1, поскольку демпфирующая сила ( F  =  cv ) также передается на основание. ${\displaystyle \delta _{st}.}$
• Каким бы ни было демпфирование, вибрация сдвинута по фазе на 90 градусов с частотой воздействия, когда отношение частот r  = 1, что очень полезно, когда дело доходит до определения собственной частоты системы.
• Каким бы ни было демпфирование, при r  ≫ 1 вибрация на 180 градусов не совпадает по фазе с частотой воздействия.
• Каким бы ни было демпфирование, при r  ≪ 1 вибрация находится в фазе с частотой воздействия

Причины резонанса

Резонанс легко понять, если рассматривать пружину и массу как элементы хранения энергии: масса хранит кинетическую энергию, а пружина хранит потенциальную энергию. Как обсуждалось ранее, когда на массу и пружину не действует внешняя сила, они передают энергию туда и обратно со скоростью, равной собственной частоте. Другими словами, для эффективной накачки энергии как в массу, так и в пружину необходимо, чтобы источник энергии подавал энергию со скоростью, равной собственной частоте. Приложение силы к массе и пружине похоже на толкание ребенка на качелях: толчок необходим в нужный момент, чтобы качели поднимались все выше и выше. Как и в случае с качелями, приложенная сила не обязательно должна быть большой, чтобы добиться больших движений, а должна просто добавлять энергию системе.

Демпфер вместо того, чтобы накапливать энергию, рассеивает ее. Поскольку сила демпфирования пропорциональна скорости, чем больше движение, тем больше демпфер рассеивает энергии. Следовательно, существует момент, когда энергия, рассеиваемая демпфером, равна энергии, добавляемой силой. В этот момент система достигла максимальной амплитуды и будет продолжать вибрировать на этом уровне до тех пор, пока приложенная сила остается прежней. Если затухания нет, то нет ничего, что могло бы рассеивать энергию, и теоретически движение будет продолжать расти до бесконечности.

Применение «сложных» сил к модели масса-пружина-демпфер

В предыдущем разделе к модели применялась только простая гармоническая сила, но ее можно значительно расширить, используя два мощных математических инструмента. Первый — это преобразование Фурье , которое принимает сигнал как функцию времени ( временная область ) и разбивает его на гармонические компоненты в зависимости от частоты ( частотная область ). Например, приложив силу к модели масса-пружина-демпфер, которая повторяет следующий цикл: сила, равная 1  ньютону, в течение 0,5 секунды, а затем отсутствие силы в течение 0,5 секунды. Этот тип силы имеет форму прямоугольной волны частотой 1 Гц .

Как прямоугольную волну частотой 1 Гц можно представить как сумму синусоидальных волн (гармоник) и соответствующего частотного спектра. Нажмите и перейдите к полному разрешению для анимации.

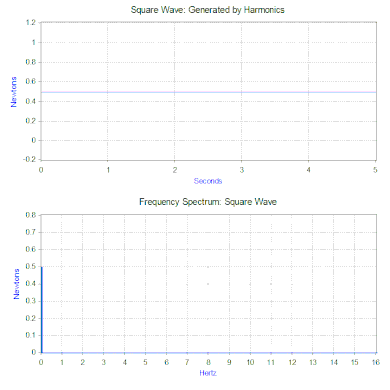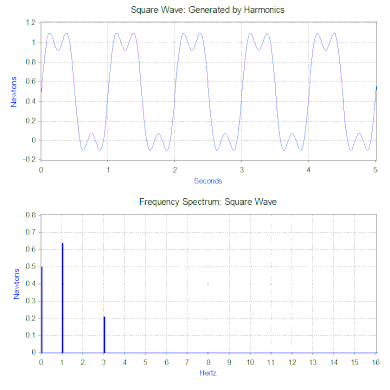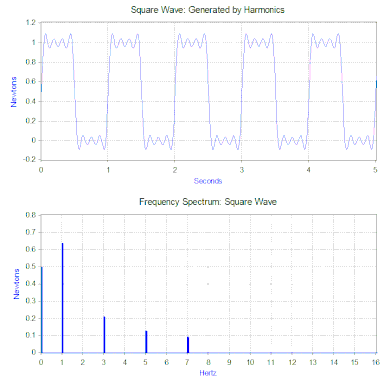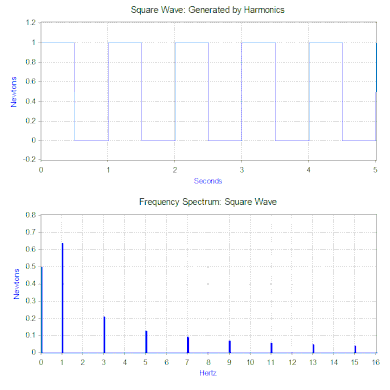
Преобразование Фурье прямоугольной волны генерирует частотный спектр , который представляет величину гармоник, составляющих прямоугольную волну (фаза также генерируется, но обычно она вызывает меньшее беспокойство и поэтому часто не отображается на графике). Преобразование Фурье также можно использовать для анализа непериодических функций , таких как переходные процессы (например, импульсы) и случайные функции. Преобразование Фурье почти всегда вычисляется с использованием компьютерного алгоритма быстрого преобразования Фурье (БПФ) в сочетании с оконной функцией .

В случае нашей прямоугольной силы первый компонент на самом деле представляет собой постоянную силу в 0,5 ньютона и представлен значением на частоте 0 Гц в частотном спектре. Следующий компонент — синусоидальный сигнал частотой 1 Гц и амплитудой 0,64. Это показано линией на частоте 1 Гц. Остальные компоненты имеют нечетные частоты, и для генерации идеальной прямоугольной волны требуется бесконечное количество синусоидальных волн. Следовательно, преобразование Фурье позволяет интерпретировать силу как сумму синусоидальных сил, приложенных вместо более «сложной» силы (например, прямоугольной волны).

В предыдущем разделе решение вибрации было дано для одной гармонической силы, но преобразование Фурье обычно дает несколько гармонических сил. Второй математический инструмент, принцип суперпозиции , позволяет суммировать решения от нескольких сил, если система линейна . В случае модели пружина-масса-демпфер система является линейной, если сила пружины пропорциональна смещению, а демпфирование пропорционально скорости в интересующем диапазоне движения. Следовательно, решение проблемы с прямоугольной волной заключается в суммировании предсказанной вибрации от каждой из гармонических сил, обнаруженных в частотном спектре прямоугольной волны.

Модель частотной характеристики

Решение проблемы вибрации можно рассматривать как соотношение ввода/вывода, где сила является входом, а выходом является вибрация. Представление силы и вибрации в частотной области (амплитуда и фаза) допускает следующее соотношение:

${\displaystyle X(i\omega )=H(i\omega )\cdot F(i\omega ){\text{ or }}H(i\omega )={X(i\omega ) \over F(i\omega )}.}$

${\displaystyle H(i\omega )}$называется функцией частотной характеристики (также называемой передаточной функцией , но технически не столь точной) и имеет как амплитудную, так и фазовую составляющую (если она представлена ​​в виде комплексного числа , вещественного и мнимого компонентов). Величина частотной характеристики (ЧЧХ) была представлена ​​ранее для системы масса-пружина-демпфер.

${\displaystyle |H(i\omega )|=\left|{X(i\omega ) \over F(i\omega )}\right|={1 \over k}{1 \over {\sqrt {(1-r^{2})^{2}+(2\zeta r)^{2}}}},{\text{ where }}r={\frac {f}{f_{n}}}={\frac {\omega }{\omega _{n}}}.}$

Фаза FRF также была представлена ​​ранее как:

${\displaystyle \angle H(i\omega )=-\arctan \left({\frac {2\zeta r}{1-r^{2}}}\right).}$

Модель частотной характеристики

Например, расчет FRF для системы масса-пружина-демпфер массой 1 кг, жесткостью пружины 1,93 Н/мм и коэффициентом демпфирования 0,1. Значения пружины и массы дают собственную частоту 7 Гц для этой конкретной системы. Применение прямоугольной волны частотой 1 Гц, использованной ранее, позволяет рассчитать прогнозируемую вибрацию массы. Рисунок иллюстрирует возникающую вибрацию. В этом примере случается, что четвертая гармоника прямоугольной волны приходится на частоту 7 Гц. Таким образом, частотная характеристика массы-пружины-демпфера выдает высокую вибрацию частотой 7 Гц, хотя входная сила имела относительно низкую гармонику частотой 7 Гц. Этот пример подчеркивает, что результирующая вибрация зависит как от функции воздействия, так и от системы, к которой применяется сила.

На рисунке также показано представление результирующей вибрации во временной области. Это делается путем выполнения обратного преобразования Фурье, которое преобразует данные частотной области во временную область. На практике это делается редко, поскольку частотный спектр предоставляет всю необходимую информацию.

Функция частотной характеристики (FRF) не обязательно должна рассчитываться на основе знания массы, демпфирования и жесткости системы, но ее можно измерить экспериментально. Например, если приложить известную силу в диапазоне частот и измерить связанные с ней вибрации, можно вычислить функцию частотного отклика, тем самым охарактеризовать систему. Этот метод используется в области экспериментального модального анализа для определения вибрационных характеристик конструкции.

Системы с несколькими степенями свободы и формы мод

Модель с двумя степенями свободы

Простая модель «масса-пружина-демпфер» является основой анализа вибрации. Описанная выше модель называется моделью с одной степенью свободы (SDOF), поскольку предполагается, что масса движется только вверх и вниз. В более сложных системах система должна быть дискретизирована на большее количество масс, которые движутся более чем в одном направлении, добавляя степени свободы. Основные концепции множественных степеней свободы (MDOF) можно понять, взглянув всего лишь на модель с двумя степенями свободы, как показано на рисунке.

Уравнения движения системы 2DOF имеют вид:

${\displaystyle m_{1}{\ddot {x_{1}}}+(c_{1}+c_{2}){\dot {x_{1}}}-c_{2}{\dot {x_{2}}}+(k_{1}+k_{2})x_{1}-k_{2}x_{2}=f_{1},}$

${\displaystyle m_{2}{\ddot {x_{2}}}-c_{2}{\dot {x_{1}}}+(c_{2}+c_{3}){\dot {x_{2}}}-k_{2}x_{1}+(k_{2}+k_{3})x_{2}=f_{2}.\!}$

Это можно переписать в матричном формате:

${\displaystyle {\begin{bmatrix}m_{1}&0\\0&m_{2}\end{bmatrix}}{\begin{Bmatrix}{\ddot {x_{1}}}\\{\ddot {x_{2}}}\end{Bmatrix}}+{\begin{bmatrix}c_{1}+c_{2}&-c_{2}\\-c_{2}&c_{2}+c_{3}\end{bmatrix}}{\begin{Bmatrix}{\dot {x_{1}}}\\{\dot {x_{2}}}\end{Bmatrix}}+{\begin{bmatrix}k_{1}+k_{2}&-k_{2}\\-k_{2}&k_{2}+k_{3}\end{bmatrix}}{\begin{Bmatrix}x_{1}\\x_{2}\end{Bmatrix}}={\begin{Bmatrix}f_{1}\\f_{2}\end{Bmatrix}}.}$

Более компактную форму этого матричного уравнения можно записать как:

${\displaystyle {\begin{bmatrix}M\end{bmatrix}}{\begin{Bmatrix}{\ddot {x}}\end{Bmatrix}}+{\begin{bmatrix}C\end{bmatrix}}{\begin{Bmatrix}{\dot {x}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{Bmatrix}x\end{Bmatrix}}={\begin{Bmatrix}f\end{Bmatrix}}}$

где и – симметричные матрицы, называемые соответственно матрицами массы, демпфирования и жесткости. Матрицы представляют собой квадратные матрицы размера NxN, где N — количество степеней свободы системы. ${\displaystyle {\begin{bmatrix}M\end{bmatrix}},}$ ${\displaystyle {\begin{bmatrix}C\end{bmatrix}},}$ ${\displaystyle {\begin{bmatrix}K\end{bmatrix}}}$

В следующем анализе рассматривается случай отсутствия демпфирования и приложенных сил (т. е. свободной вибрации). Решение вязкодемпфированной системы несколько сложнее. ^[12]

${\displaystyle {\begin{bmatrix}M\end{bmatrix}}{\begin{Bmatrix}{\ddot {x}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{Bmatrix}x\end{Bmatrix}}=0.}$

Это дифференциальное уравнение можно решить, приняв решение следующего типа:

${\displaystyle {\begin{Bmatrix}x\end{Bmatrix}}={\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}.}$

Примечание. Использование экспоненциального решения — это математический прием, используемый для решения линейных дифференциальных уравнений. Используя формулу Эйлера и принимая только действительную часть решения, мы получаем то же косинусное решение для системы с 1 степенями свободы. Экспоненциальное решение используется только потому, что им легче манипулировать математически. ${\displaystyle {\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}}$

Тогда уравнение принимает вид:

${\displaystyle {\begin{bmatrix}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}e^{i\omega t}=0.}$

Поскольку не может быть равно нулю, уравнение сводится к следующему. ${\displaystyle e^{i\omega t}}$

${\displaystyle {\begin{bmatrix}{\begin{bmatrix}K\end{bmatrix}}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0.}$

Проблема собственных значений

Это относится к проблеме собственных значений в математике и может быть представлено в стандартном формате, предварительно умножив уравнение на ${\displaystyle {\begin{bmatrix}M\end{bmatrix}}^{-1}}$

${\displaystyle {\begin{bmatrix}{\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}K\end{bmatrix}}-\omega ^{2}{\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}M\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0}$

и если: и ${\displaystyle {\begin{bmatrix}M\end{bmatrix}}^{-1}{\begin{bmatrix}K\end{bmatrix}}={\begin{bmatrix}A\end{bmatrix}}}$ ${\displaystyle \lambda =\omega ^{2}\,}$

${\displaystyle {\begin{bmatrix}{\begin{bmatrix}A\end{bmatrix}}-\lambda {\begin{bmatrix}I\end{bmatrix}}\end{bmatrix}}{\begin{Bmatrix}X\end{Bmatrix}}=0.}$

Решение задачи приводит к получению N собственных значений (т.е. ), где N соответствует числу степеней свободы. Собственные значения обеспечивают собственные частоты системы. Когда эти собственные значения подставляются обратно в исходный набор уравнений, значения, соответствующие каждому собственному значению, называются собственными векторами . Эти собственные векторы представляют формы мод системы. Решение проблемы собственных значений может быть довольно громоздким (особенно для задач со многими степенями свободы), но, к счастью, большинство программ математического анализа имеют подпрограммы для определения собственных значений. ${\displaystyle \omega _{1}^{2},\omega _{2}^{2},\cdots \omega _{N}^{2}}$ ${\displaystyle {\begin{Bmatrix}X\end{Bmatrix}}}$

Собственные значения и собственные векторы часто записываются в следующем матричном формате и описывают модальную модель системы:

${\displaystyle {\begin{bmatrix}^{\diagdown }\omega _{r\diagdown }^{2}\end{bmatrix}}={\begin{bmatrix}\omega _{1}^{2}&\cdots &0\\\vdots &\ddots &\vdots \\0&\cdots &\omega _{N}^{2}\end{bmatrix}}{\text{ and }}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}\psi _{1}\end{Bmatrix}}{\begin{Bmatrix}\psi _{2}\end{Bmatrix}}\cdots {\begin{Bmatrix}\psi _{N}\end{Bmatrix}}\end{bmatrix}}.}$

Простой пример с использованием модели с двумя степенями свободы может помочь проиллюстрировать эту концепцию. Пусть обе массы имеют массу 1 кг и жесткость всех трех пружин равна 1000 Н/м. Тогда матрица массы и жесткости для этой задачи будет равна:

${\displaystyle {\begin{bmatrix}M\end{bmatrix}}={\begin{bmatrix}1&0\\0&1\end{bmatrix}}}$и ${\displaystyle {\begin{bmatrix}K\end{bmatrix}}={\begin{bmatrix}2000&-1000\\-1000&2000\end{bmatrix}}.}$

Затем ${\displaystyle {\begin{bmatrix}A\end{bmatrix}}={\begin{bmatrix}2000&-1000\\-1000&2000\end{bmatrix}}.}$

Собственные значения для этой задачи, заданные процедурой собственных значений:

${\displaystyle {\begin{bmatrix}^{\diagdown }\omega _{r\diagdown }^{2}\end{bmatrix}}={\begin{bmatrix}1000&0\\0&3000\end{bmatrix}}.}$

Собственные частоты в единицах герц тогда (вспоминая ) и ${\displaystyle \scriptstyle \omega =2\pi f}$ ${\displaystyle \scriptstyle f_{1}=5.033\mathrm {\ Hz} }$ ${\displaystyle \scriptstyle f_{2}=8.717{\text{ Hz}}.}$

Формы двух мод для соответствующих собственных частот определяются следующим образом:

${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}\psi _{1}\end{Bmatrix}}{\begin{Bmatrix}\psi _{2}\end{Bmatrix}}\end{bmatrix}}={\begin{bmatrix}{\begin{Bmatrix}-0.707\\-0.707\end{Bmatrix}}_{1}{\begin{Bmatrix}0.707\\-0.707\end{Bmatrix}}_{2}\end{bmatrix}}.}$

Поскольку система представляет собой систему с двумя степенями свободы, существует две моды с соответствующими собственными частотами и формами. Векторы формы мод не являются абсолютным движением, а лишь описывают относительное движение степеней свободы. В нашем случае вектор формы первой моды говорит о том, что массы движутся вместе по фазе, поскольку они имеют одинаковое значение и знак. В случае вектора формы второй моды каждая масса движется в противоположном направлении с одинаковой скоростью.

Иллюстрация проблемы с множественной степенью свободы

Когда имеется много степеней свободы, одним из методов визуализации форм колебаний является их анимация с помощью программного обеспечения для структурного анализа, такого как Femap , ANSYS или VA One от ESI Group . Пример анимации форм мод показан на рисунке ниже для консольной двутавровой балки , продемонстрированной с помощью модального анализа в ANSYS. В этом случае метод конечных элементов использовался для генерации аппроксимации матриц массы и жесткости путем объединения интересующего объекта в сетку для решения дискретной задачи собственных значений . Заметим, что в этом случае метод конечных элементов дает аппроксимацию сетчатой ​​поверхности (для которой существует бесконечное число форм и частот колебаний). Таким образом, эта относительно простая модель, имеющая более 100 степеней свободы и, следовательно, столько же собственных частот и форм колебаний, обеспечивает хорошее приближение для первых собственных частот и форм ^† . Обычно для практического применения важны только первые несколько режимов.

^ Обратите внимание, что при выполнении численной аппроксимации любой математической модели необходимо убедиться в сходимости интересующих параметров.

Проблема с несколькими степенями свободы преобразована в проблему с одной степенью свободы

Собственные векторы обладают очень важными свойствами, называемыми свойствами ортогональности. Эти свойства можно использовать для значительного упрощения решения моделей с несколькими степенями свободы. Можно показать, что собственные векторы обладают следующими свойствами:

${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}},}$

${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}={\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}.}$

${\displaystyle {\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}}}$и представляют собой диагональные матрицы , содержащие значения модальной массы и жесткости для каждой из мод. (Примечание: поскольку собственные векторы (формы мод) могут масштабироваться произвольно, свойства ортогональности часто используются для масштабирования собственных векторов, поэтому значение модальной массы для каждой моды равно 1. Таким образом, матрица модальных масс является единичной матрицей . ) ${\displaystyle {\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}}$

Эти свойства можно использовать, чтобы значительно упростить решение моделей с несколькими степенями свободы, выполнив следующее преобразование координат.

${\displaystyle {\begin{Bmatrix}x\end{Bmatrix}}={\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}.}$

Использование этого преобразования координат в исходном дифференциальном уравнении свободных колебаний приводит к следующему уравнению.

${\displaystyle {\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.}$

Воспользовавшись свойствами ортогональности, предварительно умножив это уравнение на ${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}^{T}}$

${\displaystyle {\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}M\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}\Psi \end{bmatrix}}^{T}{\begin{bmatrix}K\end{bmatrix}}{\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.}$

Свойства ортогональности затем упрощают это уравнение до:

${\displaystyle {\begin{bmatrix}^{\diagdown }m_{r\diagdown }\end{bmatrix}}{\begin{Bmatrix}{\ddot {q}}\end{Bmatrix}}+{\begin{bmatrix}^{\diagdown }k_{r\diagdown }\end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}=0.}$

Это уравнение является основой анализа вибрации для систем с несколькими степенями свободы. Аналогичный результат можно получить и для демпфирующих систем. ^[12] Ключевым моментом является то, что модальные матрицы массы и жесткости являются диагональными матрицами, и поэтому уравнения были «развязаны». Другими словами, проблема превратилась из большой громоздкой задачи с несколькими степенями свободы во множество задач с одной степенью свободы, которые можно решить, используя те же методы, изложенные выше.

Решение для x заменяется решением для q , называемого модальными координатами или модальными коэффициентами участия.

Было бы яснее понять, если бы это было написано так: ${\displaystyle {\begin{Bmatrix}x\end{Bmatrix}}={\begin{bmatrix}\Psi \end{bmatrix}}{\begin{Bmatrix}q\end{Bmatrix}}}$

${\displaystyle {\begin{Bmatrix}x_{n}\end{Bmatrix}}=q_{1}{\begin{Bmatrix}\psi \end{Bmatrix}}_{1}+q_{2}{\begin{Bmatrix}\psi \end{Bmatrix}}_{2}+q_{3}{\begin{Bmatrix}\psi \end{Bmatrix}}_{3}+\cdots +q_{N}{\begin{Bmatrix}\psi \end{Bmatrix}}_{N}.}$

Записав в такой форме, можно увидеть, что вибрация на каждой из степеней свободы представляет собой просто линейную сумму форм мод. Более того, то, насколько каждый режим «участвует» в окончательной вибрации, определяется q, его модальным коэффициентом участия.

Режим твердого тела

Неограниченная система с несколькими степенями свободы испытывает как перемещение твердого тела, так и/или вращение и вибрацию. Существование моды твердого тела приводит к нулевой собственной частоте. Соответствующая форма моды называется модой твердого тела.

Смотрите также

• Акустическая инженерия
• Антивибрационный состав
• Балансировочная машина
• Базовая изоляция
• Амортизация
• Критическая скорость
• Коэффициент демпфирования
• метод Данкерли
• Сейсмостойкая инженерия
• Эластичный маятник
• Быстрое преобразование Фурье
• Машиностроение
• Механический резонанс
• Модальный анализ
• Форма режима
• Шум и вибрация на морских судах
• Шум, вибрация и резкость
• Паллестезия
• Пассивная компенсация качки
• Маятник
• Квантовая вибрация
• Случайная вибрация
• Качество езды
• Коэффициент Рэлея в анализе вибраций
• Шейкер (испытательное устройство)
• Шок
• Регистратор данных ударов и вибрации
• Простой гармонический генератор
• Звук
• Структурная акустика
• Структурная динамика
• Баланс шин
• Крутильная вибрация
• Настроенный массовый демпфер
• Калибратор вибрации
• Контроль вибрации
• Виброизоляция
• Волна
• Вибрация всего тела

Рекомендации

1. Тастин, Уэйн. Где разместить контрольный акселерометр: одно из наиболее важных решений при разработке испытаний на случайную вибрацию также является самым игнорируемым , EE-Evaluation Engineering, 2006
2. Эскюдье, Марсель; Аткинс, Тони (2019). Машиностроительный словарь (2-е изд.). Издательство Оксфордского университета. doi : 10.1093/acref/9780198832102.001.0001. ISBN 978-0-19-883210-2.
3. «Polytec InFocus 1/2007» (PDF) . Архивировано из оригинала (PDF) 24 июля 2019 г. Проверено 24 июля 2019 г.
4. Тони Араужо. Эволюция автомобильного виброоборудования , EE-Evaluation Engineering, 2019
5. Blanks, HS, «Методы эквивалентности испытаний на вибрацию», SVIC Notes, стр. 17.
6. Араужо Т. и Яо Б., «Квалификация рабочих характеристик вибрационных приспособлений – обзор передового опыта автомобильной промышленности», Технический документ SAE 2020-01-1065, 2020 г., https://doi.org/10.4271/2020-01 -1065.
7. Кроуфорд, Арт; Упрощенное руководство по анализу вибрации
8. Эшлеман, Р. 1999, Основные вибрации машин: введение в тестирование, анализ и мониторинг машин.
9. Институт Мебиуса; Аналитик вибрации, категория 2 – Краткое описание курса, 2013 г.
10. «Важность анализа вибрации при техническом обслуживании». 05.01.2021 . Проверено 08 января 2021 г.
11. Симионеску, Пенсильвания (2014). Инструменты компьютерного построения графиков и моделирования для пользователей AutoCAD (1-е изд.). Бока-Ратон, Флорида: CRC Press. ISBN 978-1-4822-5290-3.
12. Майя, Сильва. Теоретический и экспериментальный модальный анализ , Research Studies Press Ltd., 1997, ISBN 0-471-97067-0 

дальнейшее чтение

• Язык, Бенсон, Принципы вибрации , Oxford University Press, 2001, ISBN 0-19-514246-2 
• Инман, Дэниел Дж., Инженерная вибрация , Прентис Холл, 2001, ISBN 0-13-726142-X 
• Томпсон, В.Т., Теория вибраций , Nelson Thornes Ltd, 1996, ISBN 0-412-78390-8 
• Хартог, Ден, Механические вибрации , Dover Publications, 1985, ISBN 0-486-64785-4 
• Рейнольдс, Дуглас Д. (2016). Инженерные принципы механической вибрации (4-е изд.). Блумингтон, Индиана, США: Издание Trafford On Demand Publishing. п. 485. ИСБН 978-1-4907-1437-0.
• [1]
• Институт охраны труда Немецкого социального страхования от несчастных случаев : Вибрация всего тела и рук
• Манариккал И., Эльсаха Ф., Мба Д. и Лайла Д. Динамическое моделирование планетарных редукторов с треснутым зубом с использованием вибрационного анализа, (2019) Достижения в мониторинге состояния оборудования в нестационарных операциях, стр. 240–250 , Шпрингер, Швейцария; [2]

Внешние ссылки

• Бесплатные таблицы Excel для оценки модальных параметров
• Справочник по анализу вибрации – Институт Мебиуса
• Мониторинг состояния и защита оборудования – Siemens AG