Гомоморфизм

Отображение, сохраняющее структуру, между двумя алгебраическими структурами одного и того же типа.

В алгебре гомоморфизм — это сохраняющее структуру отображение между двумя алгебраическими структурами одного и того же типа (например, двумя группами , двумя кольцами или двумя векторными пространствами ). Слово гомоморфизм происходит от древнегреческого языка : ὁμός ( homos ) означает «тот же» и μορφή ( morphe ) означает «форма» или «форма». Однако это слово, по-видимому, было введено в математику из-за (неправильного) перевода немецкого слова ähnlich , означающего «похожий», на ὁμός, означающего «тот же самый». ^[1] Термин «гомоморфизм» появился еще в 1892 году, когда его приписали немецкому математику Феликсу Клейну (1849–1925). ^[2]

Гомоморфизмы векторных пространств называются также линейными отображениями , и их изучение составляет предмет линейной алгебры .

Понятие гомоморфизма было обобщено под названием морфизма на многие другие структуры, которые либо не имеют основного множества, либо не являются алгебраическими. Это обобщение является отправной точкой теории категорий .

Гомоморфизм может быть также изоморфизмом , эндоморфизмом , автоморфизмом и т. д. (см. ниже). Каждый из них можно определить таким образом, чтобы его можно было обобщить на любой класс морфизмов.

Определение

Гомоморфизм — это отображение между двумя алгебраическими структурами одного и того же типа (то есть с одинаковым именем), сохраняющее операции структур . Это означает отображение между двумя множествами , оснащенными одной и той же структурой, так что, если это операция структуры (здесь для упрощения предполагается, что это бинарная операция ), то ${\displaystyle f:A\to B}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle \cdot }$

${\displaystyle f(x\cdot y)=f(x)\cdot f(y)}$

для каждой пары элементов . ^{[примечание 1]} Часто говорят, что сохраняет операцию или совместим с операцией. ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle A}$ ${\displaystyle f}$

Формально карта сохраняет операцию арности , определенную как для, так и для if ${\displaystyle f:A\to B}$ ${\displaystyle \mu }$ ${\displaystyle k}$ ${\displaystyle A}$ ${\displaystyle B}$

${\displaystyle f(\mu _{A}(a_{1},\ldots ,a_{k}))=\mu _{B}(f(a_{1}),\ldots ,f(a_{k})),}$

для всех элементов в . ${\displaystyle a_{1},...,a_{k}}$ ${\displaystyle A}$

Операции, которые должны сохраняться гомоморфизмом, включают 0-арные операции , то есть константы. В частности, когда элемент идентификации требуется для типа структуры, элемент идентификации первой структуры должен быть отображен на соответствующий элемент идентификации второй структуры.

Например:

• Гомоморфизм полугрупп — это отображение между полугруппами , сохраняющее операцию полугруппы.
• Гомоморфизм моноида — это отображение между моноидами , которое сохраняет операцию моноида и отображает единичный элемент первого моноида в элемент второго моноида (единичный элемент — это 0-арная операция ).
• Групповой гомоморфизм — это отображение между группами , сохраняющее групповую операцию. Это означает, что групповой гомоморфизм отображает единичный элемент первой группы в единичный элемент второй группы и отображает обратный элемент первой группы в обратный образ этого элемента. Таким образом, полугрупповой гомоморфизм между группами обязательно является групповым гомоморфизмом.
• Гомоморфизм колец — это отображение между кольцами , которое сохраняет сложение колец, умножение колец и мультипликативное тождество . Сохранится ли мультипликативная идентичность, зависит от используемого определения кольца . Если мультипликативное тождество не сохраняется, то имеется гомоморфизм rng .
• Линейное отображение — это гомоморфизм векторных пространств ; то есть групповой гомоморфизм между векторными пространствами, который сохраняет структуру абелевой группы и скалярное умножение .
• Гомоморфизм модулей , также называемый линейным отображением между модулями , определяется аналогично.
• Гомоморфизм алгебры — это отображение, сохраняющее алгебраические операции.

Алгебраическая структура может иметь более одной операции, и для сохранения каждой операции требуется гомоморфизм. Таким образом, отображение, сохраняющее лишь некоторые операции, не является гомоморфизмом структуры, а лишь гомоморфизмом подструктуры, полученной при рассмотрении только сохранившихся операций. Например, отображение между моноидами, сохраняющее операцию моноида, а не единичный элемент, не является гомоморфизмом моноида, а только гомоморфизмом полугруппы.

Обозначения операций не обязательно должны быть одинаковыми в источнике и цели гомоморфизма. Например, действительные числа образуют группу для сложения, а положительные действительные числа образуют группу для умножения. Показательная функция

${\displaystyle x\mapsto e^{x}}$

удовлетворяет

${\displaystyle e^{x+y}=e^{x}e^{y},}$

и, таким образом, является гомоморфизмом между этими двумя группами. Это даже изоморфизм (см. ниже), поскольку его обратная функция , натуральный логарифм , удовлетворяет условию

${\displaystyle \ln(xy)=\ln(x)+\ln(y),}$

и также является гомоморфизмом группы.

Примеры

Моноидный гомоморфизм из моноида ( N , +, 0) в моноид ( N , ×, 1) , определенный формулой . Оно инъективно , но не сюръективно . ${\displaystyle f}$ ${\displaystyle f(x)=2^{x}}$

Действительные числа представляют собой кольцо , в котором есть как сложение, так и умножение. Множество всех матриц 2×2 также является кольцом при сложении и умножении матриц . Если мы определим функцию между этими кольцами следующим образом:

${\displaystyle f(r)={\begin{pmatrix}r&0\\0&r\end{pmatrix}}}$

где r — действительное число, то f — гомоморфизм колец, поскольку f сохраняет оба сложения:

${\displaystyle f(r+s)={\begin{pmatrix}r+s&0\\0&r+s\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}+{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)+f(s)}$

и умножение:

${\displaystyle f(rs)={\begin{pmatrix}rs&0\\0&rs\end{pmatrix}}={\begin{pmatrix}r&0\\0&r\end{pmatrix}}{\begin{pmatrix}s&0\\0&s\end{pmatrix}}=f(r)\,f(s).}$

Другой пример: ненулевые комплексные числа образуют группу при операции умножения, как и ненулевые действительные числа. (Ноль должен быть исключен из обеих групп, поскольку он не имеет мультипликативного обратного значения , которое требуется для элементов группы.) Определите функцию преобразования ненулевых комплексных чисел в ненулевые действительные числа с помощью ${\displaystyle f}$

${\displaystyle f(z)=|z|.}$

То есть, это абсолютное значение (или модуль) комплексного числа . Тогда является гомоморфизмом групп, так как сохраняет умножение: ${\displaystyle f}$ ${\displaystyle z}$ ${\displaystyle f}$

${\displaystyle f(z_{1}z_{2})=|z_{1}z_{2}|=|z_{1}||z_{2}|=f(z_{1})f(z_{2}).}$

Обратите внимание, что f нельзя расширить до гомоморфизма колец (от комплексных чисел до действительных чисел), поскольку он не сохраняет сложение:

${\displaystyle |z_{1}+z_{2}|\neq |z_{1}|+|z_{2}|.}$

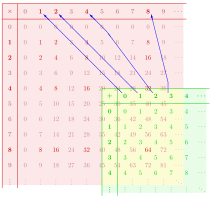
В качестве другого примера на диаграмме показан гомоморфизм моноида из моноида в моноид . Из-за разных названий соответствующих операций свойства сохранения структуры, удовлетворяемые, составляют и . ${\displaystyle f}$ ${\displaystyle (\mathbb {N} ,+,0)}$ ${\displaystyle (\mathbb {N} ,\times ,1)}$ ${\displaystyle f}$ ${\displaystyle f(x+y)=f(x)\times f(y)}$ ${\displaystyle f(0)=1}$

Композиционная алгебра над полем имеет квадратичную форму , называемую нормой , которая представляет собой групповой гомоморфизм мультипликативной группы в мультипликативную группу . ${\displaystyle A}$ ${\displaystyle F}$ ${\displaystyle N:A\to F}$ ${\displaystyle A}$ ${\displaystyle F}$

Специальные гомоморфизмы

Некоторые виды гомоморфизмов имеют особое название, которое также определено для общих морфизмов .

изоморфизм

Изоморфизм между алгебраическими структурами одного и того же типа обычно определяется как биективный гомоморфизм . ^{[3] : 134  [4] : 28}

В более общем контексте теории категорий изоморфизм определяется как морфизм , который имеет обратный, который также является морфизмом. В конкретном случае алгебраических структур эти два определения эквивалентны, хотя они могут различаться для неалгебраических структур, имеющих базовый набор.

Точнее, если

${\displaystyle f:A\to B}$

является (гомо)морфизмом, он имеет обратный, если существует гомоморфизм

${\displaystyle g:B\to A}$

такой, что

${\displaystyle f\circ g=\operatorname {Id} _{B}\qquad {\text{and}}\qquad g\circ f=\operatorname {Id} _{A}.}$

Если и имеют базовые множества и имеет обратный , то является биективным. В действительности, является инъективным , как следует , и сюръективным , поскольку для любого в имеется , и является образом элемента . ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle f:A\to B}$ ${\displaystyle g}$ ${\displaystyle f}$ ${\displaystyle f}$ ${\displaystyle f(x)=f(y)}$ ${\displaystyle x=g(f(x))=g(f(y))=y}$ ${\displaystyle f}$ ${\displaystyle x}$ ${\displaystyle B}$ ${\displaystyle x=f(g(x))}$ ${\displaystyle x}$ ${\displaystyle A}$

Обратно, если — биективный гомоморфизм между алгебраическими структурами, пусть — отображение такое, что является единственным элементом такого , что . Достаточно и осталось только показать, что g — гомоморфизм. Если — бинарная операция структуры, для каждой пары элементов из имеется ${\displaystyle f:A\to B}$ ${\displaystyle g:B\to A}$ ${\displaystyle g(y)}$ ${\displaystyle x}$ ${\displaystyle A}$ ${\displaystyle f(x)=y}$ ${\displaystyle f\circ g=\operatorname {Id} _{B}{\text{ and }}g\circ f=\operatorname {Id} _{A},}$ ${\displaystyle *}$ ${\displaystyle x}$ ${\displaystyle y}$ ${\displaystyle B}$

${\displaystyle g(x*_{B}y)=g(f(g(x))*_{B}f(g(y)))=g(f(g(x)*_{A}g(y)))=g(x)*_{A}g(y),}$

и, таким образом, совместим с Поскольку доказательство аналогично для любой арности , это показывает, что это гомоморфизм. ${\displaystyle g}$ ${\displaystyle *.}$ ${\displaystyle g}$

Это доказательство не работает для неалгебраических структур. Например, для топологических пространств морфизм является непрерывным отображением , а обратное биективному непрерывному отображению не обязательно является непрерывным. Таким образом , изоморфизм топологических пространств, называемый гомеоморфизмом или бинепрерывным отображением , является биективным непрерывным отображением, обратное к которому также непрерывно.

эндоморфизм

Эндоморфизм — это гомоморфизм, область определения которого равна кодомену , или , в более общем смысле, морфизм, источник которого равен его цели. ^{[3] : 135}

Эндоморфизмы алгебраической структуры или объекта категории образуют моноид при композиции.

Эндоморфизмы векторного пространства или модуля образуют кольцо . В случае векторного пространства или свободного модуля конечной размерности выбор базиса индуцирует кольцевой изоморфизм между кольцом эндоморфизмов и кольцом квадратных матриц той же размерности.

Автоморфизм

Автоморфизм — это эндоморфизм , который также является изоморфизмом. ^{[3] : 135}

Автоморфизмы алгебраической структуры или объекта категории образуют группу по композиции, которая называется группой автоморфизмов структуры.

Многие группы, получившие название, являются группами автоморфизмов некоторой алгебраической структуры. Например, общая линейная группа — это группа автоморфизмов векторного пространства размерности над полем . ${\displaystyle \operatorname {GL} _{n}(k)}$ ${\displaystyle n}$ ${\displaystyle k}$

Группы автоморфизмов полей были введены Эваристом Галуа для изучения корней многочленов и являются основой теории Галуа .

Мономорфизм

Для алгебраических структур мономорфизмы обычно определяются как инъективные гомоморфизмы. ^{[3] : 134  [4] : 29}

В более общем контексте теории категорий мономорфизм определяется как морфизм , который можно сократить слева . ^[5] Это означает, что (гомо)морфизм является мономорфизмом, если для любой пары морфизмов любого другого объекта в , то влечет за собой . ${\displaystyle f:A\to B}$ ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle C}$ ${\displaystyle A}$ ${\displaystyle f\circ g=f\circ h}$ ${\displaystyle g=h}$

Эти два определения мономорфизма эквивалентны для всех обычных алгебраических структур. Точнее, они эквивалентны для полей , для которых всякий гомоморфизм является мономорфизмом, и для многообразий универсальной алгебры , то есть алгебраических структур, для которых операции и аксиомы (тождества) определены без каких-либо ограничений (поля не образуют многообразия, поскольку мультипликативное обратное определяется либо как унарная операция , либо как свойство умножения, которые в обоих случаях определяются только для ненулевых элементов).

В частности, два определения мономорфизма эквивалентны для множеств , магм , полугрупп , моноидов , групп , колец , полей , векторных пространств и модулей .

Расщепляемый мономорфизм — это гомоморфизм, который имеет левый обратный и, следовательно, сам является правым обратным этому другому гомоморфизму. То есть, гомоморфизм является расщепляемым мономорфизмом, если существует такой гомоморфизм, что расщепляемый мономорфизм всегда является мономорфизмом для обоих значений мономорфизма . Для множеств и векторных пространств каждый мономорфизм является расщепляемым мономорфизмом, но это свойство не выполняется для большинства распространенных алгебраических структур. ${\displaystyle f\colon A\to B}$ ${\displaystyle g\colon B\to A}$ ${\displaystyle g\circ f=\operatorname {Id} _{A}.}$

Эпиморфизм

В алгебре эпиморфизмы часто определяются как сюръективные гомоморфизмы . ^{[3] : 134  [4] : ​​43} С другой стороны, в теории категорий эпиморфизмы определяются как сокращаемые справа морфизмы . ^[5] Это означает, что (гомо)морфизм является эпиморфизмом, если для любой пары морфизмов из в любой другой объект из равенства следует . ${\displaystyle f:A\to B}$ ${\displaystyle g}$ ${\displaystyle h}$ ${\displaystyle B}$ ${\displaystyle C}$ ${\displaystyle g\circ f=h\circ f}$ ${\displaystyle g=h}$

Сюръективный гомоморфизм всегда сокращаем справа, но обратное не всегда верно для алгебраических структур. Однако два определения эпиморфизма эквивалентны для множеств , векторных пространств , абелевых групп , модулей (доказательство см. ниже) и групп . ^[6] Важность этих структур во всей математике, особенно в линейной алгебре и гомологической алгебре , может объяснить сосуществование двух неэквивалентных определений.

Алгебраические структуры, для которых существуют несюръективные эпиморфизмы, включают полугруппы и кольца . Самый простой пример — включение целых чисел в рациональные числа , что является гомоморфизмом колец и мультипликативных полугрупп. Для обеих структур это мономорфизм и несюръективный эпиморфизм, но не изоморфизм. ^{[5] [7]}

Широким обобщением этого примера является локализация кольца мультипликативным множеством. Каждая локализация представляет собой кольцевой эпиморфизм, который, вообще говоря, не является сюръективным. Поскольку локализации являются фундаментальными в коммутативной алгебре и алгебраической геометрии , это может объяснить, почему в этих областях обычно предпочтительнее определение эпиморфизмов как сокращаемых справа гомоморфизмов.

Расщепляемый эпиморфизм — это гомоморфизм, который имеет правый обратный и, следовательно, сам является левым обратным этому другому гомоморфизму. То есть гомоморфизм является расщепляемым эпиморфизмом, если существует такой гомоморфизм, что расщепляемый эпиморфизм всегда является эпиморфизмом для обоих значений эпиморфизма . Для множеств и векторных пространств каждый эпиморфизм является расщепляемым эпиморфизмом, но это свойство не выполняется для большинства распространенных алгебраических структур. ${\displaystyle f\colon A\to B}$ ${\displaystyle g\colon B\to A}$ ${\displaystyle f\circ g=\operatorname {Id} _{B}.}$

Таким образом, у человека есть

${\displaystyle {\text{split epimorphism}}\implies {\text{epimorphism (surjective)}}\implies {\text{epimorphism (right cancelable)}};}$

последняя импликация — это эквивалентность множеств, векторных пространств, модулей, абелевых групп и групп; первое следствие — это эквивалентность множеств и векторных пространств.

Ядро

Любой гомоморфизм определяет отношение эквивалентности тогда и только тогда, когда . Отношение называется ядром . _ Это отношение конгруэнтности на . Затем фактор -множеству можно придать структуру того же типа , что и , естественным образом, определяя операции фактор-множества с помощью , для каждой операции . В этом случае образ in при гомоморфизме обязательно изоморфен ; этот факт является одной из теорем изоморфизма . ${\displaystyle f:X\to Y}$ ${\displaystyle \sim }$ ${\displaystyle X}$ ${\displaystyle a\sim b}$ ${\displaystyle f(a)=f(b)}$ ${\displaystyle \sim }$ ${\displaystyle f}$ ${\displaystyle X}$ ${\displaystyle X/{\sim }}$ ${\displaystyle X}$ ${\displaystyle [x]\ast [y]=[x\ast y]}$ ${\displaystyle \ast }$ ${\displaystyle X}$ ${\displaystyle X}$ ${\displaystyle Y}$ ${\displaystyle f}$ ${\displaystyle X/\!\sim }$

Когда алгебраическая структура представляет собой группу для некоторой операции, класса эквивалентности единичного элемента этой операции достаточно, чтобы охарактеризовать отношение эквивалентности. В этом случае частное по отношению эквивалентности обозначается (обычно читается как « mod »). Также в этом случае именно , а не , называется ядром . Ядра гомоморфизмов данного типа алгебраической структуры естественным образом наделены некоторой структурой. Этот тип структуры ядер такой же, как и рассматриваемая структура, в случае абелевых групп , векторных пространств и модулей , но отличается и получил конкретное название в других случаях, например, нормальная подгруппа для ядер групповых гомоморфизмов и идеалов . для ядер кольцевых гомоморфизмов (в случае некоммутативных колец ядрами являются двусторонние идеалы ). ${\displaystyle K}$ ${\displaystyle X/K}$ ${\displaystyle X}$ ${\displaystyle K}$ ${\displaystyle K}$ ${\displaystyle \sim }$ ${\displaystyle f}$

Реляционные структуры

В теории моделей понятие алгебраической структуры обобщается на структуры, включающие как операции, так и отношения. Пусть L — сигнатура, состоящая из символов функции и отношения, а A , B — две L -структуры. Тогда гомоморфизм из A в B — это отображение h из области определения A в область определения B такое, что

• h ( F ^A ( a ₁ ,…, an ₎ ) = F ^B ( h ( a ₁ ),…, h ( a _n )) для каждого n -арного функционального символа F в L ,
• RA ( a ₁ , …, an ) подразумевает RB ( h ( a ¹ ) , … _, h ( an ) ) для каждого ⁿ _{-арного} символа отношения R в L _.

В частном случае всего с одним бинарным отношением мы получаем понятие гомоморфизма графов . ^[8]

Формальная теория языка

Гомоморфизмы также используются при изучении формальных языков ^[9] и часто кратко называются морфизмами . ^[10] Учитывая алфавиты и , функция такая, что для всех называется гомоморфизмом на . ^{[примечание 2]} Если - гомоморфизм на и обозначает пустую строку, то называется -свободным гомоморфизмом, когда для всех в . ${\displaystyle \Sigma _{1}}$ ${\displaystyle \Sigma _{2}}$ ${\displaystyle h\colon \Sigma _{1}^{*}\to \Sigma _{2}^{*}}$ ${\displaystyle h(uv)=h(u)h(v)}$ ${\displaystyle u,v\in \Sigma _{1}}$ ${\displaystyle \Sigma _{1}^{*}}$ ${\displaystyle h}$ ${\displaystyle \Sigma _{1}^{*}}$ ${\displaystyle \varepsilon }$ ${\displaystyle h}$ ${\displaystyle \varepsilon }$ ${\displaystyle h(x)\neq \varepsilon }$ ${\displaystyle x\neq \varepsilon }$ ${\displaystyle \Sigma _{1}^{*}}$

Гомоморфизм , удовлетворяющий всем требованиям, называется -равномерным гомоморфизмом. ^[11] Если для всех (то есть 1-равномерно), то также называется кодированием или проекцией . ^{[ нужна цитата ]} ${\displaystyle h\colon \Sigma _{1}^{*}\to \Sigma _{2}^{*}}$ ${\displaystyle \Sigma _{1}^{*}}$ ${\displaystyle |h(a)|=k}$ ${\displaystyle a\in \Sigma _{1}}$ ${\displaystyle k}$ ${\displaystyle |h(a)|=1}$ ${\displaystyle a\in \Sigma _{1}}$ ${\displaystyle h}$ ${\displaystyle h}$

Набор слов, сформированный из алфавита, можно рассматривать как свободный моноид, порожденный . Здесь операция моноида — это конкатенация , а единичный элемент — пустое слово. С этой точки зрения языковой гомоморфизм — это в точности моноидный гомоморфизм. ^{[заметка 3]} ${\displaystyle \Sigma ^{*}}$ ${\displaystyle \Sigma }$ ${\displaystyle \Sigma }$

Смотрите также

• Диффеоморфизм
• Гомоморфное шифрование
• Гомоморфное разделение секретов – упрощенный протокол децентрализованного голосования
• Морфизм
• Квазиморфизм

Примечания

1. Как это часто бывает, но не всегда, здесь использовался один и тот же символ для работы обоих и . ${\displaystyle A}$ ${\displaystyle B}$
2. Символ ∗ обозначает операцию звезды Клини , а Σ ^∗ обозначает набор слов, образованных из алфавита Σ, включая пустое слово. Сопоставление терминов означает конкатенацию . Например, h ( u ) h ( v ) обозначает объединение h ( u ) с h ( v ).
3. Нас уверяют, что языковой гомоморфизм h отображает пустое слово ε ​​в пустое слово. Поскольку час ( ε ) = час ( ε ) = час ( ε ) час ( ε ), количество w символов в h ( ε ) равно числу 2 w символов в h ( ε ) h ( ε ). Следовательно, w = 0 и h ( ε ) имеет нулевую длину.

Цитаты

1. Фрике, Роберт (1897–1912). Vorlesungen über die Theorie der automorphen Functionen. Б. Г. Тойбнер. ОСЛК  29857037.
2. См.:
   • Риттер, Эрнст (1892). «Die eindeutigen automorphen Formen vom Geschlecht Null, eine Revision und Erweiterung der Poincaré'schen Sätze» [Уникальные автоморфные формы нулевого рода, пересмотр и расширение теоремы Пуанкаре]. Mathematische Annalen (на немецком языке). 41 : 1–82. дои : 10.1007/BF01443449. S2CID  121524108. Из сноски на стр. 22: «Ich will nach einem Vorschlage von Hrn. Проф. Кляйн statt der umständlichen und nicht immer ausreichenden Bezeichnungen: «holoedrisch, bezw. hemiedrisch usw isomorph» die Benennung «isomorph» auf den Fall des holoedrischen Isomorphismus zweier Gruppen einschränken, sonst aber von «Homomorphismus» sprechen,…» (По предложению проф. Кляйна вместо громоздких и не всегда удовлетворительных обозначений «голоэдрический, или полуэдрический и т. д. изоморфный», я ограничу наименование «изоморфный» случаем голоэдрического изоморфизма двух групп; в противном случае, однако, [я буду] говорить о «гомоморфизме»,…)
   • Фрике, Роберт (1892). «Ueber den arithmetischen Charakter der zu den Verzweigungen (2,3,7) und (2,4,7) gehörenden Dreiecksfunctionen» [Об арифметическом характере треугольных функций, принадлежащих точкам ветвления (2,3,7) и ( 2,4,7)]. Mathematische Annalen (на немецком языке). 41 (3): 443–468. дои : 10.1007/BF01443421. S2CID  120022176. Из стр. 466: «Hierdurch ist, wie man sofort überblickt, eine homomorphe*) Beziehung der Gruppe Γ ₍₆₃₎ auf die Gruppe der mod. n incongruenten Substitutionen mit Rational ganzen Coefficienten der Determinante 1 begründet». (Таким образом, как сразу видно, гомоморфное отношение группы Γ ₍₆₃₎ основано на группе неконгруэнтных по модулю n подстановок с целыми рациональными коэффициентами определителя 1.) Из сноски на с. 466: «*) Im Anschluss an einen von Hrn. Klein bei seinen neueren Vorlesungen eingeführten Brauch schreibe ich an Stelle der bisherigen Bezeichnung «meroedrischer Isomorphismus» die sinngemässere «Homomorphismus».» (Следуя использованию, которое было введено г-ном Кляйном в его последних лекциях, я пишу вместо прежнего обозначения «мероэдральный изоморфизм» более логичное «гомоморфизм».)
3. Биркгоф, Гарретт (1967) [1940], Теория решетки , Публикации коллоквиума Американского математического общества, том. 25 (3-е изд.), Провиденс, Род-Айленд: Американское математическое общество , ISBN. 978-0-8218-1025-5, МР  0598630
4. Стэнли Н. Беррис; HP Санкаппанавар (2012). Курс универсальной алгебры (PDF) . С. Беррис и Х. П. Санкаппанавар. ISBN 978-0-9880552-0-9.
5. Mac Lane, Сондерс (1971). Категории для работающего математика . Тексты для аспирантов по математике . Том. 5. Шпрингер-Верлаг . Упражнение 4 в разделе I.5. ISBN 0-387-90036-5. Збл  0232.18001.
6. Линдерхольм, CE (1970). Групповой эпиморфизм сюръективен. Американский математический ежемесячник , 77 (2), 176–177.
7. Даскалеску, Сорин; Нэстасеску, Константин; Райану, Шербан (2001). Алгебра Хопфа: Введение . Чистая и прикладная математика. Том. 235. Нью-Йорк, штат Нью-Йорк: Марсель Деккер. п. 363. ИСБН 0824704819. Збл  0962.16026.
8. Подробное обсуждение реляционных гомоморфизмов и изоморфизмов см. в разделе 17.3, в Gunther Schmidt , 2010. Relational Mathematics . Издательство Кембриджского университета, ISBN 978-0-521-76268-7 
9. Сеймур Гинзбург , Алгебраические и автоматно-теоретические свойства формальных языков , Северная Голландия, 1975, ISBN 0-7204-2506-9 , 
10. Т. Харью, Дж. Кархумеки, Морфизмы в Справочнике по формальным языкам , Том I, под редакцией Г. Розенберга, А. Саломаа, Springer, 1997, ISBN 3-540-61486-9 . 
11. Кригер (2006) с. 287

Рекомендации

• Кригер, Далия (2006). «О критических показателях в неподвижных точках нестирающихся морфизмов». В Ибарре, Оскар Х.; Данг, Чжэ (ред.). Развитие теории языка: 10-я международная конференция, DLT 2006, Санта-Барбара, Калифорния, США, 26–29 июня 2006 г.: материалы . Берлин: Шпрингер. п. 280-291. ISBN 978-3-540-35430-7. ОСЛК  262693179.
• Стэнли Н. Беррис; HP Санкаппанавар (2012). Курс универсальной алгебры (PDF) . С. Беррис и Х. П. Санкаппанавар. ISBN 978-0-9880552-0-9.
• Мак Лейн, Сондерс (1971), Категории для работающего математика , Тексты для выпускников по математике , том. 5, Шпрингер-Верлаг , ISBN 0-387-90036-5, Збл  0232.18001
• Фрели, Джон Б.; Кац, Виктор Дж. (2003), Первый курс абстрактной алгебры , Аддисон-Уэсли, ISBN 978-1-292-02496-7