Квантовая электродинамика

Квантовая полевая теория электромагнетизма

В физике элементарных частиц квантовая электродинамика ( КЭД ) представляет собой релятивистскую квантовую теорию поля электродинамики . ^{[1] [2] [3]} По сути, она описывает взаимодействие света и материи и является первой теорией, в которой достигнуто полное согласие между квантовой механикой и специальной теорией относительности . ^[2] КЭД ​​математически описывает все явления , включающие электрически заряженные частицы, взаимодействующие посредством обмена фотонами , и представляет собой квантовый аналог классического электромагнетизма , дающий полное описание взаимодействия материи и света. ^{[2] [3]}

С технической точки зрения, КЭД можно описать как очень точный способ расчета вероятности положения и движения частиц, даже безмассовых, таких как фотоны, и количества, зависящего от положения (поля) этих частиц, а также описываемого света и материи. за пределами корпускулярно-волнового дуализма, предложенного Эйнштейном в 1905 году. Ричард Фейнман назвал его «жемчужиной физики» за чрезвычайно точные предсказания таких величин, как аномальный магнитный момент электрона и лэмбовский сдвиг энергетических уровней водорода . ^{[2] : Глава 1} Это наиболее точная и тщательно проверенная теория в физике. ^{[4] [5]}

История

Поль Дирак

Первая формулировка квантовой теории , описывающей взаимодействие излучения и материи, приписывается британскому учёному Полю Дираку , который (в 1920 - е годы) смог вычислить коэффициент спонтанного излучения атома . ^[6] Ему также приписывают создание термина «квантовая электродинамика». ^[7]

Дирак описал квантование электромагнитного поля как ансамбль гармонических осцилляторов с введением понятия операторов рождения и уничтожения частиц. В последующие годы, благодаря вкладу Вольфганга Паули , Юджина Вигнера , Паскуаля Йордана , Вернера Гейзенберга и элегантной формулировке квантовой электродинамики Энрико Ферми , ^[8] физики пришли к убеждению, что в принципе можно выполнять любые вычисления. для любого физического процесса с участием фотонов и заряженных частиц. Однако дальнейшие исследования Феликса Блоха совместно с Арнольдом Нордсиком ^[9] и Виктором Вайскопфом [ ^10] в 1937 и 1939 годах показали, что такие вычисления были надежны только в первом порядке теории возмущений , на проблему уже указывал Роберт Оппенгеймер . ^[11] На более высоких порядках в ряду появились бесконечности, что сделало такие вычисления бессмысленными и вызвало серьезные сомнения во внутренней непротиворечивости самой теории. Поскольку в то время решение этой проблемы не было известно, казалось, что существует фундаментальная несовместимость между специальной теорией относительности и квантовой механикой .

Ганс Бете

Трудности с теорией возросли к концу 1940-х годов. Усовершенствования в микроволновой технике позволили проводить более точные измерения сдвига уровней атома водорода , ^[12] известного теперь как лэмбовский сдвиг и магнитный момент электрона. ^[13] Эти эксперименты выявили несоответствия, которые теория не смогла объяснить.

Первое указание на возможный выход было дано Гансом Бете в 1947 году ^[14] после участия в конференции на острове Шелтер . ^[15] Пока он ехал на поезде с конференции в Скенектади , он сделал первое нерелятивистское вычисление сдвига линий атома водорода, измеренное Ламбом и Ретерфордом . ^[14] Несмотря на ограничения вычислений, согласие было превосходным. Идея заключалась в том, чтобы просто придать бесконечность поправкам на массу и заряд , которые фактически были зафиксированы в результате экспериментов как конечные значения. Таким образом, бесконечности поглощаются этими константами и дают конечный результат, хорошо согласующийся с экспериментами. Эта процедура получила название перенормировки .

Фейнман (в центре) и Оппенгеймер (справа) в Лос-Аламосе .

Основываясь на интуиции Бете и фундаментальных работах по этому вопросу Синитиро Томонаги , ^[16] Джулиана Швингера , ^{[17] [18]} Ричарда Фейнмана ^{[1] [19] [20]} и Фримена Дайсона , ^{[21] [22]} это наконец стало возможным получить полностью ковариантные формулировки, конечные в любом порядке в ряду возмущений квантовой электродинамики. Шинитиро Томонага, Джулиан Швингер и Ричард Фейнман были совместно удостоены Нобелевской премии по физике 1965 года за свои работы в этой области. ^[23] Их вклад, как и вклад Фримена Дайсона , касался ковариантных и калибровочно-инвариантных формулировок квантовой электродинамики, которые позволяют вычислять наблюдаемые при любом порядке теории возмущений . Математическая техника Фейнмана, основанная на его диаграммах , поначалу казалась сильно отличающейся от теоретико-полевого операторного подхода Швингера и Томонаги, но позже Фримен Дайсон показал, что эти два подхода эквивалентны. ^[21] Перенормировка , необходимость придавать физический смысл некоторым расхождениям, возникающим в теории через интегралы , впоследствии стала одним из фундаментальных аспектов квантовой теории поля и стала рассматриваться как критерий общей приемлемости теории. Несмотря на то, что перенормировка работает очень хорошо на практике, Фейнман никогда не был полностью доволен ее математической обоснованностью, даже называя перенормировку «игрой в наперстки» и «фокус-покусом». ^{[2] : 128}

Таким образом, ни Фейнман, ни Дирак не были довольны таким подходом к наблюдениям, сделанным в теоретической физике, прежде всего в квантовой механике. ^[24]

КЭД послужила моделью и шаблоном для всех последующих квантовых теорий поля. Одной из таких последующих теорий является квантовая хромодинамика , которая возникла в начале 1960-х годов и достигла своей нынешней формы в 1970-х годах в работах Х. Дэвида Политцера , Сиднея Коулмана , Дэвида Гросса и Фрэнка Вильчека . Опираясь на новаторские работы Швингера , Джеральда Гуральника , Дика Хагена и Тома Киббла , ^{[25] [26]} Питера Хиггса , Джеффри Голдстоуна и других, Шелдон Глэшоу , Стивен Вайнберг и Абдус Салам независимо друг от друга показали, как слабая ядерная сила и квантовая сила электродинамику можно было бы объединить в одно электрослабое взаимодействие .

Взгляд Фейнмана на квантовую электродинамику

Введение

Ближе к концу своей жизни Ричард Фейнман прочитал серию лекций по КЭД, предназначенных для широкой публики. Эти лекции были расшифрованы и опубликованы под названием Фейнман (1985), КЭД: Странная теория света и материи , ^[2] классическое нематематическое изложение КЭД с точки зрения, изложенной ниже.

Ключевыми компонентами фейнмановской презентации КЭД являются три основных действия. ^{[2] : 85}

Фотон перемещается из одного места и времени в другое место и время .

Электрон перемещается из одного места и времени в другое место и время .

Электрон испускает или поглощает фотон в определенном месте и в определенное время.

Элементы диаграммы Фейнмана

Эти действия представлены в виде визуального обозначения тремя основными элементами диаграмм : волнистой линией для фотона, прямой линией для электрона и соединением двух прямых линий и волнистой линией для вершины, представляющей испускание или поглощение фотон электроном. Все это можно увидеть на соседней диаграмме.

Помимо визуального обозначения действий, Фейнман вводит еще один вид обозначения числовых величин, называемых амплитудами вероятности. Вероятность представляет собой квадрат абсолютного значения полной амплитуды вероятности, . Если фотон перемещается из одного места и времени в другое место и время , соответствующая величина записывается в сокращении Фейнмана как и зависит только от импульса и поляризации фотона. Аналогичная величина для электрона, движущегося из в, записана . Это зависит от импульса и поляризации электрона, в дополнение к постоянной, которую Фейнман называет n , иногда называемой «голой» массой электрона: она связана с измеренной массой электрона, но не совпадает с ней. Наконец, величина, которая говорит нам об амплитуде вероятности того, что электрон испустит или поглотит фотон, Фейнман называет j и иногда ее называют «голым» зарядом электрона: это константа, связанная с, но не с зарядом электрона. то же, что и измеренный заряд электрона e . ^{[2] : 91} ${\displaystyle {\text{probability}}=|f({\text{amplitude}})|^{2}}$ ${\displaystyle A}$ ${\displaystyle B}$ ${\displaystyle P(A{\text{ to }}B)}$ ${\displaystyle C}$ ${\displaystyle D}$ ${\displaystyle E(C{\text{ to }}D)}$

КЭД основана на предположении, что сложные взаимодействия многих электронов и фотонов можно представить, собрав вместе подходящий набор из трех вышеупомянутых строительных блоков, а затем используя амплитуды вероятности для расчета вероятности любого такого сложного взаимодействия. Оказывается, основную идею КЭД можно передать, предполагая, что квадрат суммы упомянутых выше амплитуд вероятностей ( P ( от A до B ), E ( от C до D ) и j ) действует точно так же, как наша повседневная вероятность ( упрощение, сделанное в книге Фейнмана). Позже это будет исправлено, включив в него конкретно квантовую математику, следуя Фейнману.

Основные правила определения амплитуд вероятности, которые будут использоваться: ^{[2] : 93}

1. Если событие может произойти посредством ряда неразличимых альтернативных процессов (так называемых «виртуальных» процессов), то его амплитуда вероятности представляет собой сумму амплитуд вероятностей альтернатив.
2. Если виртуальный процесс включает в себя ряд независимых или сопутствующих подпроцессов, то амплитуда вероятности общего (составного) процесса является произведением амплитуд вероятности подпроцессов.

Критерий неотличимости в (а) очень важен: он означает, что в данной системе нет наблюдаемого признака , который каким-либо образом «раскрывает», какая альтернатива выбрана. В таком случае невозможно наблюдать, какая альтернатива действительно имеет место, не меняя каким-либо образом экспериментальную установку (например, вводя в систему новую аппаратуру). Всякий раз, когда кто-то может наблюдать, какая альтернатива имеет место, он всегда обнаруживает, что вероятность события равна сумме вероятностей альтернатив. Действительно, если бы это было не так, сам термин «альтернативы» для описания этих процессов был бы неуместен. Что (а) говорит о том, что как только физические средства наблюдения за тем, какая альтернатива произошла , все равно нельзя сказать, что событие происходит посредством «точно одной из альтернатив» в смысле сложения вероятностей; вместо этого необходимо добавить амплитуды. ^{[2] : 82}

Точно так же критерий независимости в (b) очень важен: он применим только к процессам, которые не «запутаны».

Основные конструкции

Предположим, мы начинаем с одного электрона в определенном месте и в определенное время (этому месту и времени присвоено произвольное обозначение A ) и фотону в другом месте и в другое время (имеется обозначение B ). Типичный вопрос с физической точки зрения: «Какова вероятность найти электрон в C (в другом месте и в более позднее время) и фотон в D (еще в другом месте и в другое время)?». Самый простой процесс достижения этой цели — перемещение электрона из A в C (элементарное действие), а фотона — из B в D (еще одно элементарное действие). Зная амплитуды вероятности каждого из этих подпроцессов — E ( от A до C ) и P ( от B до D ) — мы ожидаем вычислить амплитуду вероятности того, что оба процесса происходят вместе, путем их умножения, используя правило b) выше. . Это дает простую оценку общей амплитуды вероятности, которая возводится в квадрат для получения расчетной вероятности. ^{[ нужна цитата ]}

Комптоновское рассеяние

Но есть и другие способы достижения результата. Электрон может переместиться в место и время E , где он поглотит фотон; затем двигайтесь дальше, прежде чем испустить еще один фотон в точке F ; затем переходите к C , где он обнаруживается, а новый фотон перемещается к D. Вероятность этого сложного процесса можно снова вычислить, зная амплитуды вероятности каждого из отдельных действий: трех действий электрона, двух действий фотона и двух вершин – одной эмиссии и одной поглощения. Мы ожидаем найти общую амплитуду вероятности путем умножения амплитуд вероятности каждого действия для любых выбранных положений E и F. Затем мы, используя правило а) выше, должны сложить все эти амплитуды вероятности для всех альтернатив для E и F. (На практике это не элементарно и предполагает интегрирование .) Но есть и другая возможность: электрон сначала движется в G , где он испускает фотон, который переходит в D , в то время как электрон движется в H , где он поглощает первый фотон, прежде чем перейти к C. Опять же, мы можем вычислить амплитуду вероятности этих возможностей (для всех точек G и H ). Тогда мы получим лучшую оценку общей амплитуды вероятности, добавив амплитуды вероятности этих двух возможностей к нашей исходной простой оценке. Кстати, название этого процесса взаимодействия фотона с электроном таким образом — комптоновское рассеяние . ^{[ нужна цитата ]}

Существует бесконечное количество других промежуточных «виртуальных» процессов, в которых поглощается и/или излучается все больше и больше фотонов. Для каждого из этих процессов можно построить диаграмму Фейнмана, описывающую его. Это подразумевает сложное вычисление результирующих амплитуд вероятности, но при условии, что чем сложнее диаграмма, тем меньше она вносит вклад в результат, и поиск настолько точного ответа, насколько хочется, является лишь вопросом времени и усилий. на исходный вопрос. Это основной подход QED. Чтобы вычислить вероятность любого процесса взаимодействия между электронами и фотонами, необходимо сначала отметить с помощью диаграмм Фейнмана все возможные способы, которыми этот процесс может быть построен из трех основных элементов. Каждая диаграмма включает в себя некоторые вычисления, включающие определенные правила для нахождения соответствующей амплитуды вероятности.

Эта базовая основа сохраняется и при переходе к квантовому описанию, но необходимы некоторые концептуальные изменения. Во-первых, хотя в нашей повседневной жизни мы могли бы ожидать, что будут существовать некоторые ограничения на точки, в которые частица может двигаться, в полной квантовой электродинамике это не так. Существует ненулевая амплитуда вероятности того, что электрон в точке A или фотон в точке B перемещаются в качестве основного действия в любое другое место и время во Вселенной . Сюда входят места, до которых можно было добраться только на скорости, превышающей скорость света, а также в более ранние времена . (Электрон, движущийся назад во времени, можно рассматривать как позитрон , движущийся вперед во времени.) ^{[2] : 89, 98–99}

Амплитуды вероятности

Фейнман заменяет комплексные числа вращающимися стрелками, которые начинаются при испускании и заканчиваются при обнаружении частицы. Сумма всех полученных стрелок дает окончательную стрелку, квадрат длины которой равен вероятности события. На этой диаграмме свет, излучаемый источником S , может достичь детектора в точке P , отражаясь от зеркала (синего цвета) в различных точках. С каждым из путей связана стрелка (направление которой меняется равномерно в зависимости от времени, необходимого свету для прохождения пути). Чтобы правильно рассчитать общую вероятность того, что свет достигнет точки P , начиная с точки S , необходимо просуммировать стрелки для всех таких путей. На графике ниже показано общее время, затраченное на прохождение каждого из указанных выше путей.

Квантовая механика вносит важные изменения в способ вычисления вероятностей. Вероятности по-прежнему представляются обычными действительными числами, которые мы используем для обозначения вероятностей в нашем повседневном мире, но вероятности вычисляются как квадрат модуля амплитуд вероятности , которые являются комплексными числами .

Фейнман избегает знакомить читателя с математикой комплексных чисел, используя простое, но точное представление их в виде стрелок на листе бумаги или экране. (Их не следует путать со стрелками диаграмм Фейнмана, которые представляют собой упрощенное двухмерное представление взаимосвязей между точками в трех измерениях пространства и времени.) Амплитудные стрелки имеют фундаментальное значение для описания мира, данного квантовыми числами. теория. Они связаны с нашими повседневными представлениями о вероятности простым правилом: вероятность события равна квадрату длины соответствующей амплитудной стрелки. Итак, для данного процесса, если задействованы две амплитуды вероятности, v и w , вероятность процесса будет определяться либо выражением

${\displaystyle P=|\mathbf {v} +\mathbf {w} |^{2}}$

или

${\displaystyle P=|\mathbf {v} \,\mathbf {w} |^{2}.}$

Однако правила сложения и умножения такие же, как указано выше. Но там, где вы ожидаете сложения или умножения вероятностей, вместо этого вы складываете или умножаете амплитуды вероятности, которые теперь являются комплексными числами.

Сложение амплитуд вероятности как комплексных чисел

Умножение амплитуд вероятности на комплексные числа

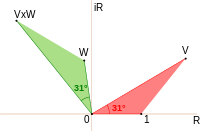
Сложение и умножение — распространенные операции в теории комплексных чисел и показаны на рисунках. Сумма находится следующим образом. Пусть начало второй стрелки будет на конце первой. Тогда сумма представляет собой третью стрелку, идущую прямо от начала первой к концу второй. Произведение двух стрел — это стрела, длина которой равна произведению двух длин. Направление продукта определяется путем сложения углов, на которые каждый из двух продуктов был повернут относительно контрольного направления: это дает угол, на который продукт повернут относительно контрольного направления.

Это изменение от вероятностей к амплитудам вероятностей усложняет математику, не меняя при этом базового подхода. Но этого изменения все еще недостаточно, поскольку оно не учитывает тот факт, что и фотоны, и электроны могут быть поляризованы, то есть необходимо учитывать их ориентацию в пространстве и времени. Следовательно, P ( от A до B ) состоит из 16 комплексных чисел или стрелок амплитуды вероятности. ^{[2] : 120–121} Есть также некоторые незначительные изменения, связанные с величиной j , которую, возможно, придется повернуть на угол, кратный 90°, для некоторых поляризаций, что представляет интерес только для детального учета.

С тем, что электрон может быть поляризован, связана еще одна небольшая необходимая деталь, связанная с тем, что электрон является фермионом и подчиняется статистике Ферми–Дирака . Основное правило заключается в том, что если у нас есть амплитуда вероятности для данного сложного процесса с участием более чем одного электрона, то когда мы включаем (как всегда необходимо) дополнительную диаграмму Фейнмана, в которой мы обмениваемся двумя электронными событиями, результирующая амплитуда является обратной – отрицательный – из первых. В простейшем случае два электрона начинаются с A и B и заканчиваются C и D. Амплитуда будет рассчитываться как «разница» E ( A и D ) × E ( B и C ) − E ( A и C ) × E ( B и D ) , чего мы и ожидаем, исходя из нашего повседневного представления о вероятностях. , что это будет сумма. ^{[2] : 112–113.}

Распространители

Наконец, нужно вычислить P ( от A до B ) и E (от C до D ), соответствующие амплитудам вероятности для фотона и электрона соответственно. По сути, это решения уравнения Дирака , описывающего поведение амплитуды вероятности электрона, и уравнения Максвелла , описывающего поведение амплитуды вероятности фотона. Их называют пропагаторами Фейнмана . Перевод обозначений, обычно используемых в стандартной литературе, выглядит следующим образом:

${\displaystyle P(A{\text{ to }}B)\to D_{F}(x_{B}-x_{A}),\quad E(C{\text{ to }}D)\to S_{F}(x_{D}-x_{C}),}$

где сокращенный символ, например, обозначает четыре действительных числа, которые обозначают время и положение в трех измерениях точки, обозначенной A . ${\displaystyle x_{A}}$

Массовая перенормировка

Электронная петля собственной энергии

Исторически возникла проблема, которая задержала прогресс на двадцать лет: хотя мы начинаем с предположения о трех основных «простых» действиях, правила игры гласят, что если мы хотим вычислить амплитуду вероятности того, что электрон попадет из A в B , , мы должны принять во внимание все возможные пути: все возможные диаграммы Фейнмана с этими концами. Таким образом, будет путь, по которому электрон достигнет точки C , испустит там фотон, а затем снова поглотит его в точке D , прежде чем перейти к точке B. Или он может сделать это дважды или больше. Короче говоря, мы имеем ситуацию, подобную фракталу , в которой, если мы внимательно посмотрим на линию, она распадается на набор «простых» линий, каждая из которых, если внимательно присмотреться, в свою очередь состоит из «простых» линий. , и так до бесконечности . Это сложная ситуация, с которой нужно справиться. Если бы добавление этой детали лишь немного изменило ситуацию, то все было бы не так уж плохо, но случилась катастрофа, когда выяснилось, что простая коррекция, упомянутая выше, привела к бесконечным амплитудам вероятности. Со временем эта проблема была «исправлена» методом перенормировки . Однако сам Фейнман остался этим недоволен, назвав это «тупным процессом» ^{[2] : 128} , а Дирак также раскритиковал эту процедуру, поскольку «в математике невозможно избавиться от бесконечностей, когда они вам не нравятся». ^[24]

Выводы

В рамках вышеизложенного физики смогли затем с высокой степенью точности рассчитать некоторые свойства электронов, такие как аномальный магнитный дипольный момент . Однако, как указывает Фейнман, это не может объяснить, почему такие частицы, как электрон, имеют такую ​​массу. «Не существует теории, которая бы адекватно объясняла эти числа. Мы используем числа во всех наших теориях, но не понимаем их – что они собой представляют и откуда они берутся. Я считаю, что с фундаментальной точки зрения это очень интересная и серьезная проблема». ^{[2] : 152}

Математическая формулировка

действие КЭД

Математически КЭД представляет собой абелеву калибровочную теорию с группой симметрии U(1) , определенной в пространстве Минковского (плоское пространство-время). Калибровочным полем , опосредующим взаимодействие между заряженными полями со спином 1/2 , является электромагнитное поле . Лагранжиан КЭД для поля со спином 1/2, взаимодействующего с электромагнитным полем в натуральных единицах, порождает действие ^{[27] : 78}

КЭД действие

${\displaystyle S_{\text{QED}}=\int d^{4}x\,\left[-{\frac {1}{4}}F^{\mu \nu }F_{\mu \nu }+{\bar {\psi }}\,(i\gamma ^{\mu }D_{\mu }-m)\,\psi \right]}$

где

• ${\displaystyle \gamma ^{\mu }}$являются матрицами Дирака .
• ${\displaystyle \psi }$биспинорное поле частиц со спином 1/2 (например, электрон - позитронное поле ).
• ${\displaystyle {\bar {\psi }}\equiv \psi ^{\dagger }\gamma ^{0}}$, называемый «пси-баром», иногда называют сопряженным Дирака .
• ${\displaystyle D_{\mu }\equiv \partial _{\mu }+ieA_{\mu }+ieB_{\mu }}$– калибровочная ковариантная производная .
  • e — константа связи , равная электрическому заряду биспинорного поля.
  • ${\displaystyle A_{\mu }}$— ковариантный четырехпотенциал электромагнитного поля, создаваемого самим электроном. Его также называют калибровочным полем или связностью. ${\displaystyle {\text{U}}(1)}$
  • ${\displaystyle B_{\mu }}$— внешнее поле, налагаемое внешним источником.
• m — масса электрона или позитрона.
• ${\displaystyle F_{\mu \nu }=\partial _{\mu }A_{\nu }-\partial _{\nu }A_{\mu }}$– тензор электромагнитного поля . Это также известно как кривизна калибровочного поля.

Расширение ковариантной производной открывает вторую полезную форму лагранжиана (внешнее поле для простоты установлено равным нулю). ${\displaystyle B_{\mu }}$

${\displaystyle {\mathcal {L}}=-{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }+{\bar {\psi }}(i\gamma ^{\mu }\partial _{\mu }-m)\psi -ej^{\mu }A_{\mu }}$

где – сохраняющийся ток, вытекающий из теоремы Нётер. Это написано ${\displaystyle j^{\mu }}$ ${\displaystyle {\text{U}}(1)}$

${\displaystyle j^{\mu }={\bar {\psi }}\gamma ^{\mu }\psi .}$

Уравнения движения

Разложение ковариантной производной в лагранжиан дает

${\displaystyle {\mathcal {L}}=-{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }+i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -e{\bar {\psi }}\gamma ^{\mu }A_{\mu }\psi -m{\bar {\psi }}\psi }$

${\displaystyle =-{\frac {1}{4}}F_{\mu \nu }F^{\mu \nu }+i{\bar {\psi }}\gamma ^{\mu }\partial _{\mu }\psi -m{\bar {\psi }}\psi -ej^{\mu }A_{\mu }.}$

Для простоты установлено нулевое значение. В качестве альтернативы мы можем поглотить новое калибровочное поле и переименовать новое поле как ${\displaystyle B_{\mu }}$ ${\displaystyle B_{\mu }}$ ${\displaystyle A'_{\mu }=A_{\mu }+B_{\mu }}$ ${\displaystyle A_{\mu }.}$

Из этого лагранжиана можно получить уравнения движения для полей и . ${\displaystyle \psi }$ ${\displaystyle A_{\mu }}$

Уравнение движения для ψ

Проще всего они возникают при рассмотрении уравнения Эйлера-Лагранжа для . Поскольку лагранжиан не содержит слагаемых, мы сразу получаем ${\displaystyle {\bar {\psi }}}$ ${\displaystyle \partial _{\mu }{\bar {\psi }}}$

${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial {\bar {\psi }}}}=0}$

поэтому уравнение движения можно записать ${\displaystyle (i\gamma ^{\mu }\partial _{\mu }-m)\psi =e\gamma ^{\mu }A_{\mu }\psi .}$

Уравнение движения для A _µ

• Используя уравнение Эйлера – Лагранжа для поля, ${\displaystyle A_{\mu }}$

производные на этот раз

$${\displaystyle \partial _{\nu }\left({\frac {\partial {\mathcal {L}}}{\partial (\partial _{\nu }A_{\mu })}}\right)=\partial _{\nu }\left(\partial ^{\mu }A^{\nu }-\partial ^{\nu }A^{\mu }\right),}$$

$${\displaystyle {\frac {\partial {\mathcal {L}}}{\partial A_{\mu }}}=-e{\bar {\psi }}\gamma ^{\mu }\psi .}$$

Замена обратно в ( 3 ) приводит к

${\displaystyle \partial _{\mu }F^{\mu \nu }=e{\bar {\psi }}\gamma ^{\nu }\psi }$

которое можно записать через ток как ${\displaystyle {\text{U}}(1)}$ ${\displaystyle j^{\mu }}$

${\displaystyle \partial _{\mu }F^{\mu \nu }=ej^{\nu }.}$

Теперь, если мы наложим калибровочное условие Лоренца

$${\displaystyle \partial _{\mu }A^{\mu }=0,}$$

$${\displaystyle \Box A^{\mu }=ej^{\mu },}$$

волновое уравнениеуравнений Максвеллакалибровке Лоренцаволновой оператор ${\displaystyle \Box =\partial _{\mu }\partial ^{\mu }}$

Картинка взаимодействия

Эту теорию можно напрямую квантовать, рассматривая бозонные и фермионные сектора ^{( необходимы пояснения )} как свободные. Это позволяет построить набор асимптотических состояний, которые можно использовать для начала расчета амплитуд вероятностей различных процессов. Для этого нам нужно вычислить оператор эволюции , который для данного начального состояния даст конечное состояние таким образом, чтобы иметь ^{[27] : 5} ${\displaystyle |i\rangle }$ ${\displaystyle \langle f|}$

$${\displaystyle M_{fi}=\langle f|U|i\rangle .}$$

Этот метод также известен как S-матрица . Оператор эволюции получается в картине взаимодействия , где эволюция во времени задается гамильтонианом взаимодействия, который представляет собой интеграл по пространству второго члена в плотности лагранжа, приведенной выше: ^{[27] : 123}

$${\displaystyle V=e\int d^{3}x\,{\bar {\psi }}\gamma ^{\mu }\psi A_{\mu },}$$

и так, имеем ^{[27] : 86}

$${\displaystyle U=T\exp \left[-{\frac {i}{\hbar }}\int _{t_{0}}^{t}dt'\,V(t')\right],}$$

где T — оператор временного порядка . Этот оператор эволюции имеет смысл только как ряд, и здесь мы получаем ряд возмущений с константой тонкой структуры в качестве параметра развития. Эта серия называется серией Дайсона .

Диаграммы Фейнмана

Несмотря на концептуальную ясность фейнмановского подхода к КЭД, почти ни один ранний учебник не следует его изложению. При выполнении вычислений гораздо проще работать с преобразованиями Фурье пропагаторов . Экспериментальные проверки квантовой электродинамики обычно представляют собой эксперименты по рассеянию. В теории рассеяния учитываются импульсы частиц, а не их положения, и удобно думать о частицах как о создании или уничтожении при их взаимодействии. Диаграммы Фейнмана тогда выглядят одинаково, но линии имеют разную интерпретацию. Электронная линия представляет собой электрон с заданной энергией и импульсом, с аналогичной интерпретацией фотонной линии. Вершинная диаграмма представляет собой уничтожение одного электрона и создание другого вместе с поглощением или рождением фотона, каждый из которых имеет определенные энергии и импульсы.

Используя теорему Вика о членах ряда Дайсона, все члены S-матрицы квантовой электродинамики можно вычислить с помощью диаграмм Фейнмана . В этом случае правила розыгрыша следующие ^{[27] : 801–802.}

К этим правилам мы должны добавить еще одно для замкнутых контуров, которое подразумевает интегрирование по импульсам , поскольку эти внутренние («виртуальные») частицы не ограничены какой-либо конкретной энергией-импульсом, даже той, которая обычно требуется специальной теорией относительности ( подробности см. в разделе « Пропагатор» ). ). Сигнатура метрики : . ${\textstyle \int d^{4}p/(2\pi )^{4}}$ ${\displaystyle \eta _{\mu \nu }}$ ${\displaystyle {\rm {diag}}(+---)}$

Из них непосредственно даются расчеты амплитуд вероятности . Примером является комптоновское рассеяние , при котором электрон и фотон подвергаются упругому рассеянию . Диаграммы Фейнмана в этом случае ^{[27] : 158–159.}

и таким образом мы можем получить соответствующую амплитуду в первом порядке ряда возмущений для S-матрицы :

$${\displaystyle M_{fi}=(ie)^{2}{\overline {u}}({\vec {p}}',s')\epsilon \!\!\!/\,'({\vec {k}}',\lambda ')^{*}{\frac {p\!\!\!/+k\!\!\!/+m_{e}}{(p+k)^{2}-m_{e}^{2}}}\epsilon \!\!\!/({\vec {k}},\lambda )u({\vec {p}},s)+(ie)^{2}{\overline {u}}({\vec {p}}',s')\epsilon \!\!\!/({\vec {k}},\lambda ){\frac {p\!\!\!/-k\!\!\!/'+m_{e}}{(p-k')^{2}-m_{e}^{2}}}\epsilon \!\!\!/\,'({\vec {k}}',\lambda ')^{*}u({\vec {p}},s),}$$

откуда мы можем вычислить сечение этого рассеяния.

Непертурбативные явления

Предсказательный успех квантовой электродинамики во многом зависит от использования теории возмущений, выраженной в диаграммах Фейнмана. Однако квантовая электродинамика также приводит к предсказаниям, выходящим за рамки теории возмущений. В присутствии очень сильных электрических полей он предсказывает, что электроны и позитроны будут рождаться спонтанно, что приведет к затуханию поля. Этот процесс, называемый эффектом Швингера ^[28] , не может быть понят в терминах любого конечного числа диаграмм Фейнмана и поэтому описывается как непертурбативный . Математически его можно получить с помощью полуклассического приближения к интегралу по путям квантовой электродинамики.

Перенормируемость

Члены более высокого порядка можно напрямую вычислить для оператора эволюции, но эти члены отображают диаграммы, содержащие следующие более простые ^{[27] : глава 10}

• 
  Однопетлевой вклад в функцию поляризации вакуума ${\displaystyle \Pi }$
• 
  Однопетлевой вклад в функцию собственной энергии электрона ${\displaystyle \Sigma }$
• 
  Однопетлевой вклад в вершинную функцию ${\displaystyle \Gamma }$

которые, будучи замкнутыми контурами, подразумевают наличие расходящихся интегралов , не имеющих математического смысла. Чтобы преодолеть эту трудность, был разработан метод, называемый перенормировкой , дающий конечные результаты, очень близко согласующиеся с экспериментами. Критерием смысла теории после перенормировки является конечность числа расходящихся диаграмм. В этом случае теория называется «перенормируемой». Причина этого в том, что для перенормировки наблюдаемых необходимо конечное число констант, чтобы сохранить предсказательную ценность теории нетронутой. Это как раз тот случай, когда квантовая электродинамика демонстрирует всего три расходящихся диаграммы. Эта процедура дает наблюдаемые, очень близко согласующиеся с экспериментом, как видно, например, для гиромагнитного отношения электронов .

Перенормируемость стала важным критерием жизнеспособности квантовой теории поля . Все теории, описывающие фундаментальные взаимодействия , за исключением гравитации , квантовый аналог которой является лишь предположением и в настоящее время находится в стадии очень активных исследований, являются перенормируемыми теориями.

Несходимость рядов

Аргумент Фримена Дайсона показывает, что радиус сходимости ряда теории возмущений в КЭД равен нулю. ^[29] Основной аргумент звучит следующим образом: если бы константа связи была отрицательной, это было бы эквивалентно отрицательной силовой постоянной Кулона . Это «перевернуло бы» электромагнитное взаимодействие, так что одинаковые заряды будут притягиваться , а разнородные — отталкиваться . Это сделало бы вакуум неустойчивым к распаду на кластер электронов на одной стороне Вселенной и кластер позитронов на другой стороне Вселенной. Поскольку теория «больна» при любом отрицательном значении константы связи, ряд не сходится, а в лучшем случае является асимптотическим рядом .

С современной точки зрения мы говорим, что КЭД не совсем определена как квантовая теория поля для сколь угодно высоких энергий. ^[30] Константа связи стремится к бесконечности при конечной энергии, что указывает на полюс Ландау . Проблема, по сути, в том, что КЭД страдает от проблем квантовой тривиальности . Это одна из причин включения КЭД в Теорию Великого Объединения .

Электродинамика в искривленном пространстве-времени

Эту теорию можно распространить, по крайней мере, как классическую теорию поля, на искривленное пространство-время. Это возникает аналогично случаю плоского пространства-времени, в результате объединения теории свободной электромагнетизма с теорией свободных фермионов и включения взаимодействия, которое переводит частную производную в теории фермионов в калибровочно-ковариантную производную.

Смотрите также

• Физический портал

• Сила Авраама – Лоренца
• Аномальный магнитный момент
• Бхабха рассеяние
• Квантовая электродинамика резонатора
• Схема квантовой электродинамики
• Комптоновское рассеяние
• Лагранжиан Эйлера – Гейзенберга
• Формализм Гупты – Блейлера
• Баранья смена
• Полюс Ландау
• Мёллеровское рассеяние
• Нерелятивистская квантовая электродинамика
• Поляризация фотонов
• Позитроний
• Прецизионные испытания QED
• КЭД-вакуум
• КЭД: странная теория света и материи
• Квантование электромагнитного поля
• Скалярная электродинамика
• Уравнение Шрёдингера
• Модель Швингера
• Уравнение Швингера – Дайсона
• Поляризация вакуума
• Вершинная функция
• Теория поглотителя Уиллера – Фейнмана

Рекомендации

1. Р.П. Фейнман (1949). «Пространственно-временной подход к квантовой электродинамике». Физический обзор . 76 (6): 769–89. Бибкод : 1949PhRv...76..769F. дои : 10.1103/PhysRev.76.769 .
2. Фейнман, Ричард (1985). КЭД: Странная теория света и материи . Издательство Принстонского университета. ISBN 978-0-691-12575-6.
3. Фейнман, Р.П. (1950). «Математическая формулировка квантовой теории электромагнитного взаимодействия». Физический обзор . 80 (3): 440–457. Бибкод : 1950PhRv...80..440F. doi : 10.1103/PhysRev.80.440.
4. Венкатараман, Ганешан (1994). Квантовая революция II — КЭД: жемчужина физики . ISBN 978-8173710032.
5. «Проверка пределов стандартной модели физики элементарных частиц с тяжелым, сильно заряженным ионом». Природа . 05.10.2023 . Проверено 23 октября 2023 г.
6. ПАМ Дирак (1927). «Квантовая теория испускания и поглощения излучения». Труды Лондонского королевского общества А. 114 (767): 243–65. Бибкод : 1927RSPSA.114..243D. дои : 10.1098/rspa.1927.0039 .
7. «Квантовая теория поля> История QFT (Стэнфордская энциклопедия философии)» . plato.stanford.edu . Проверено 22 октября 2023 г.
8. Э. Ферми (1932). «Квантовая теория излучения». Обзоры современной физики . 4 (1): 87–132. Бибкод : 1932RvMP....4...87F. doi : 10.1103/RevModPhys.4.87.
9. Блох, Ф .; Нордсик, А. (1937). «Заметка о поле излучения электрона». Физический обзор . 52 (2): 54–59. Бибкод : 1937PhRv...52...54B. дои : 10.1103/PhysRev.52.54.
10. В. Ф. Вайскопф (1939). «О собственной энергии и электромагнитном поле электрона». Физический обзор . 56 (1): 72–85. Бибкод : 1939PhRv...56...72W. дои : 10.1103/PhysRev.56.72.
11. Р. Оппенгеймер (1930). «Заметка о теории взаимодействия поля и вещества». Физический обзор . 35 (5): 461–77. Бибкод : 1930PhRv...35..461O. doi : 10.1103/PhysRev.35.461.
12. Лэмб, Уиллис ; Ретерфорд, Роберт (1947). «Тонкая структура атома водорода микроволновым методом». Физический обзор . 72 (3): 241–43. Бибкод : 1947PhRv...72..241L. дои : 10.1103/PhysRev.72.241 .
13. Фоли, HM ; Куш, П. (1948). «О собственном моменте электрона». Физический обзор . 73 (3): 412. Бибкод : 1948PhRv...73..412F. doi : 10.1103/PhysRev.73.412.
14. Х. Бете (1947). «Электромагнитный сдвиг энергетических уровней». Физический обзор . 72 (4): 339–41. Бибкод : 1947PhRv...72..339B. дои : 10.1103/PhysRev.72.339. S2CID  120434909.
15. Швебер, Сильван (1994). «Глава 5». QED и люди, которые это сделали: Дайсон, Фейнман, Швингер и Томонага . Издательство Принстонского университета. п. 230. ИСБН 978-0-691-03327-3.
16. С. Томонага (1946). «О релятивистски-инвариантной формулировке квантовой теории волновых полей». Успехи теоретической физики . 1 (2): 27–42. Бибкод : 1946PThPh...1...27T. дои : 10.1143/PTP.1.27 .
17. Дж. Швингер (1948). «О квантовой электродинамике и магнитном моменте электрона». Физический обзор . 73 (4): 416–17. Бибкод : 1948PhRv...73..416S. дои : 10.1103/PhysRev.73.416 .
18. Дж. Швингер (1948). «Квантовая электродинамика. I. Ковариантная формулировка». Физический обзор . 74 (10): 1439–61. Бибкод : 1948PhRv...74.1439S. дои : 10.1103/PhysRev.74.1439.
19. Р.П. Фейнман (1949). «Теория позитронов». Физический обзор . 76 (6): 749–59. Бибкод : 1949PhRv...76..749F. doi : 10.1103/PhysRev.76.749. S2CID  120117564.
20. Р.П. Фейнман (1950). «Математическая формулировка квантовой теории электромагнитного взаимодействия» (PDF) . Физический обзор . 80 (3): 440–57. Бибкод : 1950PhRv...80..440F. doi : 10.1103/PhysRev.80.440.
21. Ф. Дайсон (1949). «Радиационные теории Томонаги, Швингера и Фейнмана». Физический обзор . 75 (3): 486–502. Бибкод : 1949PhRv...75..486D. дои : 10.1103/PhysRev.75.486 .
22. Ф. Дайсон (1949). «S-Матрица в квантовой электродинамике». Физический обзор . 75 (11): 1736–55. Бибкод : 1949PhRv...75.1736D. doi : 10.1103/PhysRev.75.1736.
23. «Нобелевская премия по физике 1965 года». Нобелевский фонд . Проверено 9 октября 2008 г.
24. История позитрона - Поль Дирак (1975) , получено 19 июля 2023 г.
25. Гуральник, Г.С.; Хаген, Чехия; Киббл, TWB (1964). «Глобальные законы сохранения и безмассовые частицы». Письма о физических отзывах . 13 (20): 585–87. Бибкод : 1964PhRvL..13..585G. дои : 10.1103/PhysRevLett.13.585 .
26. Гуральник, Г.С. (2009). «История развития Гуральником, Хагеном и Кибблом теории спонтанного нарушения симметрии и калибровочных частиц». Международный журнал современной физики А. 24 (14): 2601–27. arXiv : 0907.3466 . Бибкод : 2009IJMPA..24.2601G. дои : 10.1142/S0217751X09045431. S2CID  16298371.
27. Пескин, Майкл; Шредер, Дэниел (1995). Введение в квантовую теорию поля (переиздание). Вествью Пресс. ISBN 978-0201503975.
28. Швингер, Джулиан (1951-06-01). «О калибровочной инвариантности и поляризации вакуума». Физический обзор . Американское физическое общество (APS). 82 (5): 664–679. Бибкод : 1951PhRv...82..664S. doi : 10.1103/physrev.82.664. ISSN  0031-899X.
29. Киносита, Тоитиро (5 июня 1997 г.). «Квантовая электродинамика имеет нулевой радиус сходимости, краткое изложение Тоитиро Киноситы» . Проверено 6 мая 2017 г.
30. Эсприу и Таррах (30 апреля 1996 г.). «Неоднозначности в КЭД: ренормалоны против тривиальности». Буквы по физике Б. 383 (4): 482–486. arXiv : hep-ph/9604431 . Бибкод : 1996PhLB..383..482E. дои : 10.1016/0370-2693(96)00779-4. S2CID  119095192.

дальнейшее чтение

Книги

• Берестецкий В.Б.; Лифшиц, Э.М. ; Питаевский, Л.П. (1982). Курс теоретической физики, Том 4: Квантовая электродинамика (2-е изд.). Эльзевир. ISBN 978-0-7506-3371-0.
• Де Бройль, Л. (1925). Recherches sur la theorie des quanta [Исследования по квантовой теории] . Франция: Wiley-Interscience.
• Фейнман, Р.П. (1998). Квантовая электродинамика (Новое изд.). Вествью Пресс. ISBN 978-0-201-36075-2.
• Грейнер, В.; Бромли, округ Колумбия; Мюллер, Б. (2000). Калибровочная теория слабых взаимодействий . Спрингер. ISBN 978-3-540-67672-0.
• Яух, Дж. М.; Рорлих, Ф. (1980). Теория фотонов и электронов . Спрингер-Верлаг. ISBN 978-0-387-07295-1.
• Кейн, GL (1993). Современная физика элементарных частиц . Вествью Пресс. ISBN 978-0-201-62460-1.
• Миллер, А.И. (1995). Ранняя квантовая электродинамика: справочник . Издательство Кембриджского университета. ISBN 978-0-521-56891-3.
• Милонни, PW (1994). Квантовый вакуум: введение в квантовую электродинамику. Бостон: Академическая пресса. ISBN 0124980805. LCCN  93029780. OCLC  422797902.
• Швебер, СС (1994). QED и люди, которые это сделали . Издательство Принстонского университета. ISBN 978-0-691-03327-3.
• Швингер, Дж. (1958). Избранные статьи по квантовой электродинамике . Дуврские публикации. ISBN 978-0-486-60444-2.
• Таннуджи-Коэн, К .; Дюпон-Рок, Жак; Гринберг, Гилберт (1997). Фотоны и атомы: введение в квантовую электродинамику . Уайли-Интерсайенс. ISBN 978-0-471-18433-1.

Журналы

• Дадли, Дж. М.; Кван, AM (1996). «Популярные лекции Ричарда Фейнмана по квантовой электродинамике: лекции Робба 1979 года в Оклендском университете». Американский журнал физики . 64 (6): 694–98. Бибкод : 1996AmJPh..64..694D. дои : 10.1119/1.18234.

Внешние ссылки

• Лекция Фейнмана, получившая Нобелевскую премию, описывающая эволюцию КЭД и его роль в ней.
• Новозеландские лекции Фейнмана по КЭД для нефизиков
• http://qed.wikina.org/ – Анимации, демонстрирующие QED